100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Интел и АМД — крупнейшие и наиболее известные производители центральных процессоров (ЦП) в мире. Обе компании имеют долгую историю в отрасли: Intel была основана в 1968 году, а AMD — в 1969 году. Несмотря на то, что они были основаны с разницей всего в год, эти две компании использовали очень разные подходы к проектированию и производству процессоров, что привело к разделению рынка компьютерных комплектующих на два основных направления.
Одним из наиболее очевидных различий между процессорами Интел и АМД является их архитектура. Именно она во многом влияет на то, какой будет на процессор цена, а также сложность его производства. Процессоры Intel традиционно используют архитектуру сложных вычислений с набором команд (CISC), ориентированную на повышение мощности процессоры при уменьшении потребляемой электроэнергии.
С другой стороны процессоры АМД обычно используют архитектуру вычислений с сокращенным набором команд (RISC), которая больше ориентирована на стоимость и простоту производства.
Покупатели выбирают себе процессор исходя из конкретных задач, которые будут перед ним поставлены.
Главное отличие между двумя производителями
Ключевое различие между продуктами Intel и AMD заключается в их производственном процессе. Intel традиционно использует более продвинутый производственный процесс с меньшими транзисторами и более высокими тактовыми частотами. Это позволило ЦП Intel быть более энергоэффективными и быстрыми, чем варианты от AMD. Однако в последние годы AMD удалось сократить разрыв, используя более совершенный производственный процесс.
С точки зрения ценообразования товары АМД обычно считаются более доступными, чем варианты от Интел. Это связано с тем, что AMD традиционно сосредоточилась на производстве комплектующих, цена которых более доступная для среднего потребителя, в то время как Intel сосредоточилась на производстве оптимальных решений для разработчиков, графических дизайнеров.
Технические особенности
Когда дело доходит до производительности, ЦП Intel обычно считаются более быстрыми.
Среди качественных отличительных особенностей:
- Более высокие тактовые частоты;
- Более совершенная архитектура;
- Большая энергоэффективность.
Такие CPU способны выполнять задачи, требующие высокого уровня вычислительной мощности, такие как игры и редактирование видео. Однако обычно считается, что процессоры AMD лучше купить для задач, требующих многозадачности и многопоточности таких, как рендеринг и научное моделирование. Среди главных преимуществ, которые можно отметить относительно ЦП AMD:
- Отличные показатели при рендеринге;
- Наличие высокопроизводительных, но доступных CPU;
- Подключение через стандартизированный сокет AM4.
Продукты обеих компаний обладают своими достоинствами. Процессоры Intel обычно считаются более быстрыми и энергоэффективными, в то время как процессоры AMD обычно считаются более доступными с точки зрения цены и лучшими для многозадачности.
Вариант 1.
С-46. № 2. ГДЗ Алгебра 7 класс Звавич. Решите систему уравнений способом подстановки. – Рамблер/класс Вариант 1. С-46. № 2. ГДЗ Алгебра 7 класс Звавич. Решите систему уравнений способом подстановки. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Решите систему уравнений способом подстановки.
Выполните проверку, подставив полученное решение в каждое из уравнений:
ответы
Держи решение:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
9 класс
11 класс
похожие вопросы 5
Помогите ответить на вопросы
1)Назовите основные формы международного сотрудничества в области охраны окружающей среды. Приведите примеры участия России в таком (Подробнее…)
ГДЗ
физика….помогите
в одном из ядерных экспериментов протон с энергией в 1МэВ движется в однородном магнитном поле по круговой траектории. какой энергией (Подробнее…)
ЕГЭЭкзаменыГДЗУчебники
Вариант 1.
С-21. № 6. ГДЗ Алгебра 7 класс Звавич. Замените значок * таким выражением, чтобы выполнялось равенство
Замените значок * таким выражением, чтобы выполнялось равенство:
1) (*)5 = a25; 2) (*)2 = а10; 3) (*)3 = а3n; 4) (*)n = (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Вариант 1. С-32. № 1. ГДЗ Алгебра 7 класс Звавич. Помогите вынести общий множитель за скобки
Вынесите общий множитель за скобки (проверьте свои действия умножением):
1) а) 2x + 3ху; б) 3ху — 5у; в) -7ху + (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Вариант 1. С-36. № 1. ГДЗ Алгебра 7 класс Звавич. Помогите записать в виде выражения.
Запишите в виде выражения:
1) сумму квадратов чисел а и b;
2) квадрат разности чисел а и b; (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Что такое метод замены? (Видео и практика)
TranscriptPractice
Привет! Добро пожаловать в это видео о решении систем уравнений с использованием метода подстановки .
Решение системы уравнений — это рассмотрение двух или более уравнений и нахождение точки или точек, в которых они пересекаются. Если вы рассматриваете линейные уравнения, то будет только одна точка пересечения, если только прямые не параллельны, и в этом случае точек пересечения не будет. Если вы рассматриваете уравнения более высокой степени, точек пересечения может быть больше.
Существует четыре метода решения систем уравнений: график, замена, исключение и матричный. Сегодня мы сосредоточимся на методе подстановки, особенно в отношении двух линейных уравнений.
При использовании метода подстановки мы собираемся заменить одну из наших переменных выражением, использующим другую переменную. Что я имею в виду? Итак, вы хотите решить одно из ваших уравнений так, чтобы либо x, либо y находились сами по себе с одной стороны, а затем подставить это выражение в другое уравнение и решить оттуда. Давайте посмотрим на несколько примеров, чтобы понять, о чем я говорю.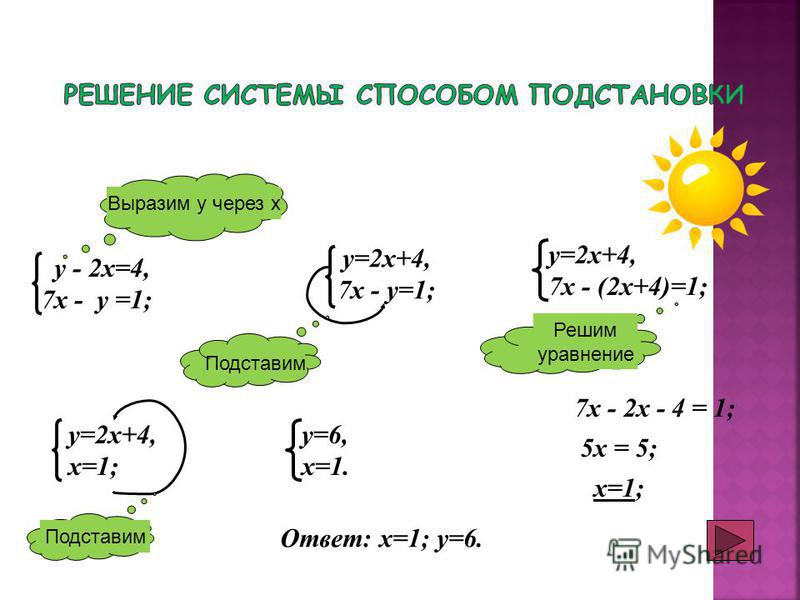
Решите следующую систему уравнений.
\(x=2y+7\)
\(2x+3y=14\)
Наш первый шаг состоит в том, чтобы одно из наших уравнений имело либо x , либо y с одной стороны. Для этого примера у нас уже есть такое уравнение \(x=2y+7\), поэтому нам не нужно делать никаких дополнительных манипуляций.
Теперь мы хотим на минутку подумать о том, что означает знак равенства. Знак равенства говорит нам, что значения по обе стороны уравнения равны другой стороне; они одинаковые! Итак, в нашем примере x равно \(2y+7\). Зная это, мы можем подставить \(2y+7\) вместо x во втором уравнении, например: только одна переменная в нашем уравнении, поэтому мы можем следовать обычным шагам решения уравнения, чтобы узнать, каково наше значение y.
\(4y+14+3y=14\)
Итак, \(4y+3y=7y.\)
\(7y+14=14\)
Если мы вычтем 14 из обеих частей, мы получим:
\(7у=0\)
И когда мы разделим на 7 с обеих сторон, у нас останется:
\(y=0\)
Помните, решить систему уравнений означает найти точку, в которой эти два уравнения пересекаются.
Это означает, что у нас есть только половина нашего ответа. Наша координата y для этой точки равна 0, но нам все еще нужно найти нашу координату x. Мы делаем это, подставляя наше вновь найденное значение y вместо y в любом из наших исходных уравнений и решая x . Я собираюсь использовать наше первое уравнение, потому что потребуется меньше манипуляций, чтобы получить наши х .
\(x=2(0)+7=0+7=7\)
Таким образом, наша координата x для этой точки равна 7. Это означает, что наш окончательный ответ, точка пересечения этих двух линий \( (7, 0)\).
Давайте рассмотрим еще один пример, чтобы попрактиковаться в использовании этого метода.
\(9x-3y=12\)
\(-6x+8y=4\)
Ни одно из наших уравнений не составлено таким образом, чтобы x или y находились на одной стороне отдельно друг от друга, поэтому мы придется манипулировать одним из них, чтобы сделать его таким. Я собираюсь решить наше первое уравнение на и .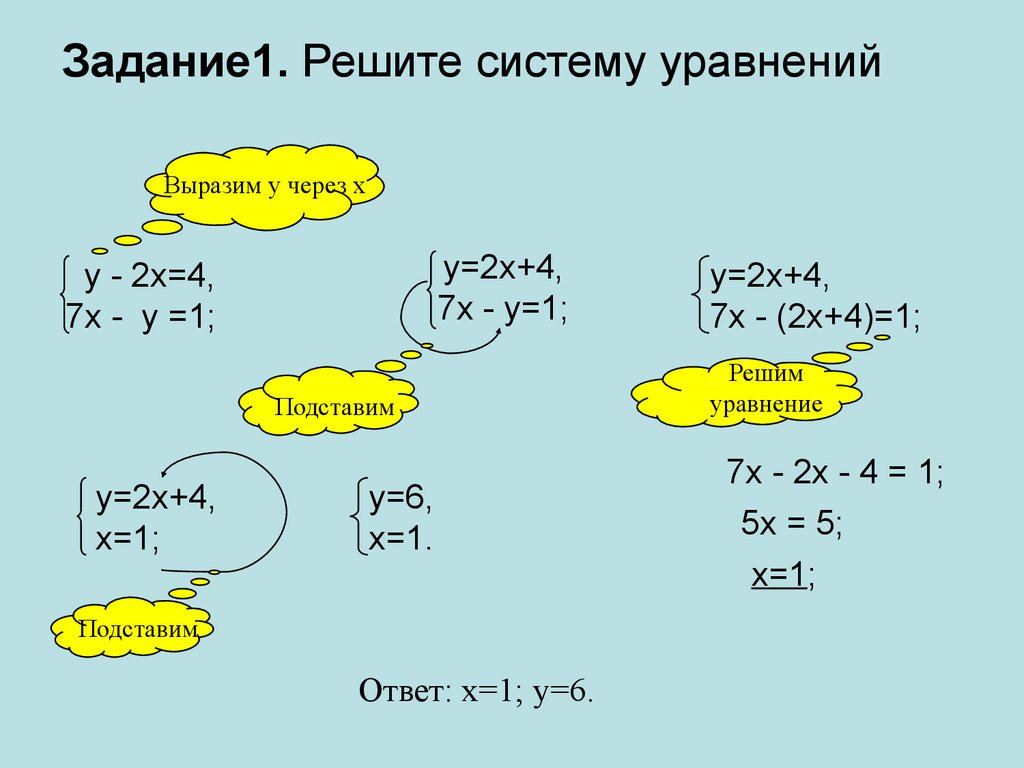
Я вычту 9 x с обеих сторон. Получается:
\(-3y=12-9x\)
А затем разделите на -3 с обеих сторон. Что дает нам:
\(y=3x-4\)
Теперь мы можем заменить это выражение на y в нашем другом уравнении.
\(-6x+8(3x-4)=4\)
\(-6x+24x-32=4\)
Сложив эти два вместе, мы получим:
\(18x-32 =4\)
Прибавьте 32 к обеим сторонам. Вы получаете:
\(18x=36\)
Разделить на 18 с обеих сторон. И мы получаем:
\(x=2\)
Теперь, когда у нас есть значение x, мы можем подставить это число в уравнение, которое мы нашли ранее для y , чтобы получить значение y. Итак:
\(y=3(2)-4=6-4=2\)
Итак, наша конечная точка равна \((2, 2)\).
Прежде чем я попрошу вас попробовать еще один вариант самостоятельно, давайте вместе сделаем еще один пример.
\(8x-3y=14\)
\(2x+y=7\)
Сначала решим одно из уравнений так, чтобы с одной стороны была независимая переменная.
Я собираюсь решить второе уравнение на и .
\(y=7-2x\)
Теперь подставим это выражение для y в наше первое уравнение и найдем x .
\(8x-3(7-2x)=14\)
\(8x-21+6x=14\)
\(14x-21=14\)
\(14x=35\)
\(x =\frac{35}{14}=\frac{5}{2}\)
Наконец, мы подставляем наше значение x в наше уравнение для y и находим y .
\(y=7-2(\frac{5}{2})=7-5=2\)
Таким образом, наша конечная точка равна \((\frac{5}{2}, 2)\) .
Теперь, когда мы вместе рассмотрели три примера, я хочу, чтобы вы попробовали один из них самостоятельно. После того, как я дам вам уравнения, остановите видео и попробуйте решить их самостоятельно. Затем, как только вы получите свой ответ, нажмите кнопку воспроизведения и посмотрите, совпадает ли он с моим.
\(x+5y=7\)
\(7x-2y=12\)
Готовы проверить свой ответ?
Сначала мы хотим решить одно из наших уравнений для независимой переменной.
Я собираюсь решить первое уравнение для x .
\(х=7-5у\)
Теперь подставьте это выражение во второе уравнение.
\(7(7-5л)-2г=12\)
\(49-35г-2г=12\)
\(49-37г=12\)
\(-37г=-37\)
\ (y=1\)
Затем подставьте значение y в уравнение для x и найдите координату x.
\(x=7-5(1)=7-5=2\)
Итак, наш окончательный ответ для системы уравнений: \((2, 1)\).
Мы рассмотрели только примеры с двумя линейными уравнениями, но этот метод можно использовать для более чем двух уравнений и для уравнений более высоких степеней. Просто выполните те же действия, что и в этом видео. Решите уравнения для независимых переменных, а затем подставьте их в другие уравнения, пока не получите сингулярную переменную для решения. Как только вы узнаете эту переменную, работайте в обратном направлении, чтобы найти все остальные переменные.
Я надеюсь, что этот обзор метода замещения был полезен. Спасибо за просмотр и удачной учебы!
Вопрос №1:
Решите следующую систему уравнений методом подстановки.
\(\begin{case}y=2x-14\\8x+3y=14\end{case}\)
(-6, 4)
(12, -11)
(4, -6 )
(-11, 12)
Показать ответ
Ответ:
Правильный ответ (4, -6). Чтобы использовать метод подстановки, сначала решите одно из уравнений для независимой переменной. Первое уравнение дается нам так. Замените \(2x-14\) вместо y во втором уравнении и найдите x .
\(8x+3(2x-14)=14\)
\(8x+6x-42=14\)
\(14x-42=14\)
\(14x=56\)
\(x= 4\)
Затем подставьте 4 in вместо x в первом уравнении.
\(y=2(4)-14=8-14=-6\)
Две прямые пересекаются в точке (4, -6).
Скрыть ответ
Вопрос №2:
Решите следующую систему уравнений методом подстановки.
\(\begin{case}12x-7y=16\\-8x+4y=8\end{case}\)
(-15, -28)
(5, -28)
(-15, 7)
(5, 7)
Показать ответ
Ответ:
-900 15, -28).
Чтобы решить эту систему, сначала переформулируйте второе уравнение так, чтобы y была изолирована с одной стороны.
\(-8x+4y=8\)
\(4y=8x+8\)
\(y=2x+2\)
Затем подставьте \(2x+2\) вместо y в первом уравнении и решить для х .
\(12x-7(2x+2)=16\)
\(12x-14x-14=16\)
\(-2x-14=16\)
\(-2x=30\)
\(x=-15\)
Наконец, подставьте -15 вместо x во втором уравнении.
\(y=2(-15)+2=-30+2=-28\)
Две прямые пересекаются в точке (-15, -28).
Скрыть ответ
Вопрос №3:
Решите следующую систему уравнений методом подстановки.
\(\begin{case}-10x-15y=75\\x-y=-25\end{case}\)
(-7, 6)
(7, -2)
(9, -7 )
(-18, 7)
Показать ответ
Ответ:
Правильный ответ (-18, 7). Чтобы решить эту систему, переформулируйте второе уравнение так, чтобы x были изолированы с одной стороны.
\(x-y=-25\)
\(x=y-25\)
Затем подставьте \(y-25\) вместо x в первое уравнение и найдите y .
\(-10(y-25)-15y=75\)
\(-10y+250-15y=75\)
\(-25y+250=75\)
\(-25y=-175\)
\(y=7\)
Наконец, подставьте 7 in вместо y в переставленном втором уравнении и найдите х .
\(x=(7)-25=-18\)
Точка пересечения этих двух прямых в (-18, 7).
Скрыть ответ
Вопрос №4:
Решите следующую систему уравнений методом подстановки.
\(\begin{case}18y-11x=12\\2x-3y=9\end{case}\)
(66, 41)
(23, 19)
(11, 27)
(59, 87)
Показать ответ
Ответ:
Правильный ответ (66, 41). Чтобы решить эту систему, сначала переформулируйте второе уравнение так, чтобы y изолирован с одной стороны.
\(2x-3y=9\)
\(-3y=-2x+9\)
\(3y=2x-9\)
\(y=\frac{2}{3}x-3\)
Затем подставьте \(\frac{2}{3}x-3\) вместо y в первое уравнение и найдите x .
\(18(\frac{2}{3}x-3)-11x=12\)
\(12x-54-11x=12\)
\(x-54=12\)
\(x= 66\)
Наконец, подставьте 66 дюймов вместо x во втором уравнении.
\(y=\frac{2}{3}(66)-3=44-3=41\)
Точка пересечения двух прямых (66, 41).
Скрыть Ответ
Вопрос №5:
Решите следующую систему уравнений методом подстановки.
\(\begin{case}x-3y=17\\2x-9y=-41\end{case}\)
(87, 63)
(8, 5)
(92, 25)
(74, 81)
Показать ответ
Ответ:
Правильный ответ (92, 25). Чтобы решить эту систему, сначала переставьте первое уравнение так, чтобы x были изолированы с одной стороны.
\(x-3y=17\)
\(x=3y+17\)
Затем подставьте \(3y+17\) вместо x во второе уравнение и найдите y .
\(2(3y+17)-9y=-41\)
\(6y+34-9y=-41\)
\(-3y+34=-41\)
\(-3y=-75\ )
\(y=25\)
Наконец, замените 25 на y в переставленном первом уравнении и найдите x .
\(x=3(25)+17=75+17=92\)
Точка пересечения этих двух прямых (92, 25).
Скрыть ответ
Возврат к алгебре I Видео
565151
Решение линейных систем подстановкой
В этом разделе мы определим полностью алгебраический метод решения систем. Идея состоит в том, чтобы решить одно уравнение для одной из переменных и подставить результат в другое уравнение. После выполнения этого шага подстановки у нас останется одно уравнение с одной переменной, которое можно решить с помощью алгебры. Это называется методом подстановки. Это средство решения линейной системы путем решения одной из переменных и подстановки результата в другое уравнение, и шаги описаны в следующем примере.
Пример 1: Решите подстановкой: {2x+y=73x−2y=−7.
Решение:
Шаг 1: Решите любую переменную в любом уравнении. Если вы выберете первое уравнение, вы можете выделить и за один шаг.
Шаг 2: Подставьте выражение −2x+7 вместо переменной y в другое уравнение .
Таким образом, у вас остается эквивалентное уравнение с одной переменной, которое можно решить с помощью ранее изученных методов.
Шаг 3: Найдите оставшуюся переменную. Чтобы найти x , сначала распределите −2:
Шаг 4: Обратное замещение Как только значение переменной найдено, подставьте его обратно в одно из исходных уравнений или эквивалентные им уравнения, чтобы определить соответствующее значение другая переменная. найти значение другой координаты. Подставьте x = 1 в любое из исходных уравнений или их эквиваленты.
Обычно мы используем эквивалентное уравнение, которое нашли при выделении переменной на шаге 1.
Решение системы (1, 5). Не забудьте представить решение в виде упорядоченной пары.
Шаг 5: Проверка. Убедитесь, что эти координаты решают оба уравнения исходной системы:
График этой линейной системы выглядит следующим образом:
Метод подстановки для решения систем является полностью алгебраическим методом. Таким образом, графическое изображение линий не требуется.
Ответ: (1, 5)
Пример 2: Решите подстановкой: {2x−y=12x−y=3.
Решение: В этом примере мы видим, что x имеет коэффициент 1 во втором уравнении. Это означает, что его можно выделить за один шаг следующим образом:
Замените 3+y на x в первом уравнении. Используйте круглые скобки и позаботьтесь о распространении.
Используйте x=3+y, чтобы найти x .
Ответ: (9, 6).
Чек остается читателю.
Пример 3: Решите подстановкой: {3x−5y=17x=−1.
Решение: В этом примере переменная x уже изолирована. Следовательно, мы можем подставить x=−1 в первое уравнение.
Ответ: (−1, −4). Построение графика этой конкретной системы является хорошим упражнением, чтобы сравнить метод подстановки с методом построения графиков для решения систем.
Попробуйте! Решите подстановкой: {3x+y=48x+2y=10.
Ответ: (1, 1)
Решение для видео
(нажмите, чтобы посмотреть видео)Алгебраическое решение систем часто требует работы с дробями.
Пример 4: Решите подстановкой: {2x+8y=524x−4y=−15.
Решение: Начните с решения x в первом уравнении.
Затем подставьте во второе уравнение и найдите y .
Обратно подставьте в уравнение, используемое на шаге подстановки:
Ответ: (−1/2, 3/4)
Как мы знаем, не все линейные системы имеют только одно упорядоченное парное решение.
Напомним, что некоторые системы имеют бесконечно много упорядоченных парных решений, а некоторые вообще не имеют решений. Далее мы исследуем, что происходит при использовании метода подстановки для решения зависимой системы.
Пример 5: Решите подстановкой: {−5x+y=−110x−2y=2.
Решение: Так как в первом уравнении есть член с коэффициентом 1, мы решили сначала решить его.
Затем подставьте это выражение вместо y во второе уравнение.
Этот процесс привел к истинному утверждению; следовательно, уравнение является тождеством, а любое действительное число является решением. Это указывает на то, что система зависима. Совместные решения имеют вид ( x
, m x + b ), или в данном случае ( x , 5 x — 1), где x — любое действительное число.Ответ: (x, 5x−1)
Чтобы лучше понять предыдущий пример, перепишите оба уравнения в форме пересечения наклона и начертите их на одном наборе осей.
Мы видим, что оба уравнения представляют одну и ту же прямую, а значит, система зависима. Теперь изучите, что происходит при решении несовместной системы методом подстановки.
Пример 6: Решите подстановкой: {−7x+3y=314x−6y=−16.
Решение: Найдите y в первом уравнении.
Подставьте во второе уравнение и решите.
Решение приводит к ложному утверждению. Это указывает на то, что уравнение является противоречием. Нет решения для x и, следовательно, нет решения для системы.
Ответ: Нет решения, Ø
Ложное утверждение означает, что система несовместима, или, говоря геометрическим языком, что прямые параллельны и не пересекаются. Чтобы проиллюстрировать это, определите форму пересечения наклона каждой линии и изобразите их на одном и том же наборе осей.
В форме пересечения наклона легко увидеть, что две линии имеют одинаковый наклон, но разные y -пересечения.
Попробуйте! Решите подстановкой: {2x−5y=34x−10y=6.
Ответ: (x, 25x−35)
Решение для видео
(нажмите, чтобы посмотреть видео)Ключевые выводы
- Метод подстановки — это полностью алгебраический метод решения системы уравнений.
- Метод подстановки требует, чтобы мы нашли решение для одной из переменных, а затем подставили результат в другое уравнение. После выполнения шага подстановки полученное уравнение имеет одну переменную и может быть решено с использованием методов, изученных до этого момента.
- Когда значение одной из переменных определено, вернитесь назад и подставьте его в одно из исходных уравнений или эквивалентные им уравнения, чтобы определить соответствующее значение другой переменной.
- Решения систем двух линейных уравнений с двумя переменными, если они существуют, представляют собой упорядоченные пары ( x , y ).
- Если процесс решения системы уравнений приводит к ложному утверждению, то система несовместна и решения нет, Ø.
- Если процесс решения системы уравнений приводит к истинному утверждению, то система зависима и существует бесконечно много решений, которые можно выразить с помощью формы (
Упражнения по теме
Часть A: Метод подстановки
Решите методом подстановки.
1. {y=4x-1-3x+y=1
2. {y=3x-84x-y=2
3. {x=2y-3x+3y=-8
4. {x=−4y+12x+3y=12
5. {y=3x−5x+2y=2
6. {y=x2x+3y=10
7. {y=4x+1−4x+ y=2
8. {y=-3x+53x+y=5
9. {y=2x+32x-y=-3
10. {y=5x-1x-2y=5
11. {y=-7x+13x-y=4
12. {x=6y+25x-2y=0
13. {y=-2-2x-y=-6
14. { x=−3x−4y=−3
15. {y=−15x+37x−5y=9
16. {y=23x−16x−9y=0
17. {y=12x+13x−6y =4
18.
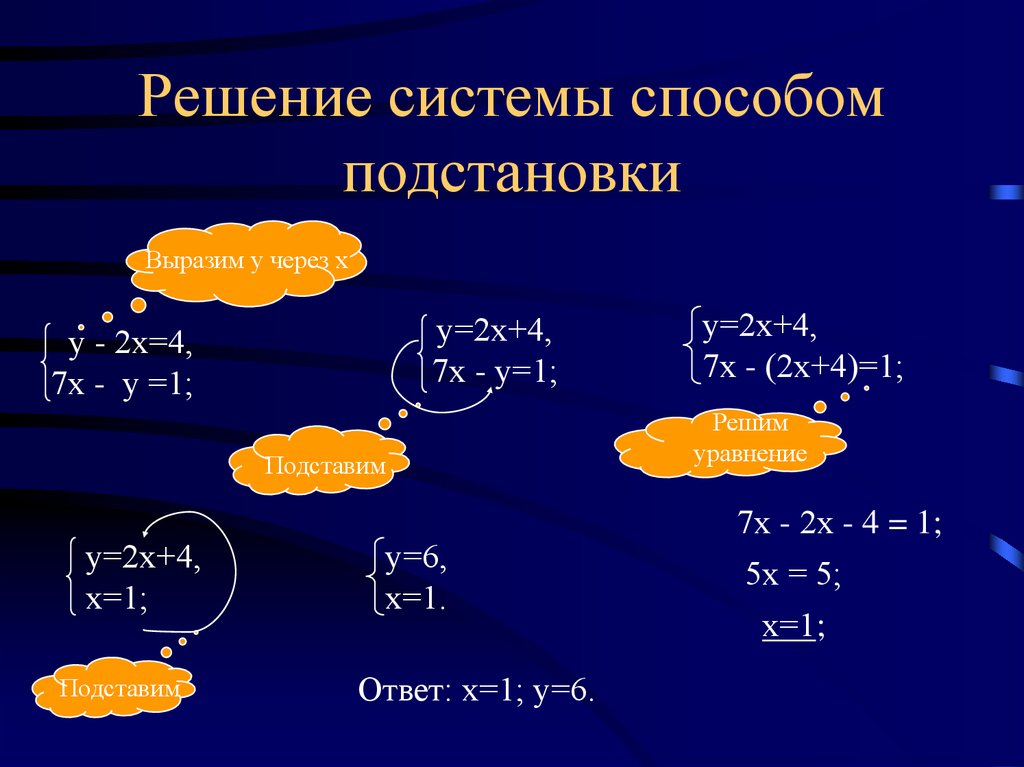{y=-38x+122x+4y=1
19. {x+y=62x+3y=16
20. {x-y=3-2x+3y=-2
21. {2x+y=23x-2y=17
22. {x-3y=-113x+5y=-5
23. {x+2y=-33x-4y=-2
24. {5x −y=129x−y=10
25. {x+2y=−6−4x−8y=2426. {x+3y=-6-2x-6y=-12
27. {-3x+y=-46x-2y=-2
28. {x-5y=-102x-10y=-20
29. {3x−y=94x+3y=−1
30. {2x−y=54x+2y=−2
31. {−x+4y=02x−5y=−6
32. {3y-x=55x+2y=-8
33. {2x-5y=14x+10y=2
34. {3x-7y=-36x+14y=0
35. {10x-y=3 −5x+12y=1
36. {−13x+16y=2312x−13y=−32
37. {13x+23y=114x−13y=−112
38. {17x−y=1214x+12y= 2
39. {−35x+25y=1213x−112y=−13
40. {12x=23yx−23y=2
41. {−12x+12y=5814x+12y=14
42. {x−y=0−x+2y=3
43. {y=3x2x −3y=0
44. {2x+3y=18−6x+3y=−6
45. {−3x+4y=202x+8y=8
46. {5x−3y=−13x+2y= 7
47. {−3x+7y=22x+7y=1
48. {y=3y=−3
49. {x=5x=−2
50. {y=4y=4
Постройте линейную систему и решите ее методом подстановки.