Равнобедренный трапеция: Равнобедренная трапеция — урок. Геометрия, 8 класс.

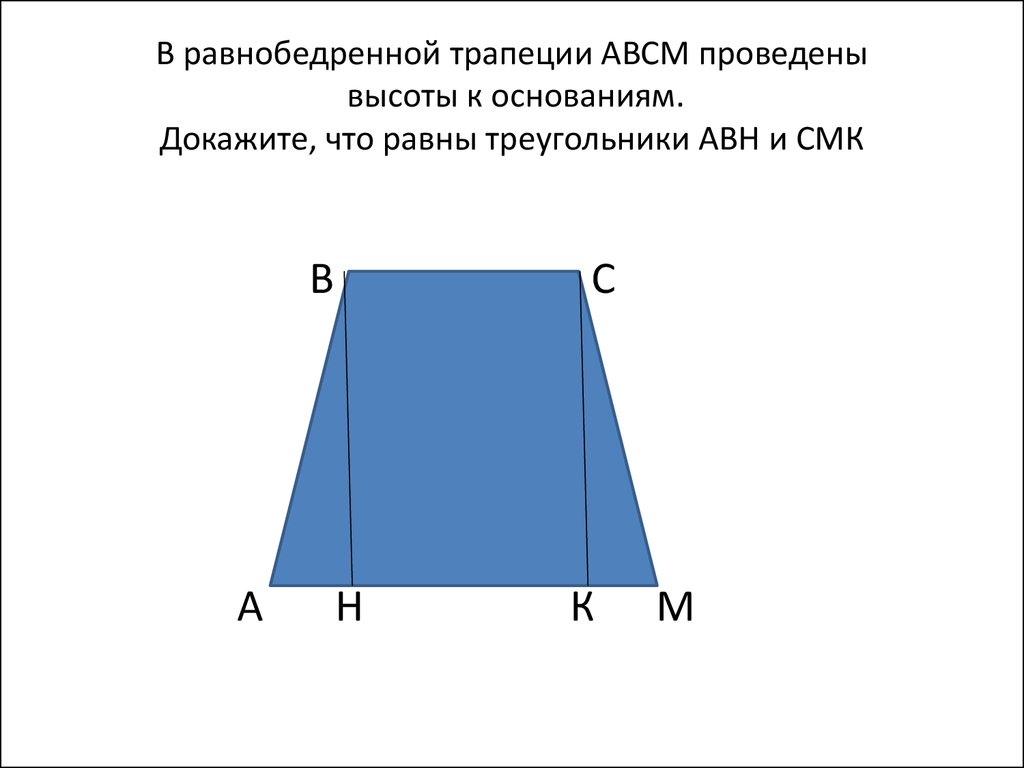
диагоналей, углов, оснований, высоты и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Свойства равнобедренной (равнобокой) трапеции

В данной публикации мы рассмотрим определение и основные свойства равнобедренной трапеции.

Напомним, трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны, т.е. AB = CD.

• Свойство 1
• Свойство 2
• Свойство 3
• Свойство 4
• Свойство 5
• Свойство 6
• Свойство 7

Свойство 1

Углы при любом из оснований равнобедренной трапеции равны.

• ∠DAB = ∠ADC = α
• ∠ABC = ∠DCB = β

Свойство 2

Сумма противоположных углов трапеции равняется 180°.

Для рисунка выше: α + β = 180°.

Свойство 3

Диагонали равнобедренной трапеции имеют одинаковую длину.

AC = BD = d

Свойство 4

Высота равнобедренной трапеции BE, опущенная на основание большей длины AD, делит его на два отрезка: первый равняется половине суммы оснований, второй – половине их разности.

Свойство 5

Отрезок MN, соединяющий середины оснований равнобокой трапеции, перпендикулярен этим основаниям.

Прямая, проходящая через середины оснований равнобедренной трапеции, называется ее осью симметрии.

Свойство 6

Вокруг любой равнобедренной трапеции можно описать окружность.

Свойство 7

Если сумма оснований равнобокой трапеции равно удвоенной длине ее боковой стороны, в нее можно вписать окружность.

Радиус такой окружности равняется половине высоты трапеции, т.е. R = h/2.

Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Поиск по сайту:

Справочник по математике

Геометрия (Планиметрия)

Четырехугольники

Основные определения и свойства трапеций

Свойства и признаки равнобедренных трапеций

Основные определения и свойства трапеций

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Трапеция		Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.       Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции
Определение	Диагонали трапеции		Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции
Определение	Высота трапеции		Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение
Свойство	Точка пересечения диагоналей		Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве
Определение	Средняя линия трапеции		Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции
Свойство			Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство
Свойство	Биссектрисы углов при боковой стороне трапеции		Биссектрисы углов при боковой стороне трапеции перпендикулярны

Определение: трапеция
	Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции
Определение: диагонали трапеции
	Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции
Определение: высота трапеции
	Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение
Свойство: точка пересечения диагоналей
	Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве
Определение: средняя линия трапеции
	Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции
Свойство: средняя линия трапеции
	Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство
Свойство: биссектрисы углов при боковой стороне трапеции
	Биссектрисы углов при боковой стороне трапеции перпендикулярны

Трапеция

Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции

Диагонали трапеции

Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции

Высота трапеции

Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение

Точка пересечения диагоналей

Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве

Средняя линия трапеции

Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство

Биссектрисы углов при боковой стороне трапеции

Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны

      Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».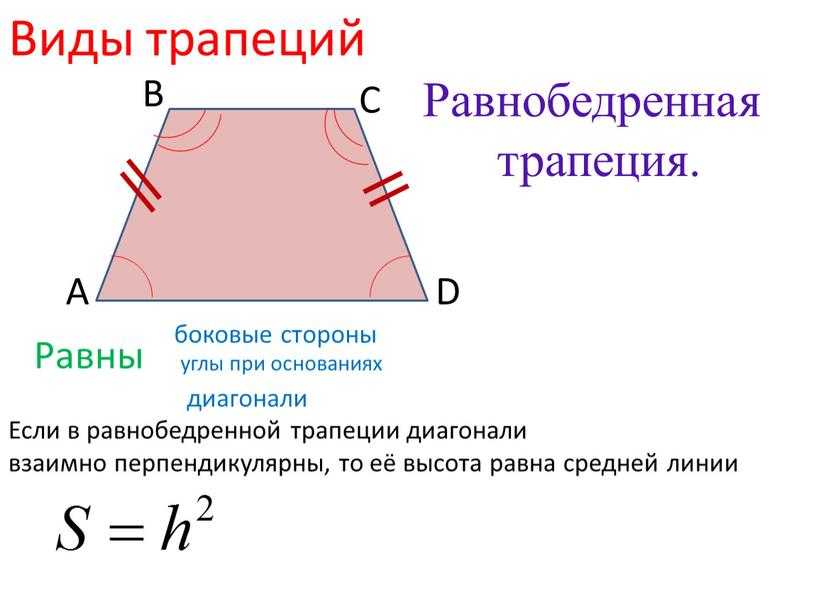

      В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.

Свойства и признаки равнобедренных трапеций

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Равнобедренная трапеция		Равнобедренной трапецией называют трапецию, у которой боковые стороны равны.
Свойство	Равенство углов при основании		Если трапеция является равнобедренной, то углы при каждом из её оснований равны.
Признак			Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной.
Свойство	Равенство диагоналей		Если трапеция является равнобедренной, то её диагонали равны.
Признак			Если у трапеции диагонали равны, то она является равнобедренной
Свойство	Углы, которые диагонали образуют с основаниями		Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований.
Признак			Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной.
Свойство	Описанная окружность		Если трапеция является равнобедренной, то около неё можно описать окружность.
Признак			Если около трапеции можно описать окружность, то она является равнобедренной.
Свойство	Высоты трапеции		Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований

Определение: Равнобедренная трапеция
	Равнобедренной трапецией называют трапецию, у которой боковые стороны равны.
Свойство: равенство углов при основании
	Если трапеция является равнобедренной, то углы при каждом из её оснований равны.
Признак: равенство углов при основании
	Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной.
Свойство: равенство диагоналей
	Если трапеция является равнобедренной, то её диагонали равны.
Признак: равенство диагоналей
	Если у трапеции диагонали равны, то она является равнобедренной
Свойство: углы, которые диагонали образуют с основаниями
	Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований.
Признак: углы, которые диагонали образуют с основаниями
	Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной.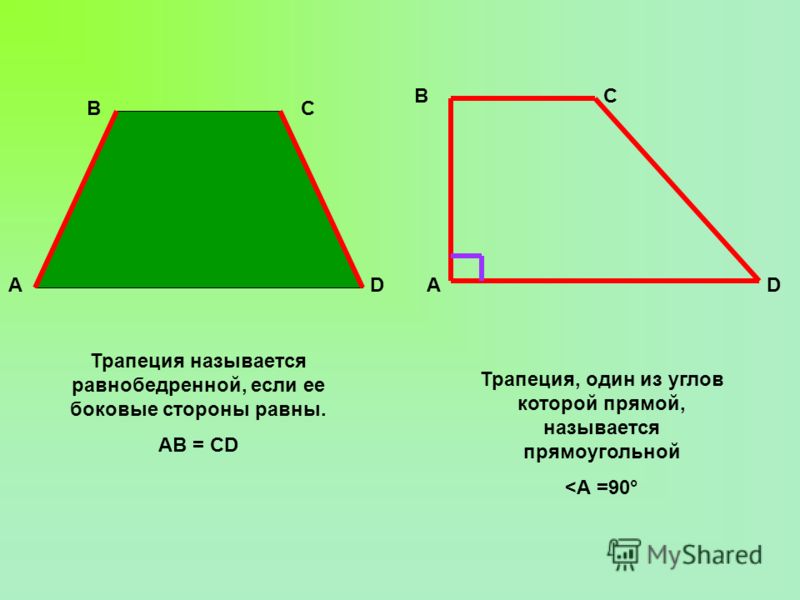
Свойство: описанная окружность
	Если трапеция является равнобедренной, то около неё можно описать окружность.
Признак: описанная окружность
	Если около трапеции можно описать окружность, то она является равнобедренной.
Свойство: высоты трапеции
	Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований

Равнобедренная трапеция

Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны.

Равенство углов при основании

Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной.

Равенство диагоналей

Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной.

Углы, которые диагонали образуют с основаниями

Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной.

Описанная окружность

Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной.

Высоты трапеции

Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

До ЕГЭ по математике осталось
дней	часов	минут	секунд

НАШИ ПАРТНЕРЫ «НПО Астек» «Fastvideo» Бюро переводов «Медтран» Независимый бизнес-консультант Е.Самаров

       

Равнобедренная трапеция: определение, формула, свойства, примеры

Что такое равнобедренная трапеция?

Равнобедренная трапеция — это трапеция, у которой верхняя и нижняя стороны параллельны, а остальные две непараллельные стороны имеют одинаковую длину.

Мы знаем, что трапеция — это четырехугольник с двумя параллельными сторонами и двумя непараллельными сторонами.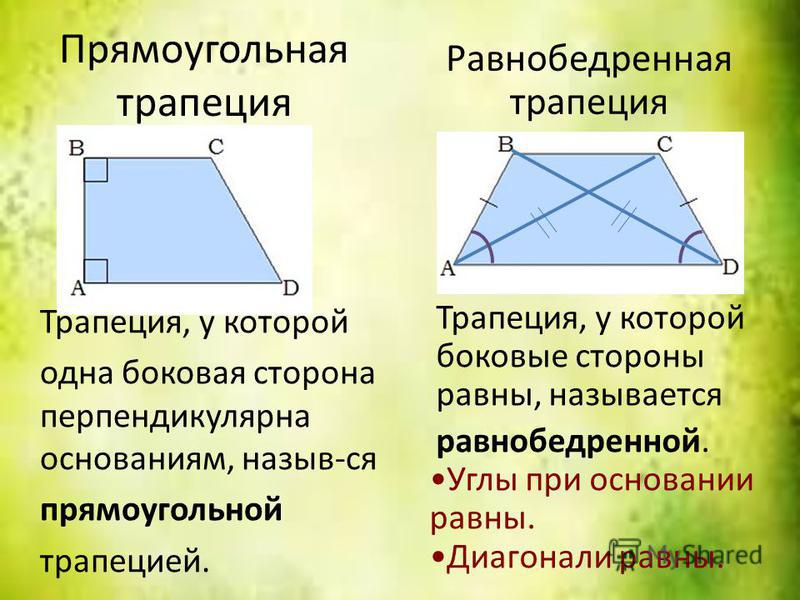 У равнобедренной трапеции непараллельные стороны равны.

Таким образом, мы можем сказать, что параллельные стороны равнобедренной трапеции не равны, а равные стороны не параллельны. Два угла при основании равнобедренной трапеции равны между собой.

Сумма углов трапеции всегда равна 360 градусов, как и любого четырехугольника.

Взгляните на следующее изображение, чтобы понять форму равнобедренной трапеции.

Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны имеют одинаковую длину; и углы при основании имеют одинаковую величину.

Родственные игры

Свойства равнобедренной трапеции

Свойства равнобедренной трапеции обсуждаются ниже. 9\circ$

Отрезки, соединяющие середины параллельных сторон, перпендикулярны сторонам основания.

Трапецию можно вписать в окружность тогда и только тогда, когда трапеция равнобедренная.

Диагонали делят друг друга на пары отрезков одинаковой длины.

Имеет ось симметрии, соединяющую середины параллельных сторон.

Похожие рабочие листы

Равнобедренная трапеция: Формулы

Давайте обсудим формулы для нахождения площади и периметра, медианы равнобедренной трапеции.

Медиана равнобедренной трапеции

Линия, соединяющая середины непараллельных сторон, образует среднюю линию или медиану. Медиана образует специальную теорему, применимую только к равнобедренным трапециям. Длина средней линии равна половине суммы двух параллельных сторон. Если мы присвоим переменные a и b измерениям параллельных сторон, то длина медианы будет равна:

$Median = \frac{a + b}{2}$

Периметр равнобедренной трапеции Формула

 $P = a + b + 2 c$ 

Где a, b и c — стороны трапеции.

Формула площади равнобедренной трапеции

$A = \frac{1}{2} h (a+b)$

где a и b — длины параллельных сторон, а h — расстояние в перпендикулярном выражении между ними.

Как найти периметр равнобедренной трапеции

Вычисление периметра фигуры просто означает нахождение длины вокруг фигуры.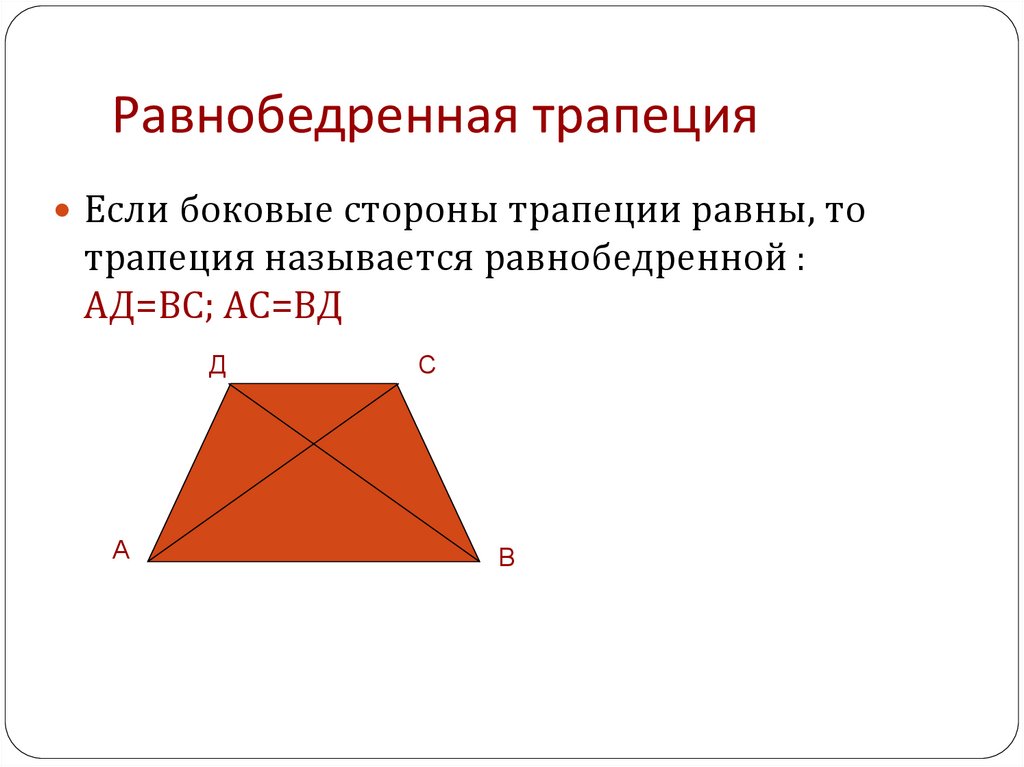 Давайте разберемся с шагами на примере.

Шаг 1: Вызовите формулу. Периметр равнобедренной трапеции равен

$P = a + b + 2c$

Длины сторон нужно просто сложить, потому что периметр равен сумме длин сторон фигуры. Стороны этой равнобедренной трапеции равны по длине, следовательно, вы можете использовать 2c в формуле, поскольку обе стороны одинаковой длины.

Шаг 2: Замените переменные известными значениями.

Шаг 3: Укажите правильную единицу измерения в соответствии с вопросом.

Пример: Найдите периметр данной равнобедренной трапеции.

Здесь $a = 16$ единиц, $b = 26$ единиц, $c = 10$ единиц

Периметр $= 16 + 26 + 10 + 10$ $ 

        $= 62$ единиц

Как найти площадь равнобедренной трапеции

Формула площади равнобедренной трапеции:  

$A = \frac{1}{2} h (a + b)$, где a и b — длины основания, h — высота.

Просто подставьте значения в формулу. Площадь измеряется в квадратных единицах. Итак, примените соответствующую единицу к ответу.

Факты о равнобедренной трапеции

• Сумма внутренних углов равнобедренной трапеции составляет 360 градусов.
• Непараллельные стороны равнобедренной трапеции равны.
• Медиана проходит параллельно обоим основаниям, и ее длина равна сумме длин оснований.
• «Трапеция» — другое название трапеции.

Заключение

В этой статье мы узнали о равнобедренной трапеции, ее свойствах и связанных с ней формулах. Давайте решим несколько примеров, чтобы применить то, что мы узнали!

Решенные примеры

на равнобедренной трапеции

1. Предположим, что площадь равнобедренной трапеции равна 128 дюймов 2 и основания длиной 12 дюймов и 20 дюймов определяют его высоту.
92$

Основания $= 12$ дюймов и 20 дюймов

мы знаем, что площадь равнобедренной трапеции $= A = \frac{1}{2} h(a + b)$

$128 = \frac{1} {2} h(12 + 20)$

Высота $= \frac{128}{16} = 8$ дюймов

2. Вычислите площадь равнобедренной трапеции с высотой 4 дюйма и основанием 3 дюйма и 5 дюймов.

Решение: Площадь равнобедренной трапеции$ = \frac{1}{2} (сумма\; параллелей\; сторон) \× высота$

дано, основания $= 3$ дюйма и 5 дюймов, высота $= 4$ дюймов 92$.

3. Вычислите периметр.

Решение: 

Периметр равнобедренной трапеции $=$ сумма всех сторон

Периметр равнобедренной трапеции $= 20 + 25 + 30 + 30 = 105$ дюймов.

4. Основания трапеции 2 дюйма и 4 дюйма. Найдите длину средней линии по формуле медианы.

Решение: Медиана равнобедренной трапеции $= \frac{a+b}{2}$.

Где a и b — параллельные стороны трапеции.

Итак, длина средней линии $= \frac{2 + 4}{2} = 3$ дюймов

5. Определить периметр равнобедренной трапеции с основаниями 10 и 15 дюймов и непараллельными сторонами 20 дюймов каждый.

Решение: Периметр равнобедренной трапеции $=$ сумма всех сторон равнобедренной трапеции

Периметр равнобедренной трапеции $= 10 + 15 + 20 + 20 = 65$ дюймов.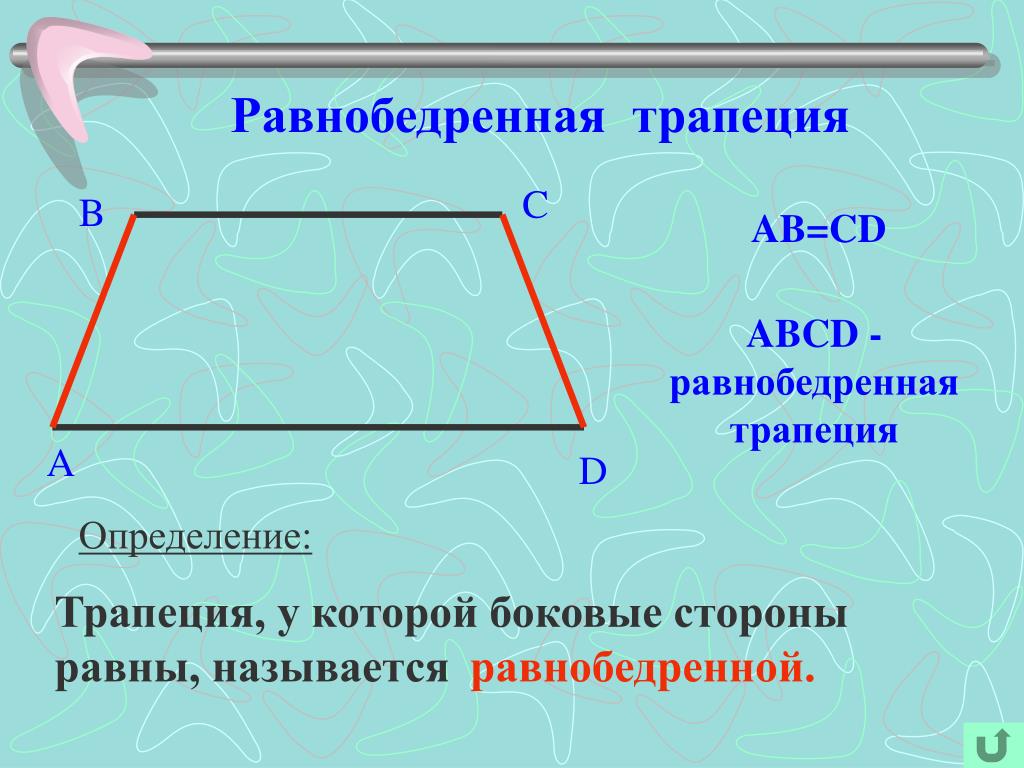

Практические задачи на равнобедренной трапеции

1

Какое из следующих свойств является свойством равнобедренной трапеции?

Противоположные стороны параллельны

Непараллельные стороны равны

И 1, и 2

Только 1

Правильный ответ: Непараллельные стороны равны друг к другу .

2

Противоположные углы равнобедренной трапеции __________________.

конгруэнтный

дополнительный

дополнительный

Ничего из вышеперечисленного

Правильный ответ: дополнительный
Противоположные углы равнобедренной трапеции являются дополнительными.

3

Трапеция имеет ножки по 8 см каждая. Его основания равны 10 см и 15 см соответственно. Вычислить его периметр.

33 дюйма

29 см

41 см

64 см

Правильный ответ: 33 дюйма
Периметр трапеции $=$ Сумма всех ее сторон $= 10 + 8 + 15 + 8 = 33$ дюймов

4

В трапеции основания равны 8 дюймам и 4 дюймам.

Найдите длину средней линии по формуле медианы.

86 дюймов

6 дюймов

14 дюймов

Нет

Правильный ответ: 6 дюймов
Медиана трапеции $= \frac{1}{2} \times $ Сумма параллельных сторон $= \frac {1}{2} \times (8 + 4) = 6$ дюймов

5

Вычислите площадь равнобедренной трапеции с высотой 6 дюймов и основаниями 8 дюймов и 4 дюйма.

86 квадратных единиц

36 квадратных единиц

14 квадратных единиц

Нет

Правильный ответ: 36 квадратных единиц им дается.

Часто задаваемые вопросы о равнобедренной трапеции

Чем отличается равнобедренная трапеция от трапеции?

У равнобедренной трапеции непараллельные стороны равны, углы при основании равны, диагонали конгруэнтны, а противоположные углы смежны.

Почему трапецию называют равнобедренной?

Isosceles означает «равные ноги». В равнобедренной трапеции непараллельные стороны (или катеты) имеют одинаковую длину. Таким образом, она называется равнобедренной трапецией.

Какими свойствами обладает равнобедренная трапеция?

Число сторон равнобедренной трапеции равно четырем. В то время как два основания (противоположные стороны) параллельны друг другу, две другие стороны равны по длине, но не параллельны друг другу.

Что такое прямая трапеция?

Прямоугольная трапеция — это трапеция, имеющая два смежных прямых угла.

Что такое разносторонняя трапеция?

Трапеция, у которой все четыре стороны имеют разную длину, называется разносторонней трапецией.

Свойства трапеций и равнобедренных трапеций

Автор: Марк Райан и

Обновлено: 09.07.2021 06 Геометрия для чайников

Геометрия для чайников

Исследуйте книгу Купить на Amazon

Трапеция — это четырехугольник (форма с четырьмя сторонами) с ровно одной парой параллельных сторон (параллельные стороны называются основаниями ).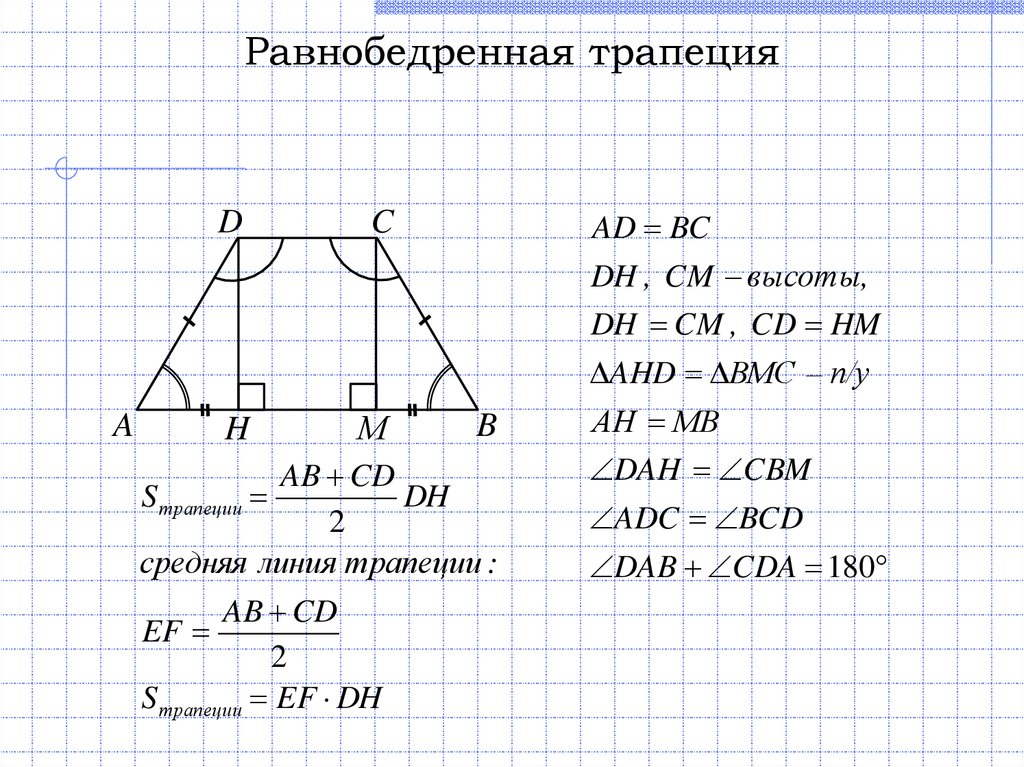 На следующем рисунке показана трапеция слева и равнобедренная трапеция справа.

• Свойства трапеции следующие:

• Свойства равнобедренной трапеции следующие:

  • Свойства трапеции применимы по определению (параллельные основания).

  • Ноги конгруэнтны по определению.

  • Нижние углы при основании равны.

  • Верхние углы при основании равны.

  • Любой нижний угол основания является дополнительным к любому верхнему углу основания.

  • Диагонали равны.

Дополнительные углы, пожалуй, труднее всего заметить на приведенных выше диаграммах. Из-за того, что стороны параллельны, последовательные углы являются односторонними внутренними углами и, таким образом, являются дополнительными. (Кстати, все специальные четырехугольники, кроме воздушного змея, содержат последовательные дополнительные углы.)

Вот вам доказательство равнобедренной трапеции:

Утверждение 1 :

Причина выписки 1 : Дано.

Утверждение 2 :

Причина утверждения 2 : Ножки равнобедренной трапеции конгруэнтны.

Утверждение 3

:

Причина утверждения 3 : Верхние углы при основании равнобедренной трапеции равны.

Заявление 4 :

Причина заявления 4 : Рефлексивное свойство.

Заявление 5 :

Причина заявления 5 : Сторона-Угол-Сторона, или SAS (2, 3, 4)

Заявление 6 :

Причина заявления 6 : CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны).

Заявление 7 :

Причина утверждения 7 : Если углы равны, то равны и стороны.

Эта статья взята из книги:

• Геометрия для чайников,

Об авторе книги:

Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством по всем математическим предметам а также подготовка к тесту.

No related posts.