Как решить систему уравнений графическим способом: 6.9.1. Решение систем линейных уравнений графическим способом.

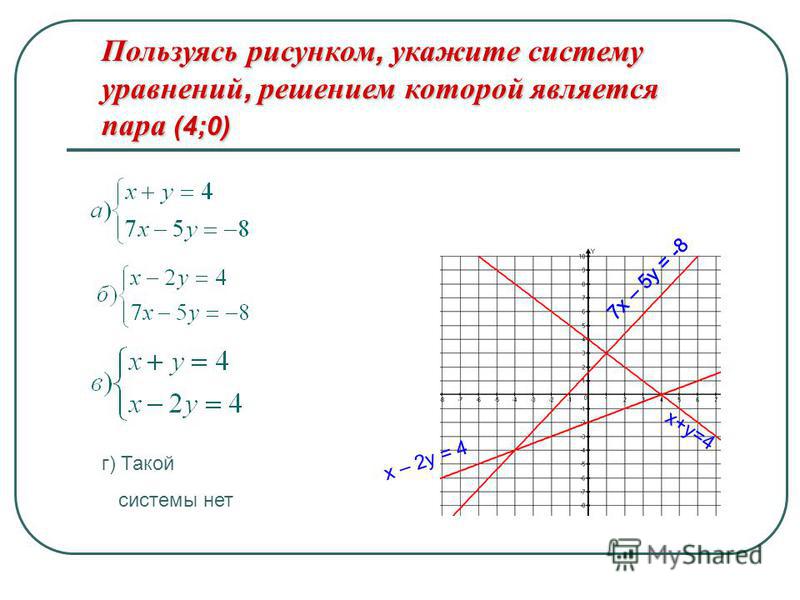
графически решить систему

Вы искали графически решить систему? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и графически решить систему уравнений, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «графически решить систему».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как графически решить систему,графически решить систему уравнений,графический способ,графический способ решения,графическим способом решите систему уравнений ответ округлите до десятых,графическое решение системы уравнений,как графически решить систему уравнений,как графическим способом решить систему уравнений,как решать графически систему уравнений,как решать графическим способом систему уравнений,как решать систему уравнений графически,как решать систему уравнений графическим способом,как решить графически систему уравнений,как решить графическим способом систему уравнений,как решить систему уравнений графически,как решить систему уравнений графическим способом,как решить систему уравнений способом графическим,решение систем уравнений графическим способом,решение системы уравнений графическим способом,решите графическим способом систему уравнений,решите систему уравнений графическим способом,решить графически систему,решить графическим способом систему,решить графическим способом систему уравнений,решить систему графически,решить систему графическим способом,решить систему уравнений графически,решить систему уравнений графическим способом,система уравнений графическая,система уравнений графическим способом,системы уравнений решение графическим способом.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и графически решить систему. Просто введите задачу в окошко и нажмите «решить» здесь (например, графический способ).

Решить задачу графически решить систему вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Решение системы уравнений графическим методом средствами MS Excel

Цели и задачи.

1. Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
2. Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
3. Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
4. Закрепить навыки создания таблиц и диаграмм.
5. Научить решать систему уравнений графическим методом, исследовать график функции.

Оборудование урока: компьютеры, мультимедиа проектор.

Программное обеспечение: Windows XP, пакет программ MS Office 2003.

Содержание урока

Организационный момент.

Здравствуйте.

Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.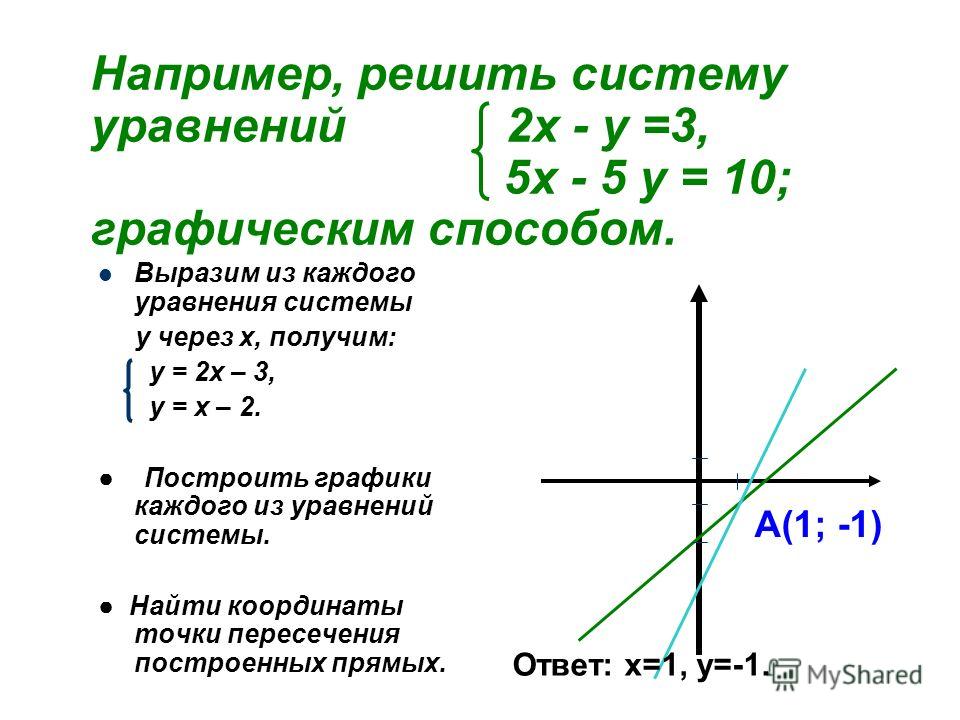

Запишите в тетради тему урока и укажите дату.

Назовите мне кого из класса сегодня нет.

Актуализация знаний.

Давайте вспомним, что такое уравнение, и как его можно решить графически.

Назовите, пожалуйста, что в математике называют

уравнением, решением уравнения и системой уравнений.

(Учащиеся приводят определения)

Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.

Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).

Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.

Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами.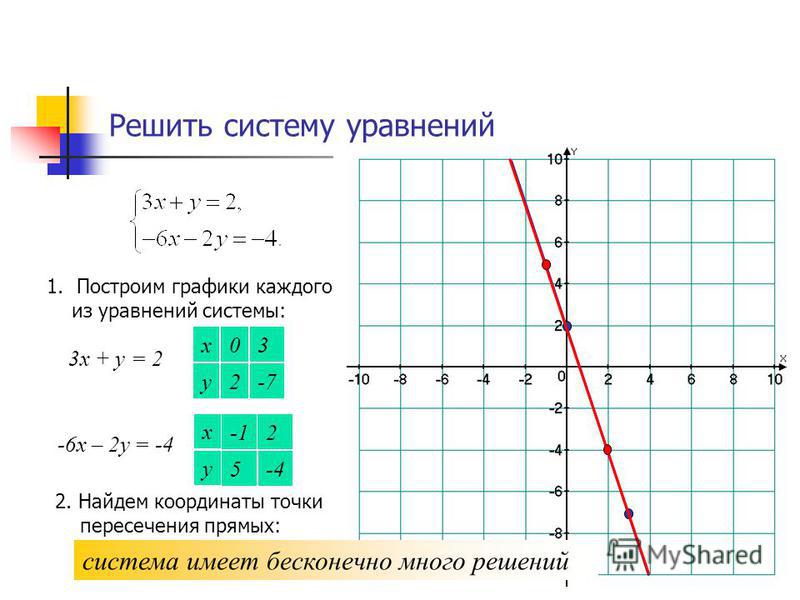 Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.

Постановка проблемы.

Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.

Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.

Но эту задачу может взять на себя ЭВМ.

Мы воспользуемся возможностями программы MS Excel.

Основная часть

Давайте разобьемся на 2 группы.

2 + 2

Y = 2 * x + 3

Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.

Сформируем начальные данные.

В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.

В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.

Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.

Приложение 1

Приложение 2

Формулы, которые нам нужно ввести приведены на рисунке.

Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.

Заполните, пожалуйста, в каждой таблице 20-25 строчек.

Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.

Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.

Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.

Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.

Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим

снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.

Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.

У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.

Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.

Мы видим, что одно из решений нашей системы уравнений равно -1,5.

Задание 1.

Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.

Сколько у вас получилось?

Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.

Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.

Приложение 1

Приложение 2

Для этого нужно внести изменения в таблицу и расчётные формулы.

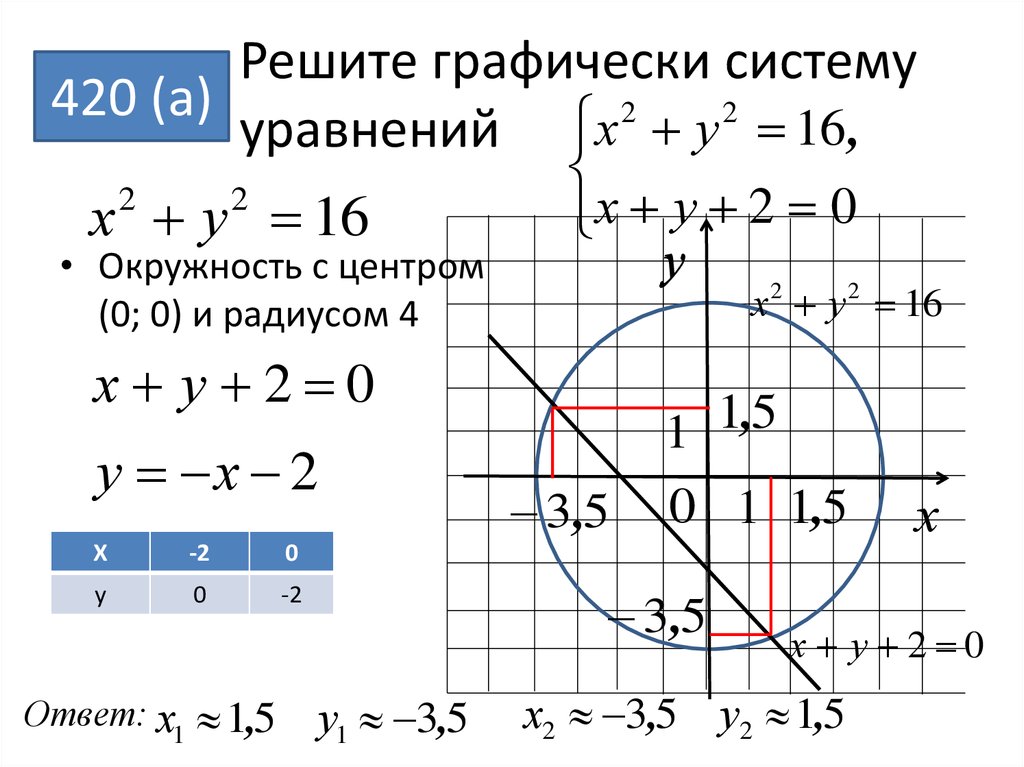Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.

Задание 2.

Самостоятельно внесите все необходимые изменения.

Задание 3.

Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.

Заключительный этап урока

Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?

А что легче для вас?

Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.

Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.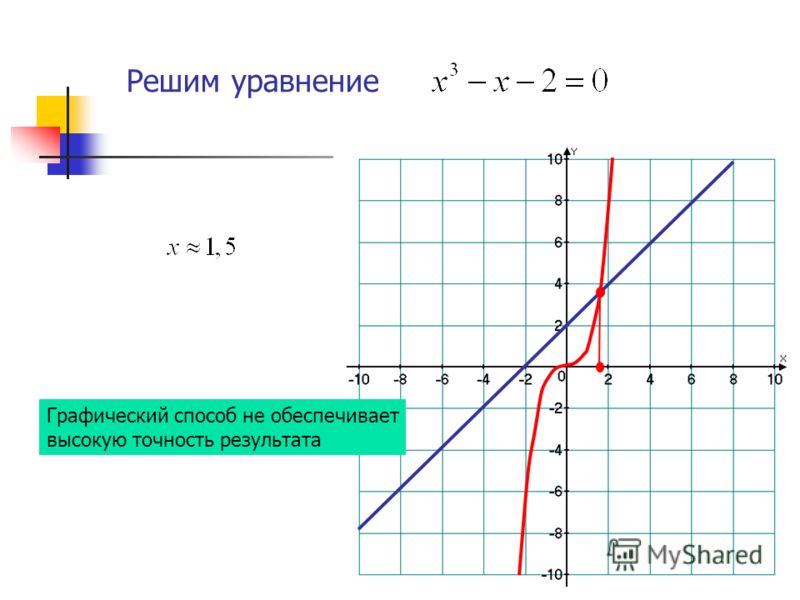

Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.

Спасибо за урок.

Решение систем линейных уравнений графически

Система уравнений представляет собой набор из двух или более уравнений. В этом курсе будут изучены линейные системы в двух уравнениях. В отличие от уравнения, где решением обычно является значение или набор значений, решение системы уравнений обычно представляет собой точку x-y или набор точек x-y. В этом разделе будет обсуждаться графическая интерпретация системы и ее решения.

Чтобы показать, что уравнения являются частью одной и той же системы, их обычно записывают друг над другом и заключают в фигурную скобку слева. Нет ничего необычного в добавлении римских цифр, чтобы иметь возможность обращаться к уравнениям по отдельности.

{x+y=3x−y=1​(I)(II)​​

Системы линейных уравнений часто содержат более одной неизвестной переменной, где решением является набор координат, который делает все уравнений истинными одновременно . В приведенном выше примере решение x=2 и y=1. Эти координаты делают стороны равными в обоих уравнениях . Решение обычно записывается в виде точки:

(2,1).​

Система линейных уравнений может быть решена как графически, так и алгебраически.

Решить систему линейных уравнений графически означает построить график, представленный системой, и определить . Рассмотрим пример системы.

{2y=-2x+8x=y−1​(I)(II)​

Для решения необходимо выполнить три шага.

Начните с написания уравнений, выделив y. Для первого разделите обе части на 2. Для второго уравнения добавьте 1 к обеим частям.

{2y=-2x+8x=y−1​(I)(II)​

(I):  Найдите y

⎩⎪⎨⎪⎧​y=2-2x+8​x=y− 1​

⎩⎪⎨⎪⎧​y=2-2x​+28​x=y−1​

⎩⎪⎨⎪⎧​y=2-2​x+28​x=y-1​

⎩ ⎪⎨⎪⎧​y=-22​x+28​x=y−1​

{y=-1x+4x=y−1​

{y=-x+4x=y−1​

(II): Решите для y

{y=-x+4x+1=y​

{y=-x+4y=x+1​

Теперь, когда оба уравнения записаны в форме пересечения наклона, они могут быть на одном и том же.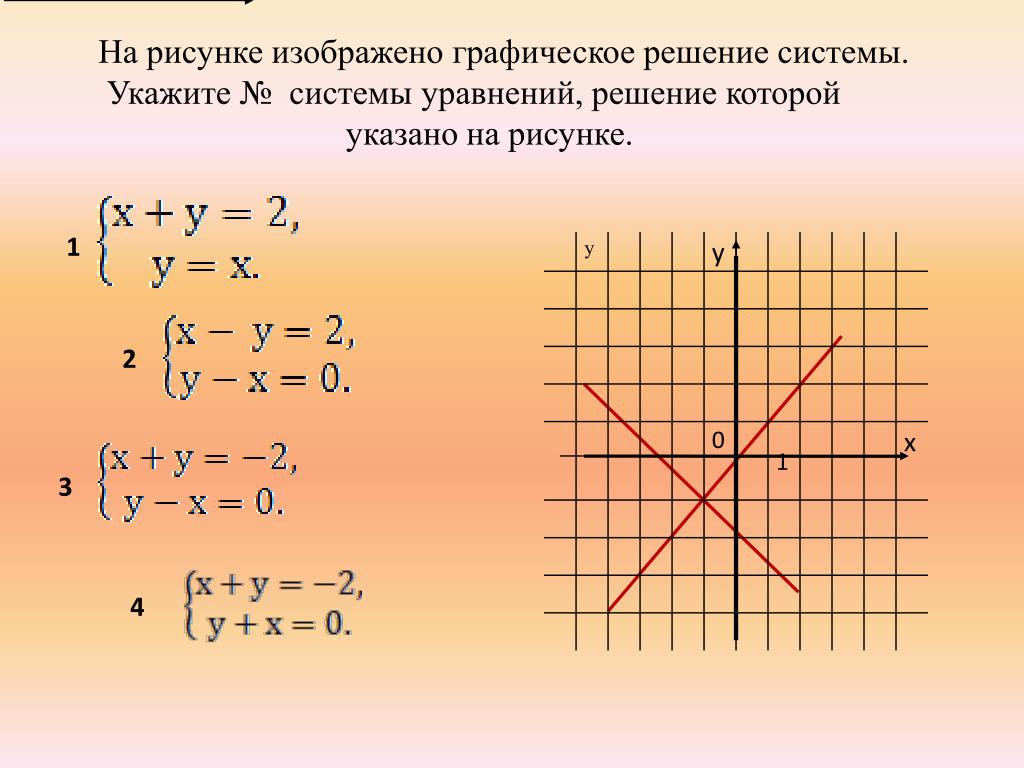

Точка пересечения прямых является решением системы.

Линии пересекаются в точках (1.5,2.5). Следовательно, это решение системы — значение x равно 1,5, а значение y равно 2,5.

Иногда точка пересечения линий не является . В этом случае решение, полученное путем графического решения системы уравнений, является приближенным.

На координатной плоскости нанесены две линии.

Используйте график для решения системы

{y=2x+5y=0,5x+2.​

Показать решение expand_more

Мы можем найти решение системы, определив .

Из графика видно, что линии пересекаются в точке (-2,1). Таким образом, эта точка является решением системы. Мы можем проверить это алгебраически, подставив x=-2 и y=1 в оба уравнения. Мы будем знать, что наш ответ правильный, если оба сделанных утверждения верны.

{y=2x+5y=0,5x+2​

{1=?2(-2)+51=?0.5(-2)+2​

{1=?-4+51=?- 1+2​

{1=11=1​

Таким образом, поскольку (-2,1) удовлетворяет обоим уравнениям, это решение системы.

В футбольном матче команда хозяев, Смертные Вомбаты, одержала победу над Бесстрашными Чайками с разницей в 13 очков. Общий счет обеих команд составил 41. Каков был итоговый счет?

Показать решение expand_more

Для начала мы будем использовать переменные для представления различных величин. Пусть w — количество очков, набранных вомбатами, а s — количество очков, набранных чайками. Вомбаты набрали на 13 очков больше, чем Чайки. Таким образом, разницу между w и s можно записать как

ш=с+13.

Общее количество баллов составило 41, поэтому сумма w и s равна

w+s=41.

Оба эти уравнения должны выполняться одновременно, что дает нам следующую систему уравнений.

{ш=с+13ш+с=41​

Мы можем решить систему, построив график. Во-первых, давайте запишем второе уравнение, вычитая s с обеих сторон.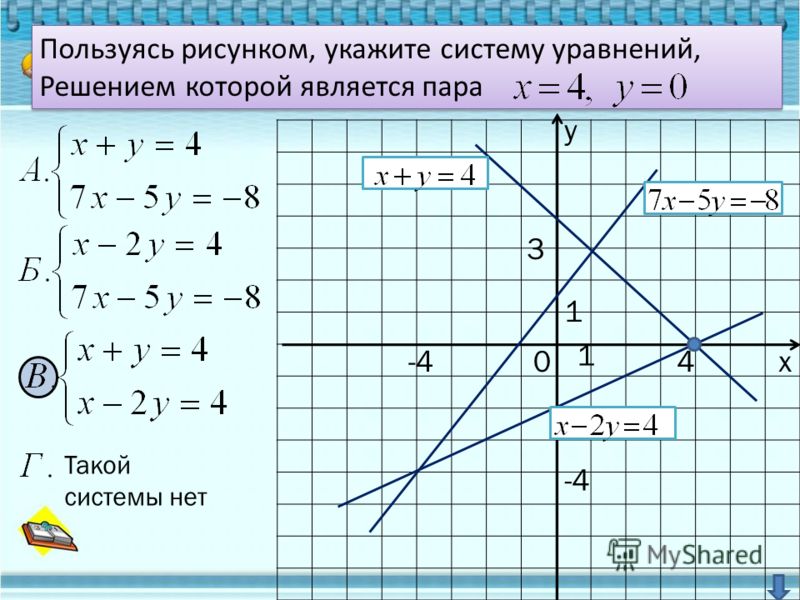

{w=s+13w=-s+41​

Теперь мы можем. Поскольку оценки не могут быть отрицательными, мы наносим линии только для положительных значений s и w.

Теперь мы можем определить файл .

Точка пересечения (14,27). Это означает, что вомбаты набрали 27 очков, а чайки — 14.

Объяснение урока: Графическое решение систем линейных уравнений

В этом объяснении мы научимся решать систему двух линейных уравнений, рассматривая их графики и определяя точку пересечения.

Когда нас просят решить систему уравнений, это означает, что мы ищем набор значений переменных, удовлетворяющих каждому уравнению. Чтобы увидеть, как мы можем решить систему уравнений графически, давайте рассмотрим следующий пример: 𝑦=𝑥+1,𝑦=−2𝑥+4.

Сначала заметим, что эти уравнения на самом деле являются линейными функциями. Поскольку есть два уравнения, мы называем это системой двух линейных уравнений.

Мы хотим найти 𝑥- и 𝑦-значения, которые удовлетворяют обоим уравнениям.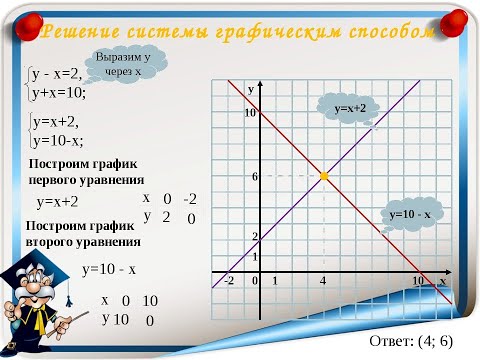 Допустим, что 𝑥=𝑎 и 𝑦=𝑏 является решением обоих уравнений. Затем мы можем определить потенциальные значения для 𝑎 и 𝑏 графически. Заметим, что, поскольку 𝑏=𝑎+1, мы знаем, что точка (𝑎,𝑏) лежит на графике первого уравнения. Сходным образом, так как 𝑏=−2𝑎+4, точка (𝑎,𝑏) лежит на графике второго уравнения. Следовательно, (𝑎,𝑏) лежит на обоих графиках, поэтому является точкой пересечения графиков.

Мы можем нарисовать графики этих уравнений, заметив, что оба уравнения представляют собой прямые линии в координатной плоскости. На самом деле они даны в наклонно-перехватная форма. Мы рисуем первую линию с 𝑦-перехватом 1 и наклоном 1, а вторую линию с 𝑦-перехватом 4 и наклоном −2. Это дает нам следующее.

Мы можем прочитать координаты точки пересечения как (1,2). Стоит отметить, что в этот момент мы рассуждали, что если (𝑎,𝑏) является решением к системе уравнений, то это точка пересечения графиков. Однако мы также хотим проверить что все точки пересечения являются решениями.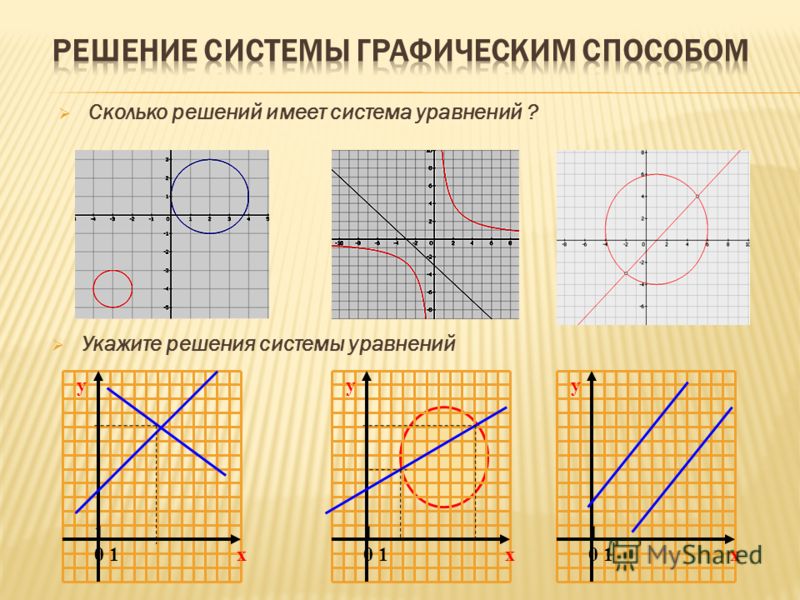 Мы можем сделать это, заметив, что если (𝑎,𝑏) является точкой пересечения, то (𝑎,𝑏) лежит на графике каждого уравнения и, следовательно, должно удовлетворять каждому уравнению; в противном случае он не будет лежать на его графике. Следовательно, каждая точка пересечения (если она существует) является решением системы уравнений.

Мы можем использовать это, чтобы заключить, что, поскольку это единственная точка пересечения, 𝑥=1, 𝑦=2 является единственным решением этой системы уравнений.

Можно также заметить, что если нет точки пересечения между всеми графиками уравнений, то нет значений переменных, которые удовлетворяют всем уравнениям. Это дает нам следующий результат.

Теорема: графическое решение системы уравнений

Каждое решение системы уравнений является точкой пересечения всех ее графиков.

Каждая точка пересечения всех графиков уравнений будет решением системы уравнений.

Если между всеми графиками нет точек пересечения, то решений системы уравнений нет.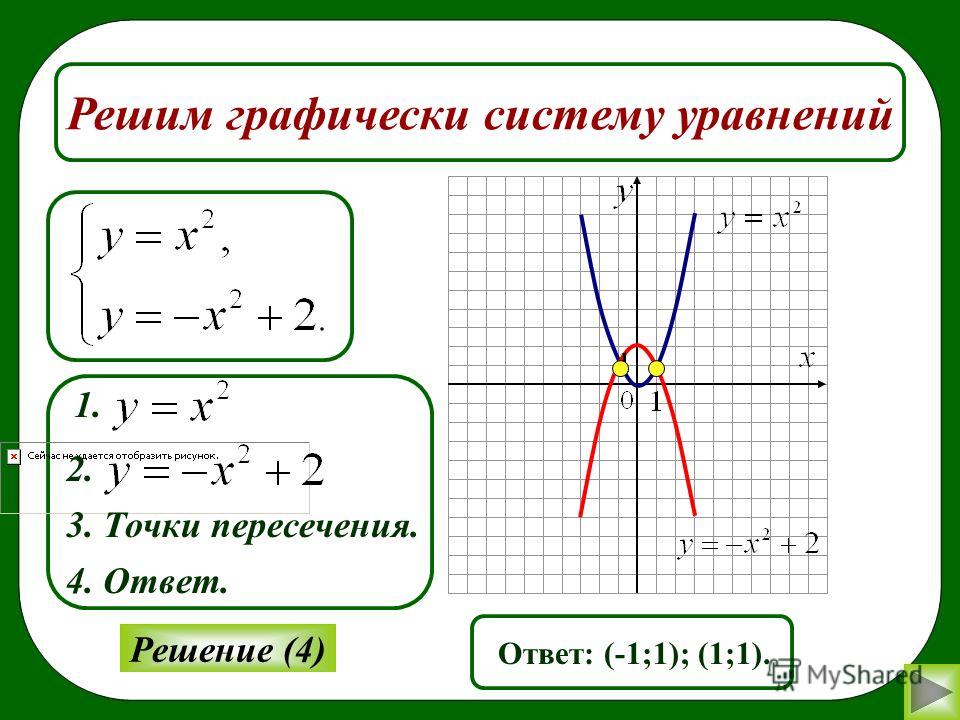

Если мы работаем с системой двух линейных уравнений, то мы знаем, что оба уравнения можно представить в виде прямых линий. Тогда мы можем вспомнить, что есть три возможности пересечения двух прямых на плоскости.

1. Линии пересекаются ровно в одной точке.
2. Линии различны и параллельны, поэтому точек пересечения нет.
3. Прямые совпадают, поэтому прямые пересекаются в каждой точке прямых.

Поскольку точки пересечения являются решениями системы уравнений, эти три возможности сообщают нам количество решений этих систем уравнений. Есть три варианта количества решений системы двух линейных уравнений; либо 0,1, либо бесконечное число решений, в зависимости от линий. Стоит отметить, что это справедливо и для более чем двух строк. Мы даем каждому из этих трех сценариев имя.

Определение: число решений системы линейных уравнений

Если система линейных уравнений имеет одно решение, то существует единственная точка пересечения между линиями, и мы называем это независимой системой линейных уравнений.

Если система линейных уравнений имеет бесконечное число решений, то все линии совпадают, и мы называем это зависимой системой линейных уравнений.

В обоих случаях у нас есть хотя бы одно решение системы, поэтому мы называем эти согласуются с системами уравнений.

Если система линейных уравнений не имеет решений, то между прямыми нет точек пересечения, и мы называем это противоречивой системой уравнений.

Решим графическим методом следующую систему двух линейных уравнений: 𝑦=4𝑥+3,2𝑥+𝑦=1.

Прежде всего заметим, что второе уравнение не представлено в форме наклона и точки пересечения, поэтому мы начнем с преобразования уравнения в эту форму путем вычитания 2𝑥 с обеих сторон уравнения, чтобы получить 𝑦=−2𝑥+1.

Затем мы рисуем обе линии на одном графике. Первая строка имеет 𝑦-перехват 3 и наклон 4, а вторая строка имеет 𝑦-перехват 1 и наклон -2, что дает нам следующий набросок.

Из графика видно, что есть одна точка пересечения, а значит, есть единственное решение системы уравнений.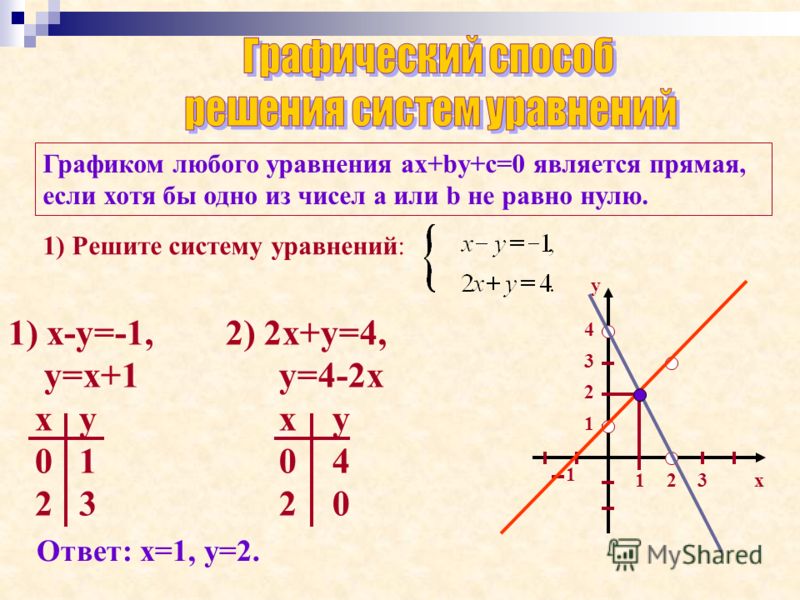 Однако мы не можем точно определить координаты этой точки пересечения. Вместо этого мы можем заметить, что 𝑥-координата точки пересечения лежит между прямыми 𝑥=−0,5 и 𝑥=0, а 𝑦-координата точки пересечения лежит между прямыми 𝑦=1,5 и 𝑦=2.

Таким образом, хотя мы не могли использовать графический метод для определения точного решения этой системы уравнений, мы могли определить, что существует единственное решение и что решение будет удовлетворять неравенствам −0,5𝑥0 и 1,5𝑦2.

Это завершает процесс графического решения системы линейных уравнений, и мы можем записать шаги следующим образом.

Как: Графическое решение системы линейных уравнений

1. Если нам не даны графики линейных уравнений, мы должны начертить графики каждой линии на тех же координатных осях. Для этого нам может понадобиться преобразовать каждое уравнение в форму наклона и пересечения.
2. Любая точка пересечения всех прямых является решением системы уравнений. В частности, если такой точки нет, то нет и решений к системе, и если прямые совпадут, то решений будет бесконечное множество.
3. Если возможно, считайте координаты точки пересечения, чтобы найти точные значения решения. Однако, если это невозможно, используйте второстепенные линии сетки, чтобы найти диапазон, в котором будут лежать решения.

Давайте теперь посмотрим, как мы можем применить этот процесс для графического определения решений системы линейных уравнений.

Пример 1. Решение системы двух линейных уравнений с использованием заданного графика

Использование графика для решения одновременных уравнений 𝑦=4𝑥−2,𝑦=−𝑥+3.

Ответ

Напомним, что решение системы уравнений задается координатами точки пересечения графиков всех уравнений. Это означает, что координаты точки пересечения двух линий сообщают нам решение уравнений.

Мы видим, что 𝑥-координата этой точки равна 1, а 𝑦-координата равна 2. Это говорит нам, что 𝑥=1 и 𝑦=2 является решением совместных уравнений, и мы могли бы проверить это, подставив эти значения в уравнения.

Если мы подставим 𝑥=1 в первое уравнение, мы получим 𝑦=4(1)−2=2, что согласуется с нашим решением. Точно так же, если мы подставим 𝑥=1 во второе уравнение, мы получим 𝑦=−(1)+3=2, что также согласуется с нашим решением. Поскольку оба уравнения верны, это подтверждает решение.

Поскольку это единственная точка пересечения, это единственное решение уравнений.

Следовательно, единственным решением является 𝑥=1 и 𝑦=2.

В нашем следующем примере мы продемонстрируем, как найти решения системы уравнений, используя систему обозначений.

Пример 2. Решение системы двух линейных уравнений с использованием их графика

Найдите набор решений двух уравнений, представленных 𝐿 и 𝐿.

Ответ

Напомним, что решение системы уравнений задается координатами точки пересечения графиков всех уравнений.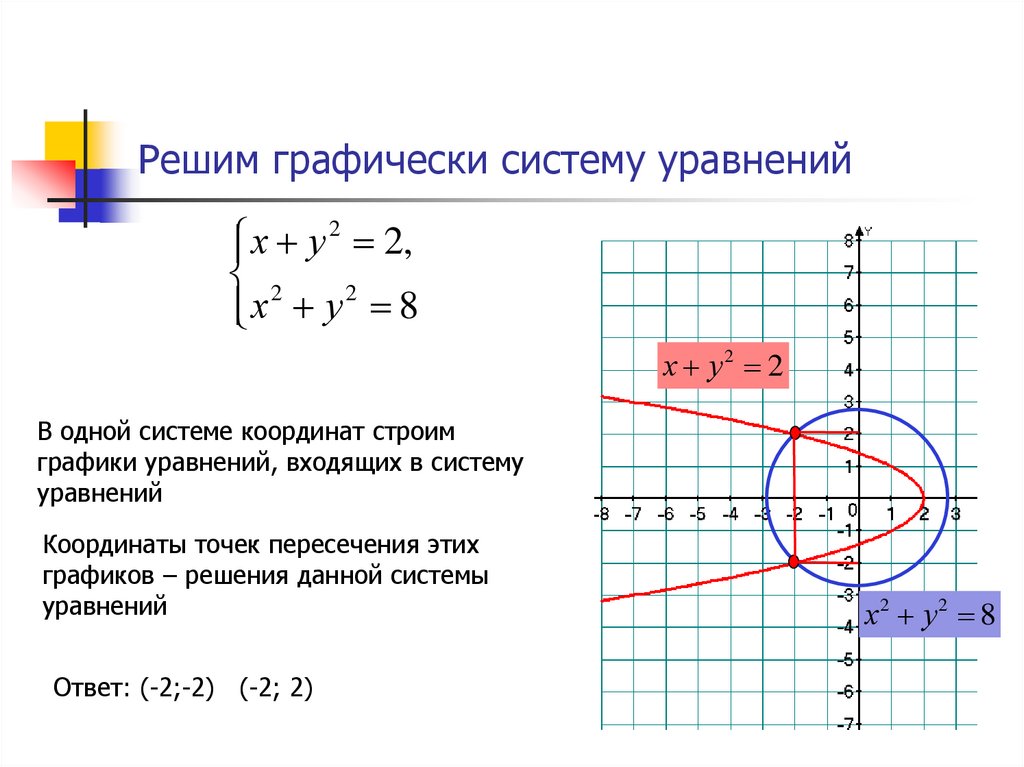 Это означает, что координаты точки пересечения двух линий дают нам решение этой системы уравнений.

Поскольку существует только одна точка пересечения, мы можем заключить, что существует только одно решение, а это, в свою очередь, означает, что множество решений будет состоять только из одного члена. Мы можем определить это единственное решение, найдя координаты точки пересечения на графике.

Мы видим, что координаты этой точки равны (2,3), а значит, пара значений 𝑥=2 и 𝑦=3 — единственное решение этой системы уравнений. Чтобы записать это в виде множества решений, вспомним, что мы можем представлять решения как упорядоченная пара, что совпадает с его координатами.

Следовательно, набор решений двух уравнений, представленных 𝐿 и 𝐿 есть {(2,3)}.

В наших предыдущих двух примерах нам даны графики линейных уравнений. Однако так будет не всегда. Давайте теперь посмотрим несколько примеров где мы решаем систему линейных уравнений, сначала рисуя графики каждого уравнения.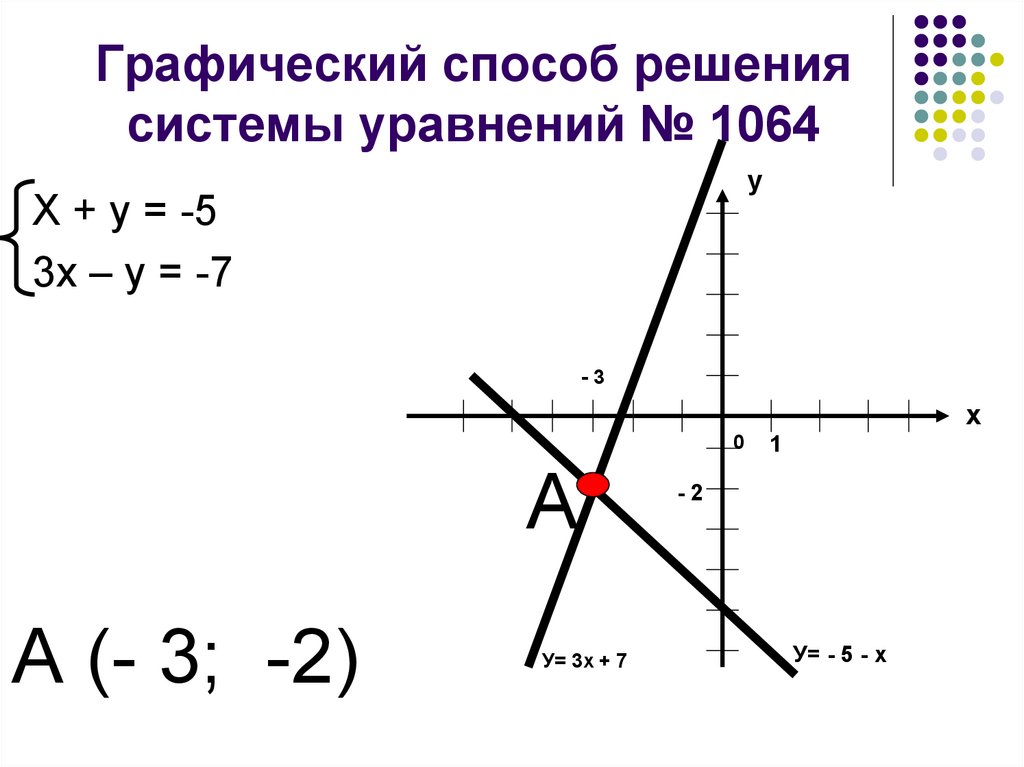

Пример 3. Решение системы двух линейных уравнений путем построения графика

Построив графики 𝑦=𝑥−1 и 𝑦=5𝑥+7, найдите точку, которая удовлетворяет обоим уравнениям одновременно.

Ответ

Напомним, что если (𝑥,𝑦) удовлетворяет обоим уравнениям одновременно, то точка должна лежать на графиках обоих уравнений. Следовательно, это будет точка пересечения обоих графиков. Точно так же, если (𝑥,𝑦) является точкой пересечения обоих графиков, тогда он удовлетворяет обоим уравнениям и, следовательно, является решением системы уравнений. Следовательно, мы можем найти решения этой системы, найдя координаты из точек пересечения. Мы сделаем это, набросав оба графика.

Существует множество различных способов построения графика прямой линии. Например, чтобы нарисовать линию 𝑦=𝑚𝑥+𝑏, мы вспоминаем, что эта линия будет иметь 𝑦-перехват 𝑏 и 𝑥-перехват −𝑏𝑚 при условии 𝑚≠0 а его наклон равен 𝑚. Соединение этих точек линией позволяет нам начертить линию.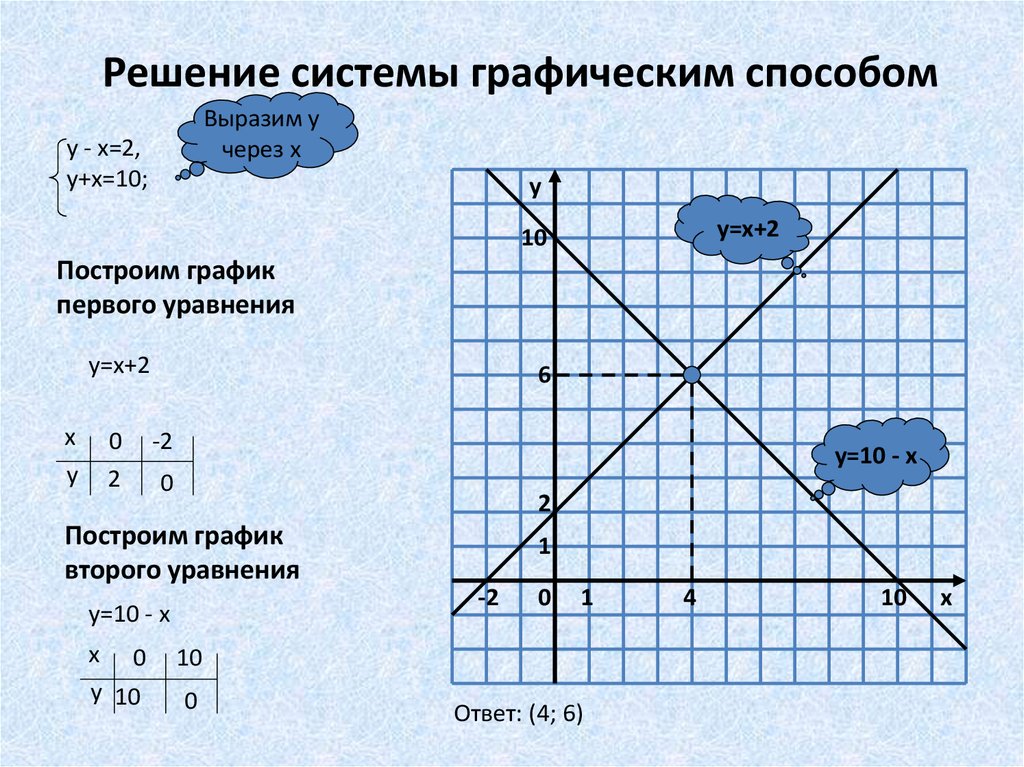

Мы можем применить это к каждой строке. Во-первых, линия 𝑦=𝑥−1 будет иметь 𝑦-перехват, равный −1. и 𝑥-перехват −(−1)1=1. Во-вторых, строка 𝑦=5𝑥+7 будет иметь 𝑦-перехват 7 и 𝑥-перехват -75.

Поскольку это не целое число, мы можем найти другую точку путем подстановки. Подставляем 𝑥=−1 в уравнение, чтобы получить 𝑦=5(−1)+7=2.

Это дает нам следующее.

Мы видим, что линии пересекаются слева от точки (−1,2). Попробуем 𝑥=−2. Подстановка 𝑥=−2 в уравнение первой строки дает 𝑦=−2−1=−3.

Подстановка 𝑥=−2 в уравнение второй строки дает 𝑦=5(-2)+7=-10+7=-3.

Отметим, что оба уравнения дают 𝑦=−3. Следовательно, 𝑥=−2 и 𝑦=−3 удовлетворяют обоим уравнениям, и мы можем сказать что точка, удовлетворяющая обоим уравнениям, равна (−2,−3).

Пример 4. Решение системы двух линейных уравнений путем построения графика

Построение графиков одновременных уравнений 𝑦=2𝑥+7,𝑦=2𝑥−4, а потом решить систему.

Ответ

Напомним, что точки пересечения графиков обоих уравнений подскажет решение системы уравнений. Это означает, что мы можем решить систему набросав оба уравнения, поскольку это линейные уравнения, приведенные в наклон-пересечение, есть много способов сделать это.

Например, чтобы нарисовать линию 𝑦=𝑚𝑥+𝑏, мы вспоминаем, что эта линия будет иметь 𝑦-перехват 𝑏 и 𝑥-перехват −𝑏𝑚, если 𝑚≠0 и его наклон равен 𝑚. Соединение этих точек линией позволяет нам начертить линию.

Для первой строки 𝑦-перехват равен 7, а 𝑥-перехват равен −72. Поскольку это не целое число, мы можем найти другую точку на прямой. Подставляем 𝑥=−1 в уравнение, чтобы получить 𝑦=2(−1)+7=5.

Во второй строке точка пересечения 𝑦 находится в точке −4, а точка пересечения 𝑥 находится в точке −(−4)2=2. Соединив точки пересечения каждой линии, мы получим следующий набросок.

Мы видим, что эти прямые параллельны; это означает, что точек пересечения нет, поэтому система не имеет решений.

На самом деле, мы могли бы сэкономить на рисовании графиков; если мы посмотрим на уравнения двух прямых, мы увидим, что они даны в наклонно-перехватная форма. Мы знаем, что коэффициент при 𝑥 говорит нам о наклоне линии, и мы видим, что в обоих случаях он равен 2. Точно так же мы можем видеть, что обе линии имеют разные 𝑦-перехваты из их уравнений. Это говорит нам о том, что эти прямые параллельны. (имеют одинаковый наклон) и различны (проходят через разные 𝑦-перехваты). Следовательно, прямые не пересекаются и система не имеет решений.

Используя любой метод, мы показали, что решений нет, поскольку оба уравнения представляют собой параллельные прямые.

В следующем примере мы покажем, как решить систему линейных уравнений, когда они не заданы. в форме наклона-перехвата.

Пример 5. Решение системы двух линейных уравнений путем построения графика

Построив графики 12𝑥−9𝑦=24 и 4𝑥−3𝑦=8, определите 𝑥- и 𝑦-координаты точки, удовлетворяющей обоим уравнениям одновременно.

Ответ

Напомним, что решение системы уравнений задается координатами точки пересечения графиков всех уравнений. Это означает, что координаты точки пересечения двух линий сообщают нам решение уравнений. Следовательно, мы можем решить эту систему, нанося каждое уравнение на один и тот же график и определяя координаты точек пересечения.

Мы построим оба графика, найдя соответствующие 𝑥- и 𝑦-перехваты. Подставляем 𝑥=0 в уравнение первой строки и решить, чтобы получить 12(0)−9𝑦=24𝑦=24−9=−83.

Поскольку это не целое число, мы будем использовать другую точку. Подставляем 𝑥=−1 в уравнение, чтобы получить 12(−1)−9𝑦=24.

Затем мы переставляем, чтобы получить 𝑦=24+12−9=−4.

Подставляем 𝑦=0 в уравнение первой строки и решаем, чтобы получить 12𝑥−9(0)=24𝑥=2412=2.

Подставляем 𝑥=0 в уравнение второй строки и решаем, чтобы получить 4(0)−3𝑦=8𝑦=8−3=−83.

Поскольку это не целое число, мы будем использовать другую точку.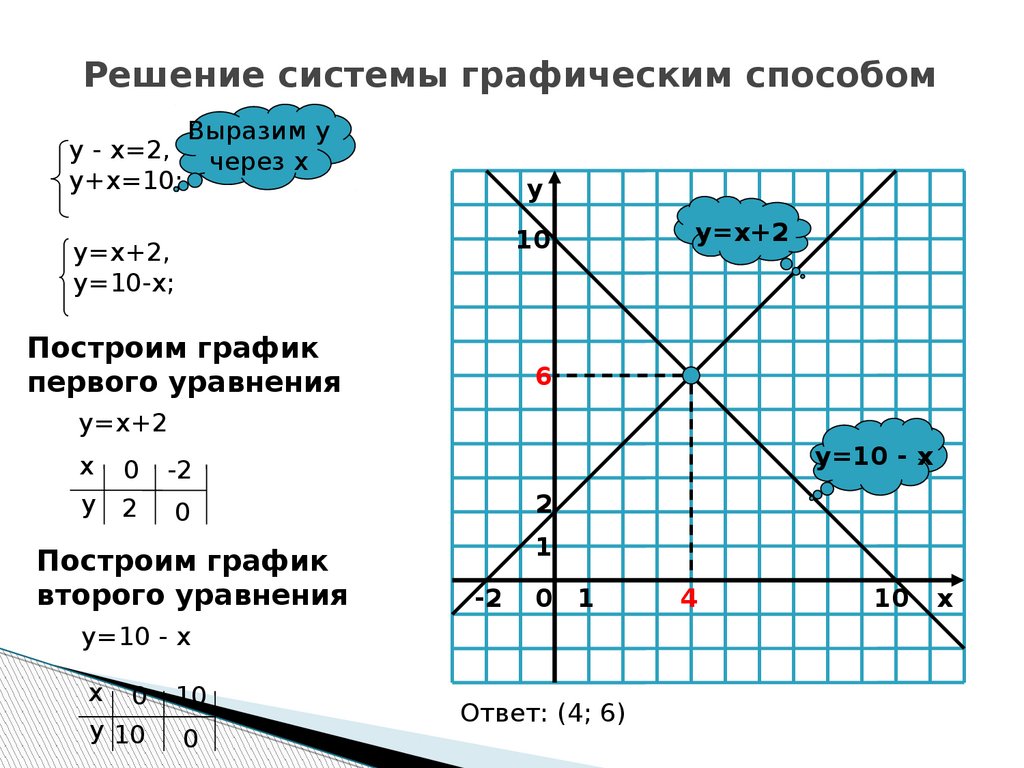 Подставляем 𝑥=−1 в уравнение, чтобы получить 4(−1)−3𝑦=8.

Затем мы переставляем, чтобы получить 𝑦=8+4−3=−4.

Подставляем 𝑦=0 в уравнение второй строки и решаем, чтобы получить 4𝑥−3(0)=8𝑥=84=2.

Итак, 𝑥- и 𝑦-перехваты обеих прямых одинаковы; следовательно, линии совпадают. Мы можем нарисовать линии следующим образом.

Каждая точка на прямой удовлетворяет обоим уравнениям, поэтому каждая точка является решением системы уравнений.

Мы могли бы также определить это из самой системы уравнений. Если мы преобразуем уравнения, которые нам даны, в форму наклона и пересечения, мы имеем 12𝑥−9𝑦=24−9𝑦=−12𝑥+24𝑦=−12𝑥+24−9𝑦=43𝑥−83 а также 4𝑥−3𝑦=8−3𝑦=−4𝑥+8𝑦=−4𝑥+8−3𝑦=43𝑥−83.

Мы видим, что оба уравнения представляют одну и ту же прямую, значит, они совпадают.

Таким образом, мы показали, что две прямые совпадают, поэтому существует бесконечное число решений.

В нашем следующем примере мы будем использовать заданный график для определения системы уравнений, для решения которой он может быть использован.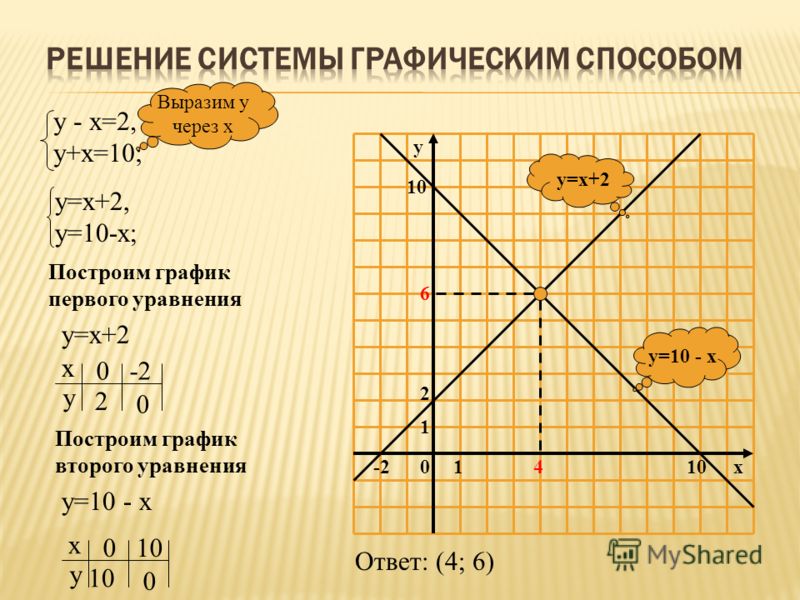

Пример 6. Определение набора одновременных уравнений, которые можно решить с помощью заданного графика

Какие из следующих систем одновременных уравнений можно решить, используя данный график?

1. 𝑦 = 2𝑥 — 4, 𝑦 = 𝑥+5
2. 𝑦 = −4𝑥+2, 𝑦 = 5𝑥 — 1
3. 𝑦 = 2𝑥 — 4, 𝑦 = −𝑥+5
4. 𝑦 = −4𝑥+2 , 𝑦=5𝑥+1
5. 𝑦=2𝑥+4, 𝑦=−𝑥+5

Ответ

Напомним, что координаты точки пересечения двух прямых сообщают нам решение уравнений, заданных уравнением уравнения линий. Следовательно, с помощью этого графика можно решить систему уравнений.

Значит, нужно определить уравнения обеих линий. Мы сделаем это, вспомнив, что уравнение прямой в форме наклона–пересечения имеет вид 𝑦=𝑚𝑥+𝑏, где 𝑚 — наклон, а 𝑏 — 𝑦-отрезок. Мы можем определить оба этих значений из диаграммы. Во-первых, синяя линия имеет 𝑦-пересечение 5, а красная линия имеет 𝑦-пересечение −4. Далее мы определяем наклон каждой линии, используя тот факт, что линия, проходящая через (𝑥,𝑦) и (𝑥,𝑦) имеет наклон 𝑚=𝑦−𝑦𝑥−𝑥. 

Синяя линия проходит через точки (0,5) и (1,4), поэтому имеет наклон 𝑚=4−51−0=−1.

Красная линия проходит через точки (0,−4) и (1,−2), поэтому она имеет наклон 𝑚=−2−(−4)1−0=2.

Следовательно, синяя линия имеет 𝑚=−1 и 𝑏=5 и уравнение 𝑦=−𝑥+5, а красная линия имеет 𝑚=2 и 𝑏=−4 и уравнение 𝑦=2𝑥−4. Это дает нам систему уравнений 𝑦=−𝑥+5,𝑦=2𝑥−4.

Решения этой системы линейных уравнений, заданные координатами точки пересечения, равны 𝑥=3 и 𝑦=2.

Это система линейных уравнений в варианте C, 𝑦=2𝑥−4, 𝑦=−𝑥+5.

В нашем последнем примере мы будем использовать заданный график системы двух линейных уравнений, чтобы найти приблизительные диапазоны, в которых находится решение.

Пример 7. Использование заданного графика для поиска подходящих диапазонов для решений заданных одновременных уравнений

Используйте показанный график, чтобы найти подходящие диапазоны для решений одновременных уравнений 𝑦=3𝑥−3,5𝑥+7𝑦=−2.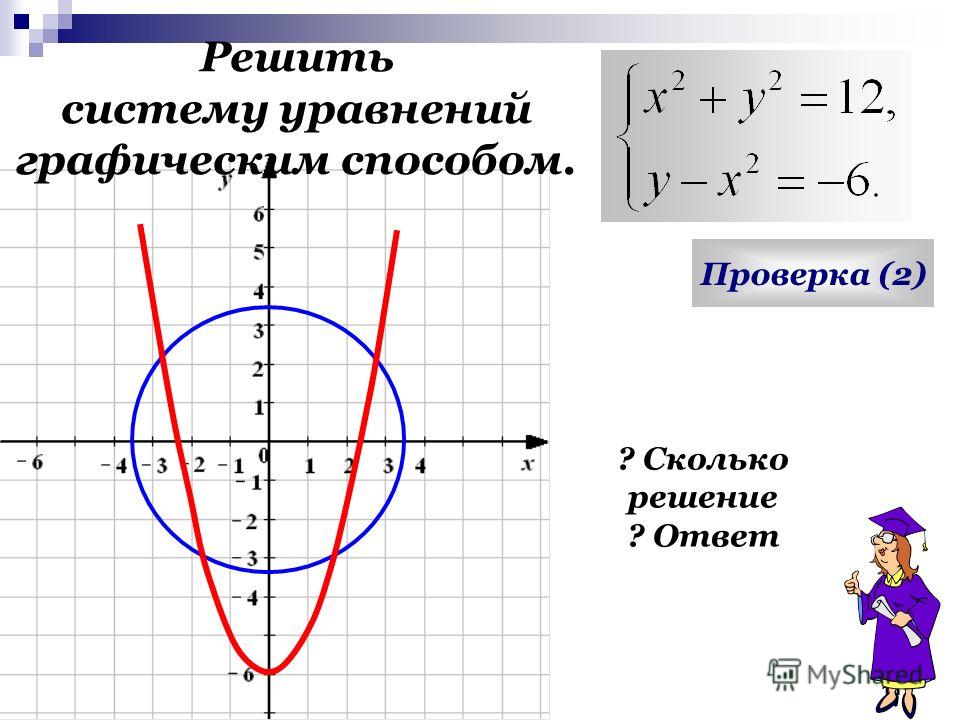

1. 0,5𝑥0,75 и −3𝑦 — 1
2. 0,5𝑥0,75 и -1𝑦 — 0,75
3. −1𝑥 — 0,75 и 0,5𝑦0,75
4. −0,75𝑥 -0,5 и 0,75𝑦19
5. −0,75𝑥 -0,5 и 0,75 40138
6. −0,75𝑥 -0,5 и 0,75 40138
7. −0,75𝑥 -0,5 и 0,75𝑦1,138
8. –0,75𝑥 -0,5 и 0,75 40138
9. –0,75 –0,5 и 0,75
10. –0,75 –0,5 и 0,5 *75
11. –0,75 –0,5, −0,5

Ответ

Напомним, что решение системы уравнений задается координатами точки пересечения графиков всех уравнений.

Однако мы не можем определить координаты этой точки пересечения непосредственно по диаграмме, так как она не лежит непосредственно на линиях сетки. Мы можем найти диапазон значений, в котором лежат координаты этой точки, используя второстепенные линии сетки.

Во-первых, отметим, что линии сетки разбивают 1 на 4 равных сегмента, поэтому каждое приращение равно 0,25. Следовательно, точка пересечения лежит между прямыми 𝑥=0,5 и 𝑥=0,75. Мы можем сделать то же самое с горизонтальными линиями.

Мы видим, что точка пересечения лежит между прямыми 𝑦=−1 и 𝑦=−0,75. Следовательно, если (𝑥,𝑦) является решением этой системы, затем 0,5𝑥0,75 и −1𝑦−0,75, что является вариантом B.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые моменты

• Каждое решение системы уравнений является точкой пересечения на всех их графиках. И наоборот, каждая точка пересечения на всех графиках уравнений будет решением системы уравнений. Следовательно, мы можем решать системы уравнений, строя их графики и находя координаты из точек пересечения.
• Если между всеми графиками нет точек пересечения, то у системы уравнений нет решений.
• Система линейных уравнений может иметь 0, 1 или бесконечное число решения в зависимости от того, параллельны ли прямые, пересекаются ли уникальная точка или совпадают. Система с 0 решениями называется несовместной системой, система с 1 решением называется независимой системой, а система с бесконечным числом решений называется зависимой системой.

  No related posts.