Как решить выражение: Нахождение значения выражения: правила, примеры, решения

Содержание

Нахождение значения выражения: правила, примеры, решения

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.

Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.

Пример 1. Значение числового выражения

Пусть нужно найти значения выражения 14-2·15÷6-3.

Выполним сначала умножение и деление. Получаем:

14-2·15÷6-3=14-30÷6-3=14-5-3.

Теперь проводим вычитание и получаем окончательный результат:

14-5-3=9-3=6.

Пример 2. Значение числового выражения

Вычислим: 0,5-2·-7+23÷234·1112.

Сначала выполняем преобразование дробей, деление и умножение:

0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112

12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.

Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:

12-(-14)+29=12+14+29=14+1318=141318.

Искомое значение найдено.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Пример 3. Значение числового выражения

Найдем значение выражения 0,5·(0,76-0,06).

В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.

0,5·(0,76-0,06)=0,5·0,7=0,35.

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

Пример 4. Значение числового выражения

Вычислим значение 1+2·1+2·1+2·1-14.

Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.

1+2·1+2·1+2·1-14=1+2·1+2·1+2·34

1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.

В нахождении значений выражений со скобками главное — соблюдать последовательность действий.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Пример 5. Значение числового выражения

Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.

Сначала вычисляем подкоренные выражения.

-2·3-1+60÷43=-6-1+153=83=2

2,2+0,1·0,5=2,2+0,05=2,25=1,5.

Теперь можно вычислить значение всего выражения.

-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Пример 6. Значение числового выражения

Сколько будет 3+13-1-1

Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.

3+13-1=3-1.

Таким образом:

3+13-1-1=3-1-1=1.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Пример 7. Значение числового выражения

Найдем значение выражения 23·4-10+161-123,5-2·14.

Начинаем вычислять по порядку.

23·4-10=212-10=22=4

16·1-123,5-2·14=16*0,53=16·18=2.

Осталось только провести операцию сложение и узнать значение выражения:

23·4-10+161-123,5-2·14=4+2=6.

Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.

Пример 8. Значение числового выражения

Вычислим значение следующего выражения: 2-25·45-1+3136.

Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.

2-25·45-1+3136=2-25·225-1+313·6

2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32

22·5-2-25+32=2-2+3=14+3=314

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Пример 9. Значение числового выражения

Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.

Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.

3,22=3,2÷2=1,6

7-2·36=7-66=16

1+2+39-6÷2=1+2+39-3=66=1.

Перепишем наше выражение и вычислим его значение:

1,6-3·16÷1=1,6-0,5÷1=1,1

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Пример 10. Значение числового выражения

Вычислим выражение 25-1-25-74-3.

Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.

25-1=25+15-15+1=25+15-1=25+24

Исходное выражение принимает вид:

25-1-25-74-3=25+24-25-74-3.

Вычислим значение этого выражения:

25+24-25-74-3=25+2-25+74-3=94-3=-34.

Выражения с логарифмами

Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.

Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:

log5-6÷352+2+7=log327+7=3+7=10.

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Пример 11. Значение числового выражения

Найдем значение выражения log2log2256+log62+log63+log5729log0,227.

log2log2256=log28=3.

По свойству логарифмов:

log62+log63=log6(2·3)=log66=1.

Вновь применяя свойства логарифмов, для последней дроби в выражении получим:

log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.

Теперь можно переходить к вычислению значения исходного выражения.

log2log2256+log62+log63+log5729log0,227=3+1+-2=2.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Пример 12. Значение числового выражения

Найдите значение выражения: tg24π3-sin-5π2+cosπ.

Сначала вычисляем значения тригонометрических функций, входящих в выражение.

tg4π3=3

sin-5π2=-1

cosπ=-1.

Подставляем значения в выражение и вычисляем его значение:

tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.

Значение выражения найдено.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Пример 13. Значение числового выражения

Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.

Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.

cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Как найти значение выражения

Корни, степени, логарифмы и т. д. заменяются их значениями.
Выполняются действия в скобках.
Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.

Разберем пример.

Пример 14. Значение числового выражения

Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.

Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?

Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.

Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.

π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π

Теперь можно узнать значение синуса:

sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.

Вычисляем значение подкоренного выражения:

2·sinπ6+2·2π5+3π5+3=2·12+3=4

Отсюда:

2·sinπ6+2·2π5+3π5+3=4=2.

Со знаменателем дроби все проще:

lne2=2.

Теперь мы можем записать значение всей дроби:

2·sinπ6+2·2π5+3π5+3 lne2=22=1.

С учетом этого, запишем все выражение:

-1+1+39=-1+1+33=-1+1+27=27.

Окончательный результат:

-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.

Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.

Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.

Нахождение значений выражений с переменными

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Пример 15. Значение выражения с переменными

Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.

Подставляем значения переменных в выражение и вычисляем:

0,5x-y=0,5·2,4-5=1,2-5=-3,8.

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.

Еще один пример. Значение выражения xx равно единице для всех положительных иксов.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Числовые выражения – как решить задачу (алгебра 7 класс) по вычислению значений числового выражения

4. 7

Средняя оценка: 4.7

Всего получено оценок: 800.

Обновлено 11 Января, 2021

4.7

Средняя оценка: 4.7

Всего получено оценок: 800.

Обновлено 11 Января, 2021

Одним из понятий алгебры 7 класса являются числовые выражения. Они используются для решения задач. Что собой представляют числовые выражения и как их использовать?

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Определение понятия

Какое же выражение является числовым в алгебре? Так обозначают запись, составленную из чисел, скобок и знаков сложения, вычитания, умножения и деления.

Понятие числового выражения допустимо только в том случае, если запись несет смысловую нагрузку. К примеру, запись 4-) не является числовым выражением, так как она бессмысленна.

Примеры числовых выражений:

25 х 13;
32 – 4 + 8;
12 х (25 – 5).

Характеристики понятия

Числовое выражение имеет несколько свойств, которые используются в решении примеров и задач. Рассмотрим эти свойства подробнее. Для этого возьмем такой пример – 45 + 21 – (6 х 2).

Значение

Так как числовое выражение содержит знаки различных арифметических действий, их можно выполнить и получить в результате какое-то число. Оно называется значением числового выражения. Как производится вычисление значений числового выражения? Оно соответствует правилам выполнения арифметических действий:

в выражениях без скобок выполняют действия, начиная с высших ступеней – умножение и деление, затем сложение и вычитание;
если имеется несколько одинаковых действий, их выполняют слева направо;
если есть скобки, сначала выполняют действия в них;
при вычислении дробей сначала выполняют действия в числителе и знаменателе, а затем числитель делят на знаменатель.

Применим эти правила к нашему примеру.

Итак, число 54 будет являться значением выражения 45 + 21 – (6 х 2).

Для того, чтобы правильно прочитать числовое выражение нужно определить, какое действие будет являться последним в подсчетах. В выражении 45 + 21 – (6 х 2) последним действием было вычитание. Соответственно, называть это выражение нужно “разность”. Если бы вместо знака “-” стоял знак “+”, выражение называли бы суммой.

Если у выражения невозможно произвести подсчет значения, его называют не имеющим смысла. Например, смысла не имеет такое выражение: 12 : (4 – 4). В скобках разность равна нулю. А по правилам математики на ноль делить нельзя. Значит, найти значение выражения невозможно.

Равенство

Так называют запись, в которой два числовых выражения разделены знаком “=”. Например, 45 + 21 – (6 х 2) = 66 – 12. Обе части записи равны числу 54, а значит, они равны друг другу. Такое равенство называют верным.

Если же написать 45 + 21 – (6 х 2) = 35 + 12, это равенство будет неверным. В левой части равенства значение выражения равно 54, а в правой – 57. эти числа не равны друг другу, значит, и равенство неверное.

Пример задачи

Для того, чтобы лучше понять тему, рассмотрим пример решения задачи. Как решить задачу числовым выражением?

Дано: две машины выезжают из одного пункта в другой. Они поедут по разным дорогам. Одной машине предстоит проехать 35 км, а другой – 42 км. Первая машина едет со скоростью 70 км/ч, а вторая – 84 км/ч Окажутся ли они в конечном пункте в одно и то же время?

Решение: нужно составить два числовых выражения, чтобы найти время в пути у каждой машины. Если они окажутся одинаковыми, значит, машины прибудут в конечный пункт одновременно. Для того, чтобы найти время, нужно расстояние разделить на скорость. 35 км : 70 км/ч = 0,5 ч. 42 км : 84 км/ч = 0,5 ч.

Итак, обе машины приехали в конечный пункт одновременно, через полчаса.

Что мы узнали?

Из темы по алгебре, изучаемой в 7 классе, мы узнали, что числовое выражение – это запись из чисел и знаков арифметических действий. С помощью числовых выражений можно решать задачи. Если последним действием в числовом выражении было вычитание (сложение), то его называют разностью (суммой). Если последним действием было бы умножение (деление), то выражение называлось бы произведением (частным).

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Ольга Кузина
10/10
Мария Гаврилова
10/10
Александра Веригина
9/10
Макс Чупин
6/10
Эдик Брага
10/10
Наталья Слинькова
10/10
Любовь Дружинина
8/10
Света Колодий
10/10
Джек Кортес
8/10
Александра Елисеева
9/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 800.

А какая ваша оценка?

Выражения в математике | О математике понятно

Числовые и алгебраические выражения и их преобразования.

Как работать с математическими выражениями?

Допустим, перед вами пример. Хоть простой, хоть суперсложный (уравнение, неравенство, интеграл, производная и т.д….). Допустими, вы не Витя Перестукин и с математикой на «ты». Сможете, глядя на пример, сразу дать ответ?

В 99% случаев — нет. Если вы не гений математической мысли, конечно.)

Почему? А потому, что вам, так или иначе, придётся решать этот пример. Что значит «решать»? Это значит, последовательно, шаг за шагом, этот пример упрощать, добираясь до окончательного ответа. Или, по-другому, преобразовывать. Естественно, все эти фокусы (т.е. преобразования) надо проделывать по определённым правилам математики. Вот насколько успешно вы проведёте эти самые преобразования, настолько вы и сильны в математике.)

Так вот, имейте в виду: если вы не умеете делать правильные преобразования выражений, в математике вы не сможете сделать НИЧЕГО. Вообще ничего. Грустная перспектива? Вот и я так думаю.

Чтобы нас с вами не постигла столь печальная участь, имеет смысл разобраться в этой теме. Тем более тема достаточно простая. Разберёмся?:)

Что такое выражение в математике?

Выражение в математике (или — математическое выражение) — это, фактически, язык, на котором говорит вся математика. Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?)

2+3 — это математическое выражение. a² — b² — это математическое выражение. И здоровенная дробь, и интеграл, и даже одно число или одна буковка — это всё математические выражения.

Например, уравнение:

3x+1 = 2x-5

состоит из двух математических выражений, соединённых знаком равенства «=» (равно).

Неравенство:

x²-4x+4≤0 – это тоже два математических выражения, соединённых знаком «≤» (меньше либо равно).

Короче говоря, термин «математическое выражение» применяется, чаще всего, чтобы не мычать, как корова и не кукарекать, как петух…

Спросят у вас, к примеру, что такое разность квадратов двух выражений. Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»

А человек в теме уверенно и с блеском в глазах ответит: «Разность квадратов двух выражений — это математическое выражение, представляющее собой произведение разности этих выражений и их суммы»!

Или: что такое квадратный корень? Квадратный корень — это математическое выражение, состоящее из подкоренного выражения и знака корня (радикала).

Согласитесь, второй вариант ответа выглядит куда более солидно и научно. )

Вот в таких вопросах фраза «математическое выражение» очень и очень удобна. Чтобы не объясняться на пальцах, как иностранные туристы в экзотической стране.

Гораздо сложнее — это конкретные математические выражения и работа с ними. Это совершенно другое дело.

Дело всё в том, что у каждого вида математических выражений имеется свой набор правил и приёмов, которому необходимо следовать при работе с ними.

У чисел — свой набор, у буквенных выражений — свой, у дробей — свой, у всяких там синусов, логарифмов, производных, интегралов — свои наборы действий. В каких-то наборах эти правила похожи или даже совпадают, а где-то — кардинально отличаются. Но пугаться этих жутких слов не надо. Эти страшные понятия мы с вами обязательно освоим в соответствующих разделах. А здесь мы с вами поработаем только с двумя видами математических выражений. А именно — с числовыми выражениями и с алгебраическими выражениями.

Что такое числовое выражение?

Что такое числовое выражение? Всё проще пареной репы.) Числовое выражение — это какое-то выражение с числами. Да-да, всего-навсего. Математическое выражение, составленное из цифр, знаков действий, скобок, знаков равенства/неравенства — это всё числовые выражения.

Например:

10-6 — числовое выражение,

(3-2,1)·0,5 — числовое выражение.

Или даже вот эти монстры:

это всё числовые выражения.

Да, в последнем примере появились специальные математические символы — радикал, значок логарифма и значок синуса. Но в этом выражении тоже нет букв. Только числа! Это самое главное.

Короче говоря, любые числа, дроби, примеры на вычисление без иксов, игреков и прочих буковок — это всё числовые выражения. Намёк понятен?)

В чём главный признак числового выражения? В том, что в нём нет букв. Вообще никаких. Математические значки (если надо) — пожалуйста. А вот букв — нету. Это ключевой признак.)

Что же можно делать с числовыми выражениями? Числовые выражения, как правило, можно (и нужно) считать. Для этого, бывает, приходится менять знаки, раскрывать скобки (или наоборот, заключать в скобки), сокращать, выносить общий множитель, раскладывать на множители т.д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)

А здесь мы с вами разберёмся с одним забавным случаем, когда с числовым выражением делать ничего не надо. Совсем! Эта приятная операция (ничего не делать)) производится, когда числовое выражение не имеет смысла.

Понятное дело, что если мы с вами напишем какую-то белиберду типа 4+)-(=), то делать ничего и не будем. Ибо непонятно, что с этим делать. Ну, разве посчитать количество скобочек. )

Однако, попадаются в математике и внешне вполне себе благопристойные выражения.

Например, такое:

Однако это числовое выражение тоже не имеет смысла. Почему? А потому, что если выписать отдельно знаменатель дроби да посчитать, получается ноль. На который делить нельзя. Нет такой операции в математике!

Или вот такое:

И это выражение тоже не имеет смысла! Догадались? А вы посчитайте, что под корнем получится.) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.

Конечно, чтобы сделать такое умозаключение, пришлось потрудиться и посчитать, что в знаменателе да под корнем получится. А в примерах может быть такого понаворочено, что… Тут уж ничего не поделаешь.)

Короче говоря, числовое выражение не имеет смысла тогда, когда в результате преобразований этого самого выражение получается запретное действие. Запретных действий в математике не так уж много: это деление на ноль, извлечение корня чётной степени из отрицательного числа, ограничения в логарифмах, в тригонометрии и в арках. Это обсуждается в соответствующих темах.

Итак, что такое числовое выражение — вникли (надеюсь).

Когда числовое выражение не имеет смысла — осознали.

Пора двигаться на следующий уровень.)

Что такое алгебраическое выражение?

Если в игру дополнительно вступают буквы, то выражение становится… Да! Оно становится алгебраическим выражением!

Например:

a+6, x+y, 2a/b, c² + 9, x²+2x+1

В общем, вы поняли…

Понятие алгебраическое выражение — более широкое, чем числовое. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)

Такие выражения ещё называют выражениями с переменными. Или просто буквенными выражениями. Почему буквенное — ясно, надеюсь. Ну, раз буквы есть.) Фраза «выражение с переменными» тоже не требует особого умственного напряжения. Если, конечно, понимать, что под буквами могут скрываться различные числа. Всякие могут скрываться: и 5, и -30 — всё что угодно. То есть, букву в алгебраическом выражении можно заменять на разные числа. Какие хотим.

В выражении х+6, например, буква икс — переменная величина. Или коротко — переменная. В отличие от шестёрки, которая — величина постоянная. Или коротко — постоянная.

Что означает термин «алгебраическое выражение»? Он означает, что, в отличие от арифметики, (которая, как известно, работает только с числами), мы должны использовать законы и правила алгебры. Непонятно? Поясняю на несложном примере:

2·3 = 3·2

Что можно сделать? Посчитать и всего делов-то.) Слева шестёрка и справа тоже. А для каких-нибудь других чисел такое выполняется? Тоже можно посчитать и сравнить. Но чисел в математике — бесконечное количество. И что же? Каждый раз считать и сравнивать?!

А вот если мы шагнём из арифметики в алгебру и распишем данное равенство через алгебраические выражения:

ab = ba,

то мы сразу решим все вопросы! Для всех чисел махом! Мощная штука — алгебра.)

А когда алгебраическое выражение не имеет смысла? Что такое ОДЗ?

С числовыми выражениями всё ясно. Там на ноль делить нельзя да корни извлекать из отрицательных чисел, ну и некоторые другие логарифмические/тригонометрические фишки. А тут как узнаешь, на что делим или из чего извлекаем…

Очень просто! Точно так же!

Возьмём, к примеру, алгебраическое выражение:

Имеет ли оно смысл? Бэ-то любое число… Любое-то любое… Но есть среди этого бесконечного набора чисел такое значение b, при котором это выражение точно не имеет смысла. Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.

А остальные b подставлять можно? Конечно! Хоть 5 возьмите, хоть -100 — наше выражение иметь смысл будет. В таких случаях говорят, что выражение имеет смысл при любом b , кроме 1.

И вот этот самый весь остальной набор чисел, которые можно подставлять в данное выражение, и который не приводит к запретному действию, в математике называется областью допустимых значений (ОДЗ) выражения. В нашем примере областью допустимых значений (ОДЗ) служат все числа, кроме единички.

Другой пример:

Видим квадратный корень. Сразу соображаем (из теории, т.е. основ), что корень квадратный извлекается только из положительных чисел и нуля. А вот из отрицательных — ни в какую!

Вот и обезопасим себя вот такой записью:

x-2≥0

x≥2

Таким образом, данный хитрое выражение имеет смысл лишь при иксах, больших (или равных) двойке. Число, скажем, 3, вполне себе прокатит, а вот ноль — никак нет: он меньше двойки. ОДЗ — штука жёсткая!

Уловили принцип? Внимательно смотрим на выражение с переменными, ищем опасные места и смотрим, при каких переменных получается запретная операция. И исключаем эти значения из ОДЗ.

А потом внимательно читаем задание. Чего хотят-то? Внимательное чтение никто не отменял, да… Если в задании спрашивают, при каких значениях переменной выражение имеет смысл, то ответом будут служить все значения, кроме запретных.

Или наоборот: при каких значениях переменных выражение не имеет смысла? Тогда найденные запретные значения и будут служить ответом к заданию. Почувствуйте разницу, что называется.)

А теперь вопрос к размышлению. А зачем нам смысл выражения? Есть он, нет его… Какая разница? Дело всё в том, что это понятие становится крайне важным в старших классах! Да и в ВУЗе тоже. Без этого важного понятия вы не сможете проделывать такие простые операции, как нахождение области определения функции, ОДЗ уравнений, неравенств. Что неизбежно будет приводить к полному провалу и непониманию всех этих серьёзных тем. Увы.)

Итак, самое главное из сегодняшнего урока:

1. Числовое выражение — это выражение с числами (т.е. без букв).

2. Если, помимо чисел, в выражении есть буквы, то оно называется алгебраическим выражением.

3. Как числовое, так и алгебраическое выражение, может иметь смысл, а может и не иметь. При встрече с алгебраическим выражением первым делом ищем его ОДЗ.

4. Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!

Ну а в различных видах преобразований выражений мы с вами подробненько разберёмся и плотно поработаем в следующих уроках этого раздела.)

Типы задач, поддерживаемые помощником по преобразованию в математические выражения

Education

Средства обучения

МАТЕМ

Типы задач, поддерживаемые помощником по преобразованию в математические выражения

OneNote для Интернета OneNote для Windows 10 Помощник по преобразованию в математические выражения Еще…Меньше

При использовании помощника по математическим формулам в OneNoteвы заметите, что в зависимости от выбранного уравнения изменяется в dropdown Select an action (Выбрать действие) под формулой. Вот некоторые из типов проблем, которые поддерживаются в зависимости от формулы, которая вы пытаетесь решить.

Примечание: Эта функция доступна только при наличии подписки на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.

Массивы	Для списка реальных чисел поддерживаются все ниже. Оценить Сортировка org/ListItem»> Среднее Медиана Мода Сумма Продукт Наибольший распространенный фактор org/ListItem»> Наименьшее общее кратное Дисперсия Стандартное отклонение Минимумы Максимум Для полиномиалов поддерживаются действия Наибольший общий фактор и Наименьший распространенный кратное. Чтобы просмотреть графики всех функций, можно также выбрать вариант График в двухдд.
Выражения	Для любого выражения доступны такие действия: org/ListItem»> Оценить Проверяем подлинность Развернуть (если применимо) Фактор (если применимо) Двухявная диаграмма (доступна только при наличии переменной) Дифференцировать (доступно только при наличии переменной) org/ListItem»> Интеграция (доступна только при наличии переменной)
Уравнения и уравнения	Для уравнений и уравнений доступны следующие действия: Решение для {переменной} Двухуголовые диаграммы. Каждая сторона равенства или разноявной разлияется в виде отдельной функции. Двухуголовые диаграммы — график уравнений или разнонавязных решений org/ListItem»> Graph Graph — пометка области решения на графике
Системы	Важно иметь одинаковое количество формул и переменных, чтобы обеспечить доступ к правильным функциям. Системы можно писать двумя способами: Одна под другой, с большой скобки или без нее перед ними В одной строке, разделенной запятой
Производные и интегралы	Производные могут быть записаны перед функцией с помощью d/dx или с помощью первой метки. Действия, доступные для производных продуктов и интегралов:
Матриц	Матрицы можно в квадратных или круглых скобках. Для матриц поддерживаются следующие действия: Оценить Вычислять определители Инвертировать матрицу Вычисления трассировки org/ListItem»> Транспонная матрица Размер матрицы Уменьшение матрицы Матричные уравнения в настоящее время не поддерживаются.
График в координатах	Для графизации функции в координатах координаты r должны быть выражены как функцияta.
Сложный режим	Примечание. Выберите Параметры, чтобы переключаться между реальными и комплексными числами. Для сложных выражений и чисел, содержащих мнимую единицу i, доступны следующие действия:

Создание математических формул с помощью рукописного ввода или текста в OneNote с использованием помощника по преобразованию в математические выражения

Решение уравнений с помощью помощника по математике в OneNote

Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения

Как упростить выражение с дробями. Как упростить математическое выражение

Главная > Утепление > Как упростить выражение с дробями. Как упростить математическое выражение

Алгебраическое выражение в записи которого наряду с действиями сложения, вычитания и умножения используют также деление на буквенные выражения, называется дробным алгебраическим выражением. Таковы, например, выражения

Алгебраической дробью мы называем алгебраическое выражение, имеющее вид частного от деления двух целых алгебраических выражений (например, одночленов или многочленов). Таковы, например, выражения

Третье из выражений ).

Тождественные преобразования дробных алгебраических выражений имеют по большей части своей целью представить их в виде алгебраической дроби. Для отыскания общего знаменателя используется разложение на множители знаменателей дробей — слагаемых с целью отыскания их наименьшего общего кратного. При сокращении алгебраических дробей может нарушаться строгая тождественность выражений: необходимо исключать значения величин, при которых множитель, на который производится сокращение, обращается в нуль.

Приведем примеры тождественных преобразований дробных алгебраических выражений.

Пример 1. Упростить выражение

Все слагаемые можно привести к общему знаменателю (удобно при этом изменить знак в знаменателе последнего слагаемого и знак перед ним):

Наше выражение равно единице при всех значениях кроме этих значениях оно не определено и сокращение дроби незаконно).

Пример 2. Представить в виде алгебраической дроби выражение

Решение. За общий знаменатель можно принять выражение . Находим последовательно:

Упражнения

1. Найти значения алгебраических выражений при указанных значениях параметров:

2. Разложить на множители.

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Yandex.RTB R-A-339285-1

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Определение 1

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , (2 + 1) 5 , (− 0 , 1) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , (a 2) 3 . А также степени с нулевым показателем: 5 0 , (a + 1) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: (0 , 5) 2 + (0 , 5) — 2 2 .

Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .

В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Пример 1

Вычислите значение степенного выражения 2 3 · (4 2 − 12) .

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · (4 2 − 12) = 2 3 · (16 − 12) = 2 3 · 4 .

Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.

Ответ: 2 3 · (4 2 − 12) = 32 .

Пример 2

Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Пример 3

Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.

Решение

Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:

9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1

Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2 + 0 , 3 · 7) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a · (a + 1) − a 2) 2 · (x + 1) и получить степенное выражение более простого вида a 2 · (x + 1) .

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

Определение 2

a r · a s = a r + s ;
a r: a s = a r − s ;
(a · b) r = a r · b r ;
(a: b) r = a r: b r ;
(a r) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Пример 4

Представьте выражение a 2 , 5 · (a 2) − 3: a − 5 , 5 в виде степени с основанием a .

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a 2) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a 2 , 5 · a − 6: a − 5 , 5 = a 2 , 5 − 6: a − 5 , 5 = a − 3 , 5: a − 5 , 5 = a − 3 , 5 − (− 5 , 5) = a 2 .

Ответ: a 2 , 5 · (a 2) − 3: a − 5 , 5 = a 2 .

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Пример 5

Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .

Решение

Если мы применим равенство (a · b) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .

Есть еще один способ провести преобразования:

3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · (3 · 7) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21

Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21

Пример 6

Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .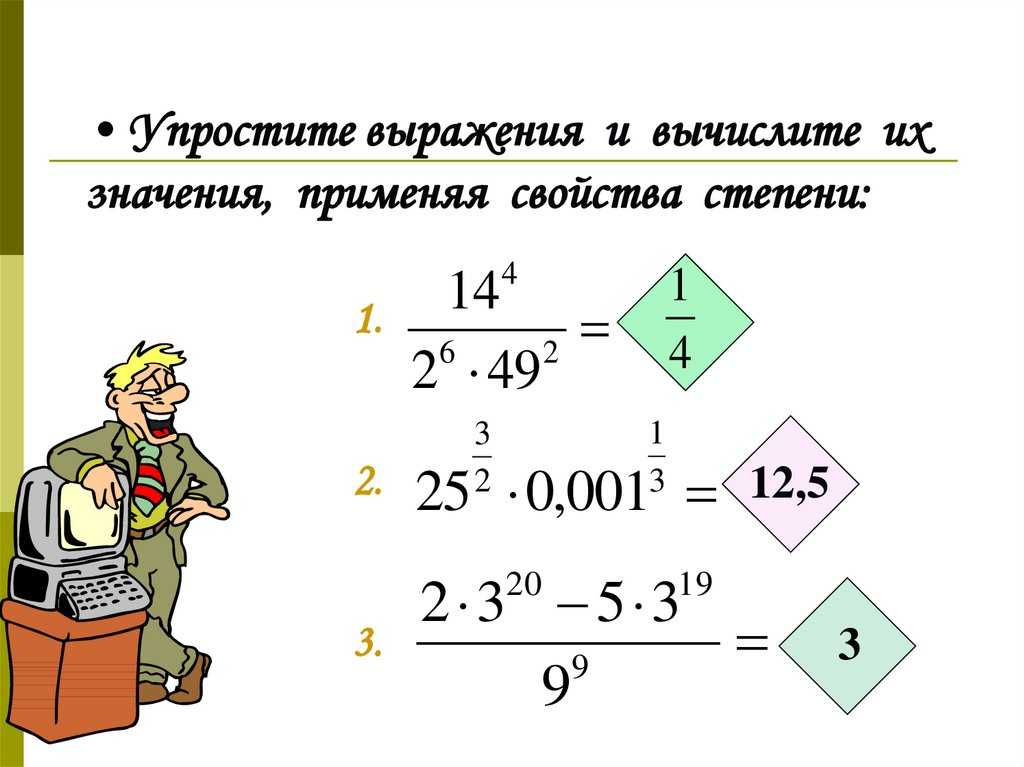

Решение

Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени (a r) s = a r · s справа налево и получим (a 0 , 5) 3: a 1 , 5 − a 0 , 5 − 6 = (a 0 , 5) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .

Ответ: t 3 − t − 6 .

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Пример 7

Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2

Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример 8

Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a 0 , 3 :

a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a

б) Обратим внимание на знаменатель:

x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2

Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.

Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2

Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .

Пример 9

Сократите дробь: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .

Получаем:

30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1)

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4

Ответ: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Пример 10

Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x 1 2 — 1 · x 1 2 + 1

Вычтем числители:

x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2

Теперь умножаем дроби:

4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2

Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .

Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1

Пример 11

Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на (x 2 , 7 + 1) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .

Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .

Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .

Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞) .

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ: x 1 9 · x · x 3 6 = x 1 3 .

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .

Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:

5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0

Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .

Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 (1 — log 3 5) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
$5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 $
$xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 $

Сумму одночленов называют многочленом. 3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения $(a + b)^2, \; (a — b)^2 $ и $a^2 — b^2 $, т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Зачастую в задачах требуется привести упрощенный ответ. Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.

Шаги

Правильный порядок выполнения математических операций

Запомните правильный порядок выполнения математических операций. При упрощении математического выражения необходимо соблюдать определенный порядок действий, так как некоторые математические операции имеют приоритет над другими и должны быть сделаны в первую очередь (на самом деле несоблюдение правильного порядка выполнения операций приведет вас к неправильному результату). Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.
- Обратите внимание, что знание правильного порядка выполнения операций позволит вам упростить большинство простейших выражений, но для упрощения многочлена (выражения с переменной) необходимо знать специальные приемы (смотрите следующий раздел).
Начните с решения выражения в скобках. В математике скобки указывают на то, что заключенное в них выражение должно быть выполнено в первую очередь. Поэтому при упрощении любого математического выражения начинайте с решения выражения, заключенного в скобки (при этом неважно, какие операции нужно выполнить внутри скобок). Но помните, что работая с выражением, заключенным в скобки, следует соблюдать порядок проведения операций, то есть члены в скобках сначала перемножаются, делятся, складываются, вычитаются и так далее.
- Например, упростим выражение 2x + 4(5 + 2) + 3 2 — (3 + 4/2) . Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
  - Выражение во второй паре скобок упрощается до 5, потому что сначала нужно разделить 4/2 (согласно правильному порядку выполнения операций). Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
- Если в скобках есть еще одна пара скобок, начните упрощение с решения выражения во внутренних скобках, а затем переходите к решению выражения во внешних скобках.
Возведите в степень. Решив выражения в скобках, перейдите к возведению в степень (помните, что у степени есть показатель степени и основание степени). Возведите соответствующее выражение (или число) в степень и подставьте результат в данное вам выражение.
- В нашем примере единственным выражением (числом) в степени является 3 2: 3 2 = 9. В данном вам выражении вместо 3 2 подставьте 9 и вы получите: 2x + 4(7) + 9 — 5.
Умножьте. Помните, что операция умножения может обозначаться следующими символами: «х», «∙» или «*». Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.
- В нашем примере присутствуют две операции умножения: 2x (два умножить на переменную «х») и 4(7) (четыре умножить на семь). Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
Разделите. Помните, что операция деления может обозначаться следующими символами: «/», «÷» или «–» (последний символ вы можете встретить в дробях). Например 3/4 – это три, деленное на четыре.
- В нашем примере операции деления больше нет, так как вы уже разделили 4 на 2 (4/2) при решении выражения в скобках. Поэтому вы можете перейти к следующему шагу. Помните, что в большинстве выражений нет сразу всех математических операций (только некоторые из них).
Сложите. При сложении членов выражения вы можете начать с самого крайнего (слева) члена, или можете сначала сложить те члены выражения, которые легко складываются. Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
- В нашем примере 2x + 28 + 9 + 5 присутствуют две операции сложения. Начнем с самого крайнего (слева) члена: 2x + 28; вы не можете сложить 2х и 28, потому что не знаете значения переменной «х». Поэтому сложите 28 + 9 = 37. Теперь выражение можно переписать так: 2х + 37 — 5.
Вычтите. Это последняя операция в правильном порядке выполнения математических операций. На этом этапе вы также можете прибавлять отрицательные числа или же делать это на этапе сложения членов – это никак не отразится на конечном результате.
- В нашем примере 2х + 37 — 5 присутствует только одна операция вычитания: 37 — 5 = 32.
На этом этапе, проделав все математические операции, вы должны получить упрощенное выражение. Но если данное вам выражение содержит одну или несколько переменных, то помните, что член с переменной останется таким, как есть. Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
- В нашем примере окончательный ответ: 2х + 32. Вы не сможете сложить два члена, пока не узнаете значение переменной «х». Узнав значение переменной, вы с легкостью упростите этот двучлен.
Упрощение сложных выражений
1. Сложение подобных членов. Помните, что вычитать и складывать можно исключительно подобные члены, то есть члены с одинаковой переменной и одинаковым показателем степени. Например, можно сложить 7x и 5x, но нельзя складывать 7x и 5x 2 (так как здесь показатели степени разные).
  - Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy 2 и -3xy 2 , но нельзя складывать 2xy 2 и -3x 2 y или 2xy 2 и -3y 2 .
  - Рассмотрим пример: x 2 + 3x + 6 — 8x. Здесь подобными членами являются 3x и 8x, поэтому их можно сложить. Упрощенное выражение выглядит так: x 2 — 5x + 6.
2. Упростите числовую дробь. В такой дроби и в числителе, и в знаменателе находятся числа (без переменной). Числовая дробь упрощается несколькими способами. Во-первых, просто разделите знаменатель на числитель. Во-вторых, разложите числитель и знаменатель на множители и сократите одинаковые множители (так как при делении числа на само себя вы получите 1). Другими словами, если и у числителя, и у знаменателя есть один и тот же множитель, его можно отбросить и получить упрощенную дробь.
  - Например, рассмотрим дробь 36/60. При помощи калькулятора разделите 36 на 60 и получите 0,6. Но вы можете упростить эту дробь и по-другому, разложив числитель и знаменатель на множители: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так как 6/6 = 1, то упрощенная дробь: 1 х 6/10 = 6/10. Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
3. Если дробь содержит переменную, можно сократить одинаковые множители с переменной. Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).
  - Рассмотрим пример: (3x 2 + 3x)/(-3x 2 + 15x). Это выражение можно переписать (разложить на множители) в виде: (x + 1)(3x)/(3x)(5 — x). Так как член 3x находится и в числителе, и в знаменателе, его можно сократить, и вы получите упрощенное выражение: (х + 1)/(5 — х). Рассмотрим другой пример: (2x 2 + 4x + 6)/2 = (2(x 2 + 2x + 3))/2 = x 2 + 2x + 3.
  - Обратите внимание, что вы не можете сокращать любые члены – сокращаются только одинаковые множители, которые присутствуют как в числителе, так и в знаменателе. Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).
4. Раскройте скобки. Для этого умножьте член, стоящий за скобкой, на каждый член в скобках. Иногда это помогает упростить сложное выражение. Это относится как к членам, которые являются простыми числами, так и к членам, которые содержат переменную.
  - Например, 3(x 2 + 8) = 3x 2 + 24, а 3x(x 2 + 8) = 3x 3 + 24x.
  - Обратите внимание, что в дробных выражениях скобки раскрывать не нужно, если и в числителе, и в знаменателе присутствует одинаковый множитель. Например, в выражении (3(x 2 + 8))/3x скобки раскрывать не нужно, так как здесь можно сократить множитель 3 и получить упрощенное выражение (x 2 + 8)/x. С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x 3 + 24x)/3x.
5. Разложите на множители многочлены. При помощи этого метода можно упростить некоторые выражения и многочлены. Разложение на множители – это операция, противоположная раскрытию скобок, то есть выражение записывается в виде произведения двух выражений, каждое из которых заключено в скобки. В некоторых случаях разложение на множители позволяет сократить одинаковое выражение. В особых случаях (как правило, с квадратными уравнениями) разложение на множители позволит вам решить уравнение.
  - Рассмотрим выражение x 2 — 5x + 6. Оно раскладывается на множители: (x — 3)(x — 2). Таким образом, если, например, дано выражение (x 2 — 5x + 6)/(2(x — 2)), то вы можете переписать его в виде (x — 3)(x — 2)/(2(x — 2)), сократить выражение (х — 2) и получить упрощенное выражение (х — 3)/2.
  - Разложение многочленов на множители применяется для решения (нахождения корней) уравнений (уравнение – это многочлен, приравненный к 0). Например, рассмотрим уравнение x 2 — 5x + 6 = 0. Разложив его на множители, вы получите (х — 3)(х — 2) = 0. Так как любое выражение, умноженное на 0, равно 0, то мы можем записать так: х — 3 = 0 и х — 2 = 0. Таким образом, х = 3 и х = 2, то есть вы нашли два корня данного вам уравнения.

Известно, что в математике никак не обойтись без упрощения выражений. Это необходимо для правильного и быстрого решения самых разнообразных задач, а также различного рода уравнений. Обсуждаемое упрощение подразумевает под собой уменьшение количества действий, необходимых для достижения поставленной цели. В результате вычисления заметным образом облегчаются, а время существенно экономится. Но, как упростить выражение? Для этого используются установленные математические соотношения, часто именуемые формулами, либо же законами, которые позволяют делать выражения гораздо короче, упрощая тем самым расчеты.

Не секрет, что состоянием на сегодняшний день не представляет труда упростить выражение онлайн. Приведем ссылки на некоторые наиболее популярные из них:

Однако обойтись так можно далеко не с каждым выражением. Поэтому рассмотрим подробнее более традиционные методы.

Вынесение общего делителя

В том случае, когда в одном выражении присутствуют одночлены, обладающие одинаковыми множителями, можно находить при них сумму коэффициентов, а потом умножать на общий для них множитель. Эта операция также носит название «вынесения общего делителя». Последовательно используя данный метод, порою можно достаточно существенно упростить выражение. Алгебра ведь вообще, в целом, построена на группировке и перегруппировке множителей и делителей.

Простейшие формулы сокращенного умножения

Одним из следствий ранее описанного метода являются формулы сокращенного умножения. Как упрощать выражения с их помощью гораздо понятнее тем, кто даже не вызубрил эти формулы наизусть, а знает, которым образом они выводятся, то есть, откуда берутся, а соответственно их математическую природу. В принципе, предыдущее высказывание сохраняет свою силу во всей современной математике, начиная от первого класса и заканчивая высшими курсами механико-математических факультетов. Разность квадратов, квадрат разности и суммы, сумма и разность кубов – все эти формулы повсеместно используются в элементарной, а также высшей математике в тех случаях, когда для решения поставленных задач необходимо упростить выражение. Примеры таких преобразований можно без труда найти в любом школьном учебнике по алгебре, либо же, что еще проще, на просторах всемирной сети.

Степени корни

Элементарная математика, если посмотреть на нее в целом, вооружена не так уж и многими способами, при помощи которых можно упростить выражение. Степени и действия с ними, как правило, удаются большинству учащихся сравнительно легко. Только вот у многих современных школьников и студентов возникают немалые трудности, когда необходимо упростить выражение с корнями. И это совершенно безосновательно. Потому как математическая природа корней ничем не отличается от природы тех же степеней, с которыми, как правило, трудностей гораздо меньше. Известно, что квадратный корень от числа, переменной или выражения представляет собой ничто иное как то же число, переменную или выражение в степени «одна вторая», кубический корень – то же самое в степени «одна третья» и так далее по соответствию.

Упрощения выражений с дробями

Рассмотрим также часто встречающийся пример того, как упростить выражение с дробями. В тех случаях, когда выражения представляют собой натуральные дроби, следует выделять из знаменателя и числителя общий множитель, а затем сокращать дробь на него. Когда же одночлены обладают одинаковыми множителями, возведенными в степени, необходимо следить при их суммировании за равенством степеней.

Упрощение простейших тригонометрических выражений

Некоторым особняком стоит разговор о том, как упростить тригонометрическое выражение. Широчайший раздел тригонометрии является, пожалуй, первым этапом, на котором изучающим математику предстоит столкнуться с несколько абстрактными понятиями, задачами и методами их решения. Здесь существуют свои соответствующие формулы, первой из которых является основное тригонометрическое тождество. Имея достаточный математический склад ума, можно проследить планомерное выведение из этого тождества всех основных тригонометрических тождеств и формул, среди которых формулы разности и суммы аргументов, двойных, тройных аргументов, формулы приведения и многие другие. Разумеется, что забывать здесь не стоит и самые первые методы, наподобие вынесения общего множителя, которые в полной мере используются наряду с новыми способами и формулами.

Для подведения итогов, предоставим читателю несколько советов общего характера:

Многочлены следует раскладывать на множители, то есть представлять их в форме произведения некоторого количества сомножителей – одночленов и многочленов. Если существует такая возможность, необходимо выносить за скобки общий множитель.
Лучше все-таки выучить на память все без исключения формулы сокращенного умножения. Их не так уж и много, но именно они при этом являются основой при упрощении математических выражений. Не стоит также забывать о способе выделения полных квадратов в трехчленах, являющемся обратным действием к одной из формул сокращенного умножения.
Все существующие в выражении дроби следует сокращать как можно чаще. При этом не забывайте, что сокращаются только множители. В том случае, когда знаменатель и числитель алгебраических дробей умножается на одно и то же самое число, которое отличается от нуля, значения дробей не меняются.
В целом все выражения можно преобразовывать по действиям, либо ж цепочкой. Первый способ более предпочтителен, т.к. результаты промежуточных действий проверяются легче.
Достаточно часто в математических выражениях приходиться извлекать корни. Следует помнить, что корни четных степеней могут извлекаться только лишь из неотрицательного числа или выражения, а корни нечетных степеней совершенно из любых выражений или чисел.

Надеемся, наша статья поможет Вам, в дальнейнем, разбираться в математических формулах и научит применять их на практике.

Урок 20. Преобразование выражений в Mathcad

Павел Демидов 29.09.2014 Уроки Mathcad 0

Преобразование выражений

Выражения в Mathcad часто имеют не тот вид, в котором Вы хотели бы их видеть. Поэтому в программе есть несколько инструментов, позволяющих преобразовывать выражения путем перестановки или замены.

Вырезать и вставить

Рассмотрим простой пример – разложение в ряд натурального логарифма в окрестности точки x=1:

Все слагаемые, кроме первых двух, кратны (x-1). По уравнению видно, что первые слагаемые тоже можно привести к такому виду. Самый простой путь сделать это – вырезать и вставить нужный фрагмент:

У такого способа есть недостаток – очень легко сделать ошибку: можно забыть скопировать знак «минус», или вставить не то выражение… Простой путь проверить, что ошибки нет – это присвоить переменной некоторое значение (лучше всего – неправильную дробь) и проверять значение выражения после каждого шага:

Если получен тот же результат, то можно быть уверенным, что ошибки нет. Однако, теперь Вы задали переменной x значение. Если Вы хотите продолжить аналитические преобразования, нужно предварительно удалить присваивание, т.е. очистить переменную, с помощью функции clear:

Можно одним действием очистить сразу несколько переменных:

Ключевые слова для приведения к нужному виду

Mathcad может сделать кое-что сам для преобразования выражения с помощью ключевых слов:

“simplify”, “expand”, “factor” и “parfrac” – для преобразования самого выражения;
“float” – для преобразования результата вычисления;
“assume” (с модификаторами) – ограничивает диапазон возможных значений переменных.

Символьное вычисление

Начальная точка всех символьных вычислений – это операция аналитического преобразования. Эта операция приводит степени и множители, а также сокращает общие множители:

Эта операция также подставляет известные соотношения для переменных. Например, есть выражение:

Нужно заменить переменные выражениями:

Mathcad выдает сообщение, что переменные не определены, но для символьных операций это не имеет значения:

В результате получаем:

Для подстановки служит также ключевое слово “substitute”, но метод, описанный выше, более гибкий. Mathcad не может заменить выражение выражением, как в символьных математических пакетах, таких как Maple.

Упростить – “simplify”

С помощью ключевого слова “simplify” можно упрощать тригонометрические выражения:

Также можно упрощать многие произведения:

(С помощью оператора аналитического преобразования так сделать нельзя. )

Раскрыть скобки – “expand”

Ключевое слово “expand” раскладывает выражение путем перемножения элементов произведения и возведения их в степень:

Разложить на множители – “factor”

Это ключевое слово раскладывает на множители многочлены и дроби с многочленами:

“factor” – обратное по отношению к “expand” действие. Однако результат этого действия не всегда полезен:

Разложение на дроби – “parfrac”

Это ключевое слово раскладывает выражение в сумму дробей:

Вычисление с плавающей запятой – “float”

Это ключевое слово выводит доступный числовой результат в десятичном формате. Количество отображаемых цифр – 20:

Такое количество может быть слишком большим, но его можно уменьшить с помощью дополнительного местозаполнителя с модификатром:

Предположить – “assume”

Ключевое слово “assume” позволяет определить диапазон переменных. На простом примере показано символьное вычисление квадратного корня:

Вы можете сочетать “assume” с другими ключевыми словами, как мы это уже делали, когда искали действительные корни уравнения:

В этом примере важен порядок ключевых слов.

Другие ключевые слова

В меню Математика –> Символьные операции находится большое число ключевых слов и модификаторов. Одна группа, о которой следует упомянуть, – это прямые и обратные преобразования:

Резюме

В этом уроке мы познакомились со способами преобразования выражений для придания им более ясного, красивого и полезного вида.

Первый способ подразумевает копирование (или помещение в буфер обмена) и вставку. Этот метод требует внимательности, поэтому лучше проверять промежуточные результаты с помощью проверочных значений.
Оператор аналитического преобразования сам по себе может упрощать выражения. Если Вы определите некоторое выражение или константу для переменной до оператора, это определение будет использовано в преобразовании.
Вы можете добавлять ключевые слова и модификаторы для символьных преобразований.
Мы рассмотрели четыре ключевых слова для преобразования выражений:

“simplify” – для упрощения тригонометрических выражений и выражений со степенями,
“expand” – перемножает множители и возводит в степень,
“factor” – раскладывает многочлен на множители,
“parfrac” — раскладывает выражение в сумму дробей.

Используйте “float,3” для вывода численного результата с трем цифрами.
Меняйте диапазон переменной для символьных вычислений с помощью ключевого слова assume и последующим модификатором, который содержит логическое выражение (можно использовать модификаторы “real” и “integer”).

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Урок 19. Символьные вычисления в Mathcad – ключевые слова и модификаторы

10 вещей, которые вам поможет сделать СПДС. Часть 1

Алгебраическое выражение – Объяснение и примеры

Алгебра – интересный и увлекательный раздел математики, в котором числа, формы и буквы используются для выражения задач. Изучаете ли вы алгебру в школе или сдаете определенный тест, вы заметите, что почти все математические задачи представлены словами.

Поэтому необходимость перевода письменных задач в алгебраические выражения возникает тогда, когда нам нужно их решить.

Большинство алгебраических текстовых задач состоят из рассказов или случаев из реальной жизни. Другие представляют собой простые фразы, такие как описание математической задачи. Эта статья научит вас писать алгебраических выражений от простых текстовых задач, а затем перейти к легким сложным текстовым задачам.

Алгебраическое выражение — это математическая фраза, в которой переменные и константы объединены с помощью операционных символов (+, -, × & ÷). В алгебраическом символе отсутствует знак равенства (=). Например, 10x + 63 и 5x – 3 являются примерами алгебраических выражений.

Многие люди взаимозаменяемо используют алгебраические выражения и алгебраические уравнения, не подозревая, что эти термины совершенно разные.

С другой стороны, алгебраика — это математическая фраза, две части которой соединены знаком равенства (=). Например, 3x + 5 = 20 — это алгебраическое уравнение, где 20 представляет правую часть (правую часть), а 3x +5 представляет левую часть (левая часть) уравнения.

Давайте рассмотрим терминологию, используемую в алгебраическом выражении:

Переменная — это буква, значение которой нам неизвестно. Например, x — это наша переменная в выражении: 10x + 63,9.0026
Коэффициент представляет собой числовое значение, используемое вместе с переменной. Например, 10 — это переменная в выражении 10x + 63.
Константа — это терм, который имеет определенное значение. В этом случае 63 является константой в алгебраическом выражении, 10x + 63.

Существует несколько типов алгебраических выражений, но основной тип включает:

Мономиальное алгебраическое выражение только одно слагаемое, например, 2х, 5х ² ,3xy и т. д.

Биномиальное выражение

Алгебраическое выражение, имеющее два непохожих члена, например, 5y + 8, y+5, 6y ³ + 4 и т. д.

Полиномиальное выражение

Это алгебраическое выражение с более чем одним членом и с ненулевыми показателями переменных. Примером полиномиального выражения является ab + bc + ca и т. д.

Другие типы алгебраических выражений:

Числовое выражение:

Числовое выражение состоит только из чисел и операторов. В числовое выражение переменная не добавляется. Примеры числовых выражений: 2+4, 5-1, 400+600 и т. д.

Выражение переменной:

Это выражение содержит переменные наряду с числами, например, 6x + y, 7xy + 6 и т. д.

Как решить алгебраическое выражение ?

Целью решения алгебраического выражения в уравнении является нахождение неизвестной переменной. Когда два выражения приравниваются, они образуют уравнение, и поэтому становится легче решать неизвестные члены.

Чтобы решить уравнение, поместите переменные с одной стороны, а константы с другой. Вы можете изолировать переменные, применяя арифметические операции, такие как сложение, вычитание, умножение, деление, извлечение квадратного корня, кубического корня и т. д.

Алгебраические выражения всегда взаимозаменяемы. Это означает, что вы можете переписать уравнение, поменяв местами левую и правую части.

Пример 1

Рассчитайте значение x в следующем уравнении.

5x + 10 = 50

Решение

Данное уравнение имеет вид 5x + 10 = 50.

Выделить переменные и константы;
Вы можете оставить переменную слева, а константы справа.

5x = 50-10

Вычесть константы;

5x = 40

Разделить обе части на коэффициент переменной;

x = 40/5 = 8

Следовательно, значение x равно 8.

Пример 2

Найдите значение y, когда 5y + 45 = 100.

Решение

изолят переменные из констант;

5y = 100 -45

5y = 55

Разделите обе части на коэффициент;

y = 55/5

y= 11

Пример 3

Определите значение переменной в следующем уравнении:

2x + 40 = 30

Решение

Отделить переменные от констант;

2x = 30 – 40

2x = -10

Обе части разделить на 2;

x = -5

Пример 4

Найти t, когда 6t + 5 = 3.

Раствор

Отдельные континта -3

6t = -2

Разделите обе части на коэффициент

t = -2/6

Упростить дробь,

t = -1/3

Как решать уравнения с скобками — часто используются в скобках

1 9 группировать части выражения. Это поможет вам найти порядок старшинства при работе с уравнениями. Когда дело доходит до оценки выражений, содержащих круглые скобки, вы можете выполнить следующие шаги:

Оцените содержимое скобок изнутри наружу.
Вычислите остальную часть выражения.

Выражения большой четверки со скобками

Аналогично, предположим, что вы хотите вычислить (1 + 15 ÷ 5) + (3 – 6) · 5. Это выражение содержит два набора скобок, так что вычисляйте их слева направо. Обратите внимание, что первый набор круглых скобок содержит выражение со смешанными операторами, поэтому оцените его в два этапа, начиная с деления:

= (1 + 3) + (3 – 6) · 5

= 4 + (3 – 6) · 5

Теперь оцените содержимое второго набора скобок:

= 4 + –3 · 5

Теперь у вас есть выражение со смешанными операторами, поэтому сначала оцените умножение (–3 · 5):

= 4 + –15

Наконец, оцените дополнение:

= –11

Итак, (1 + 15 ÷ 5) + (3 – 6) · 5 = –11.

Выражения с показателями и скобками

В качестве другого примера попробуйте следующее:

1 + (3 – 6 ² ÷ 9) · 2 ²

Начните с работы только с тем, что находится внутри скобок. Первое, что нужно оценить, это показатель степени 6 ² :

= 1 + (3 – 36 ÷ 9) · 2 ²

Продолжить работу внутри скобок, оценив деление 36 ÷ 9:

= 1 + (3 – 4) · 2 ²

Теперь можно вообще избавиться от скобок:

= 1 + –1 · 2 ²

На данный момент осталось выражение с показателем степени. Это выражение занимает три шага, начиная с показателя степени:

= 1 + –1 · 4

= 1 + –4

= –3

Так 1 + (3 – 6 ² ÷ 9) · 2 ² = –3.

Выражения со скобками, возведенными в степень

Иногда все содержимое набора скобок возводится в степень. В этом случае оцените содержимое круглых скобок перед вычислением показателя степени, как обычно. Вот пример:

(7 – 5) ³

Сначала оцените 7–5:

= 2 ³

Сняв круглые скобки, вы готовы вычислить показатель степени:

= 8

Время от времени сам показатель степени содержит круглые скобки. Как всегда, сначала оцените то, что в скобках. Например,

21 ^{(19 +} ³ ^–6 ⁾

На этот раз меньшее выражение в круглых скобках представляет собой выражение со смешанными операторами. Часть, которую вам нужно оценить в первую очередь, подчеркнута:

= 21 ^{(19 + –18)}

Теперь можно дописать то, что в скобках:

= 21 ¹

На данный момент все, что осталось, это очень простая экспонента:

= 21

Итак 21 ^{(19 + 3} ^{^–6) = 21.}

Технически вам не нужно заключать в скобки экспоненту. Если вы видите выражение в показателе степени, относитесь к нему так, как если бы оно было заключено в круглые скобки. Другими словами, 21 ^{19+ 3} ^{^–6 означает то же самое, что и 21 ^{(19 + 3} ^{^–6) .}}

Выражения с вложенными скобками

Иногда выражение имеет вложенные скобки: один или несколько наборов скобок внутри другого набора. Вот правило обработки вложенных скобок:

При вычислении выражения с вложенными круглыми скобками сначала оцените, что находится внутри самого внутреннего набора скобок, и продвигайтесь к самым внешним скобкам.

Например, предположим, что вы хотите вычислить следующее выражение:

2 + (9 – ( 7 – 3 ))

Содержимое самого внутреннего набора скобок подчеркнуто, поэтому сначала оцените это содержимое:

= 2 + (9 – 4)

Затем оцените, что находится внутри оставшегося набора скобок:

= 2 + 5

Теперь вы можете легко закончить дело:

= 7

Значит 2 + (9 – (7 – 3)) = 7

В качестве последнего примера, вот выражение, которое требует всего из этой главы:

4 + (–7 · (2 ⁽ ^{5 – 1} ⁾ – 4 · 6))

Это выражение такое сложное, какое вы когда-либо видели в преалгебре: один набор скобок, содержащий другой набор, который содержит третий набор. Для начала оцените подчеркнутую часть уравнения, которая находится в третьем наборе скобок:

= 4 + (–7 · ( 2 ⁴ – 4 · 6 ))

Остался один набор скобок внутри другого набора. Опять же, работайте изнутри наружу. Меньшее выражение здесь 2 ⁴ – 4 · 6, поэтому сначала вычислите показатель степени, затем умножение и, наконец, вычитание:

= 4 + (–7 · ( 16 – 4 · 6 ))

= 4 + (–7 · ( 16 – 24 ))

= 4 + (–7 · –8)

Остался еще один набор скобок:

= 4 + 56

На этом этапе закончить легко:

= 60

Следовательно, 4 + (–7 · (2 ^{(5 – 1)} – 4 · 6)) = 60. написание-алгебраических-выражений/содержания/

Упрощение выражений

Упрощение выражения — это еще один способ сказать решение математической задачи . Когда вы упрощаете выражение, вы, по сути, пытаетесь записать его простейшим 0008 способ возможен. В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Например, возьмем это выражение:

4 + 6 + 5

Если вы упростите , объединив термины до тех пор, пока не останется ничего, выражение будет выглядеть так:

Другими словами, 15 — это простейший способ записать 4 + 6 + 5. Обе версии выражения равны одной и той же сумме; один просто намного короче.

Упрощение алгебраических выражений — та же идея, за исключением того, что в вашем выражении есть переменные (или буквы). По сути, вы превращаете длинное выражение во что-то легко понятное. Итак, такое выражение…

(13x + -3x) / 2

…можно упростить следующим образом:

Если это кажется большим скачком, не волнуйтесь! Все, что вам нужно для упрощения большинства выражений, — это базовая арифметика — сложение, вычитание, умножение и деление — и порядок операций.

Порядок операций

Как и в любой задаче, при упрощении алгебраического выражения вам необходимо следовать порядку операций . Порядок операций — это правило, которое говорит вам правильный порядок для выполнения вычислений. Согласно порядку действий, вы должны решить задачу в следующем порядке:

Скобки
Показатель степени
Умножение и деление
Сложение и вычитание

Давайте рассмотрим задачу, чтобы увидеть, как это работает.

В этом уравнении вы должны начать с упрощения части выражения в круглых скобках : 24 — 20. 20 равно 4. В соответствии с порядком операций далее мы упростим любые показателей . В этом уравнении есть один показатель степени: 4 ² , или четыре во второй степени .

2 ⋅ 4 ² + 18 / 6 — 30

4 ² равно 16. Далее нам нужно позаботиться об умножении на и делении на . Сделаем слева направо: 2 ⋅ 16 и 18 / 6.

2 ⋅ 16 + 18 / 6 — 30

2 ⋅ 16 равно 32, а 18 / 6 равно 3. Все, что слева последний шаг в порядке операций: сложение и вычитание .

32 + 3 — 30

32 + 3 равно 35 и 35 — 30 равно 5. Наше выражение упростилось — делать больше нечего.

Это все, что нужно! Помните, вы должны следовать порядку операций при выполнении вычислений, иначе вы можете не получить правильный ответ.

Все еще немного запутались или нужно больше практики? Мы написали целый урок о порядке действий. Вы можете проверить это здесь.

Добавление похожих переменных

Чтобы добавить одинаковые переменные, вы можете просто добавляем коэффициенты . Итак, 3 х + 6 х равно 9 х . Вычитание работает так же, поэтому 5 y — 4 y = 1 y или просто y .

5y — 4y = 1y

Вы также можете умножить и разделить переменных с коэффициентами. Чтобы умножить переменные на коэффициенты, сначала умножьте коэффициенты, затем запишите переменные рядом друг с другом. Итак, 3 x ⋅ 4 y равно 12 xy .

3x ⋅ 4y = 12xy

Распределительное свойство

Иногда при упрощении выражений можно увидеть что-то вроде этого:

3(x+7)-5

внутри сначала круглые скобки. Однако в этом случае x+7 нельзя упростить, поскольку мы не можем добавить переменную и число. Итак, каков наш первый шаг?

Как вы помните, цифра 3 за скобками означает, что нам нужно умножить все внутри в скобках на 3. В скобках две вещи: x и 7 . Нам нужно умножить их и на 3.

3(x) + 3(7) — 5

3 · x равно 3x и 3 · 7 равно 21 . Мы можем переписать выражение как:

3x + 21 — 5

Далее мы можем упростить вычитание 21 — 5. 21 — 5 равно 16 .

3x + 16

Поскольку складывать переменные и числа невозможно, мы не можем еще больше упростить это выражение. Наш ответ 3x + 16 . Другими словами, 3(х+7) — 5 = 3х+16.

Продолжать
Предыдущий: Написание алгебраических выражений
Далее:Решение уравнений
/en/atomic-topics/solving-equations/content/
Использование алгебраических операций для решения задач

Основные термины

o Заказ операций
o Замена
Цели
o Просмотр порядка операций в контексте алгебры
o Узнайте, как манипулировать выражениями таким замену можно использовать в алгебре

Важным навыком в алгебре является способность выполнять математические операции с выражениями и равенствами. Когда мы имеем дело с простыми числами, такими как 2 + 9= 11 редко требуется вносить изменения для упрощения или расширения выражений (2 + 9 и 11 эквивалентны выражениям). Если мы имеем дело с алгебраическим выражением, таким как 2 + x = 9, то мы должны расширить нашу способность выполнять арифметические операции для работы с переменными, а также с числами.

Порядок операций

Полезно кратко рассмотреть порядок операций в контексте алгебры. При выполнении любого ряда операций, выраженных в математической форме, выполняйте их в следующем порядке:

1. Любые операции в скобках
2. Возведение в степень
3. Умножение/деление
4. Сложение/вычитание , просто вернитесь к первому шагу для выражения в скобках.

Практическая задача: Оцените следующее выражение, используя x = 4: 3 x ² — (4 х + 1).

Решение: Используйте правила для порядка операций. Сначала оцените выражение в скобках, используя x = 4:

4 x + 1 = 4(4) + 1 = 16 + 1 = 17

Затем оцените показатель степени в первом term:

x ² = (4) ² = 16

Теперь посмотрим на полное выражение:
3 (16) — 17
Теперь оцените продукт 3 и 16, затем вычтите 17.
3 16 — 17 = 48 — 17 = 31
. 31.

Равенства

Во-первых, мы должны признать важность «знака равенства» (=) в математике: если два выражения равны, то они действительно равны 9. Хотя этот факт может показаться очевидным, он имеет несколько важных следствий для алгебры. В качестве примера для нашего обсуждения возьмем следующее равенство:

Помните, обе части этого равенства равны друг другу. В результате, если мы выполним одну и ту же операцию, что бы это ни было , над обеими частями уравнения, результирующие выражения будут по-прежнему равными. Например, если у нас есть два банана слева и два банана справа, то количество бананов с каждой стороны одинаково. Таким образом, если убрать один банан слева , а также убери один справа, тогда у тебя останется одинаковое число с обеих сторон. В самом деле, если вы добавите бананы размером x слева и x справа, у вас все равно будет одинаковое количество бананов с каждой стороны, даже если вы не знаете, что такое x .

Итак, давайте рассмотрим приведенный выше пример с алгебраическим выражением. Поскольку обе стороны равны, мы можем делать с выражениями все, что захотим, и все равно иметь равенство , пока мы выполняем одни и те же операции в той же последовательности с обеих сторон . (Обратите внимание, что последовательность важна — лучший способ приблизиться к этому процессу — выполнить одну и только одну операцию с обеих сторон, прежде чем выполнять другую операцию. ) Что, если мы решим добавить 2 к обеим сторонам?

Полученные выражения по-прежнему равны, потому что мы выполнили одну и ту же операцию с обеих сторон. Мы можем даже упростить результат следующим образом (используя ассоциативность и коммутативность).

       Коммутативность
Ассоциативность

Все эти выражения по-прежнему равны. Хотя выражения изменились, равенство не изменилось. Обратите внимание, что в этом случае мы изменили равенство, так что постоянное числовое значение появляется только с правой стороны. Проделаем то же самое для кратных x , вычтя 3 x из обеих частей равенства. Затем мы применим наши правила действительных чисел.

Commutativity
Associativity

. по-прежнему сохраняют равенство. Обратите внимание, что окончательный результат, приведенный выше, содержит всего три члена: это более простое равенство, чем то, с которого мы начали (в котором было пять членов).

Таким же образом мы можем выполнять операции умножения и деления. Например, рассмотрим следующее равенство.

Поскольку эти выражения имеют форму дробей, с ними может быть сложно работать. Однако мы можем упростить их, применяя то, что мы знаем о равенствах. Давайте сначала умножим обе стороны на 5 x ; равенство все равно сохранится. Опять же, мы будем использовать наши правила для действительных чисел: ассоциативность, идентичность и дистрибутивность.

Ассоциативность
Идентификация
Распределение

. ) работают так же для алгебраических выражений, содержащих числа, как и для простых чисел. По мере того, как вы будете лучше знакомиться с этими и другими алгебраическими операциями, вы сможете выполнять их без необходимости узнавать конкретные правила (например, ассоциативность), которые их оправдывают.

Хотя это может показаться очевидным, а может и нет, есть еще один момент, который нам необходимо учитывать в отношении равенств. Допустим, конкретное равенство содержит переменную x . Значения x , которые удовлетворяют этому равенству , а также удовлетворяют другим равенствам, которые выводятся из этого равенства с использованием (большинства) допустимых алгебраических операций. (У этого утверждения есть некоторые ограничения, но обычно их можно решать в каждом конкретном случае.) Давайте рассмотрим пример: 3 + х = 5. Очевидно, что значение х = 2 удовлетворяет этому равенству, поскольку 3 + 2 = 5. А что, если мы проделаем какую-нибудь алгебраическую операцию? Прибавим 2 к обеим сторонам, затем умножим обе стороны на 5.

3 + x + 2 = 5 + 2
x + 5 = 7 (7)
5 x + 25 = 35

Мы знаем, что 10 + 25 = 35, поэтому мы знаем, что 5 x должно быть равно 10. Таким образом, x = 2 еще раз. Из этого примера мы можем заметить, что правильное значение (или значения) для x не меняется, если равенство манипулируется законным образом.
Практическая задача: Обосновайте помеченные шаги в следующей последовательности алгебраических манипуляций:
Учитывая
A.?
      Равенство
     B. ?
С. ?
   Равенство
        D. ?
Э. ?

Решение: Чтобы решить эту задачу, мы должны вспомнить основные правила, обсуждавшиеся в предыдущей главе, и применить их к алгебре. В случае A два термина перевернуты, поэтому оправдание коммутативность . Для B фактор t распределяется как коэффициент для каждого члена в скобках, поэтому этот шаг оправдан дистрибутивностью . В C произведение t и равно 1, что является свойством (мультипликативного) , обратного . Шаг, соответствующий D, может быть обоснован ассоциативностью , а шаг, соответствующий E, может быть обоснован (аддитивным) инверсией .

Замена

Как отмечалось выше, мы можем вносить изменения в равенство и при этом сохранять равенство. Точно так же мы можем заменить одну переменную или переменное выражение на другую переменную или переменное выражение. Например, допустим, у нас есть следующее равенство.

Теперь предположим, что мы хотим преобразовать x в другую форму (по какой-либо причине). Допустим, мы хотим, чтобы x называлось z 9.0022 вместо этого, так что x = z . Тогда

совпадает с предыдущим выражением. С другой стороны, мы можем сказать, что x = 3 y , так что

2
2
2
2
2 .
Если конкретное значение х удовлетворяет этому равенству, то соответствующее значение х (используя соотношение x = 3 y ) также удовлетворяет предыдущему выражению.

Практическая задача: Подставьте p = 3 n + 4 в выражение p + 3 – .

Решение : Постановка задачи дает нам новое выражение переменной, которое мы можем подставить в общее выражение следующим образом. Сделайте замену для каждого экземпляра p . (Обратите внимание, однако, что нет ничего принципиально неправильного в том, чтобы заменить только один экземпляр р ; это оставляет нам новое выражение, содержащее две переменные вместо одной. Однако, поскольку переменные связаны между собой, проще всего получить окончательное выражение в терминах только одной переменной.)

p + 3 – = (3 n + 4) + 3 –

Мы можем несколько упростить этот результат, используя наши правила обработки:

(3 n + 4) + 3 – = 3 n + (4 + 3) — Ассоциативность
3 N + (4 + 3) — = 3 N + 7 —
Это одно потенциальное выражение, которое получено из рамки. описано в задаче.
Что такое выражение в математике? Значение, определение, типы, примеры
Определение выражения в математике?
Выражение в математике — это предложение, содержащее не менее двух чисел или переменных и не менее одной математической операции. Эта математическая операция может быть сложением, вычитанием, умножением или делением. Структура выражения:
Экспрессия (число/переменная, математический оператор, номер/переменная)
Примеры выражения:
Пример 1: $ 7 +
Пример 2: $ 23.5 $ 23.5 $ 23.5 $ 23.5 $ 23.5 $ 23.
Пример 3: $ 37S — 6T $
Пример 4: $ 25A4 + 9 — 4 ÷ 15 $
Во всех данных выражениях, математика используется между математикой. два числа.
Не примеры выражений:
Пример 1: A
Пример 2: 4 $
Пример 3: 7,89 долл. США
Части выражения в математике
следующие:
a) Константа: it — фиксированное числовое значение.
Пример: $7, 45, 4\frac{1}{3}, −18, \sqrt{5}, 7 + \sqrt{11}$
b) Переменные: они не принимают никаких фиксированных значений . Значения назначаются в соответствии с требованием.
Пример: a, p, z
c) Термины: могут быть константами, переменными или константами, умноженными на переменную/(и). Каждый термин в выражении отделяется знаком «+» или знаком «-»
Пример: В $5a + 2b -7$ термины: $5a, 2b и 7$.
d) Операторы: Четыре операции сложения (+), вычитания (−), умножения (×), деления (÷) используются для объединения членов выражения и называются операторами.
Типы математических выражений
Числовое выражение
Числовое выражение в математике состоит из чисел и арифметических операторов. Он не содержит неизвестных переменных, символов равенства или неравенства.
Примеры:
$65 + 9 – 4$
$\frac{25}{4}+\frac{36}{5}$
$42 ÷ 7 × 4 – 9 + 7$
$14,5 + 9$
Алгебраическое выражение
Алгебраическое выражение состоит из неизвестных переменных, чисел и арифметических операторов. Он не содержит символов равенства или неравенства. 92q$
Типы алгебраических выражений
Алгебраические выражения классифицируются на основе количества терминов в выражении. Различные типы алгебраических выражений:
Мономиальные выражения содержат только один член. Например. $4x$
Биномиальные выражения содержат два непохожих члена. Например. $2xy +x$
Трехчленные выражения содержат только три непохожих члена. Например. $3т2- 4т + 9$
Полиномиальные выражения содержат два или более члена. Сюда входят также двучлены и трехчлены, а также все другие выражения с четырьмя или более терминами. Например. $2x + 3y + 5z; 4t + 5 − 4u + z$
Выражение против уравнения
Математическое выражение отличается от математического уравнения.
Разница между выражениями и уравнениями заключается в том, что выражение означает комбинацию чисел, переменных и символов операций, тогда как уравнение всегда будет использовать оператор равенства (=) между двумя математическими выражениями. Также обе стороны знака «равно» имеют одинаковое значение.
Например,
Выражение Уравнение
$ 22 + 5 $ $ 22 + 5 = 29 — 2 $
$ 99
$ 97
$ 97
.
50$ ÷ 10$ 45$ ÷ 9 = 50 ÷ 10$
15$ + 7 – 6$ 15$ + 7 – 6 = 16$
$ 25 + 7 $ $ 25 + 7 = 64 ÷ 2 $
$ 20 × 5 $ $ 20 × 5 = 100 $
, где используются явления?
Выражения помогают нам в решении текстовых задач. Математические выражения формируются с использованием слов задачи.
В качестве примера рассмотрим следующую задачу:
Давайте рассмотрим задачу со словами и научимся писать математические выражения
1. Том должен заполнить коробку апельсинами и яблоками. Количество яблок должно быть на 5 больше, чем апельсинов. Том срывает каждый раз по 3 апельсина и повторяет это 5 раз. Подсчитайте общее количество апельсинов и яблок.
Чтобы решить эту задачу, сформулируйте математические выражения следующим образом:
Количество апельсинов = $3 × 5$
Количество апельсинов = $15$
Количество яблок = Количество апельсинов $+ 5$
Количество яблок = $15 + 5$
Количество яблок = $20$
Общее количество фруктов = количество апельсинов + количество яблок
Третье математическое выражение будет:
Общее количество фруктов = $15 + 20$ количество апельсинов и яблок)
$= 35$
2. Класс учащихся собирается в путешествие. Каждый студент должен заплатить индивидуальную плату в размере $\$$8 и групповую плату в размере $\$$30. Напишите алгебраическое выражение для полной стоимости поездки. Найдите общую стоимость поездки, если в поездке едет 56 студентов.
Пусть n представляет количество студентов.
Алгебраическое выражение будет:
$\$$8 n + $\$30
Чтобы найти общую стоимость поездки, когда n = 56.
$\$8 n + $\$$30
$\$$8(56) + $\$30 \$$30
$\$$478
PEDMAS
PEDMAS — это аббревиатура, где P означает скобки, E — показатель степени, D — деление, M — умножение, A — сложение, а S — вычитание.
Порядок букв указывает порядок, в котором должна выполняться операция.
92)$
$= (5 × 4 − 7) + × (19 − 16)$
$= (20 − 7) + 3$
$= 13 + 3$
$= 16$
Применение:
Знание применения математических операций над числами является первым шагом к формированию у детей базовых арифметических рассуждений и логики. Формулирование математических выражений с использованием соответствующего навыка закладывает прочную основу для изучения алгебры и преобразования реальных задач в подходящие математические модели.
Решенные примеры выражения:
Пример 1 : Укажите, является ли каждое из них выражением или уравнением.
(a) $4 + 8$ (b) $4 + 12 = 16$ (c) $5 × 35$
(d) $919 – 8 $ 4 + 9 e) $8 × 4 ÷ 2 = 16$ (f) $72+94$
Solution:
Expression Equation
$4 + 8$ $4 + 12 = 16 $
$ 5 × 35 $ $ 8 × 4 ÷ 2 = 16 $
$ 16 ÷ 4 + 9 — 2 $
$ 72 + 94 $
94 $ 94 000 7 700077 7000777 94. фраза как выражение.
Сумма 10$ и 14$
3 больше, чем число 7$
Дважды 11$, умноженное на 1$
19 меньше, чем произведение 15$ и 4$
Частное 33$ $ и $3$
Решение:
$ 10 + 14 $
$ 7 + 3 $
$ 2 × 11 + 1 $
$ 15 × 4 — 19 $
$ 33 ÷ 3 $
Пример 3 : Классифицируйте следующее выражение. алгебраический.
$4a – 7b$
$23 + 42 – 6$
$715-911$
$2 – 5x9y$
$22 – 5 + 8$
$7y + 19x – 4z$
Solution :
Арифметика Алгебра
$23 + 42 – 6$ $4a – 7b$
$22 – 5 + 8$ $7y + 19x – 4z$
$715-911$ $2 – 5x9y$
Пример 4: Напишите члены данного выражения $4uv + 7u − 9z + 6z$ .
Решение:
$4uv, 7u, −9z$ и $6z$ — члены данного выражения.
Пример 5: В книге 250$ страниц. Рону осталось прочитать 62$ страниц. Напишите выражение, чтобы найти количество прочитанных страниц.
Решение:
$250 – 62$
Пример 6: У $X$, $Y$ и $Z$ несколько резинок для волос. У $Y$ больше резинок для волос на $20$, чем у $X$. $Z$ говорит, что у нее на пять ободков больше, чем у $X$ и $Y$ вместе взятых. Выразить это в виде выражения?
Решение : Пусть количество резинок для волос с $X$ равно $ = x$.
Тогда у $Y$ есть $(x+20)$ ободков.
$Z$ имеет ${x + (x+20)} + 5=2x+25$ ободков.
Таким образом, $Z$ имеет $(2x+25)$ ободков.
Практическая задача
$6 + 8 = 14$
$0 – 16 = –16$
$\frac{4}{7}+ \frac{4}{7}-\frac{1}{7} $
$5\text{x}-7\text{y}=15$
Правильный ответ: $\frac{4}{7}+ \frac{4}{7}-\frac{1}{ 7}$
Так как в нем есть числа (дробь) и математические операторы, другими вариантами являются уравнения, так как он имеет оператор равенства (=) между двумя математическими выражениями.
$3\текст{а}+7\текст{b}-6\текст{с}=5\текст{х}$
$9-5\text{w}$
$\frac{1}{2}+\frac{3}{4}$
$44 + 55$
Правильный ответ: $9-5\text{ w}$
Он содержит переменные, числа и математический оператор. Вариант (a) представляет собой уравнение, вариант (c) и вариант (d) представляют собой арифметические выражения, а не алгебраические, поскольку в них не участвуют переменные.
Одночлен
Бином
Трехчлен
Ни один из этих
Правильный ответ: Трехчлен
Если в выражении три члена, мы называем его трехчленным выражением.
Переменная
Константа
Член
Коэффициент
Правильный ответ: Константа
Член, который не меняет своего значения, называется константой.
$3×14$
$10 − 3 × 14$
$3 × 10 − 14$
$3 × 14 − 10$
Правильный ответ: $3 × 14 − 10$
Трижды число $1 14$.
Уменьшение на 10 равно $3 × 14 − 10$
$\$$(9,75 + 40)
$\$$(40 – 9,75)
$\$$(90,75 × 40)
$\$$(9,75 – 40)
Правильный ответ: $\$$(9,75 × 40)
Сумма, заработанная за час = $\$9,75 $
Сумма, заработанная за 40 часов = $ \$$(9,75 × 40)$
Часто задаваемые вопросы
Что такое выражение в математике?
Выражение — это набор чисел или переменных, объединенных с помощью операций $+, –, × или ÷$.
Что такое типы выражений?
Арифметическое выражение, содержащее только числа и математические операторы, и алгебраическое выражение, содержащее переменные, числа и математические операторы.
Можем ли мы решить математическое выражение?
Нет, мы не можем решить математическое выражение, так как оно не имеет знака «равно» (=), но мы можем упростить выражения.
В чем разница между арифметическим выражением и алгебраическим выражением?
Математические выражения содержат только числа и операторы, в то время как алгебраические выражения содержат как числа, так и переменные в терминах, разделенных промежуточными операторами.
Введение в алгебру | SkillsYouNeed
Многие думают, что уравнения и алгебра им не по силам — мысль о том, что придется работать с уравнениями, наполняет их страхом. Однако не нужно бояться уравнений.
Хорошей новостью является то, что уравнения на самом деле являются относительно простыми понятиями, и с небольшой практикой и применением некоторых простых правил вы можете научиться манипулировать ими и решать их.
Эта страница предназначена для того, чтобы познакомить вас с основами алгебры, и мы надеемся, что вы будете чувствовать себя более комфортно, решая простые уравнения.
Что такое уравнение?
Уравнение — это два выражения по обе стороны от символа, указывающего на их взаимосвязь.
Это отношение может быть равным (=), меньшим чем (<) или большим чем (>) или некоторой комбинацией. Например, меньше или равно (≤) или даже не равно (≠) или примерно равно (≈). Они известны как равенство символов.
Таким образом, простые уравнения включают 2 + 2 = 4 и 5 + 3 > 3 + 4.
Однако, когда большинство людей говорят об уравнениях, они имеют в виду алгебраические уравнения.
Это уравнения, в которых помимо цифр используются буквы. Буквы используются для замены некоторых чисел, когда числовое выражение было бы слишком сложным, или когда вы хотите обобщить, а не использовать конкретные числа. Их также можно использовать, когда вы знаете значения в части уравнения, но другие неизвестны и вам нужно их вычислить.
Алгебраические уравнения решаются путем определения того, какие числа представляют буквы.
Мы можем превратить два приведенных выше простых уравнения в алгебраические уравнения, подставив $x$ вместо одного из чисел:
2 + 2 = $\boldsymbol{x}$
Мы знаем, что 2 + 2 = 4, а это означает, что $x$ должно быть равно 4. Следовательно, решение уравнения равно $ \boldsymbol{x}$ = 4 .
5 + 3 > 3 + $\boldsymbol{x}$
Мы знаем, что 5 + 3 = 8. Уравнение говорит нам, что 8 больше, чем (>) 3 + $x$.
Нам нужно переставить уравнение так, чтобы $x$ было с одной стороны, а все числа с другой, иначе мы не сможем найти значение $x$. Правило перестановки уравнений то, что вы делаете с одной стороной, вы должны делать и с другой . Подробнее об этом ниже.
Отнять по 3 с обеих сторон (8 − 3 = 5) , тогда уравнение примет вид $х$ < 5 ).
Мы не можем более точно сказать, что такое $x$ с той информацией, которую нам дали. Однако в исходном уравнении, которое мы использовали в качестве примера, мы заменили $x$ на 4, что действительно меньше 5,9.0003
В использовании фигурного ‘x’ (${x}$) нет ничего волшебного. Вы можете использовать любую букву, которая вам нравится, хотя ${x}$ и ${y}$ обычно используются для представления неизвестных элементов уравнений.
Переменные и константы
Буква, используемая для замены числа в алгебре, называется переменной , потому что каждый раз она обозначает разные числа.
Это отличается от конкретной буквы, которая всегда используется для замены одного и того же числа, например, $\pi$ (pi), которое всегда равно 3,142. Такая буква называется константа .
В алгебраическом уравнении любые заданные числа также являются константами, потому что они всегда остаются неизменными.
Если вам нужно решить уравнение с константой, вам всегда сообщат ее значение.
Члены уравнения
Член представляет собой часть уравнения, которая отделена от других частей, обычно символом сложения (+) или вычитания (-).
Группа терминов называется выражением, подобно математическому предложению или описанию. Некоторые математические выражения могут выглядеть довольно устрашающе, изобилуя цифрами и буквами, некоторые из которых могут быть даже греческими. Однако ключ в том, чтобы рассматривать каждый термин отдельно и разбивать его на то, что вы знаете или что можете понять. Если вы сделаете это, вы начнете понимать, что это не всегда так сложно, как вы думали сначала.
Термины могут быть просто цифрами, буквами или комбинациями букв и цифр, например 2$\boldsymbol{x}$, 3$\boldsymbol{xy}$ или 4$\boldsymbol{x}$ ² .
В термине, включающем буквы и цифры, число известно как коэффициент , а буква является переменной . Коэффициент — это просто «множитель» — он говорит вам, сколько чего-то (переменной) у вас есть в этом термине.
Термины, имеющие точно такую же переменную, называются 92$$
Вы не можете добавлять или вычитать «непохожие термины». Однако вы можете умножить их, комбинируя переменные и перемножая коэффициенты.
Итак, например, 3$y$ × 2$x$ = 6$xy$ (потому что 6$xy$ просто означает 6 раз $x$ раз $y$ ).
Разные члены можно разделить, превратив их в дроби и сократив. Начните с цифр, затем букв.
Так, например:
$\large{6xy ÷ 3x}$
$$\frac{6xy}{3x}$$ = $$\frac{2xy}{x}$$ = $$\frac{2y}{1}$$ = $$2г$$
Разделите верхнюю часть
и нижнюю часть
на 3 Разделить верхнее
и нижнее
на x 1 можно
игнорировать, потому что
все, что делит
на 1, само является
Перестановка и решение уравнений
Во многих случаях для решения уравнения вам, вероятно, потребуется переставить его. Это означает, что вам нужно перемещать термины так, чтобы у вас остались только термины, включающие $x$ с одной стороны символа равенства (например, =, > или <), а все числа — с другой.
Этот процесс иногда называют изолирующим $x$ .
Вы можете изменить уравнения с помощью набора простых правил:
Что бы вы ни делали с одной частью уравнения, вы должен сделать то же самое с другим. Так вы сохраните отношения между ними. Неважно, что вы делаете: отнимаете 2, прибавляете 57, умножаете на 150 или делите на $х$. Пока вы делаете это с обеих сторон, уравнение остается правильным. Это может помочь думать о вашем уравнении как о наборе весов или качелях, которые всегда должны балансировать.
На нашей странице Дополнение объясняется, что не имеет значения, в каком порядке вы добавляете, ответ все тот же. Это означает, что вы можете изменить выражение, чтобы поставить похожи на члены вместе и облегчают сложение. Это относится и к Вычитание , если вы помните из нашей страницы Положительные и отрицательные числа , что вычитание равносильно добавлению отрицательного числа . Так, например, 10 − 3 = 10 + (-3).
Уравнения также работают в соответствии с BODMAS , поэтому не забывайте выполнять расчеты в правильном порядке.
Всегда придавайте своему уравнению максимально простую форму: умножайте скобки, делите вниз, сокращайте дроби и добавляйте/вычитайте все подобные члены.
Примеры работы:
Попробуйте решить эти уравнения относительно $x$, нажмите на квадраты, чтобы открыть работу и ответы.
Как и при любом расчете, сначала выполните умножение. 5 × 4 = 20
Значит $х$ + 3 = 20
Следующий шаг — убрать по три с обеих сторон
$х$ + 3 — 3 = 20 — 3
20 — 3 = 17.
Это оставляет вас с ответом: $x$ = 17
Сначала выполните вычисления с правой стороны, потому что в них не используются буквы. Здесь нет скобок, поэтому сначала умножение, а потом сложение.
6 × 5 = 30 и 30 + 3 = 33.
Вычисление слева является добавочным, поэтому вы можете перемещать члены, пока не получите все числа вместе:
5 + $x$ + 21 = $x$ + 5 + 21
и 5 + 21 = 26.
Итак, теперь у вас есть 26 + $х$ = 33
Теперь можно убрать по 26 с обеих сторон
26 + $х$ — 26 = $х$ = 33 — 26
А 33 — 26 = 7.
Следовательно, $x$ = 7
Переставьте все числа с одной стороны, убрав по пять с каждой стороны.
Теперь у вас есть
$x$ ² = 13 − 4 − 5, значит,
$х$ ² = 4
Теперь вам нужно извлечь квадратный корень из обеих частей, потому что вы хотите найти значение $x$, а не $x$ ² .
Вы знаете, что 2 × 2 = 4, а это значит, что квадратный корень из 4 = 2
$x$ = 2

Уравнения и графики
Любое уравнение, в котором есть связь только между двумя переменными $x$ и $y$, может быть представлено как линейный график, где $x$ проходит по горизонтальной оси (иногда называемой осью x) и $y$ по вертикальной оси (иногда называемой осью y).
Вы можете вычислить точки на графике, решив уравнение для определенных значений $x$.
Примеры:
$\large{y = 2x + 3}$
$x$ 0 1 2 3 4 5 6
расчет 2(0) + 3 2(1) + 3 2(2) + 3 2(3) + 3 2(4) + 3 2(5) + 3 2(6) + 3
$у$ 3 5 7 9 11 13 15
Преимущество рисования графика уравнения состоит в том, что вы можете использовать его для определения значения $y$ для любого заданного значения $x$ или даже $x$ для любого заданное значение $y$, глядя на график.
В этом примере каково значение $x$, когда $y$ = 10?
Двигайтесь вверх по оси Y, пока не достигнете 10, затем по горизонтали, пока не достигнете линии на графике. В этот момент двигайтесь вниз, пока не достигнете оси x. Это показано красными линиями на графике, и вы можете видеть, что при $y$ = 10, $x$ = 3,5. 92 + x + 4}\)
Когда $x$ = 0, $y$ = 0 + 0 + 4 = 4
когда $x$ = 1, $y$ = 1 + 1 + 4 = 6
, когда $х$ = 2, $у$ = 4 + 2 + 4 = 10
и так далее…
$х$ 0 1 2 3 4 5 6 7 8 9 10
$у$ 4 6 10 16 24 34 46 60 76 94 114

Экстраполировать
Еще одним преимуществом построения уравнения на графике является то, что вы можете экстраполировать свои данные (числовую информацию) для получения больших значений $x$ или $y$. Экстраполяция означает, что вы расширяете свой график, продолжая линию, которую вы нарисовали из своих данных, чтобы оценить значения $x$ и $y$ за пределами диапазона данных, которые у вас уже есть.
No related posts.

\(х\)	0	1	2	3	4	5	6	7	8	9	10
\(у\)	4	6	10	16	24	34	46	60	76	94	114

Нахождение значения выражения: правила, примеры, решения

Как найти значение числового выражения?

Простейшие случаи

Выражения со скобками

Выражения с корнями

Выражения со степенями

Выражения с дробями

Выражения с логарифмами

Выражения с тригонометрическими функциями

Общий случай числового выражения

Вычисление значений выражений рациональными способами

Нахождение значений выражений с переменными

Числовые выражения – как решить задачу (алгебра 7 класс) по вычислению значений числового выражения

Определение понятия

Характеристики понятия

Значение

Равенство

Пример задачи

Что мы узнали?

Тест по теме

Оценка статьи

Выражения в математике | О математике понятно

Типы задач, поддерживаемые помощником по преобразованию в математические выражения

Как упростить выражение с дробями. Как упростить математическое выражение

Что представляют собой степенные выражения?

Основные виды преобразований степенных выражений

Работа с основанием и показателем степени

Использование свойств степеней

Преобразование дробей, содержащих степени

Преобразование выражений с корнями и степенями

Преобразование степеней с переменными в показателе

Преобразование выражений со степенями и логарифмами

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

Шаги

Правильный порядок выполнения математических операций

Упрощение сложных выражений

Вынесение общего делителя

Простейшие формулы сокращенного умножения

Степени корни

Упрощения выражений с дробями

Упрощение простейших тригонометрических выражений

Урок 20. Преобразование выражений в Mathcad

About Павел Демидов

Алгебраическое выражение – Объяснение и примеры

Как решить алгебраическое выражение ?

Как решать уравнения с скобками — часто используются в скобках

Выражения большой четверки со скобками

Выражения с показателями и скобками

Выражения со скобками, возведенными в степень

Выражения с вложенными скобками

Упрощение выражений

Порядок операций

Добавление похожих переменных

Распределительное свойство

Использование алгебраических операций для решения задач

2

2

2 .

Что такое выражение в математике? Значение, определение, типы, примеры

Определение выражения в математике?

Практическая задача

Часто задаваемые вопросы

Введение в алгебру | SkillsYouNeed

Члены уравнения

Перестановка и решение уравнений

Уравнения и графики

Добавить комментарий Отменить ответ