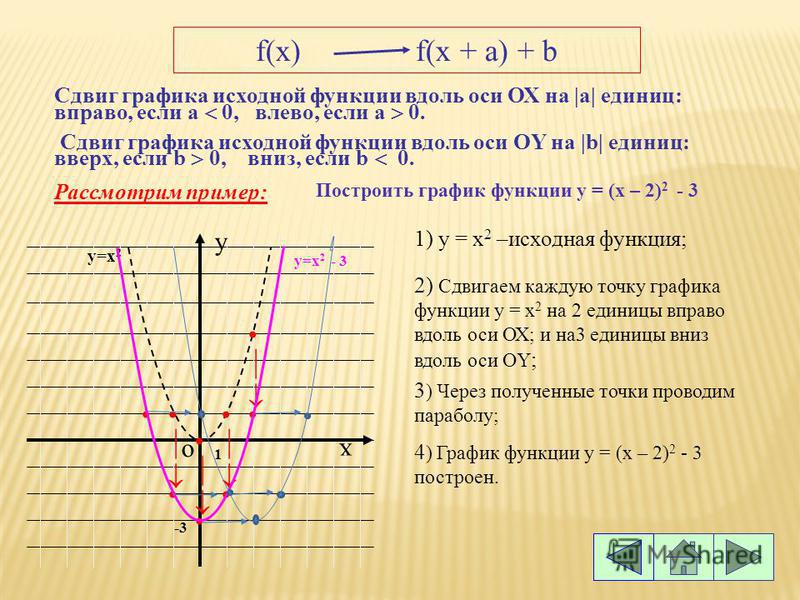
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai
03. Метод изоклин
Метод изоклин – это метод графического решения дифференциального уравнения. Семейство изоклин дифференциального уравнения (1) определяется уравнением
, где — параметр.
Метод изоклин заключается в построении семейства изоклин с нанесенными на них отрезками касательных.
Множество отрезков касательных образует поле направлений касательных интегральных кривых. Главное соединение касательных дает семейство интегральных кривых.
Рассмотрим примеры.
Пример 1. Решить методом изоклин уравнение
.
Решение. Данное уравнение определено во всей плоскости , исключая точки прямых и . В области определения его можно записать в виде:
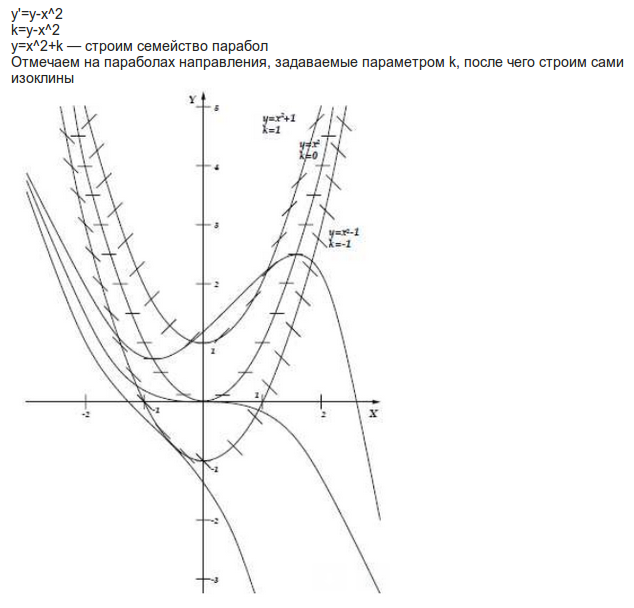
Поэтому в I и II квадрантах координатной плоскости интегральные кривые – это графики функций , а во II и IV квадрантах – графики функций (см. рис.2).
Пример 2. Решить методом изоклин уравнение:
.
Решение. Уравнение изоклины . В данном случае уравнение изоклины совпадает с уравнением нормали .
Запишем несколько уравнений изоклин для фиксированных угловых коэффициентов касательных, если
На рис.3 поле направлений касательных дает семейство интегральных кривых в виде окружностей.
Дифференциальное уравнение вида
,
В котором коэффициенты при дифференциалах распадаются на множители, зависящие только от и только от , называется уравнением с разделяющимися переменными.
Путем деления на произведение оно приводится к уравнению с разделенными переменными:
.
Общий интеграл этого уравнения имеет вид:
.
Пример 1. Решить уравнение
.
Решение. Представим данное уравнение в виде
.
Разделив обе части этого уравнения на произведение , получим уравнение с разделенными переменными
.
Интегрируя это уравнение, последовательно находим
.
Используя метод подстановки, вычислим интегралы
.
Решением данного дифференциального уравнения является функция:
.
Пример 2. Найти частное решение уравнения
,
Удовлетворяющее начальному условию .
Решение. Найти частные решения данного дифференциального уравнения – это значит решить задачу Коши.
А) Найдем общее решение данного уравнения. Запишем его иначе
.
Данное уравнение является уравнением с разделяющимися переменными. Разделим обе части этого уравнения на , получим:
.
Интегрируем:
.
Таким образом общий интеграл имеет вид :
Б) Найдем частное решение, для этого определим значение постоянной При данных начальных условиях ; будем иметь
Следовательно .
Подставив найденное значение в общее решение, получим частное решение данного дифференциального уравнения
,
Откуда
.
Из начального условия следует, что (т. к. ), поэтому перед корнем берем знак плюс. Итак, искомое частное решение:
.
| < Предыдущая | Следующая > |
|---|
DEALA Методы графического решения
Поля уклонов и построение графиков Приближенные решения
Для дифференциальных уравнений первого порядка существует простой графический метод аппроксимации кривых решений. Этот метод аппроксимации решений использует специальный график, называемый полем наклона или полем направления графиком. В частности, если мы можем написать дифференциальное уравнение в виде:
\begin{уравнение}
\ в штучной упаковке {\ dfrac {dy} {dx} = f (x, y)}
\label{eqn-gen-first-order}\tag{2.4.1}
\end{уравнение}
тогда мы можем аппроксимировать решения с помощью графика поля наклона. Так как же построить такой сюжет?
Так как же построить такой сюжет?
Ответ заключается в том, чтобы заметить, что правая часть уравнения (2.4.1) является функцией точек на плоскости \(xy\), в результате чего левая часть является в точности мгновенным наклоном \(y(x )\text{,}\) функция решения, которую мы ищем! Если нам известен наклон функции в каждой точке оси \(x\), то мы можем графически восстановить функцию решения \(y(x)\text{.}\)
Создание графика поля наклона обычно выполняется с помощью программного обеспечения на компьютере. Основной алгоритм, который использует компьютер для этого, по существу следующий:
Разделите плоскость \(xy\) равномерно на сетку квадратов.
Для каждой точки \((x_i, y_i)\) в сетке сделайте следующее:
вычислить наклон, \(dy/dx = f(x_i, y_i)\text{.}\)
Нарисуйте небольшую полосу с центром в точке \((x_i, y_i)\) с наклоном, вычисленным выше. (Каждая полоса должна быть одинаковой длины и достаточно короткой, чтобы они не перекрывались.
 {kt}.
\label{мужчины-22}\tag{2.4.3}
\end{уравнение}
Важно отметить, что никакое программное обеспечение не может отображать общие решения, потому что для построения точек компьютер должен иметь возможность генерировать пары координат. Это можно сделать, только если мы укажем значения для констант \(P_0\) и \(k\text{.}\)
{kt}.
\label{мужчины-22}\tag{2.4.3}
\end{уравнение}
Важно отметить, что никакое программное обеспечение не может отображать общие решения, потому что для построения точек компьютер должен иметь возможность генерировать пары координат. Это можно сделать, только если мы укажем значения для констант \(P_0\) и \(k\text{.}\)Иногда достаточно одной кривой решения, нанесенной на поле наклона. В этом случае команда desolve_rk4 создаст как график поля наклона, так и одну приблизительную кривую решения . Код ниже графически аппроксимирует линейное уравнение \begin{уравнение} \frac{dy}{dx} = -y + \cos x \label{мужчины-23}\tag{2.4.4} \end{уравнение} Приближенная кривая решения создается с помощью алгоритма Рунге-Кутты 4-го порядка. Мы увидим, как работает этот метод численной аппроксимации, в разделе 3.2. В приведенном ниже коде также показано, как продолжить выполнение команды на следующей строке, добавив символ «\» в конец строки.
Наконец, чаще всего нам нужно объединить график поля наклона с несколькими численно аппроксимированными кривыми решения.
 Следующий код демонстрирует это для дифференциального уравнения:
\begin{уравнение}
\frac{dy}{dx} = \cos(xy),
\label{мужчины-24}\tag{2.4.5}
\end{уравнение}
не имеет решения, выражаемого через элементарные функции. Следующий код создает график поля наклона, а затем объединяет его с выходными данными многократного вызова desolve_rk4.
Следующий код демонстрирует это для дифференциального уравнения:
\begin{уравнение}
\frac{dy}{dx} = \cos(xy),
\label{мужчины-24}\tag{2.4.5}
\end{уравнение}
не имеет решения, выражаемого через элементарные функции. Следующий код создает график поля наклона, а затем объединяет его с выходными данными многократного вызова desolve_rk4.Простой алгоритм, приведенный выше, хорош для компьютерной программы, но его очень сложно использовать на практике человеку. Однако есть более простой алгоритм, который можно выполнить вручную с помощью карандаша и миллиметровой бумаги. Основная идея состоит в том, чтобы найти изоклин в поле наклона и нанесите равномерно расположенные одинаковые бары наклона по всей длине изоклины.
Определение 2.4.2
Изоклина — это линия или кривая, на которой наклон является постоянным.
Предположим, мы хотим построить график наклона поля для дифференциального уравнения \begin{уравнение*} \frac{dy}{dx} = xy = f(x,y).
 \end{уравнение*}
Метод включает два этапа. Сначала мы создаем таблицу. Каждая строка в таблице соответствует одной изоклине. Во-вторых, для каждой строки таблицы мы начертили соответствующую изоклину и украсили ее регулярно расположенными полосами, все из которых имеют одинаковый наклон. Наклон соответствует значению в первом столбце таблицы.
\end{уравнение*}
Метод включает два этапа. Сначала мы создаем таблицу. Каждая строка в таблице соответствует одной изоклине. Во-вторых, для каждой строки таблицы мы начертили соответствующую изоклину и украсили ее регулярно расположенными полосами, все из которых имеют одинаковый наклон. Наклон соответствует значению в первом столбце таблицы.Таблица содержит данные для семи изоклин, по одной для каждого целочисленного значения уклона от \(-3, \ldots, 3\text{.}\) Мы должны изобразить каждое уравнение линии из третьего столбца и украсить его штрихами, расположенными через равные промежутки, где наклон исходит из первого столбца.
Наклон Изоклина \(м\) \(=\) \(е(х,у)\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(ч(х)\) \(-3\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х+3\) \(-2\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х+2\) \(-1\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х+1\) \(0\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х+0\) \(1\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х-1\) \(3\) \(=\) \(х-у\) \(\quad \longrightarrow \quad\) \(у\) \(=\) \(х-3\) 1
Используйте метод изоклин, чтобы вручную построить график поля наклона для следующего дифференциального уравнения первого порядка.
 \begin{уравнение*}
\ гидроразрыв {dy} {dx} = х + у
\end{уравнение*}
\begin{уравнение*}
\ гидроразрыв {dy} {dx} = х + у
\end{уравнение*}2
Используйте метод изоклин, чтобы вручную построить график поля наклона для следующего дифференциального уравнения первого порядка. \begin{уравнение*} \frac{dy}{dx} = y-x+1 \end{уравнение*} 92\cos(х) \end{уравнение*} с границами \(-\pi \lt x \lt \pi\) и \(-1 \lt y \lt 1\текст{.}\)
Решение6
В этой задаче опечатка! Границы \(y\) изменены: \begin{уравнение*} \текст{от} -3 \lt у \lt 3 \quad \text{to} \quad -30 \lt у \lt 30. \end{уравнение*}
Найдите общее решение данного линейного уравнения. Используйте Sage, чтобы создать график поля наклона для уравнения: \begin{уравнение*} \frac{dy}{dx} = y + \cos(x) \end{уравнение*} с границами \(-3 \lt x \lt 3\) и \(-30 \lt y \lt 30\text{.}\) На тех же осях графика отобразите частные решения, соответствующие начальным условиям \(y(0)=1\) и \(y(0)=-1\text{.}\)
Дифференциальные уравнения — поля направлений
Онлайн-заметки Пола
Главная / Дифференциальные уравнения / Базовые концепты / Поля направленияПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 1.2: Поля направления
Этой теме выделен отдельный раздел по нескольким причинам. Во-первых, понимание полей направлений и того, что они говорят нам о дифференциальном уравнении и его решении, важно и может быть введено без каких-либо знаний о том, как решать дифференциальное уравнение, и поэтому может быть сделано здесь, прежде чем мы приступим к их решению. Таким образом, иметь некоторую информацию о решении дифференциального уравнения, не имея фактического решения, — хорошая идея, требующая некоторого исследования.
Далее, поскольку для работы нам нужно дифференциальное уравнение, в этом разделе показано, что дифференциальные уравнения возникают естественным образом во многих случаях и как мы их получаем.
 Почти каждую физическую ситуацию, происходящую в природе, можно описать соответствующим дифференциальным уравнением. Дифференциальное уравнение может быть легко или трудно получить в зависимости от ситуации и предположений, которые делаются о ситуации, и мы, возможно, никогда не сможем его решить, однако оно будет существовать.
Почти каждую физическую ситуацию, происходящую в природе, можно описать соответствующим дифференциальным уравнением. Дифференциальное уравнение может быть легко или трудно получить в зависимости от ситуации и предположений, которые делаются о ситуации, и мы, возможно, никогда не сможем его решить, однако оно будет существовать.Процесс описания физической ситуации с помощью дифференциального уравнения называется моделированием. Мы будем рассматривать моделирование несколько раз в течение этого класса.
Одна из самых простых физических ситуаций, о которой можно подумать, — это падающий объект. Итак, давайте рассмотрим падающий объект с массой \(m\) и выведем дифференциальное уравнение, решение которого даст нам скорость объекта в любой момент времени \(t\). Будем считать, что при падении на объект будут действовать только сила тяжести и сопротивление воздуха. Ниже приведен рисунок, показывающий силы, которые будут действовать на объект.
Прежде чем определить все термины в этой задаче, нам нужно установить некоторые соглашения.
 Будем считать, что силы, действующие в направлении вниз, являются положительными силами, а силы, действующие в направлении вверх, отрицательными. Точно так же мы предположим, что объект, движущийся вниз (, т.е. падающий объект), будет иметь положительную скорость.
Будем считать, что силы, действующие в направлении вниз, являются положительными силами, а силы, действующие в направлении вверх, отрицательными. Точно так же мы предположим, что объект, движущийся вниз (, т.е. падающий объект), будет иметь положительную скорость.Теперь давайте посмотрим на силы, показанные на диаграмме выше. \({F_G}\) — сила гравитации и определяется как \({F_G} = mg\), где \(g\) — ускорение свободного падения. В этом классе мы используем \(g\) = 90,8 м/с 2 или \(г\) = 32 фута/с 2 в зависимости от того, будем ли мы использовать метрическую или имперскую систему. \({F_A}\) — сила сопротивления воздуха, и для этого примера мы будем считать, что она пропорциональна скорости \(v\), массы. Следовательно, сила сопротивления воздуха определяется выражением \({F_A} = — \gamma v\), где \(\gamma > 0\). Обратите внимание, что «-» требуется для получения правильного знака силы. И \(\gamma\), и \(v\) положительны, а сила действует вверх и, следовательно, должна быть отрицательной.
 «-» даст нам правильный знак и, следовательно, направление для этой силы.
«-» даст нам правильный знак и, следовательно, направление для этой силы.Вспомним из предыдущего раздела, что второй закон движения Ньютона можно записать как
. \[m\frac{{dv}}{{dt}} = F\left( {t,v} \right)\]
где \(F\left( {t,v} \right)\) — сумма сил, действующих на объект и может быть функцией времени \(t\) и скорости объекта, \ (в\). Для нашей ситуации у нас будет две силы, действующие на гравитацию объекта, \({F_G} = mg\). действующее в направлении вниз и, следовательно, будет положительным, а сопротивление воздуха \({F_A} = — \gamma v\), действующее в направлении вверх и, следовательно, будет отрицательным. Сведение всего этого во Второй закон Ньютона дает следующее.
\[m\frac{{dv}}{{dt}} = мг — \gamma v\]
Чтобы упростить дифференциальное уравнение, разделим массу \(m\).
\[\begin{equation}\frac{{dv}}{{dt}} = g — \frac{{\gamma v}}{m} \label{eq:eq1}\end{equation}\]
Это линейное дифференциальное уравнение первого порядка, решение которого даст скорость \(v\) (в м/с) падающего объекта массы \(м\), который имеет как силу тяжести, так и воздух действующее на него сопротивление.

Чтобы посмотреть на поля направлений (это, в конце концов, тема этого раздела….), было бы полезно иметь некоторые числа для различных величин в дифференциальном уравнении. Итак, предположим, что у нас есть масса 2 кг и что \(\gamma= 0,392\). Подстановка этого в \(\eqref{eq:eq1}\) дает следующее дифференциальное уравнение.
\[\begin{equation}\frac{{dv}}{{dt}} = 9,8 — 0,196v \label{eq:eq2} \end{equation}\]
Давайте посмотрим на это дифференциальное уравнение с геометрической точки зрения. Предположим, что в течение некоторого времени \(t\) скорость просто равна \(v = 30\) м/с. Обратите внимание: мы не говорим, что скорость когда-либо будет равна 30 м/с. Все, что мы говорим, это то, что давайте предположим, что по какой-то случайности скорость действительно равна 30 м/с в некоторый момент времени \(t\). Таким образом, если в какой-то момент времени \(t\) скорость оказывается равной 30 м/с, мы можем подставить \(v = 30\) к \(\eqref{eq:eq2}\), чтобы получить.

\[\frac{{dv}}{{dt}} = 3,92\]
Вспомните из вашего курса исчисления I, что положительная производная означает, что рассматриваемая функция, в данном случае скорость, возрастает, поэтому, если скорость этого объекта всегда равна 30 м/с в любое время \(t\), скорость должно увеличиваться в это время.
Также напомним, что значение производной при определенном значении \(t\) дает наклон касательной к графику функции в этот момент времени, \(t\). Итак, если в течение некоторого времени \(t\) скорость оказывается равной 30 м/с, то наклон касательной к графику скорости равен 3,9.2.
Мы могли бы продолжить в том же духе и выбрать различные значения \(v\) и вычислить наклон касательной для этих значений скорости. Однако давайте подойдем к этому немного более организованно. Давайте сначала определим значения скорости, которые будут иметь нулевой наклон или горизонтальные касательные. Их достаточно легко найти.
 Все, что нам нужно сделать, это установить производную равной нулю и найти \(v\).
Все, что нам нужно сделать, это установить производную равной нулю и найти \(v\).В нашем примере у нас будет только одно значение скорости, которое будет иметь горизонтальные касательные, \(v = 50\) м/с. Это означает, что ЕСЛИ (опять же, есть это слово, если) в течение некоторого времени \(t\) скорость оказывается равной 50 м/с, тогда касательная в этой точке будет горизонтальной. Каков наклон касательной временами до и после этой точки, еще неизвестно и не имеет отношения к наклону в данный конкретный момент времени \(t\).
Итак, если у нас есть \(v = 50\), мы знаем, что касательные будут горизонтальны. Мы обозначаем это на системе координат горизонтальными стрелками, указывающими в направлении увеличения \(t\) на уровне \(v = 50\), как показано на следующем рисунке.
Теперь давайте нарисуем касательные линии и, следовательно, стрелки для нашего графика для некоторых других значений \(v\). На данный момент единственный точный наклон, который нам полезен, это то, где наклон горизонтален.
 Таким образом, вместо того, чтобы искать точные наклоны для остальной части графика, мы будем следить только за общими тенденциями наклона. Наклон увеличивается или уменьшается? Как быстро наклон увеличивается или уменьшается? Для этого примера эти типы трендов очень легко получить.
Таким образом, вместо того, чтобы искать точные наклоны для остальной части графика, мы будем следить только за общими тенденциями наклона. Наклон увеличивается или уменьшается? Как быстро наклон увеличивается или уменьшается? Для этого примера эти типы трендов очень легко получить.Во-первых, обратите внимание, что правая часть \(\eqref{eq:eq2}\) является многочленом и, следовательно, непрерывна. Это означает, что он может изменить знак только в том случае, если он сначала проходит через ноль. Итак, если производная изменит знак (нет никаких гарантий, что это произойдет), она сделает это при \(v\) = 50, и единственное место, где она может изменить знак, это \(v = 50\). Это означает, что при \(v>50\) наклон касательных к скорости будет иметь тот же знак. Аналогично, для \(v
Начнем с \(v
Теперь посмотрим на \(v>50\). Первое, что нужно сделать, это выяснить, являются ли наклоны положительными или отрицательными. Мы сделаем это так же, как и в последнем бите, , т.
 е. , выберем значение \(v\), подставим его в \(\eqref{eq:eq2}\) и посмотрим, положительна ли производная или отрицательный. Обратите внимание, что вы НИКОГДА не должны предполагать, что производная изменит знак, если производная равна нулю. Это достаточно легко проверить, поэтому вы всегда должны делать это.
е. , выберем значение \(v\), подставим его в \(\eqref{eq:eq2}\) и посмотрим, положительна ли производная или отрицательный. Обратите внимание, что вы НИКОГДА не должны предполагать, что производная изменит знак, если производная равна нулю. Это достаточно легко проверить, поэтому вы всегда должны делать это.Нам нужно проверить производную, поэтому давайте использовать \(v\) = 60. Подставив это в \(\eqref{eq:eq2}\), получим наклон касательной как -1,96 или отрицательный. Следовательно, для всех значений \(v>50\) у нас будут отрицательные наклоны касательных. Как и в случае \(v
Этот график выше называется полем направления для дифференциального уравнения.
Итак, зачем нам поля направлений? Есть два полезных элемента информации, которые можно легко получить из поля направлений для дифференциального уравнения.
- Эскиз растворов . Поскольку стрелки в полях направлений на самом деле касаются реальных решений дифференциальных уравнений, мы можем использовать их в качестве руководства для построения графиков решений дифференциального уравнения.

- Долгосрочное поведение . Во многих случаях нас меньше интересуют фактические решения дифференциальных уравнений, чем то, как решения ведут себя при увеличении \(t\). Поля направлений, если мы сможем их получить, можно использовать для поиска информации об этом долгосрочном поведении решения.
Итак, вернемся к полю направлений для нашего дифференциального уравнения. Предположим, мы хотим узнать, как выглядит решение, имеющее значение \(v\left( 0 \right) = 30\). Мы можем перейти к нашему полю направления и начать с 30 по вертикальной оси. В этот момент мы знаем, что решение увеличивается, и что по мере его увеличения решение должно выравниваться, потому что скорость будет приближаться к значению \(v\) = 50. Итак, мы начинаем рисовать возрастающее решение, и когда мы нажмем стрелку мы просто следим за тем, чтобы оставаться параллельно этой стрелке. Это дает нам рисунок ниже.
Чтобы лучше понять, как ведут себя все решения, давайте добавим еще несколько решений.
 Добавление еще нескольких решений дает рисунок ниже. Набор решений, которые мы изобразили ниже, часто называют семейством кривых решения или набором интегральных кривых . Количество решений, наносимых при построении интегральных кривых, варьируется. Вы должны построить достаточное количество кривых решения, чтобы проиллюстрировать, как ведут себя решения во всех частях поля направления.
Добавление еще нескольких решений дает рисунок ниже. Набор решений, которые мы изобразили ниже, часто называют семейством кривых решения или набором интегральных кривых . Количество решений, наносимых при построении интегральных кривых, варьируется. Вы должны построить достаточное количество кривых решения, чтобы проиллюстрировать, как ведут себя решения во всех частях поля направления.Теперь либо из поля направлений, либо из поля направлений с нарисованными кривыми решения мы можем видеть поведение решения при увеличении \(t\). Для нашего падающего объекта все решения будут приближаться к \(v = 50\) по мере увеличения \(t\).
Нам часто нужно знать, будет ли поведение решения зависеть от значения \(v\)(0). В этом случае поведение решения не будет зависеть от значения \(v\)(0), но это скорее исключение, чем правило, так что не ждите этого. 92}\]
Показать решение
Во-первых, не беспокойтесь о том, откуда появилось это дифференциальное уравнение.
 Честно говоря, мы только что придумали это. Он может описывать, а может и не описывать реальную физическую ситуацию.
Честно говоря, мы только что придумали это. Он может описывать, а может и не описывать реальную физическую ситуацию.Это дифференциальное уравнение выглядит несколько сложнее, чем приведенный выше пример с падающим объектом. Впрочем, за исключением еще немного работы, он ненамного сложнее. Первый шаг — определить, где производная равна нулю. 92}\конец{выравнивание*}\]
Теперь мы можем видеть, что у нас есть три значения \(y\), при которых производная и, следовательно, наклон касательных будут равны нулю. Производная будет равна нулю при \(y\) = -1, 1 и 2. Итак, давайте начнем наше поле направлений с рисования горизонтальных касательных для этих значений. Это показано на рисунке ниже.
Теперь нам нужно добавить стрелки к четырем областям, на которые теперь разделен график. Для каждой из этих областей я выберу значение \(y\) в этой области и подставлю его в правую часть дифференциального уравнения, чтобы увидеть, является ли производная положительной или отрицательной в этой области.
 Опять же, чтобы получить точное поле направления, вы должны выбрать еще несколько значений во всем диапазоне, чтобы увидеть, как ведут себя стрелки во всем диапазоне.
Опять же, чтобы получить точное поле направления, вы должны выбрать еще несколько значений во всем диапазоне, чтобы увидеть, как ведут себя стрелки во всем диапазоне.\(y < - 1\)
В этой области мы можем использовать \(y\) = -2 в качестве контрольной точки. На данный момент мы имеем \(y’ = 36\). Таким образом, касательные в этой области будут иметь очень крутые и положительные наклоны. Также как \(y \to — 1\) наклоны будут сглаживаться, оставаясь положительными. На рисунке ниже показаны поля направлений со стрелками в этой области.
\( — 1 < y < 1\)
В этой области мы можем использовать \(y\) = 0 в качестве контрольной точки. На данный момент мы имеем \(y’ = — 2\). Поэтому касательные в этой области будут иметь отрицательный наклон и, по-видимому, не будут очень крутыми. Так как же выглядят стрелки в этом регионе? Поскольку \(y\to 1\), конечно, остается меньше 1, наклоны должны быть отрицательными и приближаться к нулю. По мере того, как мы удаляемся от 1 и приближаемся к -1, наклоны начинают становиться круче (и остаются отрицательными), но в конечном итоге снова становятся плоскими, снова оставаясь отрицательными, как \(y \to — 1\), поскольку производная должна стремиться к нулю при эта точка.
 На рисунке ниже показаны поля направлений со стрелками, добавленными к этой области.
На рисунке ниже показаны поля направлений со стрелками, добавленными к этой области.\(1 < y < 2\)
В этой области мы будем использовать \(y\) = 1,5 в качестве контрольной точки. В этот момент мы имеем \(y’ = — 0,3125\). Касательные линии в этой области также будут иметь отрицательный наклон и, по-видимому, не будут такими крутыми, как в предыдущей области. Стрелки в этой области будут вести себя практически так же, как и в предыдущей области. Вблизи \(y\) = 1 и \(y\) = 2 наклоны будут сглаживаться, и по мере того, как мы будем двигаться от одного к другому, склоны будут становиться несколько круче, прежде чем снова сгладятся. На рисунке ниже показаны поля направлений со стрелками, добавленными к этой области.
\(y > 2\)
В этой последней области мы будем использовать \(y\) = 3 в качестве контрольной точки. На данный момент мы имеем \(y’ = 16\). Итак, как мы видели, в первой области касательные линии начинаются довольно плоско около \(y\) = 2, а затем, когда мы удаляемся от \(y\) = 2, они становятся довольно крутыми.

Полное поле направления для этого дифференциального уравнения показано ниже.
Вот набор интегральных кривых для этого дифференциального уравнения.
Наконец, давайте посмотрим на долгосрочное поведение всех решений. В отличие от первого примера, долгосрочное поведение в этом случае будет зависеть от значения \(y\) в t = 0. Изучив любой из двух предыдущих рисунков, мы можем прийти к следующему поведению решений как \(t \to \infty \).
Значение \(y\)(0) Поведение как \(t\to\infty\) \(у\влево( 0 \вправо) < 1\) \(у\к — 1\) \(1 \le y\left( 0 \right) < 2\) \(г\к 1\) \(у\влево(0\вправо) = 2\) \(у\до 2\) \(у\влево(0\вправо) > 2\) \(у\до\infty\) Не забудьте отметить, что делают горизонтальные решения.
 Это часто самая упущенная часть такого рода проблем.
Это часто самая упущенная часть такого рода проблем.В обоих примерах, над которыми мы работали до этого момента, правая часть производной содержала только функцию, а НЕ независимую переменную. Когда правая часть дифференциального уравнения содержит как функцию, так и независимую переменную, поведение может быть намного более сложным, и рисовать поля направлений вручную может быть очень сложно. Компьютерное программное обеспечение очень удобно в этих случаях.
Однако в некоторых случаях их не так уж сложно сделать вручную. Давайте посмотрим на следующий пример.
Пример 2 Нарисуйте поле направлений для следующего дифференциального уравнения. Нарисуйте набор интегральных кривых для этого дифференциального уравнения. \[у’ = у — х\]
Показать решение
Чтобы набросать поля направлений для дифференциального уравнения такого типа, мы сначала определяем места, где производная будет постоянной.

- Эскиз растворов . Поскольку стрелки в полях направлений на самом деле касаются реальных решений дифференциальных уравнений, мы можем использовать их в качестве руководства для построения графиков решений дифференциального уравнения.

 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
 {kt}.
\label{мужчины-22}\tag{2.4.3}
\end{уравнение}
Важно отметить, что никакое программное обеспечение не может отображать общие решения, потому что для построения точек компьютер должен иметь возможность генерировать пары координат. Это можно сделать, только если мы укажем значения для констант \(P_0\) и \(k\text{.}\)
{kt}.
\label{мужчины-22}\tag{2.4.3}
\end{уравнение}
Важно отметить, что никакое программное обеспечение не может отображать общие решения, потому что для построения точек компьютер должен иметь возможность генерировать пары координат. Это можно сделать, только если мы укажем значения для констант \(P_0\) и \(k\text{.}\) Следующий код демонстрирует это для дифференциального уравнения:
\begin{уравнение}
\frac{dy}{dx} = \cos(xy),
\label{мужчины-24}\tag{2.4.5}
\end{уравнение}
не имеет решения, выражаемого через элементарные функции. Следующий код создает график поля наклона, а затем объединяет его с выходными данными многократного вызова desolve_rk4.
Следующий код демонстрирует это для дифференциального уравнения:
\begin{уравнение}
\frac{dy}{dx} = \cos(xy),
\label{мужчины-24}\tag{2.4.5}
\end{уравнение}
не имеет решения, выражаемого через элементарные функции. Следующий код создает график поля наклона, а затем объединяет его с выходными данными многократного вызова desolve_rk4. \end{уравнение*}
Метод включает два этапа. Сначала мы создаем таблицу. Каждая строка в таблице соответствует одной изоклине. Во-вторых, для каждой строки таблицы мы начертили соответствующую изоклину и украсили ее регулярно расположенными полосами, все из которых имеют одинаковый наклон. Наклон соответствует значению в первом столбце таблицы.
\end{уравнение*}
Метод включает два этапа. Сначала мы создаем таблицу. Каждая строка в таблице соответствует одной изоклине. Во-вторых, для каждой строки таблицы мы начертили соответствующую изоклину и украсили ее регулярно расположенными полосами, все из которых имеют одинаковый наклон. Наклон соответствует значению в первом столбце таблицы.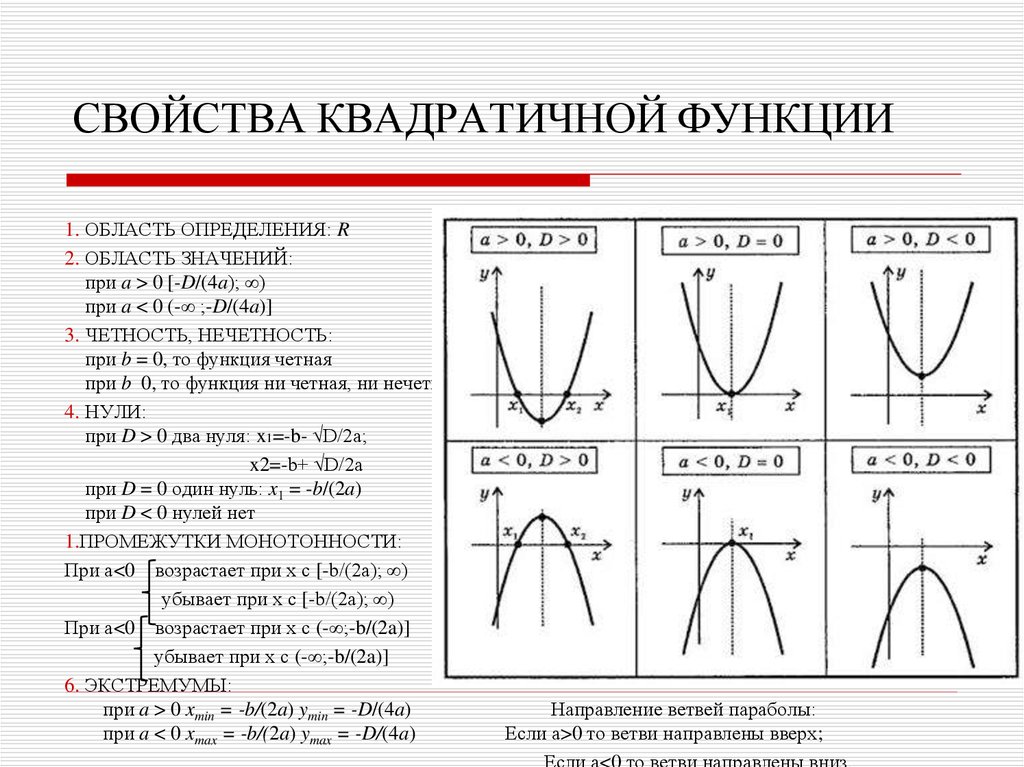 \begin{уравнение*}
\ гидроразрыв {dy} {dx} = х + у
\end{уравнение*}
\begin{уравнение*}
\ гидроразрыв {dy} {dx} = х + у
\end{уравнение*}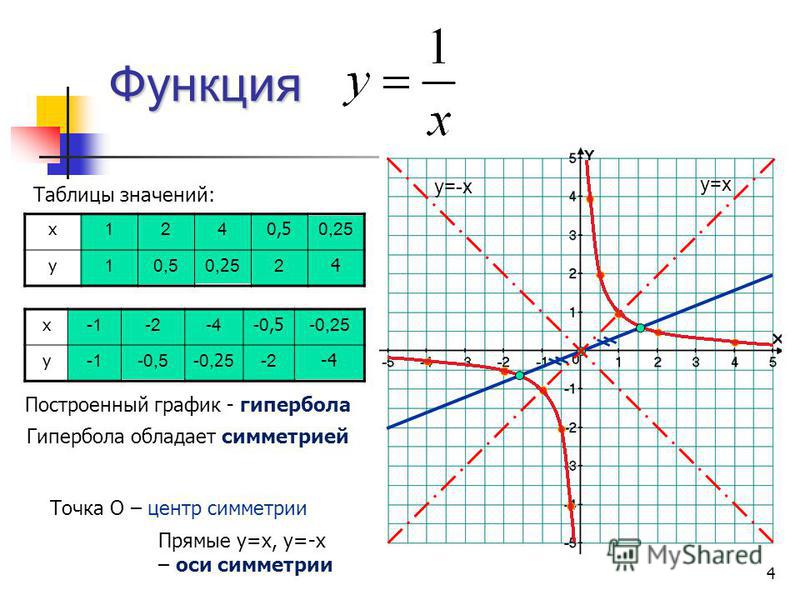 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Почти каждую физическую ситуацию, происходящую в природе, можно описать соответствующим дифференциальным уравнением. Дифференциальное уравнение может быть легко или трудно получить в зависимости от ситуации и предположений, которые делаются о ситуации, и мы, возможно, никогда не сможем его решить, однако оно будет существовать.
Почти каждую физическую ситуацию, происходящую в природе, можно описать соответствующим дифференциальным уравнением. Дифференциальное уравнение может быть легко или трудно получить в зависимости от ситуации и предположений, которые делаются о ситуации, и мы, возможно, никогда не сможем его решить, однако оно будет существовать.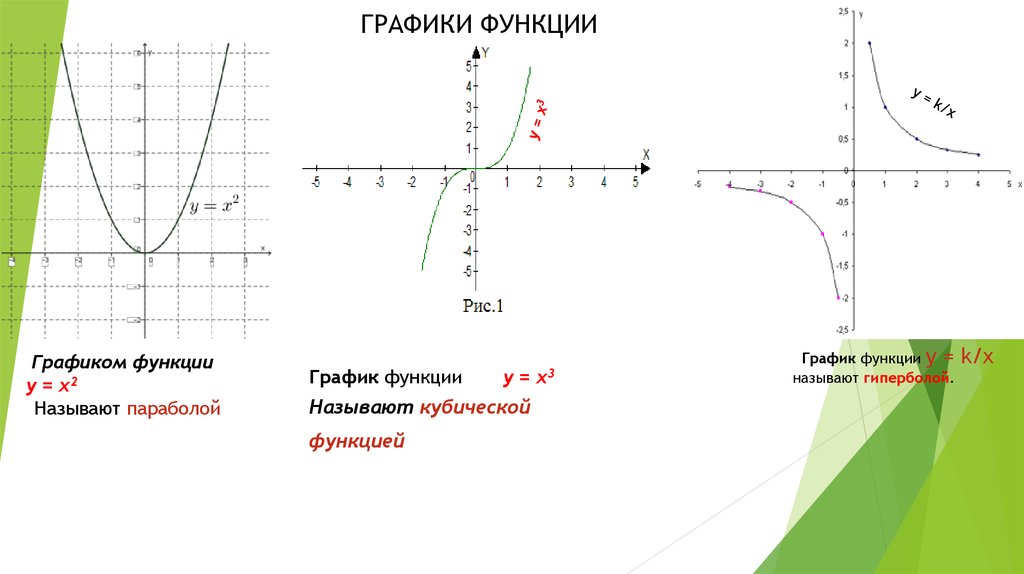 Будем считать, что силы, действующие в направлении вниз, являются положительными силами, а силы, действующие в направлении вверх, отрицательными. Точно так же мы предположим, что объект, движущийся вниз (, т.е. падающий объект), будет иметь положительную скорость.
Будем считать, что силы, действующие в направлении вниз, являются положительными силами, а силы, действующие в направлении вверх, отрицательными. Точно так же мы предположим, что объект, движущийся вниз (, т.е. падающий объект), будет иметь положительную скорость. «-» даст нам правильный знак и, следовательно, направление для этой силы.
«-» даст нам правильный знак и, следовательно, направление для этой силы.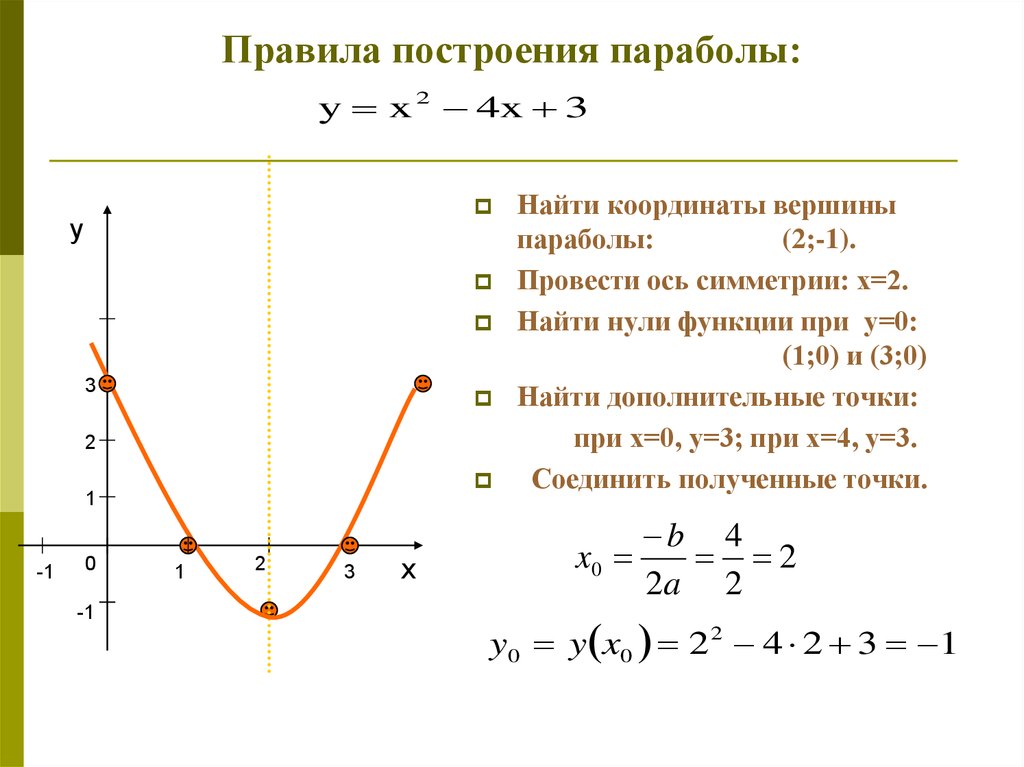

 Все, что нам нужно сделать, это установить производную равной нулю и найти \(v\).
Все, что нам нужно сделать, это установить производную равной нулю и найти \(v\). Таким образом, вместо того, чтобы искать точные наклоны для остальной части графика, мы будем следить только за общими тенденциями наклона. Наклон увеличивается или уменьшается? Как быстро наклон увеличивается или уменьшается? Для этого примера эти типы трендов очень легко получить.
Таким образом, вместо того, чтобы искать точные наклоны для остальной части графика, мы будем следить только за общими тенденциями наклона. Наклон увеличивается или уменьшается? Как быстро наклон увеличивается или уменьшается? Для этого примера эти типы трендов очень легко получить. е. , выберем значение \(v\), подставим его в \(\eqref{eq:eq2}\) и посмотрим, положительна ли производная или отрицательный. Обратите внимание, что вы НИКОГДА не должны предполагать, что производная изменит знак, если производная равна нулю. Это достаточно легко проверить, поэтому вы всегда должны делать это.
е. , выберем значение \(v\), подставим его в \(\eqref{eq:eq2}\) и посмотрим, положительна ли производная или отрицательный. Обратите внимание, что вы НИКОГДА не должны предполагать, что производная изменит знак, если производная равна нулю. Это достаточно легко проверить, поэтому вы всегда должны делать это.
 Добавление еще нескольких решений дает рисунок ниже. Набор решений, которые мы изобразили ниже, часто называют семейством кривых решения или набором интегральных кривых . Количество решений, наносимых при построении интегральных кривых, варьируется. Вы должны построить достаточное количество кривых решения, чтобы проиллюстрировать, как ведут себя решения во всех частях поля направления.
Добавление еще нескольких решений дает рисунок ниже. Набор решений, которые мы изобразили ниже, часто называют семейством кривых решения или набором интегральных кривых . Количество решений, наносимых при построении интегральных кривых, варьируется. Вы должны построить достаточное количество кривых решения, чтобы проиллюстрировать, как ведут себя решения во всех частях поля направления. Честно говоря, мы только что придумали это. Он может описывать, а может и не описывать реальную физическую ситуацию.
Честно говоря, мы только что придумали это. Он может описывать, а может и не описывать реальную физическую ситуацию. Опять же, чтобы получить точное поле направления, вы должны выбрать еще несколько значений во всем диапазоне, чтобы увидеть, как ведут себя стрелки во всем диапазоне.
Опять же, чтобы получить точное поле направления, вы должны выбрать еще несколько значений во всем диапазоне, чтобы увидеть, как ведут себя стрелки во всем диапазоне. На рисунке ниже показаны поля направлений со стрелками, добавленными к этой области.
На рисунке ниже показаны поля направлений со стрелками, добавленными к этой области.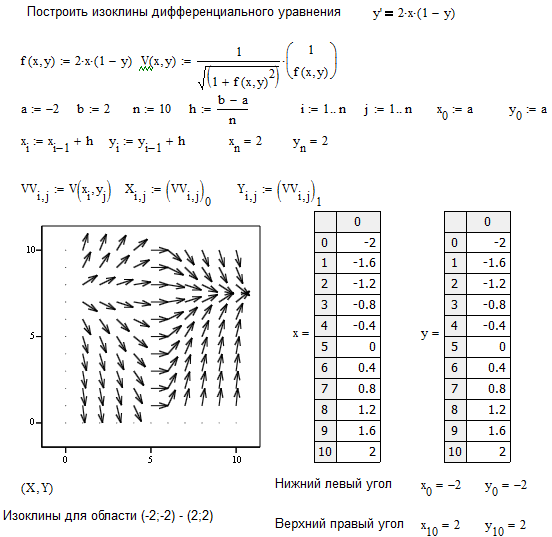
 Это часто самая упущенная часть такого рода проблем.
Это часто самая упущенная часть такого рода проблем.