Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| WinterPrimat |
| ||
02/01/23 |
| ||
| |||
| wrest |
| ||
05/09/16 |
| ||
| |||
| Gagarin1968 |
| ||
01/11/14 |
| ||
| |||
| WinterPrimat |
| ||
02/01/23 |
| ||
| |||
| Ende |
| |||||
02/02/19 |
| |||||
| ||||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Gagarin1968 |
| ||
01/11/14 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Как пользоваться логарифмической линейкой?
Не стоит забывать, что именно с помощью логарифмической линейки человек впервые ступил на Луну.
Теги:
интересное
Unsplash
Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.
Содержание статьи
Уильям Отред — изобретатель логарифмической линейки
Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.
— Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.
youtube
Нажми и смотри
История изобретения
В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.
Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы…» Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах. ..», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.
..», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.
Споры об авторстве
Авторство этого изобретения оспаривал другой его ученик — Ричард Деламэйн, опубликовавший в 1630 году книгу «Граммелогия, или Математическое кольцо». Некоторые утверждают, что он просто украл изобретение счетной линейки у учителя, но возможно, он пришел к похожему решению независимо. Еще один претендент на авторство - лондонский математик Эдмунд Уингейт, предложивший в 1626 году использовать две линейки Гюнтера, скользящие друг относительно друга. До современного состояния инструмент довели Роберт Биссакер, сделавший линейку прямой (1654), Джон Робертсон, снабдивший ее бегунком (1775), и Амеде Маннгейм, оптимизировавший расположение шкал и бегунка.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.
В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.
Как пользоваться логарифмической линейкой
Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.
СложениеПредставим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.
УмножениеДля начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg(a) + lg(b )= lg(с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.
Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.
На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).
Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).
ДелениеПусть a/b = с при a = 8, b = 4. Возведем в логарифм обе части равенства и тогда получим: Lg(a) – lg(b) = lg(с). Разность логарифмов делимого и делителя дает логарифм частного, в нашем случае — 2.
На основной шкале корпуса линейки выбирается делимое, на которое устанавливается волосок бегунка. Под волосок подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.
Результат определяется на основной шкале корпуса напротив начала или конца движка.
Читайте также:
Зачем нужен безель в наручных часах?
Невероятные механические головоломки от инженера-энтузиаста: мир шестеренок
Счет, аппроксимация, временная сложность и большое арифметическое
CSC300: счет, аппроксимация, временная сложность и большое арифметическое и возведение в степень [2/9](нажмите здесь на один слайд на страницу)
| [1/9] |
В двух частях
| Открытый список воспроизведения |
| youtube.com/embed/bQDUnEYE6Vg/?enablejsapi=1&autoplay=0&rel=0&vq=hd1080″ frameborder=»0″ allowfullscreen=»allowfullscreen»/> Открытый плейлист |
. Счет и эксплуатация [2/910 = 1024
Все мы привыкли считать, прибавляя единицу (арифметический ряд): 0 1 2 3 4 5 6 7 ... Н Также можно считать умножением на два (геометрический ряд): 1 2 4 8 16 32 64 128 ... Н Существует обратная операция, называемая логарифмом .
Люди часто пишут
lg(1) = 0 lg(тысячи) ~ 10
lg(2) = 1 lg(миллион) ~ 20
lg(4) = 2 lg(миллиард) ~ 30
lg(8) = 3 lg(триллион) ~ 40
lg(16) = 4 lg(квадриллион) ~ 50
lg(32) = 5 lg(квинтиллион) ~ 60
lg(64) = 6
lg(128) = 7
lg(256) = 8
lg(512) = 9
lg(1024) = 10
Они эквивалентны: 960 ~ 16 квинтиллионов (на самом деле 18_446_744_073_709_551_616)
С lg(N*M) = lg(N) + lg(M) у нас есть: lg(4 миллиарда) ~ lg(4) + lg(миллиард) = 2 + 30 lg(16 квинтиллионов) ~ lg(16) + lg(квинтиллионов) = 4 + 60
Вообще логи могут иметь любую базу. log_b(N) = log_a(N) / log_a(b) Например, где log_1024(N) = lg(N)/10 --- так как lg(1024) = 10 Другой пример, где log(N) ~ lg(N)/3 --- поскольку lg(10) = 3,32192809489 Кому-то может быть полезно это видео:
Вот расслабляющее введение в логарифмы, которое может вам понравиться:
Часто детали не важны Мы пишем
Мы говорим, что
Изображение из 8 временных сложностей, которые должен решить каждый программист знать Адриан Мехиа Пересмотрено: 17. Экспоненты и логарифмыЭкспоненты и логарифмы
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 02.2023, 14:18
02.2023, 14:18  Оно и убило (почти) десятичные логарифмы.
Оно и убило (почти) десятичные логарифмы.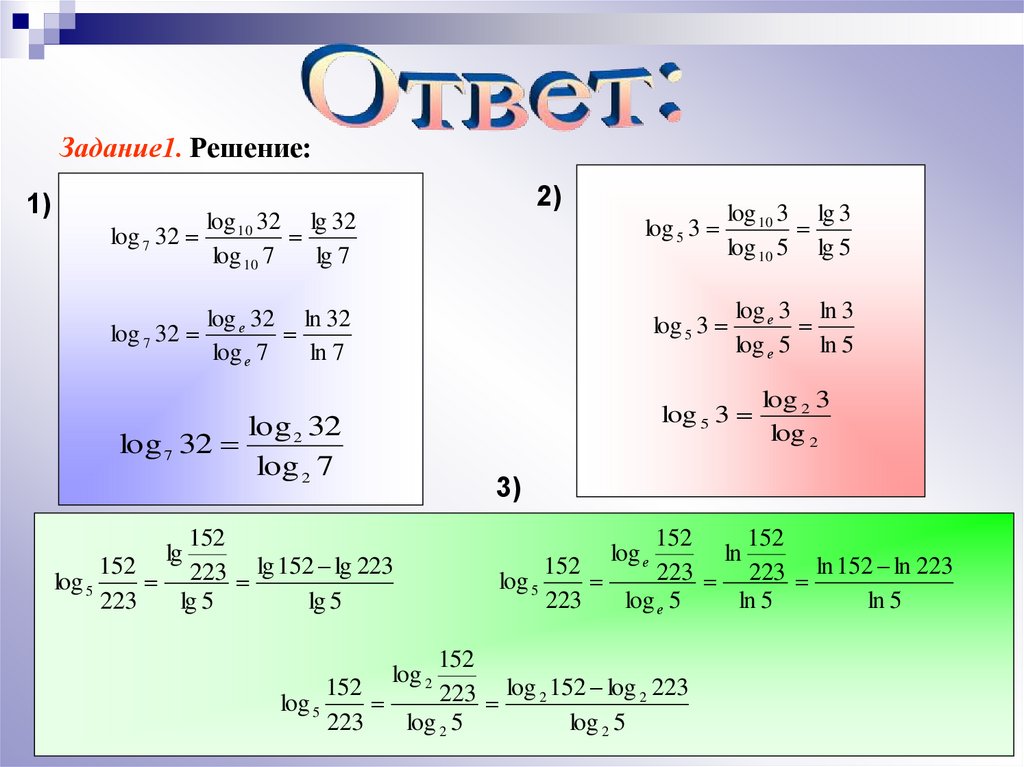 Я только неделю назад вообще узнал о таком пособии.
Я только неделю назад вообще узнал о таком пособии.
 И обращён материал к её слушателям, практикам. скажем. офицерам-расчётчикам, а не математикам. восхищающимся изяществом формулы. По ней надо получить конкретное значение. Для тех лет, когда создавалось пособие — у расчётчика была логарифмическая линейка, а на ней шкала десятичных логарифмов. Сейчас есть калькулятор, где тоже есть десятичные логарифмы, есть натуральные. А по произвольному основанию нет, по нему надо считать по приведенной ею формуле, или по аналогичной, с заменой lg на ln.
И обращён материал к её слушателям, практикам. скажем. офицерам-расчётчикам, а не математикам. восхищающимся изяществом формулы. По ней надо получить конкретное значение. Для тех лет, когда создавалось пособие — у расчётчика была логарифмическая линейка, а на ней шкала десятичных логарифмов. Сейчас есть калькулятор, где тоже есть десятичные логарифмы, есть натуральные. А по произвольному основанию нет, по нему надо считать по приведенной ею формуле, или по аналогичной, с заменой lg на ln. Грекова. Лишь гораздо позже узнал, что это псевдоним, и что её настоящее имя — Елена Сергеевна Вентцель. (Более того, думал, что она Ирина Грекова; на самом деле псевдоним образован от «игрек».)
Грекова. Лишь гораздо позже узнал, что это псевдоним, и что её настоящее имя — Елена Сергеевна Вентцель. (Более того, думал, что она Ирина Грекова; на самом деле псевдоним образован от «игрек».) С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.
С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.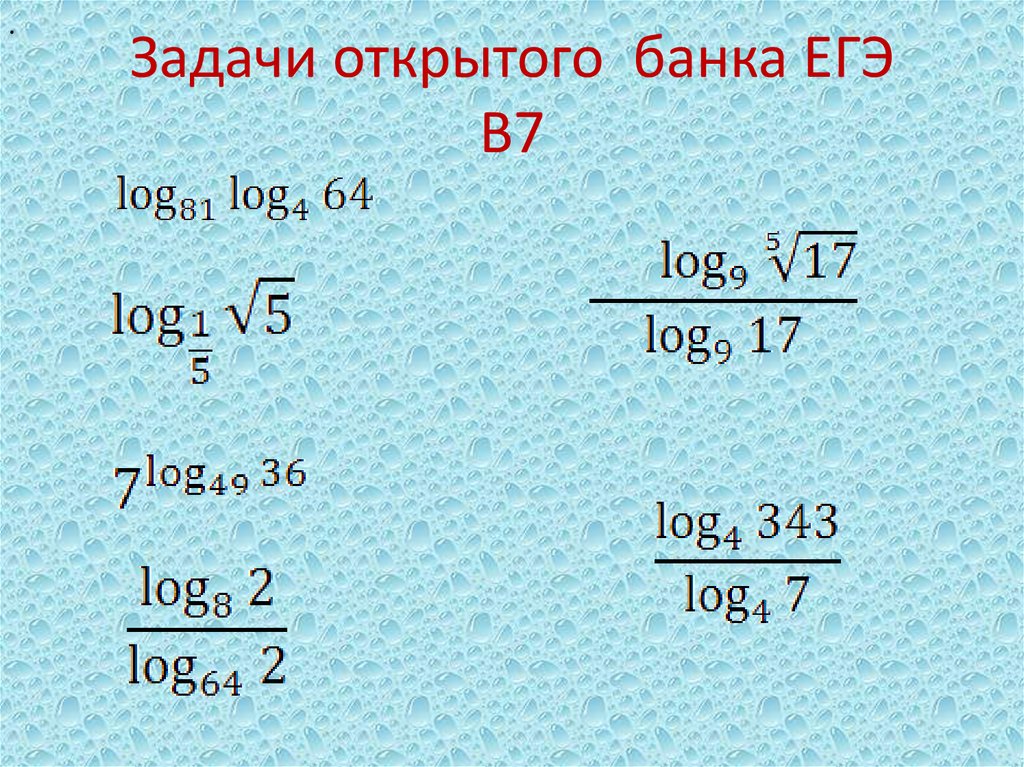 С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.
С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945. Как правило, мы пишем
Как правило, мы пишем  03.2008 13:01
03.2008 13:01 Не говоря уже о том, что вы склонны к
делать ошибки.
Не говоря уже о том, что вы склонны к
делать ошибки. 





 Вы делаете а не нужно брать 10 как основание для ввода показателя степени. Ты можешь взять любой номер .
Вы делаете а не нужно брать 10 как основание для ввода показателя степени. Ты можешь взять любой номер .


 На словах:
вторая производная определяемой функции y равна
сама функция, умноженная на некоторую константу А . Вы можете понять, что это было бы
полезно знать функцию y(x) , которая совпадает со своей производной, или dy(x)/dx = y(x) .
На словах:
вторая производная определяемой функции y равна
сама функция, умноженная на некоторую константу А . Вы можете понять, что это было бы
полезно знать функцию y(x) , которая совпадает со своей производной, или dy(x)/dx = y(x) . 
 Приз, который нужно заплатить, заключается в том, что теперь вы должны работать с
комплексные числа с вида с = с’ + ic» с i = воображаемая единица, обычно, хотя и несколько ошибочно, называемая «квадратом».
корень минус -1″. Правильно это: i 2 = 1 . И нет, это не то же самое.
Приз, который нужно заплатить, заключается в том, что теперь вы должны работать с
комплексные числа с вида с = с’ + ic» с i = воображаемая единица, обычно, хотя и несколько ошибочно, называемая «квадратом».
корень минус -1″. Правильно это: i 2 = 1 . И нет, это не то же самое. 
 х + пер. у
х + пер. у Если вы хотите рассчитать
числовое значение e , просто возьмите x = 1 .
Если вы хотите рассчитать
числовое значение e , просто возьмите x = 1 . .
. 