Как считать на калькуляторе логарифмы: Как вычислить на калькуляторе логарифм 🚩 калькулятор с логарифмами 🚩 Математика

Содержание

Что такое логарифм и как сделать лог на калькуляторе

Логарифм — это математическая процедура, которая определяет, сколько раз данное число, известное как основание, умножается само на себя, чтобы получить другое число. Поскольку логарифмы связывают геометрические и арифметические прогрессии, примеры можно найти в природе и искусстве, включая расстояние между гитарными ладами, твердость минералов, интенсивность звука, звезды, ураганы, землетрясения и кислоты. Логарифмы даже объясняют, как люди естественным образом думают о числах. Потенцирование позволяет каждому положительному целому числу иметь подлинную силу в качестве основы и всегда дает положительный результат. Это может быть выражено как logb(x). Произведение двух положительных чисел b и x всегда является действительным числом y. Десятичный или десятичный логарифм является основой логарифма. Основанием натурального логарифма является целое число e.

На графическом или научном калькуляторе функция «Лог» — это клавиша, позволяющая работать с логарифмами. Логарифмы — это средство вычисления количества степеней, необходимых для умножения заданного целого числа. Например, применение функции «Журнал» к числу 10 показывает, что для получения числа 10 необходимо один раз умножить базовое число 10 само на себя. На калькуляторе нажмите кнопку «Журнал». Число, которое вы видите сразу, является показателем степени введенного вами числа. Чтобы получить исходное число, умножьте 10 на то количество раз, которое вы видите на экране, предполагая, что базовое число равно 10 (которое всегда будет на графическом или научном калькуляторе).

Как работает логарифм?

Показатель степени или степень, до которой необходимо увеличить основание, чтобы получить определенное число, называется логарифмом. X — логарифм n по основанию b, выраженный математически. Логарифмы второго типа (то есть логарифмы по основанию 10) называются обычными или бриггсовскими логарифмами и представляются просто как log n.
Джон Нейпир ввел логарифмы в начале 17 века как способ упростить вычисления. Используя логарифмические линейки и таблицы логарифмов, навигаторы, ученые, инженеры и другие быстро освоили логарифмы, чтобы упростить вычисления. Поскольку логарифм произведения представляет собой сумму логарифмов частей, утомительные процессы многозначного умножения можно заменить поиском в таблице и более простым сложением. Натуральный логарифм остается одной из самых ценных функций математики, находящей применение в математических моделях в физических и биологических науках.

Rollenbiografie – mal anders und …

Please enable JavaScript

Rollenbiografie – mal anders und vielleicht lebendiger — Beispiel: der Prinz in „Emilia Galotti“

Калькулятор журнала

Наш калькулятор логов (https://calconcalculator.com/math/log-calculator-logarithm/) позволяет получить логарифм (положительного вещественного) целого числа, используя основание по вашему выбору (положительное, не равное 1). Этот инструмент решит вашу проблему, нужен ли вам натуральный логарифм, логарифмическая база из 2 логарифмов или логарифмическая база из 10 логарифмов. Продолжайте читать, чтобы узнать больше о формуле логарифма и рекомендациях, которым вы должны следовать. Кроме того, вы могли бы узнать что-то новое, например, почему логарифмы важны в нашей жизни и как они используются.

Как использовать лог на калькуляторе?

Вот несколько шагов, которые вы можете выполнить без регистрации вашего калькулятора:
1. Введите цифры. Включите калькулятор и введите значение, чтобы вычислить десятичный логарифм (логарифм по основанию 10) числа.
2. Активируйте кнопку «Журнал». Чтобы применить функцию журнала к числу, используйте кнопку журнала калькулятора.
3. (Необязательно) Перепроверьте ответ. Теперь вы можете продолжить и перепроверить свою работу, чтобы убедиться, что вы правильно выполнили все инструкции. Например, результат «3». Когда мы умножаем 10 на три раза, мы получаем 1000, что указывает на точность решения. Если вы хотите узнать больше об этих калькуляторах, вы можете проверить их на www.calconcalculator.com.

Функции инженерного калькулятора

Калькулятор умеет работать со степенями и логарифмами.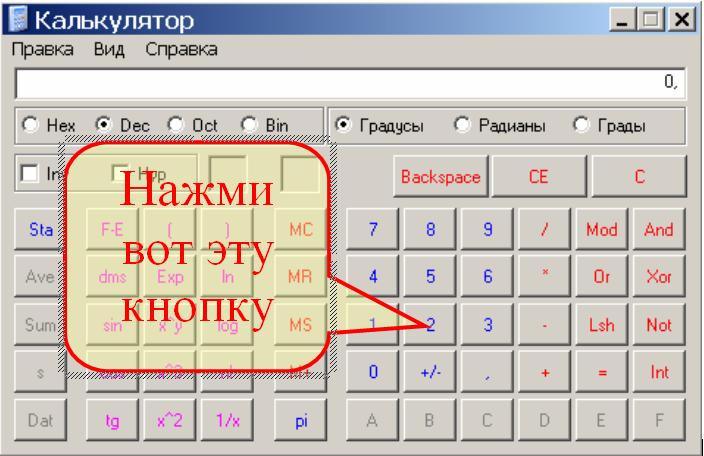 Находит синус, косинус, тангенс и котангенс, а также арксинус, арккосинус, арктангенс и арккотангенс. Поддерживает двоичные логарифмы, логарифмы по основанию. Может возвести число в 10-ю степень. Также, калькулятор позволяет просматривать число Эйлера и число Пи. Помимо этого поддерживаются стандартные арифметический действия, с помощью которых вы можете сложить и вычесть числа, умножить и разделить, а также извлечь квадратный корень онлайн.

Подробная инструкция и ознакомление с основными возможностями.

Найти корень. Чтобы найти квадратный корень числа, введите это число в калькулятор, а затем нажмите кнопку «√», которая находится в верхнем ряду основного блока, вторая справа. Допустим, если мы введем число 9, то после нажатия на эту кнопку получим число 3.
Возвести число в квадрат. Чтобы возвести число в квадрат онлайн вам необходимо воспользоваться кнопкой «X2», которая находится в левом блоке функций, в правой части третьего ряда снизу. В результате число, имевшееся на экране, будет возведено в квадрат. К примеру, на экране горит 3. В результате мы получим 9.
Возвести число в степень. Возвести число в степень можно с помощью кнопки «Xy» в правом верхнем углу калькулятора. Сначала введите число, которое нужно возвести, затем нажмите на эту кнопку и введите число самой степени. Например, если мы попробуем возвести 10 в степень 2, то получим 100.

Синус, косинус, тангенс, котангенс. Часто бывает так, что необходимо найти синус острого угла, косинус прямого угла, синус внешнего угла, а также тангенс или котангенс треугольника. На нашем калькуляторе данные вычисления можно производить с помощью кнопок «sin», «cos», «tg», «ctg». Приведем конкретный пример: допустим, нам требуется найти косинус угла в 90 градусов. Для этого, введем на калькуляторе цифру 90 и нажмем кнопку «cos» в левом блоке функций. В результате мы получим длинную цифру -0.4480736161291701. Это и есть косинус угла 90. 2=100.
Превратить число в отрицательное или положительное. Иногда требуется превратить число в отрицательное или наоборот. Чтобы не вводить его заново, просто нажмите на кнопку «+/-»
Посмотреть число Пи и число Эйлера можно с помощью кнопок «П» и «е» в правом углу левого блока.
Простые математические действия осуществляются с помощью клавиш в правом (основном) блоке. «+» — сложение, «-» — вычитание, «x» – умножение и «÷» — умножение.
Функция памяти. Пользоваться функцией памяти в нашем онлайн калькуляторе очень просто. Допустим, вы получили какое-то число, которое нужно запомнить. Чтобы сделать это нажмите «M+». Когда это число вам понадобится, просто нажмите кнопку «MR» и оно выведется на экран. После этого вы сможете совершать с ним математические операции. Также, вы можете плюсовать или вычитать имеющееся число из числа, которое уже в памяти. Допустим, в памяти у вас число 10. А на экране число 2. Если вы нажмете кнопку «M-«, то из 10 вычтется 2 и в памяти останется число 8. Точно так же происходит с кнопкой «M+». Если вы хотите очистить память — нажмите «MC» и память станет пустой.

Разделить целое на текущее. Часто в инженерной работе требуется провести довольно тривиальное вычисление: узнать, сколько текущий показатель составляет от единого целого. Для этого в нашем инженерном калькулятор существует кнопочка 1/x. Она делит единицу на текущее число. Скажем, если на табло горит 5, то функция выведет 0.2.

Как использовать вход в научный калькулятор

Последнее обновление: 11 февраля 2023 г.

Логарифмы легко понять. Это функции, которые помогают вам определить, какие показатели степени должны быть умножены на определенное число.

По мере того, как вы будете изучать сложную математику, вам нужно будет использовать научные калькуляторы для быстрого расчета значений журнала.

Эти калькуляторы сильно отличаются от обычных и бизнес-калькуляторов и оснащены функциями, помогающими решать физические, инженерные и тригонометрические задачи.

К счастью, работать с логарифмическими функциями на инженерном калькуляторе легко — после того, как вы научитесь делать это правильно.

Вычисление десятичного логарифма с помощью научного калькулятора

Шаг 1. Введите число

Включите калькулятор и введите число, для которого вы хотите вычислить десятичный логарифм.

Возьмем для примера «1000».

Шаг 2. Нажмите кнопку журнала

Чтобы применить функцию журнала к числу, нажмите кнопку журнала на калькуляторе.

Число появится на экране сразу после того, как вы нажмете кнопку журнала. Цифра представляет собой количество раз, которое вы должны умножить на 10, чтобы получить исходное число.

Шаг 3. Подтвердите ответ (необязательно)

Вы можете проверить свою работу, чтобы убедиться, что все шаги выполнены правильно. В нашем примере в качестве результата появляется «3». Умножение 10 на себя трижды дает нам 1000, а значит, ответ правильный.

Хотя в научных калькуляторах нет антилогарифмического калькулятора, вы можете использовать результат логарифмического вычисления в качестве показателя степени 10, чтобы найти антилогарифм любого журнала.

Вычисление натуральных логарифмов с помощью научного калькулятора

Натуральные логарифмы — это логарифмы с основанием «e», и на большинстве научных калькуляторов они представлены кнопкой «ln».

Чтобы использовать клавишу ln для нахождения логарифма по основанию e:

Шаг 1. Введите число

Введите число, натуральный логарифм которого вы хотите найти. Допустим, это 10.

Шаг № 2: Найдите и нажмите кнопку «ln»

Затем вы должны нажать кнопку «ln» на калькуляторе. Результат появится сразу.

Результатом является число, до которого нужно возвести иррациональное основание «е», чтобы получить аргумент.

Вычисление логарифма с другими основаниями на научном калькуляторе

Большинство научных калькуляторов поставляются только с кнопками логарифма и ln. Нет кнопки для нахождения логарифмов с другими основаниями.

Чтобы вычислить логарифм с другим основанием, вы должны использовать формулу замены основания, а именно:

a=a b

Итак, если вы хотите найти значение 3, вы должны вычислить 3 2 .

Чтобы сделать это на своем инженерном калькуляторе:

Шаг № 1: Введите числитель

Для этого введите аргумент вашего логарифма в калькулятор. В нашем примере аргумент равен 3.

Затем нажмите кнопку «ln» на калькуляторе. Но пока не нажимайте «=».

Шаг №2: Введите знаменатель

После ввода числителя найдите и нажмите кнопку «разделить» на калькуляторе. Затем вы должны ввести знаменатель в калькулятор.

Для этого сначала нажмите кнопку «ln». Естественная логарифмическая функция появится с одной скобкой. (clubdeportestolima.com.co) Затем вы должны ввести аргумент логарифма, который в этом примере равен 2.

Чтобы запустить расчет, введите закрывающую скобку в калькуляторе.

Результат появится на экране с указанием значения 3 .

Заключение

Как видите, вычислить логарифм любого числа с помощью научного калькулятора довольно просто. После того, как вы воспользуетесь им несколько раз, вы поймете, где находятся кнопки, и сможете быстро находить значения.

У нас есть различные комплексные калькуляторы, которые вы можете использовать онлайн бесплатно. Вы можете выбрать калькулятор t-теста, график, матрицу, стандартное отклонение, статистику и научные калькуляторы. Проверьте это здесь.

Быстро вычислить логарифмы без калькулятора | Советы и рекомендации MCAT

24 июня 2022 г.

20 декабря 2018 г.

Челси Майерс

Последнее обновление: Лаура Тернер, 24 июня 2022 г.

Логарифмы — одна из самых сложных математических тем на MCAT, потому что многие из нас не изучали их со средней школы и, вероятно, так и не научились вычислять логарифмы без калькулятора.

Это хорошая/плохая новость. Плохая новость заключается в том, что проблемы pH и интенсивности звука из общей химии и физики потребуют от вас работы с логарифмами без калькулятора. Хорошая новость заключается в том, что есть трюк, который упрощает вычисление логарифмов и поразит ваших друзей своими математическими способностями в уме.

Сначала краткий обзор того, что такое логарифмы и почему они важны для MCAT: десятичный логарифм или оператор «логарифма» (иногда его называют «логарифм ₁₀») наиболее полезен при описании того, что измеряется на очень крупный масштаб.

Владение логарифмами было необходимо ученым и инженерам в 19-м и начале 20-го веков, потому что их можно было использовать для упрощения всех видов сложных вычислений. Современные компьютеры сделали эти навыки устаревшими, но десятичные логарифмы по-прежнему используются в таких задачах, как расчеты pH, где основная шкала изменяется в соответствии со степенью 10.

В химии кислотность может быть измерена по линейной шкале от [H+] = 0,00000000000001M до [H+] = 1M. Однако разница в 1 млн [H+] на самом деле не имеет значения. Мы видим реальные различия в кислотности между веществами, когда [Н+] одного в 100 или 1000 (и более!) раз больше, чем [Н+] другого.

Расчет pH позволяет нам измерять кислотность по логарифмической шкале от pH=14 до pH=0. Точно так же, как более разумно измерять расстояние между Токио и Лондоном в милях, а не в дюймах, более полезно описывать кислотность, используя pH, а не [H+].

Как именно это работает? Логарифмическая функция используется для решения уравнений, в которых переменная представляет собой показатель степени с основанием 10. Например, 10 ^X = 100. Логарифмический оператор позволяет найти X и записать эквивалентное выражение в виде log(100) = X. 10 ^X = 100 — экспоненциальная форма выражения, а log(100) = X — логарифмическая форма.

Легче всего определить логарифм степени 10, потому что решение равно степени степени. Продолжая приведенный выше пример, мы можем решить уравнение, переписав log(100) как log(10 ² ) = 2.

Конечно, на MCAT вам потребуется аппроксимировать логарифм значений, которые не являются простыми степенями 10. Обратите внимание, что ключевое слово здесь —

приблизительно . Один из наиболее важных принципов овладения математикой MCAT заключается в том, чтобы помнить, что вам не нужно вычислять точный ответ на каждую задачу, вам просто нужно подобраться достаточно близко, чтобы выбрать правильный ответ из списка возможных вариантов.

Вспомним, что pH – это отрицательный логарифм [H+]. Мы можем аппроксимировать отрицательный логарифм количества, используя формулу

–log(m x 10 ^-n ) ≈ n – 0.m

, где m — число от 1 до 10, а n — целое число (целое число).

Некоторые быстрые примеры с использованием аппроксимации:

–log(3 x 10 ^-5 ) ≈ 5 – 0,3 = 4,7
–log(7,1 x 10 ^{-9 ≥ 9}0 1 8,29
– log(2,5 x 10 ^-2

) ≈ 2 – 0,25 = 1,75

Вот и все!

Давайте закончим парой проблем с pH:

Мы надеемся, что эти инструкции по вычислению логарифмов без калькулятора помогут вам победить MCAT! Обязательно ознакомьтесь с остальными сериями советов и рекомендаций MCAT:

Часть I. Преобразование единиц измерения в метрическую систему
Часть III. Использование аппроксимации для выполнения сложных вычислений
Часть IV. Преобразование единиц измерения в восьми простых шаги
Часть V – Тригонометрия

Хотите узнать больше о том, как добиться успеха на MCAT? Посмотрите этот вебинар от Student Doctor Network и MedSchoolCoach, на котором разбираются ключевые факторы для отличного результата

Text Version of Quiz

Q: What is the pH of a 4.2 x 10 ^-3 M HNO ₃ solution?

a) 1,61
b) 2,38
c) 3,42
d) 4,20

раствор равен отрицательному логарифму концентрации. В этом случае pH = –log(4,2 x 10 ^-3 ). Используя приближение, мы можем решить –log(4,2 x 10 ^-3 ) ≈ 3 – 0,42 ≈ 2,5, что ближе всего к ответу b).

Q: K _a кислоты, буфер которой имеет pH 3,62 в растворе, содержащем равные M кислоты и сопряженного основания, ближе всего к: -7
б) 3,62 х 10 ^-5
в) 2,40 х 10 ^-4
г) 7,23 х 10 ^-2

В этой задаче важно отметить, что когда кислота в растворе, содержащем равные количества кислоты и сопряженного основания, рН равен рК

и .
Следовательно, мы имеем pH = 3,62 = pK _a . Однако мы пытаемся найти K _a , а не pK _a (напомним также, что pK _a = –log(K _a ) ), и нам нужно будет использовать приближение, которое мы изучили ранее. но наоборот.
pH = n – 0,m ≈ –log(m x 10 ^-n )
Мы можем переписать значение pH 3,62 как 4 – 0,38, представив его в виде n – 0,m, показанном выше . Это дает нам
pH = 4 – 0,38 ≈ –log(m x 10 ^-n )
Теперь мы можем заменить m и n, чтобы аппроксимировать K _на в правой части.
pH = 4 – 0,38 ≈ –log(3,8 x 10 ^-4 )
Таким образом, приблизительное значение K _a равно 3,8 x 10 M — ответить в).
Chelsea Myers
Chelsea Myers, M.Stat, является автором серии электронных книг MCAT Math, доступных на сайте www.
No related posts.