Как считать пределы: Как решать пределы для чайников, примеры решений

1.6 Вычисление пределов показательно-степенной функции.

Показательно степенной функцией называется функция вида . Чаще всего при вычислении пределов от показательно степенной функции получаются неопределенности . Так как о поведении такой функции в общем случае ничего сказать нельзя (а предел описывает поведение функции вблизи заданной точки), то при вычислении предела от такой функции рекомендуется ее представить иначе, при помощи основного логарифмического тожества: . Мы будем использовать частный случай этой формулы , здесь -это константа, приближенно равная 2,71, а и называется натуральным логарифмом. Используя такое представление, получим (последнее равенство справедливо в силу свойства логарифмов ), а это уже показательная функция. Теперь достаточно знать к чему стремится ее показатель, и будем знать, к чему стремится сама функция. При этом могут возникнуть следующие ситуации:

1) если конечен, то в силу непрерывности показательной функции предел с самой функции можно переносить на ее аргумент.

Тогда ;

2) если , то получим ситуацию, которую символически можно записать так: . Учитывая поведение показательной функции, при условии, что ее показатель стремится к +∞, получим ;

3) если , то символически этот случай можно записать следующим образом: . Учитывая поведение показательной функции, получим .

Пример 1.13. Вычислить .

Решение. При дробь , так как . Тогда мы имеем неопределенность и показательно степенную функцию по условию. Прежде всего представим ее в виде степенной на основании основного логарифмического тождества, получим

Вычислим предел от показателя отдельно. Заметим, что в числителе и знаменателе дроби, стоящей в аргументе логарифма стоят многочлены первой степени, а, значит такая дробь неправильная (неправильной рациональной дробью называется дробь, у которой числитель и знаменатель — многочлены, причем старшая степень числителя не меньше старшей степени знаменателя). Из неправильной рациональной дроби можно выделить целую часть: (здесь мы использовали свойство почленного деления дроби ).

Тогда . Заметим, что , тогда аргумент логарифма представлен в виде: единица плюс бесконечно малая функция, а тогда логарифм имеет эквивалентную функцию , то есть . В нашем пределе мы имеем право переходить к эквивалентным, так как имеем дело с произведением. Тогда получим .

Окончательно .

Пример 1.14. Вычислить

Решение. Как и в предыдущем примере, мы имеем дело с показательно-степенной функцией и неопределенностью . Перейдем снова к показательной функции, применив основное логарифмическое тождество:

Вычислим предел от показателя отдельно. Выясним: можно ли заменить логарифм эквивалентной функцией. Это возможно тогда, когда аргумент логарифма может быть представлен в виде единица плюс бесконечно малая функция. . Так как при , то аргумент логарифма представлен в нужном виде , и, значит . Тогда

.

Окончательно .

объяснение, теория, примеры решений.

Понятие предела в математике

Рассмотрим функцию %%f(x)%%, определенную, по крайней мере, в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой.

Понятие предела по Коши

Число %%A \in \mathbb{R}%% называют пределом функции %%f(x)%% в точке %%a \in \mathbb{R}%% (или при %%x%%, стремящемся к %%a \in \mathbb{R}%%), если, каково бы ни было положительное число %%\varepsilon%%, найдется положительное число %%\delta%%, такое, что для всех точек проколотой %%\delta%%-окрестности точки %%a%% значения функции принадлежат %%\varepsilon%%-окрестности точки %%A%%, или

$$ A = \lim\limits_{x \to a}{f(x)} \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel{\circ}{\text{U}}_\delta(a) \Rightarrow f(x) \in \text{U}_\varepsilon (A) \big) $$

Это определение называется определением на языке %%\varepsilon%% и %%\delta%%, предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.

— (a)%% с окрестностями %%\text{U}_\varepsilon (A), \text{U}_\varepsilon (\infty), \text{U}_\varepsilon (+\infty), \text{U}_\varepsilon (-\infty)%%, получим 24 определения предела по Коши.

Геометрический смысл

Геометрический смысл предела функции

Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции %%y = f(x)%% и отметим на нем точки %%x = a%% и %%y = A%%.

Предел функции %%y = f(x)%% в точке %%x \to a%% существует и равен A, если для любой %%\varepsilon%%-окрестности точки %%A%% можно указать такую %%\delta%%-окрестность точки %%a%%, что для любого %%x%% из этой %%\delta%%-окрестности значение %%f(x)%% будет находиться в %%\varepsilon%%-окрестности точки %%A%%.

Отметим, что по определению предела функции по Коши для существования предела при %%x \to a%% не важно, какое значение принимает функция в самой точке %%a%%. Можно привести примеры, когда функция не определена при %%x = a%% или принимает значение, отличное от %%A%%. Тем не менее предел может быть равен %%A%%.

Определение предела по Гейне

Элемент %%A \in \overline{\mathbb{R}}%% называется пределом функции %%f(x)%% при %% x \to a, a \in \overline{\mathbb{R}}%%, если для любой последовательности %%\{x_n\} \to a%% из области определения, последовательность соответствующих значений %%\big\{f(x_n)\big\}%% стремится к %%A%%.

Определение предела по Гейне удобно использовать, когда возникают сомнения в существовании предела функции в данной точке. Если можно построить хотя бы одну последовательность %%\{x_n\}%% с пределом в точке %%a%% такую, что последовательность %%\big\{f(x_n)\big\}%% не имеет предела, то можно сделать вывод о том, что функция %%f(x)%% не имеет предела в этой точке. Если для двух

различных последовательностей %%\{x»_n\}%% и %%\{x»»_n\}%%, имеющих одинаковый предел %%a%%, последовательности %%\big\{f(x»_n)\big\}%% и %%\big\{f(x»»_n)\big\}%% имеют различные пределы, то в этом случае также не существует предел функции %%f(x)%%. n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.

Затем возьмем сходящуюся к той же точке последовательность $$ x»_n = \left\{ \frac{2}{(4n + 1)\pi} \right\}, $$

для которой %%\lim{x»_n} = +0%%, %%f(x»_n) = \sin{\big((4n + 1)\pi/2\big)} \equiv 1%% и %%\lim\big\{f(x»_n)\big\} = 1%%. Аналогично для последовательности $$ x»»_n = \left\{-\frac{2}{(4n + 1)\pi} \right\}, $$

также сходящейся к точке %%x = 0%%, %%\lim\big\{f(x»»_n)\big\} = -1%%.

Все три последовательности дали разные результаты, что противоречит условию определения по Гейне, т.е. данная функция не имеет предела в точке %%x = 0%%.

Теорема

Определение предела по Коши и по Гейне эквивалентны.

Доказывая свойства предела функции, мы убедились, что от проколотых окрестностей, в которых были определены наши функции и которые возникали в процессе доказательств, кроме свойств указанных во введении к предыдущему пункту 2, действительно ничего не потребовалось. Это обстоятельство служит оправданием для выделения следующего математического объекта.

а. База; определение и основные примеры

Определение 11. Совокупность В подмножеств множества X будем называть базой в множестве X, если выполнены два условия:

Иными словами, элементы совокупности В суть непустые множества и в пересечении любых двух из них содержится некоторый элемент из той же совокупности.

Укажем некоторые наиболее употребительные в анализе базы.

Если то вместо пишут и говорят, что х стремится к а справа или со стороны больших значений (соответственно, слева или со стороны меньших значений). При принята краткая запись вместо

Запись будет употребляться вместо Она означает, что а; стремится по множеству Е к а, оставаясь больше (меньше), чем а.

то вместо пишут и говорят, что х стремится к плюс бесконечности (соответственно, к минус бесконечности).

Запись будет употребляться вместо

При вместо мы (если это не ведет к недоразумению) будем, как это принято в теории предела последовательности, писать

Заметим, что все перечисленные базы обладают той особенностью, что пересечение любых двух элементов базы само является элементом этой базы, а не только содержит некоторый элемент базы. С другими базами мы встретимся при изучении функций, заданных не на числовой оси.

Отметим также, что используемый здесь термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра», а введенный ниже предел по базе есть наиболее существенная для анализа часть созданного современным французским математиком А. Картаном понятия предела по фильтру

b. Предел функции по базе

Определение 12. Пусть — функция на множестве X; В — база в X. Число называется пределом функции по базе В, если для любой окрестности точки А найдется элемент базы, образ которого содержится в окрестности

Если А — предел функции по базе В, то пишут

Повторим определение предела по базе в логической символике:

Поскольку мы сейчас рассматриваем функции с числовыми значениями, полезно иметь в виду и следующую форму этого основного определения:

В этой формулировке вместо произвольной окрестности V (А) берется симметричная (относительно точки А) окрестность (е-окрестность). Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).

Мы дали общее определение предела функции по базе. Выше были рассмотрены примеры наиболее употребительных в анализе баз. В конкретной задаче, где появляется та или иная из этих баз, необходимо уметь расшифровать общее определение и записать его для конкретной базы.

Рассматривая примеры баз, мы, в частности, ввели понятие окрестности бесконечности. Если использовать это понятие, то в соответствии с общим определением предела разумно принять следующие соглашения:

или, что то же самое,

Обычно под подразумевают малую величину. В приведенных определениях это, разумеется, не так. В соответствии с принятыми соглашениями, например, можем записать

Для того чтобы можно было считать доказанными и в общем случае предела по произвольной базе все те теоремы о пределах, которые мы доказали в пункте 2 для специальной базы , необходимо дать соответствующие определения: финально постоянной, финально ограниченной и бесконечно малой при данной базе функций.

Определение 13. Функция называется финально постоянной при базе В, если существуют число и такой элемент базы, в любой точке которого

Определение 14. Функция называется ограниченной при базе В или финально ограниченной при базе В, если существуют число с и такой элемент базы, в любой точке которого

Определение 15. Функция называется бесконечно малой при базе В, если

После этих определений и основного наблюдения о том, что для доказательства теорем о пределах нужны только свойства базы, можно считать, что все свойства предела, установленные в пункте 2, справедливы для пределов по любой базе.

В частности, мы можем теперь говорить о пределе функции при или при или при

Кроме того, мы обеспечили себе возможность применения теории пределов и в том случае, когда функции будут определены не на числовых множествах; в дальнейшем это окажется особенно ценным. К примеру, длина кривой есть числовая функция, определенная на некотором классе кривых. Если мы знаем эту функцию на ломаных, то потом предельным переходом определяем ее для более сложных кривых, например для окружности.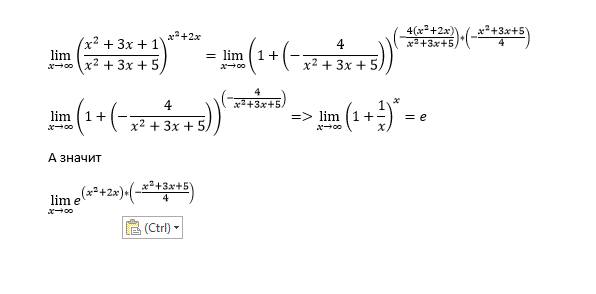

В данный же момент основная польза от сделанного наблюдения и введенного в связи с ним понятия базы состоит в том, что они избавляют нас от проверок и формальных доказательств теорем о пределах для каждого конкретного вида предельных переходов или, в нашей нынешней терминологии, для каждого конкретного вида баз.

Для того чтобы окончательно освоиться с понятием предела по произвольной базе, доказательства дальнейших свойств предела функции мы проведем в общем виде.

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.

Примеры решений

Пример 1

Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $

Решение

а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ \text{a)} \lim \limits_{x \to 0} \frac{1}{x} = \infty \text{ б)}\lim \limits_{x \to \infty} \frac{1}{x} = 0 $$

Что делать с неопределенностью вида: $ \bigg [\frac{0}{0} \bigg ] $

Пример 3

Решить $ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} $

Решение

Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. 2-1}{x+1} = \infty $$

Алгоритм вычисления лимитов

Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:

1. Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
2. Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
3. Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.

В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.

Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х о, кроме, быть может, самой точки х о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x 0 (или при х® х о), если для любой последовательности допустимых значений аргумента x n , n є N (x n ¹ x 0), сходящейся к х о последовательность соответствующих значений функции ƒ(х n), n є N, сходится к числу А

В этом случае пишут
или ƒ(х)->А при х→х о. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке х о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х о (или при х→х о), если для любого положительного ε найдется такое положительное число δ, что для все х¹ х о, удовлетворяющих неравенству |х-х о |

Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х о, что для всех х¹ хо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

Доказать, что

Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3|

Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|3.

16.2. Односторонние пределы

В определении предела функции считается, что х стремится к x 0 любым способом: оставаясь меньшим, чем x 0 (слева от х 0), большим, чем х о (справа от х о), или колеблясь около точки x 0 .

Бывают случаи, когда способ приближения аргумента х к х о существенно влияет на значение придела функции. Поэтому вводят понятия односторонних пределов.

Число А 1 называется пределом функции у=ƒ(х) слева в точке х о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х 0 -δ;x o), выполняется неравенство |ƒ(х)-А|х 0 -0 или коротко: ƒ(х о- 0)=А 1 (обозначение Дирихле) (см. рис. 111).

Аналогично определяется предел функции справа, запишем его с помощью символов:

Коротко предел справа обозначают ƒ(х о +0)=А.

Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует , то существуют и оба односторонних предела, причем А=А 1 =А 2 .

Справедливо и обратное утверждение: если существуют оба предела ƒ(х 0 -0) и ƒ(х 0 +0) и они равны, то существует предел и А=ƒ(х 0 -0).

Если же А 1 ¹ А 2 , то етот придел не существует.

16.3. Предел функции при х ® ∞

Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞ , если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|

Геометрический смысл этого определения таков: для » ε>0 $ М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).

16.4. Бесконечно большая функция (б.б.ф.)

Функция у=ƒ(х) называется бесконечно большой при х→х 0 , если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0М.

Например, функция у=1/(х-2) есть б.б.ф. при х->2.

Если ƒ(х) стремится к бесконечности при х→х о и принимает лишь положительные значения, то пишут

если лишь отрицательные значения, то

Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большой при х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко:

Например, у=2х есть б.б.ф. при х→∞.

Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность v n =n 2 +1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки х о является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)

Однако, если limƒ(х)=А при х→x 0 , где А — конечное число, то функция ƒ(х) ограничена в окрестности точки х о.

Действительно, из определения предела функции следует, что при х→ х 0 выполняется условие |ƒ(х)-А|

Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса.

Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х

будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Нахождение пределов алгебраически

Нахождение пределов алгебраически

К концу этой лекции вы должны быть в состоянии использовать уравнение функции, чтобы найти пределы для ряда различных функций, включая пределы на бесконечности, и определить, когда пределы не существуют (и когда они не существуют). существуют, чтобы объяснить, почему). Вы также должны уметь правильно использовать предельные обозначения.

Как и в предыдущей лекции, мы сразу приступим к поиску пределов конкретных функций. Но на этот раз мы собираемся дать уравнение для каждой функции, график которой мы видели в прошлой лекции, и обсудим, как найти пределы алгебраически (т. (х) ).

Прежде чем мы начнем пытаться найти пределы алгебраически, мы должны начать с размышлений о том, что мы узнали, рассматривая пределы графически. Для нас действительно важно понять, откуда берутся алгебраические правила, и часто лучший способ сделать это — представить правила графически , а затем попытаться перевести этот геометрический образ в алгебраические символы. Если вы можете переходить от графического к алгебраическому представлению функций или других математических объектов при решении задач, вы, скорее всего, будете хорошо успевать по любому изучаемому вами курсу математики.

Не используйте правило, если не понимаете, откуда оно взялось!

Если вы не понимаете, откуда берется правило, есть большая вероятность, что вы будете использовать его неправильно, по крайней мере, иногда. Кроме того, у вас есть вся дополнительная работа по запоминанию чего-то, что не имеет смысла. Тогда как если вы понимаете, откуда взялось правило, его обычно гораздо легче запомнить, а если вы забываете правило, то обычно можете придумать его самостоятельно.

Например, многие студенты, изучающие алгебру, путают правила упрощения выражений с показателями степени, как, например, эти два выражения:

1. а ² а ³

2. ( и ² ) ³

Возможно, вы помните два правила, которые применяются к этим выражениям: Одно правило гласит, что в случае a ² A ³ , вы должны добавить показатели (чтобы получить A ² A ³ = A ⁵ ), но это для ( A 9004 ⁵ ), но для этого ( A ^{333 5} ), но для этого ( A 9004 ⁵ ), но для этого ( A 9004 ⁵ ), но для этого ( A 9004 ⁵ ). 2 ) ³ , вы должны умножить степени вместо их сложения (чтобы получить ( a ² ) ³ = a 4 9003 9003). Если все, что вы знаете, это эти правила, и вы не знаете, откуда они берутся, то вам, вероятно, будет трудно запомнить, в каком случае следует умножать, а в каком — складывать. В какой-то момент вы, вероятно, забудете, что делать в какой ситуации, а затем поменяете правила и неправильно решите задачу.

Однако, если вы понимаете определение показателей степени и используете его для самостоятельного вывода правил, вы никогда не совершите эту ошибку. Например, вы можете заметить, что a ² a ³ на самом деле просто означает, что вы умножаете два на вместе, а затем вы умножаете это еще на три на — так вы умножаете всего пять и вместе. Так что в этом случае имеет смысл добавить показатели степени, потому что каждая степень просто говорит вам, сколько и перемножаются, а затем все и перемножаются вместе. Во втором случае вы можете заметить, что ( a ² ) ³ означает, что вы умножаете два на вместе три раза, чтобы в общей сложности шесть на были умножены вместе. . Так что в этом случае имеет смысл умножить показатели степени, потому что вы буквально берете два на три умножить на .

Мы можем распространить эту идею на любую область математики. Например, для этого раздела, посвященного ограничениям, нам придется придумать несколько разных методов для расчета нескольких различных типов задач с ограничениями (поскольку ни одно правило не будет работать для всех задач). Однако вместо того, чтобы запоминать правило для каждого типа задачи ограничения, попытайтесь понять правило, подумав о том, что означает определение ограничения . Некоторое запоминание — это хорошо, но вы всегда должны быть в состоянии объяснить правила или концепции, которые вы запомнили. Запоминание чего-то, чего вы не понимаете, обычно ведет к катастрофе.

Алгебраические правила (т. е. те, которые имеют дело с выражениями или уравнениями) часто можно лучше всего понять, представив задачу графически.

Иногда лучший способ понять, как и почему что-то работает, — представить это графически. Многие математики работают таким образом: если математик хочет что-то доказать, он может обнаружить, что гораздо проще увидеть закономерность или взаимосвязь на каком-либо графике. Таким образом, они могут начать с алгебраического выражения, затем придумать способ графического представления этого выражения, затем найти интересующую их закономерность или взаимосвязь, глядя на график, а затем работать над переводом закономерности или взаимосвязи (и обоснование для этого) в алгебру, чтобы они могли формально поделиться ею с другими математиками. Это похоже на подход, который мы будем использовать при решении многих математических задач.

Например, вы можете помнить теорему Пифагора: a ² + b ² = c ² для любого прямоугольного треугольника, где a и 9000 3 и 9000 две стороны. это гипотенуза. Взгляните на следующую анимацию, которая показывает графический способ показать, что это утверждение верно. (Щелкнув правой кнопкой мыши по анимации, вы сможете воспроизвести ее или вернуться назад.)

Вы заметите, что эта анимация показывает две вещи:

1. Он показывает, как отношения между и , b и c , а также отношения между ними могут быть представлены графически.
2. Он показывает, как каждый шаг этого доказательства можно перевести в алгебраические уравнения, используя символы a , b и c .

Это важно: и графические изображения, и уравнения необходимы для того, чтобы мы могли полностью понять и передать доказательство . И мы должны иметь возможность переключаться между графиком/изображением и уравнениями , чтобы понять все доказательство. Обычно это справедливо для многих математических задач, и особенно для этого класса. Если вы еще не привыкли мыслить взад и вперед между графическим и алгебраическим представлением функций и другими математическими объектами, то вам стоит начать практиковать этот навык прямо сейчас!

По мере того, как мы приступим к работе над задачами на предельные значения в этой лекции, вот что мы будем делать в каждой задаче: Мы начнем с размышлений о том, как выглядит граф, и рассмотрим, как можно представить важные особенности графа. по некоторым характеристикам уравнения. Затем мы будем использовать эти характеристики уравнения (в качестве прокси для ключевых характеристик графика), чтобы помочь нам определить, какие шаги необходимо предпринять, чтобы определить предельное поведение. Посмотрите, сможете ли вы проследить этот паттерн, пока мы работаем над следующими примерами.

Мы почти готовы приступить к решению наших первых предельных задач алгебраически, но прежде чем мы начнем с алгебраических предельных примеров, нам нужно уточнить использование некоторых конкретных обозначений, потому что эти обозначения понадобятся нам для того, чтобы правильно писать вычисления в следующие примеры:

Обозначение: → vs =

Знаки равенства используются для обозначения того, что одно число (или выражение, представляющее конкретное число, когда в выражение подставляются разные значения переменных) равно другому числу. Знак равенства используется только с алгебраическими выражениями, которые представляют определенные числа (или в других областях математики, где кто-то сначала определяет, что означает «a=b», но это не относится к нашей работе в области исчисления или алгебры в данный момент ).

Однако с ограничениями нас интересует поведение из f(x) , когда x равно близкое к c , но НЕ то, что происходит именно при x=c 4 . Поэтому в тех случаях, когда мы хотим описать это поведение, мы не можем использовать знак равенства. Например, пока мы можем написать:

LIM _{x → C} F (x) = L , чтобы означать, что «предел F (x) is l x . пришлось бы написать:

f(x) → L как x → c (без знака равенства), чтобы показать, что x 90 L 4 как 4 0 приближается к 0 приближается к c

Это потому, что f(x) на самом деле никогда не равняется L : Мы можем сказать, что предел f(x) равен L , но f(x) приближается к L на неопределенный срок , хотя на самом деле никогда не достигает потому что x никогда на самом деле не достигает c , когда мы оцениваем предел).

Таким образом, каждый раз, когда мы используем обозначение, указывающее, что мы рассматриваем предельное поведение (например, когда x близко к c , но на самом деле не равно c ), мы должны использовать знак стрелки → вместо знака равенства =.

Каждый раз, когда вы собираетесь записывать знак равенства в этом курсе, сначала спросите себя: «Действительно ли эти две величины равны ?»!

Теперь мы готовы приступить к расчету лимита!

Почему нас интересует нахождение пределов алгебраически, а не графически?

Для каждого из следующих примеров мы даем уравнение для f(x) . Мы также включаем график из предыдущей лекции; однако график не является необходимым для расчета предела, как мы увидим, и все приведенные ниже пределы могут быть вычислены исключительно из информации, приведенной в уравнении для f(x) . Мы оставляем графики здесь, чтобы помочь нам вспомнить, как характеристики формулы функции связаны с ключевыми характеристиками графика. Очевидно, что если мы все делаем правильно, мы должны получить один и тот же ответ для предела конкретной функции, независимо от того, находим ли мы его графически (смотря на картинку) или алгебраически (используя уравнение).

Нахождение пределов с помощью уравнений позволяет нам быть более точными и строгими, в то время как нахождение пределов с помощью графиков дает нам лучшее интуитивное понимание того, что на самом деле делает функция около x=c . Этот принцип верен в более общем плане в математике: просмотр графика часто является самым простым способом увидеть закономерности и другие связи, которые приведут нас к решению проблемы или к аргументу в пользу доказательства теоремы. Чтобы оправдать интуицию, которую мы получаем, глядя на график, нам часто приходится переводить это мышление в уравнения, а затем использовать алгебру, чтобы проиллюстрировать закономерности, которые мы видели графически.

Пример 1: Простой пример, где

lim _{x → c} f(x) = f(c) :

Найдите предел f(x) , когда x приближается к 1:

Чтобы увидеть, существует ли предел при x = 1, мы должны рассмотреть поведение функции вокруг x = 1 (НЕ при x = 1). Таким образом, самый важный вопрос, который мы должны задать, глядя на это уравнение: «На что будет похож график вокруг x =1?». В этом случае, поскольку f — простой многочлен, мы знаем, что график будет непрерывным, без дыр и разрывов — фактически это будет парабола. Но, в частности, мы должны подумать о том, что происходит, когда x приближается к 1 как слева, так и справа.

Поскольку здесь мы работаем с уравнениями алгебраически, нам нужен способ записать эту идею подстановки значений, которые близки, но не равны единице, в уравнение для ф . Поэтому нам нужен какой-то способ записывать символы для значений, которые произвольно близки к единице, но на самом деле не равны единице. Для этого прервемся на мгновение, чтобы ввести новый бит обозначения:

.

Обозначение: с ^— и с ⁺

Мы уже видели это обозначение внутри предельного выражения, например, вот так:

• lim _{x → c-} f(x) = L для обозначения предела f(x) , поскольку x приближается к c из слева
• lim _{x → c+} f(x) = L для обозначения предела f(x) , поскольку x приближается к
  справа от

  3 4

Мы также будем использовать его родственным, но немного другим способом при решении предельных задач алгебраически:

Когда мы заменим обозначение c ^— в выражение, мы будем использовать его для обозначения значения, сколь угодно близкого к c , но меньше c . Точно так же, когда мы подставляем обозначение c ⁺ в выражение, мы будем использовать его для обозначения значения, которое сколь угодно близко к c , но больше c .

Важно отметить, что c ^— (и c ⁺ ) НЕ имеет точного значения — это НЕ число — скорее это способ описания поведения функции вокруг c (но НЕ на c). Так, например, если c ^— встречается в выражении дважды, это может не указывать на «одно и то же» значение, которое находится «сразу слева от c ».

Например, можно написать:

(1 ^— ) ² → 1 ^—

В этом случае 1 ^— слева от стрелки НЕ совпадает с 1 ^— справа от стрелки: если 1 ^— обозначало одно конкретное число, то 1 ^— слева от стрелки будет больше, чем 1 ^— справа от стрелки (поскольку возведение в квадрат числа, которое немного меньше единицы, дает ответ, меньший, чем тот, с которого вы начали). Однако на самом деле мы не используем 1 ^— для обозначения одного конкретного числа.

Скорее, правильный способ интерпретировать это выражение состоит в том, чтобы понимать его как описание общего поведения около 1: Это выражение просто утверждает, что если возвести в квадрат любое произвольное число, которое «очень близко, но чуть меньше 1″, то в качестве ответа вы получите (другое) число, которое «очень близко, но чуть меньше 1».

Будьте осторожны! Потому что c ^— (или c ⁺ ) НЕ конкретное число, а скорее описание поведения вокруг c , как только мы подставим его в выражение мы должны использовать знак → а НЕ знак =! Итак, хотя я могу написать (1) ² = 1, я должен написать (1 ^— ) ² → 1 ^— .

А теперь вернемся к нашему примеру: если мы подумаем о поведении вокруг x = 1, мы увидим, что когда x приближается к 1 слева, f(x) будет приближаться к 2 снизу, потому что:

(1 ^— ) ² + 1 → 1 ^— + 1 → 2 ^—

(потому что что-то чуть меньше единицы, в квадрате будет чем-то немного меньше единицы , а что-то чуть меньше единицы плюс один будет чуть меньше двух ).

Точно так же, когда x приближается к 1 справа, f(x) приближается к 2 сверху, потому что:

(1 ⁺ ) ² + 1 → 1 ⁺ + 1 → 2 ⁺ .

Итак, если бы мы выписали все шаги, у нас было бы:

Поскольку f(x) непрерывно в некотором открытом интервале вокруг x = 1, поведение f(x) при приближении x к 1 из как справа, так и слева одинаково . В таком случае мы можем просто подставить 1 вместо 9.0003 x в f(x) , а значение f(1) будет таким же, как предел f(x) при x =1.

Примечание. Мы снова немного неформальны. Чтобы сделать эту теорему правильной, нам нужно доказать , что в любое время f(x) непрерывно в любом интервале около c , что предел f(x) при x приближается к c равно f(c) .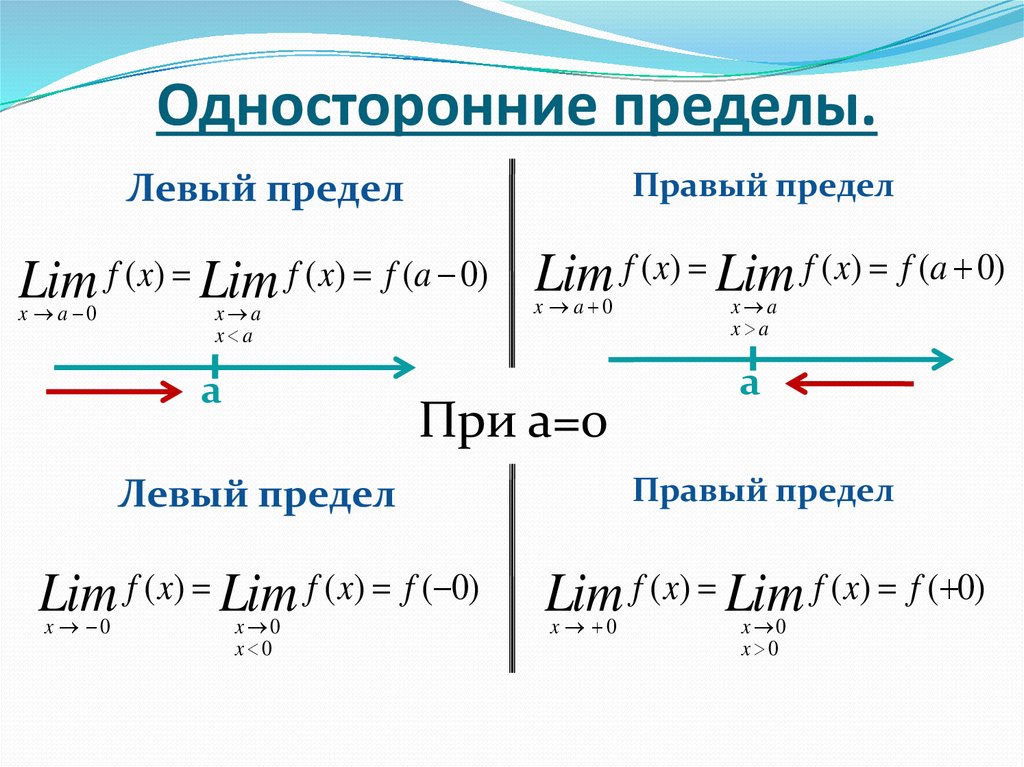 Поскольку у нас еще нет формального определения предела, мы не можем сделать это должным образом, используя строгую математику, но мы можем сделать неформальное доказательство того, почему это верно, что должно помочь нам понять, почему это верно:

Неофициальное доказательство: Если f(x) непрерывно в некотором интервале вокруг x=c , то по определению непрерывности мы должны иметь возможность положить перо на график f(x) где-то справа от x=c и проследим график (не поднимая ручки), пока не наткнемся на точку ( c , f(c) ). Мы знаем, что точка ( c , f(c) ) должна существовать, потому что иначе f(x) не была бы определена в x=c и, следовательно, f(x) не будет непрерывным при x=c , что противоречит нашему предположению, что f(x) непрерывно вокруг x=c. Итак, по определению, f(x) становится все ближе и ближе к f(c) по мере того, как x приближается к c справа, и, следовательно, предел f(x) , поскольку x приближается к c справа f(c) . Используя аналогичные рассуждения, мы можем заключить, что предел f(x) , поскольку x приближается к c слева, это также f(c) . Таким образом, по определению двусторонний предел f(x) , поскольку x приближается к c , также равен f(c) .

Обратите внимание, что, обдумывая это доказательство, мы используем мысленный образ графика для доказательства нашей точки зрения. Мы думаем о том, что значит быть непрерывным, думая о том, как будет выглядеть график вблизи предела. Это доказательство было бы намного труднее написать, если бы мы не думали о задаче 9.0017 графически !

Итак, мы можем предложить следующую неформальную теорему:

Теорема: Если f(x) непрерывна в некотором открытом интервале около x =c, тогда:

lim _x→c f(x) = f(c)

Это просто способ сказать, что если мы можем найти интервал около x=c , где f(x) непрерывно, то предел f(x) при c является просто то же, что значение f(x) при x=c.

Мы еще не доказали эту теорему формально, но как только у нас будет формальное определение предела, мы сможем доказать ее формально.

 

Пример 2: Пример с отверстием

x=c:

Найти предел f(x) при приближении x к -2:

Для этой функции f(x) не определено, когда x = -2, поэтому мы столкнемся с проблемой, если просто подставим -2 непосредственно вместо 9.0003 x в уравнении для f . Если мы попытаемся вычислить f (-2), мы получим неопределенное выражение.

Итак, чтобы найти этот предел, нам нужно подумать о том, как мы можем переписать f(x) , чтобы мы не получили что-то неопределенное, когда подставим -2 вместо x . Нам нужно будет вспомнить нашу алгебру, чтобы сделать это. Это будет повторяющаяся тема на протяжении всего исчисления.

Итак, вот наша цель: нам нужно заменить f(x) с эквивалентной функцией, такой же, как f(x) везде вокруг x=c . Это означает, что он должен быть таким же, как f(x) везде, кроме (возможно) at x=c. (Поскольку мы пытаемся найти предел, а предел сосредоточен только на поведении вокруг x=c, , а не на x=c , не имеет значения, точно ли совпадают функции при х=с )

В этом случае, когда мы подставляем -2 для x , мы получаем . Таким образом, хорошим первым шагом для нас было бы определить, есть ли способ переписать эту функцию так, чтобы при подстановке -2 для x ни верх, ни низ дроби больше не были равны нулю. А поскольку f(x) — рациональная функция, первое, что мы можем попробовать, — это разложить на множители верхнюю и нижнюю части дроби, а затем посмотреть, сможем ли мы отменить общий множитель, потому что это может помочь нам избавиться от одного из нулей вверху или внизу дроби, что позволило бы вычислить предел.

Но как мы можем связать эту алгебру обратно с графической картиной того, что мы делаем? Если вспомнить, график f(x) представлял собой линию с дыркой в ​​точке x = -2:

.

Итак, когда мы заменили f(x) на x -2, что мы на самом деле делали? Мы заменяли f(x) , то есть линию с отверстием в точке x = -2, на y = x -2, то есть та же самая линия без дырки. Эти две функции не полностью идентичны, но они идентичны везде, кроме x = -2, что имеет значение при вычислении предела. Чтобы две функции имели один и тот же предел при x = -2, все, что нам нужно, это чтобы они были идентичны в некотором интервале вокруг x = -2 (но НЕ обязательно при x = ). -2).

Пример 3: пример с функцией, которая имеет разрыв скачка в

x=c состоящий из одной точки:

Для этой функции f(x) определяется иначе, когда x = -2, по сравнению с тем, когда x ≠2, и, в результате, уравнение для f(x) , которое мы использовали бы для оценки f (x) при c отличается от уравнения, которое мы использовали бы для определения предела f(x) , когда x приближается к c .

Найти предел f(x) при приближении x к -2:

Опять же, мы хотим связать эту алгебру с графическим изображением того, что мы делаем. Оглядываясь назад, график f(x) был линией с дырой в ней при x = -2, плюс еще одна дополнительная точка при x = -2, которая не связана с графиком линии:

Как и в предыдущей задаче, мы можем заменить f(x) линией с дыркой в ​​точке x = -2, а затем «несоединенной» точкой в ​​точке 9.0003 x = -2, где y = x -2, что является той же линией без отверстия и «несоединенной» точки. Эти две функции не полностью идентичны, но они идентичны везде, кроме x = -2, что имеет значение при вычислении предела. Опять же, для того, чтобы две функции имели один и тот же предел в x = -2, все, что нам нужно, это чтобы они были идентичны в некотором интервале вокруг x = -2 (но НЕ обязательно в х = -2).

Пример 4: Пример с функцией, которая имеет разрыв скачка в

x=c и разные пределы справа и слева:

Для этой функции f(x) описывается другим уравнением слева от c и справа от c , поэтому нам нужно будет использовать разные уравнения для вычисления левостороннего и правостороннего боковые пределы.

Найдите предел f(x) как x приближается к 1:

Еще раз, мы должны попытаться напомнить себе, как наша алгебра связана с графом. График f(x) был составным набором двух функций со скачком на x = 1. Поэтому логично, что для нахождения правого предела мы должны смотреть на функцию, которая применяется только при x ≥1, а для нахождения левого предела мы должны смотреть на функцию, которая применяется только при x<1. Если эти два односторонних предела не совпадают, то двустороннего предела не будет, и это то, что мы ожидаем от графика, поскольку две функции никак не соединяются в точке 9. 0003 х = 1.

 

В этих примерах до сих пор мы видели, как нам нужно думать о том, что уравнение для функции говорит нам о графике функции, чтобы определить, что мы должны сделать алгебраически, чтобы найти предел.

Мы также видели, как мы можем решать проблемы ограничения, находя способ замены на непосредственно в x : чтобы сделать это, нам часто приходится переписывать f(x) , заменяя его на эквивалентная функция, та же самая вокруг x=c , , и нам нужно распознать, что при прямом подключении c к x мы получаем неопределенное значение. В приведенных здесь примерах мы видели, что иногда прямое подключение c к x дает нам неопределенное значение, и это было ключом к тому, что нам нужно найти способ переписать f(x) , который не дал бы нам этого неопределенное выражение. Однако при работе с лимитами нам нужно принять идею неопределенные выражения еще больше, чтобы мы могли немного лучше понять, какие неопределенные выражения действительно являются проблемой, когда мы пытаемся найти пределы, а какие не являются проблемой в контексте пределов. Следующая лекция будет посвящена этому различию, и, поняв это различие, мы сможем вычислять гораздо более широкий спектр пределов.

Калькулятор предела функции

Поиск инструмента

Поиск инструмента на dCode по ключевым словам:

Просмотреть полный список инструментов dCode

Предел функции

Инструмент для расчета пределов математических функций. Предел определяется значением функции, когда ее переменная приближается к заданному значению.

Результаты

Ограничение функции — dCode

Теги: Функции

Поделиться

dCode и многое другое решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор пределов

Найти предел функции:
Переменная
Приближение к значению
Приближение к $ + \infty $ (стремится к положительной бесконечности +∞)
Приближение к $ — \infty $ (стремится к отрицательной бесконечности -∞)

Направление

Правый предел (от больших значений стремится к X+) Левый предел (от меньших значений стремится к X-)

См. также: Область определения функции — Асимптота функции — Экстремум функции

Ответы на вопросы (FAQ)

Как рассчитать лимит?

Для расчета предела замените переменную значением, к которому она стремится/приближается (близкая окрестность).

Пример: Вычисление предела $ f(x) = 2x $, когда $ x $ стремится к $ 1 $, записано $ \lim_{x \to 1} f(x) $ для вычисления $ 2 \times 1 = 2 $, поэтому $ \lim_{x \to 1} f(x) = 2 $.

В некоторых случаях результат не определен (неопределенные пределы, см. ниже) и может свидетельствовать о существовании асимптоты.

Как рассчитать лимиты с 0 и $\infty$ бесконечностью?

Предельные расчеты обычно используют математические формы со значениями 0 или бесконечность (положительные или отрицательные), за исключением неопределенных форм, вычисления выполняются по правилам: $ -\infty — \infty = -\infty $$ $$ +\infty — \infty = ? $$ $$ -\infty + \infty = ? $$ $$ 0 + \infty = +\infty $$ $$ 0 — \infty = -\infty $$ $$ + \infty + 0 = +\infty $$ $$ — \infty + 0 = -\infty $$ $$ \pm k + \infty = +\infty $$ $$ \pm k — \infty = -\infty $$ $$ + \infty \pm k = +\infty $$ $$ — \infty \pm k = -\infty $$ $$ +\infty \times +\infty = +\infty $$ $$ +\infty \times -\infty = -\infty $$ $$ -\infty \times +\infty = -\infty $$ $$ -\infty \times -\infty = +\infty $$ $$ 0 \times +\infty = ? $$ $$ 0 \times -\infty = ? $$ $$ +\infty \times 0 = ? $$ $$ -\infty \times 0 = ? $$ $$ k \times +\infty = +\infty $$ $$ k \times -\infty = -\infty $$ $$ -k \times +\infty = -\infty $$ $$ -k \times -\infty = +\infty $$ $$ \frac{ +\infty }{ +\infty } = ? $$ $$ \frac{ +\infty }{ -\infty } = ? $$ $$ \frac{ -\infty }{ +\infty } = ? $$ $$ \frac{ -\infty }{ -\infty } = ? $$ $$ \frac{ 0 }{ +\infty } = 0 $$ $$ \frac{ 0 }{ -\infty } = 0 $$ $$ \frac{ + \infty }{ 0 } = +\infty $$ $$ \frac{ -\infty }{ 0 } = -\infty $$ 9{-\infty} = 0 $$

При $k > 0$ положительная ненулевая вещественная постоянная.

? представляют собой неопределенные формы.

Что такое неопределенные формы?

Неопределенные формы, которые появляются при расчете пределов:

$$ \frac{0}{0} $$	0 разделить на 0
$$ \frac{\pm\infty}{ \pm\infty} $$	бесконечность разделить на бесконечность
$$ 0 \times \pm\infty $$ или $$ \pm\infty \times 0 $$ 9{\pm\infty} $$	1 степень бесконечности

Как вычислить неопределенную форму?

Возможны несколько методов расчета предельных значений.

1 — Факторизация (например, с использованием инструментов выражения факторизации dCode)

2 — Использование Больничного правила (в случаях формы $ 0/0 $ или $ \ infty / \ infty $: если $ f $ и $ g $ есть 2 функции, определенные на отрезке $[a,b[$ и дифференцируемые в $a$ и такие, что $f(a) = g(a) = 0$, то если $g'(a)\ne 0$ : $$ \lim_{x \to a^+} \frac{f(x)}{g(x)} = \frac{f’ (a)}{g’ (a)} $$

3 — Использовать правило доминирующего члена (в случае сложения полиномов и когда переменная стремится к бесконечности): пределом полинома является предел его члена наибольшей степени.

4 — Расчет асимптот для вывода предельных значений

5 — Преобразование выражения (используя замечательные тождества или извлекая элементы из корней и т. д.)

Как вычислить пределы тригонометрических функций, таких как синус и косинус?

Функции синусов и косинусов, стремящиеся к $ \pm \infty $, не допускают предела, поскольку они являются периодическими (воспроизводят бесконечную закономерность) и поэтому не стремятся ни к конечному значению, ни к бесконечности. Их лимит неограничен, но иногда отмечается $\pm 1$ (не рекомендуется).

Как показать пошаговые расчеты?

Калькулятор лимита dCode применяет не школьные методы, а побитовый расчет, поэтому этапы расчета сильно отличаются и не отображаются.

Исходный код

dCode сохраняет за собой право собственности на исходный код «Limit of a Function». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Ограничение функции», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Ограничение функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.