Mathway | Популярные задачи
Популярные задачи
Элемент. математикаОсновы алгебрыАлгебраТригонометрияОсновы мат. анализаМатематический анализКонечная математикаЛинейная алгебраХимияPhysics
| Рейтинг | Тема | Задача | Форматированная задача |
|---|---|---|---|
| 1 | Решить, используя обратную матрицу | x+2y=1 , 4x+5y=13 | , |
| 2 | Перемножить матрицы | [[1/( квадратный корень из 17),-4/( квадратный корень из 17)]][[1/( квадратный корень из 17)],[-4/( квадратный корень из 17)]] | |
| 3 | Найти область определения | x+y=3 | |
| 4 | Найти область определения | x-y=3 | |
| 5 | Найти область определения | y=-2x+3 | |
| 6 | Найти область определения | y=2x+1 | |
| 7 | Записать в виде векторного равенства | x=x^2+9x+3 , x=x+2 | , |
| 8 | Найти область определения | y=2x | |
| 9 | Найти область определения | y=-3x | |
| 10 | Найти область определения | y=3x-2 | |
| 11 | Найти область определения | y=4x | |
| 12 | Найти область определения | 3x+2y=6 | |
| 13 | Trovare la 5×5 Matrice Identità | 5 | |
| 14 | Trovare la 6×6 Matrice Identità | 6 | |
| 15 | Trovare la 4×4 Matrice Identità | 4 | |
| 16 | Решить, используя обратную матрицу | 2x+y=-2 , x+2y=2 | , |
| 17 | Решить, используя обратную матрицу | 4x+4=y , y=6x | , |
| 18 | Решить, используя обратную матрицу | 4x+2=5y-3 , y=3x-1 | , |
| 19 | Найти степенное множество | (3,4) | |
| 20 | Вычислить | кубический корень из 216 | |
| 21 | Найти степенное множество | (1,3) | |
| 22 | Найти область определения | 3x-2y=12 | |
| 23 | Найти область определения | y=5x+2 | |
| 24 | Найти область определения | y=2x-3 | |
| 25 | Найти область определения | y=2x-4 | |
| 26 | Найти область определения | y=2x+5 | |
| 27 | Найти область определения | y=1/2x | |
| 28 | Найти область определения | y=1/2x-3 | |
| 29 | Найти область определения | y=2/3x-2 | |
| 30 | Найти область определения | x=2y | |
| 31 | Найти область определения | x-2y=2 | |
| 32 | Найти область определения | x-2y=6 | |
| 33 | Найти область определения | 2y+x | |
| 34 | Найти область определения | 2x+y=0 | |
| 35 | Найти область определения | y=5x+6 | |
| 36 | Найти область определения | y=x+3 | |
| 37 | Solve Using a Matrix by Elimination | y=4x+3x-2 , y=6 | , |
| 38 | Проверить линейную зависимость | B={[[-10,2],[5,-2. 5]]} | |
| 39 | Сложение | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | |
| 40 | Проверить линейную зависимость | B={[[-1,2],[0,-2.5]]} | |
| 41 | Перемножить матрицы | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | |
| 42 | Найти область определения | y=5x | |
| 43 | Найти область определения | y=7x | |
| 44 | Найти область определения | y=-x-2 | |
| 45 | Найти область определения | y=x-2 | |
| 46 | Найти область определения | y=x-3 | |
| 47 | Привести матрицу к ступенчатому виду по строкам | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | |
| 48 | Записать в виде векторного равенства | x+y+z=2 , 4x+5y+z=12 , 2x=-4 | , , |
| 49 | Найти определитель | [[0,-1,a],[3,-a,1],[1,-2,3]] | |
| 50 | Найти область определения | y=-x+2 | |
| 51 | Найти определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | |
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | |
| 53 | Найти обратный элемент | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | |
| 54 | Найти обратный элемент | [[1,2,3],[2,5,7],[3,7,9]] | |
| 55 | Привести матрицу к ступенчатому виду по строкам | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | |
| 56 | Привести матрицу к ступенчатому виду по строкам | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |
| 57 | Привести матрицу к ступенчатому виду по строкам | [[1,2,3],[4,5,6],[7,8,9]] | |
| 58 | Привести матрицу к ступенчатому виду по строкам | [[7,8]] | |
| 59 | Найти область определения | 2x+y=1 | |
| 60 | Записать в виде векторного равенства | 2x+y=-2 , x+2y=2 | , |
| 61 | Найти область определения | x-2y=4 | |
| 62 | Найти область определения | x-y=-1 | |
| 63 | Найти область определения | x+y=5 | |
| 64 | Найти область определения | x=-3y-8 | |
| 65 | Найти область определения | x=-2y-8 | |
| 66 | Найти область определения | x+y=6 | |
| 67 | Найти область определения | x+y=4 | |
| 68 | x+2y=4 | ||
| 69 | Найти область определения | x+y | |
| 70 | Найти область определения | y=7x+9 | |
| 71 | Найти область определения | y=1/2x-5 | |
| 72 | Найти область определения | y=1/2x+2 | |
| 73 | Найти область определения | y=1/2x+3 | |
| 74 | Найти область определения | x-y=-3 | |
| 75 | Найти область определения | x-y=4 | |
| 76 | Найти область определения | y=-2x | |
| 77 | Найти область определения | y=-2x+1 | |
| 78 | Найти область определения | y=2^(x+9) | |
| 79 | Найти область определения | y=10-x^2 | |
| 80 | Найти область определения | y=2x-6 | |
| 81 | Найти область определения | y=-2x-3 | |
| 82 | Найти область определения | y=3x-8 | |
| 83 | Найти область определения | y=3x | |
| 84 | Найти область определения | y=-3x+1 | |
| 85 | Найти область определения | y=4x+3 | |
| 86 | Найти область определения | y=3x-4 | |
| 87 | Найти область определения | y=4x-2 | |
| 88 | Найти область определения | y=-6x | |
| 89 | Найти область определения | y=x-4 | |
| 90 | Найти область определения | 7 корень четвертой степени из 567y^4 | |
| 91 | Найти область определения | c=5/9*(f-32) | |
| 92 | Найти область определения | f=9/5c+32 | |
| 93 | Вычислить | квадратный корень из 4 | |
| 94 | Привести матрицу к ступенчатому виду по строкам | [[-6,7],[2,6],[-4,1]] | |
| 95 | Найти собственные значения | [[2,1],[3,2]] | |
| 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | |
| 97 | Найти степенное множество | A=(2,3,4,5) | |
| 98 | Найти мощность | (2,1) | |
| 99 | Решить, используя обратную матрицу | -3x-4y=2 , 8y=-6x-4 | , |
| 100 | Решить, используя обратную матрицу | 2x-5y=4 , 3x-2y=-5 | , |
Сложение матриц
1) Определение
матрицы— Матрицей размера mxn называется
прямоугольная таблица чисел, содержащая
m
строк и n
столбцов.
Вектор-строкой называют матрицу, состоящую из одной
строки. Вектор-столбцом — из одного столбца. Матрица, у которой
количество столбцов равно количеству
строк, называется
квадратной матрицей n-ого
порядка.
Элементы матрицы, у которых номер строки
и номер столбца совпадает, называются диагональными и образуют
главную диагональ матрицы.
Если все недиагональные элементы
матрицы равны нулю, то матрицу называют диагональной.
Если у диагональной матрицы n-ого
порядка на главной диагонали все
элементы равны 1, то матрица называется единичной и обозначается Е.
Матрица любого размера, все элементы
которой равны 0, называется нуль-матрицей.
Сложение
и вычетание матриц— Сложение 2-х матриц:
условие — складывать можно только матрицы
одинакового размера. Суммой 2-х матриц
А и В называется матрица С=А+В, каждый
элемент которой находится по формуле Сij=aij+bij.
Для того, чтобы сложить 2 матрицы,
необходимо складывать между собой
элементы, стоящие на одинаковых местах.
Умножение матрицы на число- условий нет, умножить на число можно любую матрицу. Произведением матрицы А на число l называется матрица В, равная lА, каждый элемент которой находится по формуле: bij =l x aij. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы.
Произведения матриц— умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В.
Определители
2-го и 3-го порядка— Определитель—
число, характеризующее матрицу.
Определителем
матрицы 1-го порядка А=(а11)
является единственный элемент этой
матрицы. Определителем
2-го порядка называется число, характеризующее
матрицу 2-го порядка, которое находится
по следующему правилу: из произведений
элементов главной диагонали вычитается
произведение элементов второй диагонали
матрицы А.
Обратная
матрица- Матрица
А-1 называется обратной по отношению к
квадратной матрице А, если при умножении
её на заданную как справа так и слева
получатся единичная матрица. Теорема
(необходимое и достаточн.условие сущ-я
обратн.матрицы): обратная матрица А-1
сущ-т и единственна тогда и только тогда,
когда заданная матрица не вырожденная. Матрица называется вырожденной,
если её определитель равен 0, в противном
случае она – не вырожденная. Алгоритм:
1)Определитель заданной матрицы.
2)Транспонирование. 3)Алгебраические
дополнения всех элементов транспонированной
матрицы. 4) Присоед.матрица А@
(на месте каждого эл-та Ат его
алгебраич.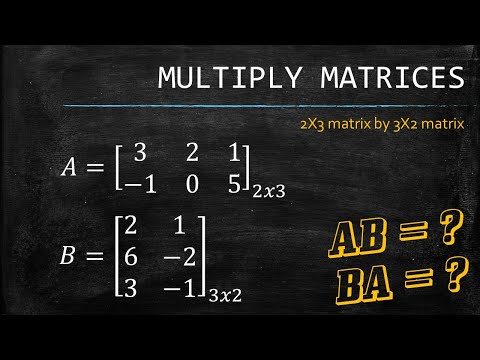
доп-я). 5) А-1=
1/DА
*A@.
6) Проверка=>А-1 *А=Е.
Понятие о матрице
Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:
aij, I – номер строки, j – номер столбца.
Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.
пример 1.
Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
пример 2.
Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной (пример 2).
Если
количество столбцов матрицы совпадают
с количеством строк, то матрица называется
квадратной (пример 1).
Количество строк или столбцов в квадратной матрице называются ее порядком.
Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).
пример3
Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).
пример 4
Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT = (2 3 5). пример 5.
Если n=1, то получается матрица-столбец (пример 6).
пример 6.
Матрицы-строки матрицы-столбцы называются векторами.
Свойства матриц:
Действия с матрицами
Матрицы одинакового размера можно складывать.
Суммой
двух таких матриц А и В называется
матрица С, элементы которой равны сумме
соответствующих элементов матриц А и
В.
Символически будем записывать
так: А+В=С.
Пример.
Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.
Вычитание матриц.
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А – В.
Пример.
3. Умножение матриц
Рассмотрим правило умножения двух квадратных матриц второго порядка.
Произведением
матрицы А на матрицу В называется матрица
С=АВ.
Правила умножения прямоугольных матриц:
Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.
В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.
4. Умножение матрицы на число
При умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число a. Например, умножим матрицу на число 2. Получим , т.е. при умножении матрицы на число множитель «вносится» под знак матрицы.
Транспонирование матрицы
Транспонированная
матрица – матрица AТ,
полученная из исходной матрицы A заменой
строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров m*n – матрица AT размеров n*m, определённая как AT[i, j] = A [j, i].
Например,
Свойства транспонированных матриц
1. (AT)T = A
2. (A + B)T = AT + BT
3. (AB)T = BTAT
4. detA = detAT
Определители 2-го и 3-го порядков.
Будем рассматривать квадратные матрицы
Определители являются основными числовыми характеристиками квадратных матриц.
Определителем (детерминантом) матрицы ,
состоящей из одного числа , называется само это число.
Определителем матрицы А= второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:
Рассмотрим матрицу третьего порядка:
Определителем матрицы A третьего порядка называется число
Данная
формула называется формулой разложения
определителя 3 порядка по элементам
первой строки.
Пример 6. Вычислить определители заданных матриц:
1.
Решение :
2.
Решение:
3.
Решение.
В первой строке определителя уже есть два нулевых элемента. Преобразуем определитель так, чтобы еще два элемента этой строки обратились в ноль. Сделать это можно путем преобразований столбцов. Оставим без изменения 2-й и 5-й столбцы (там уже стоят нули). К 3-му столбцу прибавим 1-й, умноженный на -2, к 4-му ~ первый, умноженный на 1. При этом первый столбец в преобразованном определителе останется без изменения.
Теперь разложим определитель по элементам первой строки:
В полученном определителе четвертого порядка преобразуем к нулю первые три элемента 1-й строки с помощью последнего 4-гo столбца: к 1-му прибавим 4-й, умноженный на 3, 2-ой преобразовывать не нужно, к 3-му прибавим 4-ый, умноженный на -1.
Разложим этот определитель по элементам первой строки:
Полученный
определитель третьего порядка можно
вычислить по правилу треугольников,
однако проще и здесь, получив нули (легче
всего в первом столбце), свести дело к
определителю второго порядка.
Ко 2-ой
строке прибавим 1-ю, умноженную на -4, 3-й
– первую, умноженную на 3:
Разлагаем определитель по элементам первого столбца:
И здесь можно упростить вычисления: ко 2-ой строке прибавим 1-ую, затем ко 2-му столбцу прибавим 1-ый, умноженным на 2:
Замечание 4.При использовании свойства 8, следует иметь в виду, что в преобразованном определителе меняется только та строка, к которой прибавляется другая (аналогично для столбцов). Так, если, например, к 3-ий строке прибавляется 1-ая, умноженная на 2, то в преобразованном определителе первая строка останется в неизменном виде, меняется только 3-я строка.
Умножение матриц
Умножение матрицРассмотрим произведение матрицы 2×3 и матрицы 3×4. Умножение определяется, поскольку внутренние размеры (3) одинаковы. Продукт будет быть матрицей 2×4, внешние размеры.
Так как в первой матрице три столбца и три строки во второй
матрица (внутренние размеры которой должны быть одинаковыми), каждый элемент в произведении
будет сумма трех
товары.
Строка 1, Столбец 1
Чтобы найти элемент в строке 1, столбце 1 произведения, мы возьмем строку 1 из первой матрицы и столбец 1 из второй матрицы. Мы соединяем эти значения вместе, умножаем пары значений, а затем добавляем к прибыть в 25.
Р 1 : 1 -2 3
×С 1 : 1 -3 6
---------------
1 +6 +18 = 25 Строка 2, Столбец 3
Чтобы найти элемент в строке 2, столбце 3 произведения, возьмем строку 2 из первой матрицы и столбец 3 из второй матрицы. Соединяем эти значения вместе, перемножьте пары значений, а затем добавьте к прибыть в 53.
Р 2 : 4 5 -2
×С 3 : 4 7 -1
---------------
16 +35 +2 = 53 Понимание того, откуда взялось каждое число в произведении, полезно, когда
вам нужно только определенное значение. Вам не нужно умножать полностью, если вы
нужны только определенные элементы. Просто возьмите строку из первой матрицы и
столбец из второй матрицы.
Процесс можно завершить для остальных элементов матрицы.
| Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | ||
|---|---|---|---|---|---|
| значений | [1, -3, 6] | [-8, 6, 5] | [4, 7, -1] | [-3, 2, 4] | |
| Ряд 1 | [1, -2, 3] | 1(1) — 2(-3) + 3(6) = 1 + 6 + 18 = 25 | 1(-8) -2(6) + 3(5) = -8 — 12 + 15 = -5 | 1(4) -2(7) +3(-1) = 4 — 14 — 3 = -13 | 1(-3) -2(2) + 3(4) = -3 -4 + 12 = 5 |
| Ряд 2 | [4, 5, -2] | 4(1) + 5(-3) -2(6) = 4 — 15 — 12 = -23 | 4(-8) + 5(6) — 2(5) = -32 + 30 — 10 = -12 | 4(4) + 5(7) -2(-1) = 16 + 35 + 2 = 53 | 4(-3) + 5(2) -2(4) = -12 + 10 — 8 = -10 |
Итак, конечный продукт
| 25 | -5 | -13 | 5 | ||
| -23 | -12 | 53 | -10 |
Обратите внимание, что умножение не определяется другим способом.
Вы не можете умножить
3×4
и матрица 2×3 вместе, потому что внутренние размеры не совпадают.
Этот продукт не определен.
2.1 Определения и матричная алгебра
Определение 2.1
- An m ✕ n матрица представляет собой прямоугольную сетку чисел с m строками и n столбцов.
- Вектор-столбец представляет собой матрицу м ✕1.
- Вектор-строка представляет собой матрицу 1✕ n .
- Матрица квадратных равна м ✕ м для некоторых м .
Набираем матрицы так: \[A= \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & \pi \end{pmatrix}, B=\begin{pmatrix} 1\2\3 \end{pmatrix}, C=\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \конец{pmatrix}\] это матрица 2✕3, вектор-столбец 3✕1 и 3✕3 квадратная матрица соответственно.
Определение 2.
2 i , j элементом матрицы является число в строке i и столбце j .
Например, запись 1, 2 матрицы A выше равна 2, запись 2, 1 равна 0, а запись 2, 3 — это \(\pi\). Очень часто мы пишем \(A=(x_{ij})\), чтобы обозначить, что A является матрица, чьи i , j записи равны \(x_{ij}\).
Если две матрицы A и B имеют одинаковый размер (то есть обе м ✕ n для тех же м и n ) то их складываем и вычитаем добавляя и вычитая каждую запись отдельно:
\[\begin{align*} \begin{pmatrix} 1 и 2 \\ 3 и 4 \end{pmatrix} + \begin{pmatrix} 0 и 1 \\-1 и -1 \end{pmatrix} &= \begin{pmatrix} 1 и 3 \\ 2 и 3 \end{pматрица} \\ \begin{pmatrix} 1&0 \end{pmatrix} — \begin{pmatrix} 9 и 9 \end{pmatrix} &= \begin{pmatrix} -8 и -9 \end{pматрица} \end{align*}\]
Мы также умножаем матрицы на числа по одной записи за раз («по входу»): \[2 \begin{pmatrix} 1&2&3 \\0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} 2&4&6\\0&2&0 \end{pmatrix}\]
Это называется скалярным умножением .