Как перевести синус угла в градусы
Регистрация Выслать повторно письмо для активации Что даёт регистрация на форуме? Правила раздела Visual Basic: Общие вопросы. Вопросы по Visual Basic. Обратите внимание: 1.
Поиск данных по Вашему запросу:
Как перевести синус угла в градусы
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Таблица синусов углов (градусы, значения)
- Таблицы значений тригонометрических функций.
- Как посчитать синус 5 градусов 43 минут на калькуляторе windows?
- Тригонометрические функции
- Синус угла — sin(A), формула
- Вычисление синуса, косинуса, тангенса и котангенса онлайн
- Тригонометрия в Excel: основные функции
- Тригонометрический калькулятор
- Таблица синусов углов от 0° — 360°.
Углы с шагом в 1°. Таблица значений синусов.
- Таблица Брадиса для sin, cos, tg, ctg
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Что такое радиан?
Таблица синусов углов (градусы, значения)
Данная тригонометрическая функция, как и остальные, может рассматриваться для острых углов как соотношение сторон прямоугольного треугольника. Синусом sin угла принято. Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Существует две наиболее распространенные единицы измерения углов. К ним относятся градусы и радианы. Перевести градусы в радианы достаточно просто. Он считается положительным в том случае, если угол отсчитывается против часовой стрелки.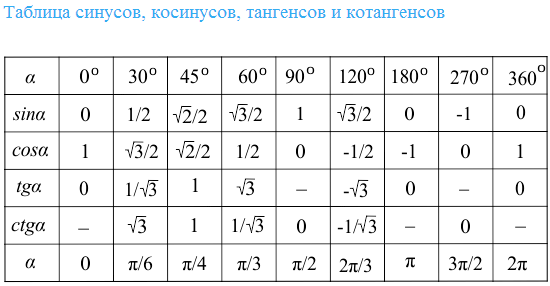
Углы могут быть также и больше градусов. Так как мы, сделав несколько полных оборотов по окружности, возвращаемся на исходную точку, которая имеет те же координаты по оси Y. В тригонометрическом круге значение синуса повторяет свое значение каждые градусов. В общем история тригонометрии насчитывает два тысячелетия. Так как большинство математических соотношений невозможно было выразить при помощи обычных алгебраических операций, были введены тригонометрические функции, которые вначале оформлялись в виде таблиц.
Современный вид тригонометрия приобрела в работах выдающегося математика, физика, астронома и механика Леонарда Эйлера. Математики Древней Индии синус называли словом «джива», что обозначало тетиву лука. В дальнейшем этот термин арабы превратили в «джиба».
А тот в дальнейшем еще превратился в «джайо», более привычное для арабского языка слово, которое означает изгиб, складку одежды. Он же и соответствует латинскому слову sinus.
Он является одной из тригонометрических функций, к которым еще относится косинус, тангенс и котангенс, а также секанс и косеканс. Леонард Эйлер Вернуться к просмотру справок по дисциплине «Геометрия».
Леонард Эйлер Вернуться к просмотру справок по дисциплине «Геометрия».
Таблицы значений тригонометрических функций.
К этой теме имеются дополнительные материалы в Особом разделе Для тех, кто сильно «не очень Продолжаем осваивать таблицу синусов и косинусов. А именно — привыкаем работать с необходимыми табличными значениями без механической зубрёжки.
Синус (sin) для острого угла рассматривается как отношение катета, который лежит напротив Перевести градусы в радианы достаточно просто.
Как посчитать синус 5 градусов 43 минут на калькуляторе windows?
Данная тригонометрическая функция, как и остальные, может рассматриваться для острых углов как соотношение сторон прямоугольного треугольника. Синусом sin угла принято. Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Существует две наиболее распространенные единицы измерения углов. К ним относятся градусы и радианы.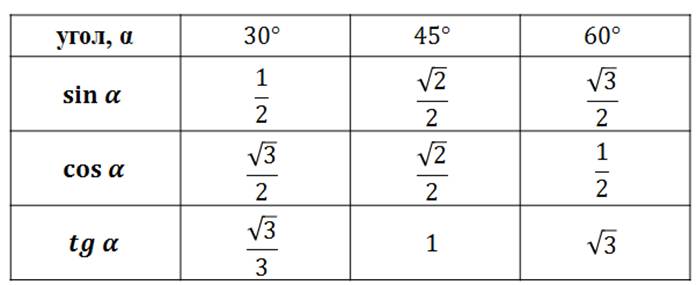 Перевести градусы в радианы достаточно просто. Он считается положительным в том случае, если угол отсчитывается против часовой стрелки. Углы могут быть также и больше градусов. Так как мы, сделав несколько полных оборотов по окружности, возвращаемся на исходную точку, которая имеет те же координаты по оси Y.
Перевести градусы в радианы достаточно просто. Он считается положительным в том случае, если угол отсчитывается против часовой стрелки. Углы могут быть также и больше градусов. Так как мы, сделав несколько полных оборотов по окружности, возвращаемся на исходную точку, которая имеет те же координаты по оси Y.
Тригонометрические функции
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение. Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение. Пример 1. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа. В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin синус и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая.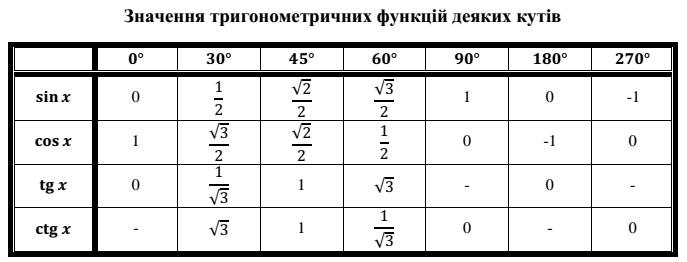
Синус угла — sin(A), формула
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов. После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций. Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов: , а котангенс нуля градусов не определен, и , а тангенс 90 градусов не определен. В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов : , и.
Вычисление синуса, косинуса, тангенса и котангенса онлайн
Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение. В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая. Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других — только приблизительные. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии. В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая. Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других — только приблизительные. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии. В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу.
калькулятор поможет перевести значение угла выраженного в градусах в Например вычислить чему равен синус 30° градусов, косинус 2-ух радиан.
Тригонометрия в Excel: основные функции
Как перевести синус угла в градусы
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. Поиск по сайту TehTab. Техническая информация Раздел.
Тригонометрический калькулятор
Формулы тригонометрии — редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна. Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel.
Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна. Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel.
Почему мы так решили?
Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
Возвращает синус указанного угла. Returns the sine of the specified angle. Угол, измеряемый в радианах. An angle, measured in radians. Синус a. The sine of a.
Таблица Брадиса для sin, cos, tg, ctg
Когда нет рядом калькулятора таблица синусов просто незаменима. Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице и все.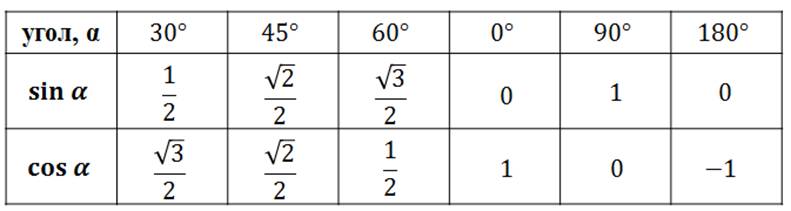 Таблица синусов — это основно материал тригонометрии, который необходимо знать или, как минимум, понимать. Пользуйтесь на здоровье таблицей значений синусов.
Таблица синусов — это основно материал тригонометрии, который необходимо знать или, как минимум, понимать. Пользуйтесь на здоровье таблицей значений синусов.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.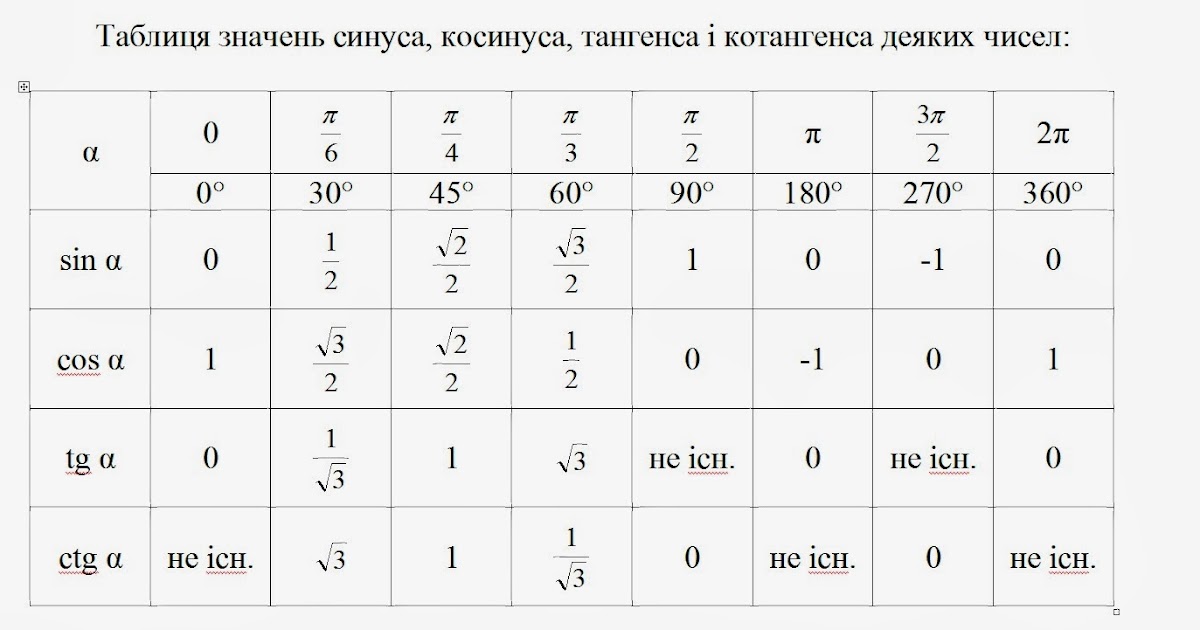 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.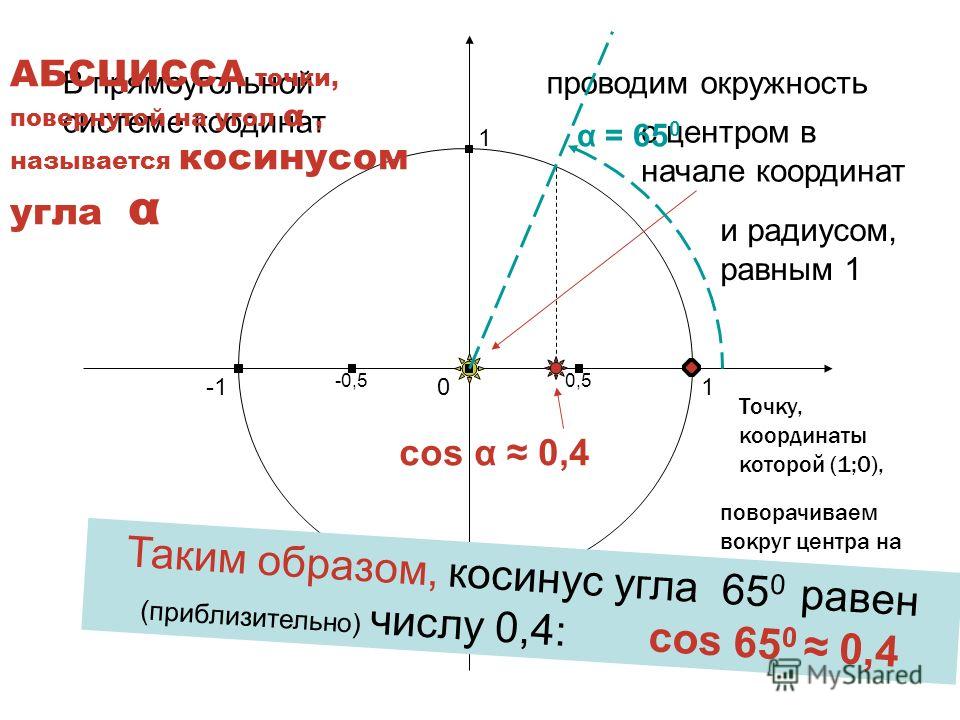 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.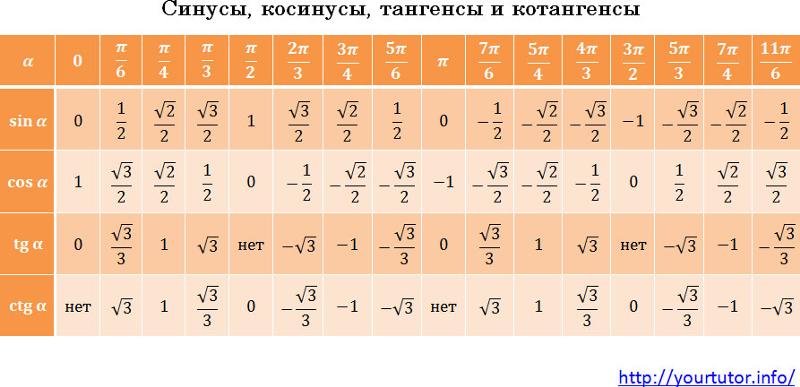 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.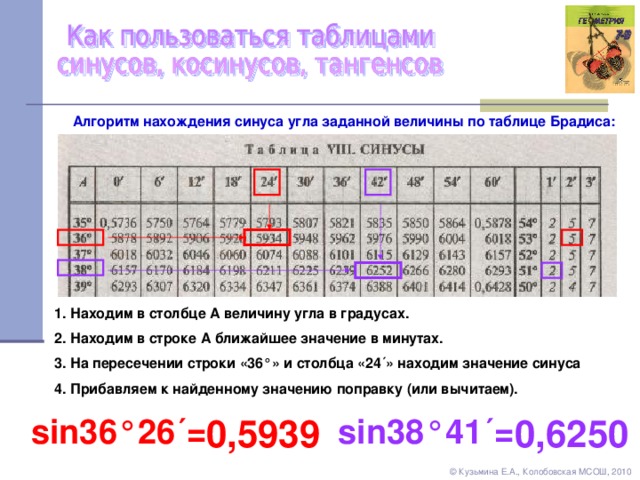 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.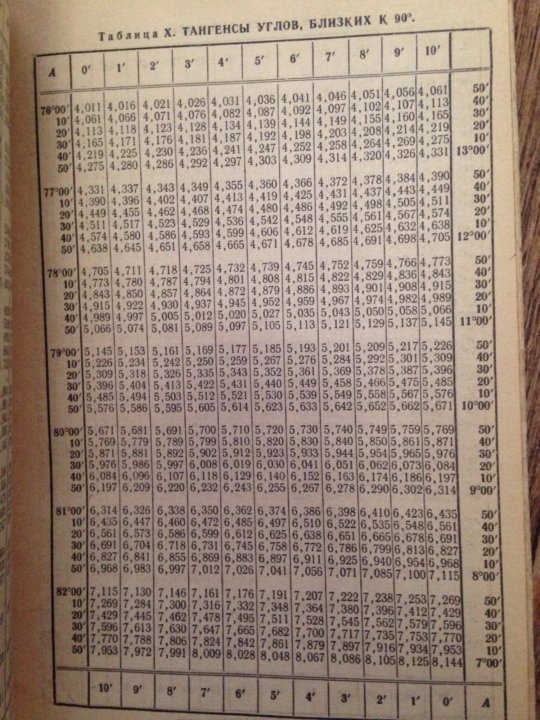 8571673007 8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
sin(11) = 0. 1908089954 1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.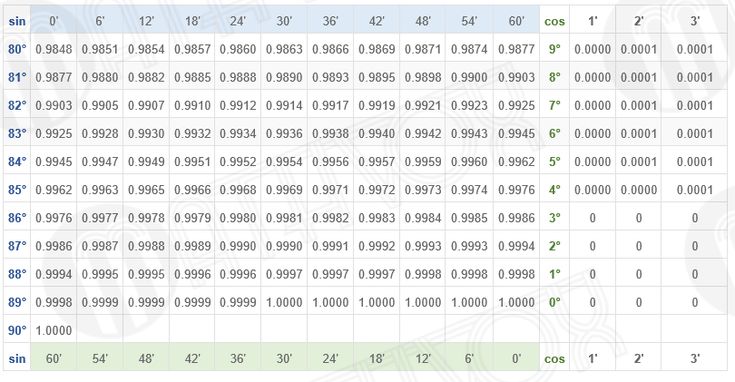 984807753 984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.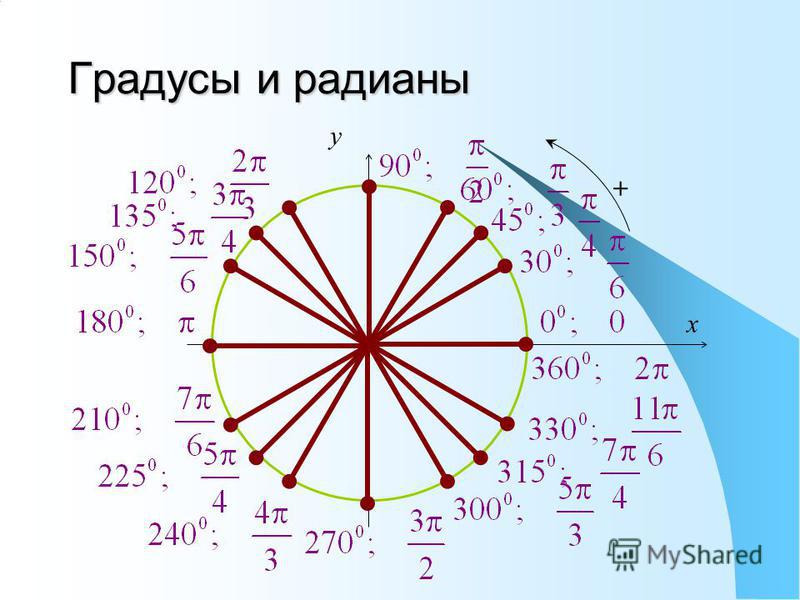 5 5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0. 3420201433 3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
sin(50) = 0. 7660444431 7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0. 8746197071 8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0. 156434465 156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
sin(79) = 0.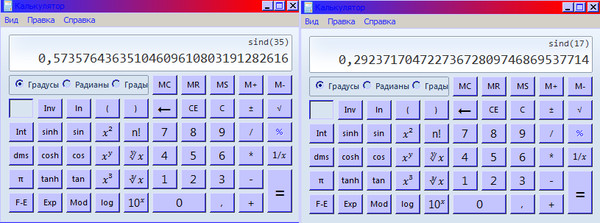 9816271834 9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.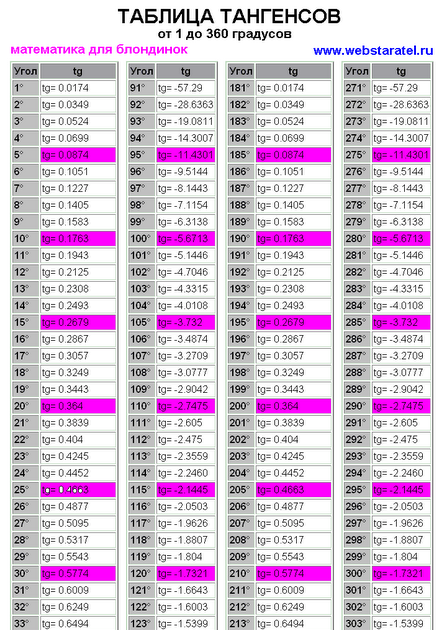 5299192642 5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.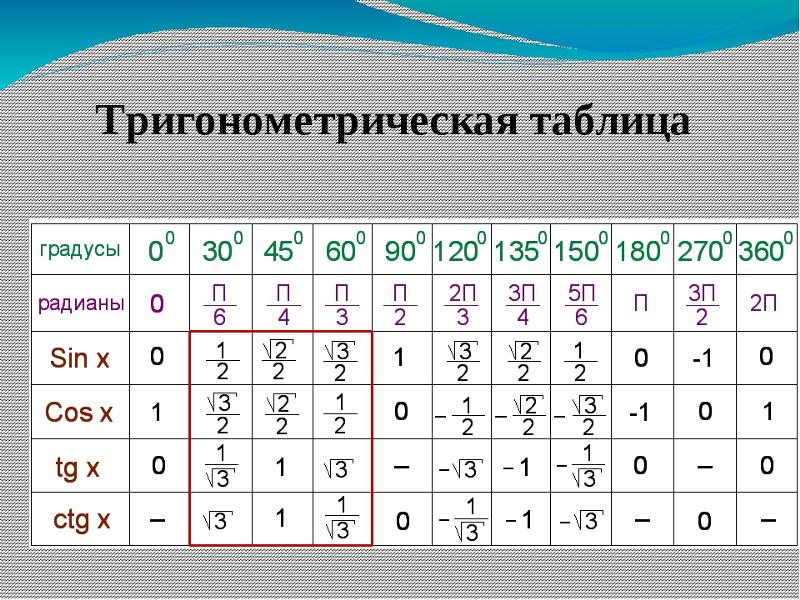 3746065934 3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.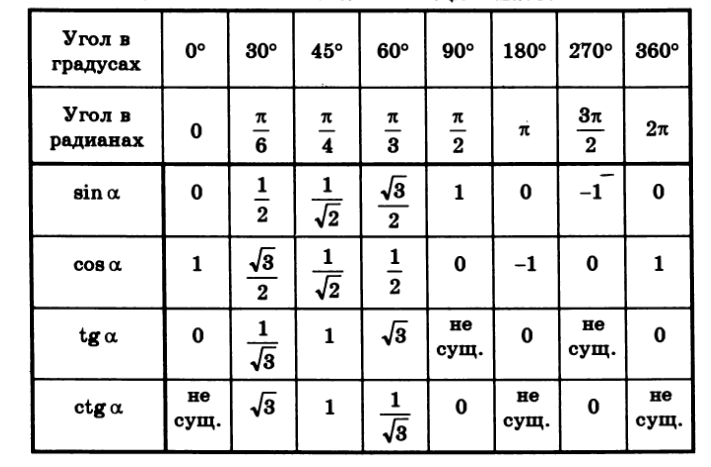 7431448255 7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
sin(118) = 0. 8829475929 8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Sin 1 градус — Найти значение Sin 1 градус
LearnPracticeDownload
Значение sin 1 градус равно 0,0174524. . . . Sin 1 градус в радианах записывается как sin (1° × π/180°), т. е. sin (0,017453…). В этой статье мы обсудим способы нахождения значения sin 1 градусов на примерах.
- Sin 1°: 0,0174524. . .
- Sin (-1 градус): -0,0174524. . .
- Sin 1° в радианах: грех (0,0174532 . . . .)
Каково значение Sin 1 градусов?
Десятичное значение sin 1 градусов равно 0,017452406. . .. Sin 1 градус также может быть выражен с помощью эквивалента заданного угла (1 градус) в радианах (0,01745 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 1 градус = 1° × (π/180°) рад = 0,0174. . .
. .
∴ sin 1 ° = sin (0,0174) = 0,0174524. . .
Объяснение:
Для sin 1 градусов угол 1° лежит между 0° и 90° (первый квадрант). Поскольку функция синуса положительна в первом квадранте, значение sin 1° = 0,0174524. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 1° как sin 1 градусов = sin(1° + n × 360°), n ∈ Z.
⇒ sin 1° = sin 361° = sin 721° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-1°) = -sin(1°).
Методы определения значения греха 1 градусов
Функция синуса положительна в 1-м квадранте. Значение sin 1° равно 0,01745. . .. Мы можем найти значение sin 1 градусов по:
- Используя тригонометрические функции
- Использование единичного круга
Sin 1° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 1 градусов как:
- ± √(1-cos²(1°))
- ± тангенс 1°/√(1 + тангенс²(1°))
- ± 1/√(1 + раскладушка²(1°))
- ± √(сек²(1°) — 1)/сек 1°
- 1/косек 1°
Примечание.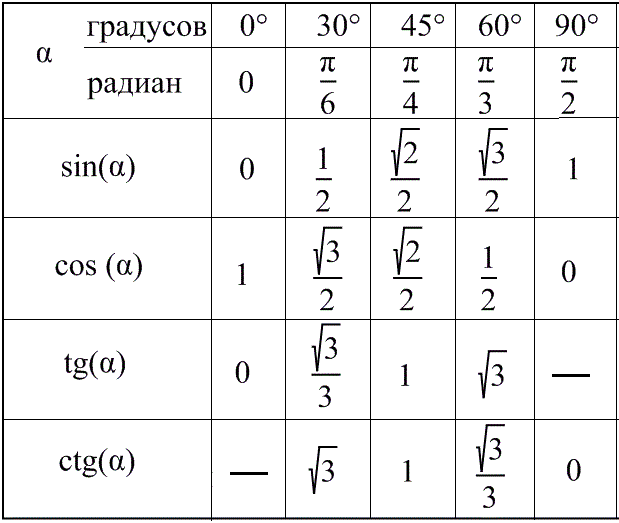 Поскольку 1° лежит в 1-м квадранте, конечное значение sin 1° будет положительным.
Поскольку 1° лежит в 1-м квадранте, конечное значение sin 1° будет положительным.
Мы можем использовать тригонометрические тождества для представления sin 1° как
- sin(180° — 1°) = sin 179°
- -sin(180° + 1°) = -sin 181°
- cos(90° — 1°) = cos 89°
- -cos(90° + 1°) = -cos 91°
Sin 1 Градусы с использованием единичной окружности
Чтобы найти значение sin 1 градусов с помощью единичной окружности:
- Поверните «r» против часовой стрелки, чтобы образовать угол 1° с положительной осью x.
- Грех в 1 градус равен координате y (0,0175) точки пересечения (0,9998, 0,0175) единичной окружности и r.
Отсюда значение sin 1° = y = 0,0175 (приблизительно)
☛ Также проверьте:
- sin 53 градуса
- грех 30 градусов
- грех 35 градусов
- грех 8 градусов
- грех 510 градусов
- грех 31 градус
Примеры использования Sin 1 градусов
Пример 1.
 Найдите значение 5 sin(1°)/7 cos(89°).
Найдите значение 5 sin(1°)/7 cos(89°). Решение:
Используя тригонометрические тождества, мы знаем, что sin(1°) = cos(90° — 1°) = cos 89°.
⇒ sin(1°) = cos(89°)
⇒ Значение 5 sin(1°)/7 cos(89°) = 5/7Пример 2. Найдите значение 2 × (sin 0,5° cos 0,5°). [Подсказка: используйте sin 1° = 0,0175]
Решение:
Используя формулу sin 2a,
2 sin 0,5° cos 0,5° = sin(2 × 0,5°) = sin 1°
∵ sin 1° = 0,0175
⇒ 2 × (sin 0,5° cos 0,5°) = 0,0175Пример 3. Найдите значение sin 1°, если cosec 1° равно 57,2986.
Решение:
Так как sin 1° = 1/csc 1°
⇒ sin 1° = 1/57,2986 = 0,0175
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 1 Degrees
Что такое Sin 1 Degrees?
Sin 1 градус — значение тригонометрической функции синуса для угла, равного 1 градусу. Значение sin 1° равно 0,0175 (приблизительно).
Как найти значение Sin 1 градусов?
Значение sin 1 градуса можно рассчитать, построив угол 1° с осью x и затем найдя координаты соответствующей точки (0,9998, 0,0175) на единичной окружности. Значение sin 1° равно координате y (0,0175). ∴ sin 1° = 0,0175.
Каково значение Sin 1° в пересчете на Cosec 1°?
Поскольку функция косеканса является обратной величиной функции синуса, мы можем записать sin 1° как 1/cosec(1°). Значение cosec 1° равно 57,29868.
Каково значение Sin 1 градусов в пересчете на Cos 1°?
Используя тригонометрические тождества, мы можем записать sin 1° через cos 1° как sin(1°) = √(1-cos²(1°)). Здесь значение cos 1° равно 0,9998476.
Здесь значение cos 1° равно 0,9998476.
Как найти Sin 1° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение sin 1° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(1°))
- ± тангенс 1°/√(1 + тангенс²(1°))
- ± 1/√(1 + раскладушка²(1°))
- ± √(сек²(1°) — 1)/сек 1°
- 1/косек 1°
☛ Также проверьте: таблицу тригонометрии
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Функция SIN в Excel | Как использовать функцию SIN в Excel?
Функция SIN в Excel (Содержание)
- Функция SIN в Excel
- Как использовать функцию SIN в Excel?
Функция синуса Excel — это еще одна математическая функция, которая дает значение синуса любого угла или значение угла в радианах. Мы все знаем, что Перпендикуляр математически вычисляет синусоидальный угол относительно гипотенузы, но это дает логику синусоидального угла. Чтобы вычислить функцию Sin, нам нужно передать значение с помощью функции радианов или умножить угол на Pi () / 180, чтобы получить фактическое значение.
Мы все знаем, что Перпендикуляр математически вычисляет синусоидальный угол относительно гипотенузы, но это дает логику синусоидального угла. Чтобы вычислить функцию Sin, нам нужно передать значение с помощью функции радианов или умножить угол на Pi () / 180, чтобы получить фактическое значение.
Базовая тригонометрическая функция
Итак, для решения тригонометрической функции Синус предоставляет функцию SIN, , которая является базовой тригонометрической функцией, но может пригодиться, особенно если вы работаете в сфере производства, навигации или связи. Но важно отметить, что Excel использует радианы, а не градусы, для вычисления любого тригонометрического выражения. Это можно сделать двумя способами:
- Напомним, что π = 180°. Итак, если угол выражен в градусах, умножьте его на π/180°, чтобы преобразовать в радианы. В Excel это преобразование можно записать как PI()/180. Например, чтобы преобразовать 60° в радианы, выражение Excel будет иметь вид 60*PI()/180, что равняется 1,0472 радианам.

- Excel также оснащен очень полезным инструментом, обычно называемым RADIANS. Он принимает угол в качестве аргумента, в котором угол относится к градусам, которые необходимо преобразовать в радианы. Возьмем пример, в котором выражение, используемое для преобразования 210° в радианы, называется «РАДИАНЫ (210)», и оно оценивается как 66 519 радиан.
С другой стороны, утилита DEGREES не менее важна. Эту функцию можно использовать, чтобы сделать прямо противоположное функции РАДИАНЫ, преобразовав радианы в градусы. Например, ГРАДУСЫ(PI()/2) оценивает 90.
Как использовать функцию SIN в Excel?
Давайте разберемся, как использовать функцию SIN в Excel, используя несколько примеров и реальных иллюстраций функции SIN в Excel.
Вы можете скачать этот шаблон Excel для функции SIN здесь — Шаблон Excel для функции SIN
Пример №1
Вычисление значения синуса с использованием функции SIN в Excel
Чтобы найти синус определенного числа, мы должны сначала написать =SIN() в конкретной ячейке.
Как видно из приведенного выше снимка экрана, функция SIN в Excel ожидает ввода числа. Это число обычно представляет значение в радианах. Итак, в этом случае мы напишем «=SIN(1,0472)», где 1,0472 — это радиан, эквивалентный 60 градусам.
Как только мы это сделаем, мы получим значение SIN 60 градусов.
Пример #2
Вычисление значения синуса с использованием функций SIN и RADIAN в Excel
Теперь давайте посмотрим, как мы можем использовать SIN более продуктивно в случае, когда мы не знаем точного значения радиана. для степени. Мы будем использовать RADIANS(), чтобы узнать значение радиана, которое мы передадим в качестве аргумента функции SIN. Итак, мы начинаем с более ранней версии SIN():
Далее мы передадим RADIANS(60) в качестве аргумента функции SIN, где 60 — это значение в градусах.
Как видно из приведенного выше примера, RADIANS() принимает значение в градусах. Итак, мы передадим 60 в качестве значения функции RADIANS().
Итак, мы передадим 60 в качестве значения функции RADIANS().
Затем нажмите Enter. Это дает следующий результат.
Итак, мы видим, что результат такой же, как и в первом примере.
Пример №3
Вычисление значения синуса с использованием SIN и PI Функция в Excel
Существует еще один способ преобразования значения градуса в радианы для использования в функции SIN. Мы помним со школьной скамьи, что π = 180°. Итак, если угол выражен в градусах, умножьте его на π/180°, чтобы преобразовать в радианы. В Excel это преобразование можно записать как PI()/180. Например, чтобы преобразовать 60° в радианы, выражение Excel будет иметь вид 60*PI()/180, что равняется 1,0472 радианам.
Начнем с написания функции SIN таким же образом, как описано выше.
Далее мы будем напрямую передавать 60° в качестве аргумента функции SIN. Но это не дало бы нам соответствующее значение 60 градусов в радианах. Следовательно, мы умножим 60 на PI()/180.
Следовательно, мы умножим 60 на PI()/180.
Это даст нам следующий результат:
Как мы видим, это то же самое, что и в приведенных выше примерах.
Пример #4
Теперь давайте рассмотрим другой пример, показывающий результаты функции SIN для различных значений.
Объяснение результатов, показанных в таблице выше:
Варианты 1 и 2:
3,14 — это значение числа Пи, и мы можем использовать оба метода, чтобы получить значение 0. Это в основном означает SIN пи радиан равен 0 .
Варианты 3 и 4:
Радианы и Пи/180 имеют одинаковое значение в математике, поэтому функция SIN дает одинаковое значение. Оба примера подразумевают SIN 30 градусов, что дает значение 0,5.
Варианты 5 и 6:
SIN 45 = 0,85 — это SIN 45 радиан, что означает, что по умолчанию Excel принимает все углы в радианах, а не в градусах. Чтобы преобразовать его в градусы, мы можем использовать функцию радиана и получить SIN 45 градусов, как показано в последней строке. т. е. SIN(RADIANS(45)) = 0,707 или 0,71
Чтобы преобразовать его в градусы, мы можем использовать функцию радиана и получить SIN 45 градусов, как показано в последней строке. т. е. SIN(RADIANS(45)) = 0,707 или 0,71
Пример №5
Скажем, например, мы хотим узнать высоту дерева на рисунке выше. Мы знаем, что если мы стоим на расстоянии 76 м от вершины дерева (x = 76 м), линия обзора вершины дерева составляет 32° по отношению к горизонту (θ = 32°). Мы знаем, что:
Следовательно, чтобы найти высоту дерева h, мы находим h= x SIN θ.
Функция SIN имеет только один аргумент, который является числом. Число требуется для расчета SIN этого. Следовательно, жизненно важно преобразовать градусы в число в радианах, прежде чем находить его синус.
Функция SIN отображает #ЗНАЧ! ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные. В приведенном ниже примере ссылка на ячейку третьей используемой строки указывает на текстовую метку в Угле 9. 0005 (Градусы) . Поскольку функции SIN поддерживают только число в качестве аргумента, SIN будет оцениваться как ошибка, в данном случае #ЗНАЧ! . Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение, как показано в примере ниже. Тригонометрические функции Excel интерпретируют пустые ячейки как ноль, а синус нуля радиан равен нулю.
0005 (Градусы) . Поскольку функции SIN поддерживают только число в качестве аргумента, SIN будет оцениваться как ошибка, в данном случае #ЗНАЧ! . Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение, как показано в примере ниже. Тригонометрические функции Excel интерпретируют пустые ячейки как ноль, а синус нуля радиан равен нулю.
Пример #6
Теперь предположим, что мы хотим узнать угол запуска рампы для водных лыж, как показано на рисунке выше. Мы знаем, что A = 3,5 м, B = 10,2 м и b = 45,0°. Теперь, чтобы найти a , мы можем использовать закон синусов. В этом сценарии его можно записать как:
Мы можем реорганизовать это уравнение как:
Используя арксинус или арксинус, мы можем найти угол α . Применяя уравнение, показанное ниже.
Пример №7
В нашем последнем тригонометрическом примере мы будем использовать Excel для проверки тригонометрического тождества: θ указывается как в радианах, так и в градусах.
Обратите внимание, что описание единиц измерения угла θ помещено в другие ячейки, чем числа. Если мы поместим числа и единицы измерения в одну и ту же ячейку, Excel не сможет отличить число от текста, и, следовательно, мы не сможем ссылаться на ячейки для использования в уравнении, и это приведет к # ЦЕННОСТЬ! ошибка.
Что следует помнить
- Имейте в виду, что функция SIN в Excel по умолчанию работает с радианами.
- Преобразуйте число, как требуется, в радианы или градусы, используя либо функцию РАДИАНОВ, либо функцию ГРАДУСОВ.
- Вы можете использовать функцию PI() для получения точных результатов функции SIN при работе с π.
Рекомендуемые статьи
Это руководство по функции SIN в Excel. Здесь мы обсудили, как использовать функцию SIN в Excel, а также практические примеры и загружаемый шаблон Excel. Вы также можете просмотреть другие наши рекомендуемые статьи —
- Функция времени в Excel
- Пользовательская функция в Excel
- Функция COS в Excel
- Функция базы данных в Excel
Функция sin() в Python: объяснение с 4 примерами
Функция sin():
- Принимает аргумент (x = число)
- и возвращает синус в радианах.

- Это часть математического модуля, поэтому эту функцию нельзя использовать напрямую.
- Вы должны импортировать математический модуль в вашей программе Python — как показано в примерах ниже.
- Чтобы получить результат в градусах, вы можете использовать функцию radians() вместе с sin(), как показано в примере в следующем разделе этого руководства.
Вот как используется функция sin():
sin(x)
Например:
math.sin(3)
Полный код приведен в примерах ниже.
Что такое функция синуса в математике? Синус — одна из самых распространенных тригонометрических функций в математике. Две другие функции косинуса (или cos) и тангенса (tan). Функция синуса основана на прямоугольном треугольнике. Вы можете узнать больше о синусоидальной функции здесь.
В приведенном ниже примере показано использование функции sin() для получения синуса нескольких чисел. Получим синус в радианах для 30, 45 и 60:
1 2 3 4 5 6 7 8 10 110003 12 13 14 199991111000114 9000 3 9000 3 9000 3 9000 2 9000 214 9000 3 9000 3 9000 29000 3 9000 3 9000 3 18 19 | # Демонстрация функции sin()
from math import sin
SINE_30 = SIN (30) SINE_45 = SIN (45) SINE_60 = SIN (60) print («Синус 45 = «, sine_45)
print («Синус 60 = «, sine_60) |
Результат:
В приведенном выше примере мы использовали сокращение для использования функции sin(). Этот код даст тот же результат:
Этот код даст тот же результат:
1 2 3 4 5 6 7 8 10 110003 12 13 14 199991111000114 9000 3 9000 3 9000 3 9000 2 9000 214 9000 3 9000 3 9000 29000 3 9000 3 9000 3 | import math
sine_30 = math.sin(30)
sine_45 = math.sin(0000) 02 SINE_60 = MATH.SIN (60) Печать («Синус 30 =», SINE_30) Печать («Синус 45 =», SINE_45) печать («Синус 60 = «, sine_60) |
Результат:
Как получить синус в градусах?Синус 30 = -0,9880316240928618
Синус 45 = 0,85045341184
Синус 60 = -0,3048106211022167
Вам может быть интересно, почему эти ответы отличаются от использования калькулятора для вычисления синуса числа? Это связано с тем, что функция Python sin() возвращает синус в радианах.
В математическом модуле есть еще одна функция radians(), которую вы можете использовать для преобразования радианов в градусы.
В приведенном ниже примере используются те же значения, что и в приведенных выше примерах, а также используется функция radians() для преобразования возвращаемого результата функцией sin() и получения значений синуса в градусах:
1 2 3 4 5 6 7 8 10 110003 12 13 14 199991111000114 9000 3 9000 3 9000 3 9000 2 9000 214 9000 3 9000 3 9000 29000 3 9000 3 9000 3 | import math
sine_30 = math.sin(math.radians(30))
sine_45 = math.sin(radians.5in4))0003 SINE_60 = MATH.SIN (Math.Radians (60)) Печать («Синус 30 в степени =», SINE_30) в степени = «, sine_45)
print («Синус 60 в степени = «, sine_60) |
Выход:
Пример округления результатаСинус 30 в градусах = 0,49999999999999994
Синус 45 в градусах = 0,7071067811865475
Синус 60 в градусах = 0,8660254037844386
В приведенном ниже примере используются три функции вместе; sin(), радианы() и round(). Функция round округляет результат, возвращаемый функцией radians(), до одинарной точности. Смотрите код и вывод:
Функция round округляет результат, возвращаемый функцией radians(), до одинарной точности. Смотрите код и вывод:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | import math
sine_30 = round(math.sin(math.radians(30)),1)
rounds,s(radians)5math.5 sine_4 1)
sine_60 = round(math.sin(math.radians(60)),1)
print («Синус 30 в градусах) 9_sine = «3, 0 0002 с одинарной точностью»0003
print («Синус 45 в градусах с одинарной точностью = «, sine_45)
print («Синус 60 в градусах с одинарной точностью = «, sine_60) |
Результат приведенного выше кода:
Синус 30 градусов с одинарной точностью = 0,5.

 Найдите значение 5 sin(1°)/7 cos(89°).
Найдите значение 5 sin(1°)/7 cos(89°).