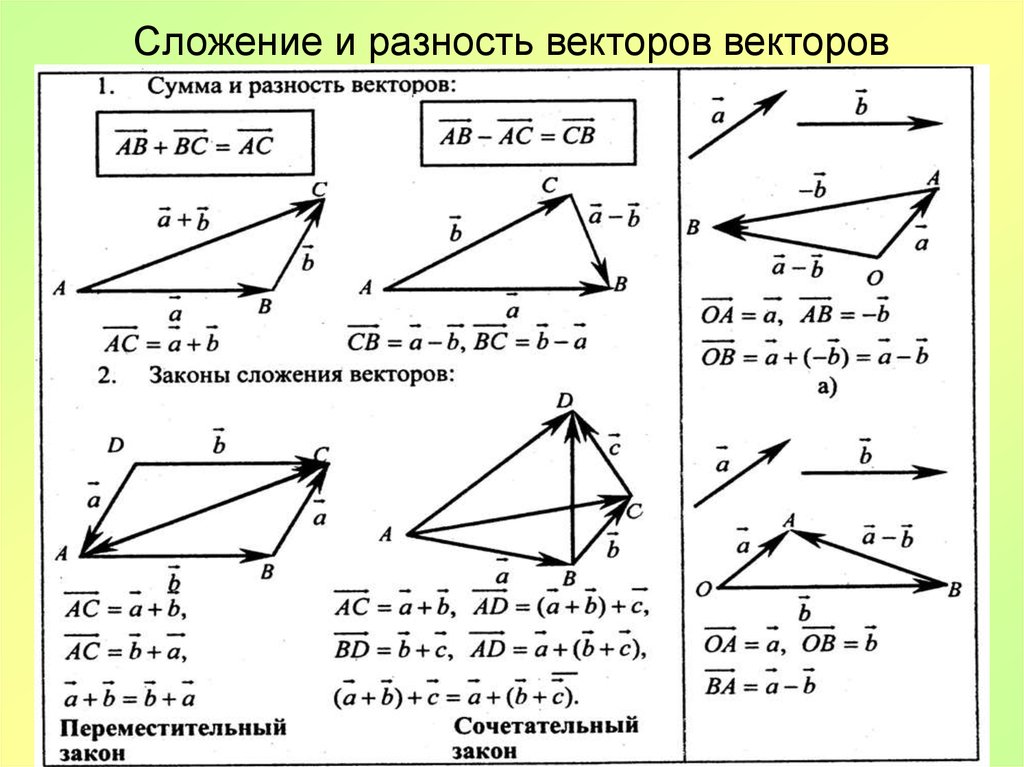
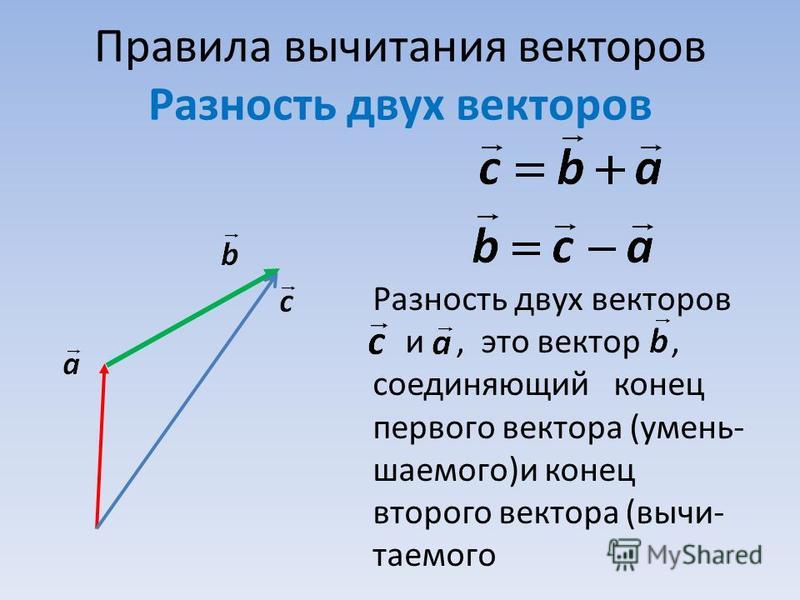
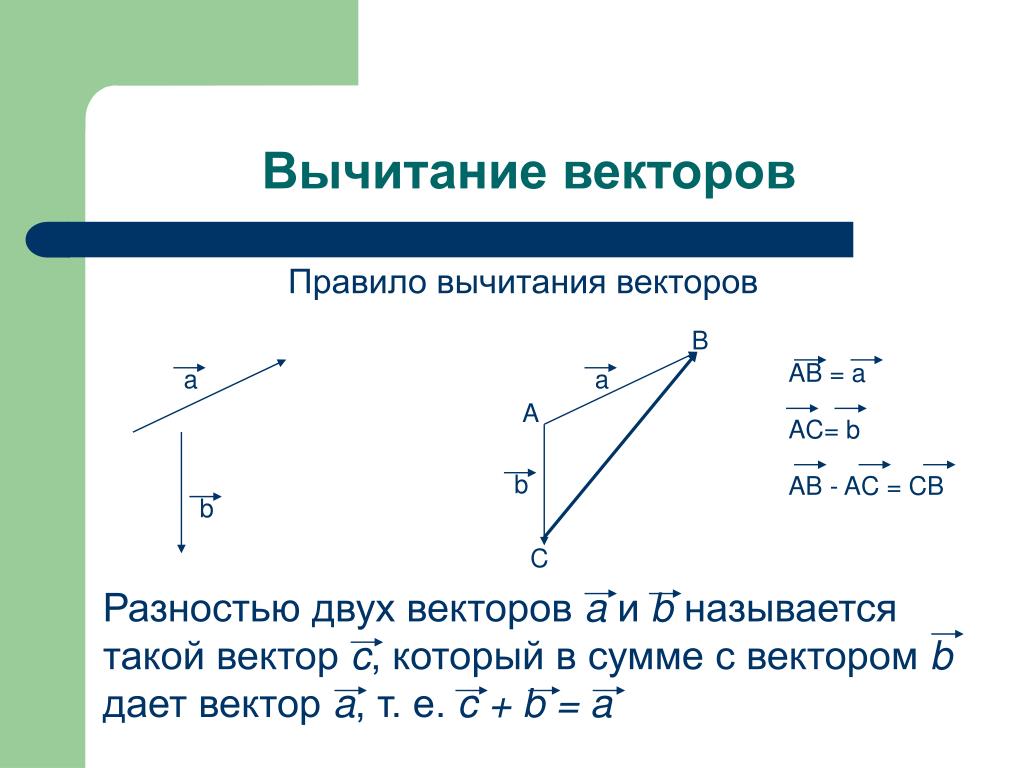
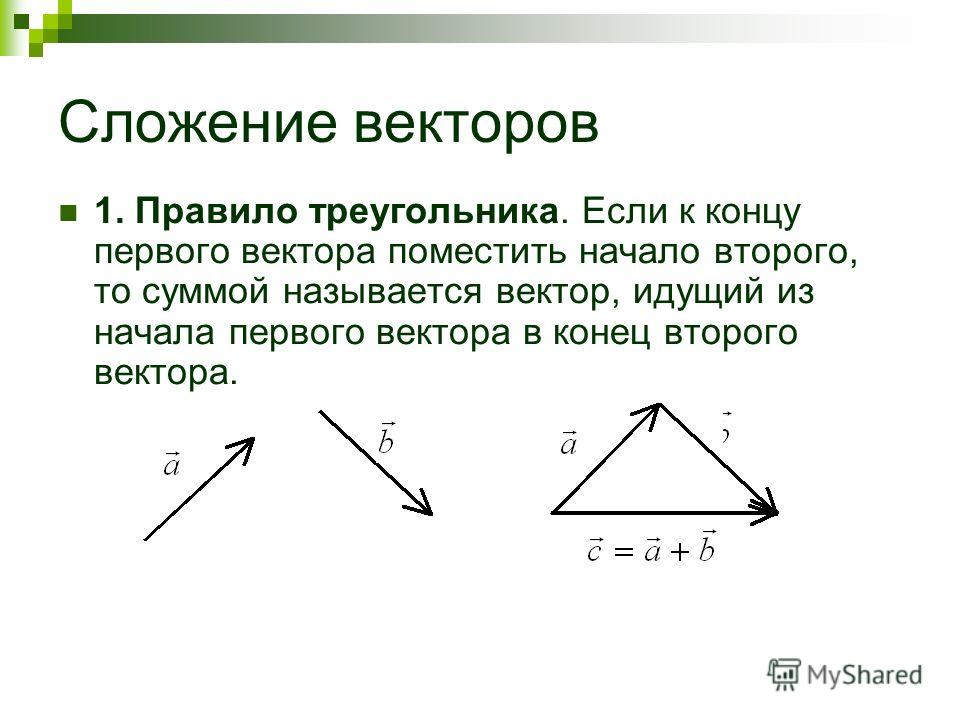
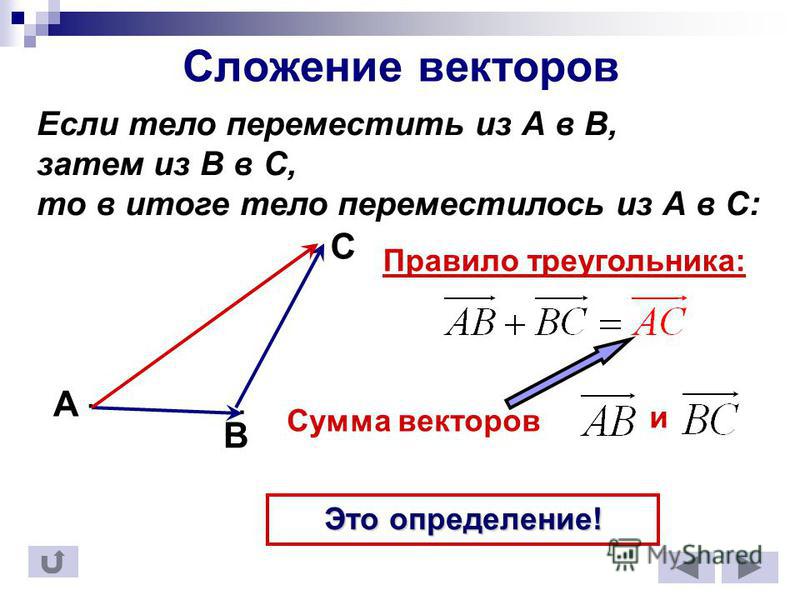
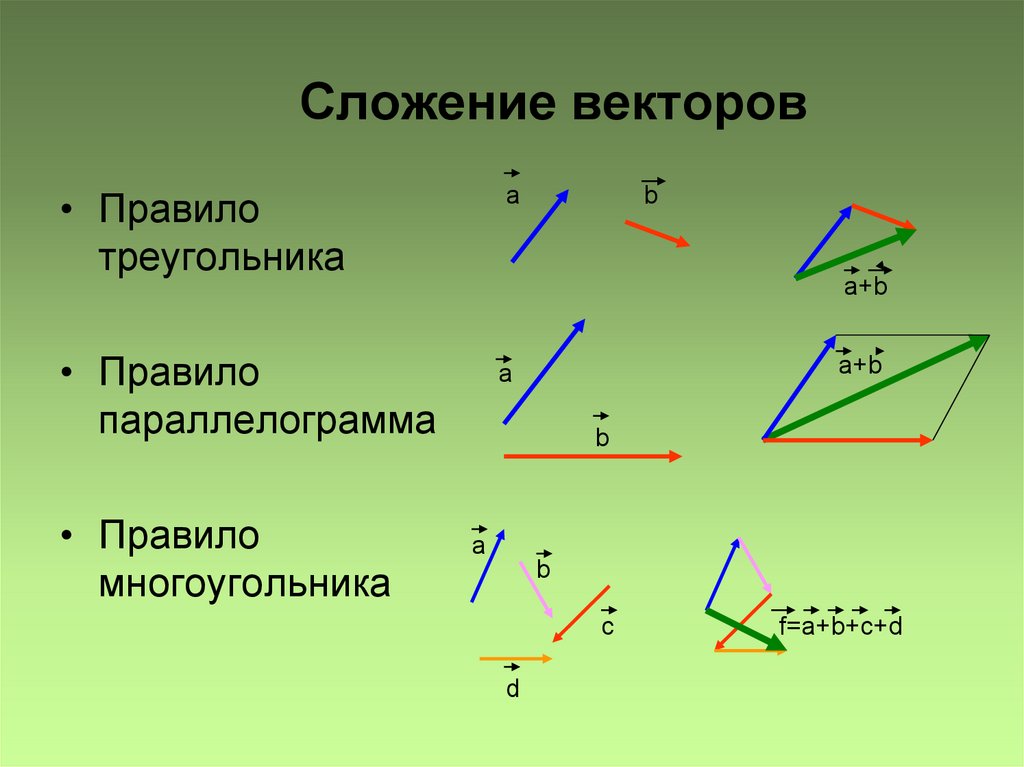
Правила сложения и вычитания векторов
Сложение (и особенно вычитание) векторов – это классика, как простые вещи иногда объясняют сложным языком. Если я спрашиваю абитуриента, как складывать (или вычитать) вектора, он нередко говорит: «Ну, правило параллелограмма, надо начало первого соединить с концом второго… Или наоборот…». В общем, дети вынуждены зазубривать правила, а все зазубренное, но не понятое, очень быстро забывается.
Итак, рассмотрим простой и понятный способ складывать и вычитать вектора. Допустим, надо найти вектор , равный сумме векторов , и . То есть, надо найти =++ (рисунок 1)
Рисунок 1
С векторами разрешен только параллельный перенос. То есть, нельзя их поворачивать и менять их длину.
Рисунок 2
Проводим стрелку из начала цепочки в конец (красная линия). Это и есть вектор суммы (рисунок 3). Все.
Рисунок 3
Тут, правда, есть один нюанс: как понимать фразу «выстраиваем вектора друг за другом»? Представьте, что по стрелкам векторов ползет жучок. Вы должны выстроить вектора так, чтобы жуку было понятно, куда ползти. Если вы выстроили вектора, например, вот так (рисунок 4):
Рисунок 4
то это не «друг за другом». Жук выползает из точки Х, двигается по стрелкам, но в точке Y ему непонятно, что делать дальше. Если вы правильно выстроили вектора «друг за другом», то жук по стрелкам проползет из начальной точки в конечную (рисунок 5).
Рисунок 5
Теперь попробуем поменять слагаемые местами и найдем =++. Как и в прошлом случае, выстраиваем вектора друг за другом (чтобы жуку было понятно) и рисуем стрелку из начала в конец пути (рисунок 6).
Рисунок 6
Как видите, суммарный вектор не зависит от очередности слагаемых. Тут как со скалярными величинами: от перемены мест слагаемых сумма не меняется. То есть, при сложении векторов их можно выстраивать в любом порядке. Результат будет одинаковым.
А как вычитать вектора? Да очень просто. Найдем, например, = —+. Чем отличается вектор
Рисунок 7
Значит, выстраиваем друг за другом (чтобы жуку было понятно) вектора , — и .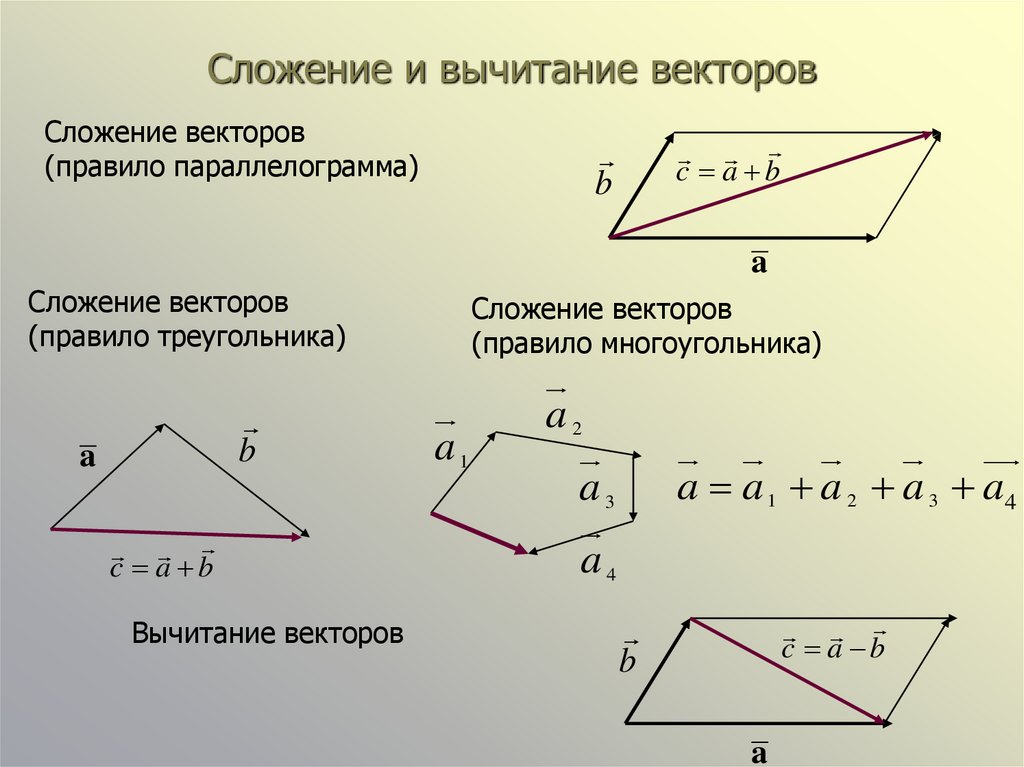 Соединяем начало и конец маршрута результирующим вектором (рисунок 8). Все.
Соединяем начало и конец маршрута результирующим вектором (рисунок 8). Все.
Рисунок 8
Фактически, тут мы нашли вектор =+(- )+.
Надеюсь, теперь у вас с векторами не будет проблем. Допустим, вам встретилась задача: на рисунке 9 изображены силы, действующие на тело; найти равнодействующую.
Рисунок 9
Просто выстраиваем вектора друг за другом (чтобы жуку было понятно) в любом порядке и строим результирующий вектор из начала в конец цепочки векторов (рисунок 10).
Рисунок 10
Красная стрелка на рисунке 10 – это вектор равнодействующей силы.
Похожая статья: что такое радиан.
—
Понравилась статья? Размести ссылку на сайт в социальных сетях
создание, сложение, вычитание, умножение и деление
В простом смысле вектор можно рассматривать, как одномерный массив.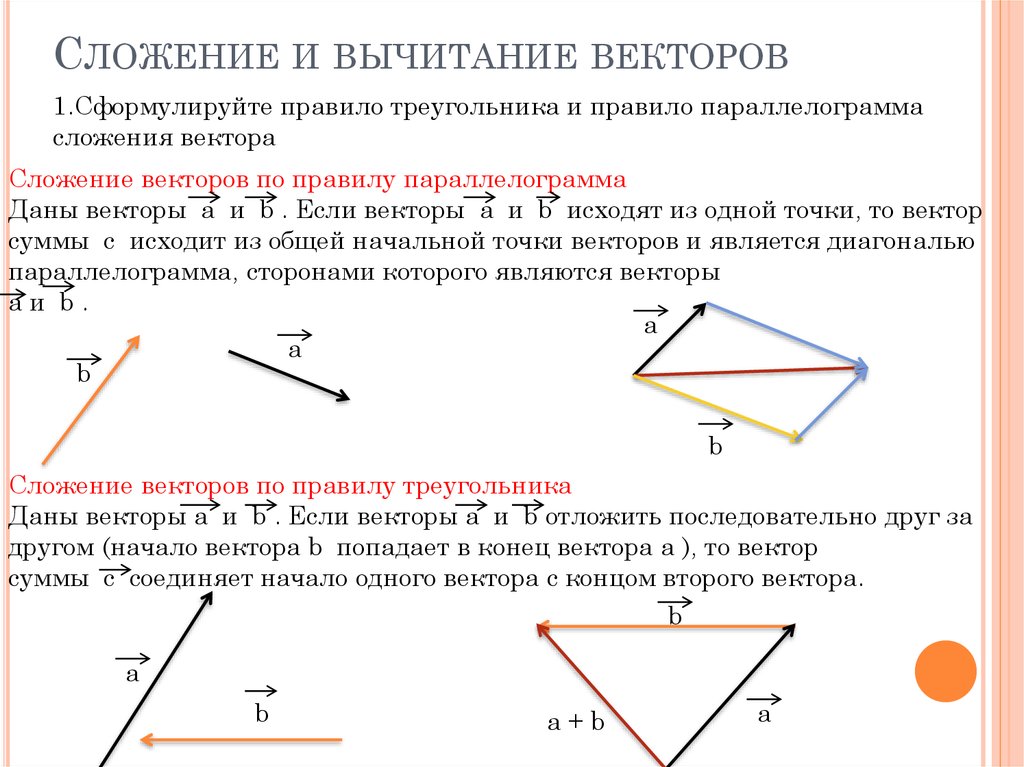 Что касается Python, вектор – это одномерный массив списков. Он занимает элементы таким же образом, как и список Python.
Что касается Python, вектор – это одномерный массив списков. Он занимает элементы таким же образом, как и список Python.
Давайте теперь разберемся с созданием вектора в Python.
Содержание
- Создание вектора
- Основные операции с вектором
- 1. Выполнение операции сложения в векторе
- 2. Выполнение вычитания двух векторов
- 3. Выполнение умножения двух векторов
- 4. Выполнение операции деления
- 5. Векторное точечное произведение
Создание вектора
Модуль NumPy в Python используется для создания вектора. Мы используем метод numpy.array() для создания одномерного массива, то есть вектора.
Синтаксис:
numpy.array(list)
Пример 1: горизонтальный вектор.
import numpy as np
lst = [10,20,30,40,50]
vctr = np.array(lst)
vctr = np.array(lst)
print("Vector created from a list:")
print(vctr)
Вывод:
Vector created from a list: [10 20 30 40 50]
Пример 2: вертикальный вектор.
import numpy as np
lst = [[2],
[4],
[6],
[10]]
vctr = np.array(lst)
vctr = np.array(lst)
print("Vector created from a list:")
print(vctr)
Вывод:
Vector created from a list: [[ 2] [ 4] [ 6] [10]]
Основные операции с вектором
Создав вектор, давайте теперь выполним некоторые базовые операции с этими векторами!
Вот список основных операций, которые можно выполнять с вектором:
- сложение;
- вычитание;
- умножение;
- деление;
- скалярное произведение и т.д.
1. Выполнение операции сложения в векторе
Ниже мы выполнили операцию сложения векторов над векторами. Операция сложения будет выполняться element-wise manner, т.е. поэлементно, и, кроме того, результирующий вектор будет иметь такую же длину, что и два аддитивных вектора.
Синтаксис:
vector + vector
Пример:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,2,3,4,5]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_add = vctr1+vctr2
print("Addition of two vectors: ",vctr_add)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Addition of two vectors: [11 22 33 44 55]
2. Выполнение вычитания двух векторов
Аналогичным образом, при вычитании также будет применяться поэлементный метод, и в дальнейшем элементы вектора 2 будут вычитаться из вектора 1.
Давайте посмотрим на его реализацию.
import numpy as np lst1 = [10,20,30,40,50] lst2 = [1,2,3,4,5] vctr1 = np.array(lst1) vctr2= np.array(lst2) print("Vector created from a list 1:") print(vctr1) print("Vector created from a list 2:") print(vctr2) vctr_sub = vctr1-vctr2 print("Subtraction of two vectors: ",vctr_sub)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Subtraction of two vectors: [ 9 18 27 36 45]
3. Выполнение умножения двух векторов
При умножении вектора элементы вектора 1 умножаются на элементы вектора 2, а вектор произведения имеет ту же длину, что и векторы умножения.
Попробуем представить себе операцию умножения:
x = [10,20] и y = [1,2] — два вектора. Таким образом, вектор произведения будет v [],
v [0] = x [0] * y [0] v [1] = x [1] * y [1]
Взгляните на приведенный ниже код:
import numpy as np lst1 = [10,20,30,40,50] lst2 = [1,2,3,4,5] vctr1 = np.array(lst1) vctr2= np.array(lst2) print("Vector created from a list 1:") print(vctr1) print("Vector created from a list 2:") print(vctr2) vctr_mul = vctr1*vctr2 print("Multiplication of two vectors: ",vctr_mul)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Multiplication of two vectors: [ 10 40 90 160 250]
4. Выполнение операции деления
При делении результирующий вектор является значениями частного после выполнения операции деления над двумя векторами.
Для лучшего понимания рассмотрим приведенный ниже пример.
x = [10,20] и y = [1,2] – два вектора. Таким образом, результирующий вектор v будет таким:
v [0] = x [0] / y [0] v [1] = x [1] / y [1].
Давайте теперь реализуем вышеуказанную концепцию.
Пример:
import numpy as np lst1 = [10,20,30,40,50] lst2 = [10,20,30,40,50] vctr1 = np.array(lst1) vctr2= np.array(lst2) print("Vector created from a list 1:") print(vctr1) print("Vector created from a list 2:") print(vctr2) vctr_div = vctr1/vctr2 print("Division of two vectors: ",vctr_div)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [10 20 30 40 50] Multiplication of two vectors: [ 1 1 1 1 1 ]
5. Векторное точечное произведение
В векторном скалярном произведении мы поэлементно производим суммирование произведения двух векторов.
Давайте посмотрим ниже.
вектор c = x. у = (х1 * у1 + х2 * у2)
Пример:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,1,1,1,1]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_dot = vctr1. dot(vctr2)
print("Dot product of two vectors: ",vctr_dot)
dot(vctr2)
print("Dot product of two vectors: ",vctr_dot)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 1 1 1 1] Dot product of two vectors: 150
Урок 22: Сложение и вычитание векторов
Во многих вопросах вам будет предложено сложить два или более векторов.
- Ваша первая реакция может состоять в том, чтобы просто взять два числа и сложить их (как если бы вы сложили 3 + 2 = 5).
- Вы абсолютно точно можете , а не сделать это!!! Вы должны помнить, что векторы большую часть времени будут указывать в разных направлениях под странными углами. Вы должны «сложить» их с помощью тригонометрии и указать направление в конце.
Сложение A + B
Давайте рассмотрим очень простой пример сложения векторов. Пока у нас даже не будет никаких чисел, мы просто нарисуем векторы с именами A и B.
Рисунок 1
Если бы вас попросили сложить A и B, вам нужно было бы сначала расположить их в виде диаграммы, показывающей A + B.
- Вы можете брать и перемещать векторы, пока они остаются одного размера и указывают в одном направлении.
- Добавляемые векторы всегда должны соприкасаться головой к хвосту.
- Вы должны быть в состоянии начать с конца первого вектора и следовать направлениям стрелок, пока не доберетесь до начала последнего.
- Я часто предлагаю людям смотреть на это как на игру в Pac Man (я знаю, я стар!), и что Pac Man может двигаться только в направлении, указанном стрелками.
Если мы будем следовать этим правилам и начертим A + B, мы должны получить что-то похожее на это…
Рис. следуйте за ним до головы.
Добавление B + A
Удивительный вопрос теперь должен звучать так: «Получите ли вы тот же ответ, если вы добавите B + A?»
- Быстрый ответ: «Да!» так как вы можете добавлять векторы в любом порядке и получать тот же ответ.

- В математике с обычными скучными старыми числами вы определенно можете сказать A + B = B + A… неважно, в каком порядке вы складываете числа.
- Это называется коммутативным свойством.
- Диаграмма будет выглядеть немного по-другому, но результат будет таким же, как и выше в Рисунок 2 . Взгляните на Рисунок 3 ниже, который показывает это.
Рисунок 3
- Здесь показано B + A, потому что мы начинаем с B, который указывает на A, и продолжается до конца.
- Даже если мы проследим от хвоста равнодействующей (B + A) к ее голове, мы все равно придем к тому же месту в конце.
Это означает, что вы можете добавлять векторы в любом порядке. Вы можете измерить другой угол, чем кто-то другой, поскольку ваша диаграмма отличается, и вы собираетесь использовать другие точки отсчета.
- Это как в прошлом уроке, где мы видели, что [N30°E] — это то же самое, что сказать [E60°N].

Вычесть A — B
Здесь все становится немного интереснее.
- Здесь нам нужно помнить, что в физике отрицательный знак просто означает «в противоположном направлении».
- Мы можем взять A — B и просто заменить его на A + -B
- Знак «минус» у B просто означает, что нам нужно взять исходный вектор B и направить его точно в противоположном направлении (на 180° от того места, где он указывает прямо сейчас).
- Затем мы просто добавим их, как мы это делали на предыдущих диаграммах (соприкасаясь, конечно, лицом к хвосту!)
Рисунок 4
Вы можете видеть, что результат, который мы получаем, отличается от показанного в Рисунок 2 и 3 .
- Также будьте осторожны, вычитание не коммутативно (это просто означает, что A — B ≠ B — A).
Решение прямоугольных (90°) треугольников
Большинство треугольников, с которыми вы будете иметь дело, будут прямоугольными.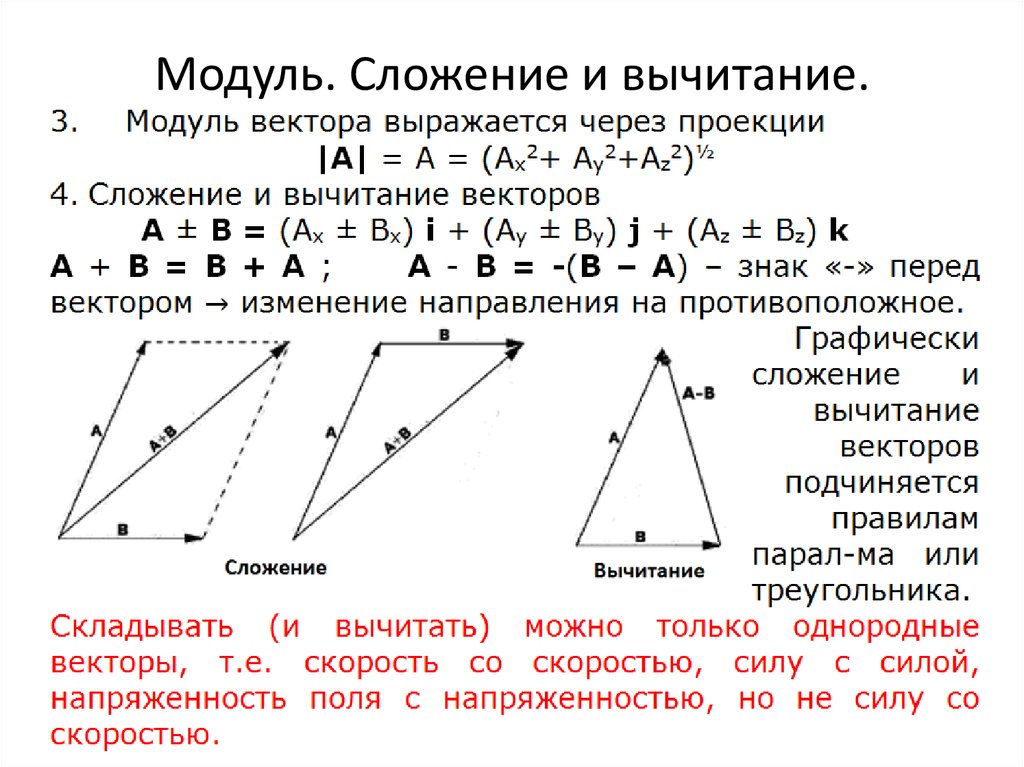
- Если они есть, просто используйте свою обычную триггерную систему (SOH CAH TOA) и пифагоров (c 2 = a 2 + b 2 ).
- Обычно вам нужно думать о физике, когда вы настраиваете свою диаграмму (так, чтобы все указывало в лоб и все такое), а затем переключаетесь на решение этой задачи, как в любой математической задаче на триггер.s
Пример 1: Автомобиль проезжает 10 км [E], а затем 7 км [N]. Определить его водоизмещение.
Сначала нарисуйте правильную схему:
Обратите внимание, как это показывает, что векторы добавляются в правильном порядке в соответствии с вопросом.
- 10 км [E] показаны впереди 7 км [N]. Начните с хвоста красной стрелки и следуйте по пути, по которому она вас ведет.
- Если вы добавите к ним 7 км [N], а затем 10 км [E], вы все равно получите тот же окончательный ответ, только с другим углом из-за другой точки отсчета.
Это определенно прямоугольный треугольник, поэтому просто используйте c 2 = a 2 + b 2 , чтобы узнать величину ( размер ) равнодействующей.
- Попробуйте сами и посмотрите, получите ли вы около 12.21 (здесь я не слишком осторожен с моими раскопками!)
Угол, который мы должны измерить, находится в левом нижнем углу.
Как подсказка, вам, вероятно, следует использовать загар, чтобы определить этот угол. Использование sin или cos потребует использования только что вычисленного результата. Если вы ошибетесь в результате, вы также ошибетесь в своем угле.
- Традиционно вы измеряете от начала равнодействующей до ее хвоста.
- Это также дает нам хорошую опорную линию, так как мы сможем сказать, на сколько градусов к северу от востока мы находимся.
- Попробуйте подсчитать и посмотрите, получилось ли около 35°.
Добавление треугольников, которые не являются прямыми углами
Если треугольник не является прямым углом, у вас есть два варианта:
- Используйте закон косинусов или закон синусов, чтобы выяснить это.

Это метод « сложных вычислений, если вы еще не сделали этого много в математике «. Если вы не знакомы с ними, щелкните здесь, чтобы посмотреть короткое видео, в котором я рассказываю вам об основах их использования. - Разбейте его на горизонтальные и вертикальные компоненты, затем используйте базовый триггер.
Это требует больше вычислений, но каждое вычисление меньше. Подробнее об этом после того, как мы рассмотрим следующий урок… а пока просто держите это в голове.
Комбинации векторов (сложение и вычитание векторов) — Криста Кинг Математика
Создание комбинации
Когда мы хотим найти комбинацию двух векторов, мы просто сопоставляем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор из начальной точки первого до конечной точки второго. Другими словами, сочетание серого и синего — фиолетовый:
Привет! Я Криста.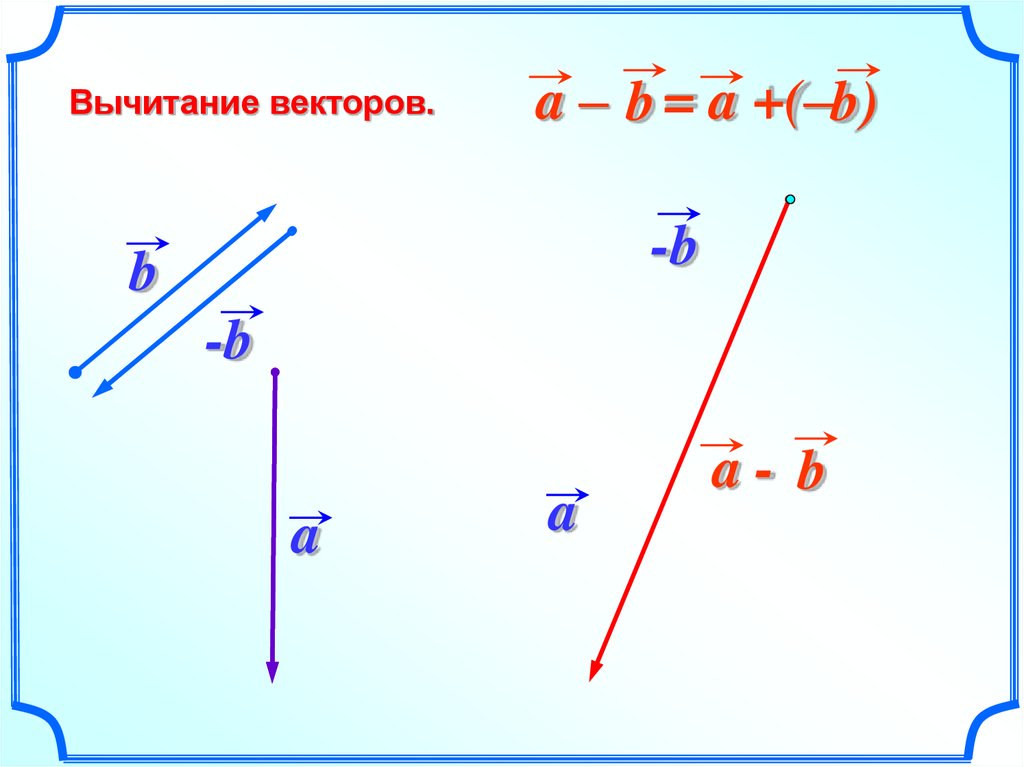
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.
Как рассчитать комбинацию векторов
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Объединение трех векторов
Пример
Найдите комбинации векторов.
???\vec{AB}+\vec{BC}???
???\vec{BC}-\vec{AC}???
???\vec{AC}+\vec{CB}-\vec{DB}???
Для ???\vec{AB}+\vec{BC}???:
Начальная точка ???\vec{AB}??? ???A???, а его конечная точка ???B???. Начальная точка ???\vec{BC}??? это б??? (конечная точка ???A???), а его конечная точка ???C???. Следовательно, комбинация этих двух векторов от начальной точки первого до конечной точки последнего равна
???\vec{AB}+\vec{BC}=\vec{AC}???
Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору.
Для ???\vec{BC}-\vec{AC}???:
Когда два вектора вычитаются, мы можем изменить отрицательный вектор на положительный, изменив направление вектора. В этом случае ???-\vec{AC}??? становится ???+\vec{CA}???. Затем мы просто объединяем их, как обычно.
???\vec{BC}-\vec{AC}=\vec{BC}+\vec{CA}???
???\vec{BC}-\vec{AC}=\vec{BA}???
Для ???\vec{AC}+\vec{CB}-\vec{DB}???:
Начнем с изменения отрицательного вектора на положительный, изменив направление вектора.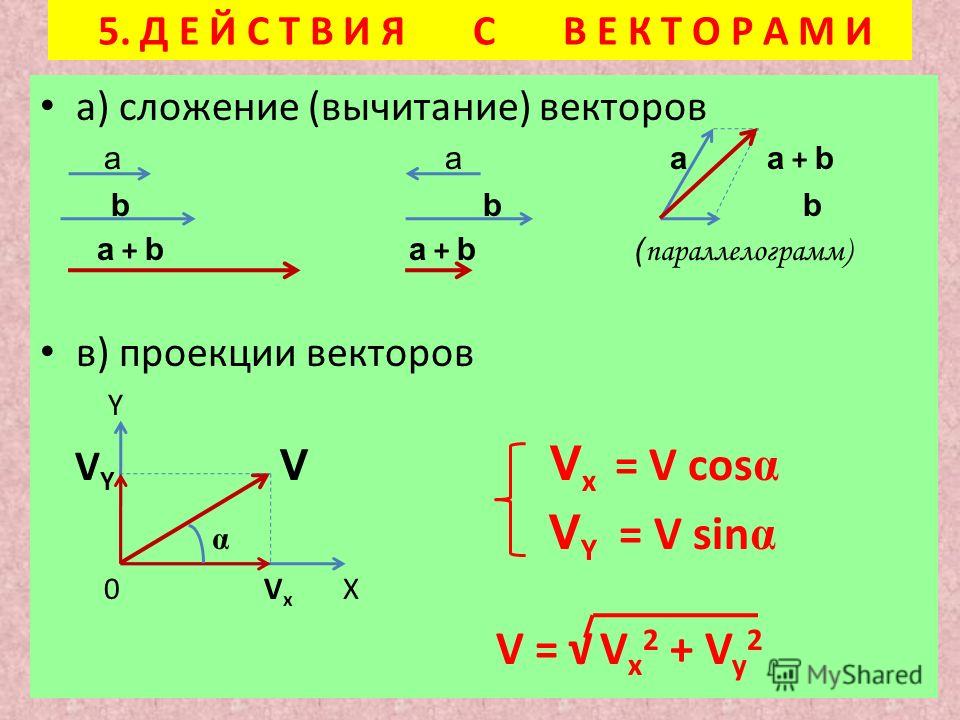

 array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_sub = vctr1-vctr2
print("Subtraction of two vectors: ",vctr_sub)
array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_sub = vctr1-vctr2
print("Subtraction of two vectors: ",vctr_sub)
 array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_mul = vctr1*vctr2
print("Multiplication of two vectors: ",vctr_mul)
array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_mul = vctr1*vctr2
print("Multiplication of two vectors: ",vctr_mul)
 array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_div = vctr1/vctr2
print("Division of two vectors: ",vctr_div)
array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_div = vctr1/vctr2
print("Division of two vectors: ",vctr_div)
 dot(vctr2)
print("Dot product of two vectors: ",vctr_dot)
dot(vctr2)
print("Dot product of two vectors: ",vctr_dot)