Как сложить числа с разными степенями: Свойства степеней, действия со степенями

alexxlab / / Разное

§ Сложение и вычитание одночленов

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

  • Геометрия: начальная школа
  • Действия в столбик
  • Деление с остатком
  • Законы арифметики
  • Периметр
  • Порядок действий
  • Разряды и классы. Разрядные слагаемые
  • Счет в пределах 10 и 20

Математика 5 класс

  • Взаимно обратные числа и дроби
  • Десятичные дроби
  • Натуральные числа
  • Нахождение НОД и НОК
  • Обыкновенные дроби
  • Округление чисел
  • Перевод обыкновенной дроби в десятичную
  • Площадь
  • Проценты
  • Свойства сложения, вычитания, умножения и деления
  • Среднее арифметическое
  • Упрощение выражений
  • Уравнения 5 класс
  • Числовые и буквенные выражения

Математика 6 класс

  • Масштаб
  • Модуль числа
  • Окружность. Площадь круга
  • Отношение чисел
  • Отрицательные и положительные числа
  • Периодическая дробь
  • Признаки делимости
  • Пропорции
  • Рациональные числа
  • Система координат
  • Целые числа

Алгебра 7 класс

  • Алгебраические дроби
  • Как применять формулы сокращённого умножения
  • Многочлены
  • Одночлены
  • Системы уравнений
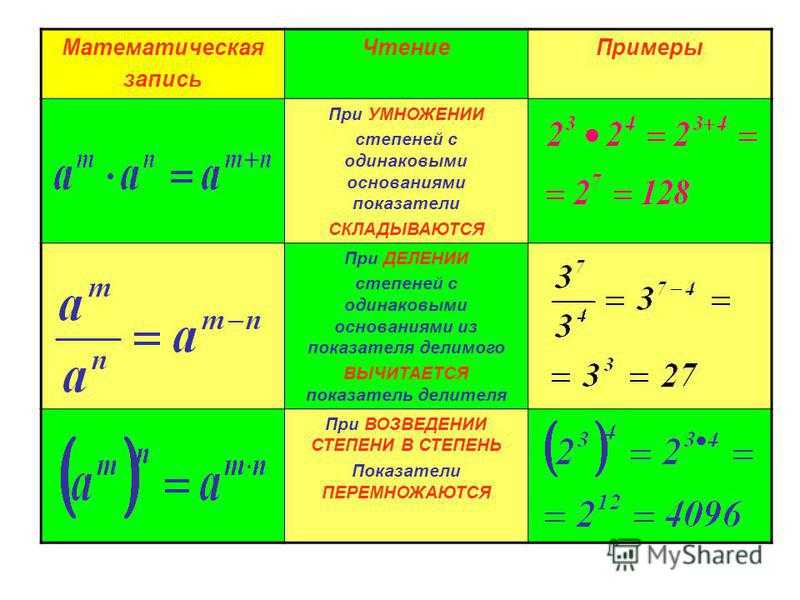
  • Степени
  • Уравнения
  • Формулы сокращённого умножения
  • Функция в математике

Геометрия 7 класс

  • Точка, прямая и отрезок
  • Что такое аксиома и теорема

Алгебра 8 класс

  • Квадратичная функция. Парабола
  • Квадратные неравенства
  • Квадратные уравнения
  • Квадратный корень
  • Неравенства
  • Системы неравенств
  • Стандартный вид числа
  • Теорема Виета

Алгебра 9 класс

  • Возрастание и убывание функции
  • Нули функции
  • Область определения функции
  • Отрицательная степень
  • Среднее
    геометрическое

Алгебра 10 класс

  • Иррациональные числа

Алгебра 11 класс

  • Факториал

А вы, наверное, думали увидеть здесь какую-нибудь умную фразу ;) Администратор

на главную

Введите тему

Русский язык Поддержать сайт

Одночлен.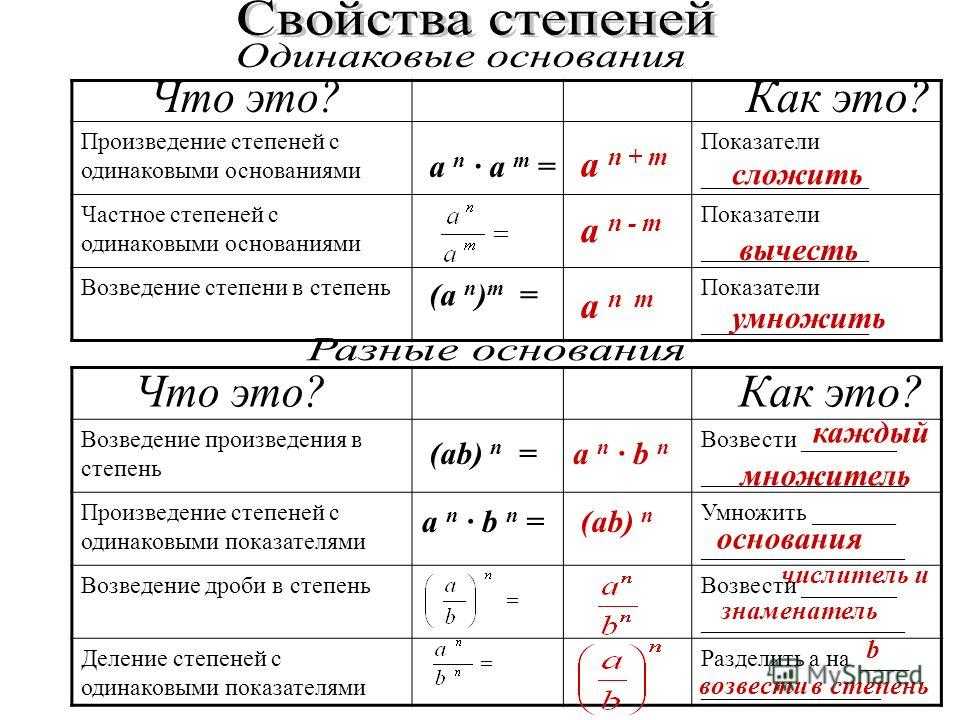 Стандартный вид одночлена Сложение и вычитание одночленов Умножение одночленов Деление одночлена на одночлен Возведение в степень одночлена

Вначале, необходимо понять, что называют подобными одночленами.

Запомните!

Одночлены, у которых одинаковый состав букв и их степеней, называют подобными.

Примеры подобных и неподобных одночленов

2ab и −3ab => Одночлены подобные. Можно вычитать.
8y2 и 7x => Одночлены не подобные. Нельзя складывать.
xy и 9xy => Одночлены подобные. Можно складывать.
4a2 и 2a => Одночлены не подобные. Нельзя складывать.

Одночлены нужно рассматривать как единое целое.

То есть, частая ошибка когда, например, одночлены 3a и 2ab считают подобными, т. к. в обоих одночленах присутствует буквенный множитель а.

Одночлены 3a и 2ab НЕ являются подобными, потому что состав букв должен полностью совпадать в обоих одночленах.

В данном примере в одночлене 3а из буквенных множителей только а, а во втором одночлене 2ab — два буквенных множителя а и b.

Запомните!

Складывать и вычитать можно только подобные одночлены.

При сложении и вычитании одночленов работаем только с их числовыми коэффициентами. Состав букв остается всегда прежним!

Разберем пример: 3a2b + 2a2b

  1. Сначала убедимся, что данные одночлены подобные.
    У первого одночлена 3a2b состав букв со степенями: a2b.
    У второго одночлена 2a2b состав букв со степенями: a2b.

    Важно!

    Состав букв и их степеней у обоих одночленов одинаков, значит, одночлены подобные и их можно складывать.

  2. Теперь рассмотрим числовые коэффициенты одночленов.
    У первого одночлена 3a2b коэффициент: 3.
    У второго одночлена 2a2b коэффициент: 2.
  3. Сложим их коэффициенты: 3 + 2 = 5
  4. Запишем окончательный ответ в виде суммы одночленов.
    3a2b + 2a2b = 5a2b

Еще раз обратите внимание, что состав букв в итоговом одночлене НЕ поменялся.
3a2b + 2a2b = 5a2b

Запомните!

Противоположные одночлены взаимно уничтожаются.

−73x2z + 73x2z = 0

Примеры сложения и вычитания одночленов

  1. 7x2y − 2x2y = 5x2y
  2. 2a3 + 3a3 − a3 = 5a3 − a3 = 5a3 − 1 a3 = 4a3
  3. ab3 + ab3 = 1ab3 + 1ab3 = 2ab3
  4. 5t − 6t = −t  (т. к. 5 − 6 = −1)
  5. 8xy − 10xy + 2xy = −2xy + 2xy = 0
    (т.к. при вычитании коэффициентов −2 + 2 = 0)

Одночлен. Стандартный вид одночлена Сложение и вычитание одночленов Умножение одночленов Деление одночлена на одночлен Возведение в степень одночлена

сложение и вычитание, умножение и деление

  • Сложение
  • Вычитание
  • Умножение
  • Деление

Сложение

При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.

Пример 1. Найти сумму рациональных чисел  2,5  и  3,2.

Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:

2,5 + 3,2 = 5,7.

Пример 2. Найти сумму отрицательных чисел  (-2,5)  и  (-3,2).

Решение: Сначала надо сложить модули слагаемых:

2,5 + 3,2 = 5,7.

Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:

(-2,5) + (-3,2) = -5,7.

Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.

При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.

Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:

Примеры:

(-4,7) + (+12) = 7,3,  так как  12 — 4,7 = 7,3;

9 + (-15) = -6,  так как  15 — 9 = 6.

Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.

Сумма двух противоположных чисел равна нулю.

Примеры:

125 + (-125) = 0;

-34 + (+34) = 0.

Вычитание

Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.

Примеры:

(+10) — (+3,4) = (+10) + (-3,4) = 6,6;

(+10) — (-3,4) = (+10) + (+3,4) = 13,4;

(-10) — (-3,4) = (-10) + (+3,4) = -6,6;

(-10) — (+3,4) = (-10) + (-3,4) = -13,4.

Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение

При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.

Примеры:

3 · 5 = 15;

3 · (-5) = -15;

-3 · 5 = -15;

-3 · (-5) = 15.

Ниже представлена схема (правило знаков при умножении):

+ · + = +
+ · — = —
— · + = —
—  · — = +

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на  -1  получится число, противоположное данному.

Примеры:

-1,5 · (-1) = 1,5;

2,5 · (-1) = -2,5.

Деление

При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

Примеры:

15 : 5 = 3;

15 : (-5) = -3;

-15 : 5 = -3;

-15 : (-5) = 3.

При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении

):

+ : + = +
+:—=—
—:+=—
—:—=+

Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на  -1  получится число, противоположное данному.

Примеры:

-1,5 : (-1) = 1,5;

2,5 : (-1) = -2,5.

Видео с вопросами: сложение чисел в стандартной форме

Стенограмма видео

Найдите значение умножения восьми на 10 в 10-й степени, прибавьте 7,1, умноженное на 10, в девятой степени, что даст ответ в стандартной форме.

Эти два числа указаны в стандартная форма. Это также известно как научный обозначение, означающее, что они представлены в виде 𝑎, умноженного на 10 в 𝑛-й степени, где абсолютное значение 𝑎 больше или равно единице и меньше 10 и 𝑛 — целое число.

Один из способов ответить на этот вопрос вопрос в том, чтобы написать эти числа так, чтобы они не были в стандартной форме. Но на самом деле у нас было бы два большие числа. Мы можем по-другому подойти к этому, но сначала нам нужно, чтобы оба этих числа были записаны с одинаковым степени 10. Обычно мы делаем это, переписывая число с наибольшей степенью 10 должно быть таким же, как степень 10 число меньшей мощности. Число с большей степенью 10 — это восемь, умноженное на 10 в 10-й степени, поэтому мы стремимся переписать это как нечто, умноженное на 10 в девятой степени, так что оно имеет ту же степень 10, что и 7,1 умножить на 10 в девятой степени. Другой способ записать 10 в Десятая степень равна 10 в степени один плюс девять.

Теперь вспомним произведение экспоненты правило: 𝑥 в степени 𝑚 умножить на 𝑥 в степени 𝑛 равно 𝑥 в 𝑚 добавить 𝑛 сила. Мы можем использовать это, чтобы записать 10 в один прибавляет девятую степень как 10 к первой степени, умноженной на 10 в девятой степени. 10 в первой степени это просто 10. Чтобы что-то закончить умножаем на 10 в девятой степени, мы умножаем восемь на 10, чтобы получить 80, умноженное на 10 в девятой степени.

Итак, теперь у нас есть два числа, которые нужно добавить вместе оба возводятся в 10 в девятой степени. Итак, теперь давайте добавим эти два числа вместе. Мы вычисляем 80 умножить на 10 в девятой степени прибавьте 7,1 умноженное на 10 в девятой степени. Потому что мы смогли написать оба наших чисел с той же степенью 10, мы можем сложить их, выполнив 80 add 7.1 умножить на 10 в девятой степени. Это дает нам 87,1, умноженное на 10. в девятой степени.

Хотя это правильно для этого расчет, мы не можем оставить наш ответ таким. Это потому, что нас попросили дайте наш ответ в стандартной форме. И это не в стандартной форме, потому что стандартная форма требует, чтобы абсолютное значение 𝑎, равное 87,1, было между 1 и 10, что не соответствует 87.1. Итак, нам нужно написать 87,1 умножить на 10 в девятой степени в стандартной форме.

Для этого мы можем использовать аналогичный к нашему первому шагу, используя правило произведения экспоненты. Поскольку 87,1 — это 8,71, умноженное на 10, начнем с записи 87,1, умноженного на 10 в девятой степени, как 8,71, умноженного на 10 умножить на 10 в девятой степени. Тогда 10 можно записать как 10 в первая мощность. И теперь мы используем произведение экспоненты правило. Это означает, что мы можем записать 10 в первую степень умножить на 10 в девятой степени как 10 к единице добавить девять сила. Но если добавить девять, будет 10. Итак, это 10 в 10-м. сила.

Давайте просто проверим, что это в стандартная форма. Значение 𝑎 равно 8,71. Таким образом, абсолютное значение 𝑎 равно больше или равно единице и меньше 10, так что все в порядке. Также 𝑛 равно 10, что является целое число. Так что это номер в стандарте форма. Итак, 8,71 умножить на 10. 10-я степень — наш окончательный ответ.

Типы чисел Экспоненты и степени

  • Главная /
  • Алгебра /
  • Типы чисел /
  • Темы /
  • Делать с реальными числами /
  • ЭКСПОНЕЕ Полномочия — целые числа

Темы

  • Введение

  • Темы
  • Различные типы чисел
  • Различные способы представления чисел
  • Сравнение фракций
  • Умножение и деление со смешанными числами
  • Десятиц
  • Перценденты
  • . С чем можно сделать с реальными числами
  • Добавление и подтронные номера
    • . сложения
  • вычитания
  • умножения
  • деления
  • остатка от длинного деления
  • степени и степени — целые числа
  • Свойства показателей
  • Факторизация простых чисел
  • Порядок операций
  • Четные и нечетные числа
  • Последовательности
  • В реальном мире

  • Примеры
  • Упражнения
  • Задачи Math Shack
  • Условия
  • Лучшее из Интернета
  • Викторины
  • Раздаточный материал
  • Содержание
  • НАЗАД
  • СЛЕДУЮЩИЙ

Эта последовательность часто встречается в математике и информатике, так что обратите внимание. Особенно, если вам нравится компьютерная наука — вы знаете, брать различные химические вещества в пипетки и капать их на свой компьютер и еще много чего.

2
2 × 2 = 4
2 × 2 × 2 = 8
2 × 2 × 2 × 2 = 16
2 × 2 × 2 × 2 × 2 = 32

Записывать все эти двойки быстро надоедает. Кто хочет выписать двадцать двоек, перемноженных вместе? (Если это вы, пожалуйста, опустите руку. Все равно вас сейчас никто не увидит.)

К счастью, есть короткий путь. Мы пишем 2 n , произносится как «2 в n », «2 в n, » или «2 в n -й степени», что означает n копий 2 умноженные вместе. И чтобы помочь вам вспомнить, что мы «увеличиваем его», мы даже буквально немного повышаем его рядом с числом, которое мы умножаем. Разве математики не мыслят? Они даже прислали тебе цветы на день рождения. Помните это?

Если у нас есть 2 n , этот маленький n называется показателем степени или степенью , 2 называется основанием , а процесс возведения числа в степень называется возведением в степень .

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *