Как сложить два числа со степенями: Свойства степеней, действия со степенями

Арифметические действия — Формулы, теоремы, определения

Типы материалов

• формулы
• теоремы
• определения
• статьи

АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ

Определение Сложение, сумма

Понятие о том, что такое сложение, возникает из таких простых фактов, что оно не нуждается в определении и не может быть определено формально.

\[слагаемое + слагаемое = сумма\]

Например

\[4 + 3 = 7\]
4 — слагаемое
3 — слагаемое
7 — сумма

Часто даются “определения” вроде таких: “сложение есть действие, посредством которого несколько чисел соединяются в одно”. или “действие посредством которого сколько единиц содержится в нескольких числах вместе”. Но тот, кто не знал бы что значит “сложить”, не знал бы и что такое “соединить числа”, так что все похожие определения сводятся лишь к замене одних слов другими.

изменить / сообщить об ошибке

Определение Вычитание

Вычитание — есть нахождение одного из слагаемых по сумме и другому слагаемому. Сумма получает название уменьшаемого, данное слагаемое — вычитаемого, искомое слагаемое — разности.

\[Уменьшаемое − Вычитаемое = Разность\]

Например

\[9 −5 = 4\]

9 — Уменьшаемое
5 — Вычитаемое
4 — Разность

изменить / сообщить об ошибке

Определение Умножение, произведение

Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемое столько раз, сколько указывает множитель. Результат называется произведением.

\[Множимое × Множитель = Произведение\]

Например

\[3 × 4 = 12\]

Или еще записывают так

\[3 · 4 = 12\]

3 — Множимое
4 — Множитель
12 — Произведение

а вычисляется так

\[3 × 4 = 3 + 3 + 3 + 3 = 12\]

Если множимое и множитель меняются ролями, произведение остается тем же.

\[4 × 3 = 4 + 4 + 4 = 12\]

изменить / сообщить об ошибке

Определение Деление с остатком

Деление с остатком есть отыскание наибольшего целого числа, которое в произведении с делителем дает число, не превышающееделимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком. Он всегда меньше делителя.

Например:

19 не делится нацело на 5.
Числа 1, 2, 3 в произведение с 5 дают 5, 10, 15,
не превосходящие делимое 19,
но уже 4 дает в произведении с 5 число 20, большее, чем 19.
Поэтому неполное частное есть 3.
Разность между 19 и произведением 3 · 5 = 15 есть 19 — 15 = 4;

поэтому остаток есть 4.

изменить / сообщить об ошибке

Определение Возведение в степень

Возвести число в целую степень (вторую, третью, четвертую и т.д.) — значит повторить это число собственным сомножителем два, три, четыре и т.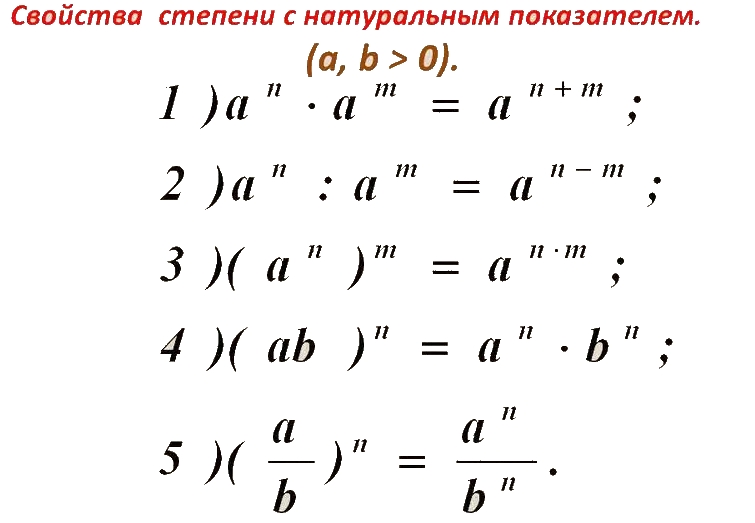 4 = 81\) (проверка извлечения корня).

Корень второй степени называется иначе квадратным, корень третьей степени — кубическим. При знаке квадратного корня показатель корня принято опускать.

Например:

\(\sqrt[2]{16} = \sqrt{16} = 4\)

 

 

 

изменить / сообщить об ошибке

Статья Порядок арифметических действий, скобки

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Например,

\[4−2+ 1= 3\]

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

\[(4−2)+ 1= 3\]

\[4−(2+ 1)= 1\]

 

Пример 1:

\[(2+ 4) · 5= 6 · 5= 30\]

\[2+(4 · 5)= 2+ 20= 22\]

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

1. в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
2. в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

1. сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
2. затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Пример 2:

\[2 · 5−3 · 3\]

 

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1

Пример 3:

\[9+ 16 : 4−2 ·(16−2 · 7+ 4)+ 6 ·(2+ 5)\]

 

Сначала выполняем действия в скобках:
\[16 — 2 · 7 + 4 = 16 — 14 + 4 = 6\]
\[2 + 5 = 7\]

Теперь выполняем остающиеся действия:
\[9 + 16 : 4 — 2 · 6 + 6 · 7 = 9 + 4 — 12 + 42 = 43\]

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки.

Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками {}. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.Пример 4:

\[5+ 2 ·[14−3 ·(8−6)]+ 32 :(10−2 · 3)\]

 

Выполняем действия в круглых скобках, имеем:
\[8 — 6 = 2\] 
\[10 — 2 · 3 = 10 — 6 = 4\]

действия в квадратных скобках дают:
\[14 — 3 · 2 = 8\]

выполняя остающиеся действия скобках находим:
\[5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29\]Пример 5:

\[[100−[35−(30−20)]]· 2\]

 

Порядок действий:
\[30 — 20 = 10\]
\[35 — 10 = 25\]
\[100 — 25 = 75\]
\[75 · 2 = 150\]

изменить / сообщить об ошибке

Сложение и вычитание

Сложение и вычитание
Далее: Умножение Up: Арифметика с плавающей запятой Предыдущий: FLOPS

Сложение с плавающей запятой аналогично сложению с использованием научного обозначение.

Например, чтобы добавить 2,25x к 1,340625x:

1. Сдвигайте запятую меньшего числа влево, пока показатели равны. Таким образом, первое число становится 0,0225x.
2. Сложите числа с выровненными десятичными точками:

3. Нормализация результата.

После того, как десятичные точки выровнены, можно выполнить сложение. игнорируя десятичную точку и используя целочисленное сложение.

Добавление двух номеров IEEE FPS выполняется аналогичным образом. Число 2,25 в IEEE FPS:

Число 134.0625 в IEEE FPS:

1. Для выравнивания двоичных точек увеличивается меньший показатель и мантисса сдвигается вправо до тех пор, пока показатели степени не сравняются. Таким образом, 2,25 становится:

2. Мантиссы складываются с помощью целочисленного сложения:

3. Результат уже в нормальной форме. Если сумма выходит за пределы положение скрытого бита, то мантисса должна быть сдвинута на один бит вправо и показатель степени увеличивается. Мантисса всегда меньше 2, поэтому сумма скрытых битов может быть не более 3 (11).

Показатели могут быть положительными или отрицательными без изменения алгоритм. Меньший показатель означает более отрицательное значение. В уклоне-127 представление, меньший показатель степени имеет меньшее значение для E, неподписанная интерпретация.

Важный случай имеет место, когда числа сильно различаются по величине. Если показатели степени отличаются более чем на 24, меньшее число будет полностью сместился вправо из поля мантиссы, создав нулевую мантисса. Тогда сумма будет равна большему числу. Таких ошибок усечения происходят, когда числа различаются более чем в , что приблизительно. Точность IEEE арифметика одинарной точности с плавающей запятой примерно 7 десятичных цифр.

Отрицательные мантиссы обрабатываются путем первого преобразования в двойки. дополнение, а затем выполнение добавления. После добавления выполняется, результат преобразуется обратно в форму со знаком.

При сложении чисел противоположного знака может произойти отмена, в результате получается сумма, которая сколь угодно мала или даже равна нулю, если числа равны по величине. Нормализация в этом случае может потребоваться сдвиг на общее количество битов в мантиссе, приводит к большой потере точности.

Когда мантисса суммы равна нулю, никакие сдвиги не дадут результата. 1 в скрытом бите. Этот случай должен быть обнаружен при нормализации шаг и набор результатов для представления для 0, E = M = 0. Это результат не означает, что числа равны; только в этом их отличие меньше, чем точность представления с плавающей запятой.

Вычитание с плавающей запятой достигается простой инверсией знака бит и выполнение сложения мантиссы со знаком, как описано выше.

---

Далее: Умножение Up: Арифметика с плавающей запятой Предыдущий: FLOPS

Учетная запись класса CS 301
Пн, 13 сентября, 11:15:41 ADT 1999

Математика с единицами измерения | GMAT Free

На GMAT, как и в реальном мире, многие числа имеют связанные с ними единицы измерения. Когда мы имеем дело с двумя числами, выраженными в единицах, если единицы одинаковы, мы можем складывать или вычитать как обычно. Однако, если единицы разные, то мы можем складывать или вычитать только в том случае, если единицы могут быть преобразованы в одинаковые единицы.

Например:

Некоторые единицы различаются, но могут быть преобразованы в общие единицы. Например,

Мы можем выполнить следующее сложение, только если мы можем конвертировать яблоки в валюту США: = 12 дюймов):

GMAT, как правило, не требует от вас знания какой-либо конкретной системы единиц, кроме основных единиц измерения времени в секундах, минутах, часах, днях, неделях, месяцах и годах. Используются как единицы США, так и метрическая система, но когда вам нужно выполнить преобразование единиц, единицы будут предоставлены вам.

Пример, в котором требуется преобразование единиц измерения:

Чтобы выполнить это вычитание, нам нужно перевести две дроби в одни и те же единицы. Первый член равен

Оба умножения, встречающиеся в этой дроби, разрешены, потому что они включают умножение на форму 1. Например, 3600 секунд равно 1 часу, поэтому дробь, умноженная на 1 час. в знаменателе просто кратно 1, что меняет единицы измерения.

Подставив эту дробь обратно в выражение, которое мы должны вычислить, мы получим:

На данный момент единицы измерения в обеих дробях одинаковы. Мы закончили преобразование единиц. Этот метод называется сокращением единиц или анализом размерностей.

Мы можем сделать важное замечание. В этот момент в этом конкретном вычислении мы можем исключить не только единиц здесь, но и коэффициентов . Дробь слева не нужно вычислять как есть; мы можем упростить его. Два множителя 10 сверху и снизу этой дроби сокращаются, что дает нам:

Более того, и числитель, и знаменатель имеют коэффициент 6, который мы можем сократить:

То, что нам нужно вычислить, было радикально упрощено! Вместо того, чтобы умножать 60 на 5280 и делить произведение на 3600, у нас есть только одно более простое деление. Мы можем закончить, разделив 528 на 6, используя деление в длинное число, чтобы получить:

Вы сможете выполнить множество упрощений, подобных этому, на GMAT. Ищите возможности аннулировать множители всякий раз, когда имеете дело с дробями.

Умножение и деление

При умножении или делении чисел на единицы единицы также умножаются или делятся.

Вот примеры, использующие одни и те же базовые единицы:

Хотя в физике имеют значение различные квадратные и кубические единицы, единственные квадратные и кубические единицы, которые вы, вероятно, встретите на GMAT, — это квадраты и кубы длины, соответствующие площади и объема соответственно.

Например, в случае прямоугольного тела:

Также можно умножать или делить число с единицами на скаляр (безразмерное число):

Поскольку показатели степени представляют умножение , операции с экспонентой применяются к единицам так же, как и умножение.