Как сложить и вычитать векторы: Вычитание векторов — урок. Геометрия, 9 класс.

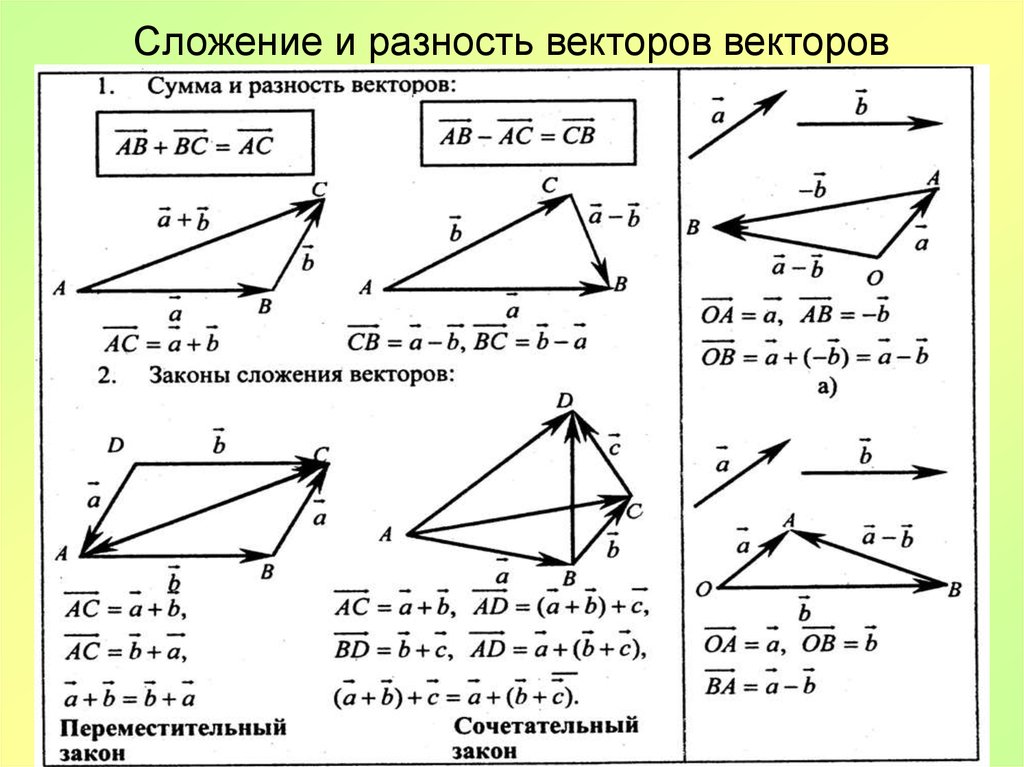
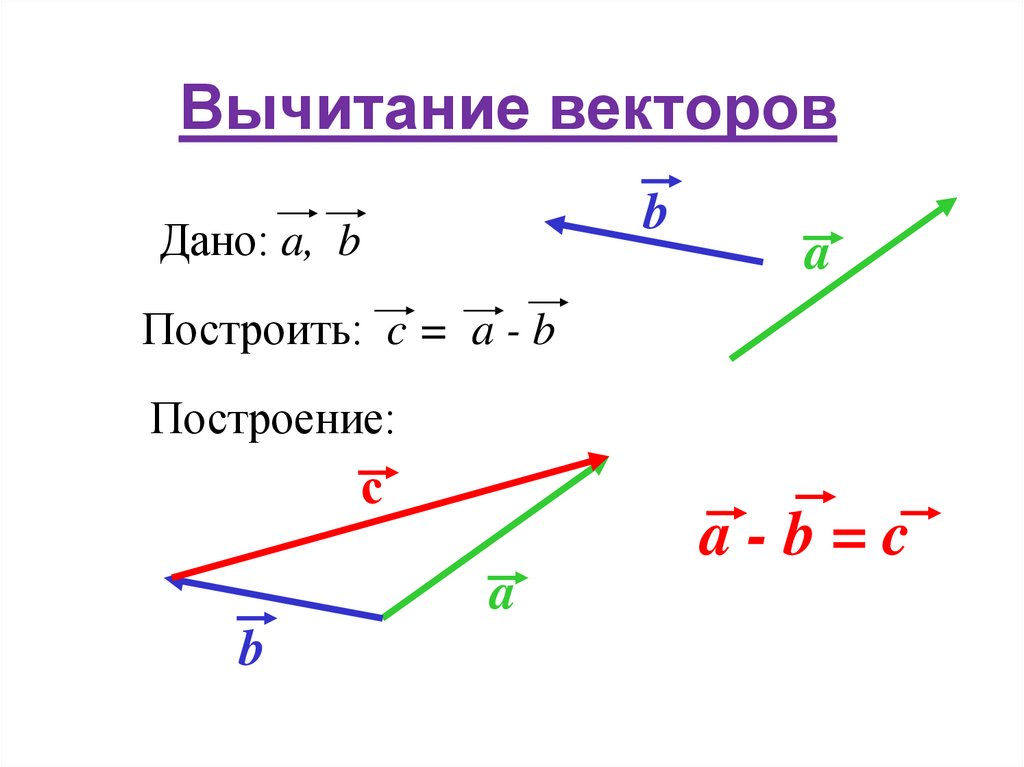
Сложение векторов

Суммой x+y векторов x и y называется вектор, проведенный из начала x к концу у, если вектор у параллельно перемещен так, что конец x и начало y совмещены.

Рис. 1

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим сумму z=x+y векторов и .

Для построения суммы векторов z=x+y, нужно переместить параллельно вектор y так, чтобы начало вектора y совпало с концом вектора x. Тогда конец полученного вектора y’ будет конечной точкой суммы векторов z=x+y.

Таким образом, для получения суммы векторов x и y достаточно сложить соответствующие координаты векторов x и y:

На рисунке Рис. 1 в двухмерном пространстве представлен процесс сложения векторов x

=(9,1) и y=(2,4).

Вычислим z=x+y=(9+2, 1+4)=(11,5). Сравним полученный результат с геометрической интерпретацией. Действительно, после параллельного перемещения вектора y на позицию y’ и сложения x и y’, получим вектор z=(11,5).

Вариант 2. Начальные точки векторов произвольные.

Рассмотрим процесс сложения двух векторов x и y. Пусть вектор x имеет начальную точку и конечную точку, а вектор y — начальную точку и конечную точку . Для того, чтобы параллельно переместить вектор y, нужно каждый элемент i точек C и D увеличить на соответствущую величину γ_i:

(1)

а для того, чтобы точка C переместилась в точку B, должны выполняться условия

(2)

Следовательно

(3)

Подставляя (3) в (1), получим:

Из выражений (4) видно, что точка C’ совпала с точкой B, и, следовательно, вектор переместился в нужную позицию BD’.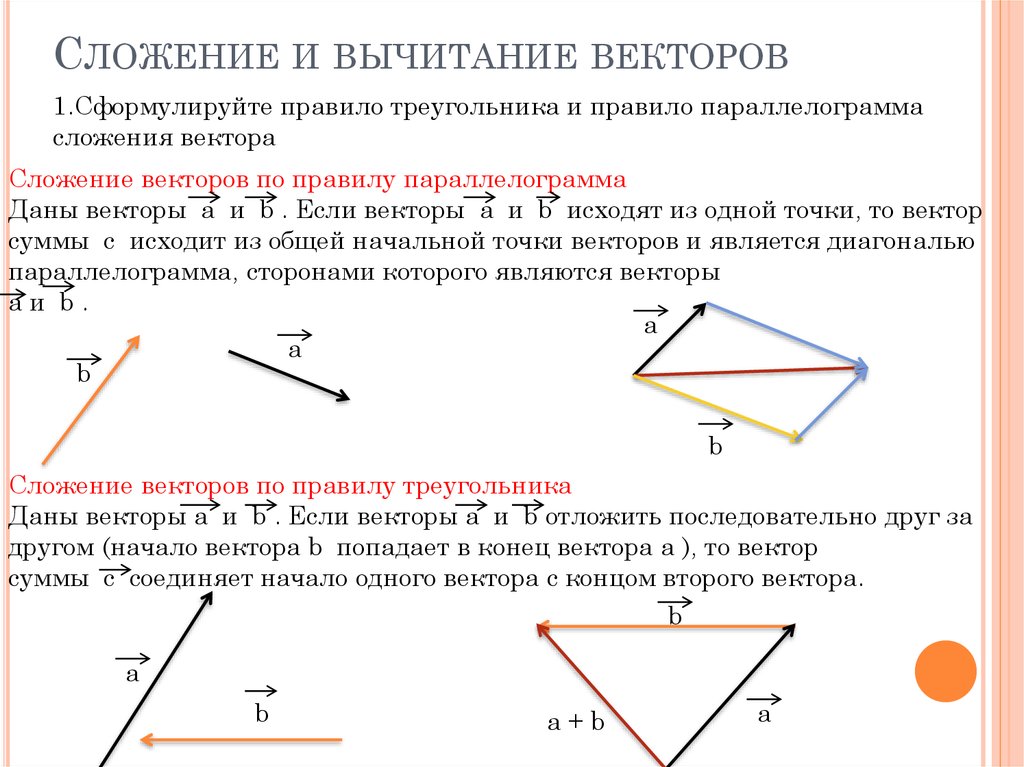 Таким образом, начальная точка вектора x+y будет точка A, а конечная точка — будет точка D’, которая вычисляется из выражения в (4).

Рис. 2

На рисунке Рис.2, для получения суммы векторов x и y, вектор y перемещается параллельно так, чтобы его начало совмещалось с концом вектора x (вектор y’ ). Вектор z=x+y получится соединив начало x и конец вектора y’.

Рассмотрим процесс сложения векторов, начальные точки которых не совпадают с началом координат. На Рис.2 представлен процесс сложения векторов x=AB и y=CD, где A(1,1), B(10,-3), C(1,2), D(2,7). Из выражений (4) вычисляем координаты точки D’:

Сумма векторов z=x+y будет иметь начальную точку A(1,1) и конечную точку D'(11,2).

Операция сложения векторов обладает следующими свойствами:

1. x+y=y+x (коммутативность).

2.(x+y)+w=x+(y+w) (ассоциативность).

3. x+0=x (наличие нулевого вектора).

4. x+(-x)=0 (наличие противоположного вектора).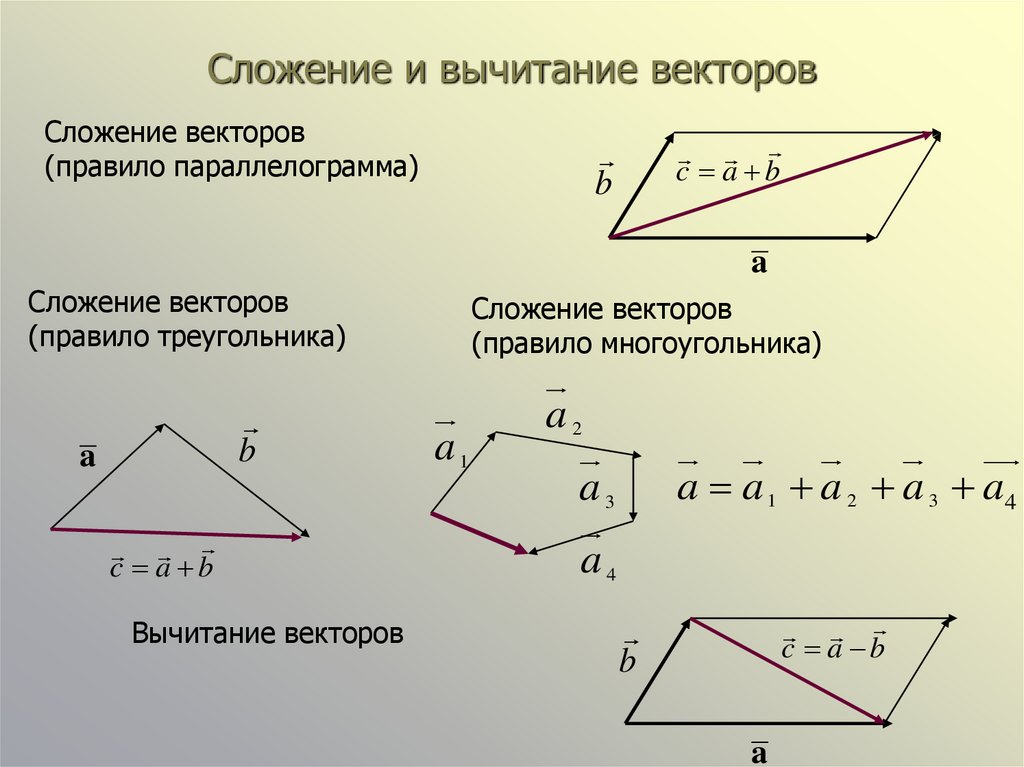

Пример 1. Вычислить сумму векторов AB и CD, где A(2,2), B(7,6), C(5,6), D(10,7).

Вычислим новое расположение точек C и D, используя выражения (4). Тогда

C'(7,6), D'(10+7-5, 7+6-6)=D(12,7).

Сумма векторов AB и CD будет вектор AD’, где A

(2,2), D‘(12,7).

Пример 2. Вычислить сумму векторов AB и у, где A(4,3), B(5,8), y=(7,3).

Так как вектор y представлен в виде координат, то это означает, что начальная точка вектора y является C(0,0) а конечная точка — D(7,3).

Вычисляя новое расположение вектора y, получим новые точки

C'(5,8), D'(7+5-0, 3+8-0)=D'(12,11).

Наконец, сумма векторов AB и y будет вектор AD’, где A(4,3), D’(12,11).

8.2. Векторы и векторные пространства

Рассматривая, как развивалось то или иное матема­тическое понятие, мы учимся понимать роль и значение всей математики. Наряду с кольцами и полями, одним из важнейших понятий в математике, физике и технике является Вектор. Эволюция этого понятия — от На­правленного отрезка до сложнейших Векторных про­странств — история интересная и поучительная.

Первоначально вектором называли направленный отрезок, прикрепленный к какой-либо точке. С помо­щью направленных отрезков удобно иллюстрировать физические величины, которые характеризуются не только величиной, но и направлением: силу, скорость, напряженность электрического поля и т. д.

Векторы, прикрепленные к одной точке, можно скла­дывать по правилу параллелограмма. С физической точки зрения сумма двух или более векторов представляет собой равнодействующую сил, действующих на точку (рис. 35).

Векторы, прикрепленные к одной точке, можно не только складывать, но и вычитать, умножать на числа. Разностью двух векторов и называется вектор — , Определяемый равенством + ( – ) = . Произведением вектора на число K называется вектор = K, при­крепленный к той же точке, что и вектор ; длина век­тора Определяется равенством | | = |K| • ||, а направле­ние совпадает с направлением вектора ||, если

K число положительное, и противоположно вектору , если K — Число отрицательное (рис. 35). При этом, каковы бы ни были векторы , , и числа K, I, всегда выполняются следующие равенства:

Математиков, которые рассматривают векторы вне их связи с физическим содержанием, не удовлетворяло, что нельзя складывать векторы, прикрепленные к разным точкам. Выход нашелся в том, чтобы сделать векторы свободными от точки прикрепления и разрешить им пе­редвигаться параллельно исходному положению. Иными словами, Свободный вектор можно представлять себе в виде совокупности всевозможных направленных отрез­ков, параллельных между собой, имеющих одну и ту же длину и одно и то же направление. Такие отрезки назы­вают Эквивалентными.

Свободные векторы просто задавать с помощью координат. Напомним, что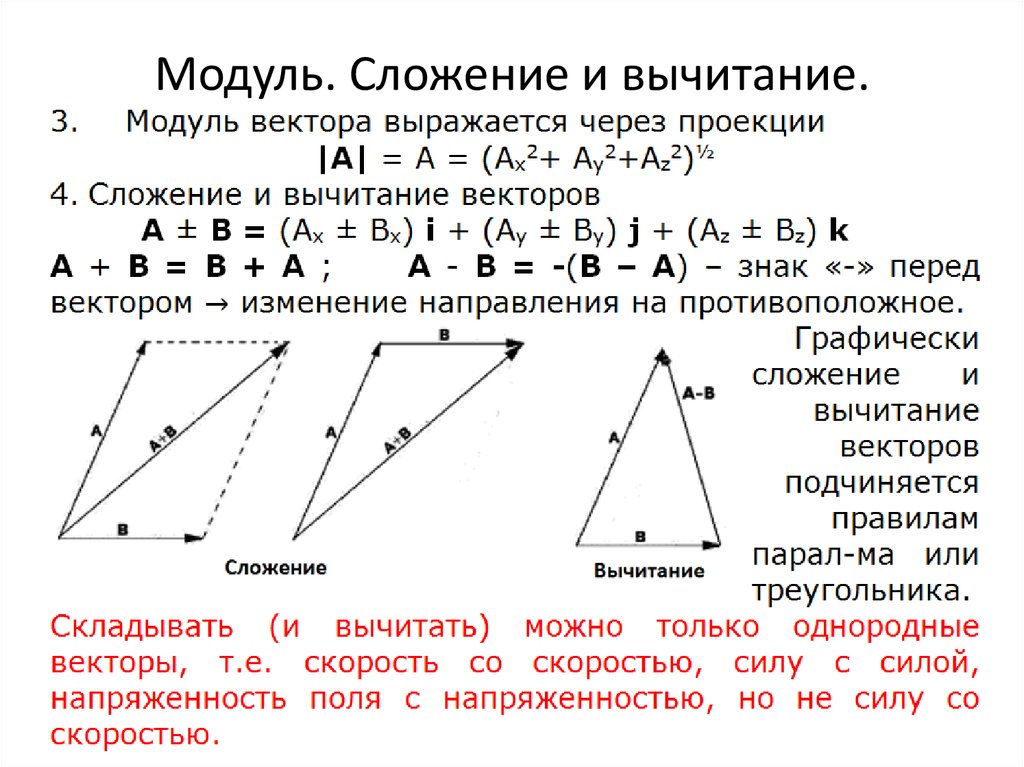

Координатами вектора — на­правленного отрезка на плоскости называются его проекции на координатные оси Х и Y (см. рис. 36). Очевид­но, что все эквивалентные направленные отрезки имеют одинаковые координаты. Поэтому последние можно счи­тать координатами соответствующего свободного вектора.

В пространстве направленный отрезок имеет три ко­ординаты: проекции на координатные оси X, Y и Z. Следовательно, свободный вектор в пространстве имеет также три координаты.

Итак, теперь вектор можно заменить эквивалентным объектом — совокупностью его координат. Вектор на плос­кости — это пара чисел (а1,а2), вектор в пространстве — тройка чисел (а1, а2, а3). Сложение векторов и умножение их на числа теперь осуществляется также просто. Чтобы сложить два вектора, нужно сложить их соответствую­щие координаты, а чтобы умножить вектор на число, нужно умножить на это число его координаты. Напри­мер, (1,2,–3) + (–4,6,4) = (–3,8,1), 2 • (1,2,–3) = (2,4,–6).

Такая точка зрения на векторы оказалась исключи­тельно плодотворной. Под определение вектора сразу по­пало много физических и математических объектов. На­пример, всякое элементарное событие, происходящее в пространстве в точке с координатами (х, у,z) в момент вре­мени T, можно рассматривать как четырехмерный вектор (X,Y,Z,T). Так мы приходим к Пространству событий — Одному из основных понятий современной физики. Дру­гой пример. Всякий технологический процесс характеризуется набором различных параметров, которые фикси­руются приборами, показывающими время, скорость процесса, давление, вязкость и т. п. Допустим, что таких параметров 10. Тогда состояние процесса определяется набором из десяти чисел, т. е. десятимерным вектором.

Количество координат вектора называется Размерностью. Векторы одной и той же размерности можно складывать и умножать на числа по тем же правилам, что двумерные и трехмерные. И при любой размерности будут выполняться свойства (2). Таким образом, мы приходим к наиболее общему аксиоматическому опреде­лению векторного пространства:

Векторным пространством называется всякое мно­жество, для элементов которого определена операция сложения и определено умножение элементов на числа таким образом, что выполняются свойства (2).

Свободный вектор называют еще Параллельным векторным полем. Термин «векторное поле» возник в фи­зике, и его смысл вполне соответствует значению этого слова в обычном языке. Мы представляем себе поле как некоторый участок земли, засеянный, скажем, пшени­цей. Теперь представим себе, что колос пшеницы — это вектор, и что колосья (векторы) растут в каждой точке участка. Это и будет векторное поле, причем не обяза­тельно параллельное. Параллельное поле получается в случае, когда все «колоски» параллельны и имеют оди­наковую длину.

Множество примеров векторных полей мы находим в физике: электрические и магнитные поля, поле тяготе­ния. Поток жидкости или газа в трубе порождает вектор­ное поле скоростей: в каждой точке потока определен вектор скорости.

Математики иногда рассматривают векторное поле как функцию, которая каждой точке пространства сопоставля­ет некоторый вектор, как бы прикрепленный к этой точке. Векторные поля представляют собой один из важнейших объектов изучения в современной физике и математике.

< Предыдущая		Следующая >

Сложение векторов — поступательное движение

Векторы можно складывать или вычитать графически, размещая их встык на наборе осей.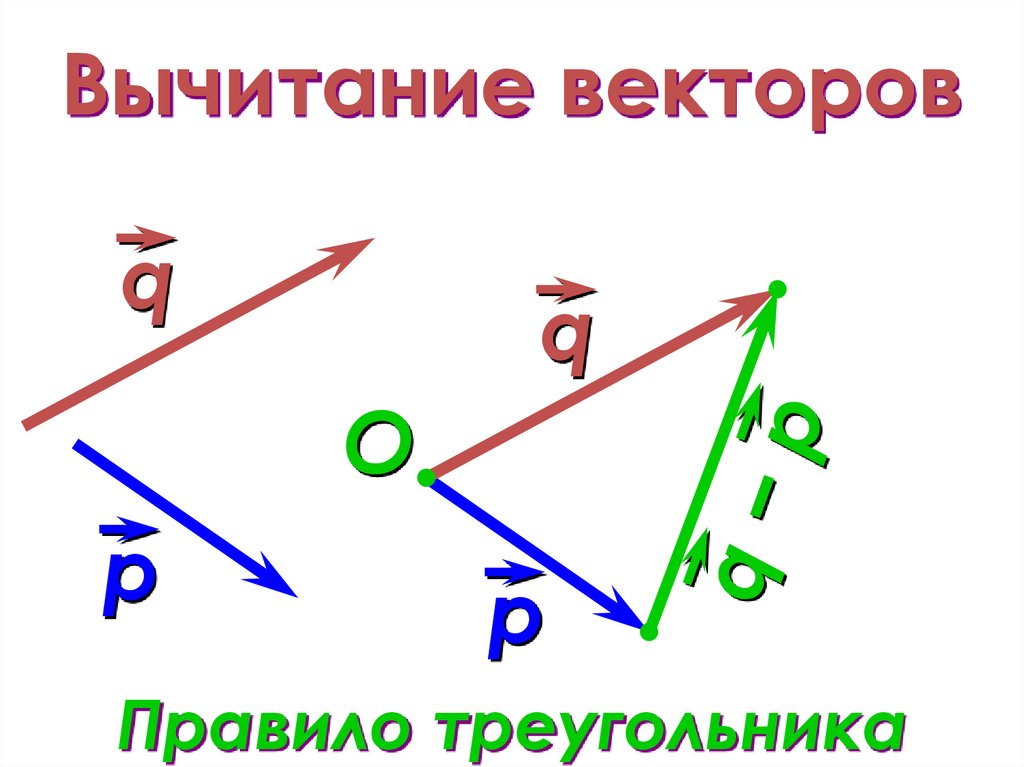

Одним из способов, которым представление физических величин в виде векторов упрощает анализ, является легкость, с которой векторы могут быть добавлены друг к другу. Поскольку векторы являются графическими визуализациями, сложение и вычитание векторов можно выполнять графически.

Графический метод сложения векторов также известен как метод «голова к хвосту». Для начала нарисуйте набор из оси координат . Затем нарисуйте первый вектор с его хвостом (базой) в начале координат осей координат. Для сложения векторов не имеет значения, какой вектор вы рисуете первым, поскольку сложение является коммутативным, но для вычитания убедитесь, что вектор, который вы рисуете первым, является тем, из которого вы вычитаете. Следующий шаг — взять следующий вектор и нарисовать его так, чтобы его хвост начинался с головы предыдущего вектора (со стороны стрелки). Продолжайте размещать каждый вектор в начале предыдущего, пока все векторы, которые вы хотите добавить, не будут соединены вместе. Наконец, нарисуйте прямую линию от начала до начала последнего вектора в цепочке. Эта новая строка является векторным результатом сложения этих векторов.

Метод вычитания векторов аналогичен. Убедитесь, что первый вектор, который вы рисуете, является тем, из которого нужно вычесть. Затем, чтобы вычесть вектор, действуйте так же, как при добавлении напротив этого вектора. Другими словами, переверните вектор, который нужно вычесть, по осям, а затем соедините его хвост к голове, как при сложении. Чтобы перевернуть вектор, просто поместите его голову туда, где был хвост, а хвост — туда, где была голова.

Помните:

• Векторная сумма всех компонентов вектора, равная самому вектору.
• Операция, включающая вектор и вектор, может привести или не привести к вектору (кинетическая энергия из квадрата векторной скорости дает скалярную энергию).
• Операция, включающая вектор и скаляр, всегда приводит к вектору.
• Операция, включающая скаляр и скаляр, всегда приводит к скаляру.

Практические вопросы

  Академия Хана

Свиной грипп в Финляндии

Официальная подготовка к MCAT (AAMC)

Пакет вопросов по физике, вопрос 116

Практический экзамен 4, раздел C/P, вопрос 12

топоров с хвостом в начале координат. Поместите следующий вектор хвостом в голову предыдущего вектора. Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.

• Чтобы вычесть векторы, действуйте, как при сложении двух векторов, но переверните вычитаемый вектор по осям, а затем соедините его хвост к началу, как при сложении.

• Добавление или вычитание любого количества векторов дает результирующий вектор.

• Векторная сумма всех компонентов вектора, равная самому вектору.

• Операция, включающая вектор и вектор, может привести к вектору, а может и не привести (кинетическая энергия, полученная путем квадрата векторной скорости, дает скалярную энергию)

• Операция, включающая вектор и скаляр, всегда приводит к вектору.

• Операция между скаляром и скаляром всегда приводит к скаляру.

Ключевые термины

Происхождение : Центр координатной оси, определяемый как координата 0 по всем осям.

Оси координат : Набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.

Сложение и вычитание векторов — Практика — Гиперучебник по физике

[закрыть]

практическая задача 1

Два человека толкают неисправную машину. Один оказывает силу 200 N на восток, другой — силу 150 N на восток. Какова результирующая сила, действующая на автомобиль? (Предположим, что трением можно пренебречь.)

раствор

Силы направлены в одном направлении, поэтому они складываются.

∑ Ж  =  Ж 1  +  F 2 ∑ F  = 200 N + 150 N ∑ F  = 350 N

Две первоначальные силы направлены на восток, поэтому результирующая — на восток.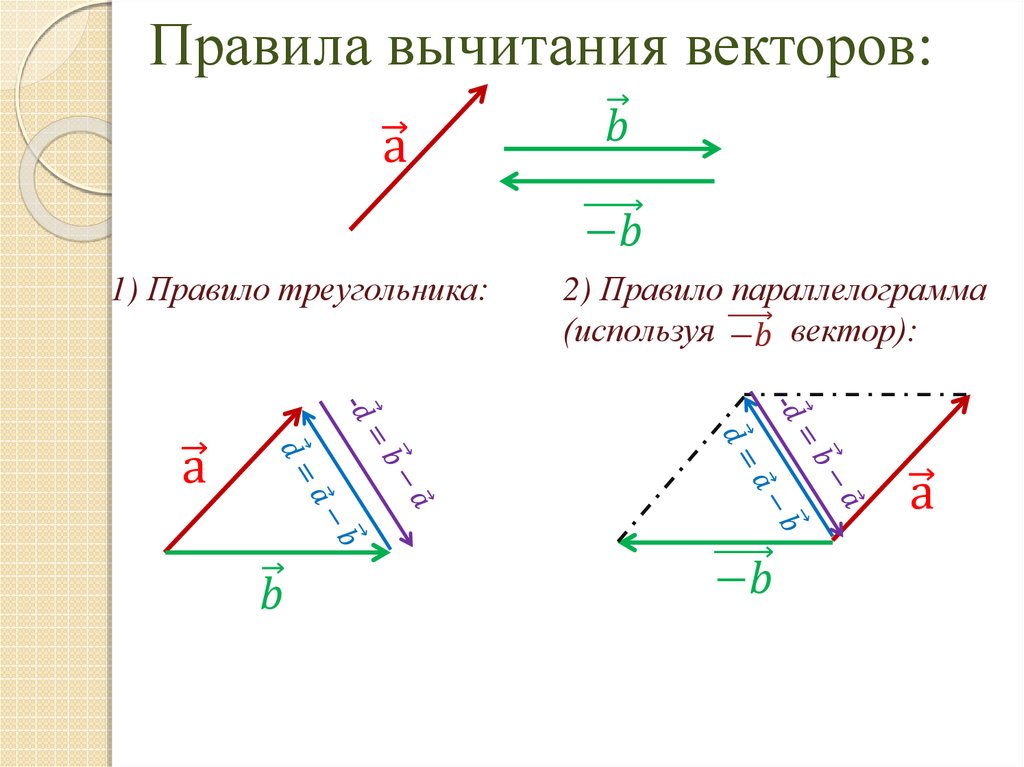

∑ Ж  = 350 Сев.-восток

Здесь никаких хитростей. Некоторые проблемы просто решить.

практическая задача 2

Два футболиста одновременно бьют по мячу с противоположных сторон. Красный №3 бьет ногой с усилием 50 Н, а Синий №5 бьет с усилием 63 Н. Какова чистая сила, действующая на мяч?

раствор

Силы направлены в противоположные стороны, поэтому они вычитаются. Другой способ думать об этом: одна из сил положительна, а другая отрицательна. Знаки — это способ указать основные направления. Я думаю, что сделаю первое положительным, а второе отрицательным, потому что, почему бы и нет?

∑ F = F RED — F Blue ∑ F = 50 N — 63 N ∑ F = —13 N ∑ F = −13 N ∑0122

Как описать это направление? Стороны света, такие как север, юг, восток или запад, не были указаны. Ничего не было сказано о левом или правом (или даже вверх или вниз).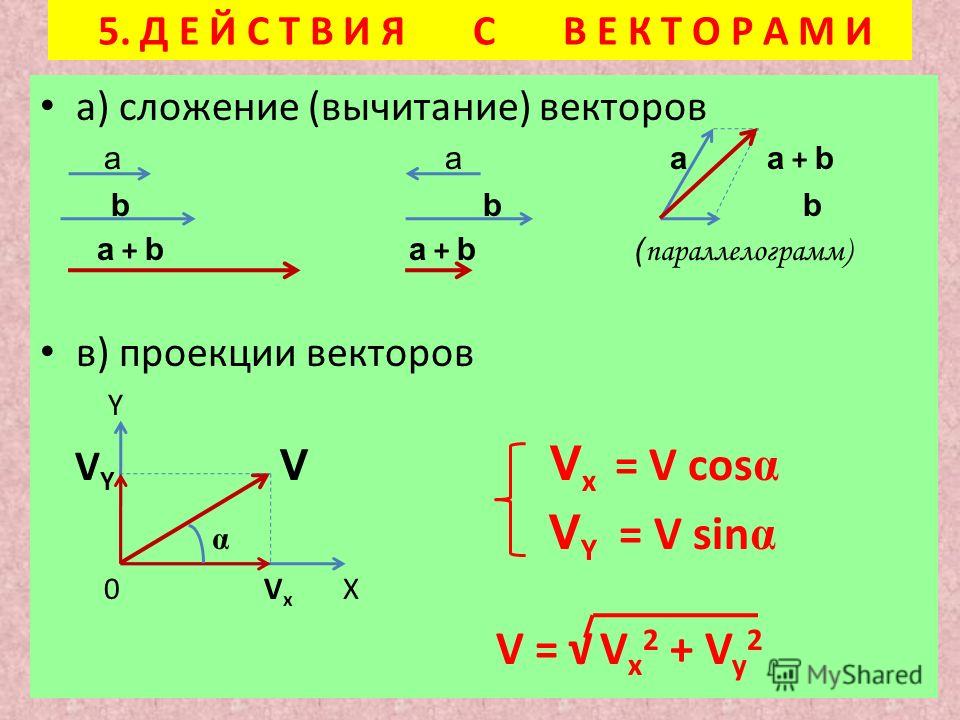 Мы произвольно присвоили отрицательное значение направлению, в котором двигался Синий № 5. Ответ был отрицательным, поэтому результирующая сила указывает в направлении, в котором пинал Синий № 5. Назовем это подальше от синего № 5.

∑ F  = 13 с.ш. от синего #5

Мы могли бы также написать…

∑ F  = 13 N в сторону красного #3

Это тоже хороший ответ. Ни одно из них не является более правильным, чем другое.

практическая задача 3

Самолет движется строго на север со скоростью 100 м/с при боковом ветре 30 м/с, дующем с востока на запад. Определить результирующую скорость самолета (относительно строгого направления на север).

раствор

Север (направление движения двигателей) перпендикулярен западу (направление ветра). Результат этих двух векторов есть гипотенуза прямоугольного треугольника. Мы используем теорему Пифагора, чтобы найти его величину…

v 2  =	в 2 самолет  +  в 2 ветер
v 2  =	(100 м/с) 2 + (30 м/с) 2
v  =	104 м/с

и тангенс, чтобы найти его направление…

тангенс θ =	напротив  =  v ветер смежный v самолет
тангенс θ =	30 м/с 100 м/с
θ =	17°

Эти 17° находятся на западной стороне севера, поэтому окончательный ответ…

v  = 104 м/с, 17° к западу от северной широты

практическая задача 4

Альпинистская экспедиция устанавливает базовый лагерь и два промежуточных лагеря, А и В.