Матрица и операции над ней
Курс данного предмета мы начнем непосредственно с матриц, потому что именно они составляют основу данной дисциплины.
Определение матрицы
Матрицей размерности называется прямоугольная таблица чисел, содержащая — строк и — столбцов, число расположенное в -ой строке и -столбце обозначается и называется элементом матрицы , т. е.
Операции над матрицами
Рассмотрим основные операции, проводимые над матрицами:
- сумма матриц;
- произведение матрицы на число;
- произведение матриц;
- транспонирование матрицы
Сумма матриц
Сумма матриц и называется матрица такая, что , где
Рассмотрим пример, чтобы стало понятнее.
ПРИМЕР 1. Найди сумму матриц А и В.
,
Как ясно из определения, чтобы найти сумму двух матриц нужно просто каждый элемент одной матрицы сложить с каждый элементом второй матрицы.
Как видите здесь сложного абсолютно ничего нет, так можно складывать и три и более матриц.
Произведение матрицы на число
Произведением матрицы на число называется матрица такая, что , где
Рассмотрим пример.
ПРИМЕР 2. Умножь матрицу А на число 2.
;
Эта операция, наверное, еще проще предыдущей. Нужно просто число умножить на каждый элемент матрицы А.
Произведение двух матриц
Произведением матрицы на матрицу называется матрица такая, что
Условие: количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы, иначе умножение невозможно!
Здесь уже более сложно так, что будьте внимательны. Чтобы сперва понять, возьмем пример самый простой с квадратными матрицами второго порядка.
ПРИМЕР 3. Вычислить произведение двух матриц.
;
Сразу, я вам не советую составлять матрицы, а делать все постепенно, подробно расписывая.
Потом, когда приловчитесь, будете записывать все кратко и большинство действий проделывать в голове.
Поэтому по-порядку, распишем каждое получаемое число:
Если записываете данные вычисления в тетради, то не забудьте выделить с обоих сторон фигурными скобками, обозначая отступление от решения { }.
Теперь можно записать получившуюся матрицу С, не забывайте — первое число элемента матрицы — это строка, второе число — столбец.
В итоге, получаем
ЗАПОМНИТЕ! При умножении матриц НЕ действует закон коммутативности (от перестановки мест множителей произведение не меняется). В матрицах произведение меняется, т. е. у вас не получится поменять местами две матрицы.
Так, думаю, стоит рассмотреть еще один пример на умножение, но уже по-сложнее, к примеру, третьей размерности возьмем матрицы.
ПРИМЕР 4. Вычислить произведение двух матриц.
;
Также распишем каждый элемент матрицы:
Вот и все, а теперь, запишем, полученную матрицу:
Транспонирование матрицы
Матрица называется транспонированной матрицей , если
, где
ПРИМЕР 5.
Транспонировать матрицу А:
Как видите первый столбец стал первой строкой, второй столбец второй строкой и так далее. Ничего сложного не вижу в этом и обычно у студентов проблем с транспонированием не возникает.
Свойства операций над матрицами
- ВНИМАТЕЛЬНО!
- ;
- ВНИМАТЕЛЬНО!
Ну думаю для первой темы вам будет предостаточно, в принципе ничего сложного, ведь все операции над матрицами сводятся к простым арифметическим операциям, которые вы надеюсь умеете выполнять еще с начальной школы.
Уроки по теории вероятности
Данная статья занесена в архив так как написана новая, возможно более понятная статья, переходите по ссылке на нее http://mathcentr.ru/matritsa-i-operatsii-nad-nej/ Как вы, наверное, уже поняли матрицы ничем не отличаются от обычных чисел, по правде говоря — это просто много цифр в одном числе))) И разумеется, существуют такие же операции над матрицами, как и над числами, но не все и
Продолжаем изучать матрицы и сегодня на уроке мы научимся находить и вычислять обратную матрицу.
Обратная матрица Матрица называется транспонированной к матрице , если выполняется условие: , для всех , где и — элементы матриц и соответственно. Проще говоря, транспонированная матрица — это перевернутая матрица, т.е. столбцы записаны строками, а строки столбцами. Пример №1 Транспонировать матрицу
Мы рассмотрели самые основные тригонометрические функции (не обольщайтесь помимо синуса, косинуса, тангенса и котангенса существует еще целое множество других функций, но о них позже), а пока рассмотрим некоторые основные свойства уже изученных функций. Тригонометрические функции числового аргумента Какое бы действительное число ни взять, ему можно поставить в соответствие однозначно определенное число . Правда, правило соответствия
Я решил, что не будем слишком долго разжевывать теоретическую часть введения в тригонометрию так, как в любом случае мало кто ее будет читать и уж тем более маловероятно, что он там все поймет. Я считаю, что лучший способ изучения математики — это не зубрежка, а работа с конкретными примерами и чем больше тем лучше.
Поэтому
Сегодня, мы рассмотрим тему «Прогрессии», которую большинство в школе либо не понимают, либо после забывают, хотя делать этого не нужно! Числовые последовательности Если каждому натуральному числу поставлено в соответствие некоторое действительное число , то говорят, что задана числовая последовательность (или просто последовательность): Кратко последовательность обозначают символом {} или (), число называют членом или элементом этой
Как создать матрицу в Python: инструкция
Матрицы являются одним из основных объектов в математике. Они используются для представления и манипулирования данными в виде таблицы, состоящей из строк и столбцов. Их используют для решения систем линейных уравнений, определения матричных действий, преобразования координат и многого другое.
В этой статье мы опишем несколько способов создать матрицу в Python. И дополнительно рассмотрим некоторые основные операции, такие как сложение, умножение и определение обратной матрицы.
Что такое матрица
Матрица — это таблица из чисел, которая используется в математике и инженерных науках для представления данных.
Матрицы имеют форму таблицы, состоящей из строк и столбцов. Каждый элемент имеет свой уникальный индекс, обозначающий строку и столбец, в котором он находится. Например, матрица размером 3×3 будет иметь 3 строки и 3 столбца, и каждый элемент будет иметь индекс вида (i, j), где i — номер строки, а j — номер столбца.
Создание матрицы
В Python существует несколько способов создания матрицы. Ниже приведены некоторые из них:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
- С помощью NumPy. NumPy — это библиотека для математических вычислений и обработки данных. В ней есть класс Array, который можно использовать для создания матрицы:
import numpy as npmatrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
Если вам нужно производить стандартные математические операции с матрицами, то стоит использовать NumPy.
Его проще использовать и все операции уже реализованы в библиотеке. А если вы хотите самостоятельно создавать методы, например, в образовательных целях, или же планируете совершать нестандартные манипуляции, то используйте вложенные списки.
Теперь рассмотрим матричные операции и поработаем с ними с помощью вложенных списков и NumPy.
Матричные операции
Вот список основных манипуляций:
- Сложение. Две матрицы можно сложить, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен сумме соответствующих элементов исходных матриц.
- Вычитание. Одну матрицу можно вычесть из другой, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен разности соответствующих элементов исходных матриц.
- Умножение на число. Каждый элемент итоговой матрицы будет равен произведению соответствующего элемента исходной матрицы на число.
- Произведение матриц.
Матрицы можно перемножить, если число столбцов первой матрицы равно числу - Транспонирование матрицы. Транспонирование — это операция, в которой строки и столбцы меняются местами. Т.е. первый столбец становится первой строкой, второй столбец — второй строкой и так далее.
- Нахождение обратной матрицы. Матрица B будет являться обратной матрицей для матрицы A, если результатом операции A*B является единичная матрица.
Матрицы можно перемножить, если число столбцов первой матрицы равно числу Сложение
Важно не забывать, что при сложении двух матриц их размеры должны совпадать.
Вот пример сложения с помощью вложенных списков и циклов:
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] + matrix2[i][j]print(result)
Результат:
[[10, 10, 10], [10, 10, 10], [10, 10, 10]]
Вот аналогичное сложение с помощью метода add() из библиотеки NumPy:
import numpy as npmatrix1 = np.
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])result = np.add(matrix1, matrix2)
print(result)
array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) Результат:
[[10 10 10]
[10 10 10]
[10 10 10]]
Вычитание
В Python можно выполнять вычитание матриц с помощью цикла или метода subtract() из библиотеки NumPy. При вычитании размеры должны совпадать.
Вычитание с помощью цикла:
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] - matrix2[i][j]print(result)
Результат:
[[-8, -6, -4], [-2, 0, 2], [4, 6, 8]]
Вычитание с помощью метода subtract() из библиотеки NumPy:
import numpy as npmatrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
matrix2 = np.result = np.subtract(matrix1, matrix2)
print(result)
array([[9, 8, 7], [6, 5, 4], [3, 2, 1]]) Результат:
[[-8 -6 -4]
[-2 0 2]
[ 4 6 8]]
Умножение на число
В Python умножение матрицы на число можно реализовать с помощью цикла или воспользоваться методом dot() из библиотеки NumPy.
При умножении матрицы на число, каждый элемент умножается на это число.
Умножение с помощью цикла:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
scalar = 2
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[i][j] = matrix[i][j] * scalarprint(result)
Результат:
[[2, 4, 6], [8, 10, 12], [14, 16, 18]]
Вот пример работы метода dot() из библиотеки NumPy с теми же вводными:
import numpy as npmatrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2result = np.
print(result)
dot(matrix, scalar)Результат:
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
Также вместо метода dot() можно использовать знак операции умножения *:
import numpy as npmatrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2result = matrix * scalar
print(result)
Результат:
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
В большинстве случаев метод dot() работает быстрее вручную реализованных циклов.
Произведение матриц
Произведение — это операция, в результате которой получается новая матрица с числом строк первой матрицы и числом столбцов второй. При матричном умножении, число столбцов первой матрицы должно совпадать с числом строк второй. Каждый элемент новой матрицы — это сумма произведения элементов строки первой матрицы и элементов столбцов второй матрицы, как на картинке ниже:
Как и прежде, реализуем произведение с помощью циклов и NumPy.
Умножение, реализованное на циклах, может иметь такой вид:
matrix1 = [[1, 2], [3, 4]]
matrix2 = [[5, 6], [7, 8]]
result = [[0, 0], [0, 0]]for i in range(len(matrix1)):
for j in range(len(matrix2[0])):
for k in range(len(matrix2)): result[i][j] += matrix1[i][k] * matrix2[k][j]print(result)
Результат:
[[19, 22], [43, 50]]
В NumPy для матричного умножения используется метода dot():
import numpy as npmatrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])result = np.dot(matrix1, matrix2)
print(result)
Результат:
[[19 22]
[43 50]]
Аналогично методу dot() работает операция @:
import numpy as npmatrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])result = matrix1 @ matrix2
print(result)
Результат:
[[19 22]
[43 50]]
Использование метода dot() или оператора @ даёт более быстрый, по сравнению с использованием вручную реализованных циклов, результат.
Не забывайте, что произведение является некоммутативной операцией, то есть порядок умножения матриц имеет значение и результат будет разным, если их переставить местами.
Транспонирование
Транспонирование — это операция, в результате которой строки исходной матрицы становятся столбцами новой матрицы, а столбцы — строками.
В Python можно выполнить транспонирование с помощью свойства T или метода transpose() из библиотеки NumPy.
Пример транспонирования с использованием свойства T:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])result = matrix.T
print(result)
Результат:
[[1 4 7]
[2 5 8]
[3 6 9]]
И пример транспонирования с использованием метода transpose():
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])result = np.transpose(matrix)
print(result)
Результат:
[[1 4 7]
[2 5 8]
[3 6 9]]
В обоих случаях результат одинаковый.
С помощью цикла транспонирование можно реализовать следующим образом:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[j][i] = matrix[i][j]print(result)
Результат:
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]
Этот метод может быть медленным и неэффективным для больших матриц, поэтому для более быстрого и эффективного решения рекомендуется использовать NumPy.
Нахождение обратной матрицы
Обратная матрица — это матрица, которая при умножении на исходную матрицу в результате дает единичную матрицу (с единицами на диагонали и нулями в остальных ячейках).
В Python можно найти обратную матрицу с помощью метода inv() из библиотеки NumPy.
import numpy as npmatrix = np.array([[1, 2], [3, 4]])
result = np.linalg.inv(matrix)
print(result)
Результат:
[[-2. 1. ]
[ 1.
5 -0.5]]Если матрица не имеет обратной матрицы, то метод inv() вызовет исключение LinAlgError: Singular matrix.
Чтобы проверить, имеет ли матрица обратную, используйте метод det() из библиотеки NumPy, который возвращает определитель матрицы. Если определитель равен нулю, то матрица вырожденная и она не имеет обратной матрицы:
import numpy as npmatrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)if determinant == 0:
print("The matrix does not have an inverse.")
else:
result = np.linalg.inv(matrix)
print(result)
Нахождение обратной матрицы с помощью циклов может быть достаточно сложным и трудоемким процессом, особенно для больших матриц. Поэтому рекомендуем использовать NumPy.
Заключение
Матрицы являются важной концепцией в линейной алгебре и часто используются в различных областях, таких как искусственный интеллект, графика и оптимизация. В Python представлено множество инструментов для работы с матрицами, включая библиотеку NumPy.
Понимание матриц и их операций может быть полезным для решения множества практических задач в различных областях.
▷ Сложение и вычитание матриц: правила, примеры и свойства
В этом посте мы объясняем, как выполнять сложение и вычитание матриц. Кроме того, вы увидите примеры сложения и вычитания матриц. Кроме того, вы обнаружите проблемы, чтобы попрактиковаться в этих матричных операциях. И, наконец, мы покажем вам все свойства сложения матриц.
Содержание
Как складывать и вычитать матрицы?
К добавить (или вычесть) две матрицы добавьте (или вычтите) элементы, которые находятся в одной и той же позиции. Таким образом, две матрицы можно складывать или вычитать только в том случае, если они обе имеют одинаковую размерность.
Примеры сложения и вычитания матриц
Пусть A и B две квадратные матрицы 2×2, их сложение и вычитание вычисляются следующим образом:
Итак, правила сложения и вычитания матриц просты: мы просто имеем чтобы добавить или вычесть соответствующие записи и поместить результат операции в ту же позицию.
Более того, чтобы сложить или вычесть две матрицы, обе они должны иметь одинаковую размерность. Например, нельзя добавить следующие матрицы, поскольку они имеют разные размеры: первая — матрица размерности 2×2, а вторая — матрица размерности 3×2.
Любопытно, что существует еще один тип сложения матриц, называемый суммой Кронекера, хотя он очень редок и мало используется в линейной алгебре.
Практика сложения и вычитания матриц
Задача 1
Добавить следующие 2 × 2 матрицы размеров:
См. Решение
, чтобы добавить две квадратные матрицы Ордена 2 Мы должны добавить соответствующие записи:
Проблема 2
. Вычтите следующие матрицы 3×2:
См. решение
Несмотря на то, что матрицы не квадратные, мы можем вычесть их, потому что они имеют одинаковую размерность:
Задача 3
Найдите следующее добавление матрицы 3 × 3:
См.
Решение
, чтобы вычислять матричную сумму Мы должны добавить элементы, которые находятся в том же положении:
6666666 Задача 4
Вычислите следующие сложения и вычитания матриц 2×2:
См. решение
В этом случае мы имеем сложение и вычитание матриц. Таким образом, мы сначала добавляем матрицы слева:
, а затем мы вычитаем матрицы:
Задача 5
Добавить и вычесть следующие матрицы размеров 3 × 3:
См. Решение
Первые, мы решаем Маттрикса. Подтоколь
И, наконец, мы вычисляем сумму матриц:
Теперь, когда вы знаете, как складывать и вычитать матрицы, вы должны увидеть умножение матриц 2×2.
Свойства сложения матриц
Сложение матриц удовлетворяет следующим характеристикам:
- Сложение матриц обладает свойством коммутативности :
Следовательно, порядок, в котором мы складываем матрицы, не имеет значения.
Чтобы доказать это свойство, мы собираемся добавить две матрицы, меняя их порядок, вы увидите, что результат тот же.
Итак, мы продолжаем складывать две матрицы:
Обратите внимание, что если мы поменяем порядок добавления матриц на обратный, результат суммирования останется прежним:
- Другим свойством матричного сложения является противоположный элемент :
То есть, если мы сложим матрицу плюс ту же матрицу, но со всеми ее элементами, поменявшими знак, результатом будет нулевая матрица. Например:
- Сложение матриц также обладает свойством нейтрального элемента :
Это свойство является наиболее очевидным и означает, что любая матрица плюс матрица, полная нулей, дает в той же матрице:
- Сложение матриц обладает ассоциативным свойством :
Следовательно, порядок сложения матриц не имеет значения.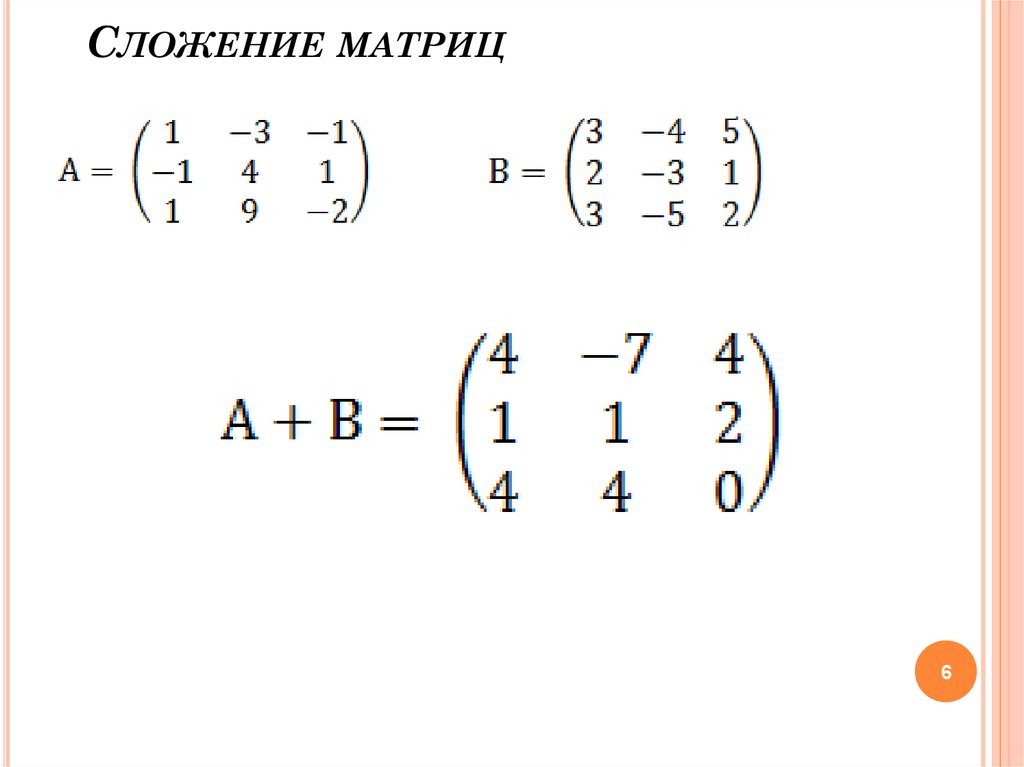
Взгляните на следующий пример, где мы складываем 3 матрицы в разном порядке, а результат тот же:
и Джон Пол Мюллер и
Обновлено: 26 марта 2016 г.
Из книги: MATLAB для чайников
MATLAB для чайников
Исследуйте книгу Купите на Amazon чтобы увидеть, как выполнять математику, используя их. Сложение и вычитание — хорошее место для начала.
Важным правилом при сложении и вычитании векторов и матриц является то, что они должны быть одного размера. Вы не можете складывать или вычитать векторы или матрицы разных размеров, потому что MATLAB отобразит сообщение об ошибке. Выполните следующие шаги, чтобы увидеть, как выполнить эту задачу:
Введите a=[1,2;3,4] и нажмите Enter.
Вы видите
а = 1 2 3 4
Введите b=[5,6;7,8] и нажмите Enter.
Вы видите
б = 5 6 7 8
Введите c = a + b и нажмите Enter.
Этот шаг добавляет матрицу a к матрице b. Вы видите
с = 6 8 10 12
Введите d = b — a и нажмите Enter.
Этот шаг вычитает матрицу b из матрицы a. Вы видите
д = 4 4 4 4
Введите e=[1,2,3;4,5,6] и нажмите Enter.
Вы видите
е = 1 2 3 4 5 6
Если вы попытаетесь добавить или вычесть матрицу e из матрицы a или матрицы b, вы увидите сообщение об ошибке. Однако следующий шаг все равно пытается выполнить задачу.
Введите f = e + a и нажмите Enter.
Как и ожидалось, вы видите следующее сообщение об ошибке:
Ошибка при использовании + Размеры матрицы должны совпадать.
Сообщения об ошибках при сложении и вычитании немного различаются, но суть одна и та же. Матрицы должны быть одинакового размера, чтобы их можно было сложить или вычесть.
