Множественная регрессия в матричной форме
1. Лекция 2. Множественная регрессия
Вопросы:1.
Классическая модель множественной линейной регрессии в матричной форме
2.
Оценка параметров МНК
3.
Ковариационная матрица
4.
Множественные коэффициенты детерминации и корреляции. Оценка значимости
множественной регрессии
5.
Оценка значимости параметров. Интервальная оценка параметров и прогноза
6.
Понятие и проблема мультиколлинеарности факторов и способы ее преодоления
7.
Коэффициент частной корреляции
8.
Свойства оценок МНК
9.
Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме.
10.
Обобщенная линейная модель. ОМНК
11.
Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
12.
Отбор наиболее существенных объясняющих переменных в модель множественной
регрессии
13.
Уравнение регрессии с фиктивными переменными.
Критерий Чоу14.
Нелинейные модели множественной регрессии. Производственные функции
15.
Вопросы для повторения и самостоятельного изучения
2. 1. Классическая модель множественной линейной регрессии в матричной форме
Yi 0 1 xi1 2 xi 2 … p xip iгде i=1,2…n – номер наблюдения, число объясняющих переменных (х) равно р.
βi-коэффициент чистой регрессии, показывает на сколько единиц изменится
зависимая переменная, если независимая – хi – изменится на единицу, при
условии, что все остальные факторы будут зафиксированы на среднем
уровне.
3. 1. Классическая модель множественной линейной регрессии в матричной форме
1 x11X 1 x21
1 x
n1
x12 … x1 p
x22 … x2 p
xn 2 … xnp
матрица
объясняющих
переменных размера
n×(p+1)
Предпосылка 6.
Векторы значений объясняющих переменных (столбцы
матрицы Х) должны быть линейно независимыми, т.е.
ранг матрицы – максимальный (X)=p+1
4.
1. Классическая модель множественной линейной регрессии в матричной формеy1 1 x11
y2
Y ; X 1 x21
…
1 x
n1
y
n
x12 … x1 p
x22 … x2 p ;
xn 2 … xnp
0
1
1
2
, тогда в матричной форме : Y X .
2 ;
…
…
n
p
Выборочная оценка : Y Xb e, где
b0
e0
b1
e1
b , e .
…
…
e
b
n
p
5. 2. Оценка параметров МНК
e en
e
1
e2
(e1e2 …en )
…
e
n
e12
e22
…en2
n
n
ei2 , условие минимизации :
i 1
2
~
(
y
y
)
e
i i i e e (Y Xb) (Y Xb) min
2
i 1
i 1
X Xb X Y
b ( X X ) 1 X Y
6. 2. Оценка параметров МНК
Пример :b0 b1 x1 у
1 х1
y1
1 х2
y2
Х
;
y
… ;
… …
1 хт
yn
1
X X
x1
1
x2
1 х1
n
1 1 1 х2
n
… xn .
.. …xi
1 хт i 1
n
Тогда X Xb X Y : n
x
i
i 1
xi
i 1
n
2
xi
i 1
n
n
xi b
yi
0 i 1
i 1
n
n
b
2
xi 1 yi xi
i 1
i 1
n
7. 2. Оценка параметров МНК
Метод Крамера :j
bj
определитель матрицы Х ;
j определитель матрицы, получающейся при замене
j й независимой переменной матрицы Х вектором Y
8. 3. Ковариационная матрица
00 01 … 0 p10 11 … 1 p
b
p 0 p1 … pp
ij M (bi M (bi ))(b j M (bJ )) , поскольку M (b j ) j
ij
M (b )(b
i
i
j
j ) M (b )(b ) ,
b M (b )(b )
так как b ( X X ) 1 X ,
получим : b ( X X ) 1 X ( X X ) 1 X
b ( X X ) 1 X M ( ) X ( X X ) 1
9. 3. Ковариационная матрица
M ( 12 ) M ( 1 2 ) … M ( 1 n )2
M ( 2 1 ) M ( 2 ) … M ( 2 n )
M ( )
M ( ) M ( ) … M ( 2 )
n 1
n 2
n
M ( i2 ) M ( i 0) 2 2
M ( ) 2 En
b 2 ( X X ) 1
10.
3. Ковариационная матрица Предпосылки множественной регрессии в матричной форме:1. случайный вектор , Х неслучайна я матрица.2.М ( ) 0n
3,4. M ( ) 2 En
5. нормально распределе нный вектор
6.r ( X ) ( p 1) n
11. 4. Множественные коэффициенты детерминации и корреляции. Оценка значимости множественной регрессии
WeWR
e e
R
1
1
,
Wy
Wy
y y
2
y (Y Y )
n 1
R 1
(1 R 2 )
n p 1
2
н
R 2 (n p 1)
F
F ; p ;n p 1
2
(1 R ) p
4. Множественные коэффициенты детерминации и корреляции. Оценка
значимости множественной регрессии
А
R 1
А11
2
R2 1
1
ryx1
ryx
2
ryx1
1
rx1x2
1
r
x1x2
ryx2
rx1x2
1
rx1x2
1
ryx2 1 ryx2 2 2ryx1 ryx2 rx1x2
1 r
2
x1 x2
13. 5. Оценка значимости параметров. Интервальная оценка параметров и прогноза
mb2j Sb2j S e2 ( X X ) 1jj
mb j Sb j S e2 ( X X ) 1
jj
e e
We
S
e
n p 1
n p 1
X п (1×1п x2 п .
..x pп ), Yп X п bm~yп S e2 X п ( X X ) 1 X п
m yп S e2 (1 X п ( X X ) 1 X п )
14. 6. Понятие мультиколлинеарности и способы ее преодоления
T 12
Rx i . x1… x i 1 , xi 1… x p
1 A
1
b X X E p 1
1
X Y
15. 7.Коэффициент частной корреляции
q yx1
r yx .x
q yy q x x
1 2
11
q yx
2
r yx .x
q yy q x x
2 1
2 2
qx x
1 2
rx x . y
qx x qx x
1 2
11 2 2
16. 7.Коэффициент частной корреляции
rij .krij rik r jk
(1 rik2 )(1 r jk2 )
17. 7.Коэффициент частной корреляции
18. 8. Свойства оценок МНК
1. Оценки b являются несмещенными, т.е.М (bi ) ,
bi оценки по всем возможным выборкам.
Y X
b ( X X ) 1 X Y ( X X ) 1 X ( X )
( X X ) 1 ( X X ) ( X X ) 1 X E ( X X ) 1 X
( X X ) 1 X , т.е. оценки параметров , найденные по выборке ,
будут содеражать случайные ошибки
Поскольку М ( ) 0, то
М (b) M ( ( X X ) 1 X ) M ( ) M ( X X ) 1 X )
M ( ) ( X X ) 1 M ( X )
Требование несмещенности гарантирует отсутствует систематических ошибок
при оценивании
19.
8. Свойства оценок МНК2. По теореме Гаусса-Маркова при выполнении предпосылок 1-4, 6несмещенная оценка МНК
b ( X X ) 1 X Y
является наиболее эффективной, т.е. обладает наименьшей дисперсией
в классе линейных несмещенных оценок.
Эффективность является решающим свойством, определяющим качество оценок.
20. 8. Свойства оценок МНК
3. Оценки b являются состоятельными, т.е. при увеличении численностивыборки сходятся по вероятности к оцениваемым параметрам:
lim P ( b ) ) 1
n
или
b
n
В случае использования состоятельных оценок оправдывается увеличение объема
выборки, так как при этом становятся маловероятными значительные ошибки при
оценивании. При построении множественной модели регрессии на каждый фактор
должно приходиться по 6-10 наблюдений.
21. 9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной детерминации. Модель регрессии в стандартизованной форме
Стандартизованные коэффициенты регрессии коэффициен ты :j bj
xj
y
Величина бета-коэффициента показывает, на сколько средних квадратических
отклонений изменится у, если хj изменится на одно среднее квадратическое отклонение.
Для парной модели регрессии β-коэффициент равен коэффициенту корреляции:
r
cov( x; y ) ( x x )( y y ) xy x y
x y
n x y
x y
cov( x; y )
b
x2
x
r b
y
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
Уравнение прямой, проходящей через точку
M ( x; y )
( y y ) b( x x )
( y y) r y ( x x)
x
( y y)
( x x)
r
y
x
t y rt x r
ty
tx
t y t x , r
r
1
n
( x x )( y y ) 1 t t t t
x y
x y
x y
txtx t y t y 1
n
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
Уравнение двухфакторной модели регрессии в стандартизованной форме:
1t x1 2t x2 t y
Параметры (бета-коэффициенты могут быть найдены методом наименьших
квадратов):
МНК : (~
ty t y ) 2 min
2
(
t
t
t
)
1 x1 2 x2 y min
t y
2t x1 ( 1t x1 2t x2 t y ) 0
1
t y 2t ( t t t ) 0
x2
1 x1
2 x2
y
2
9.
Стандартизованные коэффициенты регрессии, коэффициенты раздельнойдетерминации. Модель регрессии в стандартизованной форме
1 t x1 t x1 2 t x1 t x2 t x1 t y
txtx t yt y 1
t y t x ryx
1 t x2 t x1 2 t x2 t x2 t x2 t y
1 2 rx1x2 rx1 y 1 rx1 y 2 rx1x2
1rx1x2 2 rx2 y
( rx1 y 2 rx1x2 ) rx1x2 2 rx2 y
rx1 y rx1x2 2 rx1x2 rx1x2 2 rx2 y
2
rx2 y rx1 y rx1x2
1 rx21x2
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
1
2
rx1 y rx2 y rx1x2
2
1 rx1x2
rx2 y rx1 y rx1x2
2
1 rx1x2
rx1 y . x2
rx1 y rx2 y rx1x2
1 rx22 y 1 rx21x2
1 rx1 y . x2
2 rx2 y . x1
1 rx22 y
1
2
rx1x2
1 rx21 y
1 rx21x2
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
Коэффициенты эластичности для линейной связи определяются по формуле:
хj
Э j bj
у
Они показывают, на сколько процентов изменится признак-результат,
если признак-фактор изменится на один процент.
y x
y x
x
lim ( : ) lim ( ) f ( x )
x 0 y
x 0 x y
x
y
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
На основе множественного линейного уравнения регрессии
y b0 b1 x1 b2 x2 … bp x p
Могут быть найдены частные уравнения регрессии:
y x1 . x2… x p b0 b1 x1 b2 x 2 … bp x p
y x2 . x1x3 … x p b0 b1 x1 b2 x2 … bp x p
…………………………………………………………
y
x p . x1 … x p 1 b0 b1 x1 b2 x 2 … bp x p
y x1 . x2… x p a1 b1 x1
y x2 . x1x3 … x p a2 b2 x2
…………………………….
y
x p . x1 … x p 1 a p bp x p
a1 b0 b2 x 2 … bp x p
a2 b0 b1 x1 b3 x 3… bp x p
…………………………………….
a p b0 b1 x1 … bp 1 x p 1
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
В отличие от парной регрессии частные уравнения регрессии характеризуют
изолированное влияние фактора на результат, поскольку все остальные факторы
закреплены на среднем уровне, эффекты их влияния добавлены к свободному члену.
На основе частных уравнений регрессии могут быть найдены частные коэффициенты
эластичности (для каждого хj ):
xij
Эyx b j ~
,
ij
y xij . x1 … xi 1 , xi 1 … x p
где хij –значение j-го фактора по i-му наблюдению,
~y
xij . x1 … xi 1 , xi 1 … x p
— выравненное по частному уравнению регрессии (для xj)
значение зависимой переменной для i-наблюдения
Так, для х1 для 10 наблюдения частный коэффициент эластичности :
Эyx
10.1
x10.1
b1 ~
y x10.1 . x1 … xi 1 , xi 1 … x p
9. Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации. Модель регрессии в стандартизованной форме
Коэффициент частной детерминации определяется по формуле:
d 2j j rx j y
cov( x j ; y )
x cov( x j ; y )
d bj
bj
y x y
y2
2
j
Коэффициенты частной детерминации показывают вклад каждого фактора в
формирование коэффициента множественной детерминации:
R 2 d 2j
В коэффициенте частной детерминации смешивается чистый эффект от влияния
фактора, который выражается бета-коэффициентом, и смешанный (коэффициент
парной корреляции), поэтому существует альтернативная форма разложения
коэффициента множественной детерминации с учетом системного эффекта (η):
R 2 2j
30.
10. Обобщенная линейная модель. ОМНКОбобщенная линейная модель. Предпосылки 1,2,6 остаются неизменными, азаменяется на
3,4. M ( ) 2 En
3,4. M ( )
Ковариационная матрица оценок параметров оказывается неприемлемой в
условиях ОЛММР:
1
1
b ( X X ) X X ( X X )
Теорема Айткена
В классе линейных несмещенных оценок вектора β для обобщенной регрессионной
модели оценка
*
1
1
1
b ( X X ) X Y
Имеет наименьшую ковариационную матрицу
b*
В случае классической модели оценка b* ОМНК совпадает с оценкой b МНК,
поскольку
2
n
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
Отсутствие гетероскедастичность остатков (гомоскедастичность остатков, т.е.
постоянство дисперсий остатков , для любого i, i=1,…,n) – важное условие (3
предпосылка), которое должно выполняться при проведении регрессионного
анализа.
Чтобы выявить гетероскедастичность остатков выборочной регрессиииспользуют метод проверки статистических гипотез.
В качестве нулевой гипотезы предполагают отсутствие гетероскедастичности в
генеральной совокупности, т.е.:
Н0: 2 2
i
2
2
НА: i
Для проверки данной гипотезы можно использовать разные тесты: Уайта,
Глейзера, Спирмена, Голдфелда-Квандта и др.
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
Тест ранговой корреляции Спирмена
предполагает, что остаточная дисперсия в генеральной совокупности – это
некоторая функция от независимой переменной:
2 f ( x )
еi – оценки σi, поэтому в случае гетероскедастичности абсолютные величины
остатков (еi) и значения регрессоров xi будут коррелированы.
Для нахождения коэффициента ранговой корреляции ρx,e следует ранжировать
наблюдения по значениям переменной xi и остатков еi и вычислить
коэффициент корреляции:
x ,e
6 d i2
1 3
,
n n
где di – разность между рангами xi и остатков еi.
Коэффициент ранговой корреляции значим на уровне α при n>10, если статистика
t
x ,e n 2
1
2
x ,e
t ;n 2
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
Тест Голдфелда-Квандта
1. Исходные данные сортируются по величине независимой переменной
(нужно выделить весь диапазон значений зависимой и независимой
переменной и произвести сортировку по убыванию х):
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
2) Далее следует построить уравнение парной линейной регрессии у по х с использованием
инструмента «Регрессия», при этом нужно предусмотреть вывод остатков и построение
графика зависимости остатков от величины независимой переменной:
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
3) Раздели совокупность на три равные части и по первым m наблюдениям и последним
m наблюдениям определим суммы квадратов остатков: m=n/3=12/3=4
m
2
ei
i 1
n
2
ei
n m 1
4) Рассчитаем фактическое значение критерия Фишера:
m
F
2
ei
i 1
n
2
ei
335.
83.29
101.9
n m 1
Определим его критическое значение , где р число параметров уравнения регрессии (для парной
линейной регрессии р=2). Найдем критическое значение с помощь встроенной функции
«FРАСПОБР()», в наем случае выполнение «FРАСПОБР(0,05;2;2)» дало значение 19,00.
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
5) Альтернативная гипотеза о наличии гетероскедастичности будет принята, если:
m
F
2
ei
i 1
n
2
ei
F ; n p ; n p
n m 1
В нашем случае фактическое значение критерия Фишера (3,29) не превысило его
критическое значение (19,00), таким образом, принимаем нулевую гипотезу о
гомоскедастичности остатков уравнения парной линейной регрессии в генеральной
совокупности. Следовательно, выполняется третья предпосылка регрессионного анализа
и параметры уравнения могут быть оценены с помощь обычного метода наименьших
квадратов.
11. Гетероскедастичность. Тесты на гетероскедастичность.
ВМНКТест Глейзера
Тест Глейзера оценивает зависимость абсолютных значений остатков от
значений фактора х в виде функции:
e a bx
c
, где с задается определенным числом степени. Обычно используются значения
с, равные 1; 0,5; -1; -0,5.
Гипотеза о присутствии гетероскедастичности принимается в случае значимых
значений b. Для аппроксимации гетероскедастичности выбирается
функция с максимальным значением tb
11. Гетероскедастичность. Тесты на гетероскедастичность. ВМНК
Тест Уайта
Тест Уайта предполагает, что дисперсия ошибок регрессии представляет
собой квадратичную функцию от значений факторов. Тест Уайта для
уравнения с двумя объясняющими переменными предполагает нахождение
функции:
e 2 a b1 x1 b2 x2 b11 x12 b22 x22 b12 x1 x2 u
Гипотеза о присутствии гетероскедастичности принимается в случае
значимости уравнения по критерию Фишера.
42. 12. Отбор наиболее существенных объясняющих переменных в модель множественной регрессии
2min
R
R
2
н(k )
2k (n k 1)
2
2
(
1
R
(k ) )
2
(n 1)(n 1)
Rн2 (k )
2
Rmin
(k )
K
1
2
3 …
K0
p
43.
13. Уравнение регрессии с фиктивными переменными. Критерий Чоуy i 0 1 xi1 … p xip 1 z i1 … i z if 1 i ,где i=1…n, p – число факторных количественных переменных, f-число факторных
качественных или категориальных переменных (число фиктивных переменных
должно быть на единицу, чем число факторов)
y i 0 1 xi1 1 z i1 i ,
1, если домохозяйство расположено в городской местности
где zi1=
0, если домохозяйство расположено в сельской местности
Модель регрессии с фиктивными переменными для совокупности предприятий, по
которой проведена типизация (выделены три группы):
y i 0 1 xi1 1 z i1 2 z i 2 i ,
1, если хозяйство принадлежит первой типической группе
где zi1=
0, если хозяйство входит в другие группы
если хозяйство принадлежит второй типической группе
где zi1=
0, если хозяйство входит в другие группы
44. 13. Уравнение регрессии с фиктивными переменными. Критерий Чоу
Data from the 2000 Census, US45. 13. Уравнение регрессии с фиктивными переменными.
Критерий Чоу46. 13. Уравнение регрессии с фиктивными переменными. Критерий Чоу
H 0 : ; D( ) D( ) 2n
n 2 n1 2
2
ei ei ei n 2 p 2
i 1
i 1
i n1 1
F
F ; p 1;n 2 p 2
n1
n
2
2
e
e
i p 1
i
i n1 1
i 1
.
где р – число параметров без свободного члена,
n
2
ei
i 1
n1
e ,
i 1
2
i
— остаточная сумма квадратов при построении модели по всей совокупности,
n
2
e
i
i n1 1
— остаточные суммы квадратов для первой и второй группы.
47. 13. Уравнение регрессии с фиктивными переменными. Критерий Чоу
y b0 b1 x b2 z e.
где y — средний балл по итогам контрольной недели, х — удельный вес пропущенных
занятий
1, если студент обучается по специальности «Финансы и кредит»
где z=
0, если студент обучается по специальности «Прикладная
информатика»
~
У 4,385 0,042 х 0,317 z
( 0 , 00 )
( 0 , 00 )
Тест Чоу:
y=4,573-0,0438x – общая модель
y=4,78-0,0476x – «Финансы и кредит»
y=4,339-0,04x – «Прикладная информатика»
Fфакт=
4,15
Fкрит=
3,18
( 0 , 01)
48.
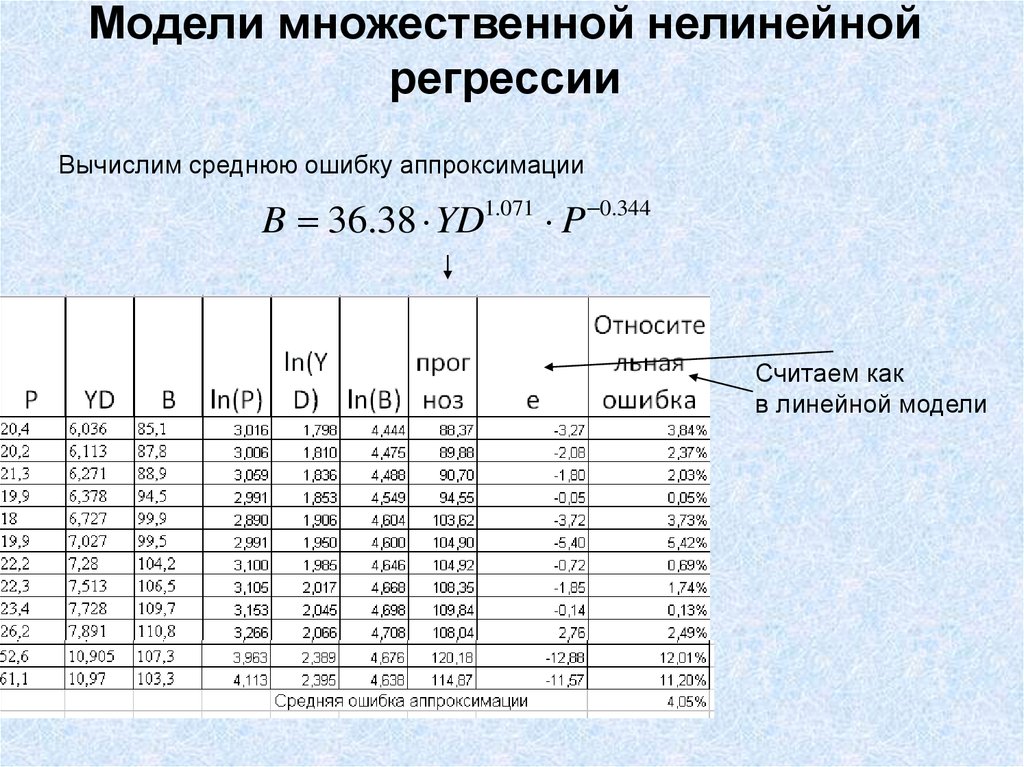14. Нелинейные модели множественной регрессии. Производственные функцииQ AK L1 Если объем производства Q будет постоянным, то дифференциал этой
функции будет равен нулю:
dQ 0 или
Q
Q
K
L 0, тогда
K
L
Q Q
K L
:
или
K L
1 K
K
L
L
49. 14. Нелинейные модели множественной регрессии. Производственные функции
Q AK L1В относительных величинах мы имеем отношение соответствующих
эластичностей:
K
1 L
K
L
— для компенсации измененияресурса труда на 1% следует изменить
ресурс капитала на –(1-α)/α процентов.
Предельная норма замены трудовых ресурсов капиталом равна:
dK
1 K
dL
L
50. 15. Вопросы для повторения и самостоятельного изучения
регрессии1. Классическая
линейная модель множественной
2.
3.
Представление и отыскание параметров модели множественной регрессии в
матричной форме
Ковариационная матрица дисперсий вектора оценок коэффициентов регрессии
, ее использование
b
4.
Свойства оценок выборочных коэффициентов регрессии, полученных методом
наименьших квадратов. Теорема Гаусса-Маркова
( X X5.) 1 Обратная матрица
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
и ее использование во множественном
регрессионном анализе
Оценка значимости множественной регрессии
Ошибки коэффициентов регрессии и прогноза в матричной форме
Ковариационная матрица вектора возмущений. Шестая предпосылка
множественного регрессионного анализа в матричной форме
Понятие мультиколлинеарности факторов. Диагностика и способы устранения
Ридж-регрессия
Факторный анализ. Построение модели регрессии на главных компонентах
Коэффициент частной корреляции: понятие и способы расчета
Стандартизованные коэффициенты регрессии, коэффициенты раздельной
детерминации
Понятие о гомо- и гетероскедастичности остатков. Последствия и подходы к
выявлению гетероскедастичнсоти остатков
Тест Гольдфельда-Квандта
Тест Спирмена
Тест Бреуша-Пагана
Тест Уайта
Тест Глейзера
Тест Парка
Обобщенная линейная модель множественной линейной регрессии
Обобщенный метод наименьших квадратов
Взвешенный метод наименьших квадратов
Отбор факторов в модель регрессии.
Пошаговые процедуры отбораЧастные уравнения регрессии, частные коэффициенты эластичности
Нелинейные модели множественной регрессии. Производственная функция
Кобба-Дугласа, замена факторов
Как выполнить множественную линейную регрессию в Excel
Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более независимыми переменными и переменной отклика .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в Excel.
Примечание. Если у вас есть только одна независимая переменная, вам следует вместо этого выполнить простую линейную регрессию .
Пример: множественная линейная регрессия в ExcelПредположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве объясняющих переменных, и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести множественную линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные для количества часов обучения, сданных подготовительных экзаменов и результатов экзаменов, полученных для 20 студентов:
Шаг 2: Выполните множественную линейную регрессию.
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для двух независимых переменных. Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны. В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии. Затем нажмите ОК .
Автоматически появится следующий вывод:
Шаг 3: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Стандартная ошибка: 5,366.
Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой.
Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку сданные подготовительные экзамены не являются статистически значимыми, мы можем принять решение удалить их из модели.
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной. Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Вот еще один способ подумать об этом: если учащийся А и учащийся Б сдают одинаковое количество подготовительных экзаменов, но учащийся А учится на один час больше, то ожидается, что учащийся А получит результат на 5,56 балла выше, чем учащийся Б.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:
экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает. Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель.
В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
С результатами этого простого линейного регрессионного анализа можно ознакомиться здесь .
Дополнительные ресурсыПосле выполнения множественной линейной регрессии есть несколько предположений, которые вы можете проверить, в том числе:
1. Тестирование на мультиколлинеарность с помощью VIF .
2. Тестирование на гетеродескедастичность с помощью теста Бреуша-Пагана .
3. Проверка нормальности с использованием графика QQ .
|
Множественная регрессия
Что такое множественная регрессия? Множественная регрессияМножественная регрессия Множественная регрессия является расширением. Какие приложения? Множественная регрессия помогает в широком диапазоне. В статистике диапазон набора данных – это разница между… Подробнее… полями. Специалисты по кадрам могут собирать данные о заработной плате сотрудника на основе таких факторов, как опыт работы и компетентность. Ваши данные могут быть использованы для построения модели и определения заработной платы сотрудников. Когда использовать линейную модель множественной регрессии Множественная регрессия относится к изучению более чем одной переменной. Основное различие между многочисленной регрессией и простой регрессией. Простая регрессия методом наименьших квадратов. Множественная регрессия отличается от простой линейной, поскольку существует бесчисленное множество независимых переменных (X), но эти независимые переменные используются для прогнозирования одной зависимой переменной (Y). Изменения в независимых переменных указывают на эволюцию зависимой переменной (Y). Как Шесть Сигм Шесть Сигм Определение: Шесть Сигм — это набор методов и т… Подробнее… Практики справляются с ситуациями, когда более одного X влияют на Y? Они используют множественную линейную регрессию, потому что она более распространена, чем одна воздействующая переменная. Вы можете создавать уравнения, включающие более одной переменной, например Y = (X1, X2) , Xn ). Множественная линейная регрессияМножественная регрессияМножественная регрессия является расширением модели… Подробнее… можно описать как расширение простой линейной модели. Например, если X1 и X2 вносят вклад в одно и то же значение Y, то можно использовать несколько линейных моделей. Yi = b0 + B1X1 +B11X12 +B2X2 +B22X22 +B12X1X2+e Уравнение включает пять типов членов:
Линия множественной регрессии. Уравнения. Они также могут вмещать трехмерные поверхности и абстрактные отношения вn -мерные пространства. Использование калькулятора уравнений множественной регрессии может быть пугающим. Линия множественной регрессии может обрабатывать практически все, они выполняются так же, как простая линейная регрессия, простая регрессия, метод наименьших квадратов. Крайне важно убедиться, что остаточные значения. «График невязок и совпадений» будет наиболее часто создаваться… Подробнее… не являются аномальными. Исходные предположения модели множественной линейной регрессии недействительны, если дисперсия остатков не равна нулю или если она не является случайной и нормальной.  Члены более высокого порядка обычно идут первыми. Менее вероятно, что квадрат или член взаимодействия будут статистически значимыми. Чтобы количественно оценить количество наблюдаемых отклонений в уравнении, используйте метрику R HTML2. Что такое скорректированный коэффициент R в квадрате?Скорректированный квадрат R измеряет объяснительную способность моделей регрессии с различным количеством предикторов. Допустим, вы хотите сравнить модель прогнозирования с пятью предикторами с более высоким R в квадрате с моделью с одним предиктором. Является ли R-квадрат выше для моделей с пятью предикторами, потому что они лучше? Является ли R в квадрате выше просто потому, что предикторов больше? Чтобы узнать это, просто сравните скорректированные значения R в квадрате! Скорректированный квадрат R — это модифицированный квадрат R, который был скорректирован с учетом количества предикторов в модели. Ниже приведен упрощенный результат регрессии наилучших подмножеств. Вы можете видеть пик и снижение в скорректированном квадрате R. Тем не менее, R в квадрате увеличивается. линейная регрессия с rЭта модель может включать только три предиктора. В моем предыдущем блоге мы видели, как плохо специфицированная модель может привести к необъективным оценкам. Слишком упрощенная модель (со слишком большим количеством переменных) приведет к снижению точности. Точность означает соответствие между измеренными количественными… Подробнее… оценками и прогнозами. Поэтому не включайте термины, которые не нужны в вашей модели. Что такое предсказанный R-квадрат? Прогнозируемый квадрат R является мерой того, насколько точно регрессионная модель предсказывает новые наблюдения. Мини-вкладка вычисляет предсказанный квадрат R путем вычитания каждого наблюдения из данных, затем оценивает уравнение регрессии и определяет, насколько хорошо оно предсказывает отсутствующее наблюдение. Прогнозируемый R-квадрат подобен скорректированному R-квадрату и может быть отрицательным. Он всегда меньше, чем R в квадрате. Даже если модель не используется для прогнозов, предсказанный R-квадрат по-прежнему дает важную информацию. Его ключевое преимущество заключается в том, что он предотвращает переобучение моделей. Переоснащение модели слишком большим количеством предикторов может привести к моделированию случайного шума. Невозможно предсказать случайный шум, поэтому R-квадрат для модели с переобучением должен уменьшаться. Прогнозируемый R в квадрате ниже, чем обычный R в квадрате, почти всегда является признаком того, что в вашей модели слишком много терминов. Множественная линейная регрессия в ExcelВ этом руководстве от Statology объясняется, как выполнить множественную линейную регрессию в Excel. Примечание. Если у вас есть только одна независимая переменная, вам следует вместо этого выполнить простую линейную регрессию в Excel. Шаг 1: Введите данные. линейная регрессия с rШаг 2: Выполните множественную линейную регрессию. Наряду с верхней лентой в Excel перейдите на вкладку Данные и нажмите Анализ данных . Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа. линейная регрессия в ExcelКак только вы нажмете Анализ данных, откроется новое окно. Выберите Регрессия и нажмите ОК. линейная регрессия с r Для Input Y Range заполните массив значений для переменной ответа. Автоматически появятся следующие выходные данные: линейная регрессия в ExcelШаг 3: интерпретируйте выходные данные. Онлайн-калькуляторы множественной регрессииКалькулятор уравнений множественной регрессииСтатистика социальных наук: Этот простой калькулятор линий множественной регрессии использует метод наименьших квадратов, чтобы найти линию наилучшего соответствия для данных, содержащих два независимых значения X и одно зависимое Y значение, позволяющее оценить значение зависимой переменной ( Y ) от двух заданных независимых (или объясняющих) переменных ( X 1 и X 2 ). Королевство статистики: Этот калькулятор множественной регрессии использует преобразование переменных и вычисляет R, линейное уравнение и p-значение. Он также вычисляет выбросы и скорректированный коэффициент Фишера-Пирсона для асимметрии. Программа интерпретирует результаты после подтверждения нормальности остатков и мультиколлинеарности. Затем он рисует гистограмму и графики остатков QQ, корреляциюКорреляция — это статистическая мера, описывающая матрицу стресса, а также график распределения. Вы можете преобразовать переменные, исключить любой предиктор или выполнить пошаговый переход назад и выбрать автоматически на основе предсказанного значения p предиктора. Stats Solver: Stats Solver — это калькулятор уравнений множественной регрессии, цель которого — быстро и легко решить любую статистическую задачу. Используйте наш интуитивно понятный интерфейс, чтобы ввести свою проблему и получить пошаговое решение. Даже если вам не нужно решать проблему, вы все равно можете учиться на других примерах. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Некоммерческое (академическое) использование этого программного обеспечения бесплатно. Единственное, что просят взамен — цитировать этот софт при использовании результатов в публикациях.
png»)
plot(kp3:nmkm3,gqarr[2], main=»критерий Гольдфельда-Квандта»,ylab=»двухстороннее p-значение»,xlab=»точка останова»)
сетка()
dev.off()
}
загрузить (файл = «создать таблицу»)
a 0) myeq H0: параметр = 0″, заголовок = ИСТИНА)
прогноз», 1, ИСТИНА)
«Ошибка предсказания», 1, ИСТИНА)
а п25) {
a»,RC.texteval(«reset_test_fitted»),»»,sep=»»))
a»,RC.texteval(«reset_test_regressors»),»»,sep=»»))
a»,RC.texteval(«reset_test_principal_components»),»»,sep=»»))
a»,RC.texteval(«vif»),»»,sep=»»))
wessa.net/rwasp_multipleregression.wasp/
(2023), Free Statistics Software, Office for Research Development and Education, 
Net 2002-2023 
.. Подробнее… является расширением простого линейного уравнения. Простой линейный анализ заключается в изучении двух переменных, где одна переменная является независимой переменной (X), а другая — зависимой переменной. Он служит для прогнозирования изменения зависимой переменной на основе разницы в независимой переменной; это также можно назвать линией множественной регрессииМножественная регрессияМножественная регрессия является расширением… Подробнее…. Подробнее… с r в Excel, а также 3 уравнения множественной регрессииВ статистическом моделировании уравнение регрессии используется для оценки… Подробнее… веб-страниц калькулятора, которые помогут вам быстро их создать.
Это больше для определенных групп сотрудников, чем норма? Есть ли сотрудники или группы, которым платят меньше нормы? 
.. Подробнее… с центром в нуле.
Скорректированный квадрат R увеличится, если новый член сделает модель лучше, чем ожидалось. Он падает, если предиктор делает модель более точной, чем это было бы случайно. Хотя скорректированный R-квадрат может быть вредным, обычно это не так. Он всегда меньше, чем R в квадрате.
Эту статистическую выборку статистики и выборку параметра совокупности для… Подробнее… можно использовать, чтобы определить, способна ли модель предсказывать новые наблюдения, но не исходные данные.
Для Input X Range заполните массив значений для двух независимых переменных. Установите флажок рядом с Ярлыки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны. Для Диапазон вывода выберите ячейку, в которой должны отображаться результаты регрессии. Затем нажмите OK .
