Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Определение 1Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R→=F1→+F2→+F3→+…+Fn→=∑i=1nFi→.
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Определение 2Для сложения 2-х сил используют правило параллелограмма (рисунок 1).
Рисунок 1. Сложение 2-х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R→=F1→2+F2→2+2F1→2F2→2cos α
Определение 3При необходимости сложения более 2-х сил используют правило многоугольника
1-й силы необходимо провести вектор, равный и параллельный 2-й силе; от конца 2-й силы необходимо провести вектор, равный и параллельный 3-й силе и т.
 д.
д.Рисунок 2. Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4-х сил: F1→, F2→, F3→, F4→. Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Определение 4Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3. Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0: ∑i=1nFi→=0→. В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0: ∑i=1nFi→=0→. В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Определение 5Разложение сил на две составляющие – это замена одной силы 2-мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2-х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2-х составляющих сил.
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b. Отрезок FA и отрезок FB изображают искомые силы.
Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b. Отрезок FA и отрезок FB изображают искомые силы.
Рисунок 4. Разложение вектора силы по направлениям
Пример 2Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2-й проекции (рисунок 5 а ).
Рисунок 5. Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F2→ силы F→.
Итак, 2-й способ решения: прибавим к силе силу, равную -F1→ (рисунок 5 в). В итоге получаем искомую силу F→.
Пример 3Три силы F1→=1 Н; F2→=2 Н; F3→= 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а) и составляют углы с горизонталью α=0°; β=60°; γ=30° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6.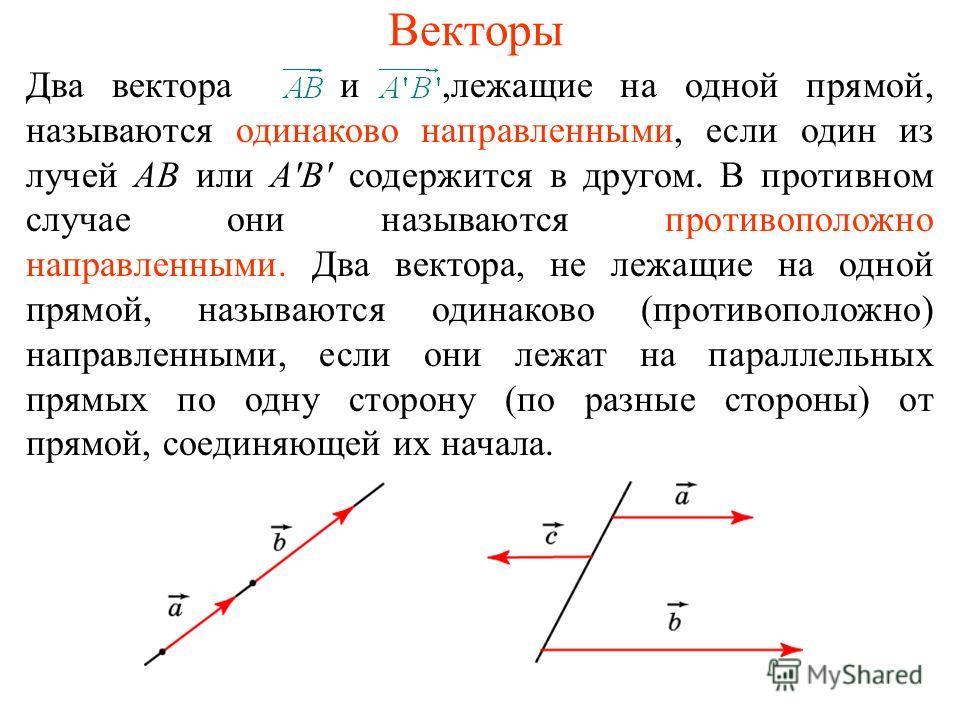 Нахождение равнодействующей силы по заданным векторам
Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси ОХ и OY таким образом, чтобы ось ОХ совпадала с горизонталью, вдоль которой направлена сила F1→. Сделаем проекцию данных сил на координатные оси (рисунок 6 б). Проекции F2y и F2x отрицательны. Сумма проекций сил на координатную ось ОХ равняется проекции на данную ось равнодействующей: F1+F2cosβ-F3cosγ=Fx=4-332≈-0,6 Н.
Точно также для проекций на ось OY: -F2sin β+F3sin γ=Fy=3-232≈-0,2 Н.
Модуль равнодействующей определим с помощью теоремы Пифагора:
F=Fx2+Fy2=0,36+0,04≈0,64 Н.
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в):
tg φ=FyFx=3-234-33≈0,4.
Пример 4Сила F=1 кН приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7.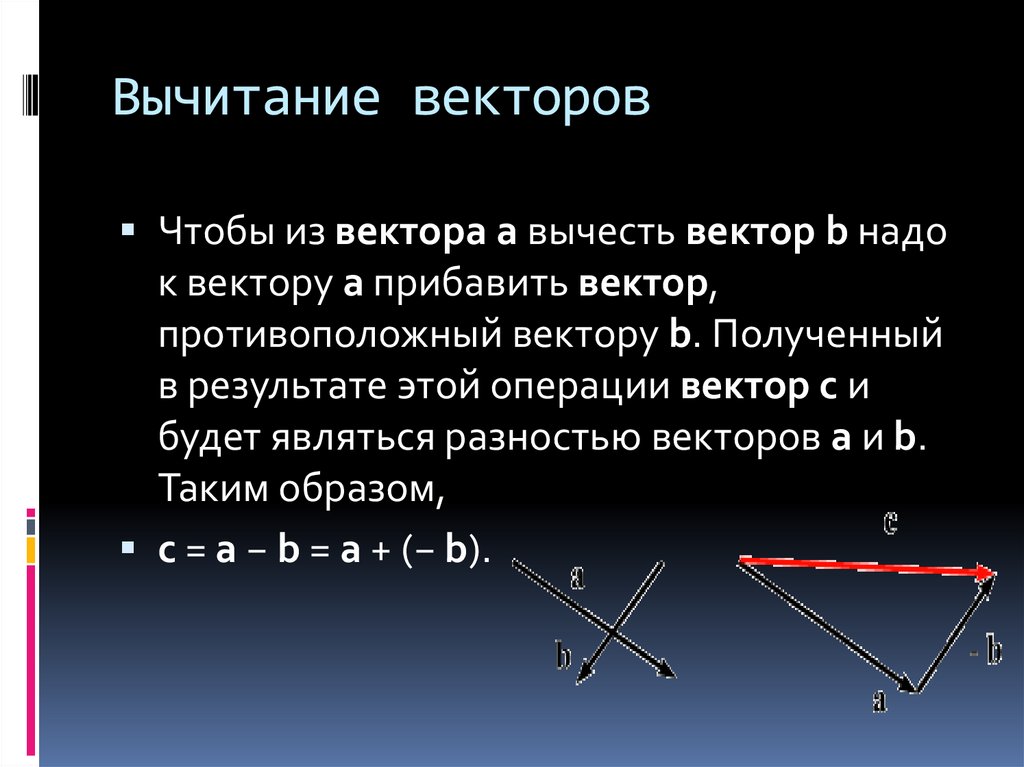 Нахождение составляющих силы F по направлениям стержней кронштейна
Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F=1 кН=1000 Н
Пускай стержни прикручены к стене в точках А и С. На рисунке 7 б изображено разложение силы F→ на составляющие вдоль направлений АВ и ВС. Отсюда понятно, что
F1→=Ftg β≈577 Н;
F2→=Fcos β≈1155 Н.
Ответ: F1→=557 Н; F2→=1155 Н.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Роман Адамчук
Преподаватель физики
Урок 3. Сложение и вычитание векторов
Первой операцией
над векторами является сложение векторов.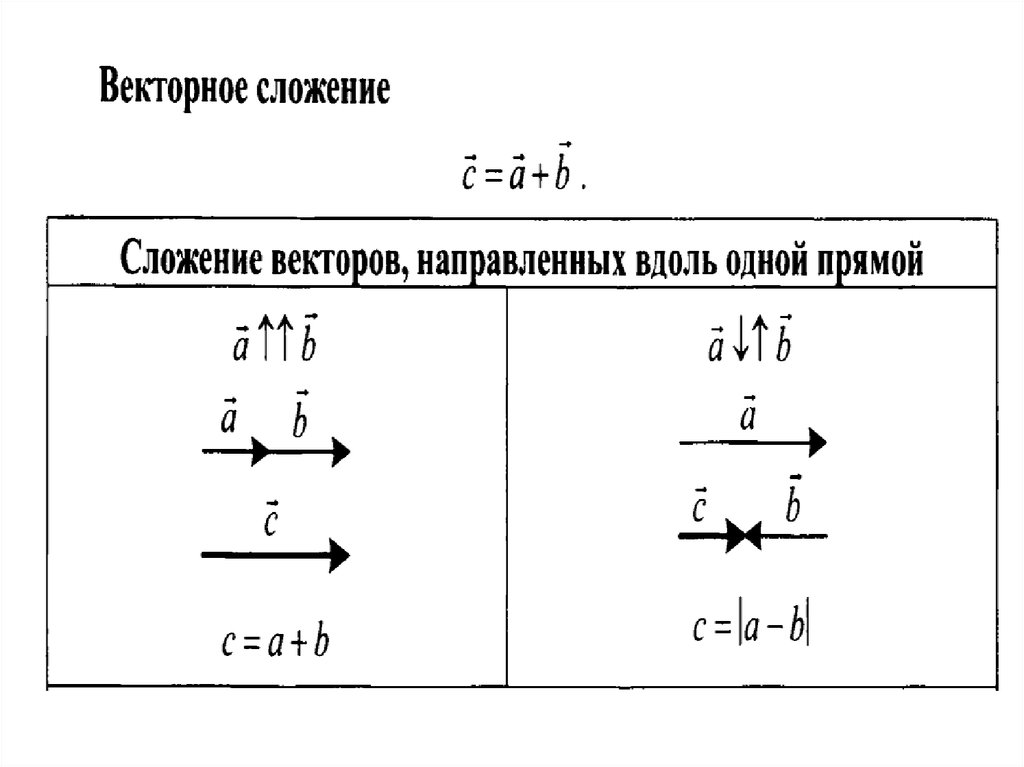
Если материальная точка переместилась из точки А в точку В, а потом из точки В в точку С, то в результате она перейдёт из точки А в точку С.
Поэтому говорят, что направленные отрезки
характеризующие эти перемещения, складываясь, дают направленный отрезок
Это записывают так:
В этом случае видно, что процесс сложения векторов происходит так:
конец первого вектора
является началом второго
а суммарный вектор
соединяет начало первого вектора и конец второго.
Правило треугольника.
Чтобы найти сумму двух векторов
нужно:
– отложить вектор
равный от произвольной точки С;
– отложить вектор
равный b, от точки D;
– построить вектор
который соединяет начало
первого слагаемого с концом второго;
– вектор
является суммой векторов ПРИМЕР:
На рисунке изображены:
ПРИМЕР:
На рисунке
изображены:
ПРИМЕР:
Пусть, двигаясь
горизонтально со скоростью 3 м/сек, кран поднимает ящик со скоростью 1 м/сек.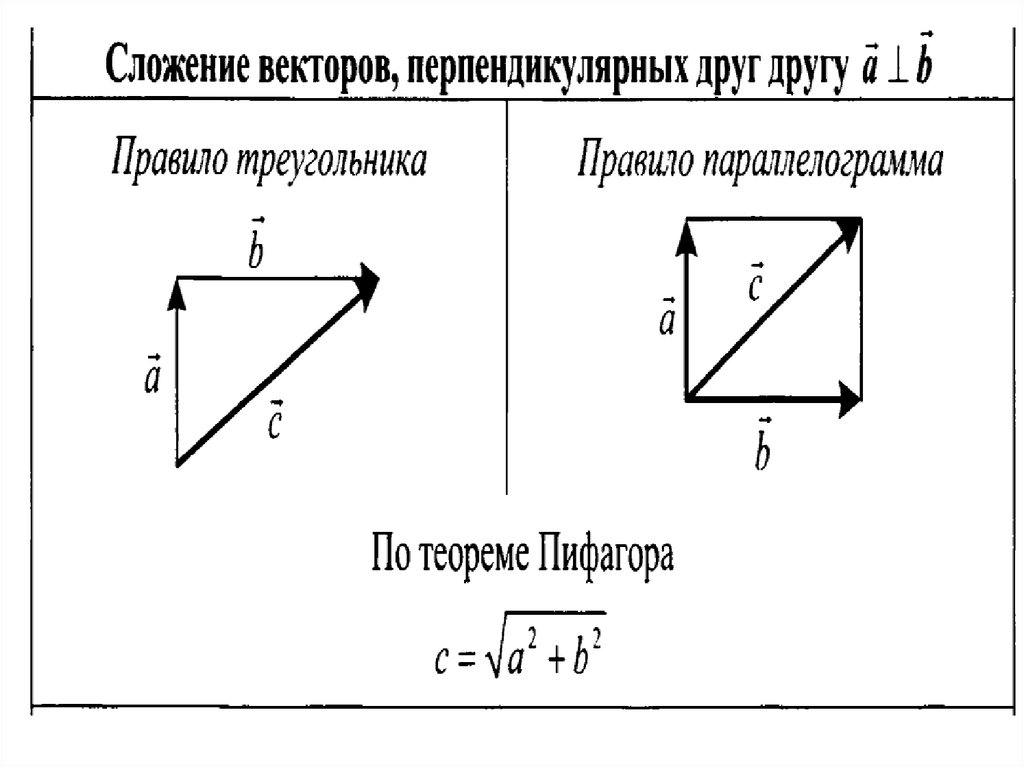 На рисунке изображены в масштабе
скорость ящика относительно крананаправленная вертикально
вверх, и скорость движения крананаправление которой совпадает с направлением движения
крана.
На рисунке изображены в масштабе
скорость ящика относительно крананаправленная вертикально
вверх, и скорость движения крананаправление которой совпадает с направлением движения
крана.
Сумма векторов– векторкоторый изображает скорость ящика относительно неподвижной системы отсчёта:
Чтобы сложить эти векторы, нужно:
1. Выбрать исходную точку А
2. От точки А отложить вектор3. От точки В отложить вектор4. Построить векторПравило параллелограмма для сложения неколлинеарных векторов.
ПРИМЕР:
Пусть нам даны векторыкоторые неколлинеарны, то есть не лежат на одной прямой.
Отложим эти векторы от
некоторой точки А, то естьТогда суммарный вектор
изобразится диагональю параллелограмма АВСD, построенного на
векторахМы получили второе
правило сложения векторов – правило
параллелограмма.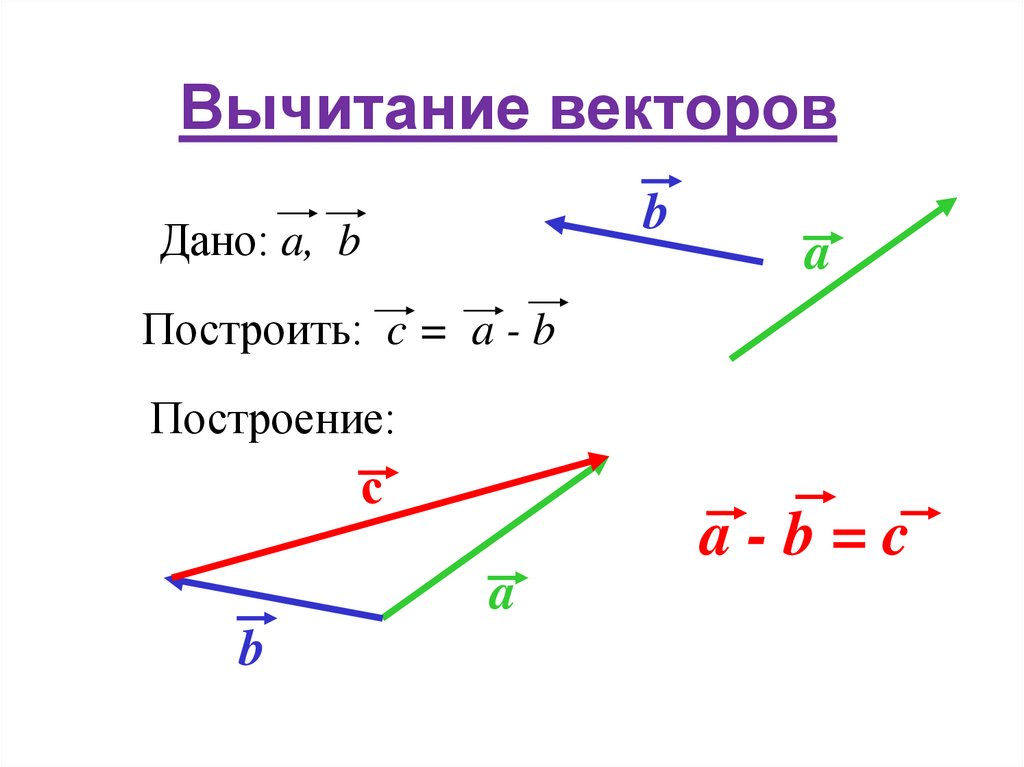
Если векторы неколлинеарные, то их сумма представляется диагональю построенного на них параллелограмма.
Чтобы найти сумму двух неколлинеарных векторов
нужно:
– отложить от произвольной точки О векторы – использовать эти векторы как стороны параллелограмма;– построить вектор
– диагональ параллелограмма, соединяющую вершины О и С: искомый вектор – сумма векторов Для любого вектора
верно равенство
Законы сложения векторов.
Переместительный закон:
Сочетательный закон:
Эти равенства справедливы для любых векторов
Правило многоугольника.
Для того, чтобы сложить любое количество векторов, надо последовательно откладывать эти векторы таким образом, чтобы каждый следующий вектор начинался от конца предыдущего. Тогда суммой всех данных векторов будет вектор, который начинается от начала первого вектора и соединяет его с концом последнего. Порядок сложения значения не имеет.
ПРИМЕР:
Чтобы сложить несколько векторов, например векторыудобно построить векторную ломаную.
Эта ломаная состоит из направленных отрезковВекторсоединяющий начало ломаной ABCD и её конец, и является суммойЕсли ломаная получилась замкнутой, то сумма векторов равна нуль-вектору,
то естьДля любого векторавыполняется равенствоПРИМЕР:
На рисунке
изображена сумма
Можно складывать в другом порядке:
Результат при этом будет тот же.
Нахождение суммы векторов с помощью координат.
При сложении векторов их соответствующие координаты складываются. А именно, если
то есть
ПРИМЕР:
Найти сумму векторов:
РЕШЕНИЕ:Разложение вектора на составляющие.
При изучении и использовании векторов часто приходится говорить о так называемом разложении вектора на составляющие.
Составляющими данного вектора называют такие векторы, сумма которых равна этому вектору.
Данный вектор <<составляется>> из составляющих как сумма слагаемых и разлагается на них как на слагаемые, поэтому говорят о разложении на составляющие.
Пусть
в плоскости α даны две прямые а и b,
пересекающиеся в точке О. Возьмём какой-нибудь вектор
Возьмём какой-нибудь вектор
и отложим его от точки О.
Если точка V не лежит ни на прямой а, ни на прямой b, то проведём через точку V прямые
и построим параллелограмм OAVB. Его диагональю будет отрезок OV, а его стороны ОА и ОВ лежат соответственно на прямых а и b. По правилу параллелограмма для сложения векторов получим
Векторы
являются составляющими вектора
по прямым а и b,
Если V ∈ a, то
а составляющая по b нулевая:
Аналогично в случае, когда
Мы
выполнили разложение вектора по двум пересекающимся прямым.
Можно разложить вектор по двум неколлинеарным векторам.
Возьмём два неколлинеарных вектора
Отложим их от точки О.
Пусть
– вектор параллельный плоскости ОВС. Отложим его от точки О.
Через точку А проведём прямые, параллельные векторам
Тогда
Векторы
коллинеарны.
Значит,
и поэтому
Такое представление вектора
через векторы
называют разложение вектора по неколлинеарным векторам.
Разность векторов.
Введём операцию разности двух векторов. Эта операция вводится так же как и
для чисел.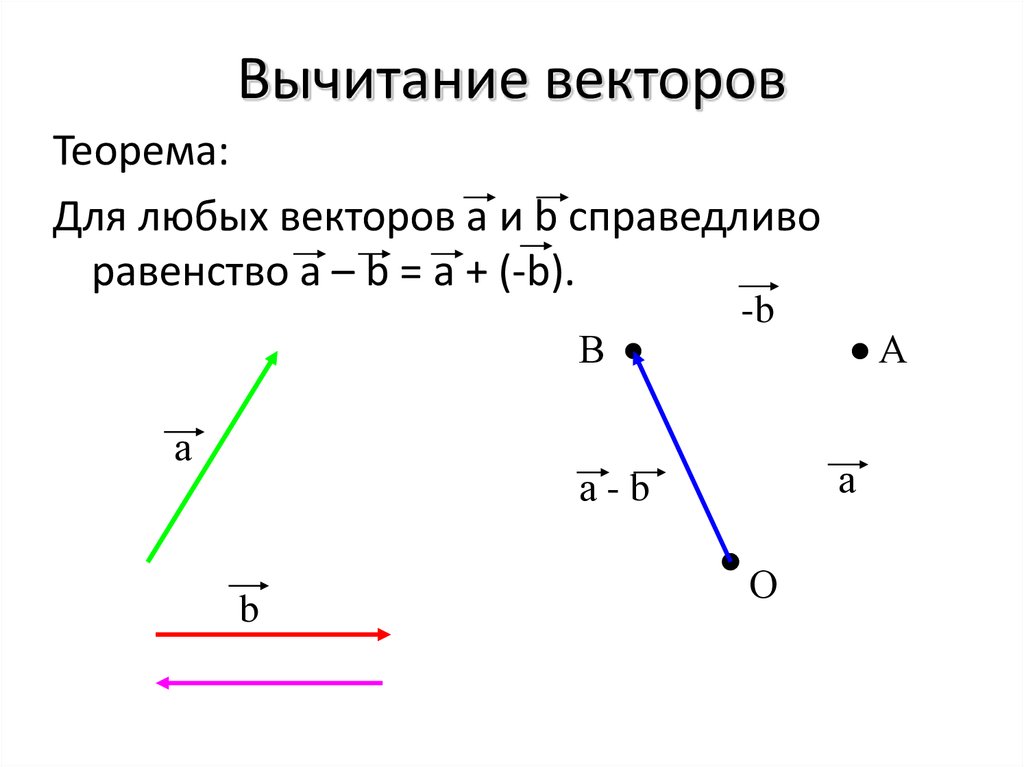
Разностью векторовназывают такой векторкоторый в сумме с вычитаемым векторомдаёт векторРазностью векторов
будет вектор
то есть вектор, который соединяет концы векторов
и направлен от вычитаемого к уменьшаемому.
ПРИМЕР:
Построим разность двух
векторовОтложим
от какой-нибудь точки О данные векторыРассмотрим векторМы видим, что(правило треугольника).
Векторбудет разностью векторовто естьЕсли
векторобозначить
черезРавенство
можно назвать правилом нахождения разности двух векторов.
Противоположные векторы – векторы, имеющие одинаковые
длины и противоположно направленные.
На рисунке
изображены два противоположных друг другу вектора.
Записывают их так:
Причём, если сложить противоположные векторы (по правилу треугольника), то в сумме получится нуль-вектор, то есть:
Верно и обратное утверждение: если сумма двух векторов равна нуль-вектору, то они противоположны.
Если
Нуль-вектор считается противоположным самому себе.
Определение разности векторов с помощью координат.
Координаты разности двух векторов равняются разности соответствующих координат вектора – уменьшаемого и вектора – вычитаемого.
Теорема о разности векторов.
Равенство
справедливо для любых векторов
Правила вычитания векторов.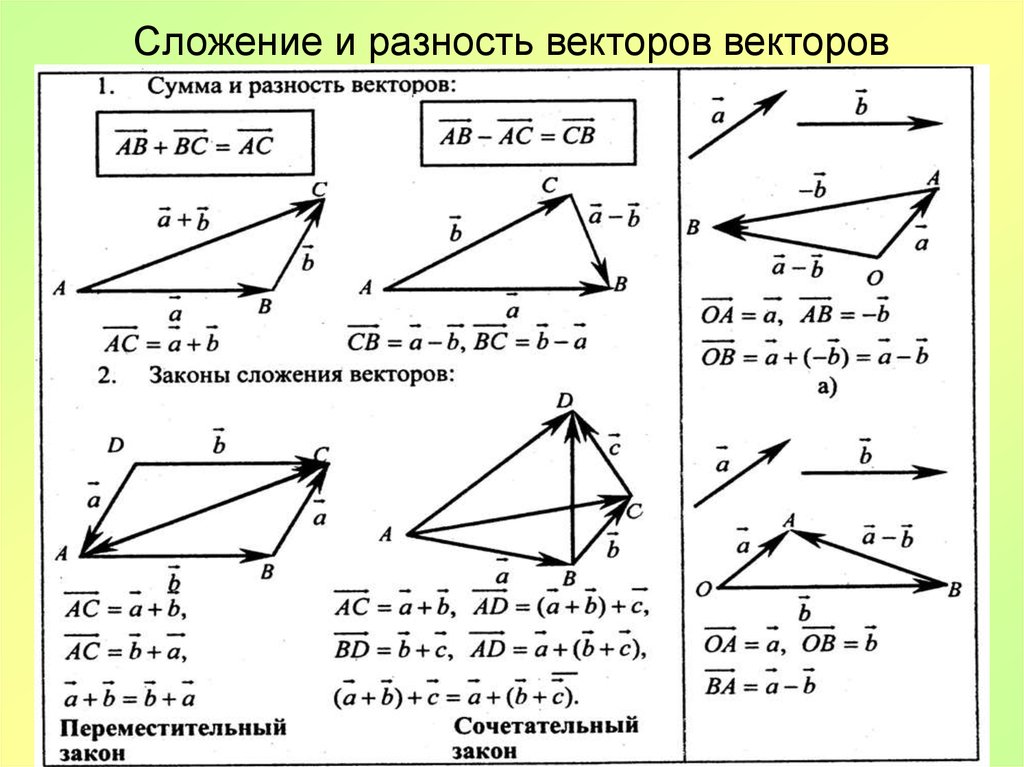
ПЕРВЫЙ СПОСОБ
Для того чтобы вычесть из одного вектора другой, надо к первому вектору прибавить вектор, противоположный второму.
ПРИМЕР:ВТОРОЙ СПОСОБ
Для того чтобы вычесть из одного вектора другой, надо из произвольной точки плоскости отложить оба вектора, затем построить вектор, который начинается на конце второго вектора (вычитаемого), а заканчивается на конце первого вектора (уменьшаемого).
ПРИМЕР:
ПРИМЕР:
Пусть даны векторы
Построить векторРЕШЕНИЕ:
Построим произвольную точку О и отложим от неё векторыСоединив точку В с точкой А, получим векторПо правилу треугольника для построения суммы двух векторов видим, чтото естьтогдаОТВЕТ:ПРИМЕР:
Пусть
Найдите вектор:
РЕШЕНИЕ:ОТВЕТ:Задания к уроку 3
Функция отмывки — ArcMap | Документация
- Обзор
- Параметры
- Узнайте больше о том, как работает отмывка
Обзор
Функция затенения рельефа создает трехмерное изображение поверхности местности в оттенках серого, при этом для затенения изображения учитывается относительное положение солнца.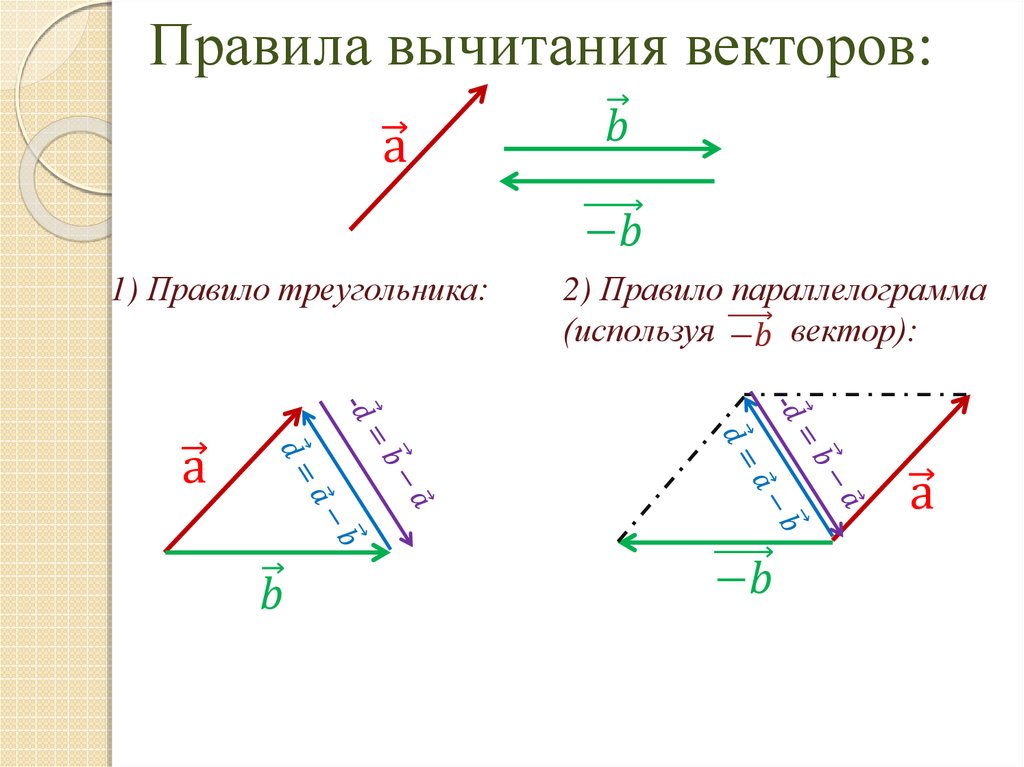 Затенение рельефа — это метод визуализации местности, определяемой источником света, а также наклоном и экспозицией поверхности возвышения. Это качественный метод визуализации топографии, который не дает абсолютных значений высоты. Эта функция предоставляет два варианта создания отмывки: традиционный и разнонаправленный. Традиционный метод вычисляет отмывку холма, используя источник освещения с одного направления, используя свойства высоты и азимута для указания положения солнца. Многонаправленный метод комбинирует свет от нескольких источников для представления заштрихованной местности. Преимущество метода разнонаправленной отмывки заключается в том, что больше деталей отображается в областях, обычно подверженных перенасыщению и глубоким теням, чем при использовании традиционного метода отмывки.
Затенение рельефа — это метод визуализации местности, определяемой источником света, а также наклоном и экспозицией поверхности возвышения. Это качественный метод визуализации топографии, который не дает абсолютных значений высоты. Эта функция предоставляет два варианта создания отмывки: традиционный и разнонаправленный. Традиционный метод вычисляет отмывку холма, используя источник освещения с одного направления, используя свойства высоты и азимута для указания положения солнца. Многонаправленный метод комбинирует свет от нескольких источников для представления заштрихованной местности. Преимущество метода разнонаправленной отмывки заключается в том, что больше деталей отображается в областях, обычно подверженных перенасыщению и глубоким теням, чем при использовании традиционного метода отмывки.
По умолчанию для отображения модели высот с отмывкой отмывки используется цветовая шкала в оттенках серого. На следующих изображениях показана модель высот с использованием традиционного метода отмывки по умолчанию, за которым следует метод многонаправленной отмывки.
Это пример традиционного изображения с отмывкой.
Это пример разнонаправленного изображения с отмывкой отмывки.
Параметры
Функция отмывки имеет следующие параметры:
| Параметр | Описание |
|---|---|
| Растр | Входной набор данных высот. |
| Тип отмывки | Управляет источником освещения для отмывки:
|
| Азимут | Азимут — это относительное положение солнца вдоль горизонта (в градусах). Этот параметр действителен, только если тип отмывки установлен на традиционный. По умолчанию 315 градусов, то есть от северо-запада. |
| Высота над уровнем моря | Высота — это угол возвышения солнца над горизонтом, который находится в диапазоне от 0 до 90 градусов. Значение 0 градусов указывает на то, что солнце находится на горизонте, то есть в той же горизонтальной плоскости, что и система отсчета. Значение 90 градусов указывает на то, что солнце находится прямо над головой. Этот параметр действителен, только если тип отмывки установлен на традиционный. По умолчанию это 45 градусов над горизонтом. |
| Масштаб | заштрихованный результат динамически масштабируется путем регулировки z-фактора с помощью один из двух вариантов:
|
| Z-фактор | z-фактор — это коэффициент масштабирования, используемый для преобразования значений высоты для двух целей:
|
| Размер пикселя Мощность | Размер пикселя Мощность учитывает изменения высоты (или масштаба) при увеличении масштаба изображения. и выйти на отображение карты. Это показатель степени, применяемый к члену размера пикселя в уравнении, который управляет скоростью изменения Z-фактора, чтобы избежать значительной потери рельефа. Этот параметр действителен, только если Тип масштабирования установлен. Значение по умолчанию — 0,664. |
| Коэффициент размера пикселя | Коэффициент размера пикселя учитывает изменения масштаба при увеличении масштаба изображения. и выйти на отображение карты. Он управляет скоростью изменения Z-фактора. Этот параметр действителен, только если Тип масштабирования установлен. |
| Отключить интерполяцию краевых пикселей по умолчанию | Использование этот параметр позволяет избежать любых артефактов передискретизации, которые могут возникнуть по краям растра. Выходные пиксели по краю растровые или рядом с пикселями NoData будут заполнены Нет данных; поэтому рекомендуется использовать этот параметр только с наборами данных мозаики высот, которые имеют перекрытие. Когда доступны перекрывающиеся пиксели, области NoData будут отображать значения перекрывающихся пикселей вместо пустых пикселей.
Результаты функции могут зависеть от данных. Если вы наблюдаете артефакты границ плитки в выходных данных, выберите альтернативное условие флажка. |
Узнайте больше о том, как работает отмывка отмывки
Тип отмывки
Многонаправленная отмывка улучшает визуализацию местности. Он сочетает в себе свет с шести разных направлений, чтобы представить улучшенную визуализацию местности и улучшить внешний вид областей с низким рельефом. Это улучшает баланс между переэкспонированными и теневыми областями карты. Результат подходит для использования в качестве рельефного фона для топографических, почвенных, гидрологических, земельных карт или других тематических карт, в которых данные будут дополнены топографией.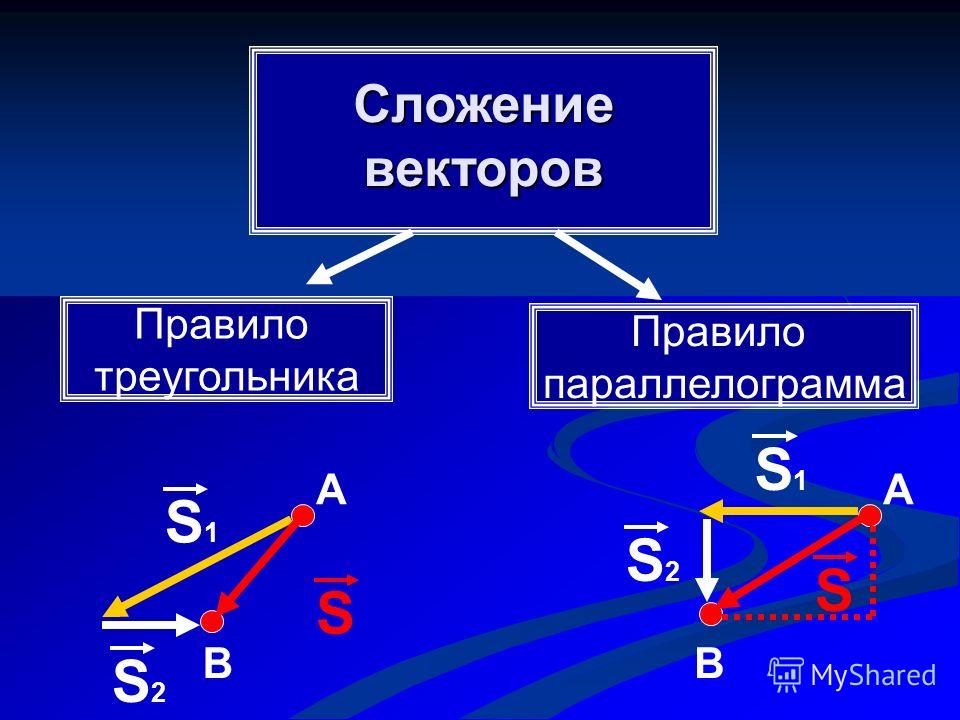
На следующих изображениях показаны два типа отмывки:
- Верхнее изображение показывает традиционный результат отмывки.
- На нижнем изображении показан результат многонаправленного затенения отмывки.
Традиционная отмывка. Исходная ЦМР предоставлена Геологической службой США (USGS).
Разнонаправленная отмывка. Исходная ЦМР предоставлена Геологической службой США (USGS).
Для получения дополнительной информации о разнонаправленной отмывке см. раздел Многонаправленная отмывка делает ваши карты популярными.
Азимут и высота
Свойства высота и азимут вместе указывают относительное положение солнца, которое будет использоваться для создания любой 3D-модели (отмывки или затененного рельефа). Высота — это угол возвышения солнца над горизонтом, который колеблется от 0 до 90 градусов. Значение 0 градусов указывает на то, что солнце находится на горизонте, то есть в той же горизонтальной плоскости, что и система отсчета. Значение 90 градусов указывает на то, что солнце находится прямо над головой.
Значение 90 градусов указывает на то, что солнце находится прямо над головой.
Азимут — это относительное положение солнца вдоль горизонта (в градусах). Это положение обозначается углом солнца, измеренным по часовой стрелке от точного севера. Азимут 0 градусов указывает на север, восток на 90 градусов, юг 180 градусов, запад 270 градусов.
Масштабирование и размер пикселя
Затененный результат динамически масштабируется путем настройки z-фактора с использованием одного из двух параметров:
Наклон — это коэффициент размера пикселя. При больших пикселях наклон
значение становится меньше, так как наклон представляет собой средний наклон по
большее расстояние. В результате на малых масштабах черты кажутся плоскими.
Картографически это приводит к значительной потере рельефа. Чтобы компенсировать это, параметр Z Factor можно изменить в соответствии с
шкала. Зависимость экспоненциальная, а не линейная. Изменение мощности размера пикселя и коэффициента размера пикселя меняет скорость изменения Z-фактора. Это означает, что необходимо установить z-фактор.
соответствующий масштабу.
Это означает, что необходимо установить z-фактор.
соответствующий масштабу.
Z-фактор
Z-фактор — это коэффициент масштабирования, используемый для преобразования значений высоты в двух целях:
- Для преобразования высоты единицы (например, метры или футы) в единицы горизонтальной координаты набора данных, которые могут быть футами, метры или градусы
- Чтобы добавить вертикальное преувеличение для визуального эффекта
Преобразование единиц
Если единицы для единиц z (высоты) такие же, как единицы x,y (линейные), то коэффициент преобразования z равен 1 , Если в вашем наборе данных используется система координат проекции, для вашего масштабирования задано значение «Нет», а ваши единицы высоты и линейные единицы различаются, вам необходимо определить коэффициент преобразования z, чтобы учесть разницу.
Для перевода из футов в метры или наоборот
наоборот, см. таблицу ниже. Например, если
единицами высоты вашей ЦМР являются футы, а единицами набора данных мозаики
метры, вы бы использовали значение 0,3048, чтобы преобразовать
единицы высоты от футов до метров (1 фут = 0,3048 метра).
Масштабирование и размер в пикселях
| Тип преобразования | Коэффициент преобразования |
|---|---|
Из футов в метры | 0.3048 |
From meters to feet | 3.28084 |
If your data is using a geographic coordinate system (such as a DTED in GCS_WGS 84), where the linear units в градусах, а ваша высота в метрах, используйте коэффициент преобразования 1, и система автоматически преобразует ваши линейные градусы в метры. Если ваши единицы высоты не в метрах, используйте функцию преобразования единиц, чтобы преобразовать высоту в метры, прежде чем использовать эту функцию.
Примечание:
Если выбрано масштабирование Скорректированное, вы можете использовать Z-фактор для преобразования единиц z в метры, и ArcGIS автоматически изменит широту и долготу на метры.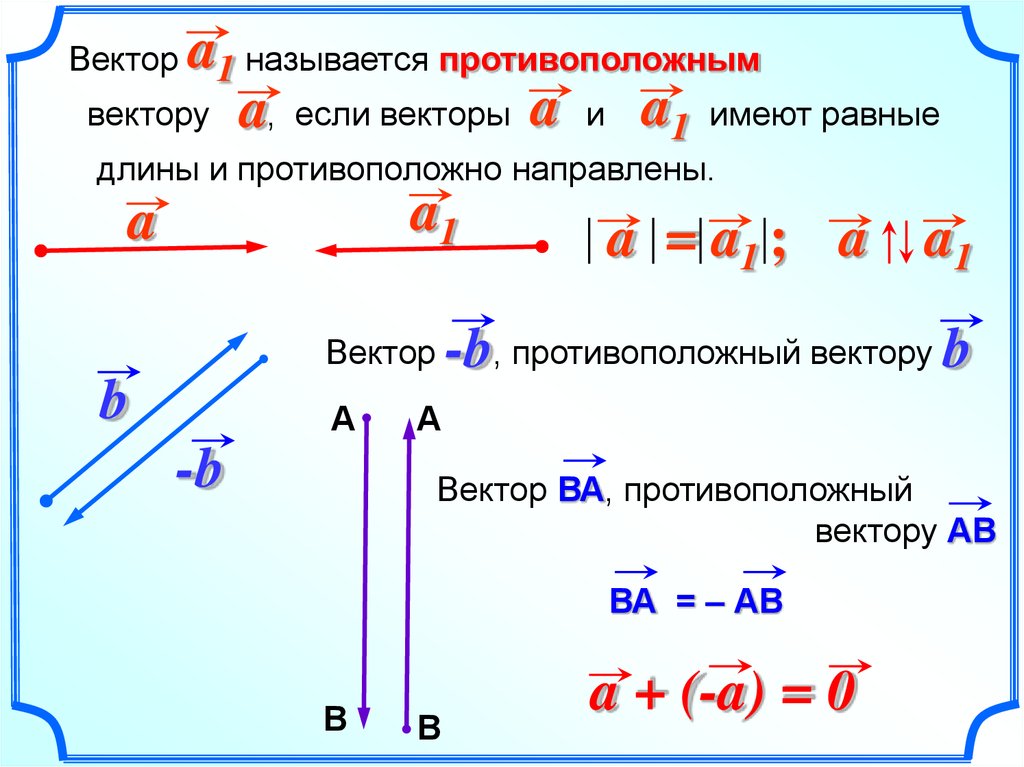
Преувеличение по вертикали
Чтобы применить преувеличение по вертикали, необходимо умножить коэффициент преобразования на коэффициент преувеличения. Например, если и высота, и координаты набора данных указаны в метрах, и вы хотите преувеличить их на кратное 10, коэффициент масштабирования будет равен коэффициенту преобразования единиц измерения (1,0), умноженному на коэффициент вертикального преувеличения (10,0), который будет равен z- коэффициент 10. Если единицами высоты являются метры, а набор данных является географическим (градусы), вы должны умножить коэффициент преобразования единиц (1,0) на коэффициент преувеличения (10,0), который будет z-фактором 10. Если ваша высота единицы не в метрах, используйте арифметическую функцию, чтобы преобразовать высоту в метры, прежде чем использовать эту функцию. Затем умножьте коэффициент преобразования единиц измерения (1,0) на коэффициент преувеличения (10,0), что даст z-фактор, равный 10,9.0013
Удалить краевой эффект
Использование этой опции позволит избежать любых артефактов передискретизации, которые могут возникнуть по краям растра. Выходные пиксели вдоль края растра или рядом с пикселями без значения будут заполнены NoData; поэтому рекомендуется использовать эту опцию только при наличии других доступных растров с перекрывающимися пикселями. Когда доступны перекрывающиеся пиксели, эти области NoData будут отображать значения перекрывающихся пикселей, а не быть пустыми.
Выходные пиксели вдоль края растра или рядом с пикселями без значения будут заполнены NoData; поэтому рекомендуется использовать эту опцию только при наличии других доступных растров с перекрывающимися пикселями. Когда доступны перекрывающиеся пиксели, эти области NoData будут отображать значения перекрывающихся пикселей, а не быть пустыми.
- Не отмечено — билинейная повторная выборка будет применяться единообразно для повторной выборки отмывки. Это значение по умолчанию.
- Отмечено — билинейная передискретизация будет использоваться внутри отмывки, за исключением краев растров или рядом с пикселями NoData. Эти пиксели будут заполнены значениями NoData и будут отображать значения высот перекрывающихся наборов данных, что уменьшит возможные эффекты резких краев.
Похожие темы
Установить разнонаправленные стрелки один два три Векторное изображение
Установить разнонаправленные стрелки один два три Векторное изображениеЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный / редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по требованию |
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69 Оплатить стандартные лицензии можно тремя способами. Цены составляют долларов США долларов США.
Цены составляют долларов США долларов США.
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00Существует два способа оплаты расширенных лицензий. Цены составляют долларов США долларов США.
| Оплата с | Стоимость изображения |
|---|---|
Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |

 Это положение обозначается углом солнца, измеренным по часовой стрелке от точного севера. Азимут 0 градусов указывает на север, на восток — 90 градусов, на юг — 180 градусов, на запад — 270 градусов.
Это положение обозначается углом солнца, измеренным по часовой стрелке от точного севера. Азимут 0 градусов указывает на север, на восток — 90 градусов, на юг — 180 градусов, на запад — 270 градусов.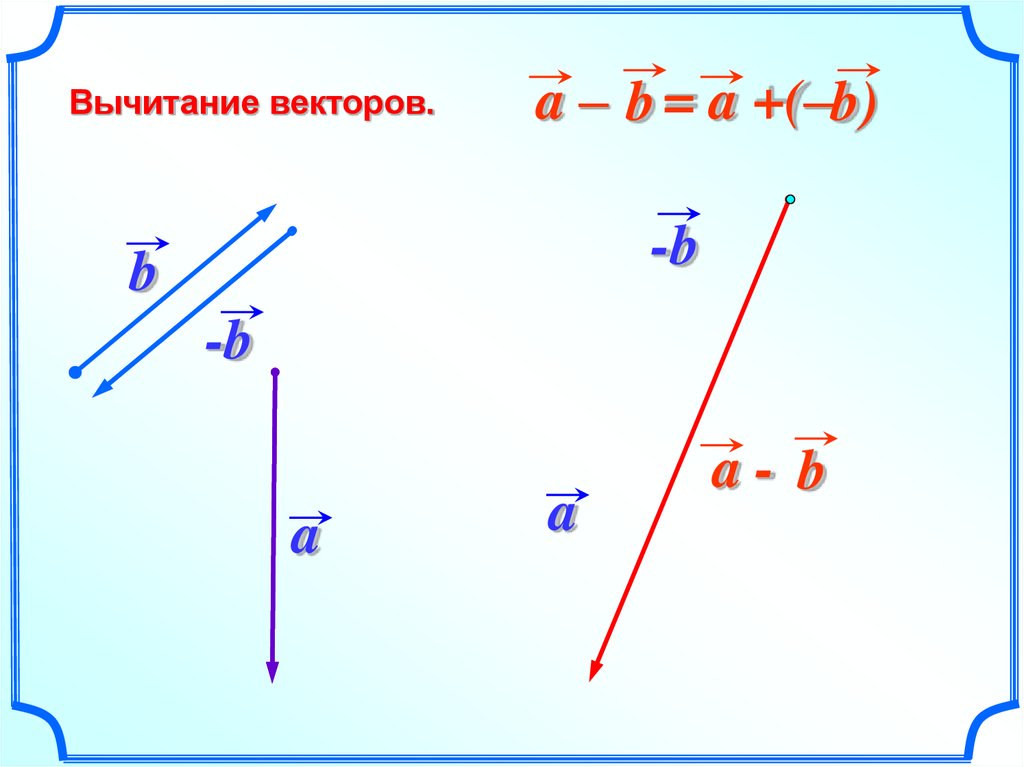 Это идеально для одного набора растровых данных, охватывающего локальную
область. Это не рекомендуется для наборов данных по всему миру с большими перепадами высот или мультимасштабом.
карты, так как он создаст рельеф местности с небольшими вариациями при небольших
Весы.
Это идеально для одного набора растровых данных, охватывающего локальную
область. Это не рекомендуется для наборов данных по всему миру с большими перепадами высот или мультимасштабом.
карты, так как он создаст рельеф местности с небольшими вариациями при небольших
Весы.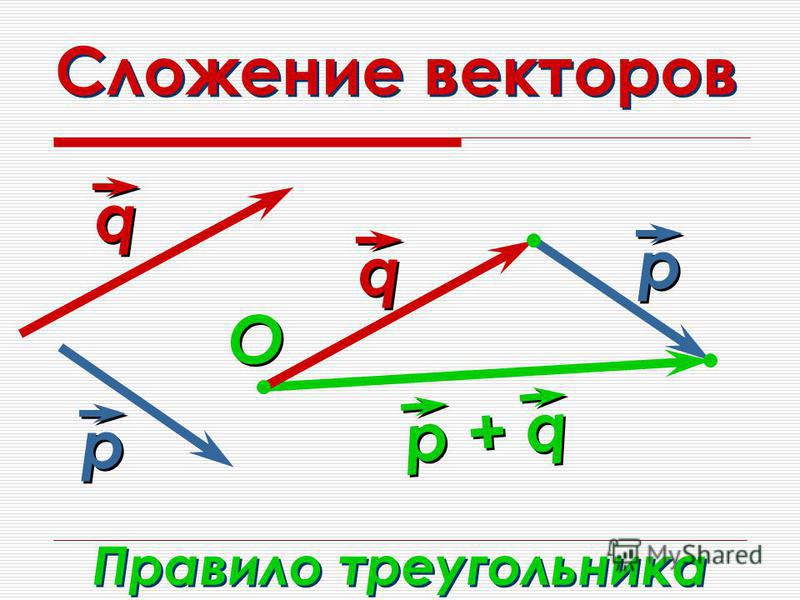
 Значение по умолчанию — 0,024.
Значение по умолчанию — 0,024.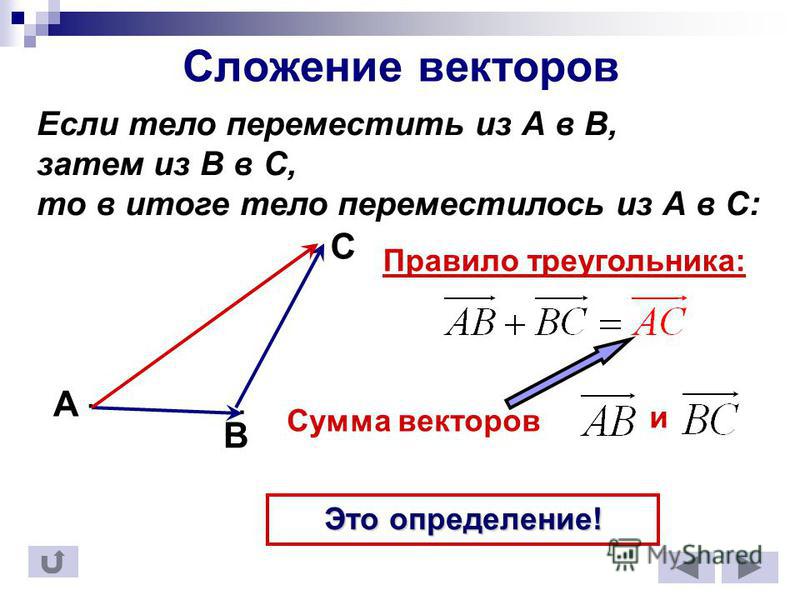 Эти пиксели будут заполнены значениями NoData и отображать перекрывающиеся значения пикселей, тем самым уменьшая
любые острые краевые эффекты, которые могут возникнуть в противном случае. Используйте эту опцию, когда набор данных мозаики, содержащий ваши растровые данные высот, состоит из перекрывающихся элементов или плиток.
Эти пиксели будут заполнены значениями NoData и отображать перекрывающиеся значения пикселей, тем самым уменьшая
любые острые краевые эффекты, которые могут возникнуть в противном случае. Используйте эту опцию, когда набор данных мозаики, содержащий ваши растровые данные высот, состоит из перекрывающихся элементов или плиток.