Произведение матриц это – примеры, алгоритм умножения на вектор, число, свойства произведения

(37)86.Что такое произведение двух матриц? При каких условиях оно определено? Примеры.

Умноже́ниема́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́ниемма́триц.

Произведением матрицы размеровна матрицуразмеровназывается матрицаразмеров, элементы которой вычисляются по формуле

(14.5)

где ,.

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матрицсогласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

 Найти произведения матриц AB и BA, если

   и   

   Р е ш е н и е: Имеем

↑ назад в содержание ↑

(38)87.Какие операции называют коммутативными? Покажите на примерах, что умножение матриц не коммутативно.

Коммутативность = Перестановочность.

Обычные числа переставлять можно: , а матрицы в общем случае не перестановочны: .

Какие матрицы можно умножать?

Чтобы матрицу   можно было умножить на матрицу  нужно, чтобы число столбцов матрицы  равнялось числу строк матрицы .

Пример:  Можно ли умножить матрицу  на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.  Например, для матриц,  и  возможно как умножение , так и умножение 

↑ назад в содержание ↑

(39)88.Что такое единичная и обратная матрицы? Как строится (по Гауссу) обратная матрица?

Пусть a – квадратная матрица порядка n. Обратной к ней матрице называется такая матрица A^-1, что A^-1*A=E (здесь A^-1 и E – квадратные матрицы того же порядка, причём E – единичная матрица).

Это определение вовсе не подразумевает, что обратная матрица существует для любой матрицы A.

Примеры

2. не существует

3. не существует

(0 0) – эта строка приводит к тому, что первая строка произведения этой матрицы на любую другую состоит из одних нулей (в единичной матрице это не так)

Определения с википедии:
Обратная матрица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Единичная матрица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Нахождение обратной матрицы методом Гаусса.

Исходная матрица А.

A =

Найдем матрицу А-1 обратную к матрице А.

Для этого напишем расширенную матрицу , в левой части которой находится наша исходная матрица А, а в правой единичная.

Применяя метод Гаусса, последовательно будем приводить нашу исходную матрицу (левую часть расширенной матрицы) к единичной матрице. Причем совершенные преобразование мы будем применять ко всей расширенной матрице.

Приведя левую часть расширенной матрицы к единичной, правая часть будет являться обратной матрицей к нашей исходной.

Последовательность приведения левой части расширенной матрицы к единичной, Вы можете проследить по выделенным серыми прямоугольниками элементам.

 Рассмотрим столбец 1.

К элементам стороки 2 прибавим соответствующие элементы строки 1 умноженные на -3.

 Рассмотрим столбец 2.

К элементам строки 1 прибавим соответствующие элементы строки 2.

Элементы строки 2 разделим на    -2 .

A-1 =

↑ назад в содержание ↑

studfiles.net

23 Matrica

МАТРИЦЫ

Оглавление.

1. Определение матриц.

2. Квадратные матрицы.

3. Действия с матрицами

4. Ранг матрицы.

5. Обратная матрица.

6. Системы линейных уравнений.

6.а. Метод Гаусса.

6.б. Формулы Крамера.

6.в. Матричный метод.

7. Системы линейных уравнений общего вида.

1. Определение матриц

Прямоугольная таблица, содержащая 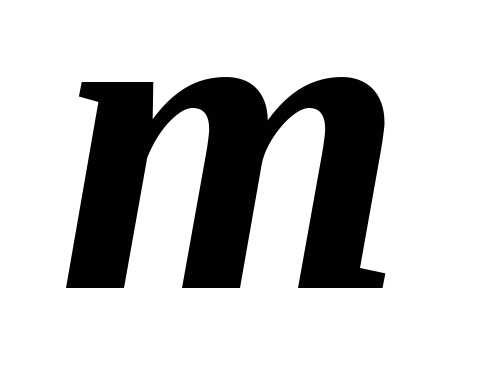строк истолбцов, называется матрицей размера.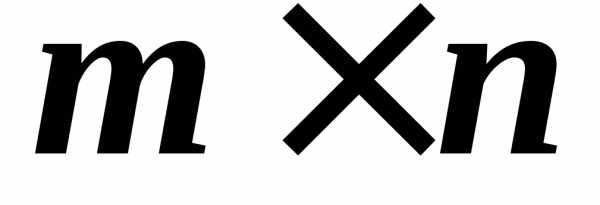

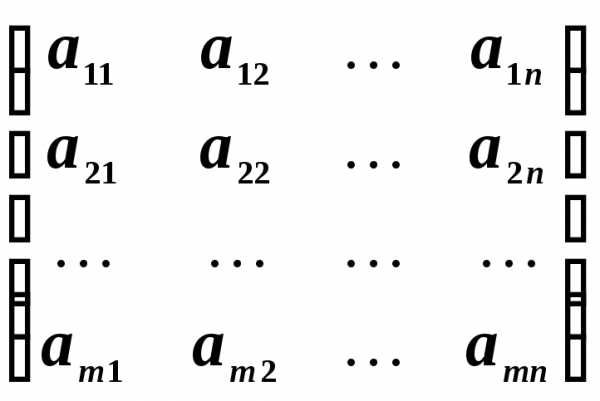
Числа называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.

Матрицы обозначают буквами ,,и т. д. Например,

или сокращенно в виде .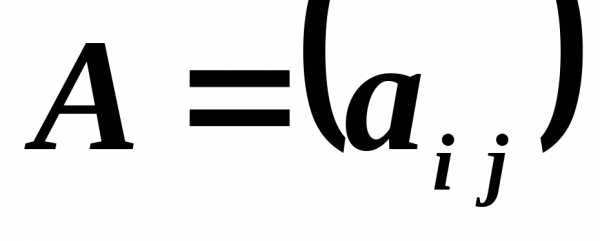

Две матрицы 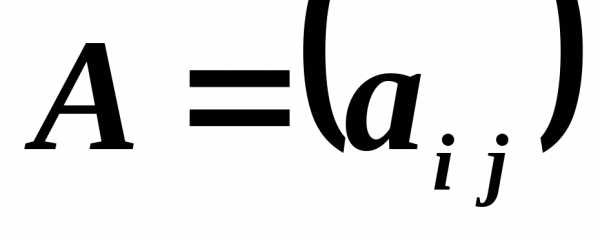и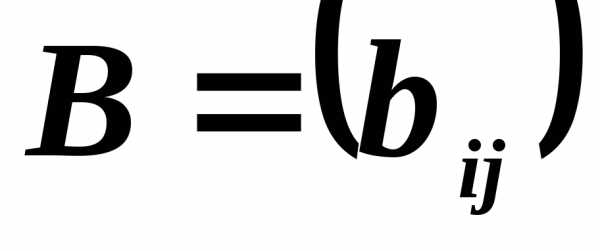считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть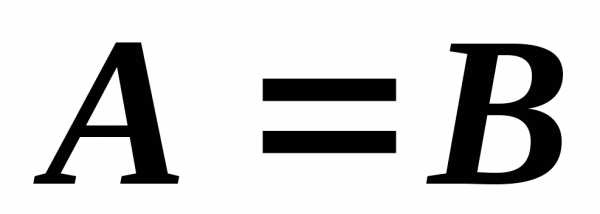, если.

Часто приходится рассматривать матрицу, столбцами которой являются строки матрицы . Эта матрица называется транспонированной ки обозначается через.

Пусть дана матрица . Переставим строки со столбцами. Получим матрицу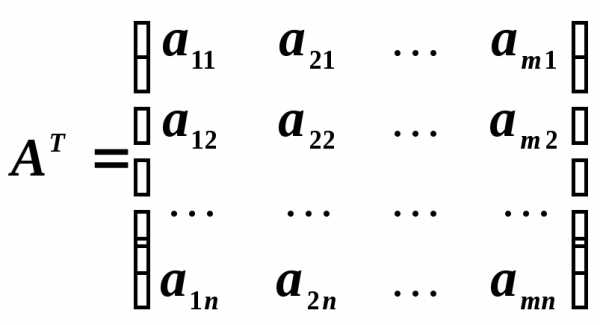

_,

которая будет транспонированной по отношению к матрице .

2. Квадратные матрицы

Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, — порядком квадратной матрицы.

Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем ее левый верхний угол с правым нижним, т. е. совокупность элементов называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, — побочной диагональю.

Квадратная матрица называется треугольной, если ее элементы, которые находятся над главной диагональю или под главной диагональю, равны нулю, т. е. матрицы вида

,

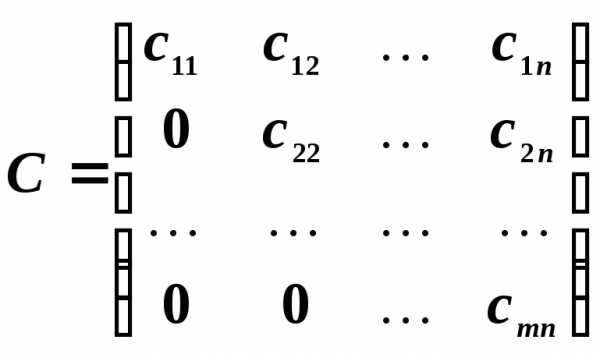
являются треугольными. Матрица называется треугольной снизу, а матрица— треугольной сверху.

Квадратная матрица называется диагональной, если ее элементы, которые находятся вне ее главной диагонали, равны .

.

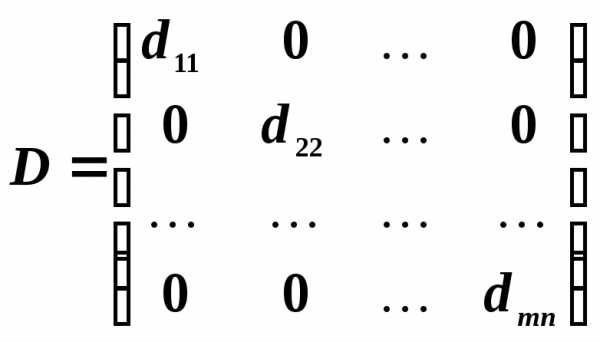3. Действия с матрицами Умножение матрицы на число и сложение матриц

По определению, чтобы умножить матрицу на число , нужно каждый элемент матрицы умножить на это число.

Пример 1. Умножить матрицу на число

Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц иназывается матрица, элементы которой равны суммам соответствующих элементов матрици:.

Пример 2. Сумма двух матриц

.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через . Для любой матрицыимеем,.

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1) ,

2) ,

3) ,

4) ,

5) .

где ,,— матрицы,,— числа.

Произведение матриц

Произведение матрицы на матрицуопределено только в том случае, когда число столбцов матрицыравно числу строк матрицы. В результате умножения получим матрицу, у которой столько же строк, как у матрицы, и столько же столбцов, как у матрицы.

По определению элемент матрицыравен сумме парных произведений элементовстроки матрицы, на соответствующие элементыстолбца матрицы.

Пример 3. Найти произведение матриц

и.

Решение. Имеем: матрица размера, матрицаразмера, тогда произведениесуществует и элементы матрицыравны

,,,

,.

, а произведениене существует.

Пример 4. Найти произведение матриц

,

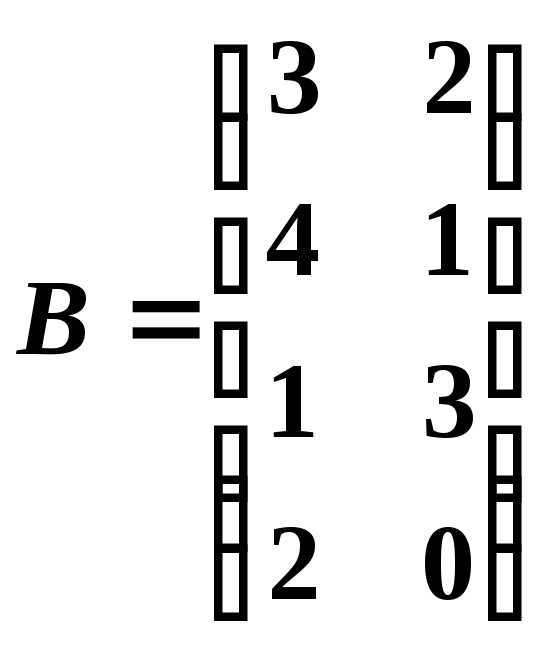
Очевидно, что произведение матриц не обладает перестановочным свойством, т.е. некоммутативно. Если все-таки выполняется равенство , то матрицыиназываются перестановочными.

Свойства произведения матриц:

1) , где-число;

2) ;

3) ;

4) .

Единичной матрицей называется диагональная матрица, у которой все элементы равны 1.

.

Свойство единичной матрицы: для любой квадратной матрицы.

Рассмотрим произвольную квадратную матрицу , порядка. Если существует такая матрица, что, то говорят, чтообратима, аназывают обратной матрицей для матрицы.

studfiles.net

Произведение матриц — это… Что такое Произведение матриц?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{— 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{— 1}AX = A ^{— 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{— 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij — b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{— 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

1. A + (B + C) = (A + B) + C
2. A + B = B + A
3. A(BC) = (AB)C
4. A(B + C) = AB + AC
5. (B + C)A = BA + CA
9. (A^T)^T = A
10. (A * B)^T = B^T * A^T

Элементарные преобразования матриц

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля
2. Прибавление одной строки к другой строке

Элементарные преобразование столбцов матрицы определяются аналогично.

Типы матриц

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис . Пусть  — произвольный вектор. Тогда его можно разложить по этому базису:

,

где x^k — координаты вектора в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть  — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

.

Вектора также разложим в выбранном базисе, получим

,

где  — j-я координата k-го вектора из .

Подставим разложение в предыдущую формулу, получим

.

Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец x^k даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.

См. также

Литература

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

Умножение матриц Википедия

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Содержание

• 1 Определение
• 2 Иллюстрация
• 3 Обсуждение
• 4 Свойства
• 5 Обратная матрица
• 6 Алгоритмы быстрого перемножения матриц
• 7 Степени матриц
• 8 См. также
• 9 Литература
• 10 Примечания

Определение[ | ]

Пусть даны две прямоугольные матрицы A{\displaystyle A} и B{\displaystyle B} размерности l×m{\displaystyle l\times m} и m×n{\displaystyle m\times n} соответственно:

A=[a11a12⋯a1ma21a22⋯a2m⋮⋮⋱⋮al1al2⋯alm],B=[b11b12⋯b1nb21b22⋯b2n⋮⋮⋱⋮bm1bm2⋯bmn].{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\ddots &\vdots \\a_{l1}&a_{l2}&\cdots &a_{lm}\end{bmatrix}},\;\;\;B={\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\end{bmatrix}}.}

Тогда матрица C{\displaystyle C} размерностью l×n{\displaystyle l\times n}:

C=[c11c12⋯c1nc21c22⋯c2n⋮⋮⋱⋮cl1cl2

ru-wiki.ru

Произведение матриц — Энциклопедия по экономике

Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. (ХЬУ=Ь Х после раскрытия скобок получим  [c.84]
Произведение матрицы АтХ =(ау) на число А. есть матрица  [c.259]

Произведение матрицы Ат =(ау) на матрицу Вп р=(Ьу) есть матрица  [c.259]

Получили, что произведения матриц АВ и ВА существуют, но являются матрицами разных размеров (порядков).  [c.260]

Доказательство заметим, что скалярное произведение векторов-столбцов а и b может быть записано в виде произведения матриц либо как аТЬ, либо как Ъта. На этом основании можно записать  [c.263]

Произведение матриц А и В обозначается АВ, т.е. С = АВ. Оно, вообще говоря, зависит от порядка сомножителей. Если АВ = ВА, то матрицы А и В называются перестановочными.  [c.54]

Вектор оптимального плана X» может быть получен согласно условию (3.4) как произведение матрицы эффективности D на вектор наличного запаса ресурсов В  [c.88]

Учитывая условие (3.4), имеем А X — — D-A°-X °. Обозначив через Н произведение матриц D и А° Л  [c.90]

Произведение матрицы на число А есть  [c.23]

Эти соотношения справедливы в том случае, когда произведения матриц определены.  [c.24]

Заметим, что в отличие от обычного произведения матриц А В, которое существует только тогда, когда число столбцов А совпадает с числом строк В  [c.53]

Определение 1. Произведением матриц А и Встроки матрицы Am на столбец матрицы BS n в соответствии с формулой  [c.385]

Произведение матриц (векторов) А, 10 и В10 1 также существует, так как внутренние индексы 10 и 10 совпадают, а размер матрицы-произведения будет 1 х 1, но это уже будет не матрица, а число (скаляр) j г  [c.386]

Произведение матриц в связи с тем, что не все матрицы согласованы для умножения не обладает свойством коммутативности, т. е. в общем случае  [c.386]

Значения А, характеризуют минимальную, но достаточную величину потребности в материально-технических ресурсах для производства продукции в объеме пятилетнего плана на текущий год. Такая экспертиза необходима, поскольку имеются случаи, когда контрольные цифры объединениям устанавливают под мощности, а материальное обеспечение ниже плана. План считается обеспеченным ресурсами, если для всех видов продукции после получения произведения матрицы норм II а, II и вектора выпусков Ц, выполняется условие ф А/, где — предельный размер (лимит) /-го ресурса, выделенного объединению Госснабом.  [c.60]

Полученное методами высшей алгебры произведение матрицы коэффициентов полных затрат на вектор (столбец) продукции, идущей в накопление и потребление, дает вектор (столбец) объемов продукции. Расчет коэффициентов полных затрат связан с громадной вычислительной работой напр., для таблицы по 44 отраслям должно быть произведено ок. 800—900 тыс. вычислительных операций. Поэтому проведение таких расчетов практически возможно лишь при использовании электронно-вычислительной техники.  [c.441]

Применяя правила матричной алгебры, систему (7) можно записать в краткой форме, представив левую часть как произведение матрицы А на вектор х, а правую — как вектор Ь  [c.12]

Замечание 1. Элемент с координатами г, j в произведении матриц АВ равен скалярному произведению г-ro вектора-строки матрицы А на j -й вектор-столбец матрицы В.  [c.491]

Замечать 2. Важным частным случаем произведения матриц является произведение квадратной п х п матрицы А на вектор Ъ. Например,  [c.491]

Таким образом, матрица перехода за m этапов равна произведению матрицы перехода за г этапов на матрицу перехода за (т — г) этапов.  [c.150]

Теорема о ранге матрицы. Нахождение ранга матрицы элементарными преобразованиями. Ранг произведения матриц. Представление прямоугольной матрицы в виде произведения двух матриц полного ранга.  [c.11]

Перестановки, инверсии, транспозиции. Число различных перестановок из п элементов. Четные и нечетные перестановки, смена четности при транспозиции. Определитель квадратной матрицы. Простые следствия из определения определителя. Линейность определителя по каждой строке и каждому столбцу, смена знака при перестановке двух столбцов или двух строк определителя. Определитель произведения столбцов или двух строк определителя. Определитель произведения матриц. Определитель особенной, неособенной, обратной матрицы. Формулы разложения определителя по столбцу (строке). Формулы Крамера.  [c.11]

Произведение матриц . . . .. 22 1 2 5 Собственные значения и собственные векторы матрицы 25 1 2 6 Ранг матрицы . 26 12 7 Понятие о ратной матрицы . . 26  [c.3]

Произведение матрицы на вектор  [c.11]

Произведение матрицы А на вектор является вектором у, т.е. у = Ах. Если у = Ах и х = Bw, то у = Abw, что справедливо для любых векторов х, у, w и любых матриц А, В.  [c.11]

В этой и последующих формулах произведения матриц перехода на вектор ILJ равны суммам строк соответствующих матриц и могут быть вычислены до начала итераций.  [c.100]

Прямое произведение матриц обладает следующими свойствами  [c.36]

Приоритет прямого произведения матриц выше, чем обычного матричного произведения.  [c.36]

Умножение на скаляр. Если А. — скаляр, то произведение матрицы на скаляр определяется как  [c.76]

МАТРИЧНАЯ АЛГЕБРА [matrix algebra] — математическая дисциплина, посвященная правилам действий пар. матрицами. Произведение матрицы [а.] на скаляр а представляет собой матрицу [аа.], т.е. матрицу, элементы которой образованы умножением всех элементов этой матрицы на скаляр сумма матриц [а.] + [Ь.] — матрицу [а.. + Ь ] умножение матриц определяется только рдяпрямоуголь-ных матриц, у которых число столбцов первого сомножителя равно числу строк второго, причем здесь не соблюдается закон коммутативности произведение матриц А я В может не быть равным произведению В на А. Если же АВ-ВА, то такие матрицы называются перестановочными.  [c.189]

Этот пример является иллюстрацией того, что операция произведения матриц, вообще говоря, некоммутативна АВ ф В А. Более того, АВ может быть определено, а В А — не определено вовсе.  [c.491]

Смещенность ошибок при наличии ошибок в факторах. Оценки Вальда. Ортогональная регрессия. Псевдопеременные. Способы устранения их линейной зависимости. Прямое произведение матриц. Главные эффекты и эффекты взаимодействия.  [c.85]

Свойства произведения матриц П сть Л, В п С мафицы соответствующих размеров (ч обы произведения мафии бы и t ределены) а а действительное чт. о Тог ы и меня место следующие снойп на произведения матриц-  [c.25]

Найти- а) вес произведения матриц, которые имею г (.мыс л, б) соответ ствующне транспонированные матрицы, в) матрицу 2G С. г) матрицу [c.47]

Л = (A.J ) — ковариационная матрица вектора (ел,…, etg ), Л / — формализованное обозначение матрицы, являющейся кронекеровским произведением матриц Л и Ig.  [c.169]

Транспонированная матрица есть матрица АТ, столбцы которой являются строками исходной матрицы при сохранении их порядка. Транспонирование является рефлексивным. Транспонирование вектор-столбца дает вектор-строку и наоборот. Транспонированная сумма матриц равна сумме транспонированных матриц. Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке, т.е. (АВ)Т = ВТАТ. Матрица называется симметрической, если транспонированная матрица равна самой матрице.  [c.11]

Прямое произведение матриц А В, имеющих размерность, соответственно, есть матрица размерности (гПАШв)х(ПАПв) следующей структуры апВ .  [c.36]

Произведение матриц. Если матрица А имеет порядок т. ° п, а матрица В имеет порядок пХр, то произведение матриц А В опртделяется как новая матрица порядка тХр, в которой элемент, стоящий на пересечении r-й строки и /-го столбца, равен  [c.76]

Таким образом, элемент произведения матриц, обладающий индексом I/, определяется как сумма попарных произведений элементе t -й строки первой матрицы на соответствующие элементы / -го столсса второй матрицы. Для того чтобы это было возможно, очевидно, необходимо равенство числа элементов в строке первой матрицы и числа элементов в столбце второй матрицы, т. е. необходимо равенство числг столбцов первой матрицы числу строк второй матрицы. Матрицы, обладающие этим свойством, называют соответственными по отношению порядок матриц при i x умножении.  [c.76]

economy-ru.info

Правила вычисления произведения матриц

Произведением двух матриц будет матрица , элементы которой равны сумме попарных произведений элементов строки первой матрицы на соответствующие элементы столбца второй матрицы :

Из этого следует что перемножить между собой можно матрицы в которых количество столбцов первой равно количеству строк второй . Новая матрица которая является произведением двух имеет размерность , где – количество строк первой матрицы, а – столбцов второй. Правила достаточно просты и для нахождения произведения матриц нужно уметь лиш умножать и прибавлять. Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика».

———————————————

Примеры.

Найти произведение матриц.

1) (1.110)

Для нахождения произведения умножаем строки первой матрицы на столбцы второй

2) (1.112)

Найдем элементы новой матрицы.

Записываем полученные значения в матрицу.

3) (1.114)

Согласно правилам — произведением будет матрица-вектор размерности . Вычислим ее элементы

Окончательно матрица примет вид

4) (1.115)

При вычислении произведения матриц-векторов получим квадратную матрицу размера. .

Простыми операциями умножения получили новую квадратную матрицу пятого порядка.

5) (1.116)

Результатом умножения в данном примере будет матрица которая содержит лиш один элемент.

На этом практическая часть урока закончена. Упражняйтесь в решении подобных примеров, ведь умножения — это одна из основных операций (не только в матрицах). В следующих статьях материал будет сложнее, поэтому начинайте знакомиться с матрицами с простого.

yukhym.com

Произведение матриц Википедия

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Содержание

• 1 Определение
• 2 Иллюстрация
• 3 Обсуждение
• 4 Свойства
• 5 Обратная матрица
• 6 Алгоритмы быстрого перемножения матриц
• 7 Степени матриц
• 8 См. также
• 9 Литература
• 10 Примечания

Определение[ | ]

Пусть даны две прямоугольные матрицы A{\displaystyle A} и B{\displaystyle B} размерности l×m{\displaystyle l\times m} и m×n{\displaystyle m\times n} соответственно:

A=[a11a12⋯a1ma21a22⋯a2m⋮⋮⋱⋮al1al2⋯alm],B=[b11b12⋯b1nb21b22⋯b2n⋮⋮⋱⋮bm1bm2⋯bmn].{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\ddots &\vdots \\a_{l1}&a_{l2}&\cdots &a_{lm}\end{bmatrix}},\;\;\;B={\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\end{bmatrix}}.}

Тогда матрица C{\displaystyle C} размерностью l×n{\displaystyle l\times n}:

C=[c11c12⋯c1nc21c22⋯c2n⋮⋮⋱⋮cl1cl2

ru-wiki.ru