Синус альфа умножить тангенс альфа… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
Помогите сделать 428 номер…
Помогите решить номер 423…
Две машины ехали с олинакрвой скоростью. 1-ая машина быоа в дороге 5 ч, а 2-ая 3. 1-ая проехала на 320км больше. сколько км проехало кажлая машина…
В детском саду 20 велосипедов — некоторые из них трехколесные а некоторые двухколесные. у всех велосипедов вместе 55 колес. сколько двухколесных велосипедов в детском саду?
AЛГЕБРАИЧЕСКИМ СПОСОБОМ!!!. ..
..
Сколько будет 48-29+37-19?…
В одной пачке 38 бумаги а в другой на 15 листов больше Сколько всего листов бумаги в пачках Реши задачу выражением…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
ЭкономикаМузыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
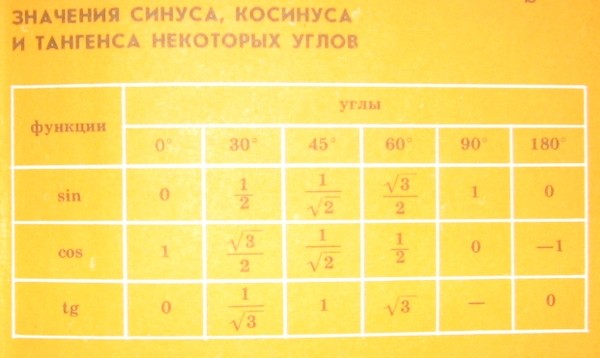
Чему равен синус тридцати пяти градусов
На вопрос, чему равен синус тридцати пяти градусов:
- Математик ответил, что синус тридцати пяти градусов не выражается алгебраическим числом.
 9}{9!}-\dots$, но упёрся в пороговое значение double. «А, так аргумент ведь в радианах брать надо было!» — догадался он, и пообещал исправить ошибку в следующей версии.
9}{9!}-\dots$, но упёрся в пороговое значение double. «А, так аргумент ведь в радианах брать надо было!» — догадался он, и пообещал исправить ошибку в следующей версии. - Математик-тролль ответил, что синус тридцати пяти градусов в точности равен косинусу пятидесяти пяти градусов.
- Юный любитель математики и будущий обладатель медали Филдса, задумав расширить табличку синусов, которую старший брат как раз изучал на уроках алгебры, построил с помощью транспортира угол в 35 градусов, достроил его до прямоугольного треугольника, измерил противолежащий катет и гипотенузу и нашёл их отношение: $\frac{39}{68}$.
- А на лекциях такого не было! — применил своё стандартное заклинание студент-первокурсник.
- Синус тридцати пяти градусов равняется, как вычислить sin 35, ышт 35 градусов посчитать, синус, косинус, математика, решение, 9 класс, скачать учебник гдз ответы на ЗНО и ЕГЭ 2016 без регистрации и смс, — написал СЕОшник.
Это была присказка. Перейдём теперь к непосредственному изложению сути этого поста.
На одном сайте о математике я увидел хитрый приём: автор сначала рассматривает какой-нибудь простой пример, а затем на два экрана со своими юмористическими комментариями перечисляет поисковые запросы, которые привели (бы?) посетителей на эту страницу.
И это работает! Даже летом на его сайт заходят по 500 человек почитать, чему равен синус тридцати градусов. А на мои «Десять букв», где столько всего интересного и необычного из мира математики, заходят в день человек по 20.
Поэтому я решил тоже создать что-то подобное, только несущее реальную пользу для людей, а не для роботов.
Ещё давно я заметил, что иногда поиск направляет посетителей не туда, куда следовало бы. Например, по запросу как вынести из-под корня посетители часто попадали на заметку о правильно-неправильном выносе из-под корня, то есть таких действиях, которые выполняются не по математическим правилам, но, тем не менее, дают верный результат.
Подытожив, какие ещё поисковые запросы приводят людей на сайт и блоги проекта «Приглашение в мир математики» и какие страницы содержат наиболее полную информацию по этим запросам, я получил следующее.
математический ряд 10 букв — это самый популярный запрос, приводящий пользователей на блог «Десять букв». Там действительно много интересных постов о математических рядах. Но, скорее всего, этот запрос родился при решении кроссворда и ответом должно быть слово «прогрессия». Кстати, скоро в нашем математическом справочнике появится пост обо всех формулах для геометрической и арифметической прогрессий.
занимательная математика — по этому запросу больше всего посетителей пришло на основной сайт проекта. Действительно, тут вы найдёте множество материалов по занимательной математике: математический юмор, истории, обзоры полезных интернет-сайтов и сервисов, нерешённые задачи, математические игры и фокусы.
Что касается блога «Эвольвента», из Яндекса и Гугла сюда (надеюсь, пока что) заходят мало, поэтому хотелось бы перечислить все запросы и поприветствовать новых посетителей.
http:// «matematika_v_shkole».html — видимо, искали сайт журнала «Математика в школе», а попали на называющийся так же раздел блога.
зно математика 2014 — хотя тестирование ЗНО является завершением изучения математики в школе, для него выделен отдельный раздел блога. Тут, помимо решений задач публикуются также органзационные материалы и новости «кухни» ЗНО. Например, в плане — пост о том, как определяется пороговый балл сдал/не сдал.
есть ли решебники по зно? — после каждого тестирования нечто подобное создаём мы сами, подробно разбирая задачи ЗНО и перечисляя темы, к которым относятся задачи и которые не мешало бы повторить перед тестированием.
моя школа зно 2014 математика — у нас задачи ЗНО разбираются полнее, чем на «моей школе» 🙂
результаты зно математика — вот результаты смотрите в своём аккаунте, который вы получили при регистрации на тестирование. Однако статистическую информацию о результатах ЗНО по стране мы найдём и скоро опубликуем.
квадрат 4 на 4 разделили на 16 единичных квадратов — интересное начало задачи, по этому запросу посетитель попал на разбор задач олимпиады Кенгуру для 5-6 класса.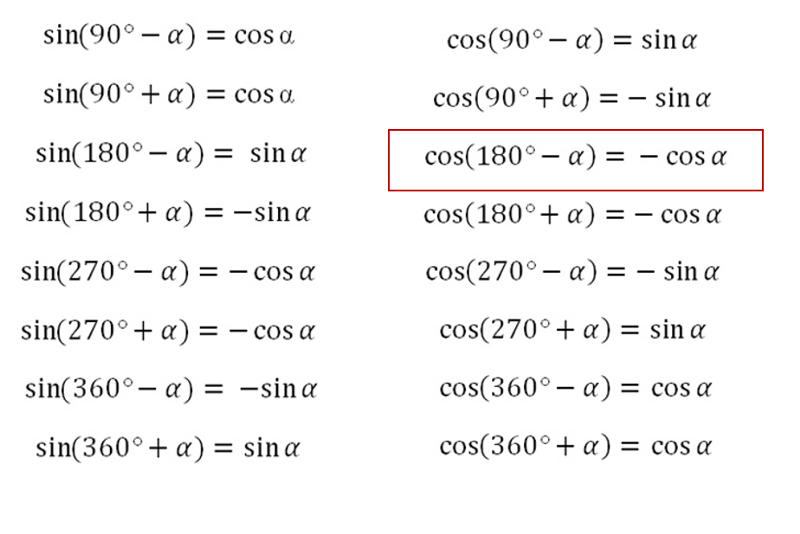 А вот задача посложнее с таким же началом: сколькими способами квадрат 4х4 можно покрыть плитками домино 1х2 без пропусков и наложений?
А вот задача посложнее с таким же началом: сколькими способами квадрат 4х4 можно покрыть плитками домино 1х2 без пропусков и наложений?
летний лагерь кенгуру — в летнем лагере «Кенгуру» собираются дети со всей страны, пропорционально участию области в олимпиаде. Здесь дети слушают лекции известных математиков по решению олимпиадных задач, играют в «математическую карусель», «Брейн-ринг» и всё это на фоне чистой горной природы.
международная ассоциация kangourou sans frontieres 14 б 4/15 — математический конкурс «Кенгуру» действительно без границ, мы писали о статистике проведения олимпиады в 50 странах мира.
регистрация на международную олимпиаду по математике 2016 кенгуру
очень большие числа в математике — наша статья о Карлсоне и триллионе начинает привлекать на сайт посетителей. Кстати, просмотрите её, возможно, некоторые их отмеченных в ней фактов вы не знали
Кстати, просмотрите её, возможно, некоторые их отмеченных в ней фактов вы не знали
формула решения задач 3 класса с дробями — о формулах решения задач на дроби в блоге тоже есть статья. Она будет полезна как третьеклассникам, так и одиннадцатиклассникам, готовящимся к тестированию
формулы сокращённого умножения алгебра 8 класс — и о формулах сокращённого умножения есть пост. Причём там формулы не просто перечисляются, а выводятся, чтобы лучше закрепить их в памяти.
приглашение по алгебре — алгебре посвящены многие материалы проекта «Приглашение в мир математики» и коллекция постоянно пополняется.
Удачного вам учебного года!
Тригонометрические функции – The Math Doctors
(Архивный вопрос недели)
В прошлый раз мы рассмотрели некоторые детали, которые редко упоминаются при формулировании правил интерпретации алгебраических выражений. Я не уместился в обсуждении самого сложного случая: тригонометрических функций, которые при записи без круглых скобок, как это было традиционно, могут вызвать несколько вопросов. (Многое из того же относится и к логарифмам.)
(Многое из того же относится и к логарифмам.)
Триггерные функции без круглых скобок
Вот вопрос, от 2010 года:
Порядок произведений, степеней и параметров тригонометрических функцийПытаюсь уточнить порядок операций применительно к тригонометрическим функциям. Я хочу знать, каков правильный порядок операций для такого выражения, как sin2x. Когда мы знаем, что умножение подразумевается? Когда в моем учебнике написано sin2x, я знаю, что это означает sin(2x). Но часто скобки отсутствуют. Правильно ли тогда предположить, что умножение всегда подразумевается в круглых скобках? Если это так, не означает ли это, что sinxcosy следует читать как sin(xcosy)? (Я тоже видел это в своем учебнике, но я знаю, что должен интерпретировать это как (sinx) (уютно).) Я знаю, что всегда следует включать символы группировки, чтобы избежать двусмысленности; но когда их нет, как правильно интерпретировать эти выражения?
Если триггерные функции были написаны с использованием обычных обозначений для функций, т. е. \(\sin(2x)\), проблем не будет. Но тригонометрические функции возникли раньше современной записи функций (или даже понятия функции), и старая запись была «унаследована», так что, хотя сегодня многие авторы рекомендуют всегда использовать круглые скобки, старая форма по-прежнему распространена. Как указал Джим, если, как в \(\sin 2x\), умножение имеет приоритет над функцией (как если бы оно было в круглых скобках), то \(\sin x \cos y\), по-видимому, подразумевает, что умножение произошло до применения функции синуса, что сделало его \(\sin(x \cos y)\). И я никогда не видел «официального» объяснения этому.
е. \(\sin(2x)\), проблем не будет. Но тригонометрические функции возникли раньше современной записи функций (или даже понятия функции), и старая запись была «унаследована», так что, хотя сегодня многие авторы рекомендуют всегда использовать круглые скобки, старая форма по-прежнему распространена. Как указал Джим, если, как в \(\sin 2x\), умножение имеет приоритет над функцией (как если бы оно было в круглых скобках), то \(\sin x \cos y\), по-видимому, подразумевает, что умножение произошло до применения функции синуса, что сделало его \(\sin(x \cos y)\). И я никогда не видел «официального» объяснения этому.
Никаких правил, только люди
Я ответил:
Я обдумывал это несколько раз и пришел к выводу, что правил не существует . Здесь мы рассматриваем язык, который развился не по преднамеренному замыслу, а органично — с согласия его пользователей — точно так же, как развивается любой естественный язык. Лингвисты могут изучать язык, чтобы выяснить его правила, но по сути они реконструируют то, что существует без явных правил.Вы можете увидеть некоторые из этих разработок в порядке операций здесь: История порядка операций http://mathforum.org/library/drmath/view/52582.html
Все, что лингвист может сделать, чтобы понять язык, — это изучить, как его используют его носители. Языки (за исключением нескольких «искусственных языков») не изобретаются с готовым сводом правил, а органически развиваются по мере того, как люди говорят на них, постоянно меняясь. Большая часть изучаемой нами английской грамматики, которая предположительно состоит из определенного набора правил, на самом деле была навязана английскому языку учеными, которые считали, что любой допустимый язык должен соответствовать категориям, известным из латыни, в результате чего она часто не соответствует как мы говорим на самом деле. То же самое относится и к PEMDAS: это набор правил, наложенных на наш «язык», предназначенных для представления того, как выполняется математика, но немного более жестких, чем реальность. А тригонометрия — это отдельный диалект! 92 x, где log x * log x и
log(log x) часто встречаются в анализе». Он говорит о том, что это сокращенное обозначение используется потому, что его достаточно, чтобы отличить часто используемые формы друг от друга: опыт говорит нам , что кто-то не имел бы в виду грех(грех(х)).
Он говорит о том, что это сокращенное обозначение используется потому, что его достаточно, чтобы отличить часто используемые формы друг от друга: опыт говорит нам , что кто-то не имел бы в виду грех(грех(х)).
Это, конечно, не главный вопрос, который мы обсуждаем, но он иллюстрирует тот факт, что нотация тригонометрии идиосинкразична и приемлема в основном потому, что «мы знаем ее, когда видим», не нуждаясь в правилах.
Правило здравого смысла
Я думаю, что основное правило здравого смысла лежит в основе небрежности в использовании других форм, таких как второй и третий примеры, которые вы упомянули: грех 2x означает грех (2x) sin x cos y означает sin(x)cos(y) Они означают то, что они делают, просто потому, что мы знаем достаточно, чтобы НЕ ожидать, что sin 2x будет означать sin(2)*x sin x cos y будет означать sin(x*cos(y)) Возможно, есть также немного типографского рассмотрения : расстояние обычно предполагает, что 2x принадлежит как единое целое, как и sinx и cosy во втором примере.
В современных учебниках (особенно по математическому анализу) могут быть сложные выражения, составленные только для того, чтобы проверить свои навыки, без ссылки на то, будут ли они когда-либо действительно использованы; в таком контексте здравый смысл может оказаться бесполезным! Тогда применяется другая часть здравого смысла: когда есть возможность неправильного толкования, используйте круглые скобки. И наоборот, если выражение не имеет круглых скобок, предполагается, что автор хотел, чтобы оно читалось наиболее естественным образом (что бы это ни было).
Таким образом, можно проанализировать все употребления с точки зрения языка и установить некоторые правила, например, «умножение предшествует триггерным функциям, за исключением случаев, когда другая триггерная функция является фактором». Но что мы действительно делаем, читая эти выражения, так это руководствуемся здравым смыслом, основанным на математическом опыте. Это вообще помогает?
Другими словами, я не думал, что стоит пытаться придумать полный набор правил.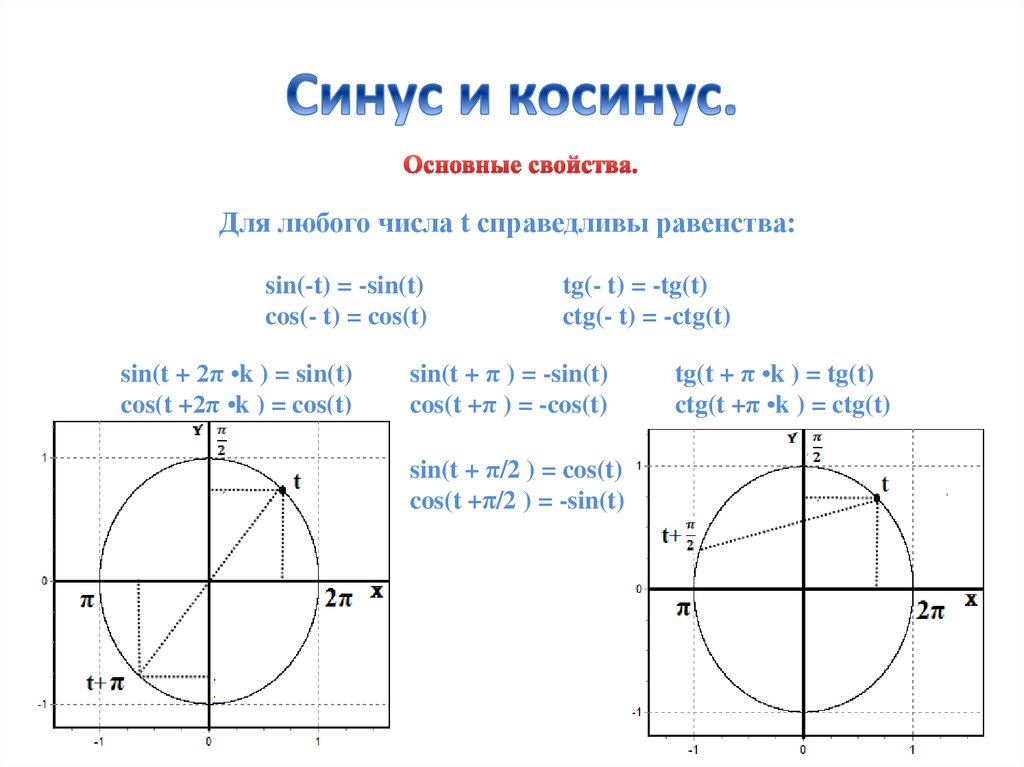 2-2)(8x)]
Я понимаю, что лучше всего использовать скобки и квадратные скобки, чтобы развеять любые сомнения, но было бы неправильно писать cos(a) (b), когда вы имеете в виду (b)cos(a)?
Когда круглые скобки не используются, например, с sin 2x, я знаю, что мы обычно принимаем это за sin(2x). Так что есть над чем подумать!
Бев
2-2)(8x)]
Я понимаю, что лучше всего использовать скобки и квадратные скобки, чтобы развеять любые сомнения, но было бы неправильно писать cos(a) (b), когда вы имеете в виду (b)cos(a)?
Когда круглые скобки не используются, например, с sin 2x, я знаю, что мы обычно принимаем это за sin(2x). Так что есть над чем подумать!
Бев
Это очень похоже на вопрос, на который я ответил, но с большим примером. Если бы мы когда-нибудь написали \(\cos(a)(b)\), то восприняли бы это как функцию произведения, как мы сделали бы с \(\cos ab\)? Если нет, то почему?
На этот конкретный вопрос есть быстрый ответ: когда круглые скобки используются с функцией, они всегда заключают в себе весь аргумент. Тот факт, что круглые скобки необязательны для триггерных функций, не имеет значения; как только вы вообще используете круглые скобки, вы теряете право думать о них как о содержащих только один фактор аргумента.
Доктор Том вместо этого ответил на более важный вопрос:
Привет, Бев!
Хороший вопрос! Вы застали нас, математиков, со спущенными штанами. Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
... тогда это может означать, верно?
f(x) = sin(x + cos(x)) Я думаю, все более или менее согласны с тем, что сложение обязательно выполняется после функции, так что \(\sin\alpha + \beta \ne \sin(\alpha + \бета)\). (С другой стороны, если известно, что \(\alpha\) и \(\beta\) являются углами, мы могли бы считать очевидным, что первая форма должна означать вторую, поскольку мы никогда не добавляем углы к отношениям.) Но такое правило обычно не указывается явно, и без таких правил возможно все.
Это прозвучит ужасно, но я так часто видел это небрежное использование, что просто «знаю», что имелось в виду.Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом: х2 Она всегда писала так: 2x Точно так же я бы никогда не написал... грех х 2 ... или даже (грех х)2 Я бы переместил 2 вперед, чтобы сделать это ... 2 грех х ... или это: 2 грех(х) Точно так же интерпретировать это... грех 2x ... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\).
Они не считаются частью порядка операций или абсолютных правил; это просто обычная практика из вежливости — своего рода «условность».
В этом случае может быть принято соглашение: всегда писать триггерную функцию последней, а не следовать за ней какими-либо множителями; таким образом, все, что следует за «sin» (до «+»), является частью аргумента.
Большинство компьютерных языков требуют круглых скобок для триггерных функций (ну, любых функций), потому что они должны быть точными. Если вы ставите круглые скобки после sin, cos и т. д., то нет никаких сомнений в том, что содержимое этих круглых скобок точно представляет параметр функции 9.2 - 2, и этот результат умножается на 8x. Мне жаль, что нет четкого и ясного ответа, но так оно и есть: уродливый скелет в шкафу математика.Я пришел к выводу:
Итак, доктор Том более или менее согласен со мной, но говорит так, что дополняет мои объяснения.Начав с рассмотрения того, почему мы следуем соглашениям, которые мы делаем, в следующий раз я рассмотрю некоторые из многих вопросов, которые у нас были о причинах порядка операций.
Анализ синусоиды для преобразования Фурье
В основе всего анализа Фурье, как ни удивительно, лежит один максимум. формула школьной тригонометрии произведения двух синусов:
sin(A) * sin(B) = 1/2 * cos(A-B) - 1/2 * cos(A+B)Вот и все, самая тяжелая математика, с которой нам нужно разобраться. Вам не нужно запоминать его, так как главное понять не саму формулу, а то, как она работает. Мы будем смотреть на это шаг за шагом.
Когда вы впервые столкнулись с этим в старшей школе, A и B относились к фиксированным углам, и это, вероятно, не выглядело слишком полезный. Но он также отлично работает с синусоидой , волнами , где углы только увеличиваются со временем и волны исходят из круговой природы функции синуса. (Видеть Основы синусоиды (подробнее)
Таким образом, формулу можно использовать для умножения двух синусоидальные волны «чистого тона» на одной частоте A и B. Это не то, с чем мы сталкиваемся в повседневной жизни, так как чаще всего мы есть волны, которые добавьте вместе.
Например, звуки два разных музыкальных инструмента сливаются в воздухе... они не размножаются.
Поскольку они складываются, у нас по-прежнему есть две отдельные волны sin(A) и sin(B) в воздухе, на их исходных частотах A и B, которые наши уши будут интерпретировать как соответствующие высоты тона. Это , а не , то же самое, что и sin(A+B) , что было бы одиночная новая волна с более высокой частотой и, следовательно, с более высоким тоном.
Но что было бы, если бы мы могли умножить на два тона, которые не происходит с нормальными звуками? В соответствии с формулой, мы получили бы два совершенно разных тона, один с частота, являющаяся суммой двух исходных частот, и в этом и есть разница. Тот факт, что они косинусны волны вместо синусоидальных волн тривиальны: косинусоидальная волна просто синусоидальная волна, которая начинается немного раньше или позже во времени... наши уши не могут отличить продолжающуюся синусоиду от продолжающейся косинусоидальная волна.
(См. иллюстрацию в разделе Фаза синусоиды.)
Предположим, что две исходные частоты тона составляют 392 Гц и 440 Гц. Гц, что эквивалентно основным частотам G и A клавиши чуть выше средней C на фортепиано. Если мы умножим эти вместе по формуле получаем "разностный" тон 48 Гц и "суммарный" тон 832 Гц... даже близко не соответствует оригиналы, которых сейчас совсем нет!
Хотя в формуле предполагается, что каждая волна имеет амплитуду в один единицы, мы могли бы легко масштабировать любой вход (или оба) вверх или вниз, и вывод будет соответственно масштабироваться. Обратите внимание, что если мы умножьте вход волны A на некоторый коэффициент Ka и волну B на Kb, умножим каждый выход на произведение этих, Ka* Кб. Это означает, что независимо от того, имеет ли один вход большой амплитуда и один имеет небольшую амплитуду, как суммарный тон, так и разница тон будет равно по амплитуде... в половина произведения исходных входных амплитуд.
Теперь предположим, что оба исходных тона имели одинаковую частота, скажем, 440 Гц.
После умножения тон "сумма" будет 880 Гц, а "разностный" тон будет ноль Гц. На нулевой частоте это уже вряд ли "тон"... будет просто постоянным значением, равным амплитуде Волна 880 Гц. (Возможно, вы помните, что косинус 0 равен 1.)
Если мы попытаемся представить каждый из них в виде звуков, волна 880 Гц будет просто тон на октаву выше, чем оригинальная волна 440 Гц. В любой заданной точке воздуха давление будет повышаться и понижаться в течение 880 циклов подъема и опускания. в секунду, а в среднем давление в этой точке был бы неизменен. Не так обстоит дело с компонентом 0 Гц, который будет означать постоянное повышение давления. Поскольку оба эти компоненты присутствуют одновременно, мы можем рассматривать что новое давление воздуха будет колебаться около более высокого ценность. Если мы измерим среднее повышение давления, мы знали бы амплитуду компонента 0 Гц, и поскольку мы зная, что обе компоненты всегда равны, мы знали бы амплитуда составляющей 880 Гц.
Обратите внимание, что если две входные частоты равны , а не , не будет выходной составляющей 0 Гц и среднее значение таким образом останется на нуле.
Конечно, мы делаем все это не со звуками и воздухом. давление, так как у нас нет удобного способа умножить их. Вместо этого мы преобразуем звук (или любую форму волны, которую мы интересует) в напряжение и преобразовать его в числа с которыми могут справиться компьютеры.
Общая стратегия такова: пусть sin(A) будет входом неизвестная частота и амплитуда, а sin(B) будет известным опорная частота единичной амплитуды. Чтобы узнать, если неизвестная частота равна эталонной, мы умножаем эти вместе и усреднить продукт с течением времени (один или несколько циклов входных волн). Если среднее значение равно нулю, частоты отличаются, и мы ничего больше не знаем. Если среднее значение не ноль, мы знаем что входная частота такая же как эталона, и что его амплитуда в два раза превышает среднюю значение (поскольку эталонная амплитуда равна единице).
Пытаясь многочисленные эталонные частоты, мы можем найти ту, которая соответствует ввод.
Следующая тема, эксперимент по умножению синусоиды, позволяет вам получить практическое представление о вышеизложенном, используя Генератор Дакарты.
См. также Спектр (преобразование Фурье) Теория
Алгебраический синус — Чтение Фейнмана
Прескриптум (от 26 июня 2020 г.): Этот пост — часть серии довольно простых постов по элементарной математике и физике — не сильно пострадал от атаки темной силы — что хорошо, потому что мне все еще нравится это. Наслаждаться !
Исходный пост :
Этот пост призван лишить формулу Эйлера магии. На самом деле, я начал делать это в своем предыдущем посте, но я думаю, что в этом посте я лучше справился с организацией цепочки мыслей. [Просто чтобы убедиться: под «формулой Эйлера» я имею в виду e i x = cos(x) + i sin(x).
Эйлер действительно вывел много формул, но эта для математики — это то же самое, что E = m c 2 для физики. :-)]
Грандиозная идея состоит в том, чтобы начать с начальной линейной аппроксимации значения комплексной экспоненты e i s рядом с s = 0 (точнее, мы будем использовать e i ε = 1 + i ε формула), а затем показать, как «магия» i – через i 2 = –1 множитель – дает нам функции синуса и косинуса. По сути, мы собираемся построить функции синуса и косинуса алгебраически.
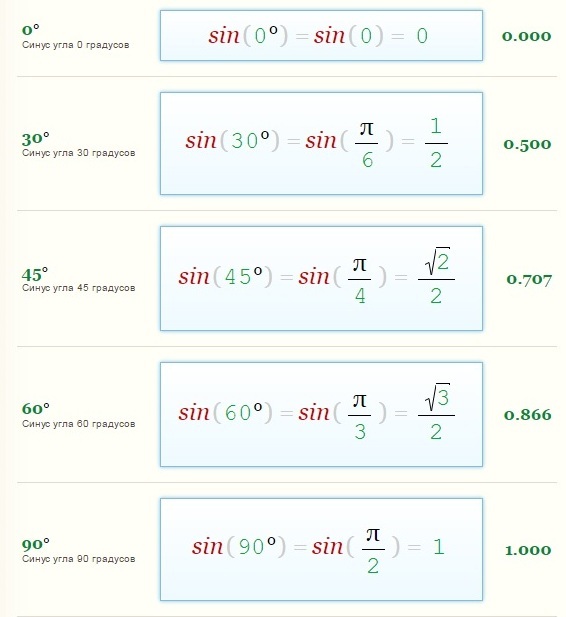
Давайте в качестве отправной точки — просто чтобы сфокусироваться — изобразим (i) действительную экспоненциальную функцию e x , то есть синий график, и (ii) действительную и мнимую части сложная экспоненциальная функция e i x = cos(x) + i sin(x), т. е.
красный и зеленый график — функции косинуса и синуса. Из этих графиков видно, что e x и e i x - два очень разных зверя.
1. e x — это всего лишь функция с действительным знаком от x, поэтому она «сопоставляет» действительное число x с некоторым другим действительным числом y = e x . Это значение y «улетает», тем самым демонстрируя силу экспоненциального роста. В 9 нет ничего особенного.0171 е х . Действительно, запись e x вместо 10 x , очевидно, выглядит лучше, когда вы ведете блог по математике или физике, но, честно говоря, нет реальной причины использовать это странное число e ≈ 2,718, когда все, что вам нужно, это просто стандартная реальная экспонента . На самом деле, если вы старшеклассник и хотите привлечь внимание какой-нибудь статьей, в которой говорится о том, что растет или сжимается, я бы рекомендовал использовать число 9.
0173 х . 🙂
2. e i x это то, что очень отличается от . Это комплексная функция от x, и речь не идет об экспоненциальном росте (хотя, очевидно, речь идет о возведении в степень, то есть о многократном умножении): y = e i x не «взрывается». Наоборот: у — просто периодическая «вещь» с двумя компонентами: синусом и косинусом. [Обратите внимание, что мы также можем изменить основание, например, на 10: тогда мы напишем 10 я х . Мы также получим что-то периодическое, но давайте не будем теряться, даже не начав.]
Действительно, два разных зверя. Как может добавление одного крошечного символа — маленького i в e i x — сделать такой большой разницей ?
У этих двух зверей есть одна общая черта: значение функции вблизи x = 0 может быть аппроксимировано одной и той же линейной формулой:
Если вам интересно, откуда это взялось, это в основном определение производной функции , как показано ниже.
В этом нет ничего особенного. Это так называемая первое приближение функции. Следует отметить, что у нас есть похожая формула для комплексной -значной функции e i x . Действительно, его производная равна d( e i x )/dx = , т.е. и . Итак… Да, главный результат в том, что мы можем эффективно записать:
e i ε ≈ 1 + i ε для малых ε
Конечно, 1 + i ε тоже другой «зверь», чем 1 + ε. Действительно, 1 + ε — это просто продолжение нашего обычного обхода вещественной оси, но 1 + i ε указывает в другом направлении (см. ниже). Этот пост покажет вам, куда он движется.
Давайте сначала снова поработаем с e x и подумаем о значении ε. Конечно, мы могли бы взять любое значение, например 0,1 или какую-то дробную часть 1/n. Мы будем использовать дробь — по причинам, которые станут понятны через мгновение.
Итак, теперь возникает вопрос: какое значение мы должны использовать для n в этой дроби 1/n? Что ж… Поскольку мы собираемся использовать это приближение в качестве начального значения в серии вычислений — будьте терпеливы: я объясню через мгновение — мы хотели бы получить достаточно малая дробь , так что наши последующие расчеты, основанные на этом начальном значении, не за горами. Но что такое достаточно маленький? Это 1/10, или 1/100 000, или 1/10 100 ? Что дает нам «достаточно хорошие» результаты? На самом деле, как мы определяем «достаточно хорошо»?
Хороший вопрос! Чтобы попытаться определить, что является «достаточно хорошим», я переверну все с ног на голову. В таблице ниже я вычисляю в обратном порядке от e 1 = e путем взятия последовательных квадратных корней из e . А? Какая? Терпение, пожалуйста! Просто пойдем немного со мной. Во-первых, я вычисляю e 1/2 , поэтому наша дробь ε, которую я просто напишу как x, равна здесь 1/2, поэтому приближение для e 1/2 равно 1 + 1/2 = 1,5.
Это выключено. Сколько? Что ж… Фактическое значение e 1/2 составляет около 1,648721 (см. таблицу ниже (или используйте калькулятор или электронную таблицу самостоятельно): обратите внимание, что, поскольку я скопировал таблицу из Excel, 9Икс). Теперь 1,648721 равно 1,5 + 0,148721, поэтому наше приближение (1,5) отличается примерно на 9 % (по сравнению с фактическим значением). Не так уж много, но давайте посмотрим, как мы можем улучшить. Возьмем еще раз квадратный корень: ( e 1/2 ) 1/2 = e 1/4 , поэтому x = 1/4. И затем я делаю это снова, так что я получаю e 1/8 , и так далее и тому подобное. Вплоть до x = 1/1024 = 1/2 10 , так что это десять итераций. Наше приближение 1 + x (см. пятый/последний столбец в таблице ниже) равно 1 + 1/1024 = 1 + 0,0009765625, который мы округлили до 1,000977 в таблице.
Фактическое значение e 1/1024 также составляет около 1,000977, как видно из третьего столбца таблицы.
Не точно , конечно, но… Ну… Точность нашего приближения здесь составляет шесть знаков после запятой, так что это эквивалентно одной миллионной. Это не плохо, но «достаточно ли хорошо»? Хм… Давайте подумаем об этом, но давайте сначала посчитаем некоторые другие вещи. Четвертый столбец в приведенной выше таблице вычисляет наклон этой линии AB на приведенном выше рисунке: его значение сходится к единице, как и следовало ожидать, потому что это наклон касательной в точке x = 0. [Итак, это значение производная от e x при x = 0. Просто проверьте это: d e x /dx = e x , очевидно, и e + 0 ] приближение x также сходится к 1 — как и должно быть!
Итак... Ну... Давайте теперь просто предположим, что нас устраивает это приближение с точностью до одной миллионной, так что давайте просто продолжим работать с дробью 1/1024 для x. Следовательно, будем писать, что e 1/1024 ≈ 1 + 1/1024 и теперь мы будем использовать это значение также для комплексной экспоненты .
А? Какая? Почему? Просто побудьте здесь немного. Потерпи. 🙂 So we'll just add the i again and, using that e i ε ≈ 1 + i ε expression, we write:
e i /1024 ≈ 1 + i /1024
Совершенно очевидно, что 1 + i /1024 — комплексное число: его действительная часть равна 1, а его мнимая часть равна 1/1024 = 0,0009765625.
Let's now work our way up again by using that complex number 1 + i /1024 = 1 + i ·0.0009765625 to calculate e i /512 , e i / 256 , e i /128 и так далее. Вплоть до x = 1, то есть e i . Я просто буду использовать другой символ для x: в таблице ниже я заменю x на s, потому что я буду время от времени обозначать действительную часть наших комплексных чисел как «x» (даже если я пишу и b в таблице ниже), поэтому я не могу использовать символ x для обозначения дроби.
[Я мог бы начать с s, но тогда… Ну… Действительные числа обычно обозначают через x, поэтому так было проще начать.] В любом случае…
The thing to note is how I calculate those values e i /512 , e i /256 , e i /128 etcetera. Я делаю это путем возведения в квадрат, т.е. просто умножаю (комплексное) число само на себя. To be very explicit, note that e i /512 = ( e i /1024 ) 2 = e i · 2/1024 = ( e i /1024 )( e i /1024 ). Итак, все, что я делаю в приведенной ниже таблице, — это умножаю комплексное число, которое у меня есть, на само себя, и затем я получаю новый результат, а затем возвожу его в квадрат еще раз, а затем снова, и снова, и так далее, и так далее.
Другими словами, возвращаясь назад, я просто беру квадрат (комплексного) числа. Конечно, вы знаете, как умножать число само на себя, но, поскольку мы говорим здесь о комплексных числах, мы должны записать его:
(A+ I · B) 2 = A 2 - B 2 + I · 2AB = A 2 - B 2 + 2AB 2 - B 2 + 2AB 2 - B 2 . было бы хорошо всегда отделять воображаемую единицу i от действительных чисел, таких как a, b или ab, но тогда я ленив, и поэтому я надеюсь, что вы всегда узнаете, что i — это воображаемая единица.] В любом случае… Когда мы возвращаемся назад (путем возведения в квадрат), действительная часть следующего числа (т. е. «x» в x + i y) — это a 2 — b 2 , а сложная часть («y») — это 2ab i . Вот что показано ниже — то есть в четвертом и пятом столбцах.
Посмотрите, что происходит.
x становится равным нулю, затем становится отрицательным, а y увеличивается до единицы. Теперь мы спустились с E 1/N = E 1 = E 1/1 по E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/176 = . мы могли бы начать с e 2 или e 4/n или любой другой. Следовательно, я должен продолжить вычисления выше, чтобы вы могли увидеть, что происходит, когда s становится равным 2, затем 3, а затем 4 и так далее и тому подобное. Вы увидите, что значение действительной и мнимой частей этой сложной экспоненты увеличивается и уменьшается между -1 и +1. Вы увидите, что обе функции представляют собой 90 171 периодическую 90 172 функции, такие как функции синуса и косинуса, которые я добавил в последние два столбца таблицы выше.
Теперь сравните эти значения a и b (т. е. второй и третий столбцы) со значениями косинуса и синуса (т. е. последние два столбца). […] Вы видите это? Вы видите, как закрыть они? Действительно, всего несколько частей на миллион.
Вы должны позволить этому утонуть на некоторое время. И я бы порекомендовал вам сделать электронную таблицу самостоятельно, чтобы вы действительно «понимали», что здесь происходит. Это все, что касается так называемой «магии» формулы Эйлера. Эта простая формула (a + i b) 2 = a 2 – b 2 + 2ab i показывает нам почему (и между действительной и мнимой частями ) и +1, как функции косинуса и синуса. На самом деле значения настолько близки, что легко понять, что следует дальше. Это же — в пределе, конечно .
Действительно, эти значения a 2 – b 2 и 2ab, т.е. действительная и мнимая части следующего комплексного числа в нашем ряду, являются тем, что Фейнман называет алгебраическими алгебраическими косинусом и , потому что мы вычисляем их как (a + i b) 2 = a 2 – б 2 + 2аб и .
Эти алгебраические значения косинуса и синуса близки к действительным значениям косинуса и синуса, особенно для малых дробей s. Конечно, там, где есть , расхождение становится — когда все сказано и сделано — мы делаем с самого начала несем небольшую ошибку, потому что остановились на 1/n = 1/1024, прежде чем вернуться обратно.
На самом деле есть гораздо более очевидный способ оценить ошибку: мы знать , что e 1/1024 должны быть некоторой точкой на самой единичной окружности. Следовательно, мы не должны приравнивать a к 1, если у нас есть некоторое значение b > 0. Или — что равнозначно тому же — если b немного больше 0, то a должно быть немного меньше 1. Таким образом, e i ε ≈ 1 + i ε является только приближением . Это не может быть точным для положительных значений ε. Это точно только при ε = 0.
Итак, мы ошибаемся, но не 92 и столбец 2ab) как –0,416553 и 0,6, но фактические значения cos(2) = –0,416146 и sin(2) = 0,7, что показывает, что наша алгебраическая функция косинуса и синуса действительно постепенно теряет точность (мы ошибаемся, как здесь одна тысячная, а не одна миллионная).
Это то, чего мы, конечно, ожидали, поскольку мы умножаем ошибки по мере того, как двигаемся «назад».
На приведенном ниже графике представлены значения таблицы.
Этот график также показывает, что по мере того, как мы постоянно удваиваем коэффициент r, точки данных разносятся все больше и больше. Это «расстояние» становится намного хуже при дальнейшем увеличении s: от s = 1 (это «самая высокая» точка на графике выше) мы перейдем к s = 2, а затем к s = 4, s = 8. , и так далее. Теперь эти значения равны , а не , как показано выше, но вы можете себе представить, где они находятся: при s = 2 мы где-то во втором квадранте, при s = 4 мы в третьем и так далее. Таким образом, 90 171, а не 90 172 составляют гладкий график. Нам нужны промежуточные точки. Итак, давайте «исправим» эту проблему, взяв только одно значение для s из таблицы (s = 1/4, например), и мы продолжим использовать это значение в качестве множителя.
Вот что сделано в таблице ниже.
Сначала это выглядит несколько пугающе, но на самом деле все просто. Во-первых, мы умножаем полученное значение на e 1/4 еще раз с самим собой, что дает нам действительную и мнимую части для e 1/8 (у нас это уже было в таблице выше, и вы можете проверить: мы получаем то же самое здесь). Мы , затем берем это значение (т. е. e 1/8 ) не , чтобы умножить его на себя, а на e 1/4 еще раз. Конечно, поскольку комплексные числа не совпадают, мы не можем использовать (a + i b) 2 = a 2 – b 2 + 2ab i правило больше. Теперь мы должны использовать более общее правило для умножения различных комплексных чисел: (a + i b)(c + i d) = (ac – bd) + i (ad + bc). Вот почему в этой таблице у меня есть столбцы a, b, c и d: a и b — компоненты первого числа, а c и d — второго (т.
е. и )
В приведенной выше таблице я позволил s диапазон от нуля (0) до семи (7) с шагом 0,25 (= 1/4). Еще раз, я добавил действительные значения косинуса и синуса для этих углов (они, конечно, выражены в радианах), потому что это то, что здесь s: угол, также известный как фаза комплексного числа . Так что можете сравнивать.
Таблица еще раз подтверждает, что мы медленно теряем точность (сейчас мы ошибаемся на 3-4 части на тысячу), но это очень только очень медленно: нам нужно было бы сделать много «петлей» вокруг центра, прежде чем мы действительно смогли бы увидеть разницу на графике. Эй! Давайте сделаем график. [Excel такой же, как , отличный инструмент, не так ли?] Вот оно: толстая черная линия, описывающая окружность на графике ниже, соединяет фактический косинус и синус значения, связанные с углом 1 /4, 1/2, 3/8 и так далее, вплоть до 7 (7 — это примерно 2,3π, так что после «петли» мы примерно на 40 градусов от исходной точки), в то время как маленькое «9Метки 0021 + ‘ — это точки данных для алгебраических косинуса и синуса.
Они идеально совпадают, потому что наш глаз не может увидеть небольшое несоответствие.
Итак… Вот и все. Конец истории.
Что?
Да. Вот и все. Конец истории. Я сделал то, что обещал. I построил функции синуса и косинуса алгебраически . Нет компаса. 🙂 Простая арифметика, включая только одно дополнительное правило: i 2 = –1. Вот и все.
Надеюсь, у меня получилось. Цель состояла в том, чтобы избавить формулу Эйлера от магии, показав, как приближение e i ε = 1 + i ε и определение i 2 = –1 дает нам сама функция косинуса и синуса по мере того, как мы движемся по единичному кругу, начиная с единичной точки на действительной оси, как показано на этом маленьком графике:
Конечно, ε, с которым мы работали, было намного меньше, чем предполагает размер стрелки (точнее, оно было равно 1/1024 ≈ 0,000977), но это просто для того, чтобы показать, как работают дифференциалы.
🙂 Неплохо, не так ли? 🙂
Post scriptum :
I. Во всяком случае, все, что в этом посте было сделано, это продемонстрировать умножение комплексных чисел. В самом деле, когда все сказано и сделано, возведение в степень — это многократное умножение — как для действительных, так и для комплексных показателей. Единственная разница в том, что… Комплексные экспоненты дают нам эти колеблющиеся вещи, потому что комплексные экспоненты эффективно добавляют функции синуса и косинуса.0005
Теперь мы можем делать с этим что угодно. В этом посте мы построили круг без компаса. Это не так хорошо, как квадратура круга 🙂, но, тем не менее, это привело бы в трепет Пифагора. Ниже я строю спираль, выполняя те же математические операции: я снова начинаю с комплексного числа, но теперь оно на больше от единичного круга (1 + 0,247434 i ). На самом деле я взял то же значение синуса, что и для e i /4 , но я заменил значение косинуса (0,969031) на 1 , ровно ).
Другими словами, мой ε здесь намного больше.
Затем я умножаю это комплексное число 1 + 0,247434 i на само , чтобы получить следующее число (0,938776 + 0,494868 i ), а затем я умножаю этот результат еще раз на мое первое число 2 (17 + 33 34 ) . i ), точно так же, как мы делали это, когда строили круг. И тогда это продолжается и продолжается и продолжается. Таким образом, единственная разница заключается в начальном значении: оно немного больше от единичный круг. [Когда мы строили круг, наше начальное значение тоже немного отличалось, но намного меньше . Здесь мы идем к гораздо большей разнице.]
Итак, вы можете видеть, что происходит: умножение комплексных чисел равносильно сложению углов и умножению величин: i δ = αγ e i (β+ δ) =|α e i β |·|γ e i δ | e i (β+ δ) | = |α||γ| e i (β+ δ) .
Итак, поскольку мы начали с комплексного числа с величиной чуть больше 1 (вы вычисляете его, используя теорему Пифагора: это 1,03, больше или меньше, что составляет 3%, в отличие от менее одной миллионной для 1). + 0,000977 i число), следующая точка, конечно, тоже немного отстоит от единичного круга, и на самом деле чуть больше 3%. И так продолжается и продолжается, и «еще немного» становится все больше и больше в процессе.
Построение графа, подобного этому, похоже на глупости, которые я проделывал, когда программировал маленькие игры на нашем Commodore 64 в 1980-х, так что я не должен слишком останавливаться на этом. На самом деле, если подумать, я должен был начать рядом — и , тогда моя спираль напоминала бы и . 🙂 И, да — для семейного чтения — это тоже как любимое хобби нашего папы: вычисление лучшего значения для π. 🙂
Однако… Единственное, пожалуй, следует отметить, что такой итерационный процесс напоминает — в какой-то мере — процесс, который системы итерационных функций (IFS) используют для создания фракталов.
Так что… ну… это просто мило, я думаю. [ХОРОШО. Это просто оправдание. Извините.]
II. Другая вещь, которую я продемонстрировал в этом посте, может показаться тривиальной, но я подчеркну ее здесь, потому что она помогла мне (хотя насчет вас не уверена) понять сущность реальных экспонент намного лучше, чем я это делал раньше. . Итак, что это?
Ну… Это довольно примечательный факт, что вычисление (реальных) иррациональных степеней сводится к бесконечной итерации. Что я имею в виду?
Ну… Помните, что мы продолжали извлекать квадратный корень из e , поэтому мы вычислили e 1/2 , а затем ( e 1/2 ) 1/2 = e 1/4 , а затем ( E 1/4 ) 1/2 = E 1/8 , а затем мы продолжили: E 7 1/8 1.17 1.9017 1.9017 1.9017 1.9017 1.9017 1/8 . e 1/32 , e 1/64 , вплоть до e 1/1024 , где мы остановились.
Это было всего 10 итераций. Однако было ясно, что мы можем продолжать и продолжать, чтобы найти тот предел, который мы так хорошо знаем: e 1/Δ стремится к 1 ( не к нулю (0) и не к e либо!) для ∆→ ∞.
Теперь e = e 1 сама является экспоненциальной, поэтому мы можем переключиться на другое основание, например, на 10, используя общее a s = (b k ) 7 s 6 = б кс 9формула 0176 = b t , где k = log b (а). Давайте возьмем основание-10: мы получим e 1 = [10 log 10 ( e ) ] 1 = 7 10 0,434294… и т. д. Теперь, поскольку e является иррациональным числом, log 10 (e) также иррационально, так что у нас действительно есть бесконечное количество десятичных знаков после запятой в 0,434294… и так далее. На самом деле e не только иррационально, но и трансцендентно : мы не можем вычислить его алгебраически, т.
е. как корень некоторого многочлена с рациональными коэффициентами. Между прочим, большинство иррациональных чисел таковы, так что не думайте, что быть «трансцендентным» — это что-то особенное. В любом случае… Это более тонкий момент, который здесь не имеет большого значения. Вы поняли идею, я надеюсь. Это следующее:
- Когда у нас есть рациональная степень m/n , полезно думать о ней как о произведении m факторов a 1/n (и, конечно, если мы хотим вычислить m/n без использования калькулятора, что, признаюсь, уже не очень модно, и поэтому никто никогда так не делает: очень плохо, потому что ручная работа действительно помогает лучше понимать вещи). Запишем: a m/n = a m·(1/n) =(a 1/n ) m = a 1/n ·a 1/n ·a 1/n ·a 1/n =·… (m раз). Это действительно просто: возведение в степень — это многократное умножение. [Конечно, если m отрицательно, то мы просто запишем m/n как 1/(a m/n ), но это не меняет общей идеи возведения в степень.
]
- Однако гораздо труднее понять, почему и как возведение в степень с иррациональными степенями равносильно повторному умножению. Довольно длинное разоблачение выше показывает… Ну, возможно, не почему , но уж точно как . [А в математике, если мы можем показать как , это обычно сводится к показу почему также , не так ли? :-)] Действительно, когда мы думаем о r (т. е. иррациональной степени некоторого (действительного) числа a), мы можем представить его как произведение бесконечного числа множителей a r/ Δ . Действительно, мы можем записать r как:
a r = a r(1/Δ + 1/Δ + 1/Δ + 1/Δ +…) = a r/Δ ·a r/Δ ·a r/Δ ·a r/Δ …
Не уверены? Let's work an example: 10 π = [ e ln10 ] π = [ e ln10 ] π = e ln10· π = e ln10 · π = e 7,233784… Конечно, если вы возьмете свой калькулятор, вы найдете что-то вроде 1385,455731, оба за 10 π и e 7,233784 (надеюсь!), но так что тут не в этом дело.
We've shown that e is an infinite product e 1/Δ · e 1/Δ · e 1/Δ · e 1/Δ ·… = e (1/Δ+ 1/Δ+1/Δ+1/Δ+…) = e Δ/Δ с Δ некоторым бесконечно большим (но целым ) числом. В нашем примере мы остановили расчет на Δ = 1024, но вы видите логику: можно было продолжать бесконечно. Следовательно, мы можем написать E 7.233784… AS
E 7,233784… = E 7,233784… ( 1/°+,171717171717171717171717171717171717,17171717171717171717,171717171717171717,1717171717171717,17171717171717,1717,1717,1717,1717,1717,1717,1717,1717,1717,1717,1717,1717, E 7.233784…/Δ · E 7,233784…/Δ · E 7.233784…/Δ 7171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717171717 2 .
Вернемся к основанию 10. Мы можем записать множители e 7,233784…/Δ как e (ln10·π)/Δ = [ e ln10 ] π/Δ = 10 π/Δ . Таким образом, наша первоначальная мощность 10 π равна: 10 π = 10 π/Δ · 10 π/Δ · 10 π/Δ · · 10 π/Δ · 6 · 100173 π/Δ · 6 · 100173. /Δ · 10 π/Δ … = 10 π(Δ/Δ) , и, конечно, 10 1/Δ также стремится к 1 при стремлении Δ к бесконечности ( не к нулю, и не до 10 тоже). 🙂 Итак, да, мы можем сделать это для любого действительного числа a и для любого r.
Опять же, это может показаться очень тривиальным для опытного математического глаза, но, как новичок в Математической Стране Чудес, я чувствовал, что должен пройти через это, чтобы действительно понять иррациональные силы. Так что это может вам помочь, а может и не помочь, в зависимости от того, где вы находитесь в MW.
[Надеюсь, доказывать, что предел для ∆/∆ стремится к 1, когда ∆ стремится к ∞, не нужно? 🙂 Но на всякий случай, если вам интересно, как могут быть связаны формулы для рациональных и иррациональных сил, мы можем просто написать m/n = a (m/n)(1/Δ + 1/Δ + 1/Δ + 1/Δ +…) = a m/nΔ ·a m/nΔ ·a m/nΔ ·a m/nΔ ·…= (a 1/Δ + 1/Δ + 1/Δ + 1/Δ +… ) m/n = a m/n , as мы ожидаем. :-)]
III. Так как же получается, что a r = a r/Δ · a r/Δ · a r/Δ · a r/Δ … формула работает для комплексных экспонент? Мы просто добавляем к , поэтому мы пишем i r но мы знаем, какой эффект это имеет: теперь у нас другой зверь. Функция с комплексным значением от r, или… Ну… Если мы сохраним показатель степени фиксированным, то это будет функция с комплексным значением от a! В самом деле, помните, что здесь у нас есть выбор (и две обратные функции!).
Однако обратите внимание, что мы можем написать i r двумя разными способами. У нас есть две интерпретации здесь на самом деле:
A. Первая интерпретация является самым простым: мы пишем I R в качестве I R = (A R ) I = I = I = I = I = . r/Δ + r/Δ + r/Δ +… ) i .
Итак, у нас есть реальная степень, r , и это некоторое действительное число , а затем мы возводим его в степень i , чтобы создать этого нового зверя: комплекснозначную функцию с двумя компоненты, одна мнимая и одна реальная. И тогда мы знаем, как связать их с функцией синуса и косинуса: мы просто меняем основание на и и все готово.
На самом деле, теперь, когда мы здесь, давайте пойдем до конца и сделаем это.
Как упоминалось в моем предыдущем посте, из этого следует a s = ( e k ) s = e ks = e t с формулой la 6 t ) – единственным эффектом изменения базы является изменение масштаба горизонтальной оси: график s полностью идентичен графику e t действительно: нам просто нужно заменить s на t = ks = ln(a)·s. Это все. Итак, у нас есть формула Эйлера для i s . Например, для основания 10 мы имеем 10 i s = cos[ln(a)·s] + i sin[ln(a)·s].
Но давайте не будем вдаваться в подробности. Идея здесь в том, что мы позволяем i «действовать» на r , так сказать . И тогда, конечно, мы можем написать r как хотим, но это не меняет суть того, с чем мы имеем дело.
B. Вторая интерпретация несколько сложнее: мы пишем A I R как I R = A I R/Δ 667673 I R/ I R/ .
·a i r/Δ ·a i r/Δ ·…
Итак, это произведение (бесконечного) числа комплексных множителей 92 i Теперь , что это интерпретация, сильно отличающаяся от приведенной выше, даже если математический результат при подстановке действительных чисел вместо a и r — очевидно — должен быть одинаковым. Если результат тот же, то что я говорю на самом деле ? Ну… Думаю, ничего особенного. Просто интерпретация возведения в степень как повторного умножения имеет смысл и для комплексных экспонент:
- 0173 I M /N = A I /N · A I /N · A I /N · A I /N · A I /N · A I /N · I /N · I /N · I /N · I /N · I .

- For irrational r, we'll have an infinite number of complex factors a i r = a i r/Δ ·a i r/Δ ·a i r/Δ ·a i r/Δ … и так далее.
Итак, разница с первой интерпретацией в том, что вместо того, чтобы смотреть на i r as a real number a r that's being raised to the complex power i , we're looking at a i r as a complex number a i , возведенное в действительную степень r. Как было сказано, математический результат при подстановке действительного числа вместо a и r, очевидно, должен быть одинаковым. [Иначе у нас были бы серьёзные проблемы: математика есть математика. Мы не можем связать одно и то же с двумя разными результатами.] Но, как было сказано, мы можем эффективно интерпретировать a i r двумя способами.
[…]
То, что я здесь делаю, это, конечно же, рассмотрение всех видов математических операций здесь — включая возведение в степень — в комплексном пространстве , а не в реальном пространстве. Итак, первый шаг — возведение комплексного числа в действительную степень (в отличие от возведения действительного числа в комплексную степень). Следующим шагом будет возведение комплексного числа в комплексную степень. Итак, мы говорим комплекснозначные функции комплексных переменных .
Вот что такое комплексный анализ, и я очень подробно написал об этом в своем посте за октябрь-ноябрь 2013 года. Поэтому я бы посоветовал вам перечитать их теперь, когда у вас, надеюсь, появилось немного больше «интуитивного» понимания комплексных чисел на фоне, изложенном в этом и моем предыдущем посте.
Комплексный анализ включает в себя отображение (т. е. отображение из одного комплексного пространства в другое), а это, в свою очередь, включает концепцию так называемых аналитических и/или голоморфных функций.

 9}{9!}-\dots$, но упёрся в пороговое значение double. «А, так аргумент ведь в радианах брать надо было!» — догадался он, и пообещал исправить ошибку в следующей версии.
9}{9!}-\dots$, но упёрся в пороговое значение double. «А, так аргумент ведь в радианах брать надо было!» — догадался он, и пообещал исправить ошибку в следующей версии. Вы можете увидеть некоторые из этих разработок в порядке операций здесь:
История порядка операций
http://mathforum.org/library/drmath/view/52582.html
Вы можете увидеть некоторые из этих разработок в порядке операций здесь:
История порядка операций
http://mathforum.org/library/drmath/view/52582.html 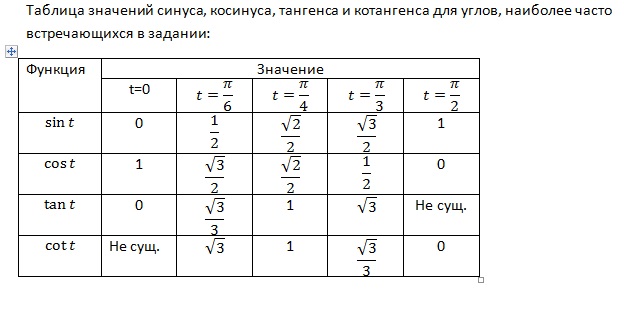
 Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
 Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом:
х2
Она всегда писала так:
2x
Точно так же я бы никогда не написал...
грех х 2
... или даже
(грех х)2
Я бы переместил 2 вперед, чтобы сделать это ...
2 грех х
... или это:
2 грех(х)
Точно так же интерпретировать это...
грех 2x
... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\).
Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом:
х2
Она всегда писала так:
2x
Точно так же я бы никогда не написал...
грех х 2
... или даже
(грех х)2
Я бы переместил 2 вперед, чтобы сделать это ...
2 грех х
... или это:
2 грех(х)
Точно так же интерпретировать это...
грех 2x
... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\). Они не считаются частью порядка операций или абсолютных правил; это просто обычная практика из вежливости — своего рода «условность».
Они не считаются частью порядка операций или абсолютных правил; это просто обычная практика из вежливости — своего рода «условность». 
 Например, звуки
два разных музыкальных инструмента сливаются в воздухе...
они не размножаются.
Например, звуки
два разных музыкальных инструмента сливаются в воздухе...
они не размножаются. (См. иллюстрацию в разделе Фаза синусоиды.)
(См. иллюстрацию в разделе Фаза синусоиды.) После умножения тон "сумма"
будет 880 Гц, а "разностный" тон будет ноль Гц. На нулевой частоте это уже вряд ли "тон"...
будет просто постоянным значением, равным амплитуде
Волна 880 Гц. (Возможно, вы помните, что косинус 0 равен 1.)
После умножения тон "сумма"
будет 880 Гц, а "разностный" тон будет ноль Гц. На нулевой частоте это уже вряд ли "тон"...
будет просто постоянным значением, равным амплитуде
Волна 880 Гц. (Возможно, вы помните, что косинус 0 равен 1.)
 Пытаясь
многочисленные эталонные частоты, мы можем найти ту, которая соответствует
ввод.
Пытаясь
многочисленные эталонные частоты, мы можем найти ту, которая соответствует
ввод. Эйлер действительно вывел много формул, но эта для математики — это то же самое, что E = m c 2 для физики. :-)]
Эйлер действительно вывел много формул, но эта для математики — это то же самое, что E = m c 2 для физики. :-)] красный и зеленый график — функции косинуса и синуса. Из этих графиков видно, что e x и e i x - два очень разных зверя.
красный и зеленый график — функции косинуса и синуса. Из этих графиков видно, что e x и e i x - два очень разных зверя. 0173 х . 🙂
0173 х . 🙂 В этом нет ничего особенного. Это так называемая первое приближение функции. Следует отметить, что у нас есть похожая формула для комплексной -значной функции e i x . Действительно, его производная равна d( e i x )/dx = , т.е. и . Итак… Да, главный результат в том, что мы можем эффективно записать:
В этом нет ничего особенного. Это так называемая первое приближение функции. Следует отметить, что у нас есть похожая формула для комплексной -значной функции e i x . Действительно, его производная равна d( e i x )/dx = , т.е. и . Итак… Да, главный результат в том, что мы можем эффективно записать: Итак, теперь возникает вопрос: какое значение мы должны использовать для n в этой дроби 1/n? Что ж… Поскольку мы собираемся использовать это приближение в качестве начального значения в серии вычислений — будьте терпеливы: я объясню через мгновение — мы хотели бы получить достаточно малая дробь , так что наши последующие расчеты, основанные на этом начальном значении, не за горами. Но что такое достаточно маленький? Это 1/10, или 1/100 000, или 1/10 100 ? Что дает нам «достаточно хорошие» результаты? На самом деле, как мы определяем «достаточно хорошо»?
Итак, теперь возникает вопрос: какое значение мы должны использовать для n в этой дроби 1/n? Что ж… Поскольку мы собираемся использовать это приближение в качестве начального значения в серии вычислений — будьте терпеливы: я объясню через мгновение — мы хотели бы получить достаточно малая дробь , так что наши последующие расчеты, основанные на этом начальном значении, не за горами. Но что такое достаточно маленький? Это 1/10, или 1/100 000, или 1/10 100 ? Что дает нам «достаточно хорошие» результаты? На самом деле, как мы определяем «достаточно хорошо»? Это выключено. Сколько? Что ж… Фактическое значение e 1/2 составляет около 1,648721 (см. таблицу ниже (или используйте калькулятор или электронную таблицу самостоятельно): обратите внимание, что, поскольку я скопировал таблицу из Excel, 9Икс). Теперь 1,648721 равно 1,5 + 0,148721, поэтому наше приближение (1,5) отличается примерно на 9 % (по сравнению с фактическим значением). Не так уж много, но давайте посмотрим, как мы можем улучшить. Возьмем еще раз квадратный корень: ( e 1/2 ) 1/2 = e 1/4 , поэтому x = 1/4. И затем я делаю это снова, так что я получаю e 1/8 , и так далее и тому подобное. Вплоть до x = 1/1024 = 1/2 10 , так что это десять итераций. Наше приближение 1 + x (см. пятый/последний столбец в таблице ниже) равно 1 + 1/1024 = 1 + 0,0009765625, который мы округлили до 1,000977 в таблице.
Это выключено. Сколько? Что ж… Фактическое значение e 1/2 составляет около 1,648721 (см. таблицу ниже (или используйте калькулятор или электронную таблицу самостоятельно): обратите внимание, что, поскольку я скопировал таблицу из Excel, 9Икс). Теперь 1,648721 равно 1,5 + 0,148721, поэтому наше приближение (1,5) отличается примерно на 9 % (по сравнению с фактическим значением). Не так уж много, но давайте посмотрим, как мы можем улучшить. Возьмем еще раз квадратный корень: ( e 1/2 ) 1/2 = e 1/4 , поэтому x = 1/4. И затем я делаю это снова, так что я получаю e 1/8 , и так далее и тому подобное. Вплоть до x = 1/1024 = 1/2 10 , так что это десять итераций. Наше приближение 1 + x (см. пятый/последний столбец в таблице ниже) равно 1 + 1/1024 = 1 + 0,0009765625, который мы округлили до 1,000977 в таблице. Не точно , конечно, но… Ну… Точность нашего приближения здесь составляет шесть знаков после запятой, так что это эквивалентно одной миллионной. Это не плохо, но «достаточно ли хорошо»? Хм… Давайте подумаем об этом, но давайте сначала посчитаем некоторые другие вещи. Четвертый столбец в приведенной выше таблице вычисляет наклон этой линии AB на приведенном выше рисунке: его значение сходится к единице, как и следовало ожидать, потому что это наклон касательной в точке x = 0. [Итак, это значение производная от e x при x = 0. Просто проверьте это: d e x /dx = e x , очевидно, и e + 0 ] приближение x также сходится к 1 — как и должно быть!
Не точно , конечно, но… Ну… Точность нашего приближения здесь составляет шесть знаков после запятой, так что это эквивалентно одной миллионной. Это не плохо, но «достаточно ли хорошо»? Хм… Давайте подумаем об этом, но давайте сначала посчитаем некоторые другие вещи. Четвертый столбец в приведенной выше таблице вычисляет наклон этой линии AB на приведенном выше рисунке: его значение сходится к единице, как и следовало ожидать, потому что это наклон касательной в точке x = 0. [Итак, это значение производная от e x при x = 0. Просто проверьте это: d e x /dx = e x , очевидно, и e + 0 ] приближение x также сходится к 1 — как и должно быть! А? Какая? Почему? Просто побудьте здесь немного. Потерпи. 🙂 So we'll just add the i again and, using that e i ε ≈ 1 + i ε expression, we write:
А? Какая? Почему? Просто побудьте здесь немного. Потерпи. 🙂 So we'll just add the i again and, using that e i ε ≈ 1 + i ε expression, we write: [Я мог бы начать с s, но тогда… Ну… Действительные числа обычно обозначают через x, поэтому так было проще начать.] В любом случае…
[Я мог бы начать с s, но тогда… Ну… Действительные числа обычно обозначают через x, поэтому так было проще начать.] В любом случае… Другими словами, возвращаясь назад, я просто беру квадрат (комплексного) числа. Конечно, вы знаете, как умножать число само на себя, но, поскольку мы говорим здесь о комплексных числах, мы должны записать его:
Другими словами, возвращаясь назад, я просто беру квадрат (комплексного) числа. Конечно, вы знаете, как умножать число само на себя, но, поскольку мы говорим здесь о комплексных числах, мы должны записать его: x становится равным нулю, затем становится отрицательным, а y увеличивается до единицы. Теперь мы спустились с E 1/N = E 1 = E 1/1 по E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/176 = . мы могли бы начать с e 2 или e 4/n или любой другой. Следовательно, я должен продолжить вычисления выше, чтобы вы могли увидеть, что происходит, когда s становится равным 2, затем 3, а затем 4 и так далее и тому подобное. Вы увидите, что значение действительной и мнимой частей этой сложной экспоненты увеличивается и уменьшается между -1 и +1. Вы увидите, что обе функции представляют собой 90 171 периодическую 90 172 функции, такие как функции синуса и косинуса, которые я добавил в последние два столбца таблицы выше.
x становится равным нулю, затем становится отрицательным, а y увеличивается до единицы. Теперь мы спустились с E 1/N = E 1 = E 1/1 по E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/N = E 1/176 = . мы могли бы начать с e 2 или e 4/n или любой другой. Следовательно, я должен продолжить вычисления выше, чтобы вы могли увидеть, что происходит, когда s становится равным 2, затем 3, а затем 4 и так далее и тому подобное. Вы увидите, что значение действительной и мнимой частей этой сложной экспоненты увеличивается и уменьшается между -1 и +1. Вы увидите, что обе функции представляют собой 90 171 периодическую 90 172 функции, такие как функции синуса и косинуса, которые я добавил в последние два столбца таблицы выше. Теперь сравните эти значения a и b (т. е. второй и третий столбцы) со значениями косинуса и синуса (т. е. последние два столбца). […] Вы видите это? Вы видите, как закрыть они? Действительно, всего несколько частей на миллион.
Теперь сравните эти значения a и b (т. е. второй и третий столбцы) со значениями косинуса и синуса (т. е. последние два столбца). […] Вы видите это? Вы видите, как закрыть они? Действительно, всего несколько частей на миллион.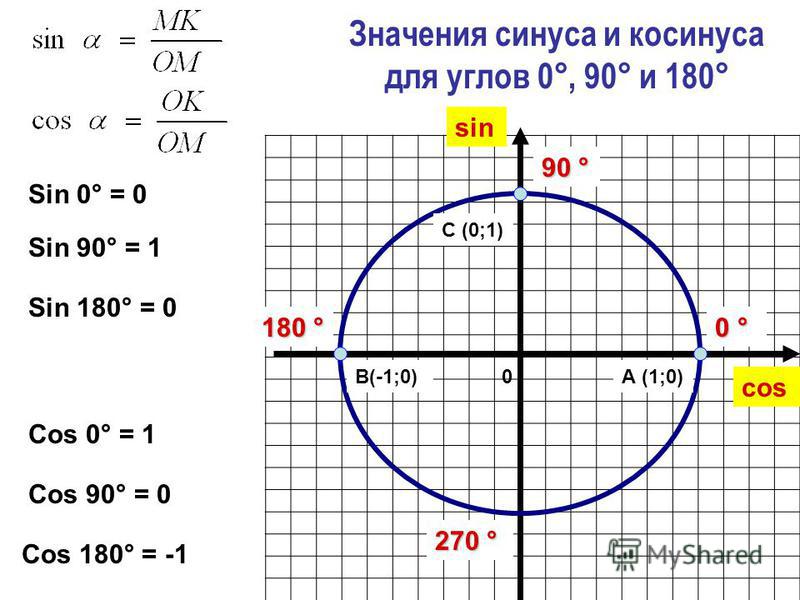 Эти алгебраические значения косинуса и синуса близки к действительным значениям косинуса и синуса, особенно для малых дробей s. Конечно, там, где есть , расхождение становится — когда все сказано и сделано — мы делаем с самого начала несем небольшую ошибку, потому что остановились на 1/n = 1/1024, прежде чем вернуться обратно.
Эти алгебраические значения косинуса и синуса близки к действительным значениям косинуса и синуса, особенно для малых дробей s. Конечно, там, где есть , расхождение становится — когда все сказано и сделано — мы делаем с самого начала несем небольшую ошибку, потому что остановились на 1/n = 1/1024, прежде чем вернуться обратно.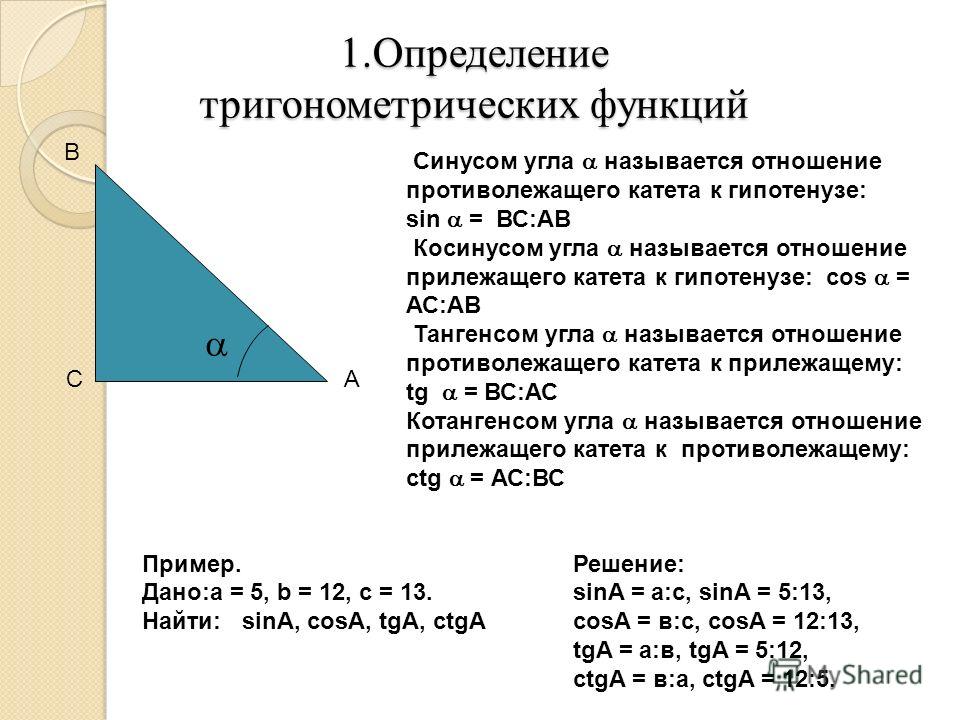 Это то, чего мы, конечно, ожидали, поскольку мы умножаем ошибки по мере того, как двигаемся «назад».
Это то, чего мы, конечно, ожидали, поскольку мы умножаем ошибки по мере того, как двигаемся «назад».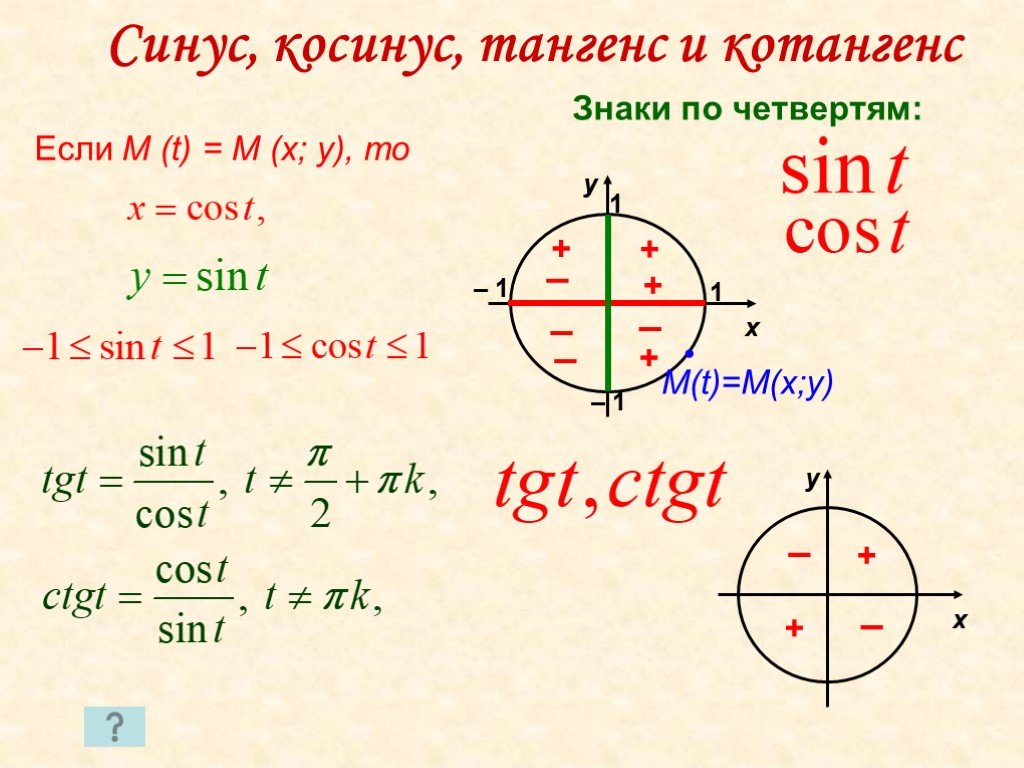 Сначала это выглядит несколько пугающе, но на самом деле все просто. Во-первых, мы умножаем полученное значение на e 1/4 еще раз с самим собой, что дает нам действительную и мнимую части для e 1/8 (у нас это уже было в таблице выше, и вы можете проверить: мы получаем то же самое здесь). Мы , затем берем это значение (т. е. e 1/8 ) не , чтобы умножить его на себя, а на e 1/4 еще раз. Конечно, поскольку комплексные числа не совпадают, мы не можем использовать (a + i b) 2 = a 2 – b 2 + 2ab i правило больше. Теперь мы должны использовать более общее правило для умножения различных комплексных чисел: (a + i b)(c + i d) = (ac – bd) + i (ad + bc). Вот почему в этой таблице у меня есть столбцы a, b, c и d: a и b — компоненты первого числа, а c и d — второго (т.
Сначала это выглядит несколько пугающе, но на самом деле все просто. Во-первых, мы умножаем полученное значение на e 1/4 еще раз с самим собой, что дает нам действительную и мнимую части для e 1/8 (у нас это уже было в таблице выше, и вы можете проверить: мы получаем то же самое здесь). Мы , затем берем это значение (т. е. e 1/8 ) не , чтобы умножить его на себя, а на e 1/4 еще раз. Конечно, поскольку комплексные числа не совпадают, мы не можем использовать (a + i b) 2 = a 2 – b 2 + 2ab i правило больше. Теперь мы должны использовать более общее правило для умножения различных комплексных чисел: (a + i b)(c + i d) = (ac – bd) + i (ad + bc). Вот почему в этой таблице у меня есть столбцы a, b, c и d: a и b — компоненты первого числа, а c и d — второго (т. е. и )
е. и ) Они идеально совпадают, потому что наш глаз не может увидеть небольшое несоответствие.
Они идеально совпадают, потому что наш глаз не может увидеть небольшое несоответствие.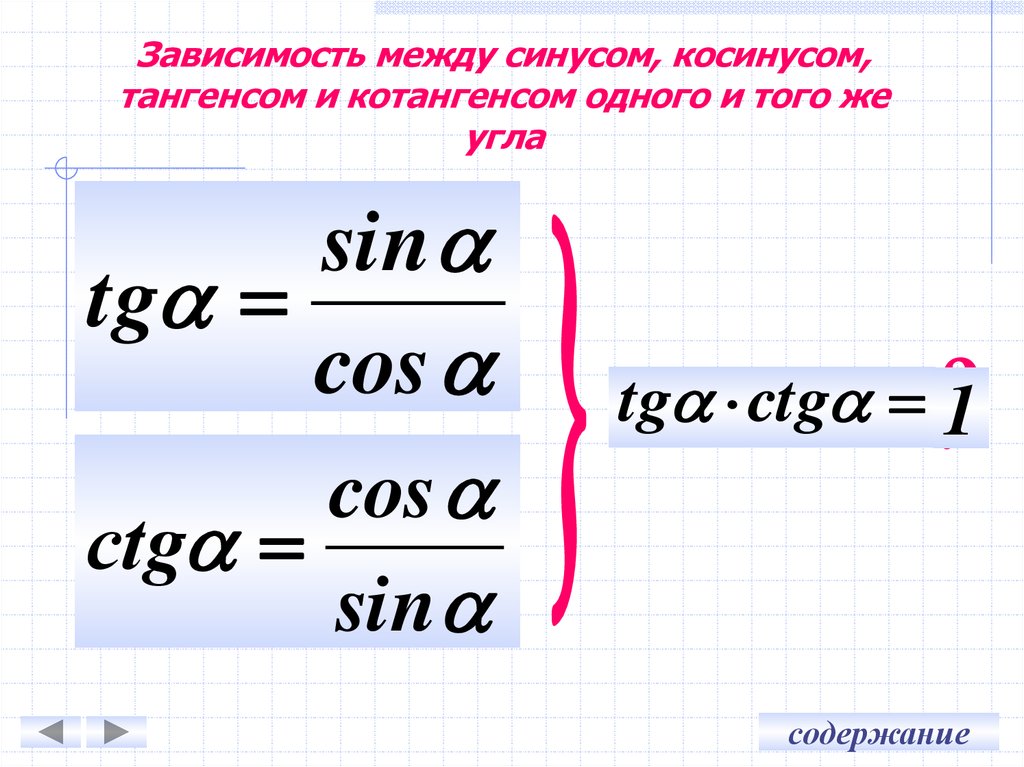 🙂 Неплохо, не так ли? 🙂
🙂 Неплохо, не так ли? 🙂 Другими словами, мой ε здесь намного больше.
Другими словами, мой ε здесь намного больше. Итак, поскольку мы начали с комплексного числа с величиной чуть больше 1 (вы вычисляете его, используя теорему Пифагора: это 1,03, больше или меньше, что составляет 3%, в отличие от менее одной миллионной для 1). + 0,000977 i число), следующая точка, конечно, тоже немного отстоит от единичного круга, и на самом деле чуть больше 3%. И так продолжается и продолжается, и «еще немного» становится все больше и больше в процессе.
Итак, поскольку мы начали с комплексного числа с величиной чуть больше 1 (вы вычисляете его, используя теорему Пифагора: это 1,03, больше или меньше, что составляет 3%, в отличие от менее одной миллионной для 1). + 0,000977 i число), следующая точка, конечно, тоже немного отстоит от единичного круга, и на самом деле чуть больше 3%. И так продолжается и продолжается, и «еще немного» становится все больше и больше в процессе. Так что… ну… это просто мило, я думаю. [ХОРОШО. Это просто оправдание. Извините.]
Так что… ну… это просто мило, я думаю. [ХОРОШО. Это просто оправдание. Извините.] Это было всего 10 итераций. Однако было ясно, что мы можем продолжать и продолжать, чтобы найти тот предел, который мы так хорошо знаем: e 1/Δ стремится к 1 ( не к нулю (0) и не к e либо!) для ∆→ ∞.
Это было всего 10 итераций. Однако было ясно, что мы можем продолжать и продолжать, чтобы найти тот предел, который мы так хорошо знаем: e 1/Δ стремится к 1 ( не к нулю (0) и не к e либо!) для ∆→ ∞. е. как корень некоторого многочлена с рациональными коэффициентами. Между прочим, большинство иррациональных чисел таковы, так что не думайте, что быть «трансцендентным» — это что-то особенное. В любом случае… Это более тонкий момент, который здесь не имеет большого значения. Вы поняли идею, я надеюсь. Это следующее:
е. как корень некоторого многочлена с рациональными коэффициентами. Между прочим, большинство иррациональных чисел таковы, так что не думайте, что быть «трансцендентным» — это что-то особенное. В любом случае… Это более тонкий момент, который здесь не имеет большого значения. Вы поняли идею, я надеюсь. Это следующее: ]
] We've shown that e is an infinite product e 1/Δ · e 1/Δ · e 1/Δ · e 1/Δ ·… = e (1/Δ+ 1/Δ+1/Δ+1/Δ+…) = e Δ/Δ с Δ некоторым бесконечно большим (но целым ) числом. В нашем примере мы остановили расчет на Δ = 1024, но вы видите логику: можно было продолжать бесконечно. Следовательно, мы можем написать E 7.233784… AS
We've shown that e is an infinite product e 1/Δ · e 1/Δ · e 1/Δ · e 1/Δ ·… = e (1/Δ+ 1/Δ+1/Δ+1/Δ+…) = e Δ/Δ с Δ некоторым бесконечно большим (но целым ) числом. В нашем примере мы остановили расчет на Δ = 1024, но вы видите логику: можно было продолжать бесконечно. Следовательно, мы можем написать E 7.233784… AS Вернемся к основанию 10. Мы можем записать множители e 7,233784…/Δ как e (ln10·π)/Δ = [ e ln10 ] π/Δ = 10 π/Δ . Таким образом, наша первоначальная мощность 10 π равна: 10 π = 10 π/Δ · 10 π/Δ · 10 π/Δ · · 10 π/Δ · 6 · 100173 π/Δ · 6 · 100173. /Δ · 10 π/Δ … = 10 π(Δ/Δ) , и, конечно, 10 1/Δ также стремится к 1 при стремлении Δ к бесконечности ( не к нулю, и не до 10 тоже). 🙂 Итак, да, мы можем сделать это для любого действительного числа a и для любого r.
Вернемся к основанию 10. Мы можем записать множители e 7,233784…/Δ как e (ln10·π)/Δ = [ e ln10 ] π/Δ = 10 π/Δ . Таким образом, наша первоначальная мощность 10 π равна: 10 π = 10 π/Δ · 10 π/Δ · 10 π/Δ · · 10 π/Δ · 6 · 100173 π/Δ · 6 · 100173. /Δ · 10 π/Δ … = 10 π(Δ/Δ) , и, конечно, 10 1/Δ также стремится к 1 при стремлении Δ к бесконечности ( не к нулю, и не до 10 тоже). 🙂 Итак, да, мы можем сделать это для любого действительного числа a и для любого r.

 Как упоминалось в моем предыдущем посте, из этого следует a s = ( e k ) s = e ks = e t с формулой la 6 t ) – единственным эффектом изменения базы является изменение масштаба горизонтальной оси: график s полностью идентичен графику e t действительно: нам просто нужно заменить s на t = ks = ln(a)·s. Это все. Итак, у нас есть формула Эйлера для i s . Например, для основания 10 мы имеем 10 i s = cos[ln(a)·s] + i sin[ln(a)·s].
Как упоминалось в моем предыдущем посте, из этого следует a s = ( e k ) s = e ks = e t с формулой la 6 t ) – единственным эффектом изменения базы является изменение масштаба горизонтальной оси: график s полностью идентичен графику e t действительно: нам просто нужно заменить s на t = ks = ln(a)·s. Это все. Итак, у нас есть формула Эйлера для i s . Например, для основания 10 мы имеем 10 i s = cos[ln(a)·s] + i sin[ln(a)·s]. ·a i r/Δ ·a i r/Δ ·…
·a i r/Δ ·a i r/Δ ·…