Зависимость между синусом, косинусом и тангенсом одного и того же угла
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Зависимость между синусом, косинусом и тангенсом одного и того же угла
2. Тригонометрические тождества
Зависимость между синусом, косинусом и тангенсом одного и того же угла
Тригонометрические функции в случае произвольного угла $-\infty
Рисунок 1.
В этом круге проведены горизонтальный и вертикальный диаметры, которые разделяют круг на квадранты. Неподвижный радиус $OA$ совпадает с горизонтальным диаметром и считается началом отсчета углов $x$, которые образует с ним подвижный радиус $OB$. {2} x=1$;
{2} x=1$;
функции $\sin x$ и $\cos x$ периодические с основным периодом $2\cdot \pi $, функции $tgx$ и $ctgx$ периодические с основным периодом $\pi $;
функции $\sin x$ и $\cos x$ являются ограниченными, то есть $\left|\sin x\right|\le 1$, $\left|\cos x\right|\le 1$;
функция $\cos x$ четная, то есть $\cos \left(-x\right)=\cos x$; остальные функции — нечетные, например, $\sin \left(-x\right)=-\sin x$;
полуоборот в любую сторону меняет знак синуса и косинуса, то есть $\sin \left(x\pm \pi \right)=-\sin x$, $\cos \left(x\pm \pi \right)=-\cos x$, и не меняет знак тангенса и котангенса, то есть $tg\left(x\pm \pi \right)=tgx$, $ctg\left(x\pm \pi \right)=ctgx$;
угол, который дополняет данный к $\frac{\pi }{2} $, меняет наименование функции, то есть $\sin \left(\frac{\pi }{2} -x\right)=\cos x$, $\cos \left(\frac{\pi }{2} -x\right)=\sin x$, $tg\left(\frac{\pi }{2} -x\right)=ctgx$, $ctg\left(\frac{\pi }{2} -x\right)=tgx$;
функция $tgx$ не существует, если $\cos x=0$, то есть $x=\frac{\pi }{2} \cdot \left(2\cdot n+1\right),\; n\in Z$; функция $ctgx$ не существует, если $\sin x=0$, то есть $x=\pi \cdot n,\; n\in Z$.
Пример 2
Доказать тождество $\sin x\cdot \left(1+tgx\cdot tg\frac{x}{2} \right)=tgx$.
\[\sin x\cdot \left(1+tgx\cdot tg\frac{x}{2} \right)=\sin x\cdot \frac{\cos x\cdot \cos \frac{x}{2} +\sin x\cdot \sin \frac{x}{2} }{\cos x\cdot \cos \frac{x}{2} } =\] \[=\sin x\cdot \frac{\cos \left(x-\frac{x}{2} \right)}{\cos x\cdot \cos \frac{x}{2} } =\sin x\cdot \frac{\cos \frac{x}{2} }{\cos x\cdot \cos \frac{x}{2} } =\frac{\sin x}{\cos x} =tgx.\]
Пример 3
Доказать тождество
\[tg\left(3\cdot \alpha \right)-tg\left(2\cdot \alpha \right)-tg\alpha =tg\alpha \cdot tg\left(2\cdot \alpha \right)\cdot tg\left(3\cdot \alpha \right).\] \[tg\left(3\cdot \alpha \right)-tg\left(2\cdot \alpha \right)-tg\alpha =\] \[=tg\left(3\cdot \alpha \right)-\frac{tg\left(2\cdot \alpha \right)+tg\alpha }{1-tg\left(2\cdot \alpha \right)\cdot tg\alpha } \cdot \left(1-tg\left(2\cdot \alpha \right)\cdot tg\alpha \right)=\] \[=tg\left(3\cdot \alpha \right)-tg\left(3\cdot \alpha \right)\cdot \left(1-tg\left(2\cdot \alpha \right)\cdot tg\alpha \right)=tg\alpha \cdot tg\left(2\cdot \alpha \right)\cdot tg\left(3\cdot \alpha \right).
Пример 5
Доказать тождество $\frac{\sin y+\sin x\cdot \cos \left(x+y\right)}{\cos y-\sin x\cdot \sin \left(x+y\right)} =tg\left(x+y\right)$.
\[\frac{\sin y+\sin x\cdot \cos \left(x+y\right)}{\cos y-\sin x\cdot \sin \left(x+y\right)} =\frac{\sin y+\frac{1}{2} \cdot \left(\sin \left(2\cdot x+y\right)-\sin y\right)}{\cos y-\frac{1}{2} \cdot \left(\cos y-\cos \left(2\cdot x+y\right)\right)} =\] \[=\frac{\sin y+\sin \left(2\cdot x+y\right)}{\cos y+\cos \left(2\cdot x+y\right)} =\frac{2\cdot \sin \left(x+y\right)\cdot \cos x}{2\cdot \cos \left(x+y\right)\cdot \cos x} =tg\left(x+y\right).\]
Пример 6
Вычислить значение выражения $arctg2+arctg3$.
Вычислим тангенс данного выражения. Получим:
\[tg\left(arctg2+arctg3\right)=\frac{tg\left(arctg2\right)+tg\left(arctg3\right)}{1-tg\left(arctg2\right)\cdot tg\left(arctg3\right)} =\frac{2+3}{1-2\cdot 3} =-1. \]
\]
Следовательно, $arctg2+arctg3=k\cdot \pi -\frac{\pi }{4} $, где $k$ — целое число или $0$. Но $\frac{\pi }{4}
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 02.03.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Может ли котангенс быть больше 1.
 Основные тригонометрические тождества, их формулировки и вывод. Соблюдение вашей конфиденциальности на уровне компании
Основные тригонометрические тождества, их формулировки и вывод. Соблюдение вашей конфиденциальности на уровне компанииГлавная > Ремонт и отделка > Может ли котангенс быть больше 1. Основные тригонометрические тождества, их формулировки и вывод. Соблюдение вашей конфиденциальности на уровне компании
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида .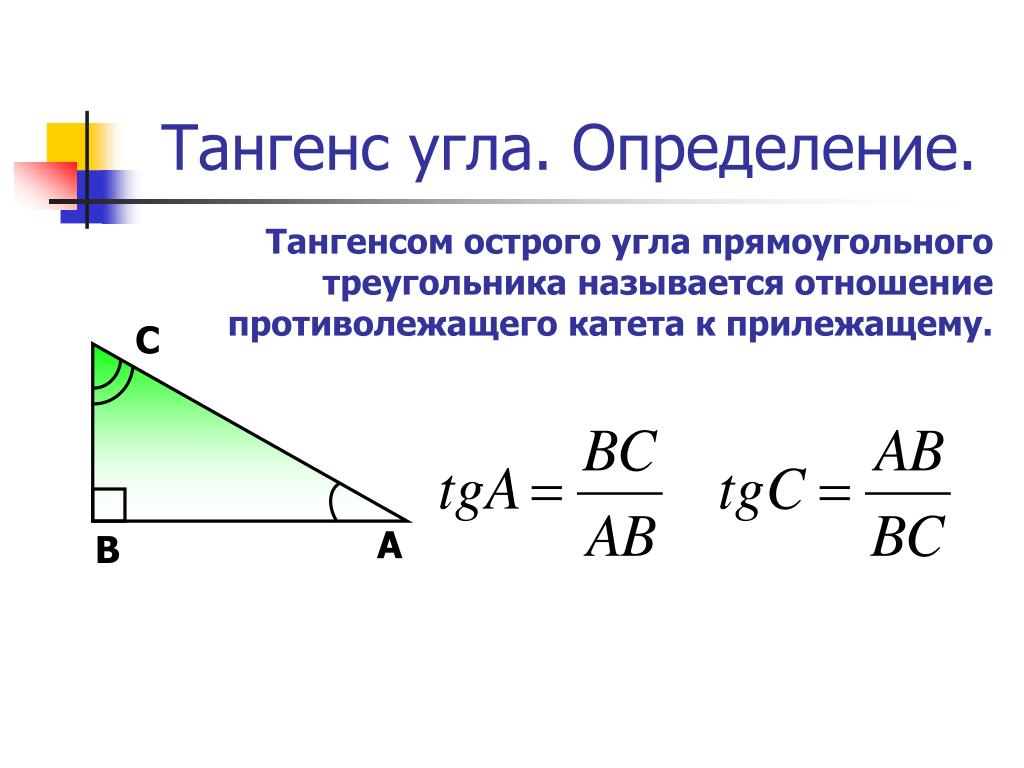 Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса.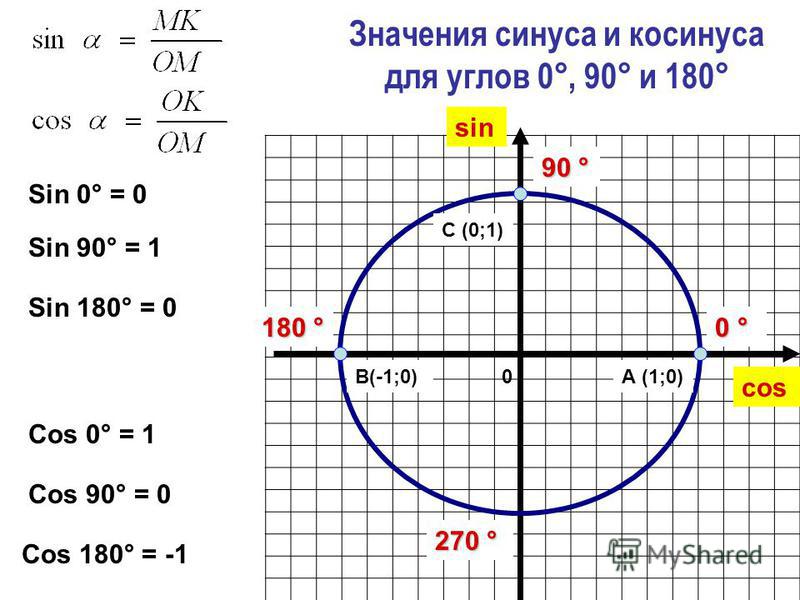 Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z — любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Первоисточник находится . Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески).
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
pozg.ru
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с .
понедельник, 7 января 2019 г.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов.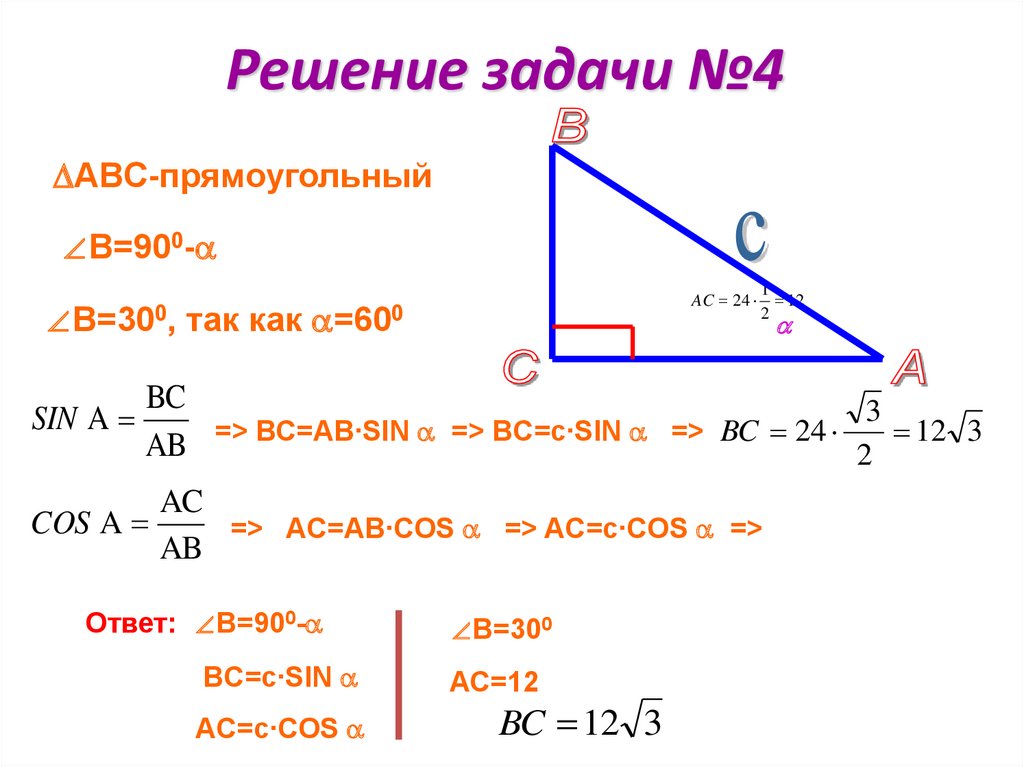 За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Я вам уже рассказывал, что , при помощи которой шаманы пытаются сортировать » » реальности. Как же они это делают? Как фактически происходит формирование множества?
Давайте внимательно разберемся с определением множества: «совокупность различных элементов, мыслимая как единое целое». А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.
А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно
Это сегодня всё, что мы не возьмем, принадлежит какому-либо множеству (как нас уверяют математики). Кстати, вы в зеркале видели у себя на лбу список тех множеств, к которым принадлежите именно вы? И я такого списка не видел. Скажу больше — ни одна вещь в реальности не имеет бирочки со списком множеств, к которым эта вещь принадлежит. Множества — это всё выдумки шаманов. Как они это делают? Давайте заглянем немного в глубь истории и посмотрим, как выглядели
элементы множества до того, как математики-шаманы растащили их по своим
множествам.
Давним-давно, когда о математике ещё никто и не слышал, а кольца были только у деревьев и у Сатурна, огромные стада диких элементов множеств бродили по физическим полям (ведь математических полей шаманы ещё не придумали). Выглядели они приблизительно так.
Выглядели они приблизительно так.
Да, не удивляйтесь, с точки зрения математики все элементы множеств больше всего похожи на морских ежей — из одной точки, как иголки, во все стороны торчат единицы измерений. Для тех, кто , напоминаю, что любую единицу измерения геометрически можно представить как отрезок произвольной длины, а число — как точку. Геометрически любую величину можно представить как пучок отрезков, торчащих в разные стороны из одной точки. Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.
Какие же единицы измерения образуют элемент множества? Всякие, описывающие данный элемент с разных точек зрения. Это и древние единицы измерения, которыми пользовались наши предки и о которых все давно забыли. Это и современные единицы измерения, которыми мы пользуемся сейчас. Это и неизвестные нам единицы измерения, которые придумают наши потомки и которыми будут пользоваться они для описания реальности.
С геометрией мы разобрались — предлагаемая модель элементов множества имеет четкое геометрическое представление. А как с физикой? Единицы измерения — это и есть прямая связь математики с физикой. Если шаманы не признают единицы измерения как полноправный элемент математических теорий — это их проблемы. Настоящую науку математику без единиц измерения лично я уже не представляю. Вот почему в самом начале рассказа о теории множеств я говорил о ней как о каменном веке.
Но перейдем к самому интересному — к алгебре элементов множеств. Алгебраически любой элемент множества представляет из себя произведение (результат умножения) разных величин.Выглядит это так.
Я умышленно не применял условные обозначения, принятые в теории множеств, поскольку мы рассматриваем элемент множества в естественной среде обитания до возникновения теории множеств. Каждая пара буковок в скобках обозначает отдельную величину, состоящую из числа, обозначенного буквой «n » и единицы измерения, обозначенной буквой «a «.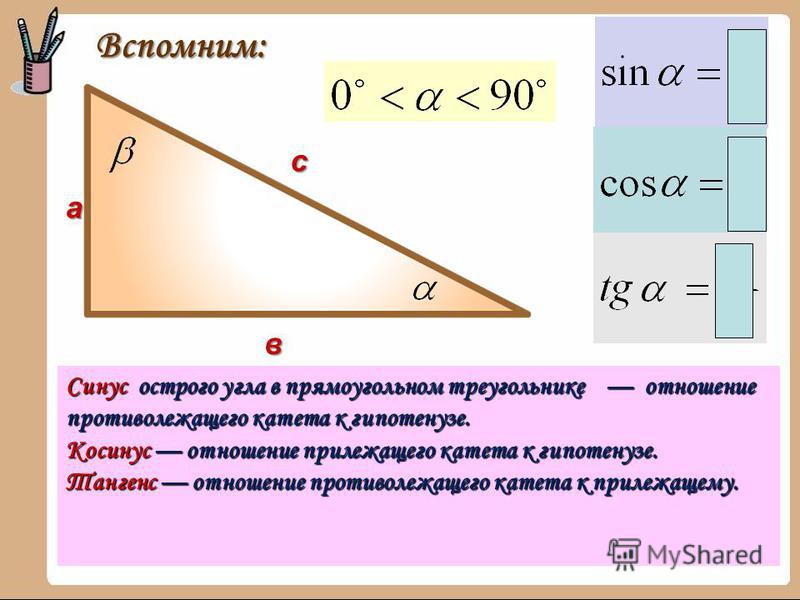 Индексы возле буковок указывают на то, что числа и единицы измерения — разные. Один элемент множества может состоять из бесконечного числа величин (на сколько у нас и наших потомков хватит фантазии). Каждая скобка геометрически изображается отдельным отрезком. В примере с морским ежом одна скобка — это одна иголка.
Индексы возле буковок указывают на то, что числа и единицы измерения — разные. Один элемент множества может состоять из бесконечного числа величин (на сколько у нас и наших потомков хватит фантазии). Каждая скобка геометрически изображается отдельным отрезком. В примере с морским ежом одна скобка — это одна иголка.
Как шаманы формируют множества из разных элементов? Фактически, по единицам измерения или по числам. Ничего не понимая в математике, они берут разных морских ежей и внимательно их рассматривают в поисках той единственной иголки, по которой они формируют множество. Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.
Как вы уже догадались, один и тот же элемент может принадлежать к самым разным множествам. Дальше я вам покажу, как формируются множества, подмножества и прочая шаманская галиматья.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом.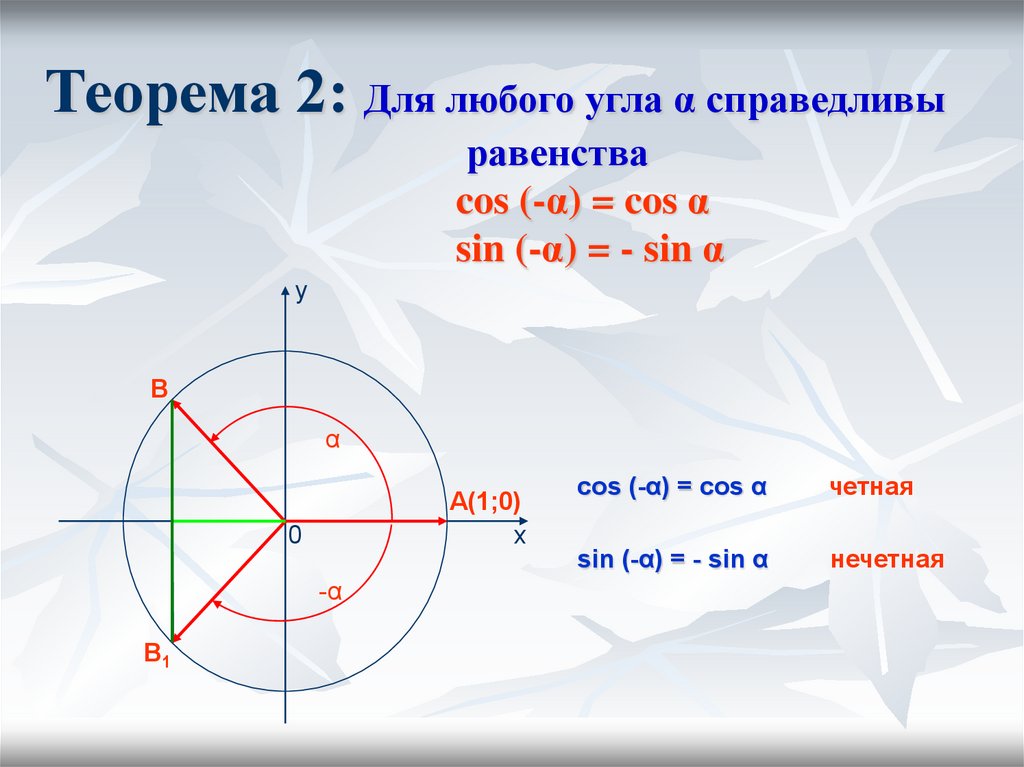 Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Если с точки Р опустить перпендикуляр на ось ОХ , то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным , если же он двигается против движения часовой стрелки — положительным .
Синусом угла ОР , является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1 , то sin(α) = y 0 .
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР , является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1 , то cos(α) = x 0 .
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб.
 заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Как найти тангенс б если известен тангенс а
Как найти тангенс через тангенс
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса, тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.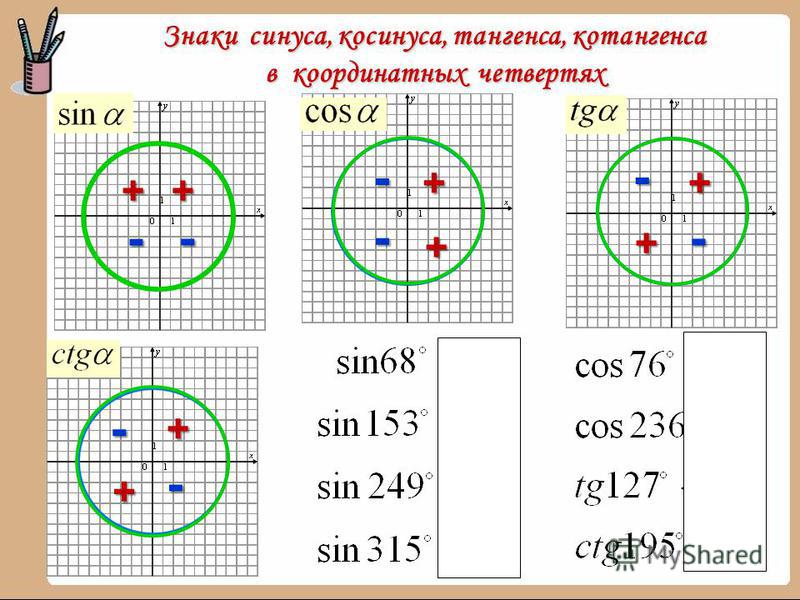
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс – это отношение синуса к косинусу.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.
Значение тангенса показывает не только раскрытие угла α , но и насколько один катет больше другого. При тангенсе угла α , равном 1 , катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.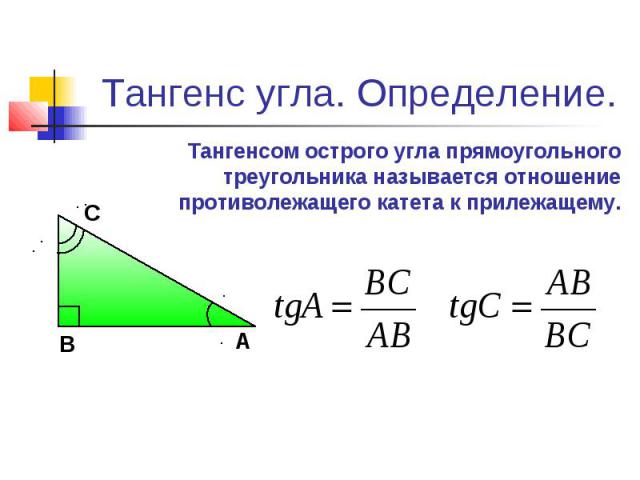
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.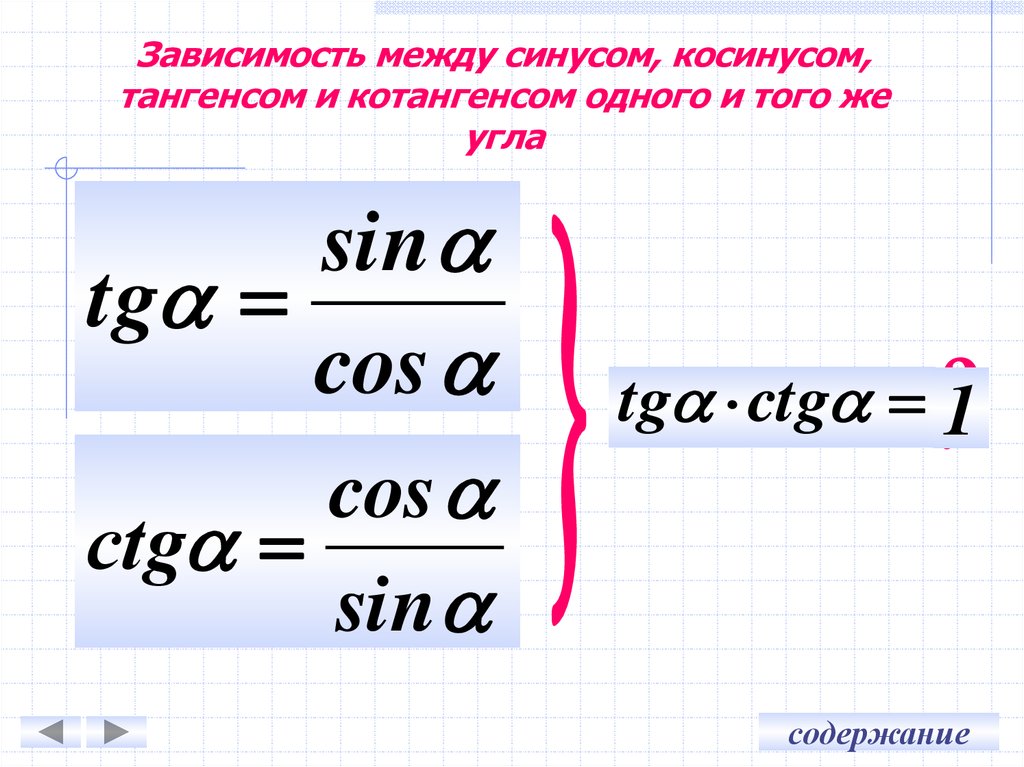
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Тангенс угла
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 90 0 . Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым.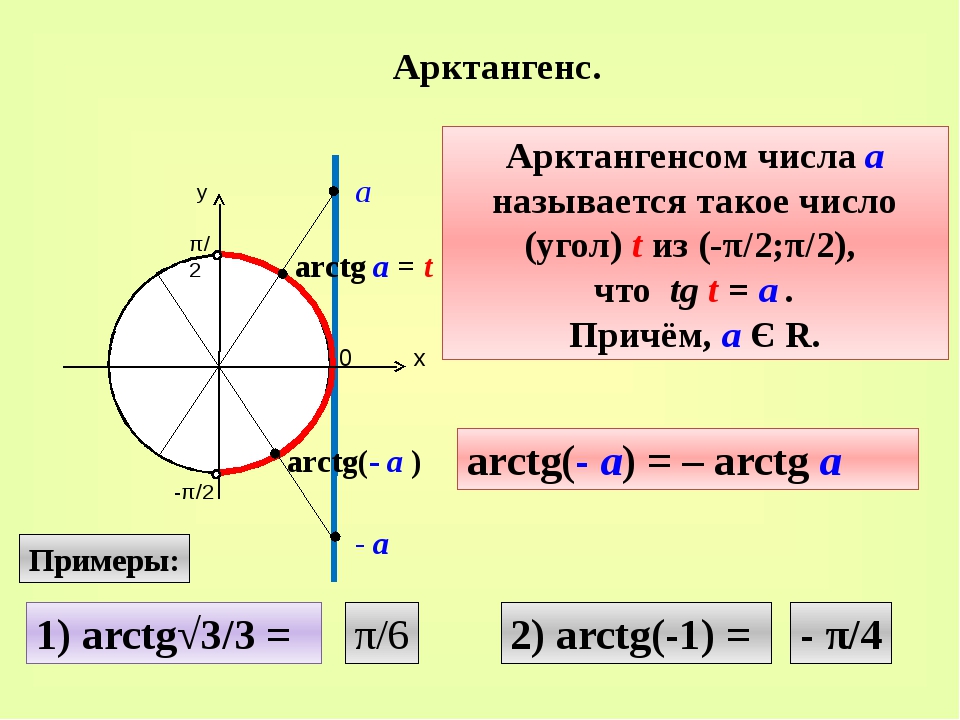 В развернутом угле 180 градусов.
В развернутом угле 180 градусов.
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла — называется катетом.
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/c
cosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса — это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly. ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:
тангенс 30 — 0,577
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.
Тригонометрическая функция: Тангенс угла (tg)
Тангенс острого угла α (tg α или tan α) – это отношение противолежащего катета (a) к прилежащему (b) в прямоугольном треугольнике.
График тангенса
Функция тангенса пишется как y = tg (x) . График в общем виде выглядит следующим образом:
Свойства тангенса
Ниже в табличном виде представлены основные свойства тангенса с формулами.
| Формула | |
| Симметричность | |
| Симметричность | |
| Тригонометрические тождества | |
| Тангенс двойного угла | |
| Тангенс суммы углов | |
| Тангенс разности углов | |
| Сумма тангенсов | |
| Разность тангенсов | |
| Произведение тангенсов | |
| ru/wp-content/uploads/2020/02/umnojenie-tg-tg-exc.png" aligncenter size-full" width="290" height="574" data-full="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-tg-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-tg-exc.png" aligncenter size-full" width="290" height="574" data-full="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-tg-exc.png" />»> | |
| Произведение тангенса и котангенса | |
| ru/wp-content/uploads/2020/02/umnojenie-tg-ctg-exc.png" aligncenter size-full" width="294" height="578" data-full="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-ctg-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-ctg-exc.png" aligncenter size-full" width="294" height="578" data-full="https://microexcel.ru/wp-content/uploads/2020/02/umnojenie-tg-ctg-exc.png" />»> | |
| Производная тангенса | |
| Интеграл тангенса | |
| Формула Эйлера |
Обратная к тангенсу функция
Если тангенс угла у равняется х ( tg y = x ), значит арктангенс x равен у :
тригонометрия — Есть ли связь между тригонометрическими функциями и их «со» функциями?
Для острых углов мы можем изобразить это отношение внутри прямоугольного треугольника.
Два угла $\theta$ и $\phi$ являются дополнительными , т.е. в сумме составляют прямой угол, так как сумма углов треугольника должна быть равна двум прямым углам. Но в зависимости от того, какой угол мы выбираем в качестве угла интереса, меняется то, какая сторона считается «прилегающей», а какая «противоположной». Итак, имеем:
$$\sin \theta \equiv \frac{\text{opp}(\theta)}{\text{hyp}} \equiv \frac{\text{adj}(\phi)}{\text{hyp }} \equiv \cos\phi\equiv\cos\left(\frac {\pi}{2} — \theta\right)$$
$$\tan \theta \equiv \frac{\text{opp} (\ theta)}{\text{adj}(\theta)} \equiv \frac{\text{adj}(\phi)}{\text{opp}(\phi)} \equiv\cot\phi\equiv \cot \left(\frac {\pi}{2} — \theta \right)$$
$$\sec \theta \equiv \frac{\text{hyp}}{\text{adj}(\theta )} \equiv \frac{\text{hyp}}{\text{opp}(\phi)} \equiv \csc \phi \equiv \csc \left(\frac {\pi}{2} — \theta\ справа)$$
Для читателей, незнакомых с радианами, замените загадочную $\frac{\pi}{2}$ на $90°$.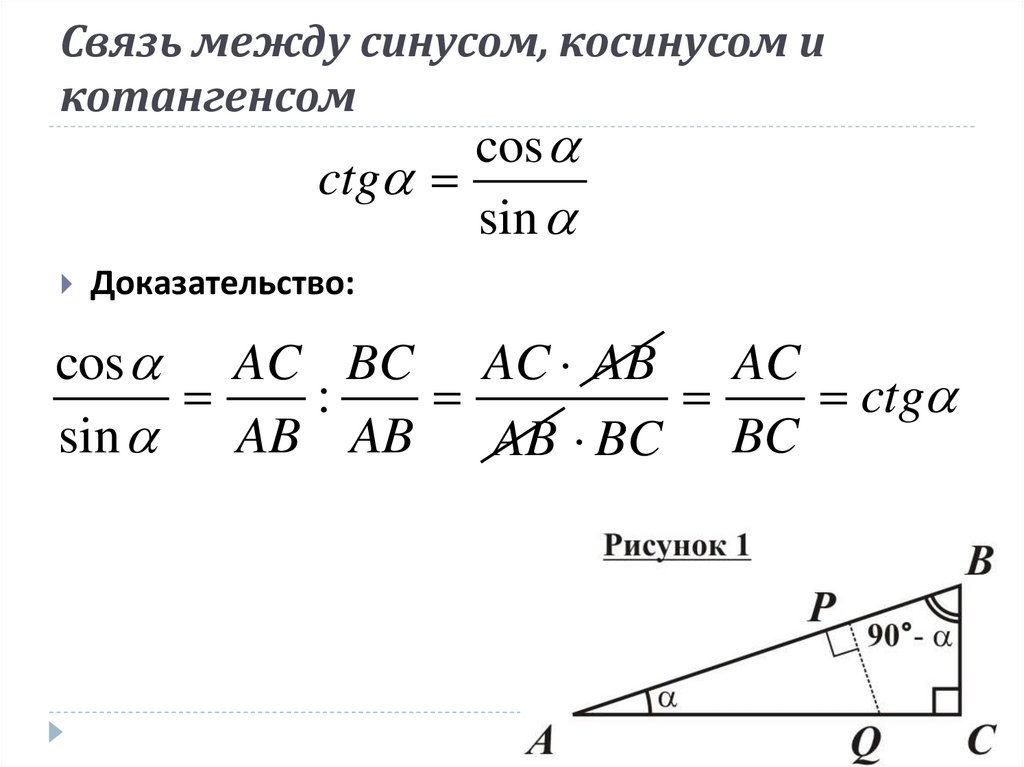 Вот почему, например, $\sin 30° = \cos 60°$. Для отрицательных углов или углов, лежащих за прямым углом, необходимо рассматривать единичную окружность, а не SOHCAHTOA, как определение тригонометрических функций (источник изображения):
Вот почему, например, $\sin 30° = \cos 60°$. Для отрицательных углов или углов, лежащих за прямым углом, необходимо рассматривать единичную окружность, а не SOHCAHTOA, как определение тригонометрических функций (источник изображения):
Радиус, образующий угол $\theta$ с положительным $ Ось x$ пересекает окружность в интересующей нас точке (отмечена красным на диаграмме). Координата $y$ этой точки определяется как $\sin\theta$. Для острых углов это длина вертикального отрезка от точки до оси $x$, но для углов в третьем и четвертом квадрантах (когда точка находится ниже оси $x$, поэтому $y$ -координата отрицательна) $\sin\theta$ это минус этой длины.
Увеличение радиуса до пересечения с (вертикальной) касательной к окружности в точке $(1,0)$ дает секущую. $y$-координата точки пересечения касательной и секущей равна $\tan\theta$ — видите проблему с $\tan 90°$ и $\tan 270°$? Для острых углов это просто длина отрезка касательной, но для углов во втором и четвертом квадрантах мы находим, что $\tan \theta$ отрицательно. Точно так же для острых углов $\sec\theta$ — это длина отрезка секущей от начала координат до касательной, но для углов во втором и третьем квадрантах это отрицательная длина этой длины (это случаи в секущая должна «выйти из задней части круга»: отрезок, который мы измеряем, пересекает окружность не в нашей первоначальной точке интереса, а в ее противоположной точке).
Точно так же для острых углов $\sec\theta$ — это длина отрезка секущей от начала координат до касательной, но для углов во втором и третьем квадрантах это отрицательная длина этой длины (это случаи в секущая должна «выйти из задней части круга»: отрезок, который мы измеряем, пересекает окружность не в нашей первоначальной точке интереса, а в ее противоположной точке).
Аналогично определяются косинус, косеканс и котангенс, но с переключением «горизонтальной» и «вертикальной», $x$- и $y$-координат и осей, а также тангенса в точке $(1,0)$, где $\theta$ — ноль, с касательной в точке $(0,1)$, где $\theta$ — прямой угол. По сути, это отражение по линии под углом 45°. Это показывает, как три приведенных выше тригонометрических тождества справедливы и для неострых углов. Вы можете нарисовать схематический график каждой тригонометрической функции, а затем набросать ее отражение через $\theta = 45°$ (которая будет вертикальной линией на вашем графике). Например, здесь отражение графика синуса (синий) дает нам график косинуса (красный). Обратите внимание, что в общем случае преобразование от $y=f(x)$ к $y=f(2k-x)$ является отражением через $x=k$, где в нашем случае $k=45°$.
Обратите внимание, что в общем случае преобразование от $y=f(x)$ к $y=f(2k-x)$ является отражением через $x=k$, где в нашем случае $k=45°$.
Я хочу привести пару практических примеров того, почему нас могут интересовать дополнительные тригонометрические тождества, но сначала в стороне. Вы могли заметить, что в моем определении тригонометрических функций из единичных окружностей я не использовал взаимные тригонометрические тождества (что $\sec$ является обратной величиной $\cos$ и т. д.). На самом деле, просмотр двух диаграмм показывает три подобных прямоугольных треугольника, дающих:
$$\cos \theta : \sin \theta : 1 \equiv \cot \theta : 1 : \csc \theta \equiv 1 : \ загар \ тета : \ сек \ тета $ $
Из этого отношения мы можем вывести взаимные тождества и такие факты, как $\frac{\sin \theta}{\cos \theta} \equiv \frac{1}{\cot \theta} \equiv \ tan \theta $ (второй член разделить на первый). Если у меня нет времени учить весь единичный круг, мое урезанное объяснение состоит в том, что $x$-координата точки интереса равна $\cos\theta$, $y$-координата равна $\sin \theta$, а градиент радиуса равен $\tan \theta$. Это затемняет геометрическое значение обратных тригонометрических функций и то, почему $\tan$ является сокращением от «тангенс», но подчеркивает тождество $\frac{\sin \theta}{\cos \theta}$ и дает аккуратный способ чтобы увидеть проблему с $\tan 90°$. К сожалению, интерпретация градиента для $\tan$ не распространяется на $\cot$, поскольку то, что было $\frac{\Delta y}{\Delta x}$, становится $\frac{\Delta x}{\Delta y }$ после отражения через линию под углом 45° (поскольку $x$ и $y$ меняются местами), что является обратной величиной градиента, а не градиента, поэтому его труднее интерпретировать. Однако этого достаточно, чтобы показать, что $\cot \theta$ (т. е. $\tan$ дополнительного угла) есть величина, обратная $\tan \theta$, без проведения касательных и секущих к единичной окружности или рассмотрения подобные треугольники. 92 \theta \equiv 1$, чтобы понять почему.
Это затемняет геометрическое значение обратных тригонометрических функций и то, почему $\tan$ является сокращением от «тангенс», но подчеркивает тождество $\frac{\sin \theta}{\cos \theta}$ и дает аккуратный способ чтобы увидеть проблему с $\tan 90°$. К сожалению, интерпретация градиента для $\tan$ не распространяется на $\cot$, поскольку то, что было $\frac{\Delta y}{\Delta x}$, становится $\frac{\Delta x}{\Delta y }$ после отражения через линию под углом 45° (поскольку $x$ и $y$ меняются местами), что является обратной величиной градиента, а не градиента, поэтому его труднее интерпретировать. Однако этого достаточно, чтобы показать, что $\cot \theta$ (т. е. $\tan$ дополнительного угла) есть величина, обратная $\tan \theta$, без проведения касательных и секущих к единичной окружности или рассмотрения подобные треугольники. 92 \theta \equiv 1$, чтобы понять почему.
Получите две тригонометрические производные по цене одной
Если вы сражались с выводом производной синуса, возможно, вам не терпится продемонстрировать производную косинуса. Но мы можем использовать тождество дополнительного угла, а затем цепное правило:
Но мы можем использовать тождество дополнительного угла, а затем цепное правило:
$$\frac{\text{d}}{\text{d}x} \cos x = \frac{\text{d}}{\ text{d}x} \sin\left(\frac{\pi}{2} — x \right) = — \cos\left(\frac{\pi}{2} — x \right) = — \sin х$$ 92 x$$
$$\frac{\text{d}}{\text{d}x} \sec x = \sec x \tan x \ подразумевает \frac{\text{d}}{\text{ d}x} \csc x = -\csc x \cot x $$
Составление и чтение математических таблиц
До эпохи карманных электронных калькуляторов тригонометрические расчеты проводились с использованием математических таблиц. Взаимосвязь между дополнительными триггерными функциями была бы очень очевидна для любого пользователя Manuale Mathematicum Маттиаса Бернеггера, опубликованного в 1612 году. Вот выдержка, которую я взял с сайта archive.org, показывающая экономию представления, которую позволяет использование дополнительных углов.
Возможно, вы привыкли представлять доли градуса в десятичной системе счисления, но здесь используется шестидесятеричная система счисления, где каждый градус разбит на 60 угловых минут (и хотя это не показано здесь, они, в свою очередь, разбиты на части).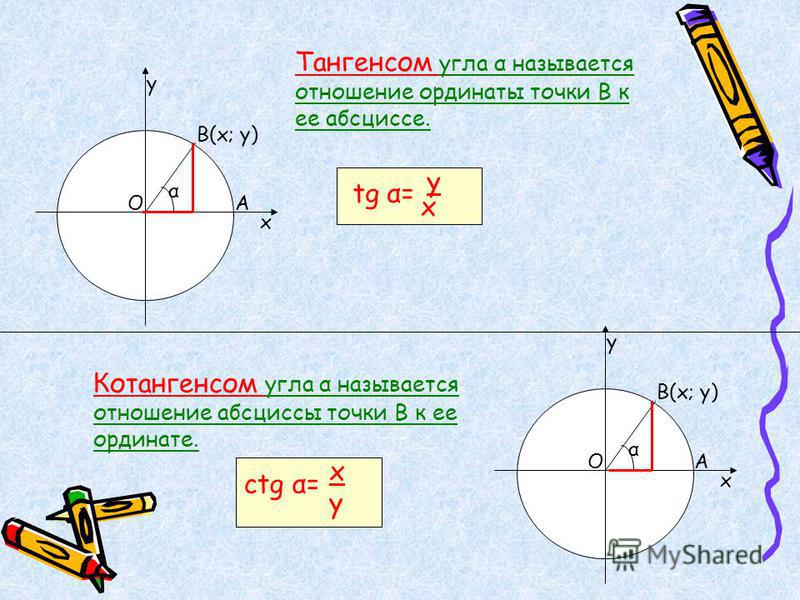 за 60 секунд). Обратите внимание, что левый столбец позволяет вам искать один угол, а правый столбец содержит его дополнение. Единственными перечисленными триггерными функциями являются sinuum , tangentium и secantium , но для каждой из них даны два значения: левая запись соответствует углу в самом левом столбце, правая запись соответствует дополнительный угол в крайнем правом столбце. Следовательно, косинус, котангенс и косеканс крайнего левого угла задаются как вторая запись под синусом, тангенсом и секущей, а записи для самого правого угла даны как первая запись .
за 60 секунд). Обратите внимание, что левый столбец позволяет вам искать один угол, а правый столбец содержит его дополнение. Единственными перечисленными триггерными функциями являются sinuum , tangentium и secantium , но для каждой из них даны два значения: левая запись соответствует углу в самом левом столбце, правая запись соответствует дополнительный угол в крайнем правом столбце. Следовательно, косинус, котангенс и косеканс крайнего левого угла задаются как вторая запись под синусом, тангенсом и секущей, а записи для самого правого угла даны как первая запись .
Например, из крайнего левого столбца можно прочитать, что $\sin (12° 42′) = 0,21985$, а из крайнего правого столбца той же строки мы видим, что $\sin (77° 18′) ) = 0,97533$. Сразу имеем, что $\cos (12° 42′) = 0,97533$, а $\cos (77° 18′) = 0,21985$. Между прочим, обе эти цифры совпали с ответом на моем электронном калькуляторе с заданным уровнем точности.
Таблица должна охватывать только от нуля до девяноста градусов, так как за пределами этой точки мы можем использовать симметрию и периодичность триггерных функций. На самом деле последняя страница таблицы останавливается, когда угол в левой колонке достигает 45 градусов; для больших углов необходимо вернуться назад по Руководству, считывая угол в крайнем правом столбце. Это использование симметрии по линии 45° уменьшает размер стола вдвое!
На самом деле последняя страница таблицы останавливается, когда угол в левой колонке достигает 45 градусов; для больших углов необходимо вернуться назад по Руководству, считывая угол в крайнем правом столбце. Это использование симметрии по линии 45° уменьшает размер стола вдвое!
Я сильно подозреваю, что для людей, занимавшихся геометрией четыреста лет назад, это тождество было бы более «очевидным» (или, по крайней мере, незаменимым инструментом в профессии), чем для тех из нас, кто родился в Кремниевом веке!
Тригонометрия
Урок № 4: Тригонометрические функции
от Ребекки Adcock
Тригонометрия.
математика, связанная с геометрией, которая изучает отношения между
стороны треугольников и их углы. Три из этих отношений являются синусоидальными,
функции косинуса и тангенса. Чтобы использовать и понимать эти функции,
Сначала нам нужно определить гипотенузу прямоугольного треугольника и ее
противоположные и смежные стороны.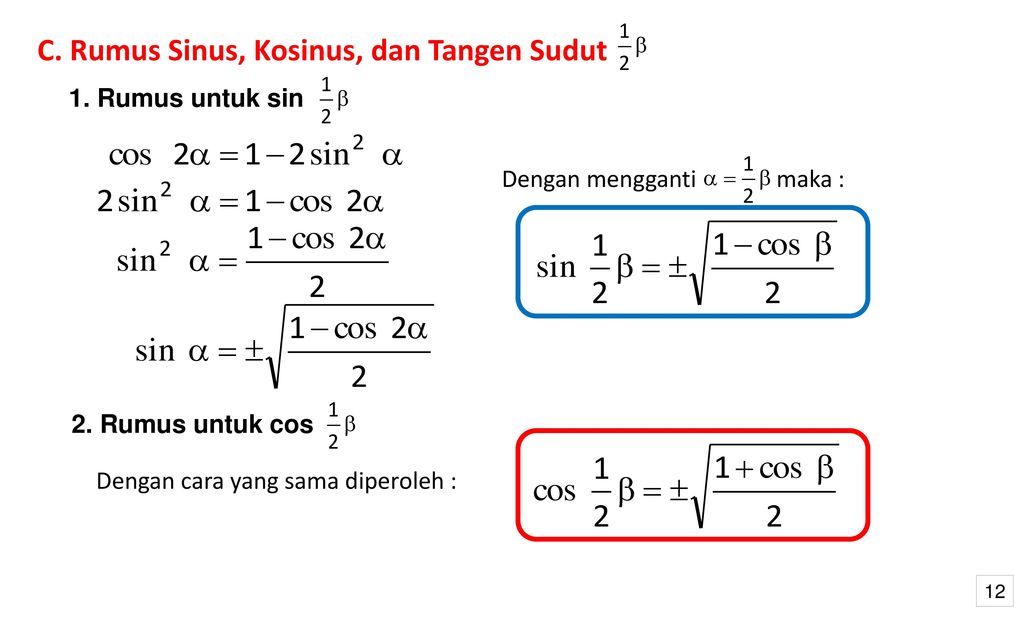
Напротив и рядом Стороны и гипотенуза
Противоположные и смежные стороны относятся к рассматриваемому углу. В примере справа мы рассматривая угол CAB.
Какая сторона будет смежной под этот угол? Мы знаем, что сторона АВ (также называемая с) является гипотенузой, потому что (1) она самая длинная сторона и (2) она лежит против прямого угла. Значит сторона АВ не соседней или противоположной стороне. (Каждая сторона может иметь только одно задание одновременно. время.) Словарь определяет смежный как рядом, примыкающий, имеющий общий конец или границу. Сторона переменного тока (также называемый b) подходит под описание. Это означает, что сторона BC (также называемая a) будет противоположная сторона.
Соотношения
Соотношение представляет собой сравнение
две величины в определенном порядке, и это может быть записано в виде дроби. В
прямоугольный треугольник, есть 6 тригонометрических соотношений.
Большая тройка и Их взаимные знаки Сокращения0100
Синусоидальный коэффициент Косеканс синус… sin
Синус = длина противоположной стороны = длина гипотенузы
длина гипотенузы гипотенуза длина противоположной стороны косинус…cos
Косинутное соотношение Отношение секущих тангенс.. tan
Косинус = длина соседней стороны Секанс = длина гипотенузы
длина гипотенузы Длина соседней стороны cosecant.csc
Коэффициент касательного отношения Котангент соотношение Secant.sec
Tangent = Длина противоположной стороны = длина прилегающей стороны
длина соседней стороны длина противоположной стороны котангенскот
Классический пример
|
Предположим, у вас есть
столб во дворе, и вы хотите узнать его высоту.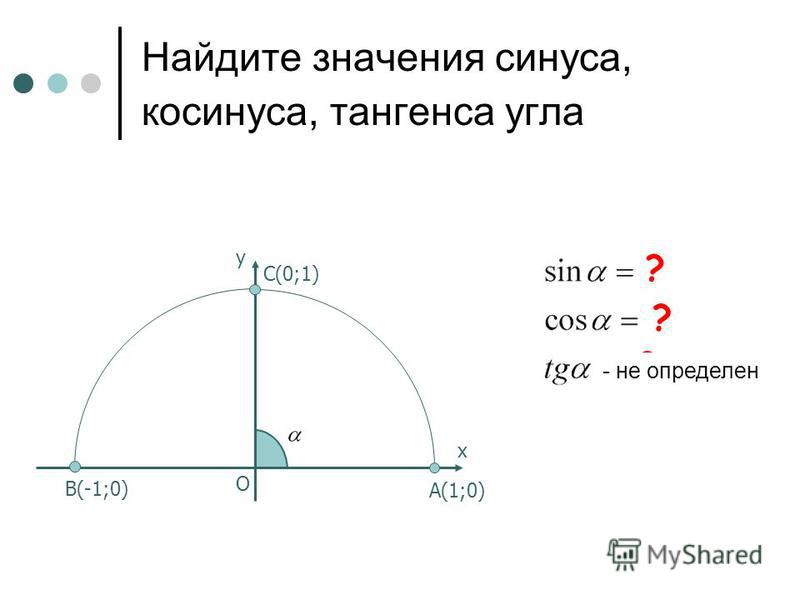 Провод от
верхняя часть шеста образует с землей угол 30° и закреплена на расстоянии 25 футов от
основание столба. Как вы оцениваете высоту столба?
Провод от
верхняя часть шеста образует с землей угол 30° и закреплена на расстоянии 25 футов от
основание столба. Как вы оцениваете высоту столба?
Поскольку столб расположен вертикально, он стоит под углом 90° к земле, и наша проблема может быть решена. представлен в виде прямоугольного треугольника.
Легенда о Сохкахтоа.
Запоминание формул для тригонометрические функции веками мучили студентов-математиков. Где-то в свое время творческий (или отчаянный) человек решил создать мнемоника для запоминания формул. Вот что такое Sohcahtoa и вот что это означает.
S S INE =
O O PPOSIT A DJACENT , разделенные на
H H Ypotenus0002 O O pposite разделить на.
A A djacent
Есть еще одна история о
Sohcahtoa Чтобы прочитать это, нажмите здесь. SOHCAHTOA http://www. pen.k12.va.us/Div/Winchester/jhhs/math/lessons/trig/legend.html
pen.k12.va.us/Div/Winchester/jhhs/math/lessons/trig/legend.html
Чтобы вернуться на эту страницу, используйте клавиша возврата в браузере.
Проверьте свое понимание. См. Урок №4 в Уроке Оценки .
Вернуться к Главная Меню .
3.1.3: Reciprocal Identities — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4174
Связь между синусом/косинусом/тангенсом и косекансом/секансом/котангенсом.
Вы уже знакомы с триггерными тождествами синуса, косинуса и тангенса. Как известно, у любой дроби есть и обратная, которую можно найти, поменяв местами местами числитель и знаменатель.
Можете ли вы перечислить отношения трех триггерных функций (синуса, косинуса и тангенса), если числители и знаменатели поменять местами?
Обратные тождества
Обратное дроби ab есть дробь ba. То есть мы находим обратную дробь, меняя местами числитель и знаменатель или переворачивая дробь. Шесть триггерных функций могут быть сгруппированы попарно как обратные.
Сначала рассмотрим определение функции синуса для углов поворота: \(\sin \theta =\dfrac{y}{r}\). Теперь рассмотрим функцию косеканса: \(\csc \theta=\dfrac{r}{y}\). В единичном круге эти значения равны \(\sin\theta=\dfrac{y}{1}=y\) и \(\csc \theta=\dfrac{1}{y}\). Эти две функции по определению являются обратными. Следовательно, значение синуса угла всегда является величиной, обратной величине косеканса, и наоборот. Например, если \(\sin \theta =\dfrac{1}{2}\), то \(\csc \theta=\dfrac{2}{1}=2\).
Следовательно, значение синуса угла всегда является величиной, обратной величине косеканса, и наоборот. Например, если \(\sin \theta =\dfrac{1}{2}\), то \(\csc \theta=\dfrac{2}{1}=2\).
Аналогично, функция косинуса и функция секанса обратны, а функции тангенса и котангенса обратны:
\(\begin{aligned}
\sec \theta &=\frac{1}{\cos \theta} & \text { или } & \cos \theta=\frac{1}{\sec \theta} \\
\cot \theta &=\frac{1}{\tan \theta} & \text { or } & \tan \theta=\frac{1}{\cot \theta}
\end{aligned}\)
Использование взаимных тождеств
Найдите значение следующих выражений, используя взаимные тождества.
1. \(\cos \theta=.3\), \(\sec \theta=?\)
\(\sec \theta=\dfrac{10}{3}\)
Эти функции обратные величины, поэтому если \(\cos\theta=.3\), то \(\sec \theta=1.3\). Легче найти обратную величину, если мы представим значения в виде дробей: \(\cos \theta=.3=\dfrac{3}{10} \Rightarrow \sec \theta=103\).
2. \(\cot \theta=\dfrac{4}{3}\), \(\tan \theta=?\)
Эти функции являются обратными, и обратная функция \(\dfrac{4} {3}\) равно \(\dfrac{3}{4}\).
Мы также можем использовать взаимные отношения для определения домена и диапазона функций.
3. \(\sin \theta =\dfrac{1}{2}\), \(\csc \theta=?\)
Эти функции являются обратными, и обратная функция \(\dfrac{1} {2}\) равно 2.
Пример \(\PageIndex{1}\)
Ранее вас просили перечислить отношения для трех тригонометрических функций, поменяв местами числители и знаменатели.
Раствор
Так как три обычные триггерные функции определены как: {adjacent}}{\text{гипотенуза}} \\ \tan&=\dfrac{\text{противоположный}}{\text{adjacent}} \end{aligned}\)
затем три функции, называемые «обратными функциями » являются:
\(\begin{align}\csc&=\dfrac{\text{гипотенуза}}{\text{напротив}} \\ \sec&=\dfrac{\text{гипотенуза}}{\text{смежный }}\\ \cot&=\dfrac{\text{смежный}}{\text{противоположный}}\end{выровненный}\)
Пример \(\PageIndex{2}\)
Укажите обратную функцию косеканса.
Решение
Функция, обратная косекансу, равна синусу.
Пример \(\PageIndex{3}\)
Найдите значение выражения, используя взаимное тождество.
\(\sec \theta=\dfrac{2}{\pi}\), \(\cos \theta=?\)
Решение
Эти функции являются обратными, и обратная функция \(\ dfrac{2}{\pi}\) равно \(\dfrac{\pi}{2}\).
Пример \(\PageIndex{4}\)
Найдите значение выражения, используя взаимное тождество.
\(\csc \theta=4\), \(\cos \theta=?\)
Решение
Эти функции являются обратными, а обратная величина 4 равна \(\dfrac{1}{4 }\).
Обзор
- Укажите обратную функцию секущей.
- Укажите обратную функцию котангенса.
- Назовите обратную функцию синуса.
Найдите значение выражения, используя взаимное тождество.
- \(\sin\theta=\dfrac{1}{2}\), \(\csc\theta=?\)
- \(\cos \theta=\dfrac{−\sqrt{3}}{2}\), \(\sec \theta=?\)
- \(\загар \тета=1\), \(\кот \тета=?\)
- \(\sec\theta=\sqrt{2}\), \(\cos\theta=?\)
- \(\csc \theta=2\), \(\sin \theta=?\)
- \(\cot \theta=−1\), \(\tan \theta=?\)
- \(\sin\theta=\dfrac{\sqrt{3}}{2}\), \(\csc \theta=?\)
- \(\cos\theta=0\), \(\sec \theta=?\)
- \(\tan \theta=\text{undefined}\), \(\cot \theta=?\)
- \(\csc \theta=\dfrac{2\sqrt{3}}{3}\), \(\sin \theta =?\)
- \(\sin\theta=\dfrac{−1}{2}\) и \(\tan\theta=\dfrac{\sqrt{3}}{3}\),\(\cos\theta=? \)
- \(\cos\theta=\dfrac{\sqrt{2}}{2}\) и \(\tan\theta=1\), \(\sin\theta=?\)
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 1. 21.
21.
Словарь
| Срок | Определение |
|---|---|
| домен | Область определения функции — это набор значений x, для которых определена функция. |
| Диапазон | Диапазон функции — это набор значений y, для которых определена функция. |
| Функция взаимного запуска | Обратная тригонометрическая функция — это функция, обратная типичной тригонометрической функции. Например, поскольку \(\sin x=\dfrac{\text{напротив}}{\text{гипотенуза}}\), обратная функция равна \(\csc x=\dfrac{\text{гипотенуза}}}{\ текст {напротив}}\) |
Дополнительные ресурсы
Интерактивный элемент
Видео: взаимное, частное и пифагорейское тождество
Эта страница под названием 3.



 заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2