Как упростить дроби? – Обзоры Вики
Вы можете упростить дробь если числитель (верхнее число) и знаменатель (нижнее число) можно разделить на одно и то же число. Шесть двенадцатых можно упростить до половины или 1 на 2, потому что оба числа делятся на 6. 6 делится на 6 один раз, а 6 на 12 дважды.
Отсюда, что такое эквивалентное отношение? Эквивалентные отношения иметь одинаковую ценность. Чтобы определить, равны ли два отношения, запишите их в виде дробей. Если дроби равны, то отношения равны.
Почему мы упрощаем дроби? Упрощение дробей процесс уменьшения числителя и знаменателя до их наименьших целых чисел, чтобы дробь была в простейшей форме.
… Это помогает другим математикам или ученым легко интерпретировать данные, а также помогает избежать путаницы, когда числа и уравнения становятся большими и сложными.
Как рассчитать коэффициент?
Разделите данные A на данные B, чтобы найти свое соотношение. В приведенном выше примере 5/10 = 0.5. Умножьте на 100, если хотите процент. Если вы хотите получить соотношение в процентах, умножьте ответ на 100.
Как упростить отношение? Соотношения можно полностью упростить, как и дроби. Чтобы упростить соотношение, разделите все числа в соотношении на одно и то же, пока они не перестанут делиться.
Как создать эквивалентное соотношение? Эквивалентные отношения (которые, по сути, являются эквивалентными дробями) — это два отношения, которые выражают одно и то же отношение между числами. Мы можем создать эквивалентные отношения с помощью умножение или деление числителя и знаменателя данного отношения на одно и то же число.
Упрощают ли пятиклассники дроби?
com/embed/sJAGR_jmR90″ frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″> Также Что такое примеры простых дробей? Говорят, что дробь имеет простейшую форму если 1 — единственный общий делитель числителя и знаменателя. Например, 89, потому что 1 — единственный общий множитель 8 и 9 в этой дроби.
Как написать дробь?
Что понимается под простейшей формой? Какая самая простая форма? Дробь в простейшей форме если верх и низ не имеют общих факторов, кроме 1. Другими словами, вы не можете больше разделить верхнюю и нижнюю части, оставив их целыми числами. Вы также можете услышать простейшую форму под названием «самые низкие условия».
Каков пример простейшей формы?
Говорят, что дробь имеет простейшую форму если его числитель и знаменатель взаимно просты , то есть у них нет общих делителей, кроме 1 .
(В некоторых книгах выражение «написано в самых низких терминах» означает то же самое.) Таким образом, 59 — простейшая форма, поскольку 5 и 9 не имеют общих делителей, кроме 1.
Что такое простая дробь?
Определение простой дроби
: дробь, имеющая целые числа в числителе и знаменателе — сравнить сложную дробь.
Как решить проблему соотношения? Чтобы использовать пропорции для решения задач соотношения слов, нам нужно выполнить следующие шаги:
- Определите известное соотношение и неизвестное соотношение.
- Настройте пропорцию.
- Перемножьте и решите.
- Проверьте ответ, подставив результат в неизвестное соотношение.
Каково соотношение 1 к 10? Таким образом, как часть 3/30 можно упростить до 1/10, соотношение 3:30 (или 4:40, 5:50, 6:60 и т. д.) можно упростить до 1:10.
Как упростить?
Чтобы упростить любое алгебраическое выражение, следующие основные правила и шаги:
- Удалите все символы группировки, такие как квадратные и круглые скобки, путем умножения множителей.
- Используйте правило экспоненты, чтобы удалить группировку, если термины содержат экспоненты.
- Объедините похожие термины сложением или вычитанием.
- Объедините константы.
Как упростить пропорции для детей?
Как найти эквивалент? Чтобы найти эквивалентные дроби для любой заданной дроби, умножьте числитель и знаменатель на одно и то же число. Например, чтобы найти эквивалент дроби 3/4, умножьте числитель 3 и знаменатель 4 на одно и то же число, скажем, на 2.
Что такое соотношение в математике?
Соотношение упорядоченная пара чисел a и b, записанная a / b, где b не равно 0. Пропорция – это уравнение, в котором два отношения равны друг другу.
Например, если есть 1 мальчик и 3 девочки, вы можете записать соотношение как: 1 : 3 (на каждого мальчика приходится 3 девочки) 1/4 мальчиков и 3/4 девочек.
Как вы находите упрощение?
Чтобы упростить математическое выражение без круглых скобок, вы соблюдать порядок действий, то есть PEMDAS (круглые скобки, экспоненты, умножение, деление, сложение, вычитание). Поскольку в выражении нет скобок, вы можете начать проверку выражения на экспоненты. Если это так, сначала упростите это.
Сокращение алгебраических дробей — Республикалық білім порталы
Раздел долгосрочного плана:
7.4С Алгебраические дроби Школа :
Дата : ФИО учителя:
Класс: 7 Количество присутствующих:
отсутствующих:
Тема урока Сокращение алгебраических дробей.
Упрощение выражений, содержаших алгебраические дроби
Тип урока Закрепление пройденного материала
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) .2.1.18
применять основное свойство алгебраической дробиac/bc=a/b,b≠0,c≠0;
7.2.1.29 Упрощение выражений содержащих алгебраические дроби
Цель урока Уметь сокращать дроби, используя основное свойства алгебраических дробей
Критерии оценивания
Знание и понимание Знает основное свойство алгебраических дробей;
Применение знания Выполняет разложение на множители числителя и знаменателя алгебраической дроби;
Применение знания Умеет сокращать и упрощать алгебраические дроби;
Языковые цели Лексика и терминология
Объясняет практическое применение сокращения обыкновенных дробей.
Приводит практические примеры алгебраических дробей.
Правильно использует следующую терминологию:
область допустимых значений;
значение переменной, при котором алгебраическая дробь не имеет смысла;
целое выражение ;
алгебраические дроби;
основное свойство дробей;
сокращение дробей;
Привитие ценностей Формирование уважения, товарищества во время работы в группе и парах, ответственность при самостоятельной работе и привитие ценностей прилежной учебы.
2= x (12 + x) В
7 27 + t3 = (3 + t)(9 – 6t + t2) н
2. Деление на группы.
Учащимся раздается элемент формулы сокращенного. Им нужно собрать 2 формулы. Затем разделиться на 2 команды с помощью формулы.
( а+ в)3 = а3 + 3а2в + 3ав2 + в3
а3 + в3 = (а+в)( а2- ав + в2)
3 . Станция «Экономическая».
В машинах находятся алгебраические выражения, их нужно погрузить в вагоны, по технике безопасности вагон перегружать нельзя, поэтому грузим только то, что получиться после упрощения выражения.
4x
8
x(x+2)
x
x² — 4
x + 2
m³k³
m²k
a² + 2ab +b²
(a + b)(a – b)
После окончания работы ученикам даются ответы и они проверяют свои работы, работают над ошибками.
4. Сфетофор.
На светофоре красный свет
Значит, ходу дальше нет,
А зеленый свет зажжется,
Если слово соберётся.
Решить уравнения и найти букву соответствующую найденному корню. Если уравнения решены верно, то из букв получиться слово.
Решите уравнение и соберите слово:
5х = 150
7х + 9 = 100
9 + 13х = 35 +26х
11х — 4х = 14
(5х – 3) + (7х – 4) = 8 – (15 – 11х)
б ь р о д
2 0 13 -2 30
5.
2+4а+16)
Презентация
Раздаточный материал
.
Приложение
Конец урока
5 минут Рефлексия. Проводится в виде мишени. У каждого учащегося на столе гвоздики с 3 цветами. Ученик выбирает тот который соответствует ему.
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? Здоровье и соблюдение техники безопасности
Здоровьесберегающие технологии.
Используемые физминутки и активные виды деятельности.
Пункты, применяемые из Правил техники безопасности на данном уроке.
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему? Используйте данный раздел для размышлений об уроке.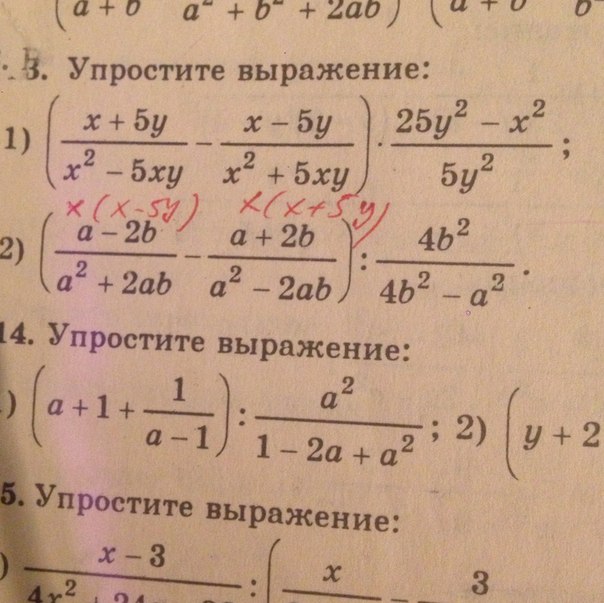
Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
7.3 Упрощение сложных рациональных выражений — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Упростите сложное рациональное выражение, записав его в виде деления
- Упростите сложное рациональное выражение с помощью ЖК-дисплея
Приготовься 7.7
Прежде чем начать, пройдите этот тест на готовность.
Упрощение: 35910.35910.
Если вы пропустили эту проблему, просмотрите пример 1.27.
Приготовься 7,8
Упрощение: 1−1342+4·5,1−1342+4·5.
Если вы пропустили эту проблему, просмотрите пример 1.31.
Приготовься 7,9
Решите: 12x+14=18,12x+14=18.
Если вы пропустили эту проблему, просмотрите пример 2.9.
Упростите сложное рациональное выражение, записав его в виде деления
Сложные дроби — это дроби, в которых числитель или знаменатель содержит дробь.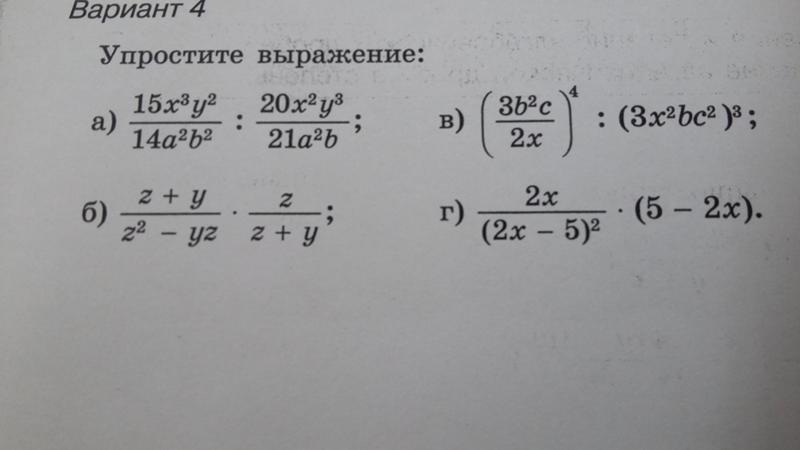
3458x2xy63458x2xy6
В этом разделе мы упростим сложные рациональные выражения, которые являются рациональными выражениями с рациональными выражениями в числителе или знаменателе.
Комплексное рациональное выражение
Комплексное рациональное выражение — это рациональное выражение, в котором числитель и/или знаменатель содержат рациональное выражение.
Вот несколько сложных рациональных выражений:
4y-38y2-91x+1yxy-yx2x+64x-6-4×2-364y-38y2-91x+1yxy-yx2x+64x-6-4×2-36
Помните, мы всегда исключаем значения, при которых любой знаменатель равен нулю.
Мы будем использовать два метода для упрощения сложных рациональных выражений.
Ранее в этой главе мы уже видели это сложное рациональное выражение.
6×2-7x+24x-82×2-8x+3×2-5x+66×2-7x+24x-82×2-8x+3×2-5x+6
Мы заметили, что дроби говорят нам делить, поэтому переписали это как задачу деления:
(6×2−7x+24x−8)÷(2×2−8x+3×2−5x+6).
(6×2−7x+24x−8)÷(2×2−8x+3×2−5x+6).
Затем мы умножили первое рациональное выражение на обратное второму, точно так же, как мы делаем это при делении двух дробей.
Это один из способов упростить сложные рациональные выражения. Мы следим за тем, чтобы комплексное рациональное выражение имело форму, в которой одна дробь находится над другой дробью. Затем мы пишем это так, как если бы мы делили две дроби.
Пример 7,24
Упростите сложное рациональное выражение, записав его в виде деления: 6x−43×2−16,6x−43×2−16.
Решение
| 6x-43×2-166x-43×2-16 | |
| Перепишите сложную дробь в виде деления. | 6x−4÷3×2−166x−4÷3×2−16 |
| Перепишите как произведение первого умножения на , обратное второму.  | 6x-4·x2-1636x-4·x2-163 |
| Фактор. | 3·2x−4·(x−4)(x+4)33·2x−4·(x−4)(x+4)3 |
| Умножить. | 3·2(x−4)(x+4)3(x−4)3·2(x−4)(x+4)3(x−4) |
| Удалить общие множители. | 3·2(x−4)(x+4)3(x−4)3·2(x−4)(x+4)3(x−4) |
| Упрощение. | 2(х+4)2(х+4) |
Существуют ли значения x , которые нельзя допускать? Исходное комплексное рациональное выражение имело знаменатели x−4x−4 и x2−16.x2−16. Это выражение было бы неопределенным, если x=4x=4 или x=-4.
x=-4.
Попробуй это 7,47
Упростите сложное рациональное выражение, записав его в виде деления: 2×2−13x+1,2×2−13x+1.
Попробуй это 7,48
Упростите сложное рациональное выражение, записав его в виде деления: 1×2−7x+122x−4,1×2−7x+122x−4.
Полосы дробей действуют как символы группировки. Итак, чтобы следовать порядку действий, мы максимально упрощаем числитель и знаменатель, прежде чем мы сможем выполнить деление.
Пример 7,25
Упростите сложное рациональное выражение, записав его в виде деления: 13+1612−13,13+1612−13.
Решение
| Упростите числитель и знаменатель. Найдите ЖК-дисплей и сложите дроби в числителе.  Найдите ЖК-дисплей и вычтите дроби в знаменателе . | |
| Упростите числитель и знаменатель. | |
| Перепишите сложное рациональное выражение в виде задачи на деление . | |
| Умножьте первое на обратное значение второго. | |
| Упрощение. | 3 |
Попробуй это 7,49
Упростите сложное рациональное выражение, записав его в виде деления: 12+2356+112,12+2356+112.
Попробуй это 7,50
Упростите сложное рациональное выражение, записав его в виде деления: 34−1318+56,34−1318+56.
Мы следуем той же процедуре, когда комплексное рациональное выражение содержит переменные.
Пример 7,26
Как упростить сложное рациональное выражение с помощью деления
Упростите сложное рациональное выражение, записав его в виде деления: 1x+1yxy-yx.1x+1yxy-yx.
Решение
Попробуй это 7,51
Упростите сложное рациональное выражение, записав его в виде деления: 1x+1y1x−1y.1x+1y1x−1y.
Попробуй это 7,52
Упростите сложное рациональное выражение, записав его в виде деления: 1a+1b1a2−1b21a+1b1a2−1b2.
Здесь мы суммируем шаги.
Как
Упростите сложное рациональное выражение, записав его в виде деления.
- Шаг 1. Упростите числитель и знаменатель.
- Шаг 2. Перепишите сложное рациональное выражение в виде задачи на деление.
- Шаг 3. Разделите выражения.
Разделите выражения.Пример 7,27
Упростите сложное рациональное выражение, записав его в виде деления: n−4nn+51n+5+1n−5.n−4nn+51n+5+1n−5.
Решение
| Упростите числитель и знаменатель. Найдите общий знаменатель числителя и знаменателя. | |
| Упростите числители. | |
| Вычесть рациональные выражения в числителе и добавить в знаменателе. | |
Упрощение. (Теперь у нас есть одно рациональное выражение на одно рациональное выражение.) | |
| Переписать как деление дроби. | |
| Умножьте первый раз на обратную величину второго. | |
| Фактор любых выражений, если это возможно. | |
| Удалить общие множители. | |
| Упрощение. |
Попробуй это 7,53
Упростите сложное рациональное выражение, записав его в виде деления: b−3bb+52b+5+1b−5.
b−3bb+52b+5+1b−5.
Попробуй это 7,54
Упростите сложное рациональное выражение, записав его в виде деления: 1−3c+41c+4+c3.1−3c+41c+4+c3.
Упростите сложное рациональное выражение с помощью ЖК-дисплея
Мы «очищали» дроби, умножая их на ЖКИ, когда решали уравнения с дробями. Мы можем использовать эту стратегию здесь, чтобы упростить сложные рациональные выражения. Умножим числитель и знаменатель на ЖК всех рациональных выражений.
Давайте посмотрим на сложное рациональное выражение, которое мы упростили одним способом в примере 7.25. Здесь мы упростим это, умножив числитель и знаменатель на LCD. Когда мы умножаем на LCDLCDLCDLCD, мы умножаем на 1, поэтому значение остается прежним.
Пример 7,28
Упростите сложное рациональное выражение с помощью ЖКИ: 13+1612−13,13+1612−13.
Решение
LCD всех дробей в целом выражении равен 6. | |
| Очистите дроби, умножив числитель и знаменатель на этот ЖК-дисплей. | |
| Распределить. | |
| Упрощение. | |
Попробуй это 7,55
Упростите сложное рациональное выражение с помощью ЖКИ: 12+15110+15.12+15110+15.
Попробуй это 7,56
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 14+3812−516,14+3812−516.
Мы будем использовать тот же пример, что и в примере 7.26. Решите, какой метод работает лучше для вас.
Пример 7,29
Как упростить сложное рациональное выражение с помощью ЖК-дисплея
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1x+1yxy-yx.1x+1yxy-yx.
Решение
Попробуй это 7,57
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1a+1bab+ba.1a+1bab+ba.
Попробуй это 7,58
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1×2−1y21x+1y.1×2−1y21x+1y.
Как
Упростите сложное рациональное выражение с помощью ЖК-дисплея.
- Шаг 1. Найдите ЖК всех дробей в сложном рациональном выражении.
- Шаг 2. Умножьте числитель и знаменатель на LCD.
- Шаг 3. Упростите выражение.
Обязательно начните с факторизации всех знаменателей, чтобы найти ЖК-дисплей.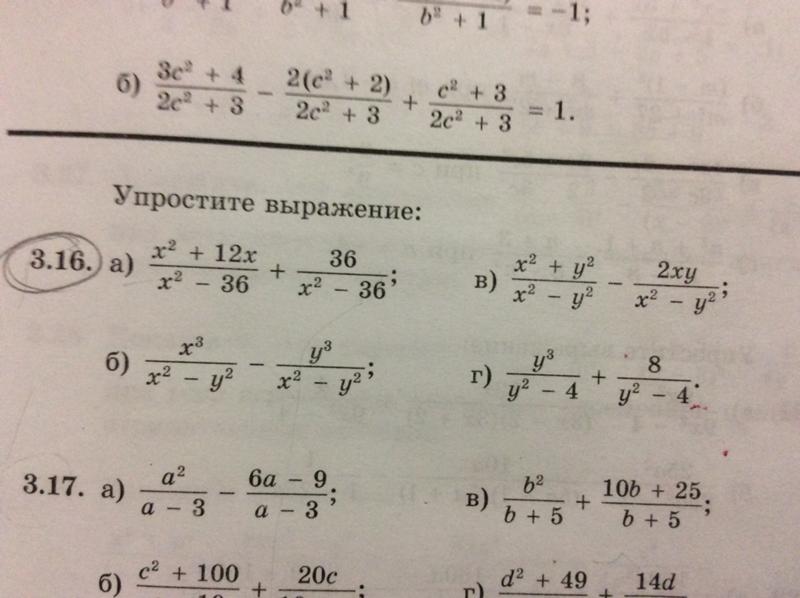
Пример 7.30
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 2x+64x−6−4×2−36,2x+64x−6−4×2−36.
Решение
| Найдите ЛК всех дробей в комплексном рациональном выражении . ЖК-дисплей равен x2-36=(x+6)(x-6)x2-36=(x+6)(x-6). | |
| Умножьте числитель и знаменатель на ЖК-дисплей. | |
| Упростите выражение. | |
Распределить в знаменателе. | |
| Упрощать. | |
| Упрощение. | |
| Чтобы упростить знаменатель, распределите и объедините подобные члены. | |
| Фактор знаменателя. | |
| Удалить общие множители. | |
| Упрощение. | |
| Обратите внимание, что больше нет общих делителей для числителя и знаменателя.  |
Попробуй это 7,59
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 3x+25x-2-3×2-4,3x+25x-2-3×2-4.
Попробуй это 7,60
Упростите сложное рациональное выражение с помощью ЖКИ: 2x−7−1x+76x+7−1×2−49,2x−7−1x+76x+7−1×2−49.
Обязательно сначала разложите знаменатели. Действуйте осторожно, так как математика может запутаться!
Пример 7.31
Упростите сложное рациональное выражение с помощью ЖКИ: 4м2-7м+123м-3-2м-4,4м2-7м+123м-3-2м-4.
Решение
| Найдите ЛП всех дробей в сложном рациональном выражении . | |
ЖК-дисплей (м-3)(м-4). (м-3)(м-4). | |
| Умножьте числитель и знаменатель на ЖК-дисплей. | |
| Упрощение. | |
| Упрощение. | |
| Распределить. | |
| Объедините похожие термины. |
Попробуй это 7,61
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 3×2+7x+104x+2+1x+5,3×2+7x+104x+2+1x+5.
Попробуй это 7,62
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 4yy+5+2y+63yy2+11y+30.
4yy+5+2y+63yy2+11y+30.
Пример 7,32
Упростите сложное рациональное выражение с помощью ЖК-дисплея: yy+11+1y-1.yy+11+1y-1.
Решение
| Найдите ЛКД всех дробей в сложном рациональном выражении. | |
| ЖК-дисплей (y+1)(y−1).(y+1)(y−1). | |
| Умножьте числитель и знаменатель на ЖК-дисплей. | |
| Распределите в знаменателе и упростите. | |
Упрощение. | |
| Упростите знаменатель и оставьте факторизованным числитель . | |
| Разложите знаменатель на множители и удалите множители , общие с числителем. | |
| Упрощение. |
Попробуй это 7,63
Упростите сложное рациональное выражение с помощью ЖК-дисплея: xx+31+1x+3.xx+31+1x+3.
Попробуй это 7,64
Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1+1x−13x+1.1+1x−13x+1.
Средства массовой информации
Получите доступ к этому онлайн-ресурсу, чтобы получить дополнительные инструкции и попрактиковаться в сложных дробях.
- Сложные дроби
Раздел 7.3 Упражнения
Практика ведет к совершенству
Упростите сложное рациональное выражение, записав его в виде деления
В следующих упражнениях упростите каждое сложное рациональное выражение, записав его в виде деления.
151.
2аа+44а2а2-162аа+44а2а2-16
152.
3bb-5b2b2-253bb-5b2b2-25
153.
5c2+5c−1410c+75c2+5c−1410c+7
154.
8d2+9d+1812d+68d2+9d+1812d+6
155.
12+5623+7912+5623+79
156.
12+3435+71012+3435+710
157.
23−1934+5623−1934+56
158.
12−1623+3412−1623+34
159.
нм+1n1n-нмнм+1n1n-нм
160.
1p+pqqp-1q1p+pqqp-1q
161.
1r+1t1r2−1t21r+1t1r2−1t2
162.
2v+2w1v2−1w22v+2w1v2−1w2
163.
х-2хх+31х+3+1х-3х-2хх+31х+3+1х-3
164.
у-2уу-42у-4+2у+4у-2уу-42у-4+2у+4
165.
2-2а+31а+3+а22-2а+31а+3+а2
166.
4+4b-51b-5+b44+4b-51b-5+b4
Упрощение сложного рационального выражения с помощью ЖК-дисплея
В следующих упражнениях упростите каждое сложное рациональное выражение с помощью ЖК-дисплея.
167.
13+1814+11213+1814+112
168.
14+1916+11214+1916+112
169.
56+29718−1356+29718−13
170.
16+41535−1216+41535−12
171.
cd+1d1d-dccd+1d1d-dc
172.
1m+mnnm−1n1m+mnnm−1n
173.
1p+1q1p2−1q21p+1q1p2−1q2
174.
2r+2t1r2−1t22r+2t1r2−1t2
175.
2x+53x−5+1×2−252x+53x−5+1×2−25
176.
5y−43y+4+2y2−165y−43y+4+2y2−16
177.
5z2−64+3z+81z+8+2z−85z2−64+3z+81z+8+2z−8
178.
3с+6+5с-61с2-36+4с+63с+6+5с-61с2-36+4с+6
179.
4a2−2a−151a−5+2a+34a2−2a−151a−5+2a+3
180.
5b2−6b−273b−9+1b+35b2−6b−273b−9+1b+3
181.
5c+2−3c+75cc2+9c+145c+2−3c+75cc2+9c+14
182.
6d−4−2d+72dd2+3d−286d−4−2d+72dd2+3d−28
183.
2+1п-35п-32+1п-35п-3
184.
nn-23+5n-2nn-23+5n-2
185.
мм+54+1м-5мм+54+1м-5
186.
7+2q−21q+27+2q−21q+2
В следующих упражнениях упростите каждое сложное рациональное выражение, используя любой метод.
187.
34−2712+51434−2712+514
188.
vw+1v1v-vwvw+1v1v-vw
189.
2а+41а2-162а+41а2-16
190.
3b2−3b−405b+5−2b−83b2−3b−405b+5−2b−8
191.
3m+3n1m2−1n23m+3n1m2−1n2
192.
2r−91r+9+3r2−812r−91r+9+3r2−81
193.
х-3хх+23х+2+3х-2х-3хх+23х+2+3х-2
194.
уу+32+1у−3уу+32+1у−3
Письменные упражнения
195.
В этом разделе вы научились упрощать сложную дробь 3x+2xx2−43x+2xx2−4 двумя способами: переписать ее как задачу на деление или умножить числитель и знаменатель на LCD. Какой метод вы предпочитаете? Почему?
196.
Эфраим хочет начать упрощать сложную дробь 1a+1b1a-1b1a+1b1a-1b, сокращая переменные в числителе и знаменателе, 1a+1b1a-1b.1a+1b1a-1b. Объясните, что не так с планом Эфраима.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?
Счет, математика и статистика — Набор академических навыков
Дроби
Главное меню ContentsToggle 1 Дроби 2 Упрощение дробей 3 Сложение и вычитание дробей 3.1 Рабочие примеры 4 Умножение дробей 4.1 Рабочие примеры 5 Деление дробей 5.1 Рабочие примеры 6 Видео примеры 7 Рабочая тетрадь 8 Проверь себя 9Внешние ресурсы
Дроби
Дробь — это выражение вида $\dfrac{p}{q}$, где $p$ и $q$ — целые числа или алгебраические выражения.
Мы называем $p$ числителем и $q$ знаменателем .
Дроби вида $\dfrac{a}{b}$, где $a$ и $b \neq 0$ — целые числа, составляют множество из рациональных чисел $\mathbb{Q}$. Такие дроби еще называют арифметическими дробями .
92-1} \end{align} В последнем примере мы требуем, чтобы $x \neq \pm 1$ иначе дробь была бы undefined .
Упрощение дробей
Мы можем упростить дробь, сократив все общие множители числителя и знаменателя. Говорят, что дробь, которая была упрощена, записывается в ее простейшей форме или низшей форме .
Арифметическая дробь имеет простейшую форму, если числитель и знаменатель не имеют общих целых делителей.
Примечание : При упрощении алгебраических дробей мы всегда должны помнить о возможности деления на ноль.
Пример 1
Упрощение: $\dfrac{24}{36}$
Решение
$24$ и $36$ имеют общий коэффициент $4$, поэтому мы можем сократить $4$ сверху и снизу: \[ \dfrac{24 \div 4}{36\div 4} = \dfrac{6}{9}\] Поскольку $6$ и $9$ имеют общий множитель $3$, мы можем сократить $3$ сверху и снизу : \[\dfrac{6\div3}{9\div3}=\dfrac{2}{3}\] Поскольку $2$ и $3$ не имеют общих делителей, эта дробь теперь имеет простейшую форму. 92+4x+3}&=\dfrac{(x+2)(x+1)}{(x+3)(x+1)}\\ &=\dfrac{x+2}{x+3} ,\;\;x \neq -1 \end{align} При сокращении общего множителя $x+1$.
Обратите внимание, что мы тщательно указываем значение $x$, при котором выражение не определено.
Сложение и вычитание дробей
Если две или более дроби имеют одинаковый знаменатель, говорят, что они имеют общий знаменатель .
Складывать и вычитать дроби просто, если все они имеют общий знаменатель: мы просто складываем или вычитаем числители.
Пример : $\dfrac{1}{5} + \dfrac{3}{5} = \dfrac{4}{5}$
Пример : \begin{align} \frac{y+ z-xy}{y+z+1}+\frac{1+xy}{y+z+1}&=\dfrac{(y+z-xy)+(1+xy)}{y+z+ 1}\\ &=\dfrac{y+z+1}{y+z+1}\\ &=1,\;\;y+z+1 \neq 0 \end{align}
Если знаменатели различны, простое сложение или вычитание числителей вместе не имеет смысла — каким должен быть знаменатель результата? Решение состоит в том, чтобы привести обе дроби к общему знаменателю, прежде чем выполнять сложение (или вычитание). Этот общий знаменатель равен произведению знаменателей дробей, которые мы складываем (или вычитаем).
Например, предположим, что мы хотим вычислить: \[\frac{3}{5}+\frac{7}{10}\] Общий знаменатель будет $5\times 10=50$. Чтобы переформулировать первую дробь в этом знаменателе, мы должны умножить и числитель, и знаменатель на $10$: \[\frac{3\times 10}{5 \times 10}=\frac{30}{50}\] вторую дробь над этим знаменателем, мы должны умножить и числитель, и знаменатель на $5$: \[\frac{7\times 5}{10 \times 5}=\frac{45}{50}\] Поскольку знаменатели две дроби, которые мы хотим сложить, одинаковы ($50$), мы можем просто сложить числители и записать результат над общим знаменателем, чтобы теперь у нас была одна дробь: \[\frac{30}{50}+\frac {45}{50}=\frac{75}{50}\] Последний шаг — записать эту дробь в простейшей форме, убрав все общие множители в числителе и знаменателе (если они есть). Наибольший общий делитель 75$ и 50$ равен 25$, поэтому: \[\frac{75}{50}=\frac{75 \div 25}{50\div 25}=\frac{3}{2} \] Таким образом, \[\frac{3}{5}+\frac{7}{10}=\frac{3}{2}\]
В сводке :
1) Умножьте знаменатели, чтобы получить общий знаменатель.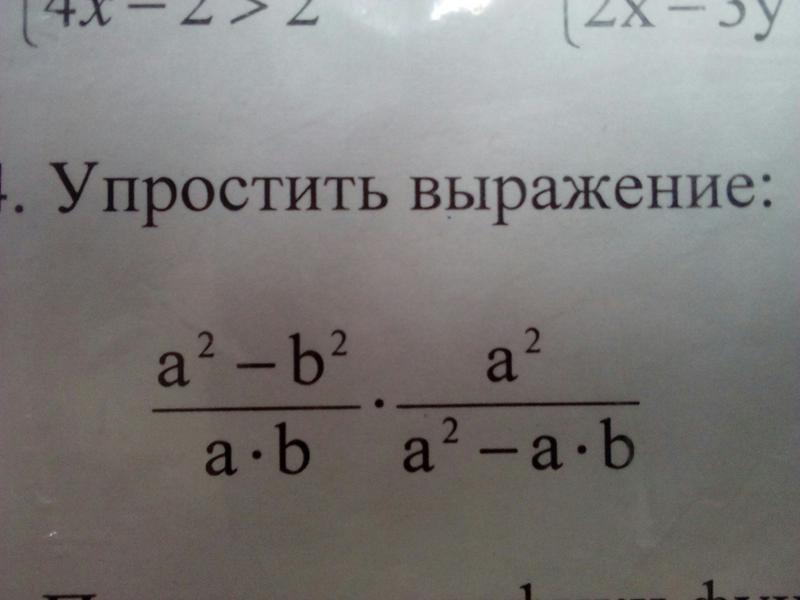
2) Сформулируйте каждую дробь под общим знаменателем.
3) Сложите (или вычтите) числители и запишите результат над общим знаменателем.
4) При необходимости упростите дробь.
Примеры работы
Пример 1
Вычислить $\dfrac{3}{5}+\dfrac{1}{4}$.
Решение
\begin{align} \frac{3}{5}+\frac{1}{4} &= \frac{3\times4}{5 \times 4} + \frac{1 \times 5 }{5\times4}\\ &= \frac{12}{20} + \frac{5}{20} \\ &=\frac{12+5}{20}\\ &=\frac{17} {20} \end{выравнивание} 92+y}{xy} \end{align}
Пример 3
Вычислить $\dfrac{5}{6}-\dfrac{2}{3}$.
Решение
\begin{align} \frac{5}{6}-\frac{2}{3}&= \frac{5}{6} — \frac{2\times 2}{3 \times 2} \\ &= \frac{5}{6} — \frac{4}{6} \\ &=\frac{5-4}{6}\\ &=\frac{1}{6} \ end{align}
Примечание: , как вы можете видеть в этом примере, не всегда необходимо умножать знаменатели вместе, чтобы получить общий знаменатель. Здесь $3$ делится на $6$ без остатка, поэтому разумнее было использовать $6$ в качестве общего знаменателя, а не $6 \times 3=18$.
Если бы мы использовали $18$ в качестве общего знаменателя, мы бы получили тот же результат, но с одним дополнительным шагом:
\begin{align} \frac{5}{6}-\frac{2} {3}&= \frac{5\times 3}{6 \times 3} — \frac{2\times 6}{6 \times 3}\\ &= \frac{15}{18} — \frac{ 12}{18} \\ &=\frac{15-12}{18}\\ &=\frac{3}{18}\\ &=\frac{1}{6} \end{align}
Пример 4
Запишите $\dfrac{x+y}{xy-x}-\dfrac{xy-1}{y-1}$ как одну алгебраическую дробь.
В этом примере мы находим общий знаменатель $x(y-1)$, на который делятся оба знаменателя. 92y}{x(y-1)} \end{align}
Умножение дробей
Правило умножения дробей: умножить числители вместе и умножить знаменатели вместе:
\[\frac{a}{b} \ раз \frac{c}{d} = \frac{ac}{bd}\]
Примеры работы
Пример 1
Вычислить $\dfrac{3}{7} \times \dfrac{5}{3} $.
Решение
\begin{align} \frac{3}{7} \times \frac{5}{3} &= \frac{3\times5}{7\times3}\\ &= \frac{15 }{21}\\ &= \frac{5}{7} \end{align} 92y}{z} \qquad \textrm{ (При сокращении общего члена }y\textrm{ в числителе и знаменателе)} \end{align}
Деление дробей
Правило деления дробей: \[\frac {a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}.
\]
Это легко запомнить как «перевернуть вторую дробь» , затем умножить».
Иногда это может быть записано как дробь поверх дроби, но правило остается тем же: \[\frac{a/b}{c/d}=\frac{a}{b}\times\frac {д}{с}\текст{.}\]
Примеры работы
Пример 1
Вычислить $\dfrac{1}{3}\div\dfrac{1}{4} $.
Решение
\begin{align} \frac{1}{3}\div\frac{1}{4} &=\frac{1}{3}\times\frac{4}{1}\\ \\ &=\frac{1\times4}{3\times1}\\\\ &=\frac{4}{3}. \end{align}
Пример 2
Вычислить $\dfrac{3}{5} \div \dfrac{2}{3}$.
Решение
\begin{align} \frac{3}{5}\div\frac{2}{3} &=\frac{3}{5}\times\frac{3}{2}\\ \\ &=\frac{3\times3}{5\times2}\\\\ &=\frac{9{10}. \end{align}
Пример 3
Упростите дробь $\dfrac{2/3}{2-5/7}$.
Решение
Начните с замены дроби на символ деления, чтобы увидеть обе части рядом. \[\frac{2}{3} \div \left(2-\frac{5}{7}\right)\] Вычтите $\frac{5}{7}$ из $2$, положив их на общую знаменатель.
\begin{align} 2 — \frac{5}{7} &= 2 \times \frac{7}{7} — \frac{5}{7} \\ &= \frac{14}{7} — \frac{5}{7} \\ &= \frac{14 — 5}{7} \\ &= \frac{9}{7}. \end{align} Теперь у нас есть: \[\frac{2}{3} \div \frac{9}{7}\] Используйте правило деления дробей. \begin{align} \frac{2}{3} \div \frac{9}{7} &= \frac{2}{3} \times \frac{7}{9} \\ \\ &= \ frac{2 \times 7}{3 \times 9} \\ \\ &= \frac{14}{27}. \end{align}
Пример 4
Выразите $\dfrac{4}{1-2x} — 3$ в виде одной дроби.
Решение
Сначала приведем все к одному знаменателю $1-2x$, затем раскроем скобки в числителе и упростим.
\begin{align} \frac{4}{1-2x} — 3 & = \frac{4}{1-2x} — \frac{3(1-2x)}{1-2x}\\\ \ &=\frac{4-3(1-2x)}{1-2x}\\\\ &=\frac{4-3+6x}{1-2x}\\\\ &=\frac{1 +6x}{1-2x} \end{align} $1+6x$ и $1-2x$ не имеют общих множителей, поэтому дробь имеет простейшую форму. 92-1}$.
Пример 3
Профессор Робин Джонсон вычисляет $2 \div \dfrac{1}{4}$ и $3 \div \dfrac{2}{5}$.