Как узнать перпендикулярны ли векторы: Как найти вектор перпендикулярный вектору? Ответ на webmath.ru

Условие перпендикулярности плоскостей | matematicus.ru

Skip to content

11.04.2019 Artman Аналитическая геометрия в пространстве

Если плоскости

  A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0

перпендикулярны, то и их нормальные векторы (нормали) перпендикулярны, т.е.

N₁{A₁;B₁;C₁} ⊥ N₂{A₂;B₂;C₂},

тогда условие перпендикулярности плоскостей запишем:

  A₁⋅A₂+B₁⋅B₂+C₁⋅C₂=0 

---

Пример 

  Плоскости  2x-y-2z+5=0 и 2x+2y+z+3=0 перпендикулярны, так как

2⋅2+(-1)⋅2+(-2)⋅1=0

 

Объём параллелепипеда построенного на векторах

Объём параллелепипеда, построенного на трех векторах

a₁={X₁;Y₁;Z₁}, a₂={X₂;Y₂;Z₂} и a₃={X₃;Y₃;Z₃} равен модулю смешанного произведения векторов и  находится по формуле:

где координаты векторов в соответствии с рисунком

вычисляются следующим образом

a₁=$\overrightarrow {AA_1} $={X₁=X_a1-X_a; Y₁=Y_a1-Y_a; Z₁=Z_a1-Z_a; }

a₂=$\overrightarrow {AD} $={X₂=X_d-X_a; Y₂=Y_d-Y_a; Z₂=Z_d-Z_a; }

a₃=$\overrightarrow {AB} $={X₃=X_b-X_a; Y₃=Y_b-Y_a; Z₃=Z

b-Z_a; }

  Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.

---

Пример

  Найти объём параллелепипеда, построенного на векторах a₁={2;3;2}, a₂={-1;-4;3} и a₃={3;1;2}

Решение

$V =  \pm \left| {\begin{array}{*{20}{c}}2&3&2 \\  { — 1}&{ — 4}&3 \\ 3&1&2 \end{array}} \right| =  $

$=\pm \left( {2\left| {\begin{array}{*{20}{c}} { — 4}&3 \\ 1&2 \end{array}} \right| — 3\left| {\begin{array}{*{20}{c}}{ — 1}&3 \\ 3&2 \end{array}} \right| + 2\left| {\begin{array}{*{20}{c}}{ — 1}&{ — 4} \\ 3&1 \end{array}} \right|} \right) = $

$ =  \pm \left( {2\cdot\left( {\left( { — 4} \right)\cdot2 — 1\cdot3} \right) — 3\left( {\left( { — 1} \right)\cdot2 — 3\cdot3} \right) + 2\left( {\left( { — 1} \right)\cdot1 — 3\cdot\left( { — 4} \right)} \right)} \right) = -33$

  Так как определитель отрицателен, берем перед ним знак «—».

Тогда объём параллелепипеда равен  V=33

3472

15.

Скалярное произведение векторов и его свойства.Условие перпендикулярности векторов.Угол между векторами.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла фи между ними

Скалярное произведение равно сумме произведений соответствующих координат этих векторов.

Скалярный квадрат вектора равен квадрату его длины.

свойства проекций:

1)     Равные векторы имеют равные проекции на одну и ту же ось.

2)     прпр пр .

3)     прпр , .

4)     пр , где  – угол между вектором и осью.

Заметим, что проекция вектора на ось и его составляющая связаны соотношением сост

пр .

Условие перпендикулярности векторов

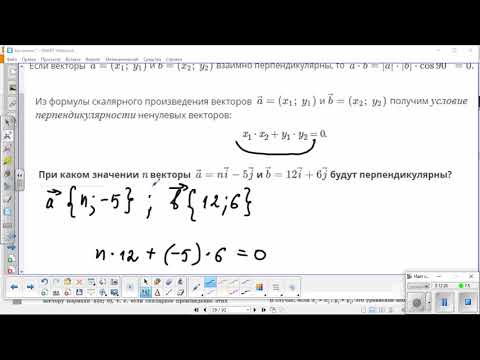
• Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

• Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_b + y_ay_b = 0.

Углом между двумя ненулевыми векторами  и  называется наименьший угол ( ), на который надо повернуть один из векторов до его совпадения со вторым. Предварительно нужно привести векторы к общему началу О (рис. 7).

Рис. 7

Под углом между вектором  и осью  понимают угол между векторами  и  (рис. 8).

 

16.Векторное произведение и его свойства.

Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левой (начала векторов тройки предполагаются совмещенными). Так, на рис. 16 тройка , ,  – правая, а тройка , , – левая (из конца вектора  кратчайший поворот от  к  виден по часовой стрелке).

Рис. 16Векторным произведением двух векторов называется вектор, который обозначается  или и определяется следующим образом: 1)     где  – длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними; 2)      , – этот вектор перпендикулярен каждому из перемножаемых векторов; 3)     векторы , ,  образуют правую тройку. Из условия (1) следует, что модуль вектора

численно равен площади параллелограмма, построенного на векторах  и  как на сторонах (рис 17): , .

Свойства векторного произведения:

1)     ;

2)     ;

3)     ;

4)     , или , или ;

4a) .

17.Смешанное произведение и его свойства.

Условие компланарности векторов.

Смешанным, или векторно-скалярным произведением трех векторов (обозначается ) называется произведение вида .

 Свойства:

• Коммутативность

• ассоциативность

Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю

Доказательство. Необходимость. Пусть векторы , ,  компланарны. Можно считать, что они лежат в одной плоскости. Тогда вектор  перпендикулярен этой плоскости, следовательно, ,

а значит, их скалярное произведение равно нулю, то есть .

Достаточность. Пусть . Предположим, что векторы некомпланарны. Но тогда существует параллелепипед, построенный на этих векторах, объем которого , а это противоречит условию . Следовательно, предположение неверно, и векторы компланарны.

Перекрестное произведение перпендикулярных векторов

Вектор — это двумерный объект, имеющий как величину, так и направление. Геометрию вектора можно проиллюстрировать как направленный отрезок линии со стрелкой, указывающей в правильном направлении, и длиной, равной величине вектора. Направление векторов от хвоста к голове. Под прямым углом перпендикулярные линии пересекаются друг с другом.

В трехмерном ориентированном евклидовом векторном пространстве перекрестное произведение или векторное произведение представляет собой бинарную операцию над двумя векторами. Третий вектор, перпендикулярный двум исходным векторам, представляет собой векторное произведение двух векторов. Площадь параллелограмма между ними определяет его величину, а правило большого пальца правой руки определяет его направление.

Перекрестное произведение перпендикулярных векторов

Он перпендикулярен обоим векторам v и w, если векторное произведение v,w двух ненулевых векторов v и w также является ненулевым вектором. Когда два вектора перпендикулярны друг другу, угол, образованный между ними, равен 90 градусов.

Перекрестное произведение двух векторов равно произведению их модулей и синуса угла между ними, как мы все знаем. Перекрестное произведение дает вектор, перпендикулярный обоим векторам, потому что вектор площади любой поверхности определяется в направлении, перпендикулярном этой поверхности. и величина которого равна площади параллелограмма, смежные стороны которого являются этими двумя векторами.

Рисунок 1

Если A и B являются двумя независимыми векторами, результат их поперечного продукта (a × b) перпендикулярно обоим векторам и нормальным по отношению к плоскости, в которой они оба находятся.

А ×В= |А| |Б| sin θ n

 

|A| = длина вектора A

B= длина вектора B

θ= угол между A и B

n = единичный вектор, перпендикулярный плоскости, содержащей a и b

 

Например, если два вектора лежат в плоскости X-Y, их векторное произведение даст результирующий вектор в направлении оси Z, который перпендикулярна плоскости XY.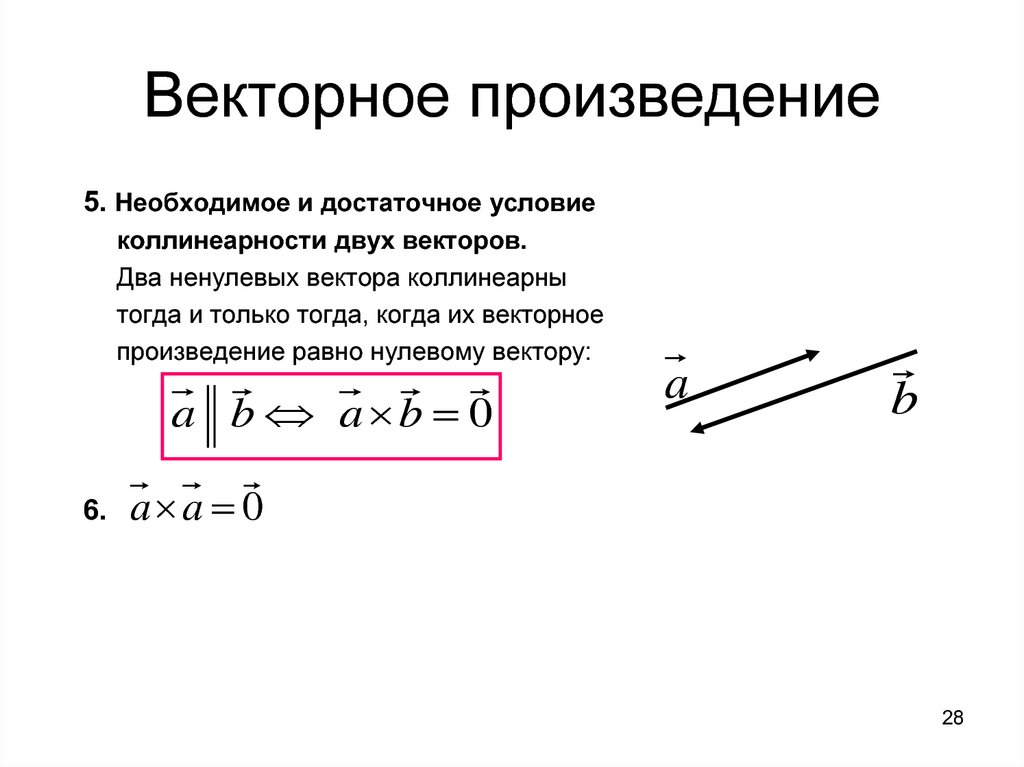 Между исходными векторами используется символ . Перекрестное произведение двух векторов, также известное как векторное произведение, обозначается как:

ab=c

 

Величина перекрестного произведения перпендикулярных векторов

Мы получаем еще один вектор, выровненный перпендикулярно плоскости, содержащей два вектора, когда находим векторное произведение двух векторов. Величина результирующего вектора равна произведению синуса угла между векторами и величины двух векторов. а × б = | а | |б| грех θ.

Величина векторного произведения максимальна, когда a и b перпендикулярны, как показывает эта формула. С другой стороны, перекрестное произведение является нулевым вектором, если a и b параллельны или если любой из векторов является нулевым вектором. Не существует уникальной прямой, перпендикулярной как к a, так и к b, если векторы параллельны или один вектор является нулевым вектором. Более того, поскольку существует только один вектор нулевой длины, векторное произведение однозначно определяется определением.

 

 

Угол, образованный углами a и c, всегда равен 90 градусов.

Угол между точками b и c всегда равен 90 градусам.

Мы можем выровнять a и b параллельно друг другу или под углом 0°, что приведет к нулевому вектору.

Исходные векторы должны быть перпендикулярны (угол 90°), чтобы векторное произведение двух векторов было наибольшим.

Перекрестное произведение перпендикулярных векторов пример

Пример: найти векторное произведение. Затем используйте скалярное произведение, чтобы проверить перпендикулярность.

Решение: 

Теперь проверьте перпендикулярность.

Заключение

В этой статье мы заключаем, что когда два вектора перпендикулярны друг другу, угол между ними составляет 90 градусов. Как мы все знаем, перекрестное произведение двух векторов равно произведению их модулей плюс синус угла между ними. Вектор, перпендикулярный основанию плоскости, также перпендикулярен всей плоскости. В результате перекрестное произведение двух (линейно независимых) векторов ортогонально плоскости, которую они охватывают, потому что оно ортогонально каждому из них.

 

Векторная проекция — JCCC MATH/PHYS 191

FOLT СОДЕРЖАНИЕ Параллельная проекция Перпендикулярная проекция БОЛЬШИЕ ТОЧКИ Линии в 2D и плоскостях в 3D Линии 2D или 3D БОЛЬШЕ Практика УРЕБЛЕНИЕ

Перпендикулярная проекция вектора $\vec{u}$ на другой вектор $\vec{v}$ дает нам вектор, параллельный вектору $\vec{v}$, длина которого равна длине вектора $\vec{u}$ продолжается в направлении $\vec{v}$. Это показано ниже.

Возможно, проецируемый вектор простирается в направлении, противоположном вектору, на который он проецируется. В этом случае проекция выглядит примерно так.

Теперь разработаем формулу для параллельной проекции. Мы знаем, что результат будет параллелен $\vec{v}$. Нам просто нужно определить величину. Для этого мы можем использовать тригонометрию прямоугольного треугольника. Используя следующую картинку в качестве руководства,

(1)

\begin{eqnarray} \cos \theta =\frac{|\mbox{Proj}_\vec{v} \vec{u}|}{|\vec{u}|}\\ |\mbox{Proj }_\vec{v} \vec{u}|=|\vec{u}|\cos \theta\\ |\mbox{Proj}_\vec{v} \vec{u}|=|\vec{ u}|\frac{\vec{u} \cdot \vec{v}}{|\vec{u}\|\vec{v}|}\\ |\mbox{Proj}_\vec{v} \ vec{u}|=\frac{\vec{u} \cdot \vec{v}}{|\vec{v}|}\\ \end{eqnarray} 92}\vec{v}\\ \end{align}

Пример
Найти параллельную проекцию $<3,5,-2>$ на $<4,0,1>$

Решение

В то время как параллельная проекция дала нам вектор, параллельный вектору на плоскость, перпендикулярная проекция дает нам вектор, перпендикулярный вектору на плоскость. Эта перпендикулярная проекция с величиной, соответствующей количеству $\vec{u}$, простирается в направлении, перпендикулярном $\vec{v}$

Получить перпендикулярную проекцию из параллельной проекции довольно просто с помощью вектора дополнение следующим образом.

(3)

\begin{align} \mbox{Proj}_\vec{v} \vec{u} + \bot \mbox{Proj} _\vec{v} \vec{u} = \vec{u}\\ \bot \mbox{Proj} _\vec{v} \vec{u} = \vec{u}-\mbox{Proj}_\vec{v} \vec{u} \end{align}

Пример
Найти перпендикулярную проекцию $<3,5,-2>$ на $<4,0,1>$

Решение

Использование векторной проекции может значительно упростить процесс нахождения ближайшей точки на линии или плоскости от заданной точки. Мы рассмотрим два подхода. Первый подход использует направление, нормальное к рассматриваемому объекту. Это будет включать линии в 2D и плоскости в 3D. Второй подход использует направление, параллельное объекту, что применимо к линиям в 3D.

Прямые в 2D и плоскости в 3D

В этих задачах у нас будет некоторая точка в 2D или 3D, которую мы назовем $Q$ и либо прямая в 2D линия, либо плоскость в 3D. Оба эти объекта могут быть описаны в терминах точки на объекте $P$ и направления нормали к объекту. Направление нормали будем представлять вектором $\vec{n}$. Мы будем пытаться определить ближайшую точку $S$ на объекте от точки $Q$. На приведенном ниже рисунке видно, что вектор $\vec{S}$, указывающий на ближайшую точку $S$, задается как $\vec{S}=\vec{Q}-\mbox{Proj} _{\vec{n}}\vec{PQ}$

Если бы нас интересовало расстояние от точки $Q$ до точки $S$, нам нужно было бы только вычислить $|\mbox{Proj}_{\vec{n}}\vec{PQ}|$

Пример
Найдите точку на плоскости $x+2y-3z=4$, ближайшую к точке $(0,1,-1)$

Решение

Линии в 2D или 3D

В этих задачах у нас будет некоторая точка в 2D или 3D, которую мы назовем $Q$, и линия либо в 2D, либо в 3D. Обе линии можно описать в терминах точки на прямой $P$ и направления, параллельного этой прямой. Мы будем представлять параллельное направление вектором $\vec{d}$. Мы будем пытаться определить ближайшую точку $S$ на объекте от точки $Q$. На приведенном ниже рисунке видно, что вектор $\vec{S}$, указывающий на ближайшую точку $S$, задается как $\vec{S}=\vec{P}+\mbox{Proj} _{\vec{d}}\vec{PQ}$

Если бы нас интересовало расстояние от точки $Q$ до точки $S$, нам нужно было бы вычислить только $|\vec{Q} — \vec{S}|$

Пример
Найдите точку на прямой $<1+t,4-3t,2t>$, ближайшую к точке $(5,6,7)$

Решение

На следующей странице представлены инструменты для отработки различных векторных операций.
Практика векторных операций

1. Найти параллельную проекцию $\vec{u}=<1,4,-2>$ на вектор $\vec{v}=<0,3,5>$
2. Найти перпендикулярную проекцию $\vec{u}=<1,4,-2>$ на вектор $\vec{v}=<0,3,5>$
3. Запишите $\vec{u}=<1,4,-2>$ как сумму вектора, параллельного и перпендикулярного $\vec{v}=<0,3,5>$
4. При каких условиях $\mbox{Proj} _\vec{v} \vec{u} =\vec{0}$
5. Найдите точку на прямой, проходящей через (1,4,-8) и (3,2,1), ближайшую к точке (0,0,0).

   No related posts.