Сложение и вычитание векторов решение задач: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 10 класс.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Методическая разработка урока геометрии по теме «Сложение векторов» 9 класс | План-конспект урока по геометрии (9 класс):

Задание 20 №1

Укажите номера верных утверждений.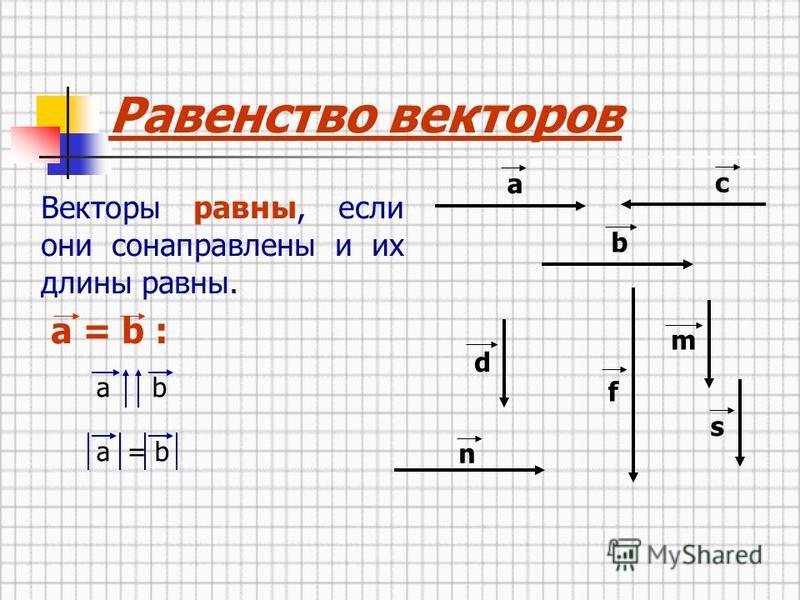

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.

 

Ответ: 12.

Задание 20 № 2

Укажите номера верных утверждений.

 

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.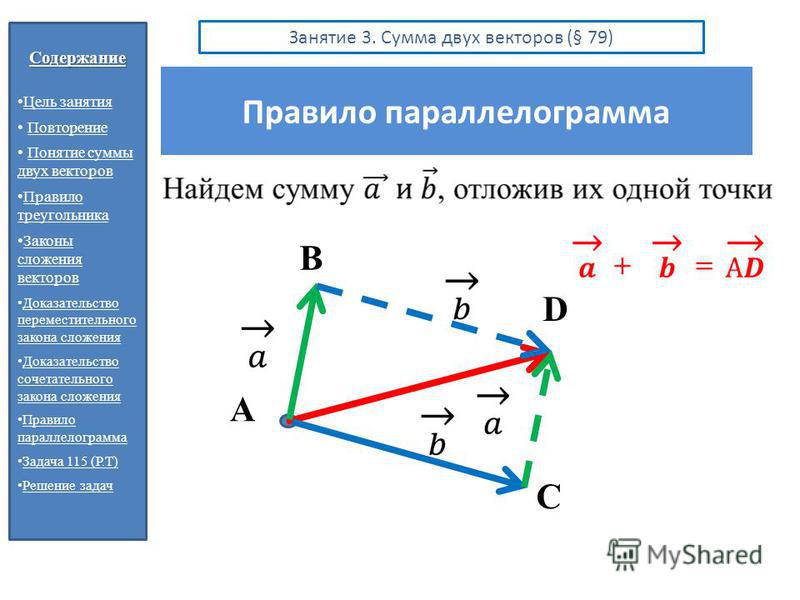

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существует квадрат, который не является прямоугольником» — некорректное утверждение, корректное — «Существует прямоугольник, который не является квадратом».

2) «Если два угла треугольника равны, то равны и противолежащие им стороны» — верно, т. к. треугольник, два угла которого равны является равнобедренным, причём равные стороны лежат напротив равных углов.

3) «Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны» — верно, это теорема планиметрии.

 

Ответ: 23.

Задание 20 № 3

Укажите номера верных утверждений.

 

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.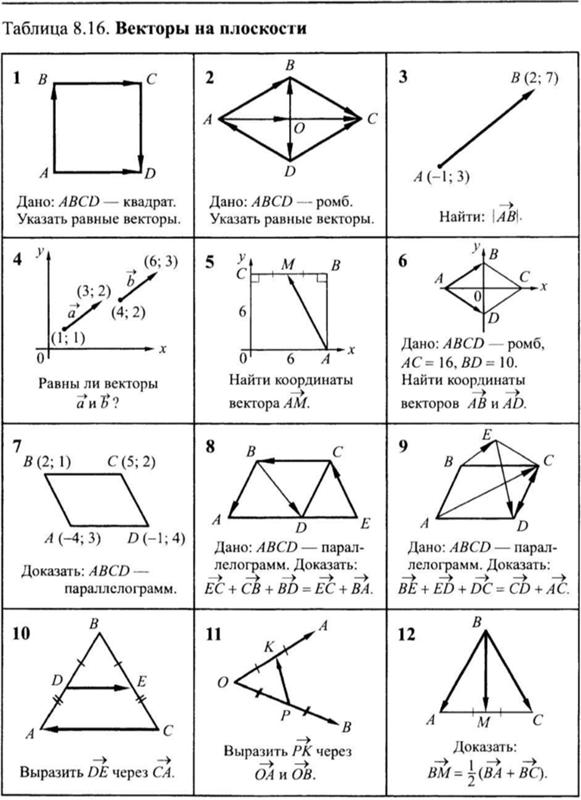

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно по свойству равнобедренного треугольника.

2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это утверждение справедливо исключительно для ромба, а не для прямоугольника.

3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу» — верно, т. к. окружность — множество точек, находящихся на заданном расстоянии от данной точки.

 

Ответ: 13.

Задание 20 № 4

Укажите номера верных утверждений.

 

1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Центры вписанной и описанной окружностей равностороннего треугольника совпадают» — верно, т.к. совпадают точки пересечения биссектрис и серединных перпендикуляров этого треугольника.

2) «Существует квадрат, который не является ромбом» — неверно; верным будет утверждение: «Существует ромб, который не является квадратом».

3) «Сумма углов любого треугольника равна 180°» — верно по свойству треугольника.

 

Ответ: 13.

Задание 20 № 5

Укажите номера верных утверждений.

 

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если угол острый, то смежный с ним угол также является острым» — неверно, т.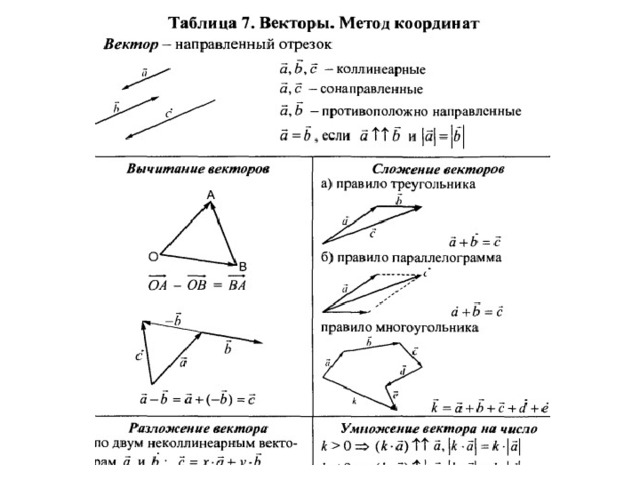  к. смежные углы в сумме составляют 180°.

2) «Диагонали квадрата взаимно перпендикулярны» — верно, т. к. квадрат — частный случай ромба.

3) «В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности» — верно, т. к. окружность — это множество точек, находящихся на заданном расстоянии от данной точки.

 

Ответ: 23.

Задание 20 № 6

Укажите номера верных утверждений.

 

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

 

1) «Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны» — верно, по первому признаку подобия треугольников.

2) «Сумма смежных углов равна 180°» — верно по свойству смежных углов.

3) «Любая высота равнобедренного треугольника является его биссектрисой» — неверно, это утверждение справедливо только для равностороннего треугольника.

 

Ответ: 12.

Задание 20 № 7

Какие из следующих утверждений верны?

 

1) Если угол равен 45°, то вертикальный с ним угол равен 45°.

2) Любые две прямые имеют ровно одну общую точку.

3) Через любые три точки проходит ровно одна прямая.

Решение.

Проверим каждое из утверждений.

1) «Если угол равен 45°, то вертикальный с ним угол равен 45°» — верно, по теореме о вертикальных углах.

2) «Любые две прямые имеют ровно одну общую точку» — неверно, утверждение справедливо только для пересекающихся прямых.

3) «Через любые три точки проходит ровно одна прямая» — неверно, не всегда через три точки можно провести одну прямую.

4) «Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.» — неверно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.

 

Ответ: 1.

Задание 20 № 8

Какие из следующих утверждений верны?

 

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.» — верно, так как если соответственные углы равны, то прямые параллельны.

2) «Любые две прямые имеют не менее одной общей точки.» — неверно, две прямые имеют не более одной общей точки.

3) «Через любую точку проходит более одной прямой.» — верно, через одну точку проходит множество пересекающихся в этой точке прямых.

 

Ответ: 13.

Сложение и вычитание векторов: графические методы

Векторы в двух измерениях

Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рисунке 2 показано графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный символ, такой как D , обозначает вектор. Его величина представлена ​​курсивным символом D , а его направление — θ .

Векторы в этом тексте

В этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором F , который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ .

Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º к северу от востока.

Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, рассмотренному на рисунке 2, нарисуйте стрелку, представляющую вектор полного перемещения Д . Используя транспортир, нарисуйте линию под углом θ  относительно оси восток-запад. Длина D  стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ составляет 29,1º к северу от востока.

Сложение векторов: метод «голова к хвосту»

Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на Рисунке 4 ниже и в следующих шагах.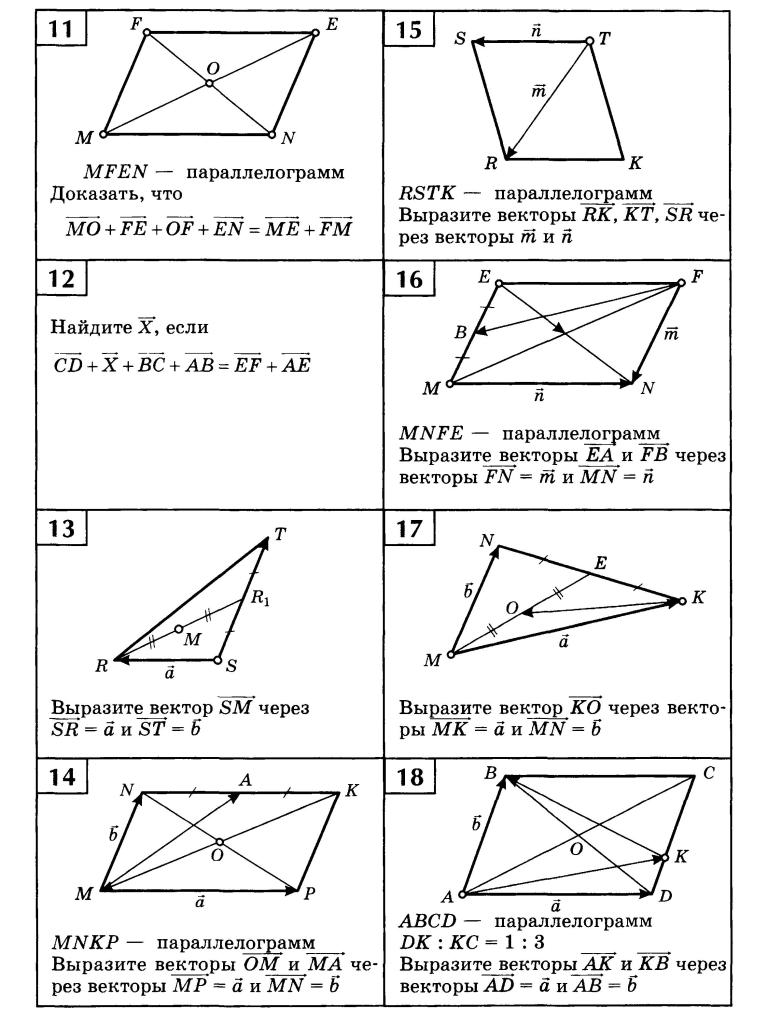 хвост вектора является начальной точкой вектора, а начало (или кончик) вектора является конечным заостренным концом стрелки.

Рис. 4. Метод «голова к хвосту». Метод графического сложения векторов «голова к хвосту» проиллюстрирован для двух перемещений человека, идущего по городу, показанного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, равно 29,1º.

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .

Рисунок 5

Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .

Рисунок 6

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .

Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это равнодействующее или сумма других векторов.

Рисунок 7

 

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)

Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета с помощью транспортира. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 1. Графическое сложение векторов с использованием метода «голова к хвосту»: прогулка женщины ровное поле. Сначала она проходит 25,0 м в направлении 49..0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , делая длины пропорциональными расстоянию и направлениям, указанным относительно линия восток-запад. Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенного цифрой 9.0013 Р .

Решение

(1) Нарисуйте три вектора смещения.

Рисунок 8.

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рис. 9.

(3) Нарисуйте результирующий вектор R .

Рисунок 10.

(4) Используйте линейку для измерения величины R и транспортир для измерения направления R . Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.

Рисунок 11

 

В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено в направлении 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение.

Рисунок 12.

Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.

A + B = B + A.

(Это верно и для сложения обычных чисел — вы получите тот же результат, сложите ли вы, например, 2 + 3 или 3 + 2 ) .

Это видео можно использовать для просмотра. Он включает в себя основы работы с векторами — рисование векторов/добавление векторов. Вы узнаете об основном понятии вектора, о том, как графически складывать векторы, а также о том, что графически означает умножение вектора на скаляр.

Вычитание векторов

Вычитание векторов является прямым расширением сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть B из A, записанного A – B), мы должны сначала определить, что мы подразумеваем под вычитанием.0007 отрицательный вектора B определяется как –B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, B имеет ту же длину, что и -B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рис. 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, B является минусом 9.0013 –В ; он имеет ту же длину, но противоположное направление.

Затем вычитание вектора B из вектора A просто определяется как сложение –B с A . Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.

A – B = A + (-B)

Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.

Пример 2. Графическое вычитание векторов: женщина, плывущая на лодке

Женщина, плывущая на лодке ночью, следует указаниям к причалу. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0° к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112° к северу от востока (или 22,0° к западу от севера). Если женщина совершит ошибку и поедет в направлении против направления на второй этап поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 14.

Стратегия

Мы можем представить первый этап поездки вектором A , а второй этап поездки вектором B . Док находится по адресу A+B . Если женщина по ошибке едет в направлении , противоположном , для второго этапа пути, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от востока. Мы представляем это как –B , как показано ниже. Вектор –B имеет ту же величину, что и B, но в противоположном направлении. Таким образом, она окажется в локации A + (–B) , или A – B .

Рисунок 15

 

Выполним сложение векторов, чтобы сравнить местоположение причала, A + B , с местоположением, в которое по ошибке прибыла женщина, A + (-B) .

Решение

(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы А и –В .

(2) Разместите векторы лицом к хвосту.

(3) Нарисуйте результирующий вектор R .

(4) С помощью линейки и транспортира измерьте величину и направление R .

Рисунок 16

В этом случае R = 23 . 0 м и θ = 7 . 5º к югу от востока.

(5) Чтобы определить местоположение дока, мы повторяем этот метод, чтобы добавить векторы A и B . Получаем результирующий вектор 9Рисунок 17

Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Умножение векторов и скаляров

Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0 º к северу от востока. Это пример умножения вектора на положительный

скаляр . Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор A умножается на скаляр c ,

• , величина вектора становится абсолютной величиной c A ,
• если c положительно, направление вектора не меняется,
• , если c отрицательно, направление меняется на противоположное.

В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.

Разложение вектора на компоненты

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например компоненты x – и y , или компоненты север-юг и восток-запад.

Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0º к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.

PhET Explorations: Maze Game

Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Нажмите, чтобы загрузить. Запуск с использованием Java.

Резюме

• Графический метод сложения векторов   A и B включает в себя рисование векторов на графике и их сложение методом «голова к хвосту». Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
• Графический метод вычитания вектора B  из A включает добавление противоположного вектора B , который определяется как -B . В этом случае А – В = А + (-В) = R
  . Затем обычным образом применяется метод сложения «голова к хвосту» для получения результирующего вектора R .
• Сложение векторов коммутативно, так что A + B = B + A .
• Метод сложения векторов «голова к хвосту» заключается в том, что первый вектор рисуется на графике, а хвост каждого последующего вектора помещается в начало предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
• Если вектор A  умножить на скалярную величину c , величина произведения будет равна cA . Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .

Концептуальные вопросы

1. Что из следующего является вектором: рост человека, высота над уровнем моря, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?

2. Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.

3. Что общего между векторами и скалярами? Чем они отличаются?

4. Два отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый по своему пути, как показано ниже. Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?

Рисунок 18.

5. Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 19.. Какая еще информация ему понадобится, чтобы добраться до Сакраменто?

Рисунок 19.

6. Предположим, вы делаете два шага A и B (то есть два ненулевых перемещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить нуль? Максимальное расстояние, которое вы можете пройти от начальной точки A + B , равно сумме длин двух шагов?

7. Объясните, почему нельзя добавить скаляр к вектору.

8. Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше?

Задачи и упражнения

Используйте графические методы для решения этих задач. Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр.

1. Найдите следующее для пути A на рис. 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.

Рисунок 20. Различные линии обозначают пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м.

2. Найдите следующее для пути B на рисунке 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.

3. Найдите северную и восточную составляющие смещения для туристов, показанных на Рисунке 20.

4. Предположим, вы прошли 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения

A и B , как на рисунке 21, то эта задача требует от вас найти их сумму R = A + B .

Рисунок 21. Два смещения A и B складываются, чтобы получить общее перемещение R , имеющее величину R и направление θ .

5. Предположим, вы сначала прошли 12,0 м в направлении 20° к западу от севера, а затем 20,0 м в направлении 40,0° к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 22, то эта задача находит их сумму R = A + B . )

Рисунок 22.

6. Повторите задачу выше, но поменяйте порядок двух шагов ходьбы; показать, что вы получаете тот же конечный результат. То есть вы сначала проходите отрезок B , который составляет 20,0 м в направлении точно на 40º к югу от запада, а затем проходите отрезок A , который составляет 12,0 м в направлении ровно 12,0 к западу от севера. (Эта задача показывает, что A + B = B + A .)

7. (a) Повторите задачу двумя предыдущими задачами, но на втором этапе вы пройдете 20,0 м в направлении 40° к северу от востока (что эквивалентно вычитанию B из A , т. е. к нахождению R’ = A – B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала пройдете 20,0 м в направлении на 40º к югу от запада, а затем 12,0 м в направлении на 20º к востоку от юга (что эквивалентно вычитанию A из B — это есть, чтобы найти R” = B – A = R’  Покажите, что это так.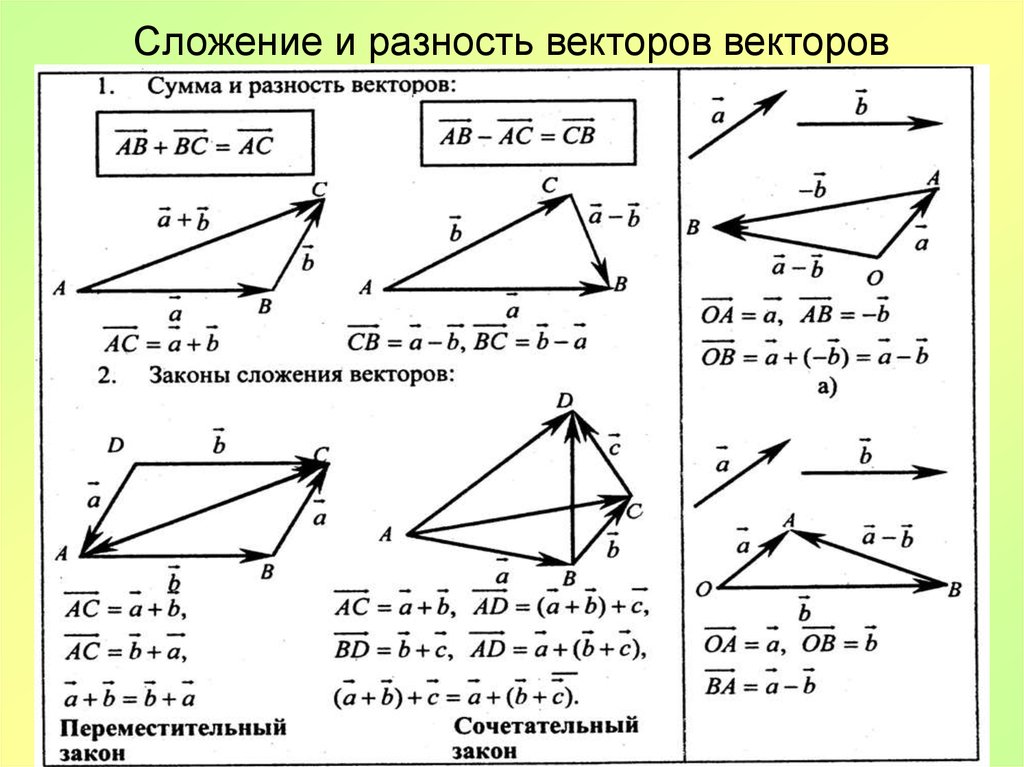

8. Показать, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство, выбрав любые три вектора  A , B и C , а также [latex]\mathbf{C}[/latex] , имеющие разную длину и направление. Найдите сумму A + B + C , затем найдите их сумму при сложении в другом порядке и покажите, что результат тот же. (Есть еще пять порядков, в которых A , B и C  можно добавить; выберите только один.)

9. Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.

10. Найдите модули скоростей на рисунке 23.

Рисунок 23. Две скорости V _A  и V _B складываются, чтобы получить общее значение V _к .

11. Найдите компоненты v _tot  along the x – and y -axes in Figure 23.

12. Find the components of v _tot  along a set of perpendicular axes rotated 30º counterclockwise relative тем, что на рис. 23.

Глоссарий

компонент (двумерного вектора):

часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов

коммутативный:

относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 647

направление (вектора):

ориентация вектора в пространстве

голова (вектора):

конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»

метод «голова к хвосту»:

метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора

величина (вектора):

длина или размер вектора; величина является скалярной величиной

результат:

сумма двух или более векторов

Результирующий вектор:

векторная сумма двух или более векторов

скаляр:

количество с величиной, но без направления

хвост:

начальная точка вектора; напротив наконечника или наконечника стрелки

Избранные решения задач и упражнений

1. (a) 480 м (b) 379 м, 18,4º к востоку от севера

3. северная составляющая 3,21 км, восточная составляющая 3,83 км

5,19,5 м, 4,6 к югу от запада

7. (а) 26,6 м, 65,1° к северу от востока (б) 26,6 м, 65,1° к югу от запада

9. 52,9 м, 90,1º относительно оси x .

11.  x — составляющая 4,41 м/с,  y — составляющая 5,07 м/с

 

3.3: Сложение и вычитание векторов – аналитические методы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1493

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Понимать правила сложения и вычитания векторов с использованием аналитических методов.
• Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
• Применение аналитических методов для определения величины и направления результирующего вектора.

Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.

Разложение вектора на перпендикулярные компоненты

Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, имея такой вектор, как \(\displaystyle A\) на рисунке, мы можем захотеть найти, какие два перпендикулярных вектора, \(\displaystyle A_x\) и \(\displaystyle A_y\), нужно сложить, чтобы получить его.

Рисунок \(\PageIndex{1}\): вектор \(\displaystyle A\) с хвостом в начале системы координат x, y показан вместе с его x- и y-компонентами, \ (\displaystyle A_x\) и \(\displaystyle A_y\). Эти векторы образуют прямоугольный треугольник. Аналитические отношения между этими векторами резюмируются ниже.

\(\displaystyle A_x\) и \(\displaystyle A_y\) определяются как компоненты \(\displaystyle A\) по осям x и y. Три вектора \(\displaystyle A, A_x\) и \(\displaystyle A_y\) образуют прямоугольный треугольник:

\(\displaystyle A_x + A_y = A.\)

Обратите внимание, что эта связь между компонентами вектора и результирующий вектор верен только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если \(\displaystyle A_x=3 м\) на восток, \(\displaystyle A_y=4 м\) на север и \(\displaystyle A=5 м\)на северо-восток, то верно, что векторы \(\displaystyle A_x + A_y = A\). Однако неверно, что сумма величин векторов также равна. то есть

\(\displaystyle 3 м+4 м ≠ 5 м\)

Таким образом,

\(\displaystyle A_x+A_y≠A\)

Если вектор \(\displaystyle A\) известен, то его величина \(\displaystyle A\) (его длина) и его угол \(\displaystyle θ\) (его направление) известны. Чтобы найти \(\displaystyle A_x\) и \(\displaystyle A_y\), его x- и y-компоненты, мы используем следующие отношения для прямоугольного треугольника.

\(\displaystyle A_x=Acosθ\)

и

\(\displaystyle A_y=Asinθ.\)

Рисунок \(\PageIndex{2}\): Величины компонентов вектора \(\displaystyle A_x\) и \(\displaystyle A_y\) могут быть связаны с результирующим вектором \(\displaystyle A\) и углом \(\displaystyle θ\) с тригонометрическими тождествами.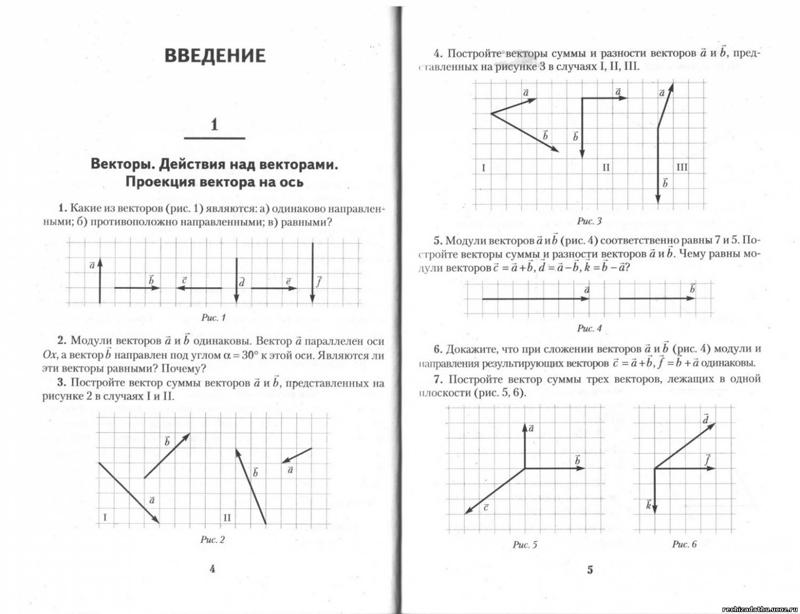 Здесь мы видим, что \(\displaystyle A_x=Acosθ\) и \(\displaystyle A_y=Asinθ.\)

Предположим, например, что A представляет собой вектор, представляющий полное перемещение человека, идущего по городу, рассматриваемому в Кинематика в двух измерениях: введение и сложение и вычитание векторов: графические методы.

Рисунок \(\PageIndex{3}\): Мы можем использовать отношения \(\displaystyle A_x=Acosθ\) и \(\displaystyle A_y=Asinθ\) для определения величины векторов горизонтальной и вертикальной составляющих в этом примере .

Затем \(\displaystyle A=10,3\) блоков и \(\displaystyle θ=29,1º\), так что

\(\displaystyle A_x=A\cos θ=(10,3 блока)(\cos 29,1º)= 9,0\) блоков

\(\displaystyle A_y=A\sin θ=(10,3 блоков)(\sin 29,1º)=5,0\) блоков.

Вычисление результирующего вектора 9{–1}(A_y/A_x)\) используются для нахождения вектора по его перпендикулярным компонентам, то есть для перехода от \(\displaystyle A_x\) и \(\displaystyle A_y\) к \(\displaystyle A\ ) и \(\displaystyle θ\).

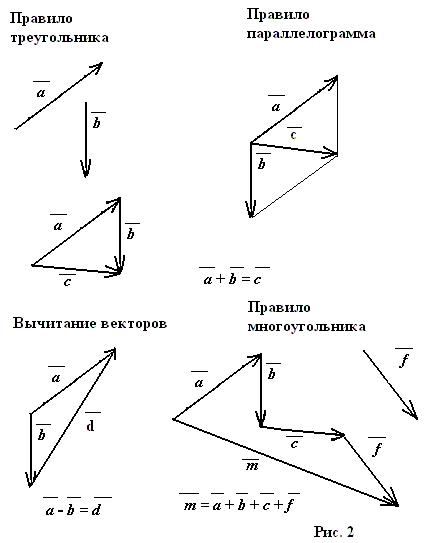Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.

Добавление векторов с использованием аналитических методов

Чтобы увидеть, как складывать векторы с использованием перпендикулярных компонент, рассмотрите рисунок, на котором векторы \(\displaystyle A\) и \(\displaystyle B\) складываются для получения результирующего \(\ стиль отображения R\).

Рисунок \(\PageIndex{5}\): Векторы \(\displaystyle A\) и\(\displaystyle B\) — это два участка пути, а \(\displaystyle R\) — результирующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления \(\displaystyle R\).

Если \(\displaystyle A\) и \(\displaystyle B\) представляют два этапа ходьбы (два перемещения), то \(\displaystyle R\) является общим перемещением. Человек, совершающий прогулку, оказывается на вершине R. Есть много способов попасть в одну и ту же точку. В частности, человек мог идти сначала в направлении x, а затем в направлении y.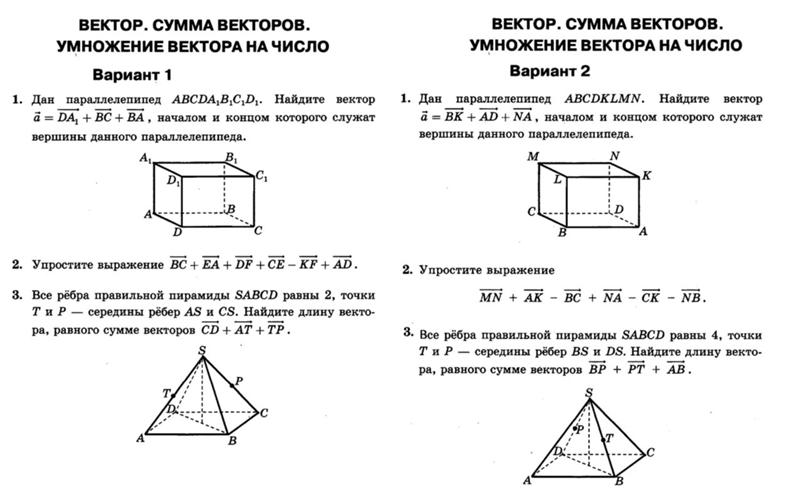 {– 1} (A_y / A_x) \). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.

Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей. Используйте уравнения \(\displaystyle A_x=Acosθ\) и \(\displaystyle A_y=Asinθ\), чтобы найти компоненты. На рисунке это компоненты \(\displaystyle A_x, A_y, B_x\) и \(\displaystyle B_y\). Углы, которые векторы \(\displaystyle A\) и \(\displaystyle B\) образуют с осью x, составляют \(\displaystyle θ_A\) и \(\displaystyle θ_B\) соответственно.

Рисунок \(\PageIndex{6}\): Чтобы добавить векторы \(\displaystyle A\) и \(\displaystyle B\), сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы \(\displaystyle A_x, A_y, B_x\) и \(\displaystyle B-y\), показанные на изображении.

Шаг 2.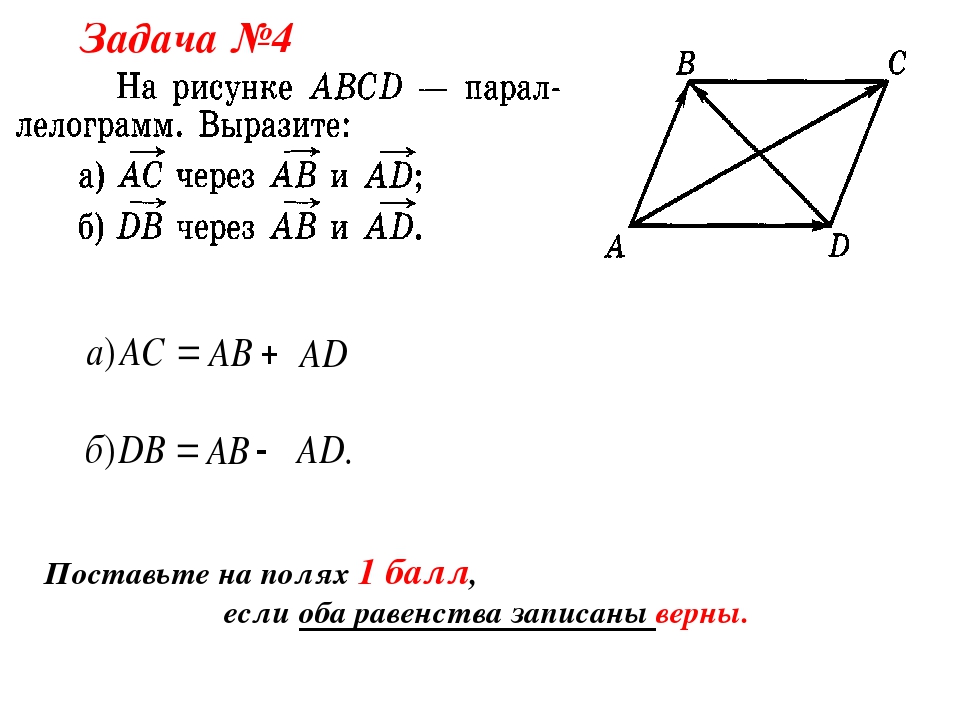 Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси. То есть, как показано на рисунке,

\(\displaystyle R_x=A_x+B_x\)

и

\(\displaystyle R_y=A_y+B_y.\)

Рисунок \(\PageIndex{7}\): Величина векторов \(\displaystyle A_x\) и \(\displaystyle B_x\) сложить чтобы задать величину \(\displaystyle R_x\) результирующего вектора в горизонтальном направлении. Точно так же величины векторов \(\displaystyle A_y\) и \(\displaystyle B_y\) складываются, чтобы получить величину \(\displaystyle R_y\) результирующего вектора в вертикальном направлении.

Компоненты вдоль одной оси, скажем, x — оси, являются векторами вдоль одной линии и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси y . (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении. ) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты R известны, можно найти его величину и направление. 9{−1}(R_y/R_x)\).

В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.

Пример \(\displaystyle \PageIndex{1}\): добавление векторов с помощью аналитических методов

Добавьте вектор \(\displaystyle A\) к вектору \(\displaystyle B\), показанному на рисунке, используя перпендикулярные компоненты вдоль оси x — и y — . Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор \(\displaystyle A\) представляет собой первый этап прогулки, на которой человек идет \(\displaystyle 53,0 м\) в направлении \(\displaystyle 20,0º\) к северу от востока. Вектор \(\displaystyle B\) представляет второй отрезок, смещение \(\displaystyle 34,0 м\) в направлении \(\displaystyle 63,0º\) к северу от востока.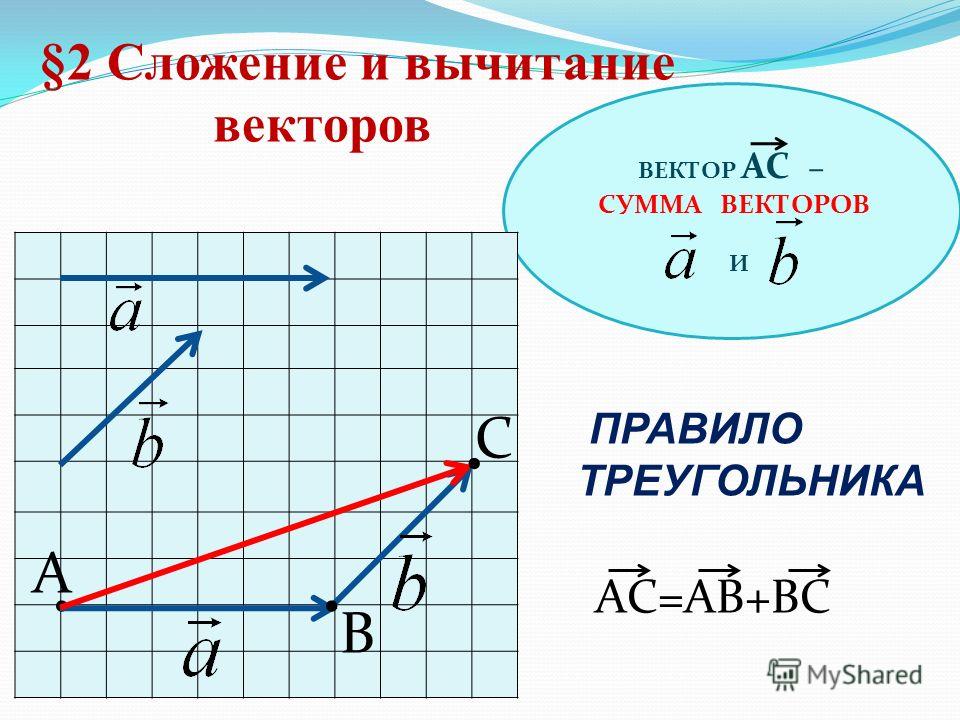

Рисунок \(\PageIndex{8}\): Вектор \(\displaystyle A\) имеет величину \(\displaystyle 53,0 м\) и направление \(\displaystyle 20,0º\) к северу от х — ось. Вектор B имеет величину \(\displaystyle 34,0 м\) и направление \(\displaystyle 63,0º\) к северу от оси x. Вы можете использовать аналитические методы для определения величины и направления \(\displaystyle R\).

Стратегия

Компоненты \(\displaystyle A\) и \(\displaystyle B\) вдоль x- и y -оси представляют ходьбу строго на восток и строго на север, чтобы добраться до одной и той же конечной точки. После обнаружения они объединяются для получения результирующего.

Решение

Следуя описанному выше методу, мы сначала находим компоненты \(\displaystyle A\) и \(\displaystyle B\) по осям x- и y-. Обратите внимание, что \(\displaystyle A=53,0 м, θ_A=20,0º, B=34,0 м,\) и \(\displaystyle θ_B=63,0º\).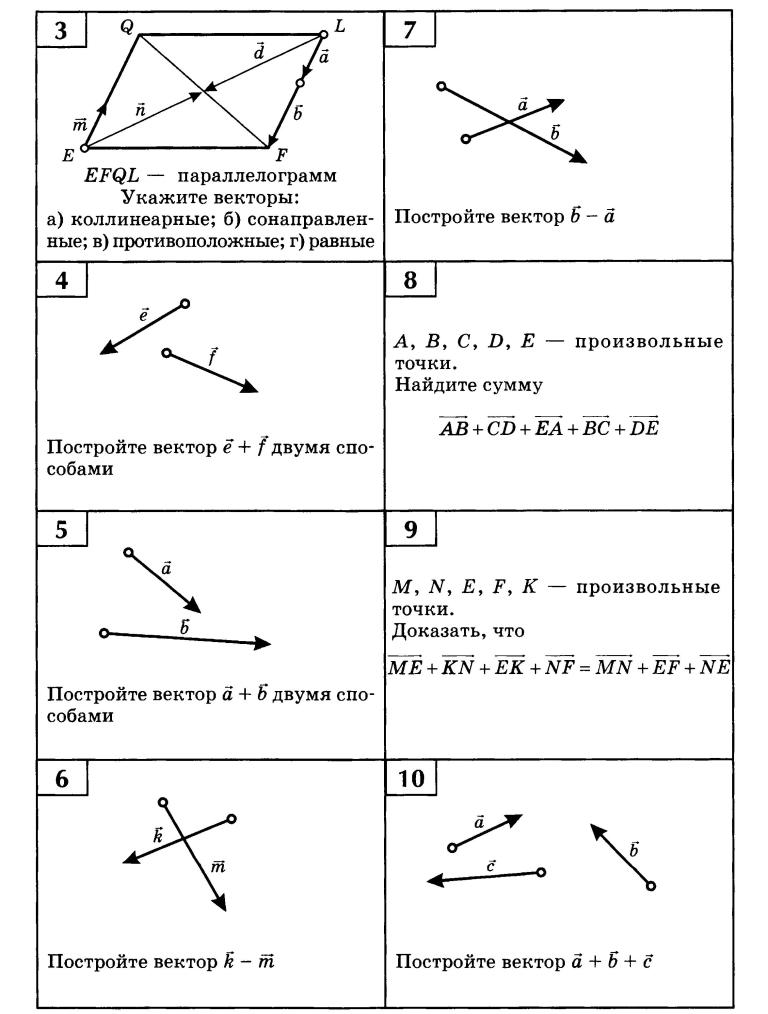 Мы находим компоненты x-, используя \(\displaystyle A_x=Acosθ\), что дает

\(\displaystyle A_x=Acosθ_A=(53,0 м)(cos 20,0º)(53,0 м)(0,940)=49,8 м\)

и

\(\displaystyle B_x=Bcosθ_B=(34,0 м)(cos 63,0º)(34,0 м)(0,454)=15,4 м.\)

Точно так же компоненты y- находятся с помощью \(\displaystyle A_y=Asinθ_A\):

\(\displaystyle A_y=Asinθ_A=( 53,0 м)(sin 20,0º)(53,0 м)(0,342)=18,1 м\)

и

\(\displaystyle B_y=Bsinθ_B=(34,0 м)(sin 63,0º)(34,0 м)(0,891)= 30,3 м.\)

х- 9{−1}(0,742)=36,6º.\)

Рисунок \(\PageIndex{9}\): Используя аналитические методы, мы видим, что величина \(\displaystyle R\) равна \(\displaystyle 81,2 м\ ) и его направление \(\displaystyle 36,6º\) к северу от востока.

Обсуждение

Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.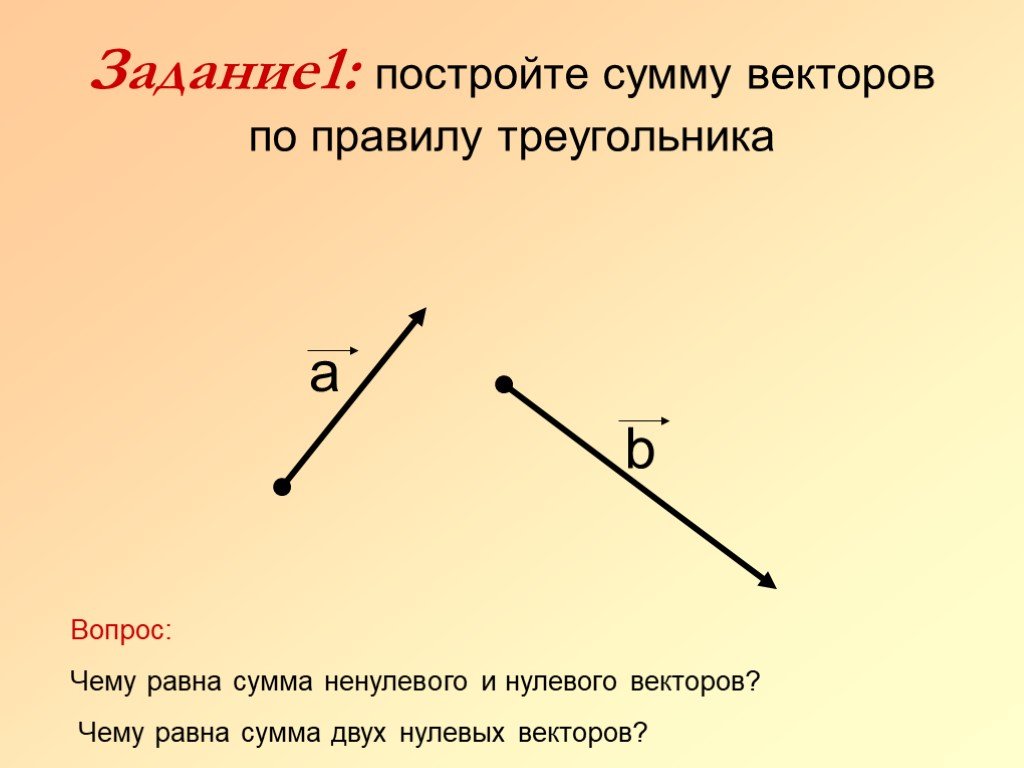

Вычитание векторов осуществляется добавлением отрицательного вектора. То есть \(\displaystyle A−B≡A+(–B)\). Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения. Компоненты \(\displaystyle –B\) являются минусами компонентов \(\displaystyle B\). Компоненты x- и y- результирующего \(\displaystyle A−B = R\) равны

\(\displaystyle R_x=A_x+(-B_x)\)

и

\(\ displaystyle R_y=A_y+(–B_y)\)

, а в остальном описанный выше метод идентичен методу сложения. (См. рис.)

Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль Projectile Motion — один из многих, в котором использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.

Рисунок. Компоненты \(\displaystyle –B\) являются минусами компонентов \(\displaystyle B\). Метод вычитания такой же, как и для сложения.

ИССЛЕДОВАНИЯ PHET: ДОБАВЛЕНИЕ ВЕКТОРА

Узнайте, как добавлять векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.

Рисунок \(\PageIndex{11}\): Сложение векторов

Резюме

• Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
• Чтобы добавить векторы \(\displaystyle A\) и \(\displaystyle B\) с помощью аналитического метода, выполните следующие действия:

Шаг 1: Определите систему координат для векторов. Затем определите горизонтальную и вертикальную составляющие каждого вектора, используя уравнения \(\displaystyle B_y=Bsinθ.\)

Шаг 2: Сложите горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты Rx и Ry результирующего вектора, R: 9{−1}(R_y/R_x)\).

Глоссарий

аналитический метод

метод определения величины и направления результирующего вектора с использованием теоремы Пифагора и тригонометрических тождеств

---

Эта страница под названием 3.3: Сложение и вычитание векторов — аналитические методы распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. аналитический метод
   2. источник@https://openstax.

      No related posts.