Как вычесть 2 отрицательных числа? – Обзоры Вики
Если вычесть отрицательное число, два негатива объединяются, чтобы создать положительный. −10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.
Точно так же почему 2 отрицательных числа дают положительный результат при вычитании? Правило 3: вычитание отрицательного числа из отрицательного числа — знак минус, за которым следует знак минус, превращает два знака в знак плюс. Таким образом, вместо вычитания минуса вы добавляете плюс.
Почему минусы отменяются? Негативы отменяются
После появления вы умножаете отрицательное число на положительное число, отрицательное число переворачивает знак, и ваш результат будет отрицательным числом.
Однако, когда вы умножаете два отрицательных числа вместе, первое изменяет знак с положительного на отрицательное, а второе — обратно.
Что дают два плюса?
Если два положительных числа умноженные или разделенные, ответ положительный. Если два отрицательных числа умножить или разделить, ответ будет положительным. Если положительное и отрицательное число умножаются или делятся, ответ будет отрицательным.
тогда каковы четыре правила математики? Четыре правила математики сложение, вычитание, умножение и деление. На следующих веб-страницах вы можете узнать, как это сделать вручную (без калькулятора), а также другую важную информацию о порядке приоритета этих операций.
Как добавить минусы? Добавление отрицательного числа то же, что вычитание положительного числа — то есть идти вниз (влево) по числовой строке.
Это правило работает независимо от того, начинаете ли вы с положительного или отрицательного числа.
Как добавить отрицательное число?
Сложить два отрицательных числа вместе? Только что сложите абсолютное значение каждого числа вместе, поставь перед собой знак минус, и у тебя есть ответ!
Какова сумма двух отрицательных чисел?
Правильный ответ:
Объяснение: Сумма двух отрицательных чисел всегда отрицательный, следовательно, это правильный выбор. Что касается других вариантов: произведение или частное двух отрицательных чисел всегда положительно.
Негатив отменяет позитив? Когда вы вычитаете положительное число из отрицательного числа, это то же самое, что складывать отрицательное число. Другими словами, это делает отрицательное число еще более отрицательным. Вычитание отрицательного числа из положительного числа нейтрализует отрицательные знаки и становится простым дополнением.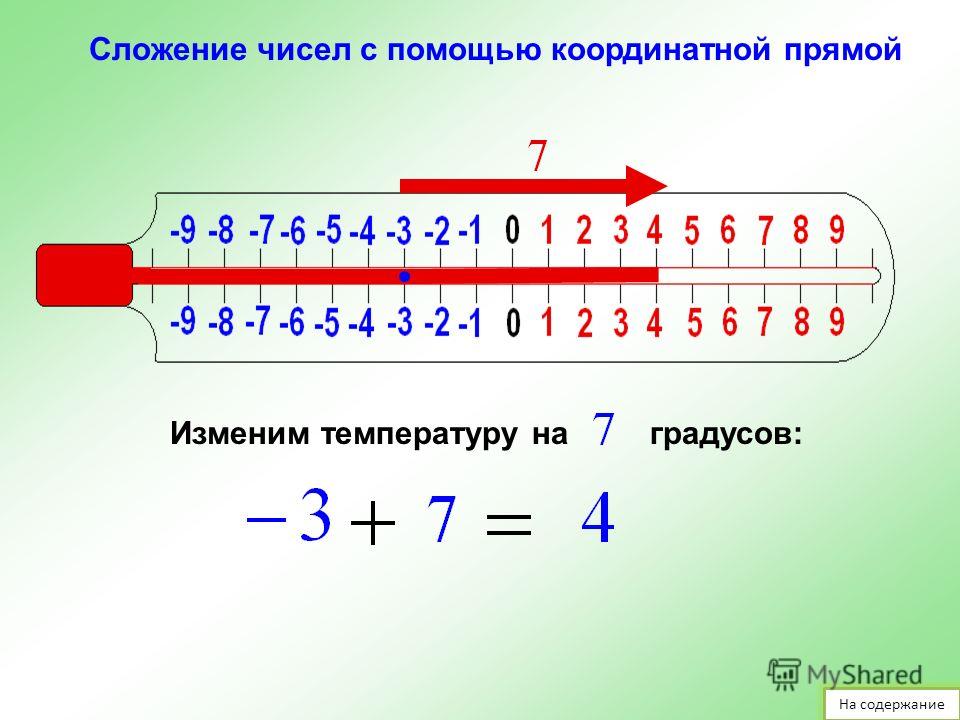
Чему равно произведение двух отрицательных чисел?
Произведение двух отрицательных целых чисел равно положительное целое число. Пример: (-2)×(-2) = +4.
Как вычесть вручную?
Какое правило для плюса и минуса?
Правила:
| Правило | Пример | |
|---|---|---|
| + (+) | Два подобных знака становятся положительным знаком | 3 + (+ 2) = 3 + 2 = 5 |
| — (-) | 6 — (- 3) = 6 + 3 = 9 | |
| + (-) | Два непохожих знака становятся отрицательным знаком | 7 + (- 2) = 7 — 2 = 5 |
| — (+) | 8 — (+ 2) = 8-2 = 6 |
com/embed/DBSviXhkubg» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″> Что такое A/(BC?
Итак, а/(б/с) = (а×с)/ b.
Какой минус плюс минус? Когда вы добавляете отрицательное число к отрицательному числу, оно становится вычитание, где вы начинаете с отрицательной точки на числовой строке и двигаетесь влево. Например, -3 + (-2). Это читается как «минус три плюс минус 2». …Затем вычитаем 2. Ответ равен -5.
Как складывать и вычитать отрицательные числа?
Каковы основные математические формулы? Некоторые примеры основных математических формул:
- Периметр прямоугольника = 2 (длина + ширина)
- Площадь прямоугольника = длина × ширина.
- Периметр квадрата = 4 × длина стороны.
- Площадь квадрата = длина стороны × длина стороны.
- Объем прямоугольного параллелепипеда = длина × ширина × высота.
- Прибыль = Цена продажи – Себестоимость.
Каково правило DMAS?
правило DMAS следует, когда в данной задаче присутствует несколько арифметических операций, таких как сложение, вычитание, умножение и деление. В нем говорится, что они должны выполняться в порядке деления, умножения, сложения и вычитания.
Как вычесть отрицательные числа?
Как вычесть отрицательные числа?
Имеет место следующее правило вычитания отрицательных чисел: чтобы из числа a вычесть отрицательное число b, нужно к уменьшаемому a прибавить число −b, противоположное вычитаемому b. В буквенном виде правило вычитания отрицательного числа b из произвольного числа a выглядит так: a−b=a+(−b).
Как из отрицательного числа вычесть положительное число?
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.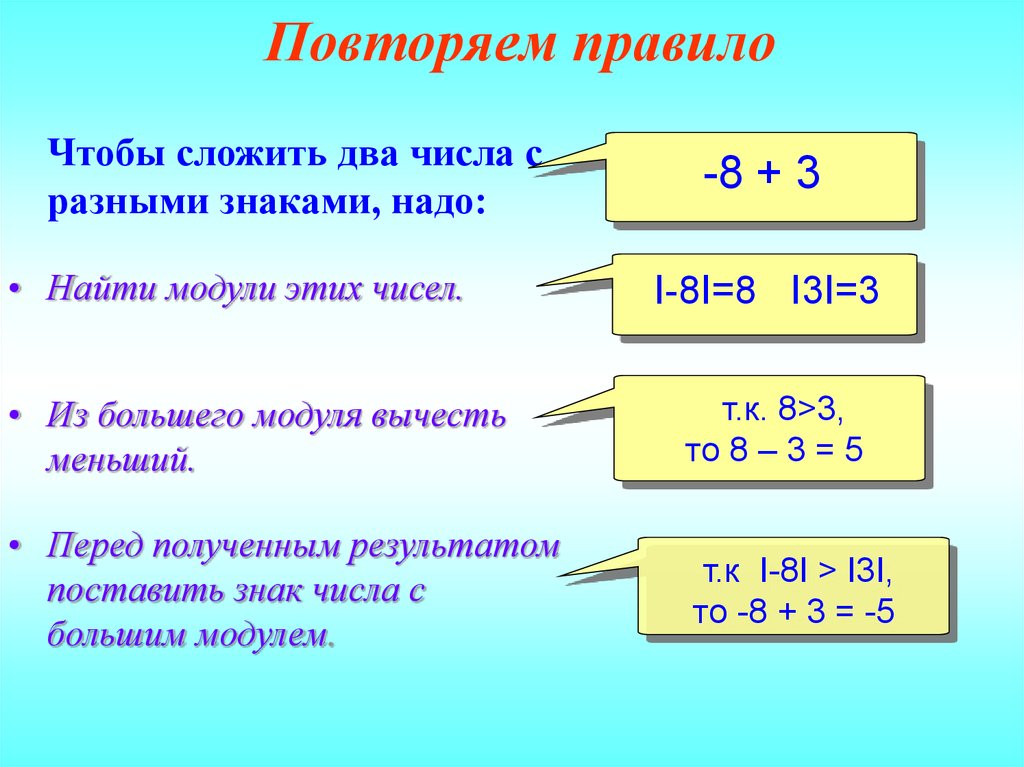
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Как поделить два отрицательных числа?
Чтобы разделить отрицательное число на отрицательное (два отрицательных числа), надо разделить модуль делимого на модуль делителя.
Как разделить две отрицательные дроби?
Чтобы разделить два числа с разными знаками, надо:
- модуль делимого разделить на модуль делителя;
- перед результатом поставить знак «−».
Какой знак будет если минус делить на минус?
»−−»− при делении минус на минус результат становится положительным; »−+»−при делении минуса на плюс результат становится отрицательным; «+−»−при делении плюса на минус результат становится отрицательным; «++»− при делении плюса на плюс результат становится положительным.
Как делить минус на минус?
Итак, правило деления чисел с разными знаками имеет следующую формулировку: чтобы разделить положительное число на отрицательное или отрицательное число на положительное, надо модуль делимого разделить на модуль делителя, и перед полученным числом поставить знак минус.
Чему равно частное двух отрицательных чисел?
1) разделить модуль делимого на модуль делителя. 2. разделить. Частное двух отрицательных чисел — это положительное число.
Как найти частное двух чисел с разными знаками?
Ответ: 1) Чтобы найти частное двух чисел с разными знаками, надо разделить их модули и поставить перед полученным числом знак минус.
Как делить отрицательные дроби на положительные?
При умножении отрицательной дроби на положительную результат будет отрицательным. Пример. То есть при умножении положительной дроби на отрицательную результат будет отрицательным. Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Что будет если умножить два отрицательных числа?
Правила знаков для умножения Плюс на минус даёт минус. В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
Как делить отрицательные числа с остатком?
Правило деления с остатком целых отрицательных чисел, примеры
- Находим модули делимого и делителя.
- Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. …
- К полученному неполному частному прибавляем единицу, это число есть искомое неполное частное от деления исходных целых отрицательных чисел.
Как можно сократить дробь?
Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби. К примеру, возьмем обыкновенную дробь 624 и сократим ее.
В каком случае можно сократить дробь?
Если числитель и знаменатель представлены числовыми или буквенными выражениями, то на слагаемое сокращать нельзя.
Сумму (разность), если возможно, надо преобразовать в произведение и сократить на общий множитель числителя и знаменателя дроби. Числитель и знаменатель преобразовали в произведение.
Что делать если дробь не сокращается?
Чтобы сделать дробь несократимой, нужно поделить её числитель и знаменатель на их наибольший общий делитель.
Как сократить дробь 2 6 18?
Переводим: 18*2+6=42, то есть получается 42/18. Все это можем сократить на 6, получается: 7/3.
Как сокращать дроби в умножении?
При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.
Как сократить простую дробь?
Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число. Это число является наибольшим общим делителем числителя и знаменателя данной дроби.
Как объяснить ребенку как сократить дробь?
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей.
Как вычитать отрицательные числа
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
SAT Math Help » Арифметика » Целые числа » Отрицательные числа » Как вычитать отрицательные числа
Если x — отрицательное целое число, что еще должно быть отрицательным целым числом?
Возможные ответы:
x — x
x²
x² — x
x — (–x)
Правильный ответ:
x – (—x)
9000 3 9000 3 9000 3 9000 3
Объяснение:Выбрав случайное отрицательное число, например: –4, мы можем ввести число в каждый вариант и посмотреть, получится ли другое отрицательное число. Когда мы подставляем -4 вместо x, мы получим -4 — (-(-4)) или -4 — 4, что равно -8. Подключение других опций дает положительный ответ. При необходимости вы можете попробовать другие отрицательные числа, чтобы убедиться, что это все еще работает.
Отчет о ошибке
–7 — 7 = x
–7 — (–7) = y
Что такое x и y, соответственно
Возможные ответы:
x = 0, 0,0. у = 0
х = –14, у = 14
х = 14, у = –14
у = 0, х = 14
х = –14, у = 0
Правильный ответ: х = –14, у = 0 Объяснение: x: –7 – 7= –7 + –7 = –14 y: –7 – (–7) = –7 + 7 = 0 при вычитании отрицательного числа превратить его в задачу на сложение
Объяснение: Преобразование в отдельные знаки. Сообщить об ошибке Вычесть: Возможные ответы: 
Помните, что двойное отрицание превратится в положительное.
Объяснение:
Вычитание отрицательного числа перемещает число дальше влево от нуля в числовой строке.
Ответ:
Сообщить об ошибке Объяснение:
Упростите выражение, убрав двойные отрицательные знаки. Два отрицательных числа, умноженные друг на друга, дадут положительное число.
Преобразование знаков.
Добавьте правую часть уравнения.
Ответ .
Сообщить об ошибке
Упростите следующее выражение:
Возможные ответы:
Правильный ответ:
Объяснение:
Упростите следующее выражение:
Чтобы вычесть отрицательные числа, мы должны помнить, что вычитание отрицательных чисел такое же, как сложение положительных.
Уведомление об авторских правах
View SAT Репетиторы по математике
Zachary
Сертифицированный репетитор
Йельский университет, бакалавр наук, биология, общие.
Посмотреть Репетиторы по математике SAT
Zane
Сертифицированный преподаватель
Университет Невада-Рино, бакалавр наук, машиностроение. Вандербильт, магистр биомедицинской инженерии.
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
Вычитание целых чисел — правила, шаги, примеры
Вычитание целых чисел — это процесс нахождения разницы между двумя целыми числами. Это может привести к увеличению или уменьшению значения, в зависимости от того, являются ли целые числа положительными или отрицательными или смесью. Вычитание целых чисел — это арифметическая операция, выполняемая над целыми числами с одинаковым или разными знаками для нахождения разницы.
| 1. | Правила вычитания целых чисел |
| 2. | Вычитание целых чисел из числовой строки |
| 3. | Часто задаваемые вопросы о вычитании целых чисел |
Правила вычитания целых чисел
При вычитании двух целых чисел необходимо соблюдать определенные правила. Целые числа — это полные числа, не имеющие дробных частей. Он включает в себя положительные целые числа, ноль и отрицательные целые числа. Правила вычитания целых чисел приведены ниже:
- Если мы вычтем 0 из любого целого числа, ответом будет само целое число.
- Если мы вычтем любое целое число из 0, мы найдем добавку, обратную или противоположную целому числу.
- Вычитание целых чисел осуществляется изменением знака вычитаемого. После этого шага, если оба числа имеют один и тот же знак, то мы добавляем абсолютные значения и присоединяем общий знак. Если оба числа разного знака, то находим разность абсолютных чисел и подставляем в результат знак большего числа.
Если оба числа разного знака, то находим разность абсолютных чисел и подставляем в результат знак большего числа.В приведенной ниже таблице показаны правила вычитания целых чисел с примерами.
Вычитание целых чисел с одинаковым знаком
Когда мы вычитаем два целых числа с одинаковым знаком, мы вычитаем их абсолютные значения и помещаем в результат общий знак. Абсолютное значение числа — это положительное значение данного числа. Например, абсолютное значение 6 равно 6, абсолютное значение -6 равно 6 и т. д. При вычитании целых чисел мы меняем знак вычитаемого. Например, -2 -(-5) можно записать как -2 + 5. Теперь абсолютное значение 5 равно 5, а -2 равно 2. Вычитая 2 из 5, мы получаем 3. Так как 5 >
2 знак ответа будет таким же, как и знак 5, что положительно. Следовательно, -2 -(-5) = 3,Здесь важно отметить, что каждый факт вычитания может быть записан как факт сложения. Например, 4 — 7 равно 4 + (-7).
Ниже приведены некоторые примеры вычитания целых чисел с одинаковым знаком:
- (-1) — (-6) = -1 + 6 = 5
- 3 — 8 = -5
- 24 — 17 = 7
Вычитание целых чисел с разными знаками
Вычитание двух целых чисел с разными знаками выполняется путем изменения знака вычитаемого целого числа.
Затем нам нужно проверить, станут ли оба целых числа положительными, результат будет положительным, а если оба целых числа отрицательными, то результат будет отрицательным. Например, если мы хотим вычесть -9от 5, то есть 5 — (-9), изменим знак 9 и затем сложим целые числа, значит будет 5 + 9 = 14. Следовательно, 5 — (-9) = 14.
Это также можно понять с помощью другого метода, в котором мы добавляем абсолютные значения, а затем присоединяем к результату знак уменьшаемого. Например, если мы хотим вычесть -9 из 5, сначала мы найдем абсолютные значения обоих. Абсолютное значение -9 равно 9, а 5 равно 5. Теперь найдите сумму этих абсолютных значений, которая равна 9 + 5 = 14. Поскольку 5 — это уменьшаемое здесь с положительным знаком, поэтому знак ответа будет положительным. . Следовательно, 5 — (-9) = 14.
Вычитание целых чисел из числовой строки
Вычитание целых чисел на числовой прямой основано на данных принципах:
- Каждый факт вычитания может быть записан как факт сложения.
- Добавление положительного числа будет выполняться путем перемещения к правой стороне (или положительной стороне) числовой строки.
- Добавление отрицательного целого числа будет выполняться путем перемещения к левой стороне (или отрицательной стороне) числовой строки.
- Любое из заданных целых чисел можно взять за базовую точку, с которой мы начинаем движение по числовой прямой.
Теперь давайте научимся вычитать целые числа из числовой строки. Первым шагом является выбор шкалы на числовой прямой. Например, если мы хотим отобразить числа, кратные 1, 5, 10, 50 и т. д., в зависимости от заданных целых чисел. Например, вычитая 10 из -30 , мы можем использовать шкалу 10 на числовой прямой, чтобы упростить нашу работу. Однако, если нам нужно вычесть -2 из 7, мы можем взять шкалу счета чисел, начиная с 1. Затем нам нужно выразить данное выражение вычитания в факте сложения, изменив знак вычитаемого.
Следующий шаг — найти любое целое число в числовой строке, предпочтительно число с большим абсолютным значением.
Например, если вам нужно вычесть 4 из 29, будет лучше, если мы сначала найдем 29 в строке, а затем сделаем 4 прыжка влево, а не найдем -4, а затем сделаем 29 прыжков.
Третий и последний шаг состоит в том, чтобы добавить второе целое число к числу, полученному на предыдущем шаге, путем прыжков влево или вправо в зависимости от того, положительное это число или отрицательное.
Давайте рассмотрим пример, чтобы лучше понять это.
Пример: Вычесть -4 из -7
Решение: Для вычитания целых чисел на числовой прямой выполните шаги, указанные ниже:
- Шаг 1: Выражение может быть записано как -7 — (-4). Нарисуйте числовую линию с масштабом 1.
- Шаг 2: Выразите -7 — (-4) как выражение сложения, изменив знак вычитаемого с отрицательного на положительный. Получаем -7+4.
- Шаг 3: Начните с -7, сделайте 4 прыжка вправо, так как мы добавляем 4 к -7.
Следовательно, требуемый ответ -3.
☛ Статьи по теме
- Калькулятор вычитания целых чисел
- Сложение и вычитание целых чисел
- Умножение и деление целых чисел
Примеры вычитания целых чисел
Пример 1: Вычтите указанные целые числа, используя правила вычитания целых чисел.
Вычесть -56 из -90
Решение: Этот вопрос основан на вычитании двух целых чисел с одинаковым знаком. Вот если записать в виде выражения, то получится -90 — (-56). Это можно записать как -90 + 56. Найдем разницу между абсолютными значениями. Итак, 90 — 56 равно 34. Поскольку 90 > 56, знак ответа будет таким же, как и знак 90, то есть отрицательный. Поэтому -90 — (-56) = -34.
Пример 2: Используя правила вычитания целых чисел, узнайте, какое число нужно прибавить к 43, чтобы получить -20 в качестве ответа?
Решение: Пусть x будет числом, которое нужно прибавить к 43, чтобы получить -20.
Итак, мы можем составить уравнение относительно х.x + 43 = -20
Чтобы найти пропущенное значение, нам нужно решить уравнение.
х + 43 = -20
х = -20 -43
х = -63
Следовательно, к 43 нужно прибавить -63, чтобы получить -20.
Пример 3: Вычтите -7 из -12, используя правила вычитания целых чисел.
Решение: Этот вопрос основан на вычитании целых чисел с одинаковым знаком. Здесь нам нужно вычесть два целых числа с одинаковым знаком, -12 и -7.
-12 — (-7) = -12 + 7
= -5
Следовательно, разница между -12 и -7 равна -5.
Итак, мы можем составить уравнение относительно х.перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по вычитанию целых чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о вычитании целых чисел
Как вычитать целые числа?
Вычитание целых чисел требует соблюдения определенных правил.
Основные правила вычитания целых чисел приведены ниже:
- Если мы вычтем 0 из любого целого числа, ответом будет само целое число.
- Если мы вычтем любое целое число из 0, мы найдем добавку, обратную или противоположную целому числу.
- Вычитание целых чисел осуществляется изменением знака вычитаемого. После этого шага, если оба числа имеют один и тот же знак, то мы добавляем абсолютные значения и присоединяем общий знак. Если оба числа разного знака, то находим разность абсолютных чисел и подставляем в результат знак большего числа.
Каково правило вычитания отрицательных целых чисел?
Если оба целых числа отрицательные, то для их вычитания мы сначала запишем это как факт сложения. Затем мы находим разницу между их абсолютными значениями и присоединяем к результату знак числа с большим абсолютным значением. Например, давайте вычтем -45 из -23. Это можно записать как -23 — (-45). Мы можем переписать его как -23 + 45. Теперь разница между абсолютными значениями составляет 45 — 23 = 22.
Поскольку 45 > 23, знак ответа будет таким же, как и знак 45, что положительно. Следовательно, -23 — (-45) = 22,
Каково общее правило вычитания целых чисел?
Общее правило для вычитания целых чисел дается следующим образом:
Вычитание целых чисел производится изменением знака вычитаемого. После этого шага, если оба числа имеют один и тот же знак, то мы добавляем абсолютные значения и присоединяем общий знак. Например, 1 — (-9) может быть записано как 1 + 9 после изменения знака вычитаемого, что дает результат как 1 + 9 = 10. В другом примере, если после изменения знака вычитаемого мы получаем оба числа с разными знаками, то находим разность модулей и записываем знак большего числа. Например, в -4 — (-8), Здесь мы получаем -4 + 8, поэтому после нахождения разницы абсолютных значений мы получаем 4, а знак большего числа положительный, поэтому мы запишем ответ как 4.
Каково правило вычитания целых чисел с разными знаками?
Для вычитания целых чисел с разными знаками мы следуем шагам, указанным ниже.
Вычтем -5 из 6. Это означает 6 — (-5)
- Шаг 1: Во-первых, мы изменим знак вычитаемого, который равен -5. Получается 5.
- Шаг 2: Найдите сумму новых целых чисел, то есть 6 + 5 = 11.
- Шаг 3: Результат 11.
Каково правило вычитания целых чисел с одинаковым знаком?
Чтобы вычесть целые числа с одинаковым знаком, мы сначала меняем знак вычитаемого. Затем найдите разницу между абсолютными значениями обоих целых чисел. Прикрепите к ответу знак числа с большей абсолютной величиной. Например, (-9) — (-3) = -9 + 3 = -6.
Как вычитание целых чисел связано со сложением целых чисел?
Сложение и вычитание являются обратными операциями. Это означает, что каждое выражение сложения может быть выражено вычитанием и наоборот. Вычитание целых чисел связано со сложением целых чисел, потому что оба они могут быть выражены в форме друг друга. Например, мы можем написать 12 + (-9) как 12 — 9. Точно так же мы можем записать — 23 — 5 как -23 + (-5).