вычисление определителя 3 порядка
Вы искали вычисление определителя 3 порядка? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определителя 3 порядка матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление определителя 3 порядка».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление определителя 3 порядка,вычисление определителя 3 порядка матрицы,вычислить определители третьего порядка,вычислить определитель 3 порядка,вычислить определитель получив нули в какой либо строке или столбце,вычислить определитель третьего порядка по правилу треугольника,как вычислить определитель 3 порядка,как вычислить определитель второго порядка,как вычислить определитель третьего порядка,как вычислять определители,как найти определитель 3 порядка,как найти определитель матрицы 3х3 треугольником,как посчитать определитель 3 порядка,как решать определители,как решать определители 3 порядка,как решить определитель 3 порядка,как считать определитель 3 порядка,как считать определитель матрицы 3 порядка,матрица 3 порядка,матрица 3 порядка примеры,матрицы определитель 3 порядка,матрицы определитель третьего порядка,матрицы правило треугольников,матрицы третьего порядка,определители 3 порядка,определители 3 порядка как решать,определители 3 порядка примеры,определители как решать,определители примеры,определители третьего порядка,определитель 3 порядка,определитель 3 порядка как считать,определитель 3 порядка матрицы,определитель 3 порядка это,определитель матрицы первого порядка,определитель матрицы порядка 3,определитель матрицы третьего порядка,определитель первого порядка,определитель первого порядка матрицы,определитель правило треугольника,определитель правило треугольников,определитель третьего порядка,определитель третьего порядка вычислить,определитель третьего порядка как найти,определитель третьего порядка матрицы,определитель третьего порядка примеры,определитель третьего порядка это,правило саррюса вычисления определителя третьего порядка,правило треугольника определитель,правило треугольников определитель,примеры определители,примеры определитель,примеры определитель третьего порядка,способы вычисления определителей,способы вычисления определителя,формула определителя матрицы 3 порядка.
Решить задачу вычисление определителя 3 порядка вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
|
Заглавная страница
Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 2 из 7Следующая ⇒ Рассмотрим квадратную матрицу размера
Определение 2.2. Определителем (или детерминантом) высшего порядка, соответствующим данной квадратной матрице, называют число, получаемое из элементов матрицы А по определенному закону — закону раскрытия определителя. Это число обозначается
Прежде, чем формулировать закон раскрытия определителей высшего порядка, введем понятие минора и алгебраического дополнения. Определение 2.3. Минором, соответствующим данному элементу определителя n-го порядка, называется определитель (n-1)-го порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Миноры обозначаются буквой Мij с индексами, соответствующими вычеркнутым номерам строк и столбцов. Так, например, минор М12, соответствующий элементу а12 определителя (2.4), есть определитель
Он получается из определителя (2.4) вычеркиванием первой строки и второго столбца. Определение 2.4. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, в которых стоит элемент, четна, и со знаком минус, если эта сумма нечетна. Алгебраическое дополнение элемента аij обозначается через Aij. Здесь i означает номер строки, а j —номер столбца, на пересечении которых находится данный элемент.Связь между алгебраическим дополнением элемента и его минором выражается следующим равенством:
Определение 2.5. Определитель квадратной матрицы равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения:
Определение 2.6. Матрица называется невырожденной, если ее определитель отличен от нуля. В качестве примера использования формул (2.7) и (2.8) приводятся формулы разложения определителя третьего порядка
по элементам первой строки
и элементам второго столбца
Поработаем с формулой (2.10) и раскроем миноры по формуле (3.2): Итак, раскрыв скобки, получим.
Для запоминания правила вычисления определителя третьего порядка используют модель Саррюса, которая приведена на рис. 2.1. Элементы определителя изображены точками. Перемножают элементы, соединенные линиями, и полученные произведения складывают, снабдив их соответствующими знаками.
Пример 2.2. Вычислить определитель третьего порядка для матрицы:
Воспользуемся формулой (2.7) и раскроем определитель, например, по элементам третьей строки (i=3):
Предварительно вычислим алгебраические дополнения: Подставим полученные числовые значения алгебраических дополнений в формулу (3.14) и вычислим определитель
Полученное решение можно проверить по формуле (2.12).
Свойства определителей Сформулируем основные свойства определителя:
Обратная матрица Понятие обратной матрицы вводится только для квадратных матриц. Определение 3.3. Если А — квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая А-1и удовлетворяющая условию
Теорема 3.1. (об обратной матрице): Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы ее определитель был отличен от нуля. Для простоты на примере матрицы третьего порядка приведем последовательность вычислений, которая позволяет построить обратную матрицу. Пусть
Невырожденная матрица, т. е. её определитель
Составим новую матрицу В, заменяя в матрице А каждый ее элемент аij его алгебраическим дополнением Аij, деленным на определитель |A| матрицы А:
Построим матрицу ВТ, транспонированную по отношению к матрице В:
Покажем, что матрица ВТ, является обратной матрице А. Для этого составим произведение: Так как. числители элементов на главной диагонали равны |A| (раскрытие определителя по элементам строки), а числители всех остальных элементов равны нулю (сумма произведений элементов одной строки или столбца на алгебраические дополнения другой строки или столбца равна нулю). Таким образом, откуда Итак, способ построения обратной матрицы получен:
Пример 3.1.Дана матрица Найти обратную матрицу. Вычислим определитель матрицы А: Находим алгебраические дополнения элементов этого определителя по формулам Следовательно,
11. При вычислении обратной матрицы, как правило, приходится вычислять большое число определителей. Чтобы облегчить этот процесс, применяют специальные приемы, которые называют элементарными преобразованиями матриц. Элементарными называются следующие преобразования: · умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля; · прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число; · перемена местами строк (столбцов) матрицы; · отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю. Матрицы, получающиеся одна из другой при элементарных преобразованиях, называются эквивалентными. Пример 4.1.Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы не вычислять много миноров.
Теперь к третьей строке прибавим первую строку, умноженную на :
И, наконец, к четвертой строке прибавим первую, умноженную на :
Определитель полученной матрицы равен произведению элемента на его алгебраическое дополнение: Пример 4.2.Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы под главной диагональю стояли нули. ПоДля этого в первом столбце во второй, третьей и четвертой строках получим нули.
Теперь к третьей строке прибавим первую строку, умноженную на :
И, наконец, к четвертой строке прибавим первую, умноженную на : Ранг матрицы Рассмотрим матрицу размера
Выделим в ней несколько миноров. Определение 3.1. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Определение 3.2. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Пример 4.4.Найти ранг матрицы:
Определитель матрицы (3.2) равен нулю. Все миноры 3-го порядка равны нулю, например: Есть минор 2-го порядка, отличный от нуля: Значит, . Свойства ранга матрицы
Использование этих свойств позволяет в ряде случаев упростить вычисления ранга.
Пример 4.5.Найти ранг матрицы:
Определитель матрицы (4.3) равен нулю, поскольку матрица имеет пропорциональные строки, например, первую и третью. Значит ранг матрицы (4.3) будет меньше 4. Выполним некоторые элементарные преобразования: к третьей строке матрицы прибавим первую строку, умноженную на , к четвертой строке прибавим вторую строку, умноженную на 2. Получим: Полученная матрица, очевидно, имеет ранг 2. Итак, . Метод окаймления При вычислении ранга можно использовать метод окаймления, состоящий в следующем. Пусть матрица имеет ненулевой минор порядка .Тогда можно рассматривать только миноры порядка , которые содержат упомянутый ненулевой минор порядка . Если все миноры большего порядка равны нулю, то . Пример 4.6.Найти ранг матрицы, используя метод окаймления:
Эта матрица имеет ненулевой минор Теперь достаточно рассмотреть не все миноры третьего порядка, а только миноры, которые содержат указанный ненулевой минор второго порядка: Итак, . Система линейных уравнений Система n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения. Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет бесчисленное множество решений. Две совместные системы уравнений называются равносильными, если решение первой системы является решением второй и наоборот. С помощью теорем линейной алгебры можно доказать, что следующие преобразования, которые принято называть элементарными, приводят к равносильным системам: · перемена местами двух любых уравнений; · умножение обеих частей уравнений на произвольное число, отличное от нуля; · прибавление к обеим частям одного из уравнений другого уравнения, умноженного на любое действительное число. ⇐ Предыдущая1234567Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0. |
Определение реакций опор и моментов защемления
15)
16)
6)
Элементарные преобразования матриц
Для этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на :
Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на :
2)
3)
004 с.)linear алгебра — Вычисление характеристического уравнения матрицы 3×3
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 62к раз
$\begingroup$
Может ли кто-нибудь помочь мне объяснить, как решить эту проблему ниже:
Пусть матрица $\mathbf{A}$ задана как $$\mathbf{A}=\begin{bmatrix}0&-1&-1\\1&2&1\\1&1&2\end{bmatrix}$$ 1. Вычислите характеристическое уравнение.
Правильно ли это?
$$(\lambda-2)(\lambda-2)(\lambda-0)-\ldots$$
Но я не уверен.
- линейная алгебра
$\endgroup$
2
92+5x-2=0$$\endgroup$
6
$\begingroup$
Быстрый способ: Обратите внимание, что сумма каждого столбца $A$ равна $2$, следовательно, $\lambda_1=2$ является собственным значением $A$.
2(x-2)$$
$\endgroup$
4
$\begingroup$
Характеристическое уравнение используется для нахождения собственных значений квадратной матрицы A .
Во-первых: Знайте, что собственный вектор некоторой квадратной матрицы A является ненулевым вектором x таким, что Ax = λx .
Секунда: С помощью стандартных математических операций мы можем выйти из этого: Ax = λx , к этому: (A — λI)x = 0
Решения уравнения det( A — λI ) = 0,0 дадут3 ваше собственное значение 0,0 Ранее упомянутое уравнение является характеристическим уравнением.
— ПЕРЕЙДИТЕ К ЭТОМУ ПУНКТУ ДЛЯ КОРОТКОГО ОТВЕТА —
Для некоторой квадратной матрицы A характеристическое уравнение имеет вид det( A — λI ) = 0 .
Пример:
$$ A = \begin{bmatrix} а и б \\ CD \\ \end{bmatrix}$$$$ λI = \begin{bmatrix} λ & 0 \\ 0 и λ \\ \end{bmatrix}$$
$$ A — λI = \begin{bmatrix} а-λ и б \\ с & d-λ \\ \end{bmatrix}$$
$$det\begin{bmatrix} а-λ и б \\ с & d-λ \\ \end{bmatrix} = 0$$ Характеристическое уравнение: $$(a-λ)(d-λ) — (c)(b) = 0$$
Источник цитируется: Lay, David C., et al. . Линейная алгебра и ее приложения, пятое издание. Пирсон, 2016.
$\endgroup$
$\begingroup$
Неверно. Характеристическое уравнение получается из вычисления значений $\lambda$, необходимых для получения определителя матрицы, равного нулю.
$$\begin{vmatrix} -\lambda & -1 & -1 \\ 1 & 2 — \lambda & 1 \\ 1 & 1 & 2- \lambda \end{vmatrix} = 0 $$
Обратите внимание, что при $\lambda = 1$ все три столбца становятся идентичными, и мы можем получить два собственных вектора.
Придумать последнее собственное значение должно быть легко, если мы воспользуемся тем фактом, что след матрицы представляет собой сумму собственных значений.
Таким образом, собственные значения этой матрицы равны $\lambda_1 = 1, \lambda_2 = 1, \lambda_3 = 2$, поскольку они делают матрицу сингулярной.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Математика — Алгебра матриц — Определители
Определитель — это скалярное число, вычисляемое из матрицы. Это число может определить, разрешима ли система линейных уравнений, другими словами, можно ли инвертировать матрицу.
Расчет определителя
Здесь показана формула определителя:
- для матрицы 2×2
- для матрицы 3х3
- для матрицы 4×4
Обозначение
Это скалярное число представлено матрицей с вертикальными линиями с каждой стороны: |M|
Альтернативные подходы
Как и многие математические понятия, существуют разные способы понимания определителей:
Решение линейных уравнений
Если у нас есть n уравнений с n неизвестными, то мы можем решить эти уравнения при условии, что все эти уравнения независимы, если их нет, то одно уравнение выводится из другого и поэтому не дает никакой дополнительной информации.
Геометрическая интерпретация
Детерминанты, возможно, чаще всего связаны с матрицами, но у них есть геометрическая интерпретация, которая полностью не зависит от матриц (эта геометрическая интерпретация обсуждается на этой странице).
Независимость векторов (ортогональность) | Возможно, мы получили ключ к этой геометрической интерпретации, когда рассмотрели вращения, чистое вращение всегда имеет определитель, равный единице. Это связано с ситуацией, когда у нас есть набор взаимно ортогональных единичных векторов, определитель матрицы, образованной из этих векторов, равен единице. |
Объем, заключенный в вектора | |М| — это объем, заключенный между векторами. Однако знак значим, он может быть отрицательным, если инвертировано нечетное количество координат, «объем» будет отрицательным. Это связано с трехмерным вектором трехмерной алгебры Клиффорда. |
Используется для вычисления обратной матрицы
Формула для вычисления обратной матрицы [M] включает умножение на скалярный коэффициент 1/|M| поэтому, если |М| = 0 все компоненты инверсии будут равны бесконечности, что указывает в этом случае на то, что [M] не имеет инверсии.
Вычисление определителей с помощью рекурсии
Мы можем вычислить определитель n×n из матрицы (n-1)×(n-1) и так далее до определителя матрицы 1×1, который является просто самим термином. Этот рекурсивный метод также известен как расширение минорами.
Сначала немного терминологии. Если мы удалим одну строку и один столбец, оставшийся определитель будет называться второстепенным, а элемент на пересечении удаляемых строк и столбцов будет называться кофактором.
| м11 | м12 | м13 |
| м21 | м22 | м23 |
| м31 | м32 | м33 |
где:
- кофактор
- младший
Чтобы вычислить определитель рекурсивно, мы сначала выбираем любую строку или столбец, затем мы превращаем каждый член в строке или столбце в кофактор.
Определитель вычисляется из суммы миноров, умноженных на связанные с ними кофакторы (чередующиеся знаки), взятые в выбранной строке или столбце.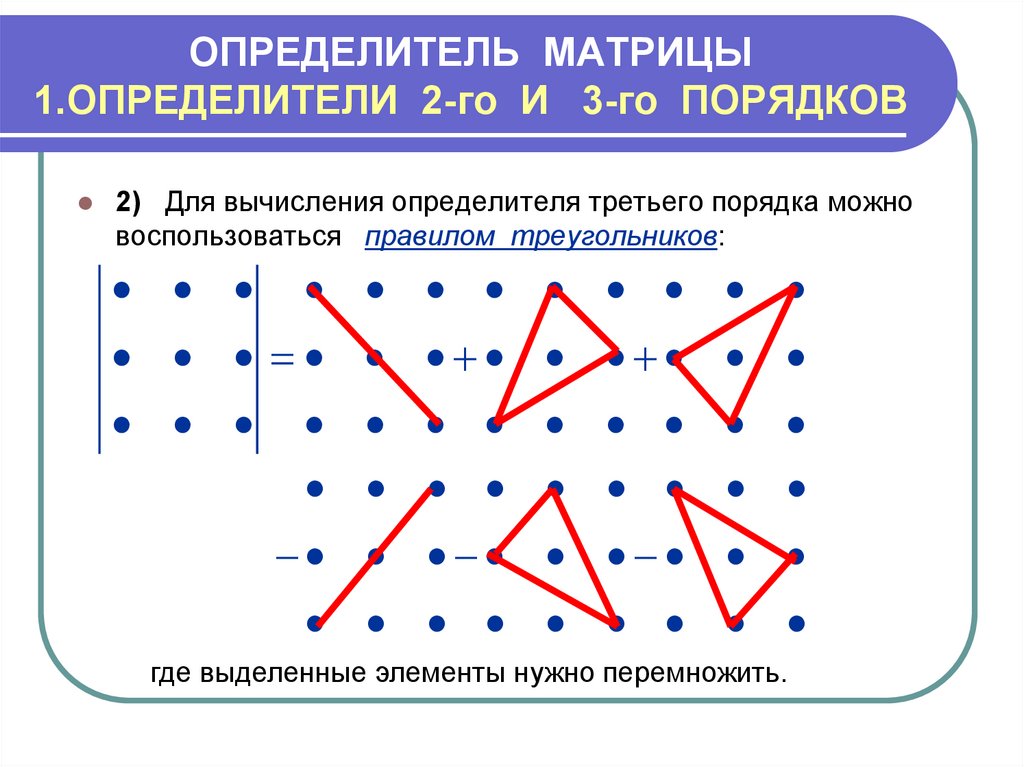
|А| = ∑ aij·Cij
где:
- aij = минор A (строка i и столбец j удалены)
- Cij = кофактор (со знаком) = (−1) i+j · mij
- mij = элемент в строке i и столбце j
Пример матрицы 3×3
Определитель:
| м11 | м12 | м13 |
| м21 | м22 | м23 |
| м31 | м32 | м33 |
вычисляется из
| первый срок | второй срок | третий срок | ||||||||||||||||||||||||||||
| знак | + | — | + | |||||||||||||||||||||||||||
| кофактор | м11 | м12 | м13 | |||||||||||||||||||||||||||
| второстепенный (удалить термины с желтым фоном) |
|
|
|
получаем
| = м11 |
| — м12 |
| + м13 |
|
и переход на следующий уровень дает:
|M| = m11 m22 m33 + m12 m23 m31 + m13 m21 m32 — m11 m23 m32 — m12 m 21 m33 — м13 м22 м31
Расширение Лапласа
Мы можем либо расширить по любому столбцу (j = 1,2 .
. n):
| п | ||
| дет(М) = | Σ | М С |
| i=1 |
или любой ряд (j = 1,2 .. n):
| н | ||
| дет(М) = | Σ | М да С да |
| i=1 |
где:
- M ij = минор элемента ij
- C ji = кофакторы элемента ij = (-1) i+j M ij
Свойства определителей
Все матрицы вращения имеют определитель 1
Например, |R| = cos(a) 2 + sin(a) 2 = 1
Использование определителей для решения одновременных уравнений
Для 3 неизвестных
x | -у | с | -1 | |||||||||||||||||||||||||||||||||||||||
|
|
|
|
Детерминанты и алгебра Клиффорда
| = A/\B = псевдоскалярный множитель |
На этой странице обсуждаются детерминанты и алгебра Клиффорда.