Как вычислить определитель четвертого порядка
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .
Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»:
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке.
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу:
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.
Автор: Емелин Александр
(Переход на главную страницу)
Профессиональная помощь по любому предмету – Zaochnik.com
Часто в математических и прикладных задачах возникает необходимость использовать матрицы. Дадим определение матрицы.
Матрица – это прямоугольная таблица скаляров (элементов некоторого поля), состоящая из заданного количества столбцов и заданного количества строк.
Выделяют разные матрицы. Нам пригодятся понятие следующих:
- если матрица имеет единственный элемент, то она является совпадающей со своим единственным скаляром;
- квадратной матрицей называют такую матрицу, у которой количество столбцов совпадает с количеством строк.

Алгебраические операции над матрицами имеют свой алгоритм и порядок, отличающийся от тех же операций над обычными числами. Помимо алгебраических операций, существуют и другие операции над матрицами. Например, операция транспонирования матрицы.
Часто учащиеся сталкиваются с задачами по нахождению определителя матриц разных порядков. Под матрицами первого, второго, третьего, четвёртого и т.д. порядка понимаются квадратные матрицы. Дадим определение определителю.
Попробуй обратиться за помощью к преподавателям
Определитель или детерминант матрицы – это определённое число, которое можно поставить в соответствие какой-либо квадратной матрице. Если элементы матрицы действительные числа, то и определитель будет действительным числом. Определитель обозначают $det A$ или $|A|$.
Определитель первого порядка равен скаляру данной матрицы. Определители второго и третьего порядка высчитываются в определённом порядке, то есть по известным формулам.
Для вычисления определителя больше третьего порядка, необходимо понимание минора матрицы.
Минор матрицы третьего порядка – это определитель второго порядка, полученной из заданной матрицы третьего порядка вычеркиванием $i$-ой строки и $j$-го столбца. Минор обозначают $M$.
Формула для определителя четвёртого порядка:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Определителем матрицы второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ;
.
Пример: .
Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу
Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.
В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.
Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.
Пример:
Разложение определителя по элементам некоторой строки (столбца).
Минором Мij элемента аij квадратной матрицы А называется определитель, составленный из элементов матрицы А, оставшихся после вычеркивания i-ой строки и j-го столбца.
Например, минором к элементу а21 матрицы третьего порядка будет определитель .
Будем говорить, что элемент аij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) – четное число, нечетное место, если i+j – нечетное число.
Алгебраическим дополнением Аij элемента аij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).
Пример:
– алгебраическое дополнение элемента а23= 4;
– алгебраическое дополнение элемента а22= 1.
Теорема Лапласа. Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.
Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом
Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.
Пример:
Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n-го порядка, сводя его к вычислению n определителей (n-1)-го порядка
Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.
Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.
Пример. Вычислить определитель четвертого порядка.
Разложим определитель по элементам третьей строки
Свойства определителей:
1. Определитель не изменится, если его строки заменить столбцами и наоборот.
2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.
3. Определитель с двумя одинаковыми строками (столбцами) равен 0.
4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.
5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10568 – | 7328 – или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Вычислить определитель разложением по строке или столбцу. Разложение определителя по строке. Вычисление определителя матрицы при помощи метода Гаусса
Рубрика: Мифы и легенды
Задание. Вычислить определитель , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно
выполним элементарные преобразования
над строками определителя, сделав как
можно больше нулей либо в строке, либо
в столбце. Для этого вначале от первой
строки отнимем девять третьих, от второй
— пять третьих и от четвертой — три третьих
строки, получаем:
Для этого вначале от первой
строки отнимем девять третьих, от второй
— пять третьих и от четвертой — три третьих
строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
Ответ.
12. Слау 3 порядка
1. Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
2. Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
3. Разложение
определителя по строке или столбцу
Разложение
определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель
Решение.
Ответ.
4.Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получаем
нули во втором столбце на месте элементов,
стоящих под главной диагональю. И снова,
если диагональный элемент будет равен ,
то вычисления будут более простыми. Для
этого меняем местами вторую и третью
строки (и при этом меняется на
противоположный знак определителя):
И снова,
если диагональный элемент будет равен ,
то вычисления будут более простыми. Для
этого меняем местами вторую и третью
строки (и при этом меняется на
противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
1.Теорема разложения:
Всякий определитель равен сумме парных произведений элементов какого-либо ряда на их алгебраические дополнения.
Для i- й строки:
или для j -го столбца:
Пример 7.1. Вычислить определитель разложением по элементам первой строки:
1∙(1+12+12 ) ∙(2+16+18 )+
3∙(4+8+27 ) ∙(8+4+18 )=
Теорема разложения позволяет заменить вычисление одного определителя n- го порядка вычислением n определителей (n- 1)-го порядка.
Однако для упрощения вычислений целесообразно для определителей высоких порядков использовать метод «размножения нулей», основанный на свойстве 6 раздела 5. Его идея:
Сначала «размножить нули» в некотором ряду, т.е. получить ряд, в котором только один элемент не равен нулю, остальные нули;
Затем разложить определитель по элементам этого ряда.
Следовательно, на основании теоремы разложения исходный определитель равен произведению ненулевого элемента на его алгебраическое дополнение.
Пример7.2. Вычислить определитель:
.
«Размножим нули» в первом столбце.
От второй строки вычтем первую, умноженную на 2, от третьей строки вычтем первую, умноженную на 3, а от четвертой строки вычтем первую, умноженную на 4. При таких преобразованиях величина определителя не изменится.
По свойству 4 раздела 5 можем вынести за знак определителя из 1-го столбца, из 2-го столбца и из 3-го столбца.
Следствие: Определитель с нулевым рядом равен нулю.
2. Теорема замещения:
Сумма парных произведений каких-либо чисел на алгебраические дополнения некоторого ряда определителя равна тому определителю, который получается из данного, если в нем заменить элементы этого ряда взятыми числами.
Для -й строки:
1. Теорема аннулирования:
Сумма парных произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.
Действительно, по теореме замещения получаем определитель, у которого в k -й строке стоят те же элементы, что и в i -й строке
Но по свойству 3 раздела 5 такой определитель равен нулю.
Т.о., теорему разложения и ее следствия можно записать следующим образом:
8. Общие сведения о матрицах. Основные определения.
Определение 8.1 . Матрицей называется следующая прямоугольная таблица:
Применяют также следующие обозначения матрицы: , или , или .
Строки и столбцы матрицы именуются рядами.
Величина называется размером матрицы.
Если в матрице поменять местами строки и столбцы, то получим матрицу, называемую транспонированной . Матрица, транспонированнаяс , обычно обозначается символом .
Например:
Определение 8.2 . Две матрицы A и B называются равными , если
1) обе матрицы одинаковых размеров, т.е. и ;
2) все их соответствующие элементы равны, т.е.
Тогда . (8.2)
Здесь одно матричное равенство (8.2) эквивалентно скалярных равенств (8.1).
9. Разновидности матриц.
1) Матрица, все элементы которой равны нулю, называется ноль-матрицей:
2) Если матрица состоит только из одной строки, то она называется матрицей-строкой, например . Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столбцом, например .
Транспонирование переводит матрицу-столбец в матрицу-строку и наоборот.
3) Если m = n , то матрица называется квадратной матрицей n-го порядка.
Диагональ членов квадратной матрицы, идущая из левого верхнего угла в ее правый нижний угол, называется главной . Другая же диагональ ее членов, идущая из левого нижнего угла в ее правый верхний угол, именуется побочной .
Для квадратной матрицы может быть вычислен определитель det(A) .
Определение1. 7 . Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение: выбранный элемент определителя, его минор.
Пример. Для
Определение1. 8. Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т. е.
е.
Рассмотрим еще один способ вычисления определителей третьего порядка – так называемое разложение по строке или столбцу. Для этого докажем следующую теорему:
Теорема 1.1 . Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.
где i=1,2,3.
Доказательство.
Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.
Найдем алгебраические дополнения к элементам первой строки:
Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.
Пример. Вычислим определитель с помощью разложения по первому столбцу. Заметим, что при этом искать не требуется, так как следовательно, и Найдем и Следовательно,
Определители более высоких порядков .
Определение1. 9 . Определитель n-го порядка
есть сумма n! членов каждый из которых соответствует одному из n! упорядоченных множеств полученных r попарными перестановками элементов из множества 1,2,…,n.
Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.
Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.
Пример. Вычислим определитель 4-го порядка с помощью разложения по 2-му столбцу. Для этого найдем и :
Следовательно,
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году , хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
олнение минора определяется следующим образом:
Справедливо следующее утверждение.
Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать столбцов из , то есть биномиальному коэффициенту .
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Разложение определителя по строке (столбцу) (Следствие 1)
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть — квадратная матрица размера . Пусть также задан некоторый номер строки либо номер столбца матрицы . Тогда определитель может быть вычислен по следующим формулам.
Задание. Вычислить
определитель ,
разложив его по элементам какой-то
строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
Ответ.
12. Слау 3 порядка
1. Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
2. Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
3. Разложение
определителя по строке или столбцу
Разложение
определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель
Решение.
Ответ.
4.Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Дальнейшие свойства связаны с понятиями минора и алгебраического дополнения
Минором элемента называется определитель, составленный из элементов, оставшихся после вычеркивания стоки и столбца, на пересечении которых находится этот элемент. Минор элемента определителя порядка имеет порядок . Будем его обозначать через .
Минор элемента определителя порядка имеет порядок . Будем его обозначать через .
Пример 1. Пусть , тогда .
Этот минор получается из A путём вычёркивания второй строки и третьего столбца.
Алгебраическим дополнением элемента называется соответствующий минор, умноженный на , т.е , где –номер строки и -столбца, на пересечении которых находится данный элемент.
VІІІ. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.
Пример 2. Пусть , тогда
Пример 3. Найдём определитель матрицы , разложив его по элементам первой строки.
Формально эта теорема и другие свойства определителей применимы пока только для определителей матриц не выше третьего порядка, поскольку другие определители мы не рассматривали. Следующее определение позволит распространить эти свойства на определители любого порядка.
Определителемматрицы порядка называется число, вычисленное с помощью последовательного применения теоремы о разложении и других свойств определителей.
Можно проверить, что результат вычислений не зависит от того, в какой последовательности и для каких строк и столбцов применяются вышеуказанные свойства. Определитель с помощью этого определения находится однозначно.
Хотя данное определение и не содержит явной формулы для нахождения определителя, оно позволяет находить его путём сведения к определителям матриц меньшего порядка. Такие определения называют рекуррентными.
Пример 4. Вычислить определитель:
Хотя теорему о разложении можно применять к любой строке или столбцу данной матрицы, меньше вычислений получится при разложении по столбцу, содержащему как можно больше нулей.
Поскольку у матрицы нет нулевых элементов, то получим их с помощью свойства VII . Умножим первую строку последовательно на числа и прибавим её ко строкам и получим:
Разложим получившийся определитель по первому столбцу и получим:
так как определитель содержит два пропорциональных столбца.
Некоторые виды матриц и их определители
Квадратная матрица, у которой ниже или выше главной диагонали стоят нулевые элементы ()называется треугольной.
Их схематичное строение соответственно имеет вид: или
.
Помогите решить / разобраться (М)
| NNDeaz |
| ||
13/06/10 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| NNDeaz |
| ||
13/06/10 |
| ||
| |||
| SomePupil |
| ||
07/01/15 |
| ||
| |||
| NNDeaz |
| ||
13/06/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| NNDeaz |
| ||
13/06/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
4, \quad (c,x)\in \varDelta _1. \end{выровнено}$$
- (я)
На вершинах \(\varDelta _1,\)
$$\begin{aligned} \begin{aligned}&h(0,0)=1296, \quad h(0,x_1(0))= h( 0,1)=1296,\quad h(2,0)=1296,\\&h(2,x_1(2))=h\left( 2,\frac{1}{8}\left( \sqrt{ 57}-3\right) \right) =\frac{9}{32}\left( 3461+113\sqrt{57}\right) \примерно 1213,349.
 \end{выровнено} \end{выровнено}$$
\end{выровнено} \end{выровнено}$$ - (ii)
На стороне \(x = 0,\)
$$\begin{aligned}h(c,0)=1296, \quad c\in (0,2).\end{aligned}$$ 92+7296t-9216.\end{aligned}$$
Так как \(\varrho _1’\) имеет только два действительных нуля в точках \(c\приблизительно -12,8436\) и \(c\приблизительно -5,43834,\) и \(\varrho _1′(0)<0,\), поэтому \(\varrho _1\) убывает на (0, 2). Это с \(\varrho _1(0)<0\) дает
$$\begin{aligned} \varrho _1(c)<0,\quad c\in (0,2). \end{aligned}$$
(20)
Так как \(\varrho _2’>0\) для \(c\in [0,2],\), то \(\varrho _2\) увеличивается от \ (\varrho _2(0)=-9216\) в \(\varrho _2(2)=87296.\) Таким образом, \(\varrho _2(c)\le 0\) для \(c\in (0,c ‘]\) и \(\varrho _2(c)> 0\) для \(c\in (c’,2),\), где \(c’\приблизительно 0,627225\) является уникальным нулем \(\ гамма _2\) в (0, 2).92-208896t-262144,\quad t\in \mathbb R.\end{aligned}$$
Как легко видеть, \(\varrho _3′(c)<0\) для \(c\in (0,6, 2),\), так что \(\varrho _3\) убывает на (0,6, 2), и, следовательно, на \((c',2).
 \) Это и \(\varrho _3(0,6)<0\) дает
\) Это и \(\varrho _3(0,6)<0\) дает$$\begin{aligned}\varrho _3(c)<0,\quad c\in (c',2),\end{aligned}$$
что подтверждает (21), (22) и завершает доказательство (19) тем самым (18).
Подведение итогов,
$$\begin{aligned}h(c,x_1)=\gamma (c)\le \gamma (2)<1296,\quad c\in (0,2).\end{aligned }$$ 93=0 \конец{массив}\справа. } \end{aligned}$$
имеет решения \((c_i,x_i), i=1,2,3,\) только тогда, когда
$$\begin{aligned} {\left\{ \begin{array }{ll} c_1=0\\ x_1=0 \end{массив}\right. }\quad {\left\{ \begin{массив}{ll} c_2=0\\ x_2=-3 \end{массив}\right. }\quad {\left\{ \begin{массив}{ll} c_3=0\\ x_3=3 \end{массив}\right. } \end{align}$$
, поэтому h не имеет критических точек внутри \(\varDelta _1.\)
D2. Предположим, что \(y_w\ge 1\), т. е. эквивалентно тому, что \(x\in [x_1(c),1].\) Пусть \(\varDelta _2:=\{(c,x): 0\ le c\le 2,\ x_1(c)\le x\le 1\}.\) Тогда 94.\end{выровнено}$$
- (я)
На вершинах \(\varDelta _2,\)
$$\begin{aligned} \begin{aligned}&g(0,x_1(0))=g(0,1)=1024,\quad g( 2,1)=1008,\\&g(2,x_1(2))=g\left( 2,(\sqrt{57}-3)/8\right) =\frac{9}{32}\left ( 3461+113\sqrt{57}\right) \ приблизительно 1213,349.
 3&{} =0 \конец{массив}\справа. } \end{выровнено}$$ 93\cdot 1296=1. \end{aligned}$$
3&{} =0 \конец{массив}\справа. } \end{выровнено}$$ 93\cdot 1296=1. \end{aligned}$$(25)
Ясно, что равенство для верхней оценки в (12) выполняется для тождественной функции, а для нижней оценки для функции (9).
\(\площадь \)
Детерминанты — Значение, определение | Матрица 3х3, Матрица 4х4
Детерминанты — это скалярные величины, полученные суммой произведений элементов квадратной матрицы и их сомножителей по заданному правилу. Они помогают найти сопряженную, обратную матрицу. В дальнейшем для решения линейных уравнений методом обращения матриц нам необходимо применить эту концепцию. Перекрестное произведение двух векторов легко запоминается путем вычисления определителей.
В этой статье давайте узнаем больше о процессе нахождения определителей разных порядков и их свойствах, а также поработаем над несколькими решенными примерами.
1. 
Что такое детерминанты? 2. Как рассчитать определитель 3. Умножение определителей 4. Свойства определителей 5. Правила операций над определителем 6. Часто задаваемые вопросы об определителях Что такое детерминанты?
Детерминанты рассматриваются как коэффициент масштабирования матриц. Их можно рассматривать как функции растяжения и сжатия матриц. Детерминанты принимают квадратную матрицу на входе и возвращают одно число на выходе.
Определение определителей
Для каждой квадратной матрицы C = [\(c_{ij}\)] порядка n×n определитель может быть определен как скалярное значение, которое является действительным или комплексным числом, где \(c_ {ij}\) — это (i, j) -й -й элемент матрицы C. Определитель можно обозначить как det(C) или |C|, здесь определитель записывается путем взятия сетки чисел и размещения их внутри полосы абсолютного значения вместо использования квадратных скобок.

Рассмотрим матрицу C = \(\left[\begin{array}{ll}1 & 2 \\ \\ 3 & 4\end{array}\right]\)
Тогда его определитель можно представить как:
|C| = \(\left|\begin{массив}{ll}1 & 2 \\ 3 & 4\end{массив}\right|\)
Как рассчитать определитель?
Для простейшей квадратной матрицы порядка 1×1, которая имеет только одно число, определитель становится самим числом. Давайте научимся вычислять определители для матриц второго, третьего и четвертого порядка.
Вычисление определителя матрицы 2×2
Для любой квадратной матрицы 2×2 или квадратной матрицы порядка 2×2 мы можем использовать формулу определителя для вычисления ее определителя:
C = \(\left[\begin{array}{ll}a & b \\ \\c & d\end{массив}\right]\)
Его определитель 2×2 можно вычислить как:
|C| = \(\left|\begin{массив}{ll}a & b \\c & d\end{массив}\right|\) = (a×d) — (b×c)
Например: C = \(\left[\begin{array}{ll}8 & 6 \\ \\3 & 4\end{array}\right]\)
Его определитель можно вычислить как:
|С| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\)
|C| = (8×4) — (6×3) = 32 — 18 = 14
Вычисление определителя матрицы 3×3
Для любой квадратной матрицы 3×3 или квадратной матрицы порядка 3×3 \(C = \left[\ begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_ {3}\end{массив}\right] \), определитель представляется в виде:
|C| (или) det C = \(\left|\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \ \a_{3} & b_{3} & c_{3}\end{массив}\right| \)
Вот шаги по вычислению определителя матрицы 3×3 .

- a 1 фиксируется как номер привязки и определитель 2×2 его подматрицы (минор 1 ).
- Аналогично вычислите миноры b 1 и c 1 .
- Продолжайте умножать малый определитель на номер привязки и на его знак \(\left|\begin{array}{ccc}+ &-& + \\- & + & — \\+ &-& + \end{array }\вправо|\)
- Наконец, суммируйте их.
|С| = \(a_{1} \cdot\left|\begin{array}{ll}b_{2} & c_{2} \\b_{3} & c_{3}\end{массив}\right|-b_ {1} \cdot\left|\begin{array}{cc}a_{2} & c_{2} \\a_{3} & c_{3}\end{array}\right|+c_{1} \ cdot\left|\begin{array}{ll}a_{2} & b_{2} \\a_{3} & b_{3}\end{array}\right|\)
|C| = \(a_{1}\left(b_{2} c_{3}-b_{3} c_{2}\right)-b_{1}\left(a_{2} c_{3}-a_{3 } c_{2}\right)+c_{1}\left(a_{2} b_{3}-a_{3} b_{2}\right)\)
Рассмотрим этот пример:
\(B = \left[\begin{array}{ccc}3 & 1 & 1 \\4 & -2 & 5 \\2 & 8 & 7\end{array}\right ] \)
Его определитель вычисляется как:
|B| = \(\left|\begin{массив}{ccc}3 & 1 & 1 \\4 & -2 & 5 \\2 & 8 & 7\end{массив}\right| \)
= \(3 \cdot\left|\begin{array}{ll}-2 & 5 \\8 & 7\end{array}\right|-1 \cdot\left|\begin{array}{cc}4 & 5 \\ 2 & 7\end{массив}\right|+1 \cdot\left|\begin{array}{ll} 4 & -2 \\2 & 8\end{массив}\right|\)
= 3 × ((-2)(7) — (5)(8)) -1 × ((4)(7) — (5)(2)) + 1 × ((4)(8) — (-2)(2))
= 3 × ((-14) — (40)) -1 × ((28) — (10)) + 1 × ((32) — (-4))
= 3 × (-54) -1 × (18) + 1 × (36)
= — 162 — 18 + 36
= -144
Обратите внимание, что мы вычислили определитель матрицы 3×3, используя первую строку здесь.
 Но любую строку/любой столбец можно использовать для вычисления определителей.
Но любую строку/любой столбец можно использовать для вычисления определителей.Вычисление определителя матрицы 4×4
Рассмотрим приведенную ниже квадратную матрицу 4×4 или квадратную матрицу порядка 4×4. При нахождении 9 следует помнить о следующих изменениях.0393 определитель матрицы 4 × 4 :
B = \(\left[\begin{array}{cccc}a_{1} & b_{1} & c_{1} & d_{1} \\a_{ 2} и b_{2} и c_{2} и d_{2} \\a_{3} & b_{3} & c_{3} & d_{3} \\a_{4} & b_{4} & c_{4} & d_{4}\end{массив}\right]\)
- плюс 1 , умноженный на определитель матрицы 3×3, полученный удалением строки и столбца, содержащего 1
- минус b 1 умножить на определитель матрицы 3×3, полученный удалением строки и столбца, содержащего b 1
- плюс c 1 умножить на определитель матрицы 3×3, полученный удалением строки и столбца, содержащего c 1
- минус d 1 умножить на определитель матрицы 3×3, полученный удалением строки и столбца, содержащего d 1
\(\begin{align}|B| = &a_{1} \cdot\left|\begin{array}{lll}b_{2} & c_{2} & d_{2} \\b_{3} & c_{3} & d_{3} \\b_{4} & c_{4} & d_{4}\end{массив}\right|-b_{1} \cdot\left|\begin{массив}{ ccc}a_{2} & c_{2} & d_{2} \\a_{3} & c_{3} & d_{3} \\a_{4} & c_{4} & d_{4}\end {массив}\right|\\&+c_{1}\cdot\left|\begin{массив}{ccc}a_{2} & b_{2} & d_{2} \\a_{3} & b_{ 3} & d_{3} \\a_{4} & b_{4} & d_{4}\end{массив}\right|-d_{1} \cdot\left|\begin{массив}{ccc}a_ {2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3} \\a_{4} & b_{4} & c_{4}\end{массив} \право|\конец{выравнивание}\)
Мы можем использовать метод, упомянутый в предыдущем разделе, чтобы найти определитель матриц 3×3.
 Вот простой способ найти его.
Вот простой способ найти его.Умножение определителей
Мы используем метод, называемый умножением массивов, для умножения двух определителей квадратных матриц. Давайте посмотрим на правило умножения строк на столбцы для умножения двух определителей квадратных матриц A и B:
Умножение определителей 2×2
Рассмотрим две квадратные матрицы A и B порядка 2×2, сначала обозначим их определители как |A| и |Б| как показано ниже:
|A| = \(\left|\begin{array}{ll}\mathrm{a}_{1} & \mathrm{~b}_{1} \\\mathrm{a}_{2} & \mathrm{~ b}_{2}\end{массив}\right|\)
|B| = \(\left|\begin{array}{ll}\mathrm{p}_{1} & \mathrm{~q}_{1} \\\mathrm{p}_{2} & \mathrm{~ q}_{2}\end{массив}\right|\)
|A| × |В| = \(\left|\begin{array}{ll}\mathrm{a}_{1} & \mathrm{~b}_{1} \\\mathrm{a}_{2} & \mathrm{~ b}_{2}\end{массив}\right| \times\left|\begin{array}{cc}p_{1} & \mathrm{~q}_{1} \\p_{2} & \ mathrm{~q}_{2}\end{массив}\right|=\left|\begin{массив}{ll}\mathrm{a}_{1} p_{1}+\mathrm{b}_{ 1} p_{2} & \mathrm{a}_{1} \mathrm{~q}_{1}+\mathrm{b}_{1} \mathrm{~q}_{2} \\\mathrm {a}_{2} p_{1}+\mathrm{b}_{2} p_{2} & \mathrm{a}_{2} \mathrm{~q}_{1}+\mathrm{b }_{2} \mathrm{~q}_{2}\end{массив}\right|\)
Умножение определителей 3×3
Рассмотрим две матрицы C и D порядка 3×3, сначала обозначим их соответствующие определители как |C| и |Д| как показано ниже:
|C| = \(\left|\begin{array}{lll}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{массив}\right|\)
|D| = \(\left|\begin{array}{lll}p_{1} & q_{1} & r_{1} \\p_{2} & q_{2} & r_{2} \\p_{3} & q_{3} & r_{3}\end{массив}\right|\)
|С| × |Д| = \(\left|\begin{массив}{lll}
a_{1} p_{1}+b_{1} p_{2}+c_{1} p_{3} & a_{1} q_{1}+b_{1} q_{2}+c_{1} q_ {3} & a_{1} r_{1}+b_{1} r_{2}+c_{1} r_{3} \\a_{2} p_{1}+b_{2} p_{2}+ c_{2} p_{3} и a_{2} q_{1}+b_{2} q_{2}+c_{2} q_{3} & a_{2} r_{1}+b_{2} r_ {2}+c_{2} r_{3} \\a_{3} p_{1}+b_{3} p_{2}+c_{3} p_{3} и a_{3} q_{1}+ b_{3} q_{2}+c_{3} q_{3} & a_{3} r_{1}+b_{3} r_{2}+c_{3} r_{3}\end{массив}\ right|\)Вот некоторые моменты, которые следует помнить при умножении двух определителей:
- Чтобы умножить два определителя, нам нужно убедиться, что они имеют один и тот же порядок
- Значение определителя не меняется, когда строки и столбцы меняются местами, поэтому мы можем также следовать правилам умножения столбец за строкой, строку за строкой или столбец за столбцом, чтобы умножить два определителя.

Свойства определителей
Для квадратных матриц разных типов при вычислении ее определителя они вычисляются на основе некоторых важных свойств определителей. Вот список некоторых важных свойств определителей:
Свойство1: «Определитель единичной матрицы всегда равен 1»
Рассмотрим определитель единичной матрицы I = \(\left[\begin{array}{ll}1 & 0 \\\\0 & 1\конец{массив}\справа]\), |I| = (1)(1) — (0)(0) = 1,
Таким образом, определитель любой единичной матрицы всегда равен 1,
Свойство 2: «Если любая квадратная матрица B порядка n×n имеет нулевая строка или нулевой столбец, то det(B) = 0″
Рассмотрим определитель единичной матрицы B,
|Б| = \(\left|\begin{array}{ll} 2 & 2 \\0 & 0\end{array}\right|\)
|B| = (2)(0) — (2)(0) = 0
Здесь квадратная матрица B имеет одну нулевую строку, и, таким образом, определитель этой квадратной матрицы обращается в нуль.
Свойство 3: «Если C является верхней или нижнетреугольной матрицей, то det(C) является произведением всех ее диагональных элементов»
Рассмотрим верхнюю треугольную матрицу C с диагональными элементами 3, 2 и 4 Определитель |C| можно найти как:
|С| = \(\left|\begin{array}{ccc}3 & 1 & 1 \\0 & 2 & 5 \\0 & 0 & 4\end{array}\right| \)
|C| = 3 × 2 × 4 = 24
Свойство 4: «Если D — квадратная матрица, то если ее строку умножить на константу k, то константу можно вынести из определителя»
|Д| = \(\left|\begin{массив}{ll}k×a & k×b \\c & d\end{массив}\right|\) |Д| = k × \(\left|\begin{array}{ll}a & b \\c & d\end{array}\right|\) |Д| = \(\left|\begin{массив}{ll}2 и 4 \\1 и 5\конец{массив}\right|\)
= (2)(5) — (4)(1)
= 10 — 4 = 6
|Д| = 2 × \(\left|\begin{array}{ll} 1 & 2 \\1 & 5\end{array}\right|\)
= 2 × ((1)(5) — (2)(1))
= 2 × (5-2) = 2 × 3 = 6
Таким образом, определитель остается одним и тем же в обоих случаях.

Другими важными свойствами определителей являются:
- Квадратная матрица C считается обратимой тогда и только тогда, когда det(C) ≠ 0.
- Если B и C — две квадратные матрицы порядка n × n, то det(BC) = det(B) × det(C) = det(C) × det(B)
- Связь между определителем матрицы D и присоединенным к ней adj(D) может быть представлена как D × adj(D) = adj(D) × D = |D| × I. Здесь D — квадратная матрица, а I — единичная матрица.
Правила операций над определителем
Следующие правила полезны для выполнения операций со строками и столбцами над определителями.
- Значение определителя не изменится, если строки и столбцы поменять местами.
- Знак определителя меняется, если поменять местами любые две строки или (два столбца).
- Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
- Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.

- Если элементы строки или столбца выражены в виде суммы элементов, то определитель может быть выражен в виде суммы определителей.
- Если элементы строки или столбца сложить или вычесть с соответствующими кратными элементами другой строки или столбца, то значение определителя остается неизменным.
Важные примечания к определителю:
Вот несколько моментов, которые следует помнить при изучении определителя:
- Определитель можно рассматривать как функцию, которая принимает квадратную матрицу в качестве входных данных и возвращает одно число. как его выход.
- Квадратная матрица может быть определена как матрица, имеющая одинаковое количество строк и столбцов.
- Для простейшей квадратной матрицы порядка 1×1, которая имеет только одно число, определитель становится самим числом.
☛ Похожие темы:
- Матричный калькулятор
- Формула матрицы
- Калькулятор диагональной матрицы
- Калькулятор матрицы транспонирования
Примеры определителей
Пример 1: Найдите определитель матрицы A, где \(A=\left[\begin{array}{ll}4 & 1 \\ \\3 & 2\end{array}\right]\)
Решение:
У нас есть
\(|\mathrm{A}|=\left|\begin{array}{ll}4 & 1 \\ \\ 3 & 2\end{array}\right|\)
найдите это, просто умножьте диагонали и вычтите произведения.

|А| = (4 × 2) — (3 × 1)
= 8 — 3
= 5
Ответ: |A| = 5.
Пример 2: Какой определитель матрицы 2×2 \(C = \left[\begin{array}{ll}4 & -2\\ \\ -8 & 4\end{array}\right]\ )?
Решение:
По формуле определителя матрицы 2×2,
\(|\mathrm{C}|=\left|\begin{array}{ll}4 & -2\\ \\-8 & 4\конец{массив}\право|\)
|C| = ((4)(4)-(-8)(-2)) = 16 — 16 = 0.
Ответ: |C| = 0,
Пример 3: Найдите определитель матрицы 3×3 A, где \(A=\left[\begin{array}{ll}1 & 3 & 2 \\-3 & -1& -3\\2 & 3 & 1 \end{массив}\right]\).
Решение:
Разложим определитель данной матрицы 3х3 по первой строке.
|С| = \(1 \cdot\left|\begin{array}{ll}-1 & -3 \\3 & 1\end{array}\right|-3 \cdot\left|\begin{array}{cc} -3 & -3 \\2 & 1\end{массив}\right|+2 \cdot\left|\begin{array}{ll} -3 & -1 \\2 & 3\end{массив}\right |\)
= 1.
 (-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))
(-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))= 1. (-1 +9) — 3. (-3 +6) + 2 .(-9 +2)
= 8 — 9 -14
= -15
Ответ: |A| = -15.
Пример 4: Использование свойств определителей и оценка значения определителя \(\left|\begin{array}{ccc}
а-б&б-в&в-а\
б-в&в-а&а-б \\
в-а и а-б и б-с
\end{массив}\right|\).Решение:
Применим элементарное преобразование строки R 1 → R 1 + R 2 + R 3 (по одному из свойств определителей элементарные преобразования строк не меняют значения определителя). Тогда указанный выше определитель превращается в:
\(\left|\begin{array}{ccc}
0&0&0\
б-в&в-а&а-б \\
в-а и а-б и б-с
\end{array}\right|\)По другому свойству определителей, если строка/столбец матрицы полностью с нулями, то ее определитель равен 0. Следовательно, значение вышеуказанного определителя равно 0,
Ответ: 0.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по детерминантам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об определителях
Что такое детерминант?
Определитель квадратной матрицы C = [\(c_{ij}\)] порядка n×n может быть определен как скалярное значение, которое является действительным или комплексным числом, где \(c_{ij }\) является (i,j) -м -м элементом матрицы C. Он обозначается как det(C) или |C|, здесь определитель записывается путем взятия сетки чисел и размещения их внутри абсолютного значения полосы вместо квадратных скобок. Определитель квадратной матрицы \(C = \left[\begin{array}{ll} 4 & 2\\ \\ 5 & 3\end{array}\right]\) можно записать как: \(|C| = \left|\begin{массив}{ll} 4 & 2\\5 & 3\end{массив}\right|\).
 Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений.
Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений.Для чего используются определители?
Детерминанты играют важную роль в линейных уравнениях, где они используются для регистрации изменений переменных в целых числах и того, как линейные преобразования изменяют объем или площадь. Детерминанты особенно полезны в приложениях, где используются обратные и сопряженные матрицы. Перекрестное произведение двух векторов также вычисляется с помощью определителей.
Какая формула определителя матрицы 2×2?
Для любой квадратной матрицы 2×2 или квадратной матрицы порядка 2×2 мы можем использовать эту формулу определителя для вычисления ее определителя:
\(C = \left|\begin{array}{ll}a & b\\c & d\end{array}\right|\). Формула для вычисления определителя 2×2: |C| = (a×d) — (b×c)
Каковы примеры определителей?
Рассмотрим пример квадратной матрицы D, D = \(\left[\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right]\).
 Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.
Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.Являются ли детерминанты коммутативными?
Да, умножение определителей коммутативно, и это можно легко понять с помощью следующего свойства: если B и C — две квадратные матрицы порядка n × n, то det(BC) = det(B) × det(C) = det (С) × дет(В).
Каковы свойства определителей?
Вот список некоторых важных свойств определителей:
- Определитель единичной матрицы всегда равен 1
- Если любая квадратная матрица B порядка n×n имеет нулевую строку или нулевой столбец, то det(B) = 0,
- Если C является верхнетреугольной или нижнетреугольной матрицей, то det(C) является произведением всех ее диагональных элементов.
- Если D — квадратная матрица, то если ее строку умножить на константу k, то константу можно вынести из определителя.
- Квадратная матрица C считается обратимой тогда и только тогда, когда det(C) ≠ 0.

- Если B и C — две квадратные матрицы порядка n × n, то det(BC) = det(B) × det(C) = det(C) × det(B)
- Связь между определителем матрицы D и присоединенным к ней adj(D) может быть представлена как D × adj(D) = adj(D) × D = |D| × I. Здесь D — квадратная матрица, а I — единичная матрица.
Как вы оцениваете определители матрицы 3×3?
Любой определитель 3×3 можно вычислить следующим образом:
\(C = \left[\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{ 2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{массив}\right] \)
Его определитель можно вычислить как:- a 1 фиксируется как номер привязки, и вычисляется определитель 2×2 его подматрицы, которая представляет собой квадратную матрицу.
- Берется следующий номер привязки по порядку, теперь это b 1 и вычисляется малый определитель, и, наконец, в качестве номера привязки берется c 1 и вычисляется его определитель 2×2.
- Продолжайте попеременно умножать меньший определитель на номер привязки и на его знак \(\left|\begin{array}{ccc}+ &-& + \\- & + & — \\+ &-& + \end{ массив}\справа|\).

- |С| = \(\left|\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{массив}\right| \)
|С| = \(a_{1} \cdot\left|\begin{array}{ll}b_{2} & c_{2} \\b_{3} & c_{3}\end{массив}\right|-b_ {1} \cdot\left|\begin{array}{cc}a_{2} & c_{2} \\a_{3} & c_{3}\end{array}\right|+c_{1} \ cdot\left|\begin{array}{ll}a_{2} & b_{2} \\a_{3} & b_{3}\end{array}\right|\) - Наконец, просуммируйте их. |С| = \(a_{1}\left(b_{2} c_{3}-b_{3} c_{2}\right)-b_{1}\left(a_{2} c_{3}-a_{3 } c_{2}\right)+c_{1}\left(a_{2} b_{3}-a_{3} b_{2}\right)\)
Каковы правила выполнения операций со строками и столбцами над определителями?
Следующие правила полезны для выполнения операций со строками и столбцами над определителями.
- Если строки и столбцы поменять местами, то значение определителя не изменится
- При перестановке любых двух строк или (двух столбцов) знак определителя меняется
- Значение определителя матрицы, в которой две строки/столбца равны, равно нулю.

- Если каждый элемент определенной строки или столбца матрицы умножается на константу, то ее определитель также умножается на константу.
- Если элементы строки или столбца выражены в виде сумм, то определитель можно разбить на два или более определителей.
- Если строку (или столбец) умножить на число, а полученные элементы добавить к другой строке (или столбцу), то определитель не изменится.
Где мы можем найти калькулятор определителя?
Чтобы найти определитель матрицы, используйте следующий калькулятор: Калькулятор определителя. Это поможет нам найти определитель матрицы 3×3.
Что такое определитель треугольной матрицы?
Определитель треугольной матрицы можно найти, вычислив произведение всех ее диагональных элементов. Это применимо как к верхнетреугольным, так и к нижнетреугольным матрицам.
Могут ли определители быть отрицательными?
Определители представляют скалярную величину, которая является действительным числом.
 Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель.
Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель.M4 Определитель матрицы
14 июля 2021 г. — 11:09я — ЭйДжей (e67821)
Open image
Определитель — это число, которое можно вычислить для любой квадратной матрицы. Определитель используется при вычислении векторных перекрестных произведений, собственных значений, собственных векторов и решении одновременных уравнений.
Определитель матрицы \(2\times2\)
Определитель матрицы \(2\times2\) называется определителем второго порядка.
Пусть \[\begin{align*} A & =\left[\begin{массив}{cc} а и б\\ CD \end{массив}\right].
 \end{align*}\] Определитель \(A\) обозначается \(\det A\) или \(\left|A\right|\) и определяется как \[\begin{align* }
\влево|А\вправо| & =\left|\begin{массив}{cc}
а и б\\
CD
\конец{массив}\справа|\\
& = ad-bc.
\end{выравнивание*}\]
\end{align*}\] Определитель \(A\) обозначается \(\det A\) или \(\left|A\right|\) и определяется как \[\begin{align* }
\влево|А\вправо| & =\left|\begin{массив}{cc}
а и б\\
CD
\конец{массив}\справа|\\
& = ad-bc.
\end{выравнивание*}\]Примеры
\(\left|\begin{array}{cc} 2 & 3\\ 1 & 5 \end{array}\right|=2\times5-1\times3=10-3=7 .\)
\(\left|\begin{array}{cc} 3 & 2\\ -1 & 1 \end{array}\right|=3\times1-\left(-1\right)\times2=3- \влево(-2\вправо)=3+2=5.\)
\(\left|\begin{array}{cc} -2 & -1\\ 6 & 3 \end{array}\right|=\left(-2\right)\times3-6\times\left (-1\справа)=-6+6=0.\)
Сингулярные матрицы
Матрица с нулевым определителем называется сингулярной матрицей.11 Сингулярные матрицы не имеют обратной. Если определитель не равен нулю, матрица называется невырожденной.
См. упражнение 1 для практики.
Определитель матрицы \(3\x3\)
Определитель матрицы \(3\x3\) называется определителем третьего порядка.

Пусть \[\begin{align*} B & =\left[\begin{массив}{ccc} а_{1} и б_{1} и в_{1}\\ а_{2} и б_{2} и в_{2}\\ а_{3} и б_{3} и в_{3} \конец{массив}\справа] \end{align*}\], то определитель \(B\) вычисляется путем расширения по любой строке или столбцу и оценки результирующего определителя второго порядка.22 Удивительно, что значение определителя остается одним и тем же независимо от того, какой строку или столбец мы расширяем вдоль.
Расширение по первой строке. Умножаем \(a_{1}\) на определитель второго порядка, полученный путем игнорирования строки и столбца, занимаемых \(a_{1}.\). Мы получаем \[ a_{1}\left|\begin{массив}{cc} б_{2} и с_{2}\\ б_{3} и в_{3} \конец{массив}\право|. \]
Теперь умножьте \(b_{1}\) на определитель второго порядка, полученный путем игнорирования строки и столбца, занимаемых \(b_{1}.\). Мы получаем \[ b_{1}\left|\begin{массив}{cc} а_{2} и с_{2}\\ а_{3} и в_{3} \конец{массив}\право|. \]
Теперь умножьте \(c_{1}\) на определитель второго порядка, полученный путем игнорирования строки и столбца, занимаемых \(c_{1}.
 \). Мы получаем \[
c_{1}\left|\begin{массив}{cc}
а_{2} и б_{2}\\
а_{3} и б_{3}
\конец{массив}\право|.
\]
\). Мы получаем \[
c_{1}\left|\begin{массив}{cc}
а_{2} и б_{2}\\
а_{3} и б_{3}
\конец{массив}\право|.
\]Тогда определитель \(B\) равен \[\begin{align*} \влево|В\вправо| & =\left|\begin{массив}{ccc} а_{1} и б_{1} и в_{1}\\ а_{2} и б_{2} и в_{2}\\ а_{3} и б_{3} и в_{3} \конец{массив}\справа|\\ & =a_{1}\left|\begin{массив}{cc} б_{2} и с_{2}\\ б_{3} и в_{3} \end{массив}\right|-b_{1}\left|\begin{массив}{cc} а_{2} и с_{2}\\ а_{3} и в_{3} \end{массив}\right|+c_{1}\left|\begin{массив}{cc} а_{2} и б_{2}\\ а_{3} и б_{3} \конец{массив}\право|. \end{align*}\] Обратите внимание на изменение знака во втором члене. На самом деле при вычислении определителей полезно иметь в виду следующую картину: \[ \left|\begin{массив}{ccc} + & — & +\\ — & + & -\\ + & — & + \конец{массив}\право| \] эти знаки должны затем применяться к соответствующим элементам.
В приведенном выше случае мы расширились по первой строке. Мы получаем одно и то же значение определителя независимо от того, по какой строке или столбцу мы расширяем.
 Теперь мы расширяем столбец \(2\), чтобы получить: \[\begin{align*}
\влево|В\вправо| & =\left|\begin{массив}{ccc}
а_{1} и б_{1} и в_{1}\\
а_{2} и б_{2} и в_{2}\\
а_{3} и б_{3} и в_{3}
\конец{массив}\справа|\\
& =-b_{1}\left|\begin{массив}{cc}
а_{2} и с_{2}\\
а_{3} и в_{3}
\end{массив}\right|+b_{2}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{3} и в_{3}
\end{массив}\right|-b_{3}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{2} и в_{2}
\конец{массив}\право|.
\end{align*}\] Опять же, обратите внимание на изменение знака.
Теперь мы расширяем столбец \(2\), чтобы получить: \[\begin{align*}
\влево|В\вправо| & =\left|\begin{массив}{ccc}
а_{1} и б_{1} и в_{1}\\
а_{2} и б_{2} и в_{2}\\
а_{3} и б_{3} и в_{3}
\конец{массив}\справа|\\
& =-b_{1}\left|\begin{массив}{cc}
а_{2} и с_{2}\\
а_{3} и в_{3}
\end{массив}\right|+b_{2}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{3} и в_{3}
\end{массив}\right|-b_{3}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{2} и в_{2}
\конец{массив}\право|.
\end{align*}\] Опять же, обратите внимание на изменение знака.Пример 1
Вычислить определитель \[ A=\left[\begin{массив}{ccc} 2 и 1 и 3\\ 1 и -1 и 2\\ 2 и 1 и 4 \end{массив}\right]. \]
Решение 1:
Расширяя первую строку, получаем: \[\begin{align*} \влево|А\вправо| & =\left|\begin{массив}{ccc} 2 и 1 и 3\\ 1 и -1 и 2\\ 2 и 1 и 4 \конец{массив}\справа|\\ & =2\влево|\begin{массив}{cc} -1 и 2\\ 1 и 4 \end{массив}\right|-1\left|\begin{массив}{cc} 1 и 2\\ 2 и 4 \end{массив}\right|+3\left|\begin{массив}{cc} 1 и -1\\ 2 и 1 \конец{массив}\справа|\\ & =2\влево(\влево(-1\вправо)\раз4-1\время2\вправо)-\влево(1\время4-2\время2\вправо)+3\влево(1\время1-2\время\ влево(-1\вправо)\вправо)\\ & =2\влево(-4-2\вправо)-\влево(4-4\вправо)+3\влево(1+2\вправо)\\ & =-12+9\\ & =-3.
 \end{align*}\]
\end{align*}\]Решение 2:
На этот раз мы расширим столбец 2, чтобы получить: \[\begin{align*} \влево|А\вправо| & =\left|\begin{массив}{ccc} 2 и 1 и 3\\ 1 и -1 и 2\\ 2 и 1 и 4 \конец{массив}\справа|\\ & =-1\left|\begin{массив}{cc} 1 и 2\\ 2 и 4 \end{массив}\right|-1\left|\begin{массив}{cc} 2 и 3\\ 2 и 4 \end{массив}\right|-1\left|\begin{массив}{cc} 2 и 3\\ 1 и 2 \конец{массив}\справа|\\ & =-1\влево(1\время4-2\время2\вправо)-\влево(2\время4-2\время3\вправо)-1\влево(2\время2-1\время3\вправо)\\ & =-1\влево(4-4\вправо)-\влево(8-6\вправо)-1\влево(4-3\вправо)\\ & =-2-1\\ & =-3. \end{align*}\] как и раньше.
Пример 2
Вычислить определитель \[ B=\left[\begin{массив}{ccc} 1 и 3 и -2\\ 1 и -1 и 3\\ 2 и 6 и -4 \end{массив}\right]. \]
Решение:
Расширяя столбец 1, получаем: \[\begin{align*} \влево|В\вправо| & =\left|\begin{массив}{ccc} 1 и 3 и -2\\ 1 и -1 и 3\\ 2 и 6 и -4 \конец{массив}\справа|\\ & =1\влево|\begin{массив}{cc} -1 и 3\\ 6 и -4 \end{массив}\right|-1\left|\begin{массив}{cc} 3 и -2\\ 6 и -4 \end{массив}\right|+2\left|\begin{массив}{cc} 3 и -2\\ -1 и 3 \конец{массив}\справа|\\ & =1\влево(\влево(-1\вправо)\раз\влево(-4\вправо)-6\раз3\вправо)-1\влево(3\раз\влево(-4\вправо)-6\ раз\влево(-2\вправо)\вправо)+2\влево(3\раз3-\влево(-1\вправо)\раз\влево(-2\вправо)\вправо)\\ & =\влево(4-18\вправо)-\влево(-12-\влево(-12\вправо)\вправо)+2\влево(9-2\справа)\\ & =-14+14\\ & =0.
 \end{align*}\] Обратите внимание, что строка \(3\) строки \(B\) кратна строке \(1.\). В общем, когда строка кратна другой строке, определитель равен нулю . Также, если столбец кратен другому столбцу, определитель равен нулю.
\end{align*}\] Обратите внимание, что строка \(3\) строки \(B\) кратна строке \(1.\). В общем, когда строка кратна другой строке, определитель равен нулю . Также, если столбец кратен другому столбцу, определитель равен нулю.Пример 3
Вычислить определитель \[ C=\left[\begin{массив}{ccc} 1 и 5 и 6\\ 3 и -2 и 2\\ 4 и 0 и 1 \end{массив}\right]. \] Решение:
На этот раз лучше расширить столбец \(2\) или строку \(3.\). Это связано с тем, что столбец \(2\) или строка \(3\) содержит ноль, что делает расчет проще. Раскладывая по строке \(3\), получаем: \[\begin{align*} \влево|С\вправо| & =\left|\begin{массив}{ccc} 1 и 5 и 6\\ 3 и -2 и 2\\ 4 и 0 и 1 \конец{массив}\справа|\\ & =4\влево|\begin{массив}{cc} 5 и 6\\ -2 и 2 \end{массив}\right|-0\left|\begin{массив}{cc} 1 и 6\\ 3 и 2 \end{массив}\right|+1\left|\begin{массив}{cc} 1 и 5\\ 3 и -2 \конец{массив}\справа|\\ & =4\влево(5\times2-\влево(-2\вправо)\times6\вправо)+1\влево(1\times\влево(-2\вправо)-3\times5\вправо)\\ & =4\влево(10+12\вправо)+1\влево(-2-15\вправо)\\ & =88-17\\ & =71.
 \end{выравнивание*}\]
\end{выравнивание*}\]Для практики см. упражнение 2.
Оценка определителей более высокого порядка
Определители четвертого порядка могут быть оценены с использованием определителей третьего порядка и пятого порядка с использованием четвертого порядка и так далее. При этом необходимо применять следующие знаки \[ \left|\begin{массив}{ccccc} + & — & + & — & \cdots\\ — & + & — & + & \cdots\\ + & — & + & — & \cdots\\ — & + & — & + & \cdots\\ \vdots & \vdots & \vdots & \vdots & \ddots \конец{массив}\право| \]
Калькуляторы, способные выполнять матричную алгебру, также можно использовать для вычисления определителей.
Упражнение 1
Оцените следующие определители:
\[\begin{align*} \begin{массив}{lllll} а)\,\влево|\begin{массив}{cc} 2 и 5\\ 1 и 2 \конец{массив}\право| & b)\,\left|\begin{массив}{cc} -1 и 1\\ -2 и 5 \конец{массив}\право| & c)\,\left|\begin{массив}{cc} 2 и -3\\ -2 и 6 \конец{массив}\право| & d)\,\left|\begin{массив}{cc} 0 и -3\\ 1 и 0 \конец{массив}\право| & e)\,\left|\begin{массив}{cc} 1 и -3\\ -3 и 9\конец{массив}\право|.

- (я)





 07.2018, 17:15
07.2018, 17:15 

 youtube.com/watch?v=shW_yVZiJKQ&t=50m15s
youtube.com/watch?v=shW_yVZiJKQ&t=50m15s

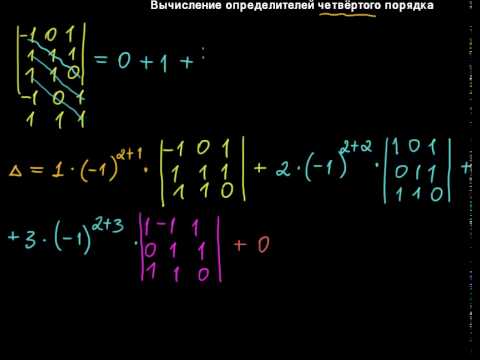 \end{выровнено} \end{выровнено}$$
\end{выровнено} \end{выровнено}$$ \) Это и \(\varrho _3(0,6)<0\) дает
\) Это и \(\varrho _3(0,6)<0\) дает 3&{} =0 \конец{массив}\справа. } \end{выровнено}$$ 93\cdot 1296=1. \end{aligned}$$
3&{} =0 \конец{массив}\справа. } \end{выровнено}$$ 93\cdot 1296=1. \end{aligned}$$


 Но любую строку/любой столбец можно использовать для вычисления определителей.
Но любую строку/любой столбец можно использовать для вычисления определителей. Вот простой способ найти его.
Вот простой способ найти его.

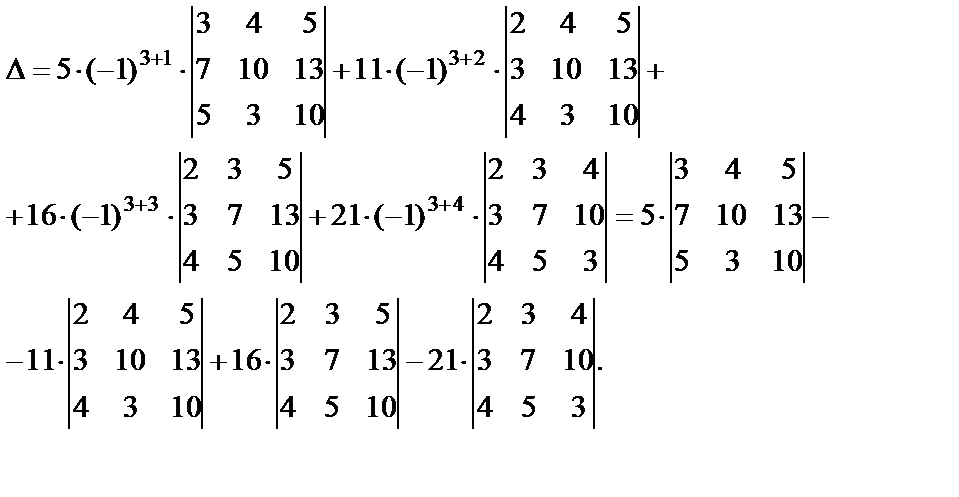

 (-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))
(-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))
 Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений.
Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений. Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.
Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.


 Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель.
Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель. \end{align*}\] Определитель \(A\) обозначается \(\det A\) или \(\left|A\right|\) и определяется как \[\begin{align* }
\влево|А\вправо| & =\left|\begin{массив}{cc}
а и б\\
CD
\конец{массив}\справа|\\
& = ad-bc.
\end{выравнивание*}\]
\end{align*}\] Определитель \(A\) обозначается \(\det A\) или \(\left|A\right|\) и определяется как \[\begin{align* }
\влево|А\вправо| & =\left|\begin{массив}{cc}
а и б\\
CD
\конец{массив}\справа|\\
& = ad-bc.
\end{выравнивание*}\]
 \). Мы получаем \[
c_{1}\left|\begin{массив}{cc}
а_{2} и б_{2}\\
а_{3} и б_{3}
\конец{массив}\право|.
\]
\). Мы получаем \[
c_{1}\left|\begin{массив}{cc}
а_{2} и б_{2}\\
а_{3} и б_{3}
\конец{массив}\право|.
\] Теперь мы расширяем столбец \(2\), чтобы получить: \[\begin{align*}
\влево|В\вправо| & =\left|\begin{массив}{ccc}
а_{1} и б_{1} и в_{1}\\
а_{2} и б_{2} и в_{2}\\
а_{3} и б_{3} и в_{3}
\конец{массив}\справа|\\
& =-b_{1}\left|\begin{массив}{cc}
а_{2} и с_{2}\\
а_{3} и в_{3}
\end{массив}\right|+b_{2}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{3} и в_{3}
\end{массив}\right|-b_{3}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{2} и в_{2}
\конец{массив}\право|.
\end{align*}\] Опять же, обратите внимание на изменение знака.
Теперь мы расширяем столбец \(2\), чтобы получить: \[\begin{align*}
\влево|В\вправо| & =\left|\begin{массив}{ccc}
а_{1} и б_{1} и в_{1}\\
а_{2} и б_{2} и в_{2}\\
а_{3} и б_{3} и в_{3}
\конец{массив}\справа|\\
& =-b_{1}\left|\begin{массив}{cc}
а_{2} и с_{2}\\
а_{3} и в_{3}
\end{массив}\right|+b_{2}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{3} и в_{3}
\end{массив}\right|-b_{3}\left|\begin{массив}{cc}
а_{1} и с_{1}\\
а_{2} и в_{2}
\конец{массив}\право|.
\end{align*}\] Опять же, обратите внимание на изменение знака. \end{align*}\]
\end{align*}\] \end{align*}\] Обратите внимание, что строка \(3\) строки \(B\) кратна строке \(1.\). В общем, когда строка кратна другой строке, определитель равен нулю . Также, если столбец кратен другому столбцу, определитель равен нулю.
\end{align*}\] Обратите внимание, что строка \(3\) строки \(B\) кратна строке \(1.\). В общем, когда строка кратна другой строке, определитель равен нулю . Также, если столбец кратен другому столбцу, определитель равен нулю. \end{выравнивание*}\]
\end{выравнивание*}\]