Как вычитать числа со степенями: Свойства степеней, действия со степенями

О степенях свободы в статистике / Хабр

В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.

Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?

По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.

Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:

Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:

Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0. 004.

Но почему n минус один?

Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?

В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:

“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.

Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?

Причем тут распределение Хи-квадрат Пирсона?

Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:

имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.

Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?

Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона.

Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:

Где O — наблюдаемые, E — ожидаемые частоты.

Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.

Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:

При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.

Пришло время вычесть единичку!

Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.

Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.

Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.

Все становится на свои места

Теперь, вооружившись этими знаниями, вернемся к t-тесту:

в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики.

Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.

Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.

Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.

Онлайн курсы по статистике: объясняем сложные темы простым языком

Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!

Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.

Одночлен

Поделиться решением

Произведение чисел, буквенных выражений и их степеней называется одночленом.

 – примеры одночленов.

Просто число, отдельная буква – тоже одночлен.

Приведение одночлена к стандартному виду

Предположим, дано выражение и необходимо привести этот одночлен к стандартному виду.

Для этого сначала записываем само число (16), потом ту букву, у которой была самая большая степень из представленных (), затем букву со степенью поменьше(), а далее – с самой маленькой степенью().

То есть одночлен будет выглядеть следующим образом: .

Разберём еще один пример, , в нём уже два числа, поэтому сначала умножим их

8 * 2 = 16.

Также тут несколько переменных «x» с разными степенями, также выполняем их умножение, используя свойства степеней.

Больше никаких действий выполнить нельзя, записываем одночлен в стандартном виде по правилам, сначала число 16, потом буква в старшей степени () , ну а затем в младшей().

Получим

Задание для самопроверки:

Запишите в стандартном виде:

Сложение и вычитание одночленов

Для того, чтобы понять, как выполняется сложение одночленов, рассмотрим пример:

23ab + 6ab

Мы видим, что и буквы и их степени полностью совпадают, в этом случае суммируем цифры, стоящие перед ними, а буквенную часть просто переписываем.

23ab + 6ab = (23 + 6)ab  = 29ab

Если же буквы или их степени отличались у слагаемых, складывать, да и вычитать их нельзя!

12x + 5y просчитать невозможно.

Теперь попробуем найти разность двух слагаемых, то есть вычесть одночлены, так как  совпадает у обоих выражений, действие выполнить можно:

11xz – 3xz = (11 – 3)xz = 8xz

Если же перед буквой не было никакого числа, то мы принимаем его за 1.

x = 1x

Задание для самопроверки:

Выполните сложение одночленов:

Выполните вычитание:

Умножение одночленов

Также как и числа, одночлены можно умножать.

Как же это делать правильно?

• Рассмотрим пример

В первую очередь, перемножим все имеющиеся числа, 2 * 2 * 7 = 4 * 7 = 28

Затем найдем одинаковые буквы и тоже найдем их произведение, пользуясь свойствами степеней.

После выполнения всех необходимых действий, запишем одночлен в стандартном виде.

• Еще один

Задание для самопроверки:

Выполните умножение одночленов:

Деление одночленов

Аналогично умножению, научимся выполнять деление одночленов на конкретном примере:

Разделим числа, 12 на 3

12 : 3 = 4

Затем найдем первую пару одинаковых букв, воспользуемся свойством деления степеней, основание оставим прежним, а степенные выражения вычтем

Также поступим и с другими буквами

Получили 

Задание для самопроверки:

Выполните деление одночленов:

Как складывать и вычитать многочлены — Криста Кинг Математика

Сложение и вычитание многочленов заключается в определении похожих членов

При сложении и вычитании многочленов вы просто ищете сходные члены для объединения. 1???.

Как складывать и вычитать многочлены

Пройти курс

Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Сложение многочленов, когда оба являются квадратичными

Пример

Упростите выражение. 92-10х+5???

Получить доступ к полному курсу Алгебра 1

Начать

Изучение математикиКриста Кинг 26 мая 2020 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, многочлены, сложение многочленов, вычитание многочленов, сложение и вычитание многочленов, объединение многочленов, подобные термины, объединение подобных термины, добавление подобных терминов, вычитание похожих терминов

0 лайков

Сложение и вычитание чисел в экспоненциальном представлении

Сложение или вычитание чисел в экспоненциальном представлении требует, чтобы числа имели сходные основания и показатели степени.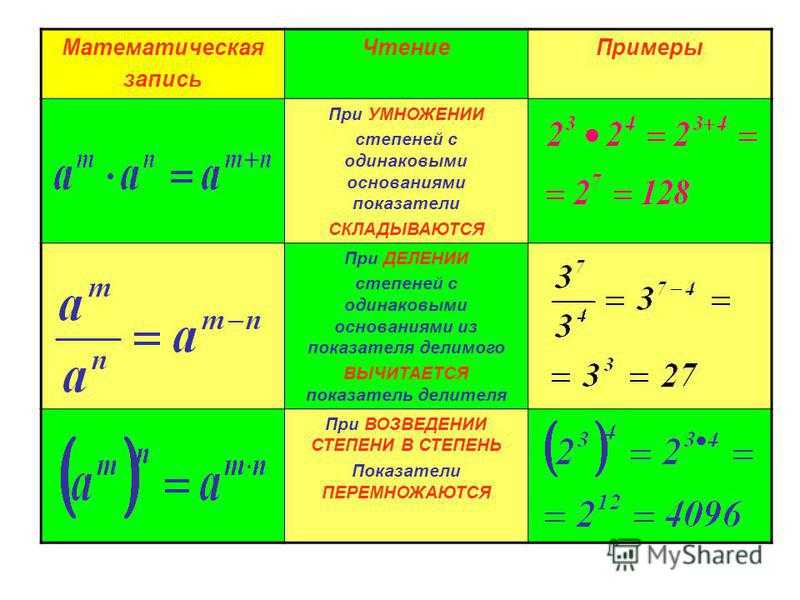 Это необходимо для того, чтобы соответствующие целые числа в своих коэффициентах имели одинаковое разрядное значение.

Добавление в экспоненциальном представлении с примерами

При добавлении чисел в экспоненциальном представлении необходимо выполнить несколько шагов:

1. Проверьте, равны ли степени чисел.
2. Если они равны, вынесите числа на множители, используя распределительное свойство умножения (a ^m x a ⁿ  = a ^{m + n} ).
3. Добавьте коэффициенты. Если они не равны, показатели степени должны быть равны путем перемещения десятичной точки. Самый простой способ сделать десятичные дроби равными — это сделать меньшую степень равной большей, сдвигая десятичную дробь влево.

Давайте разберемся с концепцией на нескольких примерах.

с равными показателями

Пример — 1

Добавить: (4,7 x 10 ³ ) + (1,89 x 10 ³ )

1. . распределительное свойство умножения; числа разложены, как показано ниже:

(4,7 x 10 ³ ) + (1,89 x 10 ³ )

(4,7 + 1,89) × 10 ³

• Adding the coefficients and multiplying by the power of 10, we get = 6.59 × 10 ³

Thus, the answer is 6.59 × 10 ³

With Unequal Exponents

Пример – 2

Добавить: (8,8 x 10 ³ ) + (6,25 x 10 ⁵ )

Здесь степени чисел разные. Таким образом, нам нужно манипулировать мощностью с большим показателем.

Используя свойство показателей степени:  а ^M x A ^N = A ^{M + N} , переписывание более крупного показателя 10 ⁵ в (10 ² × 10 ³ )

= (8,8 x 10 ³ ) (8.8 x 10 ³ ) (8.8 x 10 ³ ) + (8.8 x 10 ³ ) + (8. 8 x 10 ³ ). 6,25 x 10 ⁵ )

= (8,8 x 10 ³ ) + (6,25 x 10 ² × 10 ³ )

= (8,8 x 10 ³ ) + [(6.25 x 10 ² ) × 10 ³ ]

= (8,8 x 10 ³ ) + (625 × 10 ³ )

= (8,8 + 625) × 10 ³

Adding the coefficients and multiplying by the power of 10, we get

 = 633.8 × 10 ³

Thus, the answer is 633.8 × 10 ³

(3.769 x 10 ⁵ ) + (4,21 x 10 ⁵ )

Решение:

Эти два числа имеют одинаковые показатели степени
Используя распределительное свойство умножения; числа вынесены за скобки, как показано ниже:
(3,769 x 10 ⁵ ) + (4,21 х 10 ⁵ )
(3,769 + 4,21) х 10 ⁵
Складывая коэффициенты и умножая на степень 10, получаем = 7,979 х 10 ⁵ 3, таким образом, ответ IS 7,979 × 10 ⁵

Добавить: (5,5 x 10 ² ) + (1,25 x 10 ⁴ )

Решение:

Здесь. Таким образом, нам нужно манипулировать мощностью с большим показателем.
Используя свойство показателей: A ^M x A ^N = A ^{M + N} , переписывая более крупный показатель 10 ⁵ в (10 ² × 10 ³ )
= (5,5 x 1003 ² ) + (1,25 x 10 ⁴ )
= (5,5 x 10 ² ) + (6,25 x 10 ² × 10 ³ )
= (8,8 x 100102 3 ) + [((8,8 x 100102 3 ) + 6,25 х 10 ² ) х 10 ³ ]
= (8,8 х 10 ³ ) + (625 х 10 ³ )
= (8,8 + 625) х 10 ³
Складывая коэффициенты и умножая на степень 10, получаем
 = 633,8 × 10 ³
Таким образом, ответ равен 633,8 × 10 ³

Вычитание в научной нотации с примерами 9 вычитание двух или более чисел в экспоненциальном представлении такое же, как сложение, за исключением того, что сложение заменяется вычитанием.

Рассмотрим несколько примеров.

С равными показателями

Пример – 1

Вычесть: (4 x 10 ^-2 ) – (2,89 x 10 ^-2 )

1. Эти два числа имеют сходное свойство дистрибутивности

   ; числа разлагаются, как показано ниже:

= (4,4 x 10 ² ) – (2,89 x 10 ² )

= (4,4 – 2,89) × 10 ^{2 9091038 и сложение коэффициентов умножая на степень 10, получаем = 1,51×10 2}

Таким образом, ответ составляет 1,51 × 10 ²

с неравными показателями

Пример — 2

Подряд: (7.35 x 10 ^{7903) — 5.8. 4} )

Здесь степени чисел разные. Таким образом, нам нужно манипулировать мощностью с большим показателем.

Используя свойство показателей степени: a ^m x a ⁿ  = a ^{m + n} , переписав больший показатель степени 10 ⁷ в (10 ³ × 10 ⁴ )

= (7,35 x 10 ⁷ ) — (5,8 x 10 ⁴ )

= (7,35 x 10 ³ × 10 ⁴

= (7,35 x 10 ³ × 10 ⁴

= (7,35 x 100102 3 × ⁴

. ) — (5,8 x 10 ⁴ )

= [(7,35 x 10 ³ ) × 10 ⁴ ] — (5,8 x 10 ⁴ )

= (7350 × 10 ⁴ ) — ( 5,8 х 10 ⁴ )

= (7350 – 5,8) × 10 ⁴

Складывая коэффициенты и умножая на степень 10, получаем = 7344,2 × 10 ⁴

Та. два числа имеют одинаковые показатели степени
Использование дистрибутивного свойства умножения; числа разлагаются на множители, как показано ниже:
= (6 x 10 ⁵ ) – (4,49 x 10 ⁵ )
= (6 – 4,49) × 10 ⁵
Складывая коэффициенты и умножая на степень 10, получаем = 1,51×10 ⁵
Thus, the answer is 1.51 × 10 ⁵

Subtract: (3.25 x 10 ⁵ ) – (9.8 x 10 ² )

Solution:

Here, степени чисел разные. Таким образом, нам нужно манипулировать мощностью с большим показателем.