Как выглядят острые тупые и прямые углы: Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный

Содержание

Классифицирующие углы как острые, тупые, правые или рефлексы

пропустить до контента

Опубликованы на по математике с мамой

классификационные углы как острые, тупые, правые или рефлексы

Примервидеокетские

. Поделиться в Google Классе

Углы классифицируются по количеству градусов, которые они содержат.
Острый угол меньше 90°.
Прямой угол равен ровно 90°.
Тупой угол больше 90°, но меньше 180°.
Прямая линия составляет ровно 180°.
Угол рефлекса больше 180°, но меньше 360°
Полный оборот равен точно 360°

Измерьте величину угла в градусах и сравните это значение с таблицей выше, чтобы решить, к какой категории он относится в. .

Первый угол равен 315°, что находится между 180° и 360°. Это рефлекторный угол.

Второй угол равен ровно 90°. Это прямой угол.
Третий угол равен ровно 360°. Это полный оборот.
Четвертый угол равен ровно 180°. Это прямая линия.
Пятый угол равен 150°, что находится между 90° и 180°. Это тупой угол.
Конечный угол равен 40°, что меньше 90°. Это острый угол.

Классификация углов Рабочие листы и ответы

Какие бывают виды углов?

Существует 7 основных различных типов углов:

Нулевые углы
Острые углы
Прямые углы
Тупые углы
Прямые линии
Полные обороты

Тип уголка	Размер в градусах
Нулевой угол	Ровно 0°
Острый угол	Меньше 90°
Прямоугольный	Ровно 90°
Тупой угол	Больше 90° и меньше 180°
Прямоугольный	Ровно 180°
Угол рефлекса	Больше 180° и меньше 360°
Полный оборот	Ровно 360°

Как классифицировать угол

Чтобы классифицировать угол, сначала измерьте его размер в градусах. Затем сравните этот угол со следующими значениями:

Если угол меньше 90°, то это острый угол.
Если угол равен 90°, то это прямой угол.
Если угол находится в диапазоне от 90° до 180°, это тупой угол.
Если угол равен 180°, это прямая линия.
Если угол ровно 360°, то это полный оборот.

Хотя вы можете поворачиваться на угол, превышающий 360°, нового названия для угла, превышающего 360°, не существует.

Например, поворот на 360° — это один полный оборот, а полный поворот на 720° — два полных оборота, потому что 2 партии по 360° — это 720°.

Вот сводная таблица различных типов углов.

Вот несколько примеров определения типов углов.

Угол в левом верхнем углу равен 315°. Этот угол больше 180°, но меньше 360°. Это означает, что он открывается шире, чем прямая линия, но это не совсем полный оборот. Угол является рефлекторным углом.

Угол в правом верхнем углу показывает поворот, который полностью вернулся к тому месту, где он начался.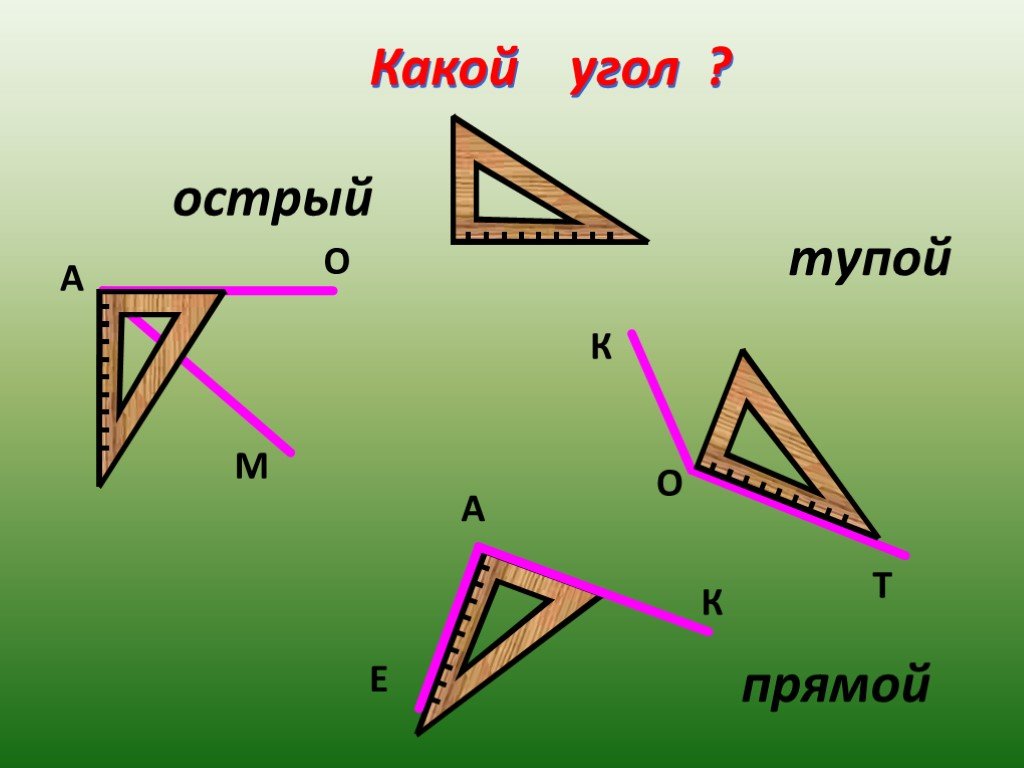 Он показывает полный оборот. Полный оборот составляет 360°.

Угол посередине прямой. Это потому, что это ровно 90°. Он также отмечен квадратом в углу угла, который говорит нам, что это прямой угол.

Угол в левом нижнем углу представляет собой прямую линию. Прямые линии составляют ровно 180°.

Угол в нижней середине равен 150°. 150° больше 90°, но меньше 180°. Он больше прямого угла, но не так велик, как прямой угол. Это тупой угол.

Угол в правом нижнем углу равен 40°. 40° меньше 90°, значит, этот угол острый.

Вот еще один пример классификации угла.

Этот угол равен 60°.

Этот угол меньше 90°, поэтому этот угол классифицируется как острый угол.

Кроме нулевого угла, нет меньшего угла, чем острый угол. Поскольку нулевые углы выглядят как прямая линия, с ними трудно работать, и они обычно не встречаются в типичных вопросах классификации углов.

Вот еще один пример определения типа угла.

Здесь у нас есть угол 280°.

280° больше прямого угла 180° и меньше полного оборота 360°. Это рефлекторный угол.

Важно убедиться, что вы измеряете правильный угол при измерении углов рефлекса. Мы измеряем отмеченную стрелку, показанную красным на схеме. Мы повернулись вокруг прямой линии, чтобы добраться до этой точки.

Острые углы

Острые углы относятся к любому углу, который меньше 90°. Это означает, что острый угол меньше прямого угла.

Вот несколько примеров острых углов.

При обучении острым углам мы можем помнить, что это наименьший тип классификации углов, и поэтому они являются «симпатичными» углами. Связывание идеи быть маленьким и милым может сделать это имя легко запоминающимся.

Острые углы наряду с прямыми углами, вероятно, являются самыми простыми типами углов для изучения в первую очередь, потому что они чаще всего встречаются в повседневной жизни.

Прямые углы

Прямые углы равны ровно 90°. Они составляют четверть полного оборота и показаны квадратиком в углу угла.

Прямые углы обычно встречаются в доме, например, на углах столов, полок, книг и коробок. По этой причине они могут быть одним из самых простых типов углов для обучения в первую очередь.

Название прямого угла первоначально происходит от латинского слова «angulus rectus». Rectus означает прямой. При измерении от горизонтального положения прямой угол является вертикальным, отсюда и название прямого угла.

Тупые углы

Тупой угол больше 90°, но меньше 180°. Следовательно, тупой угол больше прямого, но не такой большой, как прямой.

Вот несколько примеров тупых углов.

Типичным примером тупого угла в реальной жизни является кончик крыши дома.

Прямые уголки

Прямой угол равен ровно 180° и называется так, потому что выглядит как прямая линия. Когда объект вращается под прямым углом, он повернулся на 180° и, следовательно, изменил свое первоначальное направление.

Вот фото прямого угла.

Прямой угол, или прямая, должны быть ровно 180. Если чуть больше или меньше этого, то в углу угла будет отклонение и это не будет прямой линией.

Прямые линии встречаются повсюду, и детям может быть трудно думать о прямых углах как об углах, а не как о линиях. Чтобы обучать прямолинейным углам, полезно отметить центр прямой линии как угол угла. Также полезно показать угол поворота между 179° и 181°. Между ними должно быть 180°.

Рефлекторные углы

Углы рефлекса больше 180° и меньше 360°. Это означает, что рефлекторные углы открываются шире, чем прямая линия, но недостаточно велики, чтобы совершить полный оборот.

Вот несколько примеров рефлекторных углов.

Рефлекторные углы иногда путают по названию с тупыми углами. Это два наиболее часто путаемых названия при обучении классификации углов. При обучении полезно показывать примеры как рефлекторных, так и тупых углов.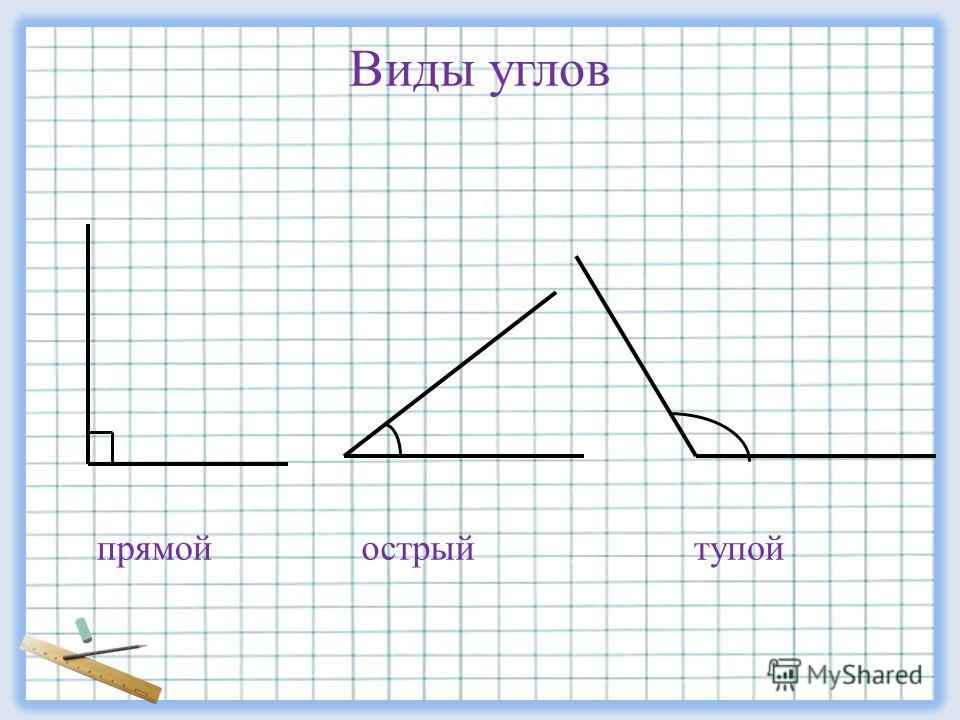

Полные обороты

Полный оборот составляет ровно 360°. После завершения полного поворота объект смотрит в том же направлении, что и изначально.

Вот схема, показывающая полный оборот.

Полные повороты иногда трудно нарисовать или объяснить, поскольку два плеча угла находятся непосредственно друг над другом.

Теперь попробуйте наш урок на Почему углы в треугольнике Добавьте к 180 градусам , где мы узнаем об углах в треугольнике.

: Контент защищен !!

Обсуждение углов

Обсуждение углов

Наставник: Сегодня мы будем изучать углы.

Студент: Я знаю, что такое угол! Это два луча, соединенные вместе.

Наставник: Хорошая работа! Вы прочитали это из своей книги?

Студент: Да.

Наставник: Ну, есть три категории углов: острый, тупой и верно.

Давайте сначала узнаем, что такое прямой угол. Прямые углы присутствуют во многих местах в реальной жизни. Посмотрите на углы этой комнаты или края ваших книг. Прямой угол – это угол, равный 90 градусов. Прямой угол выглядит так:

Наставник: Второй тип угла — острый. Острый угол – это угол, градусная мера которого менее 90 градусов. Острый угол выглядит так:

Студент: Дайте угадаю! Третий тип – это угол, градусная мера которого больше 90 градусов.

Наставник: Да, и название того угла тупое. Тупой угол выглядит так:

Наставник: У нас также есть имена для пар углов. Углы образуются при пересечении прямых. Рассмотрим углы, образованные двумя параллельными линии пересекает третья линия, называемая секущей . На этом рисунке красные линии параллельны, а синяя — поперечна.

Студент: Эти линии образовали 8 углов.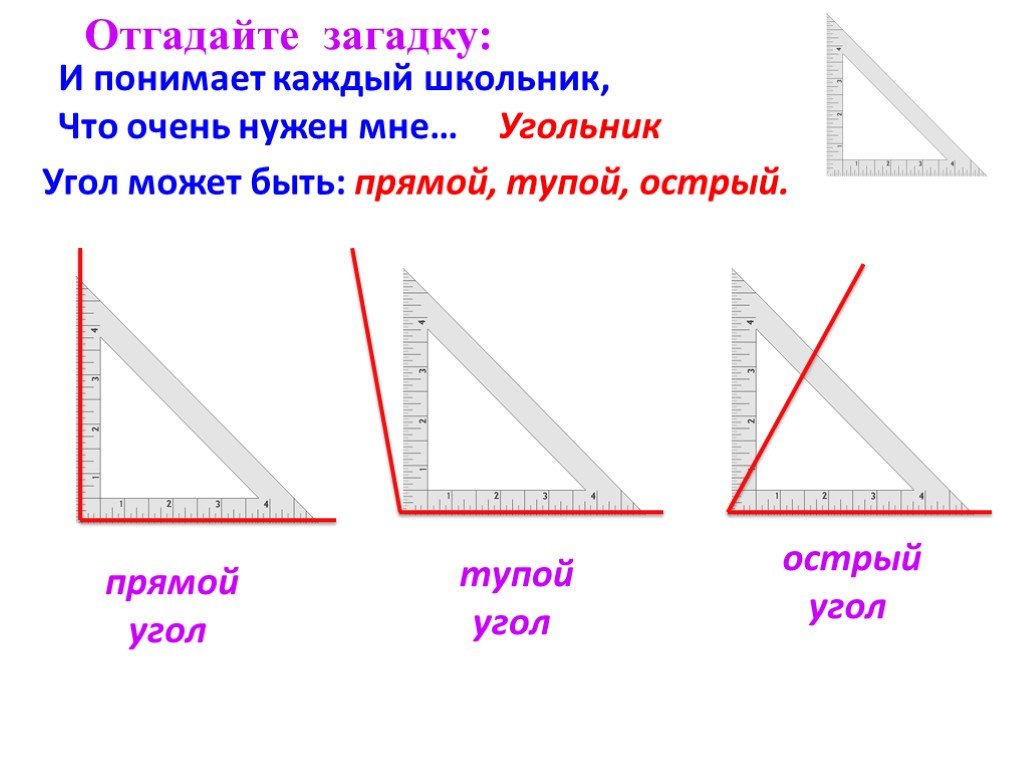

Наставник: Хорошая работа. А кто мне покажет острый угол?

Студент: Я могу! Это тот, что справа вверху.

Наставник: Опять верно. Кто может показать мне тупой угол?

Ученик 2: Кажется, тот, что слева вверху.

Наставник: Правильно. Нам нужен более простой способ обозначения углов, о которых мы говорим. Итак, с этого момента мы будем обозначать наши углы. Углы а и b равны смежные углы.

Наставник: Углы f и h также являются смежными углами. Кто-нибудь знает, что это означает, что пара углов должна быть смежной?

Студент: Значит ли это, что они рядом?

Mentor: Да, смежные углы — это углы, у которых есть общий луч. Кто-нибудь может подскажите еще пару углов, которые являются смежными?

Студент: Да, углы c и d смежные.

Студент2: Я тоже могу; углы b и d смежные.

Наставник: Хорошая работа, углы c и d смежные, а также углы b и d.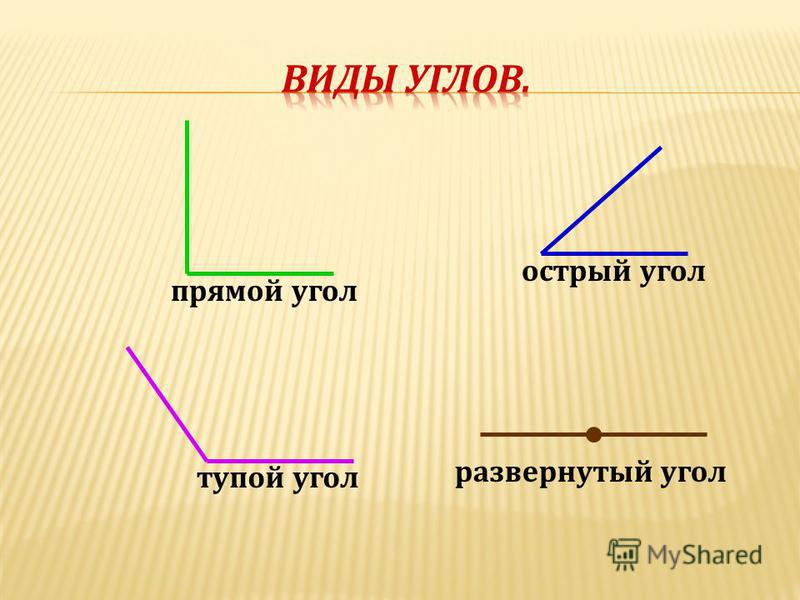 Там на рисунке много пар смежных углов. Теперь давайте поговорим о вертикальные углы. Углы а и d являются вертикальными углами.

Наставник: Углы f и g также являются вертикальными углами. Кто-нибудь может догадаться, что это значит чтобы пара углов была вертикальной?

Студент: Являются ли вертикальные углы противоположными друг другу?

Наставник: Хорошая работа! Вертикальные углы имеют только одну общую точку. Эта точка называется вершиной. Может ли кто-нибудь назвать другую пару вертикальных углов?

Студент 2: Я могу; углы b и c являются вертикальными углами.

Студент: Углы e и h также являются вертикальными углами.

Наставник: Да, углы b и c являются вертикальными углами, как и углы e и ч. Теперь, когда мы знаем, что такое смежный и вертикальный углы, давайте поговорим о альтернативные внутренние углы. Углы c и f равны альтернативные внутренние углы.

Наставник: Углы d и e также являются альтернативными внутренними углами.