Как выразить одну переменную через другую? Как выразить переменную из формулы?
Этот урок — полезное дополнение к предыдущей теме «Тождественные преобразования уравнений».
Умение делать такие вещи — штука не просто полезная, она — необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях — как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула — это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и тождественные преобразования уравнений. Вот и применяем их в удобном нам порядке и — готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка — для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
3x — 2y = 5
Здесь две переменные — икс и игрек.
Допустим, нас просят выразить x через y.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа — что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
3x – 2y = 5
Здесь нам мешаются тройка перед иксом и —2y.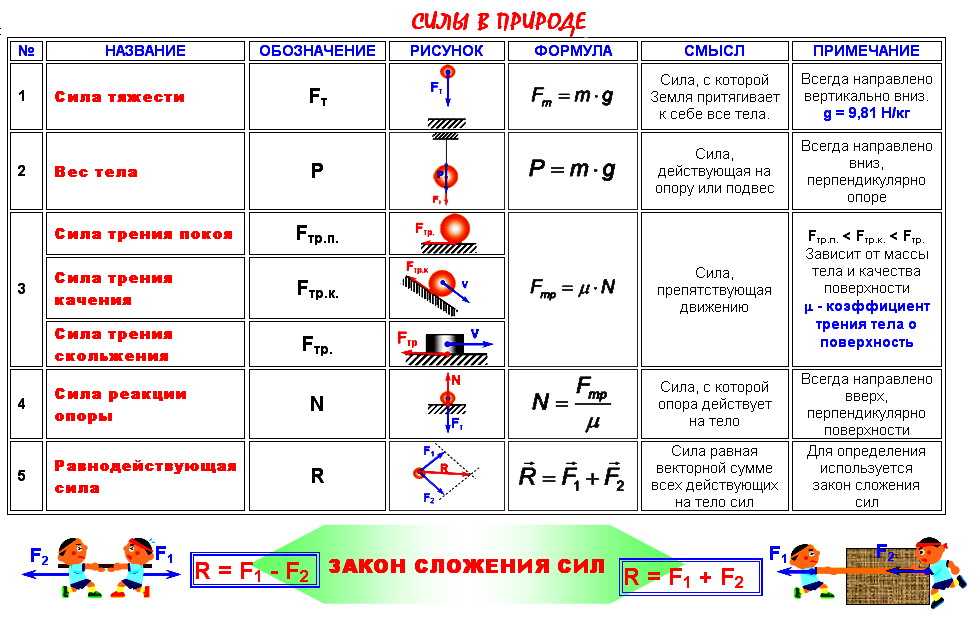
Начнём с —2у, это попроще будет.
Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
3x = 5 + 2y
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и делим:
Вот и всё. Мы выразили икс через игрек. Слева — чистый икс, а справа — что уж получилось в результате «очищения» икса.
Можно было бы сначала поделить обе части на тройку, а затем — переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем.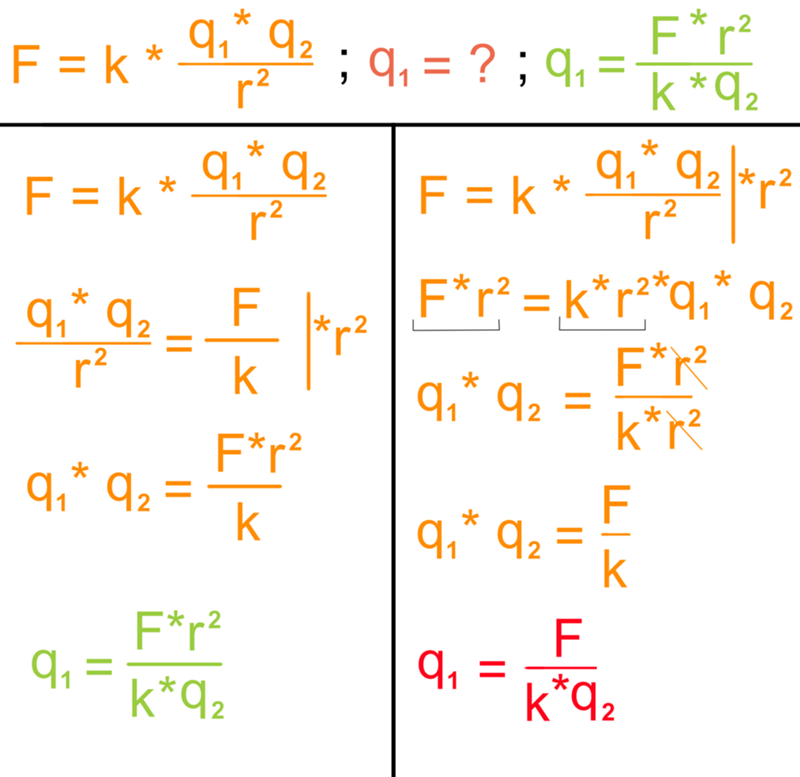
Самое главное — не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
3x – 2y = 5
выразить y через x?
А почему — нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:
–2y = 5 — 3x
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула — тоже уравнение.
Например, такое задание:
Из формулы
выразить переменную с.
Формула — тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа — что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.
Получим:
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби — нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать.
Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с — скорость звука в воде,
f0 — частота испускаемых импульсов (в МГц),
f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы — это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы.
Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там — видно будет. Для этого применяем второе преобразование — умножаем обе части на знаменатель.
Получим:
А вот тут — очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с. Что и выражается скобками в правой части.
)
А вот теперь скобки и раскрыть можно:
Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f — справа. Займёмся переносом:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем. Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v—c) и — дело в шляпе!
В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно «причесать» полученное выражение — вынести f0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Ответ: 751 МГц
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Простенькая задачка:
Из формулы
выразить переменную а и найти её значение при S=300, V0=20, t=10.
Задачка посложнее:
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V1 и V2 — средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с-1), а R — радиус окружности.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы — это как-нибудь сами…)
Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Кинематика
- Динамика
- Статика
- Гидростатика
- Импульс
- Работа, мощность, энергия
- Молекулярная физика
- Термодинамика
- Электростатика
- Электрический ток
- Магнетизм
- Колебания
- Оптика
- Атомная и ядерная физика
- Основы специальной теории относительности (СТО)
- Равномерное движение по окружности
- Расширенная PDF версия документа «Все главные формулы по школьной физике»
Кинематика
К оглавлению.
..
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
К оглавлению.
..
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса.
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ).
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы.
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения.
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A.
Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1.
В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т.
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению.
..
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом.
Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению.
..
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом.
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т.
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению.
..
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению.
..
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению.
..
Преобразование номера столбца в букву с помощью формулы в Excel
Советы и руководства по Excel
Редактировать
Добавить в избранное Избранное
Автор: дон
Курс макросов Excel и VBA (скидка 80 %)
Как получить букву столбца из числа в Excel с помощью простой формулы.
Это важно уметь делать при работе со сложными формулами в Excel, особенно с функцией ДВССЫЛ().
Разделы:
Основная формула — работает для всех столбцов
Более сложная формула — работает для всех столбцов
Примечания
Основная формула — работает для всех от А до Я
Формула:
=СИМВОЛ(64+A1)
A1 — это ячейка, содержащая номер столбца, для которого вы хотите получить букву.
Результат:
Вы также можете записать эту формулу следующим образом:
=СИМВОЛ(64+10)
Вам просто нужно ввести номер столбца непосредственно в формулу.
Функция CHAR() получает букву на основе ее номера, определенного набором символов вашего компьютера; однако вам не нужно знать это, чтобы использовать эту функцию.
Использование COLUMN()
Если вы создаете динамическую формулу, вы можете захотеть автоматически определить букву определенного столбца для использования в другой функции, например в функции ДВССЫЛ().
В этом случае вы можете использовать функцию COLUMN() для получения номера определенного столбца или текущего столбца:
=СИМВОЛ(64+СТОЛБЦ(A1))
Это позволит получить букву столбца для ячейки A1, то есть A.
Удалите ссылку на ячейку из функции COLUMN(), и вы получите букву текущего столбца.
=СИМВОЛ(64+СТОЛБЦ())
Результат:
Однако помните, что это будет работать только для столбцов от A до Z, а в некоторых случаях это может не работать в зависимости от локализованных настроек компьютера. Следующий пример не имеет этих ограничений.
Более сложная формула — работает для всех столбцов
Этот пример является более универсальным, поскольку он работает для всех столбцов в Excel, но он несколько сложнее.
Формула:
=ПОДСТАВИТЬ(АДРЕС(1,A3,4),"1","")
A3 — это примерная ячейка, которая содержит номер столбца, для которого мы хотим получить букву (буквы).
Результат:
Эта формула использует функции ПОДСТАВИТЬ() и АДРЕС() для получения букв столбца. Это изящный маленький трюк, который позволяет вам получить буквы для любого столбца, используя только число в качестве ссылки для него.
Функция АДРЕС() дает нам адрес ячейки на основе номера столбца и строки, а функция ПОДСТАВИТЬ() заменяет числовую часть ссылки на ячейку ничем, что удаляет номер. Если вы хотите увидеть это в Excel, просто разделите эти две функции на отдельные ячейки и посмотрите на результаты:
Использование COLUMN()
(это почти то же самое, что и раздел COLUMN() выше, только с новой формулой)
Если вы создаете динамическую формулу, вы можете захотеть автоматически определить букву определенный столбец для использования в другой функции, такой как функция ДВССЫЛ().
В этом случае вы можете использовать функцию COLUMN() для получения номера определенного столбца или текущего столбца:
=ПОДСТАВИТЬ(АДРЕС(1,СТОЛБЦ(A3),4),"1","")
Это позволит получить букву столбца для ссылки на ячейку A1, то есть A.
Вы также можете удалить ссылку на ячейку из функции COLUMN(), чтобы получить буквы для столбца в котором в данный момент находится формула.
=ПОДСТАВИТЬ(АДРЕС(1,СТОЛБЦ(),4),"1","")
Это вернет D, потому что формула находится в столбце D.
Эти последние два примера могут показаться тривиальными, но они очень полезны, когда вы копируете формулу в ячейку и столбец, которые неизвестны, поскольку вы не знаете, в каком столбце будет формула, когда она будет использована или скопирована.
Примечания
Это мощная вещь, которую можно сделать в Excel, получить букву (буквы) столбца из их номера. Вы не будете использовать это каждый день, и это может не помочь базовым пользователям Excel, но для всех вас, кто хочет или должен поднять Excel на следующий уровень, сохраните это руководство, особенно для второй формулы, той, которая использует ПОДСТАВИТЬ () и АДРЕС().
Обязательно загрузите прилагаемую книгу, чтобы работать с этими примерами в Excel.
Функция Excel: АДРЕС(), СИМВОЛ(), СТОЛБЦ(), ПОДСТАВИТЬ()
Версия Excel: Эксель 2003, Эксель 2007, Эксель 2010, Эксель 2013, Эксель 2016
Курс Excel VBA — от новичка до эксперта
200+ видеоуроков 50+ часов обучения Более 200 руководств Excel Станьте мастером VBA и макросов в Excel и узнайте, как автоматизировать все свои задачи в Excel с помощью этого онлайн-курса.
(Опыт работы с VBA не требуется.)
Посмотреть курс
Аналогичный контент на TeachExcel
Преобразование названия месяца в число и наоборот в Excel
Учебник: как преобразовать название месяца, например, январь, в число с помощью формулы в Excel; аль…
Функция ROMAN() и ARABIC() в Excel
Руководство:
Преобразование римских цифр в обычные числа (арабские), а также как преобразовать обычные числа…
5 советов по оценке сложных формул в Excel
Активировать или перейти к рабочему листу с помощью макросов VBA в Excel
Учебное пособие. Сделайте определенный рабочий лист видимым с помощью макроса в Excel.
Это называется активировать wo…
Возврат минимального или максимального значения с помощью поиска в Excel — ПОИСКПОЗ ПО ИНДЕКСУ
Руководство:
Найдите минимальное или максимальное значение в диапазоне и на его основе верните значение из другого диапазона.
..
Получить день недели (от 1 до 7) для даты в Excel — WEEKDAY
Учебник: используйте функцию в Excel, чтобы получить номер дня в неделе от 1 до 7.
Это позволяет…
Подпишитесь на еженедельные уроки
БОНУС: подпишитесь сейчас, чтобы загрузить нашу электронную книгу Top Tutorials!
Детали руководства
Функция Excel:
АДРЕС(), СИМВОЛ(), СТОЛБЦ(), ПОДСТАВИТЬ()Версия Excel: Эксель 2003, Эксель 2007, Эксель 2010, Эксель 2013, Эксель 2016
Курс Excel VBA — от новичка до эксперта
200+ видеоуроков
50+ часов видео
Более 200 руководств Excel
Станьте мастером VBA и макросов в Excel и узнайте, как автоматизировать все свои задачи в Excel с помощью этого онлайн-курса.
(Опыт работы с VBA не требуется.)
Посмотреть курс
Как преобразовать номер столбца Excel в букву
В этом руководстве мы рассмотрим, как изменить номера столбцов Excel на соответствующие буквенные символы.
При построении сложных формул в Excel иногда может потребоваться получить букву столбца определенной ячейки или из заданного числа. Это можно сделать двумя способами: используя встроенные функции или пользовательскую.
Как преобразовать номер столбца в алфавит (однобуквенные столбцы)
Если имя столбца состоит из одной буквы от A до Z, вы можете получить его, используя эту простую формулу:
СИМВОЛ(64 + col_number )
Например, чтобы преобразовать число 10 в букву столбца, используйте следующую формулу:
=СИМВОЛ(64 + 10)
Также можно ввести число в какую-либо ячейку и ссылаться на эту ячейку в формуле:
=СИМВОЛ(64 + A2)
Как работает эта формула:
Функция CHAR возвращает символ на основе кода символа в наборе ASCII.
Значения ASCII заглавных букв английского алфавита от 65 (A) до 9.0 (З). Итак, чтобы получить код заглавной буквы A, вы добавляете 1 к 64; чтобы получить код символа верхнего регистра B, вы добавляете 2 к 64 и так далее.
Как преобразовать номер столбца Excel в букву (любой столбец)
Если вы ищете универсальную формулу, которая работает для любого столбца в Excel (1 буква, 2 буквы и 3 буквы), вам нужно использовать немного более сложный синтаксис:
ПОДСТАВИТЬ (АДРЕС (1, col_number , 4), «1», «»)
С буквой столбца в A2 формула принимает следующий вид:
=ЗАМЕНИТЬ(АДРЕС(1, A2, 4), "1", "")
Как работает эта формула:
Сначала вы создаете адрес ячейки с номером интересующего столбца. Для этого предоставьте функции АДРЕС следующие аргументы:
.- 1 для row_num (номер строки особого значения не имеет, поэтому можно использовать любой).
- A2 (ячейка, содержащая номер столбца) для column_num .
- 4 для абс_номер аргумент для возврата относительной ссылки.
С указанными выше параметрами функция АДРЕС возвращает в качестве результата текстовую строку «A1».
Поскольку нам нужна только буква столбца, мы удаляем номер строки с помощью функции ПОДСТАВИТЬ, которая ищет «1» (или любой другой номер строки, который вы жестко закодировали в функции АДРЕС) в тексте «А1» и заменяет его на пустая строка («»).
Получить букву столбца из номера столбца с помощью пользовательской функции Пользовательская функция
Если вам необходимо регулярно преобразовывать номера столбцов в алфавитные символы, пользовательская пользовательская функция (UDF) может значительно сэкономить ваше время.
Код функции довольно простой и понятный:
Общедоступная функция ColumnLetter (col_num) Буква столбца = Разделить (Ячейки (1, номер_столбца). Адрес, «$») (1) Конечная функция
Здесь мы используем свойство Cells для ссылки на ячейку в строке 1, указанный номер столбца и Свойство Address для возврата строки, содержащей абсолютную ссылку на эту ячейку (например, $A$1).
Затем функция Split разбивает возвращаемую строку на отдельные элементы, используя знак $ в качестве разделителя, и мы возвращаем элемент (1), который является буквой столбца.
Вставьте код в редактор VBA, и ваша новая функция ColumnLetter готова к использованию. Подробное руководство см. в разделе Как вставить код VBA в Excel.
С точки зрения конечного пользователя, синтаксис функции очень прост:
ColumnLetter(col_num)
Где col_num — это номер столбца, который вы хотите преобразовать в букву.
Ваша реальная формула может выглядеть следующим образом:
= Буква столбца (A2)
И он вернет точно такие же результаты, как и встроенные функции Excel, рассмотренные в предыдущем примере:
Как получить букву столбца определенной ячейки
Чтобы определить букву столбца конкретной ячейки, используйте функцию СТОЛБЦ, чтобы получить номер столбца, и передайте этот номер функции АДРЕС.
Полная формула примет следующий вид:
ПОДСТАВИТЬ (АДРЕС (1, СТОЛБЦ ( адрес_соты ), 4), «1», «»)
В качестве примера найдем букву столбца ячейки C5:
=ЗАМЕНИТЬ(АДРЕС(1, СТОЛБЦ(C5), 4), "1", "")
Очевидно, результат «C» 🙂
Как получить букву столбца текущей ячейки
Для вычисления буквы текущей ячейки формула почти такая же, как в приведенном выше примере. Единственное отличие состоит в том, что функция COLUMN() используется с пустым аргументом для ссылки на ячейку, в которой находится формула:
=ПОДСТАВИТЬ(АДРЕС(1, СТОЛБЦ(), 4), "1", "")
Как создать ссылку динамического диапазона из столбца номер
Надеюсь, предыдущие примеры дали вам новые темы для размышлений, но вас могут интересовать практические применения.
В этом примере мы покажем вам, как использовать формулу «число столбцов в букву» для решения реальных задач. В частности, мы создадим динамическую формулу XLOOKUP, которая будет извлекать значения из определенного столбца на основе его номера.
Предположим, что вы хотите получить показатель прибыли для данного проекта (h3) и недели (h4).
Для выполнения задачи необходимо указать XLOOKUP диапазон, из которого возвращаются значения. Поскольку у нас есть только номер недели, соответствующий номеру столбца, мы сначала преобразуем этот номер в букву столбца, а затем создадим ссылку на диапазон.
Для удобства разобьем весь процесс на 3 простых шага.
- Преобразование номера столбца в букву
С номером столбца в h4 используйте уже знакомую формулу, чтобы изменить его на буквенный символ:
=ЗАМЕНИТЬ(АДРЕС(1, h4, 4), "1", "")Совет. Если число в вашем наборе данных не соответствует номеру столбца, обязательно внесите необходимые исправления. Например, если бы у нас были данные за неделю 1 в столбце B, данные за неделю 2 в столбце C и т. д., мы бы использовали h4+1, чтобы получить правильный номер столбца.
- Создание строки, представляющей ссылку на диапазон
Чтобы создать ссылку на диапазон в виде строки, вы объединяете букву столбца, возвращаемую приведенной выше формулой, с номерами первой и последней строки.
. В нашем случае ячейки данных находятся в строках с 3 по 8, поэтому мы используем следующую формулу:=ЗАМЕНИТЬ(АДРЕС(1, h4, 4), "1", "") & "3:" & ПОДСТАВИТЬ(АДРЕС(1, h4, 4), "1", "") & "8"Учитывая, что h4 содержит «3», которая преобразуется в «C», наша формула претерпевает следующее преобразование:
="С"&"3:"&"С"&"8"И создает строку C3:C8.
- Создание эталона динамического диапазона
Чтобы преобразовать текстовую строку в действительную ссылку, которую может понять Excel, вложите приведенную выше формулу в функцию ДВССЫЛ, а затем передайте ее аргументу 3 rd функции XLOOKUP:
.=XLOOKUP(h3, E3:E8, INDIRECT(h5), "Не найдено")Чтобы избавиться от лишней ячейки, содержащей строку возвращаемого диапазона, вы можете поместить формулу ПОДСТАВИТЬ АДРЕС в саму функцию ДВССЫЛ:
=XLOOKUP(h3, E3:E8, INDIRECT(ПОДСТАВИТЬ(АДРЕС(1, h4, 4), "1", "") & "3:" & ПОДСТАВИТЬ(АДРЕС(1, h4, 4), "1 ", "") & "8"), "Не найдено")
В нашем случае ячейки данных находятся в строках с 3 по 8, поэтому мы используем следующую формулу:С нашей пользовательской функцией ColumnLetter вы можете получить более компактное и элегантное решение:
=XLOOKUP(h3, E3:E8, INDIRECT(ColumnLetter(h4) & "3:" & ColumnLetter(h4) & "8"), "Not found")
Вот как найти букву столбца из число в экселе.