Как выразить из формулы одну величину через другие онлайн: Выразить переменную из уравнения | Онлайн калькулятор

Как выразить одну переменную через другую? Как выразить переменную из формулы?

        Этот урок — полезное дополнение к предыдущей теме «Тождественные преобразования уравнений».

        Умение делать такие вещи — штука не просто полезная, она — необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях — как базовом, так и профильном.

        Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.

        Удивляемся, но запоминаем:

        Любое равенство с буквами, любая формула — это ТОЖЕ УРАВНЕНИЕ!

        А где уравнение, там автоматически и тождественные преобразования уравнений. Вот и применяем их в удобном нам порядке и — готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка — для вас.

        Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.

        Начнём с простого.

 

Как выразить одну переменную через другую?

        Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:

        3x — 2y = 5

        Здесь две переменные — икс и игрек.

        Допустим, нас просят выразить x через y.

        Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа — что уж получится.

        И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.

        Анализируем левую часть уравнения:

        3x – 2y = 5

        Здесь нам мешаются тройка перед иксом и —2y. Начнём с —2у, это попроще будет.

        Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:

        3x = 5 + 2y

        Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.

        Вот и делим:

        

        Вот и всё. Мы выразили икс через игрек. Слева — чистый икс, а справа — что уж получилось в результате «очищения» икса.

        Можно было бы сначала поделить обе части на тройку, а затем — переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.

        Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное — не порядок применения тождественных преобразований, а их правильность!

        А можно из этого же равенства

        3x – 2y = 5

        выразить y через x?

        А почему — нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.

        Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:

        –2y

= 5 — 3x

        Осталась двойка с минусом. Делим обе части на (-2):

        И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.

 

Как выразить переменную из формулы?

        Не проблема! Точно так же! Если понимать, что любая формула — тоже уравнение.

 

        Например, такое задание:

        Из формулы

        

        выразить переменную с.

        Формула — тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа — что уж получится, то и получится…

        Однако… Как нам эту самую с вытаскивать-то?

        Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.

        Получим:

        

        Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби — нету и числителя.) Умножаем обе части формулы на 2:

        

        Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:

        

       Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и — ответ готов:

        

      

        Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:

        Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле

        

        где с = 1500 м/с — скорость звука в воде,

        f₀ — частота испускаемых импульсов (в МГц),

        f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).

        Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.

       

        «Многа букафф», да… Но буквы — это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:

        

        Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там — видно будет. Для этого применяем второе преобразование — умножаем обе части на знаменатель.

        Получим:

        

        А вот тут — очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)

        Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…

        Справа же, после умножения, дробь исчезла и остался одинокий числитель.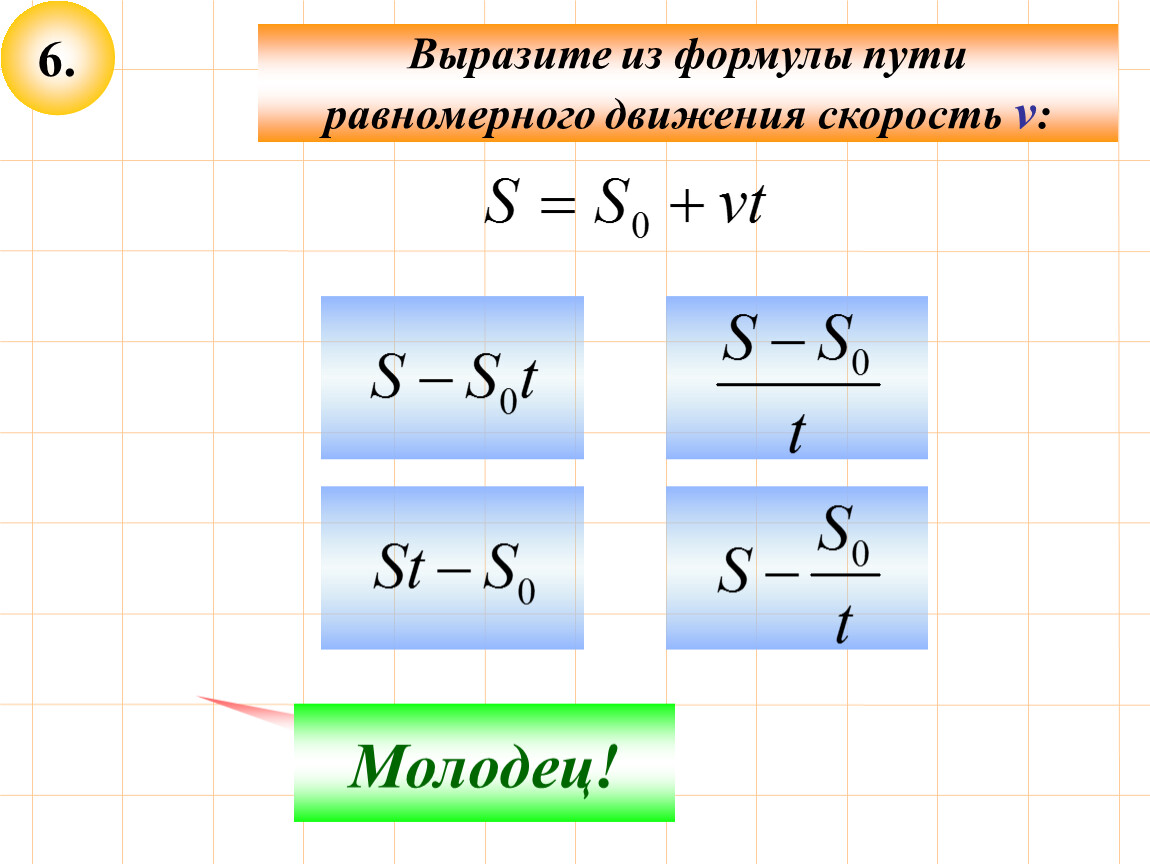 Который, опять же, весь

целиком умножается на буковку с. Что и выражается скобками в правой части.)

        А вот теперь скобки и раскрыть можно:

        

        Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f — справа. Займёмся переносом:

        

        Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем. Выносим её за скобки:

        

        Осталось всего ничего. Делим обе части на скобку (v—c) и — дело в шляпе!

        

        В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно «причесать» полученное выражение — вынести f₀ за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:

        

        Вот такое выражение. А вот теперь и числовые данные подставить можно.

Получим:

        

        Ответ: 751 МГц

 

        Вот и всё. Надеюсь, общая идея понятна.

        Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.

 

        В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях. 

        Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны

.

        Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…

        Подобные преобразования будут рассматриваться в соответствующих темах.

        А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.

 

        Простенькая задачка:

        Из формулы

        

        выразить переменную а и найти её значение при S=300, V₀=20, t=10.

 

        Задачка посложнее:

        Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:

        

        где V₁ и V₂

 — средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?

 

        Задача на основе реального варианта ОГЭ:

        Центростремительное ускорение при движении по окружности (в м/с²) можно вычислить по формуле a=ω²R, где ω — угловая скорость (в с^-1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с^-1, а центростремительное ускорение равно 289 м/с².

 

        Задача на основе реального варианта профильного ЕГЭ:

        К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:

        

        При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.

 

        Ответы (в беспорядке): 4; 15; 2; 10.

        А уж где числа, километры в час, метры, омы — это как-нибудь сами…)

Выражение неизвестной величины из формулы.

         Выражение неизвестной величины из формулы.

Для очень многих учеников это неумение является камнем преткновения при решении задач.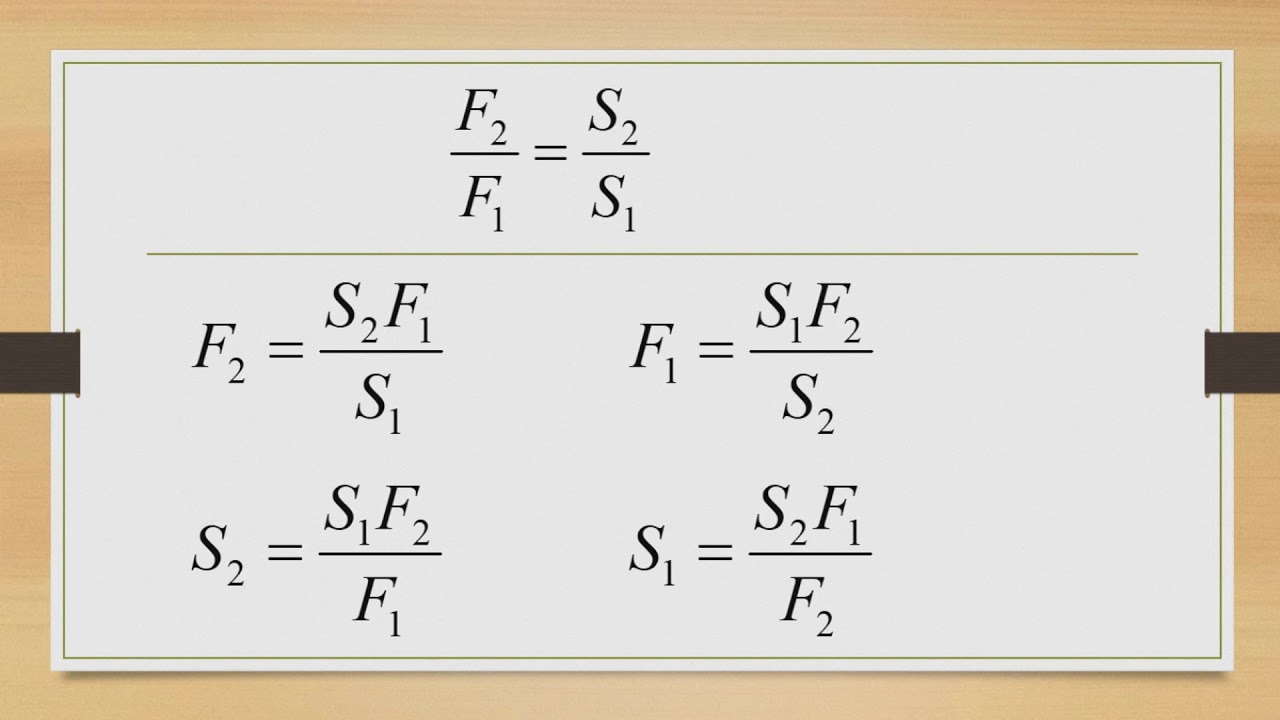

Хотя нужно уметь применять всего лишь два правила решения уравнений, которые изучаются еще в 7-м классе на алгебре и заменяют собой шесть правил нахождения неизвестной величины, знакомых вам  с начальных классов.

А ведь любая физическая формула по сути – это уравнение.

Вот они: эти правила.

1. Если слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.

В дополнение ко второму правилу добавляем еще правило сокращения дробей.

И в некоторых формулах потребуется извлечение корня.

Смотрите видеоурок.

На уроках математики ученики худо-бедно применяют эти правила, но и то часто делают ошибки. А уж если нужно перенести данную информацию на задачу с физическим содержанием, то многие впадают в полный ступор.

Давайте сегодня с вами решим эту проблему раз и навсегда. После этого мастер-класса у вас не будет никаких непоняток в плане выражения неизвестной величины из формулы.

Первая часть:

Начнем с самых простых формул, которые включают в себя три буквы.

Формула пути при равномерном движении:

 

Если нужно из этой формулы выразить время, то применяем второе правило: обе части уравнения делим на одно и то же число  (на одну и ту же букву). Делим на ту букву, от которой нужно избавиться. Затем сокращаем. В данном случае нужно избавиться от величины скорости.

Пишем короче:

Рассмотрим формулу давления столба жидкости.

 

Рассмотрим формулу плотности.

Чтобы выразить массу, нужно обе части уравнения умножить на объем. Затем сократить.

 

Если нужно выразить величину, которая стоит в знаменателе дроби, то сначала перетащим ее из знаменателя в числитель.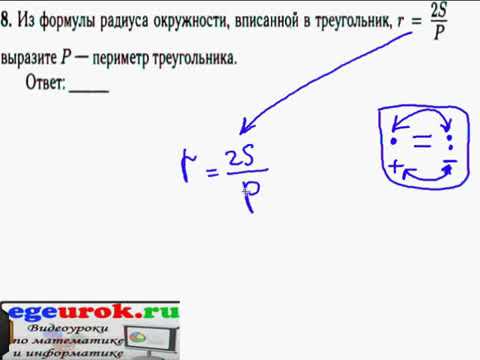

Итак, выражаем величину объема. Обе части уравнения умножаем на объем, извлекая его таким образом из знаменателя.

Сокращаем дробь в правой части на v.

Теперь, чтобы избавиться от плотности, делим на нее обе части

 

Встречаются формулы, в которых какая-то величина в степени.

Например, формула кинетической энергии

Нужно выразить скорость. Сначала выражаем квадрат скорости. Для этого обе части уравнения разделим на массу и умножим на 2.

 

Сокращаем на m и на 2, и получаем

Мы выразили квадрат скорости. Чтобы найти скорость, нужно избавиться от квадрата. Для этого из обеих частей уравнения извлекаем квадратный корень.

Записывается, конечно, все это короче.

 

На первых порах вы можете расписывать все подробно, когда же эти правила доведете до автоматизма, тогда уже сокращайте записи.

Для тренировки выпишите все известные вам формулы, похожие на те, которые мы сегодня разбирали и потренируйтесь в выражении. 2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(a/tan⁡α √(2c(a/tan⁡α +c) ))/(a/tan⁡α +c)=(a√(2c(a/tan⁡α +c) ))/(a+c tan⁡α ) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(a√(2c(a+a/sin⁡α ) ))/(a+a/sin⁡α )=(a sin⁡α √(2c(a+a/sin⁡α ) ))/(a sin⁡α+a)

Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tan⁡α ) M_c=c/2=a/(2 sin⁡α )

Радиус вписанной окружности равен разности катетов и гипотенузы, деленной на два, а чтобы найти радиус описанной окружности, нужно разделить на два гипотенузу. Заменяем второй катет и гипотенузу на отношения катета a к синусу и тангенсу соответственно. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+a/tan⁡α -a/sin⁡α )/2=(a tan⁡α sin⁡α+a sin⁡α-a tan⁡α)/(2 tan⁡α sin⁡α ) R=c/2=a/2sin⁡α

Электростатика — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению. ..

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов. Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

 

Закон Кулона

К оглавлению. ..

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

 

Электрическое поле и его напряженность

К оглавлению…

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика — напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

• Силовые линии электростатического поля никогда не пересекаются.
• Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
• При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
• Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
• В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

 

Принцип суперпозиции

К оглавлению. ..

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).

 

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

 

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

• φ – потенциал электрического поля.
• ∆φ – разность потенциалов.
• W – потенциальная энергия заряда во внешнем электрическом поле.
• A – работа электрического поля по перемещению заряда (зарядов).
• q – заряд, который перемещают во внешнем электрическом поле.
• U – напряжение.
• E – напряженность электрического поля.
• d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

 

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0.  Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

 

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

 

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.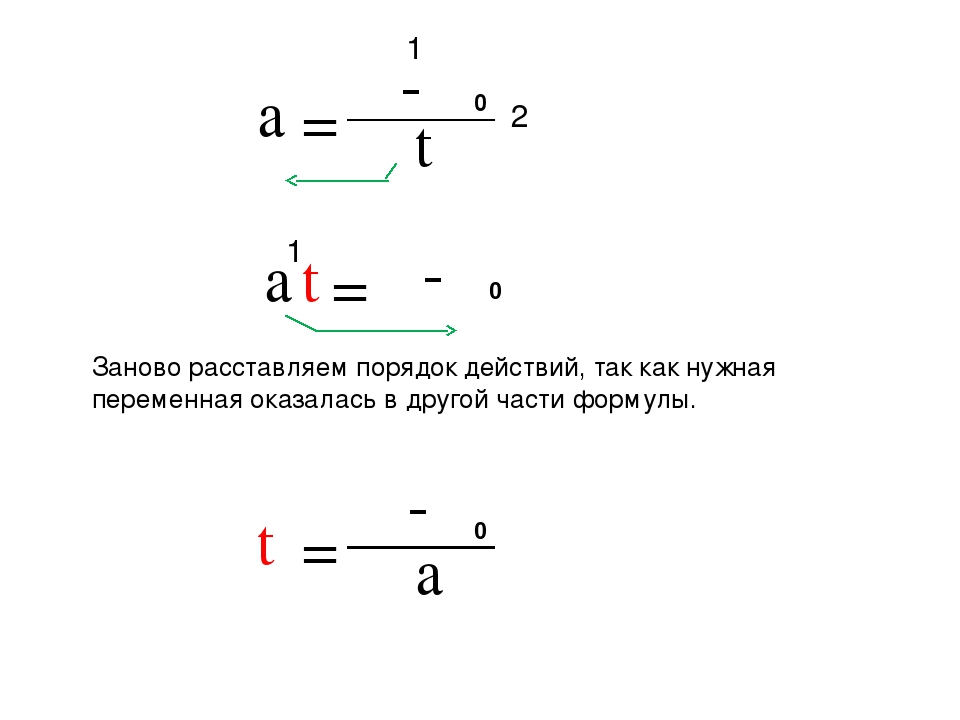

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

 

Свойства проводника в электрическом поле

К оглавлению…

1. Внутри проводника напряженность поля всегда равна нулю.
2. Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
3. Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
4. Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
5. Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

 

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

• Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
• Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии. 3$, давление при этом было равно одой атмосфере ($p_1=1\ атм.$). Какую силу следует приложить к поршню для того чтобы удержать его при смещении?

Решение. В результате перемещения поршня влево появляется избыточное давление на поршень со стороны газа внутри сосуда. Это давление можно компенсировать, если приложит к поршню силу, равную:

\[F=\Delta pS=S\left(p_2-p_1\right)\left(1.1\right),\]

где $p_2$ — давление, которое под поршнем после того как его сдвинули в левую сторону.

Будем считать, что процесс, который проводят в нашей системе, является изотермическим, а газ под поршнем идеальным. Тогда поведение газа подчиняется закону Бойля — Мариотта:

\[p_1V_1=p_2V_2\left(1.2\right),\]

где $V_2$ — давление, которое занимает газ после того, как поршень передвинули. Его можно найти как:

\[V_2=V_1-\Delta lS\ \left(1.3\right).\]

Выразим давление $p_2$ из (1.2), примем во внимание формулу (1.3), имеем:

\[p_2=\frac{p_1V_1}{V_2}=\frac{p_1V_1}{V_1-\Delta lS}\ \left(1. 2м}=Н.\]

Ответ. F=32 Н

как сдать ОГЭ по математике — Учёба.ру

Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Ольга Евсеева,

преподаватель математики физико-математической школы Института довузовской подготовки

Московского технологического университета (МИРЭА, МИТХТ, МГУПИ)

По вашему мнению, насколько хорошо девятиклассники сейчас знают математику? Насколько сложен для них этот ОГЭ?

Не сказала бы, что школьники не знают математику. Как правило, к нам на занятия приходят ребята с неплохим начальным уровнем, с хорошими навыками выполнения арифметических действий и преобразования выражений, знакомые с методами решения линейных, квадратных уравнений и неравенств — то есть со всем тем, что они должны знать к началу 9 класса. Конечно, глубина знаний и умение ими пользоваться напрямую зависят от количества часов математики в школе: при изучении предмета на базовом уровне это три-четыре часа алгебры и два часа геометрии в неделю, на углубленном уровне — пять-семь часов алгебры и три часа геометрии. Поскольку ОГЭ состоит из двух частей, первая из которых проверяет базовый уровень подготовки, а вторая включает более сложные задания, ребятам, изучающим в школе базовую математику, необходимо выделить дополнительное время для подготовки.

Иногда школьных уроков и самостоятельной работы достаточно, чтобы сдать ОГЭ на хорошо и отлично. В качестве подспорья можно использовать различные сайты и учебную литературу в открытом доступе. Возникающие вопросы можно обсудить на форумах или со школьным учителем. Но занятия на курсах помогают последовательно разобрать темы, систематизировать материал, проверить глубину его усвоения. Ведь после ОГЭ ребят через два года ждет более трудное испытание — ЕГЭ, в котором часть базовых заданий аналогичны заданиям повышенной и высокой сложности из ОГЭ. Девятиклассники впервые сдают экзамен, содержащий так много заданий, и его длительность составляет 3 часа 55 минут. Безусловно, для ребят это непросто.

Расскажите про структуру экзамена и систему начисления баллов. За какие задания на ОГЭ по математике ставится наибольшее количество баллов?

Всего школьникам предлагается 26 заданий. До недавнего времени экзамен состоял из трех частей — «Математика», «Реальная математика» и «Геометрия». С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».

Ребятам предстоит решить 17 задач по алгебре (14 задач в части 1 и три в части 2) и девять задач по геометрии (шесть задач в части 1 и три в части 2). Задания части 1 требуют краткого ответа в виде числа или последовательности цифр, которые вносятся в бланк ответов № 1. Развернутые решения заданий части 2 и ответы к ним записываются на бланке ответов № 2. За правильный ответ на каждое из заданий № 1-20 ставится 1 балл. Эти задания проверяются автоматически при сканировании бланков. Задания № 21-26 проверяют двое независимых экспертов, хотя при значительном расхождении оценок назначается проверка третьим экспертом. Эти задания могут быть оценены от 0 до 2 баллов. Таким образом, максимально за работу можно получить 32 первичных балла. Пятерка ставится за результат от 22 баллов, четверка — от 15 баллов, тройка — от 8 баллов (из них не менее 4 баллов по алгебре и 2 баллов по геометрии).

Как видите, для положительной оценки достаточно решить лишь восемь задач из части 1, а для пятерки — безошибочно выполнить базовую часть экзамена и только одно из заданий повышенной сложности. Вроде бы задача «сдать ОГЭ на отлично» не кажется такой уж сложной. Однако с заданиями повышенной сложности из части 2 ребятам придется снова столкнуться на ЕГЭ, уже в его базовой части. Например, задание № 22 повышенного уровня сложности — «текстовая задача» — аналогично заданию № 11 из части 1 ЕГЭ. Поэтому, как мне кажется, ребятам уже в 9 классе надо освоить методы и приемы решения заданий из части 2.

По вашему опыту преподавания, какие разделы математики самые сложные для школьников и вызывают наибольшее затруднение? Какие темы самые простые?

В модуле «Алгебра» это, прежде всего, исследование функций и построение их графиков. Задания на эту тему входят и в часть 1, и в часть 2 ОГЭ. В задании № 10 нужно установить соответствие между графиками функции и формулами, которые их задают. Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.

В модуле «Геометрия» в части 1 включены задачи, относящиеся к ключевым разделам курса геометрии. И все же, если в задании встречаются такие темы, как «вписанная и описанная окружности», «вписанные углы», «соотношения между сторонами и углами прямоугольного треугольника», «подобие треугольников», показатель его решаемости падает.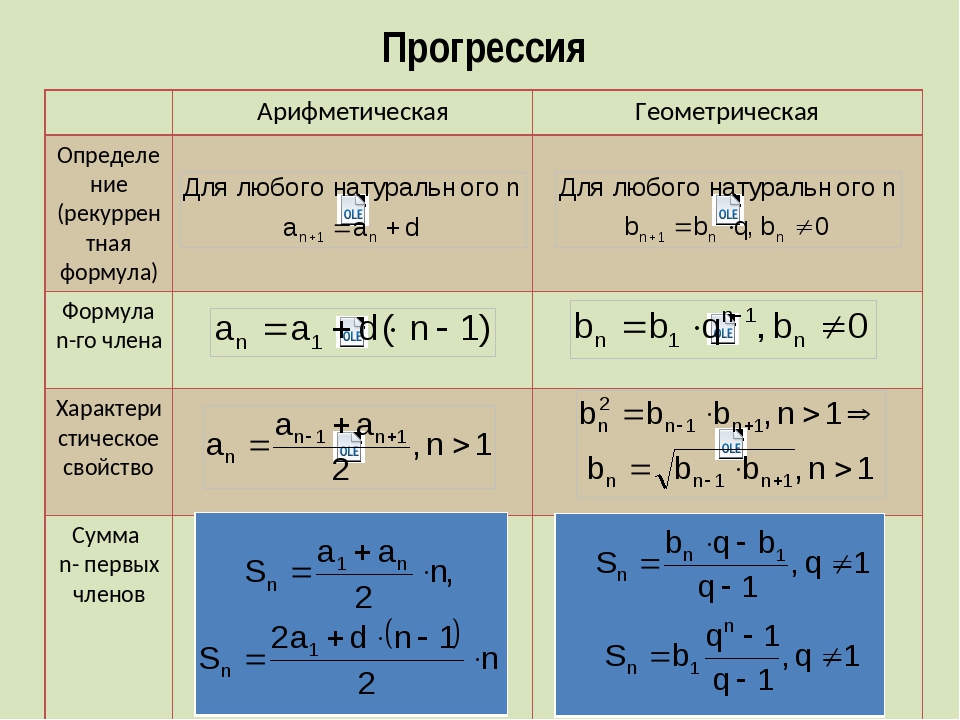

Меньше всего ошибок девятиклассники допускают в заданиях на чтение таблиц и диаграмм, нахождение вероятности случайного события.

Какие есть «подводные камни» в заданиях части 2? На что нужно обратить внимание при подготовке к заданиям повышенной сложности?

Задание № 21	В этом задании необходимо решить уравнение или неравенство, преобразовать алгебраическое выражение. При решении рациональных и дробно-рациональных уравнений, а также уравнений высших степеней необходимо обращать внимание на возможность потери решения (при сокращении на выражение, которое может быть равным нулю) или получение посторонних решений (которые обнуляют знаменатель или обращают исходное уравнение в выражение, не имеющее смысла). При решении неравенств надо помнить, что при умножении неравенства на отрицательное выражение оно меняет знак. Зачастую школьники либо просто не обращают внимание на знак величины, на которую умножают неравенство, либо умножают неравенство на выражение, содержащее переменную.
Задание № 22	Это текстовая задача, как правило, на «движение», «работу», «концентрации растворов» или «смеси и сплавы». Для ее решения необходимо составить уравнение или систему уравнений. Я бы посоветовала ребятам для наглядности обязательно заполнять таблицу, в которую вносятся известные по условию величины, выбранная переменная или переменные, после чего в пустые клетки вписываются соответствующие им величины, выраженные через введенные переменные, и только потом приступать к составлению уравнения (или системы).
Задание № 23	Построение графика функции. Для правильного выполнения этого задания необходимо знать свойства следующих функций: линейная, квадратичная, либо функция, описывающая обратно пропорциональную зависимость. Также необходимо уметь строить графики этих функций, знать правила преобразования графиков. Очень часто встречаются задания, в которых формулу, задающую исходную функцию, можно преобразовать, после чего она значительно упрощается. Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать.
Задание № 24	Геометрическая задача вычислительного характера. Школьник должен решить планиметрическую задачу, применяя различные теоретические знания из курса геометрии.
Задание № 25	Геометрическая задача на доказательство с использованием стандартных приемов. Здесь надо обратить внимание на умение математически грамотно и ясно записать решения, приведя все необходимые обоснования и пояснения.
Задание № 26	Для решения этой задачи школьникам нужно владеть широким спектром приемов и способов рассуждений. Здесь возможно потребуются и дополнительные построения, и знание утверждений, не так часто используемых в школьном курсе. Например, теорема об угле между касательной и хордой; теорема о секущих и касательной; свойства высоты прямоугольного треугольника, опущенной из прямого угла; свойства биссектрис, медиан, высот треугольника; теорема Чевы; теорема Менелая.

Что нужно делать школьнику, чтобы подготовиться к экзамену наилучшим образом? Как вы посоветуете им распределить свое время?

На занятиях со школьниками я обычно придерживаюсь следующей стратегии. Во-первых, мы полностью проходим программу 9 класса, начиная с отработки основных навыков и умений по следующим темам: преобразование алгебраических выражений, решение уравнений и неравенств, числовые последовательности, функции, их свойства и графики, элементы статистики и теории вероятностей. Постепенно повышая уровень заданий, мы переходим к решению задач повышенной и высокой сложности и стараемся уделить этим заданиям как можно больше внимания. Не менее трети времени следует посвятить геометрии, и здесь также нужно двигаться «от простого к сложному».

Во-вторых, необходимо готовиться к самому формату ОГЭ, к его структуре. Если ученик хорошо умеет решать задачи, но ни разу не пробовал написать работу в этом формате, ему сложно будет оценить количество затрачиваемого времени на часть 1 и 2. Обязательно нужно научиться правильно распределять свои силы.

Многие девятиклассники не используют предлагаемое на экзамене время полностью, у них просто не хватает усидчивости. Ребята сдают работу раньше, хотя еще остались нерешенными задания повышенной сложности. Зачастую и в заданиях части 1 бывают ошибки по невнимательности, которые сам школьник не смог найти и исправить. На ЕГЭ же складывается обратная ситуация. Выпускники прилежно готовятся к экзамену, считают, что времени мало. Им хочется еще раз проверить свои решения и подумать над заданиями высокой сложности.

Какие источники вы рекомендуете использовать для самостоятельной подготовки к экзамену?

• «Сайт ФИПИ». На нем вы найдете открытый банк заданий ОГЭ.
• Сборник «ОГЭ. Математика 2018. Типовые и тестовые задания». Таких сборников очень много, нужно обращать внимание на гриф «рекомендовано ФИПИ».
• Учебные пособия Центра непрерывного математического образования. Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения.
• «Сайт Alexlarin.net». Здесь каждую неделю выкладывается новый вариант ОГЭ и новый вариант ЕГЭ. Ребятам дается семь дней на размышление. Они могут обсуждать свои решения на специальном форуме. Потом вывешиваются правильные ответы.
• «РешуЕГЭ». На сайте доступен большой банк заданий. Тесты можно составлять самостоятельно, выбирая лишь те темы, над которыми необходимо поработать. Небольшой минус — тесты часто получаются похожими друг на друга.

Решение «буквенных» уравнений в Wolfram|Alpha

Задача «выразить х из уравнения (с несколькими неизвестными)» встречается довольно часто. Ее можно рассматривать, как решение уравнения с буквенными коэффициентами. Поэтому логично, что Wolfram|Alpha использует для решения таких «буквенных» уравнений запрос solve, который обычно служит для решения уравнений с одним неизвестным.

Вот простой пример такой задачи.

Дано:

Найти x.

Запрос solve применительно к этому уравнению дает такой результат:

solve 2x+3y-1=0

Здесь Wolfram|Alpha отдает приоритет отысканию переменной y. Возможно, полагая, что y это — функция, а x — ее аргумент? Кстати, тот же самый результат дает и запрос solve 2x+3y-1.

Если же из данного уравнения нужно найти именно х, то это следует указать явно. И вот, каким образом:

solve 2x+3y-1 for x

При этом, в отличие от первого варианта, здесь Wolfram|Alpha дает возможность посмотреть пошаговое решение задания с подробным текстовым комментарием:

(Эта замечательная особенность Wolfram|Alpha уже обсуждалась в одном из предыдущих постов Математика с Wolfram|Alpha: шаг за шагом…)

Итак, рассмотренный выше пример уже дает представление о том, как легко Wolfram|Alpha справляется с «буквенными» уравнениями. Однако, пойдет ли дело так же гладко, если вместо x и y взять другие буквы?

Запрос solve 2a+3b-1 дает следующее:

Однако, абсолютно аналогичный по структуре запрос solve 2n+3m-1 выводит совсем другой результат:

Конечно же! Логика здесь есть: Wolfram|Alpha по умолчанию считает неизвестным то, что обозначено буквой, расположенной ближе к концу алфавита. y=0

И т.д. и т.п.

Выражение одной величины в процентах от другого числа

В школе 56 из 70 учителей — женщины. Какой процент учителей — женщины? Какой процент из них — мужчины? Доля учителей-женщин в школе составляет 56/70, поэтому, изменив эту долю на процентную долю, мы получим

$$ \ frac {{56}} {{70}} $$ x 100% = 80%

80% учителей — женщины, а процент учителей-мужчин (100% -80%) = 20%

В общем, чтобы выразить одно количество «$$ a $$» в процентах от другого количества «$$ b $$», мы:

1. Запишите дробь $$ \ frac {a} {b} $$
2. Умножьте дробь $$ \ frac {a} {b} $$ на 100%, чтобы преобразовать ее в процент.

Пример :
108 студентов из 150 сдали математику и 96 из 160 сдали английский. Найдите процент сдавших экзамен студентов.

Решение :
Процент студентов, сдавших математику = $$ \ frac {{108}} {{150}} $$ x 100% = 72%
Процент студентов, сдавших английский язык = $$ \ гидроразрыв {{96}} {{160}} $$ x 100% = 60%

Определение процента числа:

Чтобы найти процент ($$ a \% $$) другого числа «$$ b $$», у нас есть следующий метод.

1. Умножьте $$ a \% $$ на $$ b $$, т.е. $$ b {\ text {x}} a \% $$
2. Упростите, если возможно.

Пример:
Если 75% учеников в классе из 40 сдали тест по математике, сколько из них не выдержали?

Решение:
Всего студентов = 40
Процент студентов, сдавших тест = 75%
Количество студентов, прошедших тест = 75% из 40 студентов = $$ \ frac {{75}} {{100}} $ $ x 40 = 30
Количество неуспешных студентов = 40 — 30 = 10

Пример:
Найдите (1) 25% от 21.60 (2) $$ 37 \ frac {1} {2} $$% x 1,60

Раствор:

1. 25% от 21,60 = $$ \ frac {{25}} {{100}} $$ x 21,60 = 5,40

2. $$ 37 \ frac {1} {2} $$% x 1.60 = $$ \ frac {{75}} {2} $$% x 1.60 = $$ \ frac {{75}} {{2 {\ text {x 100}}}} $$ x $$ \ frac {{160}} {{100}} $$ = = 0,60

Выражение одной величины как дроби другой — Дроби — CCEA — Редакция математики GCSE — CCEA

1h4h845bwjm.0.0.0.1:0.1.0.$0.$1.$0″> Из группы из 20 человек пять человек выбрали для изучения искусства на GCSE.Какая часть класса будет сдавать Art GCSE?

Всего пять человек из 20. Мы можем записать это как \ (\ frac {5} {20} \).

Эту дробь можно упростить, разделив числитель и знаменатель на одно и то же значение: \ (\ frac {5 ÷ 5} {20 ÷ 5} = \ frac {1} {4} \)

Вопрос

В июне дожди идут восемь дней. В какой части месяца шел дождь?

Показать ответ

В июне 30 дней, из них восемь дней шел дождь.

Это записывается как \ (\ frac {8} {30} \)

Это может быть упрощено до:

\ [\ frac {8 ÷ 2} {30 ÷ 2} = \ frac {4} { 15} \]

Важно убедиться, что обе величины указаны в одних и тех же единицах.

Например, мы не можем сравнить время в минутах с количеством часов. Сначала мы должны преобразовать время из часов в минуты.

Обычно мы переключаемся на меньшую единицу, чтобы не работать с десятичными знаками.

Вопрос

Джонни опаздывает на 20 минут на съемку двухчасового фильма. Какую часть фильма он пропускает?

Показать ответ

2 часа = 2 × 60 = 120 минут.

\ [\ frac {20} {120} = \ frac {2} {12} = \ frac {1} {6} \]

Пропорциональные отношения

Пропорциональная зависимость — это такая, при которой две величины изменяются напрямую друг с другом. Мы говорим Переменная у изменяется прямо как Икс если:

у знак равно k Икс

для некоторых постоянный k , называемая константой пропорциональности.

(Некоторые учебники описывают пропорциональную зависимость, говоря, что » у изменяется пропорционально Икс » или это » у прямо пропорциональна Икс . «)

Это означает, что как Икс увеличивается, у увеличивается и как Икс уменьшается, у уменьшается — и соотношение между ними всегда остается неизменным.

График уравнения пропорциональной связи представляет собой прямую линию, проходящую через начало координат.

Пример 1:

Учитывая, что у варьируется пропорционально Икс , с участием константа пропорциональности k знак равно 1 3 , найти у когда Икс знак равно 12 .

Напишите уравнение пропорциональной зависимости.

Переменная Икс изменяется пропорционально у с константой пропорциональности, равной 1 3 .

Так,

Заменить данный Икс значение.

Пример 2:

Учитывая, что у варьируется пропорционально Икс , Найти константа пропорциональности если у знак равно 24 а также Икс знак равно 3 .

Напишите уравнение пропорциональной зависимости.

у знак равно k Икс

Заменить данный Икс а также у значения и решить для k .

24 знак равно k ⋅ 3 k знак равно 8

Пример 3:

Предполагать у изменяется пропорционально Икс , а также у знак равно 30 когда Икс знак равно 6 . В чем ценность у когда Икс знак равно 100 ?

Напишите уравнение пропорциональной зависимости.

у знак равно k Икс

Заменить данный Икс а также у значения и решить для k .

30 знак равно k ⋅ 6

k знак равно 5

Уравнение у знак равно 5 Икс . Теперь замените Икс знак равно 100 и найти у .

у знак равно 5 ⋅ 100 у знак равно 500

математических навыков: как вычислять, преобразовывать и использовать проценты

Если вы слушаете радио, смотрите телевизор или читаете газету, вы не можете не слышать или видеть такие фразы, как «25% скидка только сегодня» или «10% скидка на все товары» или «выход из бизнеса со скидками. 50% «. Что все это значит?

Процент означает «части на сотню».«Что вам нужно сделать, так это представить себе одно целое как разделенное на 100 частей. Если у вас есть все 100 из этих частей, у вас есть 100%. Обратите внимание на символ, который мы используем для процента (%). Если у вас есть только 95 из запчасти, у вас 95%.

Преобразование десятичных дробей в проценты

Чтобы превратить число (целое или десятичное) в процент, просто умножьте его на 100. Это то же самое, что переместить десятичную запятую на две позиции вправо.Возможно, вам потребуется округлить до желаемой точности. Добавьте знак процента (%).

0,32 в процентах составляет 32%

38,59 = 3859%

0,002 = 0,2%

Чтобы превратить процент в целое или десятичное число, просто разделите на 100. Это то же самое, что переместить десятичную точку на две позиции влево. Снимите знак процента (%).

50% в виде десятичной дроби 0,50

3,5% = 0,035

250% = 2,50

Преобразование дробей в проценты

Чтобы преобразовать дробь в процент, разделите числитель дроби на знаменатель.Затем умножьте на 100 или переместите десятичную запятую на два разряда вправо. Округлите ответ до желаемой точности. Добавьте знак процента (%).

Термины — процент, база, ставка

Если стоимость товара составляет 32,99 доллара США, вы заплатите на 5% больше, чем указанная сумма с добавленным налогом. Сначала вы вычисляете размер налога, беря 5% от $ 32,99:

.

0,05 х 32.99 = 1,6495

Помните, что вы имеете дело с деньгами, поэтому округлите это число до ближайшего пенни, чтобы получилось 1,65 доллара. Затем вы должны добавить это к 32,99 доллара, чтобы узнать, сколько вы будете платить: 32,99 доллара + 1,65 доллара = 34,64 доллара. Это окончательная цена с учетом налога с продаж.

Другой способ рассчитать это — представить цену как 100%, а налог с продаж — как 5%, так что общая цена, которую вы заплатите, составит 105%. Затем вы можете умножить первоначальную цену на 105%:

105% х 32.99 = 1,05 (32,99) = 34,6395 = 34,64 доллара США

Если вы работаете в розничном магазине, вас могут попросить сделать наценку. Это когда вы берете оптовую цену и увеличиваете ее на определенный процент, чтобы получить розничную цену в магазине, в котором вы работаете. Это повышение цены покрывает вашу зарплату и другие расходы по эксплуатации магазина (аренда, свет, отопление и т. Д.).

Свитер может стоить 15 долларов оптом, но ваш магазин получает от него 65% прибыли. Следовательно, для получения розничной цены на него должна быть наценка на 65%.

65% x 15 долларов = 0,65 (15) = 9,75 долларов

Теперь добавьте к 15 долларам: 9,75 доллара + 15 долларов = 24,75 доллара

Наценка составляет 9,75 доллара, а розничная цена — 24,75 доллара.

Или вы можете посмотреть на это как 165% x 15 долларов, что даст вам 24,75 доллара за один шаг.

Во многих магазинах есть уценки или скидки, называемые распродажами. Это работает противоположно наценкам и налогу с продаж, поскольку процент вычитается из первоначальной цены, а не прибавляется к ней.

Допустим, такой же свитер продается со скидкой 30%. Это означает, что вам нужно найти 30% его розничной цены и вычесть ее из розничной цены.

30% x 24,75 доллара = 0,30 (24,75) = 7,425 доллара или 7,43 доллара

24,75 доллара — 7,43 доллара = 17,32 доллара

В этом случае вы должны вычесть 30% из 100%, чтобы сделать это за один шаг:

(100% — 30%) x 24,75 доллара = 70% x 24,75 доллара = 0,7 (24,75) = 17,325 доллара = 17,33 доллара

Это будет зависеть от того, как запрограммирован кассовый аппарат (компьютер), будет ли с вас снята сумма в размере 17 долларов.32 или 17,33 доллара, но таким способом вы можете рассчитать стоимость с точностью до копейки.

Комиссия — еще одно место, где используются проценты. Комиссионные с продаж выплачиваются продавцам в зависимости от цены проданного товара. В некоторых отраслях, например в страховании, они выплачиваются вместо заработной платы. Во многих отраслях это мотивирует продавать больше и выплачивается в дополнение к обычной зарплате.

Если агент по недвижимости получает комиссию в размере 7% от проданного им дома стоимостью 175 000 долларов, он получает

.

Процент = 7% x 175 000 $ =.07 (175 000) = 12 250 9000 долларов США 3

Еще одно место, где все используют проценты, — это вычисление чаевых. Чаевые даются людям, которые нас обслуживают — официантам в ресторане, грумеру собак, бармену, водителю такси, парковщику и т. Д. Большинство чаевых составляют 15% или 20%. Если вы оплачиваете обед, а официант приносит счет и забирает счет, вы можете просто оплатить счет и дать ему чаевые. Однако, если официант принесет счет, и вы оплатите его в кассе, вам следует оставить чаевые на столе, а затем пойти оплатить счет.

Простой способ вычислить чаевые без использования калькулятора: округлите счет до ближайшего доллара или полдоллара, затем переместите десятичную запятую на одно место влево, чтобы определить 10% суммы счета. Если вы даете чаевые 20%, удвойте это. Если вы даете чаевые 15%, оцените половину и прибавьте ее к 10%.

Если ваш счет составляет 35,95 доллара, округлите его до 36 долларов. Переместите десятичную запятую на одну позицию влево, чтобы получить 3,60 доллара. Это 10%. Поскольку 2 x 36 равно 72, вы получите чаевые в размере 7,20 доллара США за 20% чаевых.

Половина 3,60 доллара составит 1 доллар.80, поскольку ½ из 36 равно 18. Чтобы дать чаевые 15%, добавьте 1,80 доллара к 3,60 доллара (для оценки округлите до 1,50 и 4 доллара) и чаевые 5,40 доллара — ваша оценка в 5,50 доллара достаточно близка для использования.

Проценты — это наибольшее использование процентов в повседневной жизни. Когда вы вкладываете деньги, вы получаете проценты — проценты выплачиваются вам. Это происходит, если у вас есть сберегательный счет или вы покупаете процентные облигации, казначейские векселя (TB) или депозитные сертификаты (CD).

Однако, если вы занимаете деньги, например, взяли ссуду на машину, лодку или дом, вы платите проценты.А если вы используете платежную карту и не оплачиваете платежи в установленный срок, с вас будут взиматься проценты.

Если ваша ссуда предоставлена ​​на очень короткий период времени или является личной ссудой от члена семьи, вы можете выплачивать простые проценты. Если это связано с банком или финансовым учреждением, вы, вероятно, будете платить сложные проценты. Простой процент начисляется на всю сумму денег (называемую основной суммой) один раз, а затем сумма делится на количество платежей и добавляется к каждому платежу.Сложные проценты начисляются на основную сумму, затем после первого платежа они рассчитываются на оставшуюся часть основной суммы, а после следующего платежа они снова рассчитываются на оставшуюся основную сумму и так далее.

Чтобы рассчитать проценты, вы должны знать сумму денег (основную сумму), период времени, на который она была взята в долг (время), и процентную ставку, которая взимается или выплачивается. Формула:

Проценты = Основная сумма x Ставка x Время

Если заимствовано 500 долларов на 2 года под 12% годовых:

Процентная ставка = 500 долларов США x 12% x 2

Проценты = (500) (0.12) (2) = 120 9000 долл. США 3

Сумма долга в конце будет 500 + 120 долларов или 620 долларов.

Расчет сложных процентов .

Сложные проценты начисляются на основную сумму плюс накопленных процентов. Сумма возврата рассчитывается по следующей формуле:

A = P (1 + i) ⁿ

Например, вы получаете 10% годовых на инвестиции в размере 1000 долларов США в первый год. Вы реинвестировали эти деньги обратно в свои первоначальные вложения.На второй год вы получите 10% годовых на 1 000 * плюс * 100 долларов, которые вы реинвестировали. С годами сложные проценты принесут вам гораздо больше денег, чем простые проценты, потому что вы реинвестируете любые проценты, которые приносите. Давайте рассмотрим это на следующем примере:

A = P (1 + i) ⁿ

A — окончательная сумма, включая основную сумму.

P — это основная сумма (то, что вы изначально инвестировали).

i — годовая процентная ставка.

n — количество вложенных лет. Помните, что n — показатель степени.

Пример:

Допустим, у вас есть 2 500,00 долларов для инвестирования на 5 лет по ставке 7% сложных процентов.

A = 2500 (1 + 0,07) ⁵ = 3506,38 долларов США

Вы можете видеть, что ваши 2500,00 долларов теперь стоят 3 506,38 долларов после 5 лет при 7% годовых.

Коэффициенты

| Purplemath

Purplemath

Пропорции строятся на основе соотношений. «Отношение» — это просто сравнение или соотношение двух разных вещей. Например, кто-то может посмотреть на группу людей, сосчитать носы и сослаться на «соотношение мужчин и женщин» в группе. Предположим, есть тридцать пять человек, пятнадцать из которых — мужчины.Остальные — женщины, итак:

… в группе двадцать женщин. Выражение «отношение (этого) к (этому)» означает, что (это) стоит перед (этим) в сравнении. Итак, если бы можно было выразить «соотношение мужчин и женщин», то соотношение, выражаясь английскими словами, было бы «15 мужчин к 20 женщинам» (или просто «15 к 20»).

MathHelp.com

Порядок элементов в соотношении очень важен и должен соблюдаться; какое бы слово ни было первым в соотношении (если оно выражено словами), его номер должен стоять первым в соотношении. Если бы выражение было «отношение женщин к мужчинам», то словесным выражением было бы «20 женщин к 15 мужчинам» (или просто «20 к 15»).

Если соотношение мужчин и женщин выражается как «15 к 20», это соотношение выражается словами. Есть два других обозначения этого отношения «15 к 20»:

обозначение шансов: 15: 20

дробное представление:

¹⁵ / ₂₀

Вы должны уметь распознать все три обозначения; вы, вероятно, должны будете знать их и как конвертировать между ними в следующем тесте.Например:

• В одном парке 16 уток и 9 гусей. Выразите соотношение уток и гусей через двоеточие, через дробь (не уменьшать) и прописью.

Они хотят «соотношение уток и гусей», поэтому число уток идет первым (или, для дробной формы, сверху). Итак, мой ответ:

---

• Рассмотрим вышеупомянутый парк с 16 утками и 9 гусями.Выразите соотношение гусей и уток во всех трех форматах.

На этот раз они хотят, чтобы я дал им «соотношение гусей и уток». Я буду использовать те же числа, но в этом случае количество гусей идет первым (или, для дробной формы, сверху). Итак, мой ответ:

Числа были одинаковыми в каждом из двух приведенных выше упражнений, но порядок , в котором они были перечислены, различается в зависимости от порядка, в котором были выражены элементы соотношения.В соотношениях очень важен порядок.

---

Давайте вернемся к 15 мужчинам и 20 женщинам в нашей первоначальной группе. Я выразил это отношение дробью, а именно:

¹⁵ / ₂₀ . Эта фракция уменьшается до ³ / ₄ . Это означает, что мы также можем выразить соотношение мужчин и женщин в группе как ³ / ₄ , 3: 4 или «3 к 4».

Это указывает на одну важную вещь о соотношениях: числа, используемые в соотношении, могут не совпадать с абсолютными измеренными значениями .Соотношение «15 к 20» относится к абсолютному количеству мужчин и женщин, соответственно, в группе из тридцати пяти человек. Упрощенное или сокращенное соотношение «3 к 4» говорит нам только о том, что на каждых трех мужчин приходится четыре женщины. Упрощенное соотношение также говорит нам, что в любой репрезентативной выборке из семи человек (3 + 4 = 7) из этой группы трое будут мужчинами. Другими словами, мужчины составляют

³ / ₇ человек в группе. Эти отношения и рассуждения — то, что мы используем для решения многих словесных задач:

• В определенном классе соотношение положительных и отрицательных оценок составляет 7 к 5.Сколько из 36 студентов не прошли курс?

Соотношение «7 к 5» (или 7: 5 или

⁷ / ₅ ) говорит мне, что из каждой репрезентативной группы студентов пять не смогли. Под «репрезентативной группой» я подразумеваю группу, в которой количество учеников такое же, как и во всем классе. Я могу определить размер этой группы, используя указанное мне соотношение. Размер репрезентативной группы будет суммой ее частей:

Итак, в репрезентативной группе 12 студентов, из которых 7 сдали экзамен, а 5 — нет.В частности, доля отказавшейся группы определяется путем деления количества отказавшихся студентов на общее количество студентов в репрезентативной группе. То есть:

Итак,

завалили 5/12 группы и, поскольку эта группа репрезентативна, завалили 5/12 всего класса. Это означает, что теперь я могу найти количество студентов во всем классе, которые провалились (это упражнение удручает!), Умножив долю из репрезентативной группы на размер всего класса:

Итак, из 36 учеников класс не прошли:

---

Соотношение репрезентативной группы также можно использовать для получения процентной информации.

• Какой процент учащихся в вышеприведенном классе сдали его? (Округлите ответ до одного десятичного знака.)

Я уже знаю, что в репрезентативной группе 12 учеников, из которых 7 сдали класс. Преобразуя это в проценты (разделив, а затем переместив десятичную точку, как описано здесь), я получу:

7/12 = 0.583333 … = 58,3333 …%

Они хотят, чтобы ответ был округлен до одного десятичного знака, поэтому мой ответ:

---

• В парке, упомянутом ранее, соотношение уток и гусей составляет 16 к 9. Сколько из 300 птиц гуси?

Это соотношение говорит мне, что из каждой репрезентативной группы из 16 + 9 = 25 птиц 9 — гуси.То есть

⁹ / ₂₅ птиц — гуси. Я могу использовать эту дробь из репрезентативной группы, чтобы найти ответ для всей группы:

Это номер, который им нужен. Всего в парке насчитывается:

---

Как правило, проблемы с соотношениями сводятся только к их установлению или упрощению. Например:

• Выразите в простейшей форме следующее соотношение: от 10 до 45 долларов

Это упражнение требует, чтобы я записал отношение в виде уменьшенной дроби.Итак, сначала я сформирую дробь, а затем сделаю отмену, которая приведет к «простейшей форме».

Знаки доллара тоже погасли, потому что они были одинаковыми, верхняя и нижняя, в дробной форме отношения. Итак, мой ответ:

Эта уменьшенная дробь является выражением отношения в простейшей дробной форме. Единицы (являющиеся знаками «доллар») отменены на дроби, потому что единицы (а именно, символы «$») были одинаковыми для обоих значений.

Если оба значения в соотношении имеют одну и ту же единицу измерения или обозначение, в сокращенной форме отношения не должно быть единиц или обозначения. Единицы не являются факторами, но они отменяются так же, как и факторы.

---

• Выразите в простейшей форме следующее соотношение: 240 миль к 8 галлонам

Члены этого соотношения имеют разные единицы измерения, поэтому они не отменяются; будут единицы на моем упрощенном соотношении.Мое упрощение выглядит так:

(240 миль) / (8 галлонов)

= (30 миль) / (1 галлон)

Это конкретное соотношение единиц, «(мили) / (галлон)», имеет свою упрощенную форму; а именно «миль на галлон», сокращенно «миль на галлон». Итак, на стандартном английском мой ответ:

.

В отличие от ответа в предыдущем упражнении, в ответе этого упражнения должны были быть единицы измерения, так как единицы на двух частях отношения (а именно, «мили» и «галлоны») не были то же самое, и, таким образом, не отменяли друг друга.Когда соотношение заканчивается единицами (или размерами) на нем, это соотношение также может называться «ставкой». В случае с упражнением, описанным выше, тариф представлял собой пройденное расстояние на единицу объема топлива.

---

Коэффициенты пересчета — это упрощенные соотношения, поэтому они могут быть рассмотрены примерно в то же время, когда вы изучаете соотношения и пропорции. Например:

• Какова длина игрового поля на поле для американского футбола в футах (т. Е. Длина поля без учета «концевых» зон)?

Я знаю, что длина поля для американского футбола, не считая «конечных» зон, составляет 100 ярдов.Я также знаю, что 3 фута равны 1 ярду. Я могу представить это равенство в виде отношения. Поскольку они дали мне измерение в «ярдах», я хочу, чтобы единицу «ярды» вычитали в моем умножении. Из-за этого я укажу свое соотношение (ярдов к футам) с указанием «футов» сверху:

Теперь я могу умножить предоставленную мне длину на мой коэффициент преобразования (указанное выше соотношение) и упростить:

[(3 фута) / (1 ярд)] [100 ярдов]

= (3 фута) (100) = 300 футов

Это значение — это число, которое они хотят, поэтому мой ответ:

.

Дополнительную информацию по этой теме см. В уроке «Отмена / преобразование единиц».

---

Соотношения — это сравнение одного показателя с другим (мили к галлонам, футы к ярдам, утки к гусям и т. Д.). Но их истинная полезность заключается в установлении и решении пропорций.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании отношений, выраженных в нотации «шансов», в дробную форму. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Преобразовать в упрощенную дробь», чтобы сравнить свой ответ с ответом Матвея.(Или пропустите виджет и перейдите на следующую страницу.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

---

---

URL: https://www.purplemath.com/modules/ratio.htm

Обучение линейным уравнениям в математике

Для многих учеников 8-х классов и выше числа и формы, которые они узнали, действительно начинают сходиться, когда они составляют и решают линейные уравнения.Эта тема объединяет идеи об алгебре, геометрии и функциях, и многим детям — и взрослым может быть сложно осмыслить. В этой статье объясняется, что такое линейное уравнение, и рассматриваются различные примеры. Затем он предлагает учащимся идеи уроков по введению и развитию концепции линейных уравнений с одной переменной.

Что такое линейное уравнение?

Как и любое другое уравнение, линейное уравнение состоит из двух равных друг другу выражений.Есть некоторые ключевые особенности, общие для всех линейных уравнений:

1. Линейное уравнение имеет только одну или две переменные.
2. Никакая переменная в линейном уравнении не возводится в степень больше 1 или не используется в качестве знаменателя дроби.
3. Когда вы находите пары значений, которые делают линейное уравнение истинным, и наносите эти пары на координатную сетку, все точки лежат на одной линии. График линейного уравнения представляет собой прямую линию.

Линейное уравнение с двумя переменными можно описать как линейное соотношение между x и y , то есть двумя переменными, в которых значение одной из них (обычно y ) зависит от значение другого (обычно x ).В этом случае x является независимой переменной, а y зависит от нее, поэтому y называется зависимой переменной.

Независимая переменная, помеченная ли она как x , обычно отображается по горизонтальной оси. Большинство линейных уравнений являются функциями. Другими словами, для каждого значения x существует только одно соответствующее значение y . Когда вы присваиваете значение независимой переменной x , вы можете вычислить значение зависимой переменной y .Затем вы можете нанести точки, названные каждой парой ( x , y ), на координатной сетке.

Описание линейных отношений

Студенты уже должны знать, что любые две точки определяют линию. Таким образом, для построения графика линейного уравнения на самом деле требуется всего лишь найти две пары значений и провести линию через точки, которые они описывают. Все остальные точки на линии предоставят значения x и y , которые удовлетворяют уравнению.

Графики линейных уравнений всегда представляют собой линии.Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).

Как выглядит линейное уравнение?

Пример 1: расстояние = скорость × время

В этом уравнении для любой заданной постоянной скорости соотношение между расстоянием и временем будет линейным.Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этой взаимосвязи будут отображаться только точки в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо. Линии, идущие в этом направлении, имеют положительный наклон . Положительный наклон указывает, что значения на обеих осях увеличиваются слева направо.

3 простых формулы для расчета диапазона значений в Excel

Важным навыком, который должен знать любой пользователь Excel, является определение диапазона значений в Excel.У большинства компаний нет времени тратить время на сортировку строк и строк в Excel, чтобы найти самые высокие и самые низкие значения дохода, продаж или другой информации. Разница между наибольшим и наименьшим значениями в группе данных — диапазон — может иметь важное значение для принятия точных решений, составления бюджета и прогнозирования.

Представим, что вы менеджер по закупкам Revelation, Inc., небольшого предприятия, занимающегося продажей компьютеров. Вы можете назначать оптовые цены на сырье, что значительно увеличит прибыль Revelation.Чем раньше вы сможете приобрести материалы, тем лучше, потому что цена увеличивается по мере приближения к дате отгрузки. Вы можете использовать данные о продажах за предыдущий финансовый год для бюджета на сырье, и диапазон может помочь вам спрогнозировать продажи в следующем году на основе результатов этого года. Вы можете использовать средние продажи в месяц, чтобы понять, какое сырье вам понадобится и когда. Выявление этого конкретного пробела также отлично подходит для установления стандартов производительности, потому что вы можете выяснить, как вы работаете по сравнению с другими месяцами.

Поскольку Excel предлагает несколько способов написания формул диапазона в соответствии с вашими индивидуальными потребностями, вот три варианта формулы диапазона, которые помогут вам начать работу!

1. Формулы минимума и максимума

Revelation ведет электронную таблицу с информацией, включая состояние, модель, количество единиц, цену за единицу и общий доход для каждого продукта в каждом штате. Продажи продукции в прошлом году распределены следующим образом:

Вам необходимо определить, какие товары пользуются наибольшим и наименьшим спросом.Это небольшой список, но если вы продаете или перепродаете много товаров, следующая формула может оказаться неоценимой. Вы можете легко найти минимальные и максимальные единицы с помощью функций MIN () и MAX ().

• В ячейке B15 введите «= MIN (C2: C13)».
• В ячейке B16 введите «= МАКС (C2: C13)».

Теперь у вас есть быстрый отчет о наименьшем количестве проданных единиц в штате (102 планшета в Айове) и о наибольшем (450 ноутбуков в Иллинойсе).

2. Верхний

k и нижний k Формулы

Предположим, вас интересует больше данных — не только о наименее продаваемых товарах, но и о трех наименее продаваемых товарах.Вы можете найти их с помощью функции НАИМЕНЬШИЙ (). Чтобы использовать SMALL (), вам понадобятся два параметра:

1. Тот же диапазон или список значений, что и для MIN ().

Примечание. Если вы используете несколько значений вместо одного непрерывного диапазона, вам нужно будет заключить каждый набор в круглые скобки.

2. Значение k , которое является желаемой позицией снизу списка. Если вы ищете наименьшее значение, тогда k = 1. Чтобы найти второе наименьшее значение, k = 2 и т. Д.

Чтобы найти три наибольших значения, используйте функцию НАИБОЛЬШИЙ () с теми же параметрами, что и НАИМЕНЬШИЙ ().

Обратите внимание, что SMALL () с k = 1 дает точно такой же результат, что и MIN (). Точно так же LARGE () с k = 1 дает то же, что и MAX ().

3. Формулы условного минимума и максимума

В некоторых ситуациях может потребоваться минимальное значение, отвечающее определенным критериям. Например, вы можете узнать наименьшее количество единиц, проданных за весенний квартал или для определенного типа продукта.

Excel предоставляет СУММЕСЛИ (), СЧЁТЕСЛИ () и другие полезные условные формулы. К сожалению, здесь нет MINIF () или MAXIF (), но вы можете создать тот же эффект с помощью немного более сложного метода, называемого формулой массива. Формула массива оценивает диапазон ячеек вместо одной ячейки.

Обычно формула IF () проверяет значение истинности отдельной ячейки, но, как формула массива, мы можем заставить ее оценивать каждую ячейку в диапазоне. При использовании формулы массива вы получите сообщение об ошибке, если просто нажмете клавишу ввода — #VALUE !.Не забудьте нажать CTRL, SHIFT и ENTER после завершения формулы массива.

Найдем минимальное значение для настольных компьютеров. Сначала введите соответствующее значение (рабочий стол) в ячейку, с которой вы сравниваете свою функцию. Если вы ищете значения рабочего стола, введите «рабочий стол» в B18. Приведенная ниже формула сравнит эту ссылку на ячейку с тестируемым диапазоном. Вложите инструкции MIN () и IF () следующим образом: «= MIN (IF (B2: B13 = B18, C2: C13))» и нажмите — — .

Три формулы в строках 18, 19 и 20 вычисляют минимальное количество проданных настольных компьютеров, ноутбуков и планшетов.Вы можете написать идентичные формулы с помощью MAX (), чтобы найти наибольшее количество каждого проданного продукта.

Следующие шаги

Теперь вы можете использовать три различных метода (формулы минимума и максимума, формулы верхнего k и нижнего k , формулы условного минимума и максимума), чтобы найти диапазон значений в любом наборе данных.

Советы и рекомендации по работе с Excel от Pryor.com

Excel Tips & Tricks написан экспертами Microsoft® Excel® из Fred Pryor Seminars и CareerTrack.Известные своим обширным обучением в области Excel, мы предлагаем одни из лучших в отрасли. Не тратьте драгоценное время на то, чтобы разобраться во всем самостоятельно. Посетите один из наших замечательных курсов по Excel и получите знания, необходимые для более эффективного и действенного использования Excel.

No related posts.