Геометрическое место точек
Тема: Геометрическое место точек
Теория
Задачи
p/q=/= 1 есть окружность с центром на прямой АВ. Выразить диаметр этой окружности через длину a отрезка АВ. Исследовать также случай
p/q= 1 Смотреть решение →
razdupli.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом.
Геометрические места точек на плоскости
| Дано | Найти | Ответ (ГМТ) | Рисунок |
| Точка и число r | Геометрическое место точек, находящихся на расстоянии r от данной точки. | Окружность радиуса r | |
| Угол | Геометрическое место точек, равноудалённых от сторон данного угла. | Биссектриса угла | |
| Пара пересекающихся прямых | Геометрическое место точек, равноудалённых от пары данных пересекающихся прямых. | Две перпендикулярных прямых (биссектрисы углов, образованных данными прямыми) | |
| Отрезок | Геометрическое место точек, равноудалённых от концов данного отрезка. | Серединный перпендикуляр к отрезку | |
| Прямая и число d | Геометрическое место точек, находящихся на расстоянии d от данной прямой. | Пара параллельных прямых | |
| Пара параллельных прямых | Геометрическое место точек, каждая из которых равноудалена от двух данных параллельных прямых. | Прямая | |
| Отрезок и угол, величина которого равна α | Геометрическое место точек, из которых данный отрезок виден под данным углом | Две дуги окружностей одинакового радиуса, для которых данный отрезок является общей хордой, причём из дуг исключены концы отрезка. |
| ||||
| ||||
| ||||
| ||||
|
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Материал по математике «Геометрические места точек»
Геометрическим местом точек
В решении задач ГМТ должны присутствовать три момента:
1) предъявлено множество Р, про которое мы утверждаем, что оно-искомое;
2) доказано, что каждая точка множества Р обладает заданным свойством;
3) доказано, что нет других точек, обладающих данным свойством.
Важнейшими ГМТ в пространстве являются следующие:
а) ГМТ, удаленных на расстояние R > 0 от данной точки О, есть (по определению) сфера радиуса R с центром в точке О.
б) ГМТ, равноудаленных от двух различных точек А и В есть плоскость Р, перпендикулярная отрезку АВ и проходящая через его середину.
в) ГМТ, равноудаленных от трех не лежащих на одной прямой точек А, В и С есть прямая, перпендикулярная плоскости АВС и проходящая через центр окружности, описанной около треугольника АВС.
г) ГМТ, равноудаленных от сторон двугранного угла, есть его биссектральная плоскость.
д) Геометрическим местом точек М (х, у, z) пространства с системой координат Охуz таких, что Ах + Ву + Сz + D = 0 (А, В, С, D – числа такие, что А2 + В2 + С2 не равно 0) является плоскостью, перпендикулярная вектору n {A,B.C}.
е) Уравнение (х – а) 2 + (у – b) 2 + (z – с) 2 = R2, где R Ю 0, задает сферу радиуса R с центром в точке O (а, b, с).
Если мы знаем ГМТ, М1, определяемое свойством Р1 и ГМТ М2, определяемое свойством Р2, то ГМТ, для которых одновременно выполняются свойства Р1 и Р2, есть пересечение множеств М1 и М2.
Как правило, можно понять, как устроено искомое ГМТ, если разбить данное свойство на более простые, найти соответствующие более простые ГМТ и из них построить искомое. Иногда удается ввести систему координат и записать данное свойство в виде формулы f(х, у, z ) = 0. Иногда нужно угадать хорошую геометрическую закономерность, присутствующую в данном свойстве.
Задача 1. Найти геометрическое место оснований перпендикуляров, опущенных из точки А на всевозможные прямые, проходящие через фиксированную точку В.
Решение. Искомое ГМТ есть сфера, построенная на отрезке АВ как на диаметре. В самом деле, если мы проведем произвольную плоскость через прямую АВ, то из всех точек искомого ГМТ в этой плоскости отрезок АВ будет виден под прямым углом, так что пересечение искомого ГМТ с плоскостью, проходящей через прямую АВ есть окружность, построенная на АВ как на диаметре.
Теперь уже ясно, что ГМТ обязано быть сферой радиуса AB/2 с центром в середине АВ.
Ответ: сфера, построенная на отрезке АВ как на диаметре.
Задача 2. В пространстве даны две точки А и В. Найдите геометрическое место таких точек М, что АМ2 – ВМ2 = b2, где b > 0.
Решение. Возьмем такую же систему координат, как в предыдущей задаче. Точка М (х, у, z ) принадлежит искомому ГМТ, если и только если
МА2 – МВ2 = b2 — ((х + а ) 2 + у2 + z2 ) – ((х – а ) 2 + у2 + z2 ) = b2
Очевидно, это уравнение плоскости, пертендикулярной оси Ох, т. е. прямой АВ. Точка пересечения этой плоскости с прямой АВ зависит от числа b2/4a.
Ответ: плоскость, перпендикулярная прямой АВ, пересекающая ее правее середины отрезка АВ на расстоянии b2/2AB от нее.
Задачи для самостоятельного решения.
Дана сфера. Найдите геометрическое место центров сфер, вписанных в тетраэдры, вписанные в данную сферу.
В провтранстве дана точка А. Найдите геометрическое место проекций А на всевозможные плоскости, проходящие через прчмую f, не содержащую точку А.
В пространстве дана точка О и две прямые. Найдите геометрическое место точек М, для которых сумма длин проекций отрезка ОМ на данные прямые есть величина постоянная.
Найдите геометрическое место середин общих касательных к двум заданным сферам.
Найдите геометрическое место центров сфер, касающихся двух данных пересекающихся прямых.
videouroki.net
Геометрическое место точек » Страница 2
Тема: Геометрическое место точек
Теория
Задачи
- вершины А и В закреплены;
- вершина А закреплена.
razdupli.ru
Геометрическое место точек — это… Что такое Геометрическое место точек?
Геометри́ческое ме́сто то́чек (ГМТ) — фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.
Примеры
Формальное определение
В общем случае, геометрическое место точек формулируется параметрическим предикатом, аргументом которого является точка данного линейного пространства. Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант , где — точка, — дифференциалы, то искомую фигуру задают в виде: « — геометрическое место точек , таких, что ». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек , для которых для каждого конкретного набора значений высказывание обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.
В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.
Пример: параболу зададим как множество всех таких точек , что расстояние от до точки равно расстоянию от до прямой . Тогда дифференциалы параболы — и ; детерминант — предикат , где — расстояние между двумя точками (метрика), — расстояние от точки до прямой. И говорят: «Парабола — геометрическое место точек , равноудалённых от точки и прямой . Точку называют фокусом параболы, а прямую — директрисой».
Ссылки
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011. |
dic.academic.ru
Метод геометрических мест точек
Поиск ЛекцийОдним из методов решения задач на построение является метод геометрических мест. Понятие геометрического места является одним из важнейших в геометрии. Термин «геометрическое место точек» был введен еще древнегреческим ученым и философом Аристотелем (384-222 гг. до новой эры), который представлял себе линию, как некоторое «место», где могут быть размещены точки. Понятие линии как следа движущей точки или совокупность точек, возникли значительно позже.
Геометрическим местом точек (сокращенно ГМТ), обладающих определенным свойством, называется множество всех точек, которые обладают этим свойством.
Сущность метода состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X , удовлетворяющую двум условиям. ГМТ, удовлетворяющих первому условию, есть некоторая фигура A, а ГМТ, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит A и B, т.е. является их точкой пересечения.
При решении задач этим методом надо знать основные геометрические места точек на плоскости:
1. ГМТ, равноудаленных от двух данных точек.
2. ГМТ, находящихся на данном расстоянии oт данной точки.
3. ГМТ, удаленных на расстояние d oт данной прямой.
4. ГМТ, равноудаленных от двух данных параллельных прямых.
5. ГМТ, равноудаленных от сторон угла.
6. ГМТ, из которых данный отрезок виден под данным углом.
Некоторые геометрические места точек, часто используемые
Рассмотрим построение основных ГМТ, перечисленных в предыдущем пункте.
1. Геометрическим местом точек, равноудаленных от двух данных
точек, является серединный перпендикуляр к отрезку с концами в этих
точках.
2. Геометрическим местом точек, находящихся на данном расстоянии
oт данной точки, является окружность с центром в данной точке и радиусом, равном данному отрезку.
3. Геометрическим местом точек, удаленных на расстояние d oт
данной прямой в выбранной полуплоскости, является прямая
параллельная данной и находящаяся на расстоянии d от нее.
А выбираем произвольно.
4. Геометрическим местом точек, равноудаленных от двух данных
параллельных прямых, является прямая, находящаяся на одинаковом
расстоянии от данных прямых (ось симметрии этих прямых).
ОА=ОВ
5. Геометрическим местом точек, равноудаленных от сторон угла,
является биссектриса этого угла. (См. построение 4).
6. Геометрическим местом точек, из которых данный отрезок виден под
данным углом, является дуга окружности, опирающейся на этот отрезок.
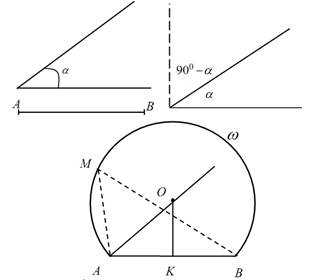I случай:
— данный угол,
АВ – данный отрезок.
Построение:
Действительно, ∟АМВ, как угол, вписанный в окружность, измеряется
половиной малой дуги АВ, так как центральный угол ∟АОВ = 2α, то
∟АМВ = α.
При этом заметим, что центр окружности О и вершина М угла лежат по
одну сторону от данного отрезка
II случай:
1. О – середина АВ.
Полуокружность
(Любой угол, опирающийся на диаметр –
прямой).
III случай:
Действительно, ∟АОВ = 2( 900 – (α — 900)) = 2(1800 — α). Тогда большая дуга
АВ равна 3600 – 2(1800 — α) = 2α и угол АМВ, опирающийся на большую дугу АВ, измеряется половиной этой дуги, т.е. равен α.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК — это… Что такое ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК?
- ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК, в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее нахождения до центра остается неизменным.
Научно-технический энциклопедический словарь.
- ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ
Смотреть что такое «ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК» в других словарях:
геометрическое место точек — местоположение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы местоположение EN locus … Справочник технического переводчика
Геометрическое место точек — (ГМТ) фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством. Примеры Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов… … Википедия
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК — понятие, иногда используемое в геометрии. Обычно под Г. м. т. понимают множество точек (образующих кривую или поверхность), выделяемых из всех точек пространства к. л. геометрич. требованием. Напр., эллипс может быть определен как Г. м. т.… … Математическая энциклопедия
кривая круговых точек — circle point curve Геометрическое место круговых точек на движущейся плоской фигуре. Шифр IFToMM: 2.3.31 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
Середина моста — геометрическое место точек, равноудаленных от начала и конца моста. Источник: Справочник дорожных терминов … Строительный словарь
Середина пролета — геометрическое место точек, равноудаленных от смежных опорных частей. Источник: Справочник дорожных терминов … Строительный словарь
График LM(LM SCHEDULE) — геометрическое место точек всех комбинаций уровней реального дохода и процентных ставок, соответствующих состоянию равновесия на денежном рынке … Современные деньги и банковское дело: глоссарий
кривая инверсии — Геометрическое место точек на термодинамической диаграмме, отображающих состояния вещества, в которых дроссельный эффект меняет свой знак … Политехнический терминологический толковый словарь
кривая фазового равновесия — Геометрическое место точек, отображающих на термодинамической диаграмме состояния сосуществующих фаз … Политехнический терминологический толковый словарь
КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… … Энциклопедия Кольера
dic.academic.ru