2+n-72)=1/(n+9)Венозный синус склеры — vet-Anatomy
ПОДПИСАТЬСЯ
ПОДПИСАТЬСЯ
Анатомия животных
Sinus venosus sclerae
Определение
Определение этой анатомической структуры пока отсутствует
Я даю согласие на уступку прав, связанных с моим участием в проекте, в соответствии с Правила и условия пользования сайтом.
Я даю согласие на уступку прав, связанных с моим участием в проекте, в соответствии с Правила и условия пользования сайтом.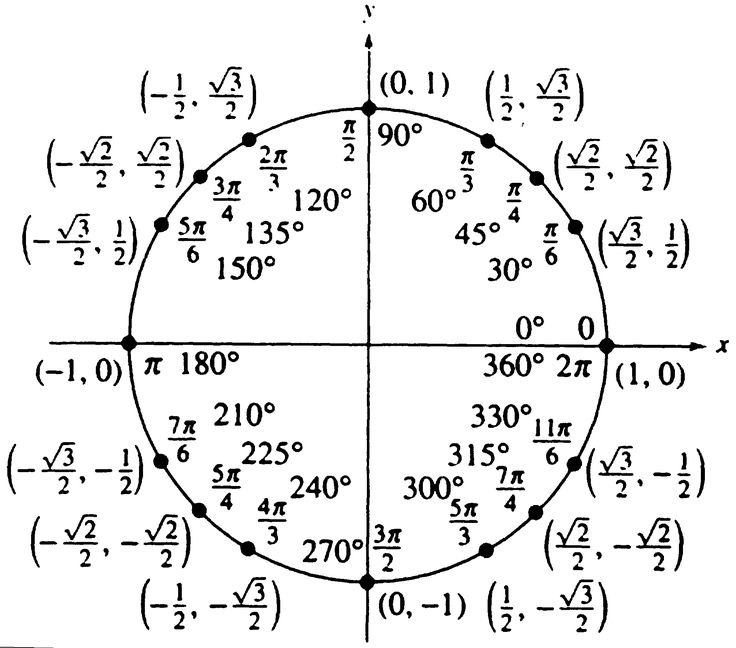
Анатомическая иерархия
Органы чувств > Орган зрения > Глаз > Глазное яблоко > Фиброзная оболочка глаза > Склера > Венозный синус склеры
Основные структуры: Нет анатомических терминов, относящихся к этой части тела
Сравнительная анатомия человека
- Венозный синус склеры
Переводы
Заметили ошибку?
Не стесняйтесь предложить поправку, свою версию перевода или решение по улучшению контента.
Сообщить об ошибке
Ваши комментарии помогают нам улучшить содержимое сайта. Не стесняйтесь предлагать поправки. Мы их внимательно рассмотрим.
Пожалуйста, опишите ошибкуПоказать больше
Показать меньше
IMAIOS и некоторые третьи лица используют файлы cookie или подобные технологии, в частности для измерения аудитории. Файлы cookie позволяют нам анализировать и сохранять такую информацию, как характеристики вашего устройства и определенные персональные данные (например, IP-адреса, данные о навигации, использовании и местонахождении, уникальные идентификаторы). Эти данные обрабатываются в следующих целях: анализ и улучшение опыта пользователя и/или нашего контента, продуктов и сервисов, измерение и анализ аудитории, взаимодействие с социальными сетями, отображение персонализированного контента, измерение производительности и привлекательности контента.
Вы можете дать, отозвать или отказаться от согласия на обработку данных в любое время, воспользовавшись нашим инструментом для настройки файлов cookie. Если вы не согласны с использованием данных технологий, это будет расцениваться как отказ от имеющего правомерный интерес хранения любых файлов cookie. Чтобы дать согласие на использование этих технологий, нажмите кнопку «Принять все файлы cookie».
Аналитические файлы сookie
Эти файлы cookiе предназначены для измерения аудитории: статистика посещаемости сайта позволяет улучшить качество его работы.
- Google Analytics
тригонометрия — построение основных синусоидальных и косинусоидальных кривых.
Воспользуемся определением, что синус угла в стандартном положении (вершина в начале координат, начальная сторона на положительной оси $x$) есть $y$-координата точки пересечения конечной стороны угла единичный круг.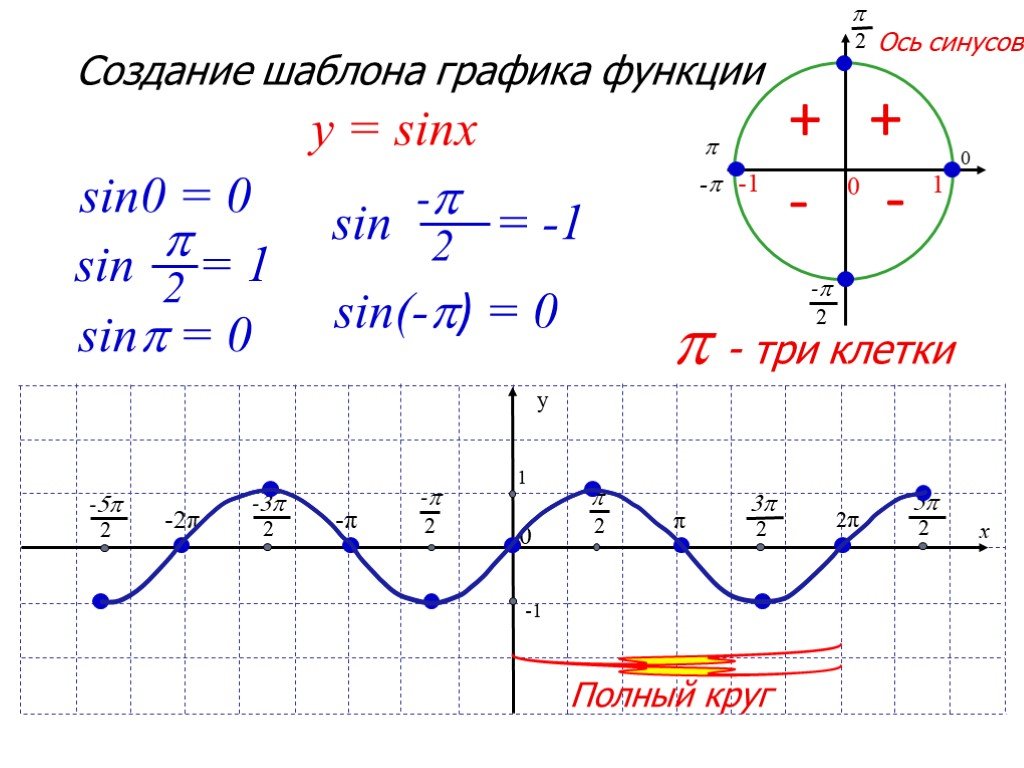
Таким образом, график синусоидальной функции $f(x) = \sin x$ получается отслеживанием $y$-координат точки, в которой конечная сторона угла пересекает единичную окружность при ее вращении вокруг круг.
После завершения полного оборота окружности продолжение вращения конечной стороны угла вокруг окружности приводит к повторению значений. Следовательно, функция синуса является периодической. Поскольку в полном круге содержится $2\pi$ радиан,
$$f(x + 2\pi) = \sin(x + 2\pi) = \sin x = f(x)$$
Так как не существует меньшего положительного значения $p$ такого, что $f(x + p ) = f(x)$ для каждого $p$ в своей области определения синусоидальная функция имеет период $2\pi$.
Вас попросили ограничить область определения функции интервалом $[2\pi, 4\pi]$, что дает график, показанный ниже.
Назовем функцию в вашем примере $g$. Тогда $g: [2\pi, 4\pi] \to [-1, 1]$ — это функция, определяемая равенством $g(x) = \sin x$.
Так как $0$ не находится в домене $g$, у него нет $y$-перехвата.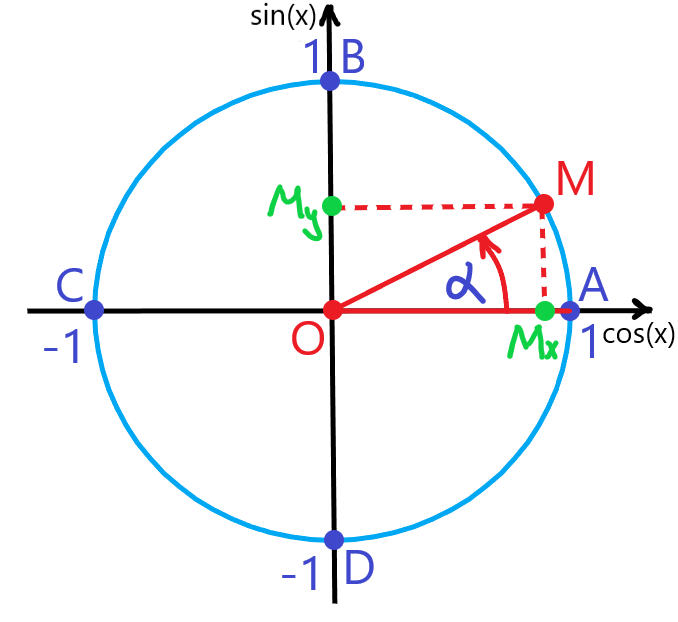
Функция синуса $f(x) = \sin x$ имеет точку пересечения $x$ в каждой точке, где конечная сторона угла лежит на оси $x$, что происходит при $x = n\pi , п \in \mathbb{Z}$. Три значения, при которых это происходит в области определения $g$, это $2\pi$, $3\pi$ и $4\pi$.
Синусоидальная функция $f(x) = \sin x$ достигает своего максимального значения $1$ всякий раз, когда конечная сторона угла лежит на положительной оси $y$, что происходит, когда \начать{выравнивать*} х & = \arcsin (1) + 2n\pi, n \in \mathbb{Z}\\ & = \frac{\pi}{2} + 2n\pi, n \in \mathbb{Z} \конец{выравнивание*} где член $2n\pi$ используется для учета периодичности функции синуса, поскольку все углы, которые отличаются на целое число, кратное $2\pi$, имеют одинаковое значение синуса. Единственным таким значением в области определения $g$ является $$\frac{\pi}{2} + 2\pi = \frac{5\pi}{2}$$
Синусоидальная функция $f(x) = x$ достигает своего минимального значения $-1$ всякий раз, когда конечная сторона угла лежит на отрицательной оси $y$, что происходит, когда
\начать{выравнивать*}
х & = \arcsin(-1) + 2n\pi, n \in \mathbb{Z}\\
& = -\frac{\pi}{2} + 2n\pi, n \in \mathbb{Z}
\конец{выравнивание*}
Единственным таким значением в области определения $g$ является
$$x = -\frac{\pi}{2} + 4\pi = \frac{7\pi}{2}$$
Опять же, член $2n\pi$ используется для учета периодичности синусоидальной функции.
Я ответил на ваши второй и третий вопросы выше. Что касается вашего первого вопроса, обратите внимание, что функция обратного синуса $h: [-1, 1] \to [-\frac{\pi}{2}, \frac{\pi}{2}]$, обозначаемая $ h(x) = \arcsin x$, определяется формулой $$\arcsin x = y \iff\sin y = x, -\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$$
Поскольку $0$ — единственный угол в интервале $[-\frac{\pi}{2}, \frac{\pi}{2}]$ с синусом, равным нулю, $\arcsin(0) = 0$. Поскольку синусоидальная функция имеет период $2\pi$, знание того, что арксинус нуля равен нулю, означает, что $g$ будет иметь $x$-пересечений в точках $2\pi$ и $4\pi$. Это не говорит вам, что $g$ также имеет ноль в точке $3\pi$. Для этого значения вы можете использовать сделанное выше наблюдение о том, что функция синуса равна нулю, когда конечная сторона угла лежит на оси $x$.
Видео с вопросами: Распознавание тригонометрических функций по их графикам
Стенограмма видео
Рассмотрим следующие рисунки (a) и (b).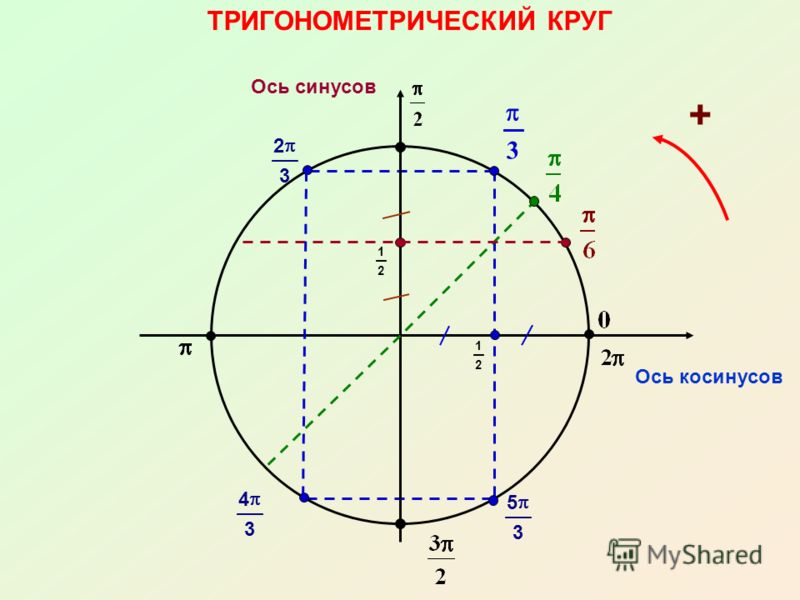
Какую функцию представляет график на графике (рис. а)? (A) синус или (B) косинус. Назначьте каждой области графика на рисунке (а) соответствующий квадрант единичного круга на рисунке (б).
Итак, во-первых, нам нужно определить, представляет ли график на рисунке (a) функцию синуса или косинуса. Напомним, что графики этих двух функций имеют одинаковую основную форму и много одинаковых признаков. Например, они оба колеблются между минимальным значением отрицательной единицы и максимальным значением положительной единицы. Чтобы определить, какую из двух функций представляет этот график, рассмотрим корни. Мы видим, что значения этой функции равны нулю, когда угол равен двум 𝜋 и трем 𝜋. Продолжая движение по оси 𝑥, также будут корни в четырех 𝜋, пяти 𝜋 и так далее, по существу, во всех целых числах, кратных 𝜋.
Глядя конкретно на значение двух 𝜋, нам нужно определить, является ли синус двух 𝜋 или cos двух 𝜋 равным нулю. И это скажет нам, является ли синусоидальная или косинусная функция изображена на рисунке (а).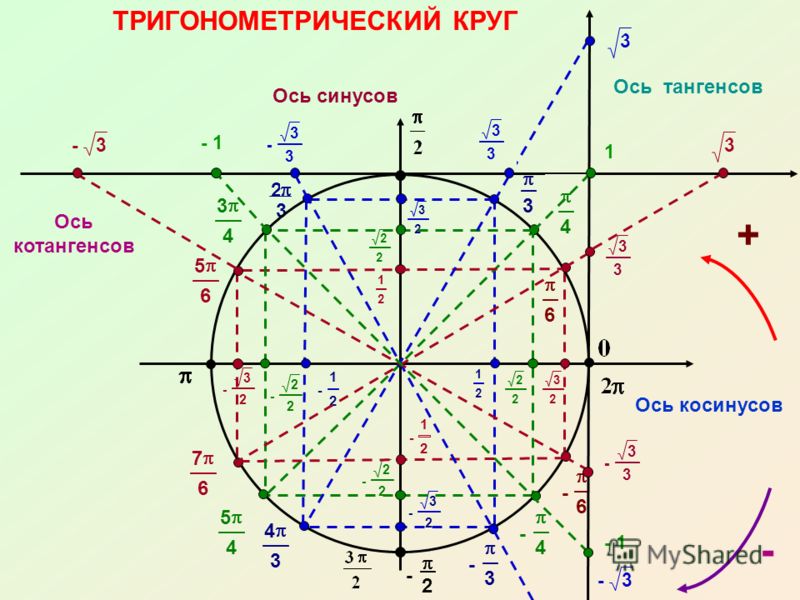
Для этого воспользуемся единичным кругом. Напомним, что точки на единичной окружности имеют координаты cos 𝜃, sin 𝜃, где 𝜃 — угол против часовой стрелки между положительной осью 𝑥 и радиусом, соединяющим точку с началом координат. Положительные углы измеряются против часовой стрелки от положительной оси 𝑥. Угол в два 𝜋 радиана соответствует одному полному обороту против часовой стрелки, который возвращает нас на положительную 𝑥-ось.
Точка на единичной окружности, лежащая на положительной оси 𝑥, имеет координаты единица, ноль. Таким образом, это говорит нам о том, что cos двух 𝜋 должен быть равен единице; это 𝑥-координата. А грех двух 𝜋 должен быть равен нулю; это 𝑦-координата. Затем мы обнаружили, что именно синусоидальная функция равна нулю, когда угол равен двум 𝜋, и поэтому эта функция представлена на рисунке (а).
Теперь рассмотрим вторую часть вопроса, в которой нас просят сопоставить каждой области графика на рисунке (а) соответствующий квадрант единичного круга на рисунке (б).
Прежде всего, если рассматривать область А, она содержит все углы между тремя 𝜋 более чем двумя и двумя 𝜋 радианами. Мы уже говорили, что угол в два 𝜋 радиана соответствует одному полному обороту против часовой стрелки от положительной 𝑥-оси, возвращая нас к положительной 𝑥-оси. Угол в три 𝜋 на два радиана будет соответствовать трем четвертям оборота против часовой стрелки, что приводит нас к отрицательной оси 𝑦. Таким образом, углы между тремя 𝜋 больше двух и двумя 𝜋 радиан лежат в четвертом квадранте единичной окружности. Таким образом, область А относится к четвертому квадранту.
Далее мы рассмотрим область B, которая содержит все углы между двумя 𝜋 радианами и пятью 𝜋 более чем на два радиана. Мы уже знаем, что угол, равный двум 𝜋, возвращает нас к положительной оси 𝑥. Угол в пять 𝜋 больше двух радиан — это угол в два 𝜋 плюс еще один 𝜋 на два. Это еще четверть оборота против часовой стрелки от положительной оси 𝑥. Мы проходим весь путь один раз, а затем снова четверть пути.