Какая статистика используется при проверке гипотезы о значении генеральной: 2. Проверка гипотезы о значении генеральной дисперсии нормально распределённой совокупности.

2. Проверка гипотезы о значении генеральной дисперсии нормально распределённой совокупности.

Пусть из генеральной совокупности, значения которой распределены по нормальному закону с неизвестной дисперсией , взята случайная выборка изn независимых наблюдений и вычислена выборочная дисперсия S².

Требуется проверить нулевую гипотезу , где- определённое значение генеральной дисперсии. Для проверки нулевой гипотезы используют статистику

, (10)

которая при выполнении гипотезы имеет распределениесстепенями свободы.

В зависимости от конкурирующей гипотезы рассматривают левостороннюю, правостороннюю или двустороннюю критические области. Границы критических областей определяют по таблице распределения — Пирсона.

Рассмотрим три случая:

1. Если , то выбирают правостороннюю критическую область инаходят из условия

.

Правила проверки гипотезы заключаются в следующем:

1) если , то нулевая гипотеза не отвергается;

2) если , то нулевая гипотеза отвергается.

2. Если , то строят левостороннюю критическую область инаходят из условия

.

Правила проверки гипотезы заключаются в следующем:

1) если , то гипотеза не отвергается;

2) если , то гипотеза отвергается

3. Если , то строят двустороннюю критическую область и её границыинаходят из условий:

;

Правила проверки гипотезы заключается в следующем:

Если , то гипотеза не отвергается, в противном случае отвергается.

Пример 1. Точность работы автоматической линии проверяют по дисперсии контролируемого признака, которая не должна превышать 0,1 мм

2. По результатам выборочного контроля получены следующие данные:

Контролируемый размер xi	43,0	43,5	43,8	44,4	44,6
Частота mi	3	7	10	8	2

Требуется проверить на уровне значимости 0,01, обеспечивает ли линия требуемую точность.

Решение: Задача состоит в проверке гипотезы о значении генеральной дисперсии . Автоматическая линия не обеспечивает требуемую точность, если, следовательно, в данном случае строим правостороннюю критическую область.

Для вычисления статистики по формуле (10), необходимо найти выборочную дисперсию. Примем значениеC = 43,8, а вычисление оформим в таблице:

43,0	3	— 0,8	— 2,4	1,92
43,5	7	— 0,3	— 2,1	0,63
43,8	10	0	0	0
44,4	8	0,6	4,8	2,88
44,6	2	0,8	1,6	1,28
Итого:	30	—	1,9	6,71

По таблице — распределения при заданном уровне значимостииполучаем.

Сравнивая и, делаем вывод о том, что гипотезаотвергается. Это значит, что генеральная дисперсия не равна 0,1, линия не обеспечивает заданную точность и требуется её регулировка.

Мощность критерия может быть вычислена только при проверке простых гипотез: гипотезы о значении генеральной средней и гипотезы о генеральной дисперсии и только при односторонней критической области.

Проверка гипотез

Общий обзор

Определение нулевой и альтернативной гипотезы, уровня статистической значимости

Получение статистики критерия, определение критической области

Получение значения р (достигнутого уровня значимости)

Применение значения р

Проверка гипотез против доверительных интервалов

Общий обзор

Часто делают выборку, чтобы определить аргумен­ты против гипотезы относительно популяции (генеральной совокупности).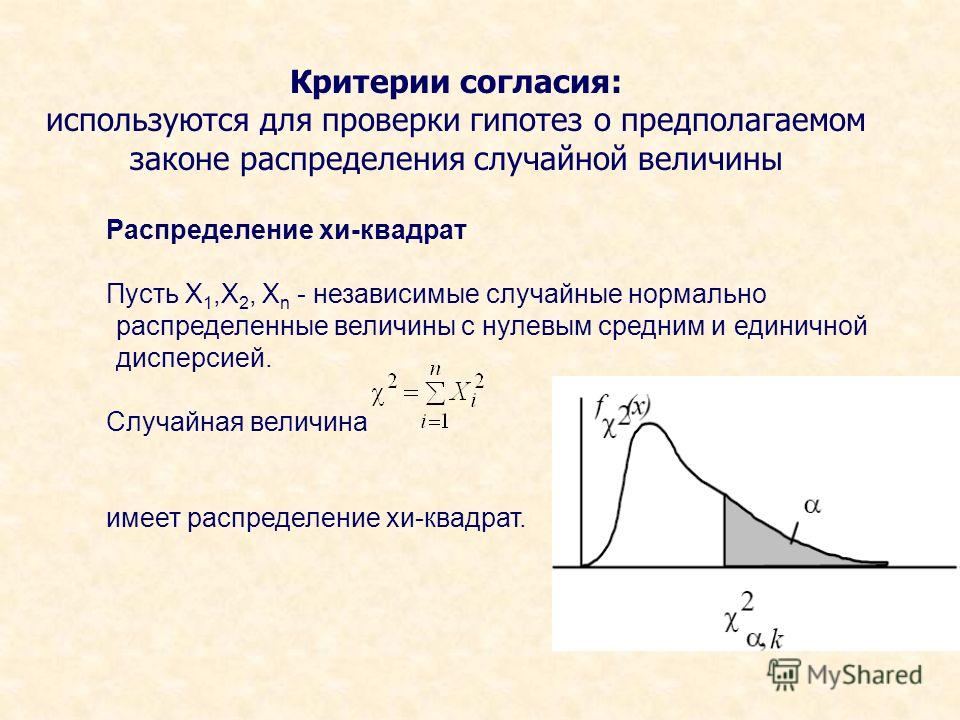 Этот процесс известен как проверка гипотез (проверка статистических гипотез или проверка значимости), он представляет количественную меру аргументов про­тив определенной гипотезы.

Установлено 5 стадий при проверке гипотез:

1. Определение нулевой () и альтернативной гипотезы () при исследовании. Определение уровня значимости критерия.
   
2. Отбор необходимых данных из выборки.
3. Вычисление значения статистики критерия, отвечающей .
4. Вычисление критической области, проверка статистики критерия на предмет попадания в критическую область.
   
5. Интерпретация достигнутого уровня значимости р и результатов.

Определение нулевой и альтернативной гипотез, уровня статистической значимости

При проверке значимости гипотезу следует формулировать независимо от используемых при ее проверке данных (до проведения проверки). В таком случае можно получить действительно продуктивный результат.

Всегда проверяют нулевую гипотезу (), которая отвергает эффект (например, разница средних равняется нулю) в популяции.

Например, при сравнении показателей курения у мужчин и женщин в популяции нулевая гипотеза означала бы, что показатели курения одинаковые у женщин и мужчин в популяции.

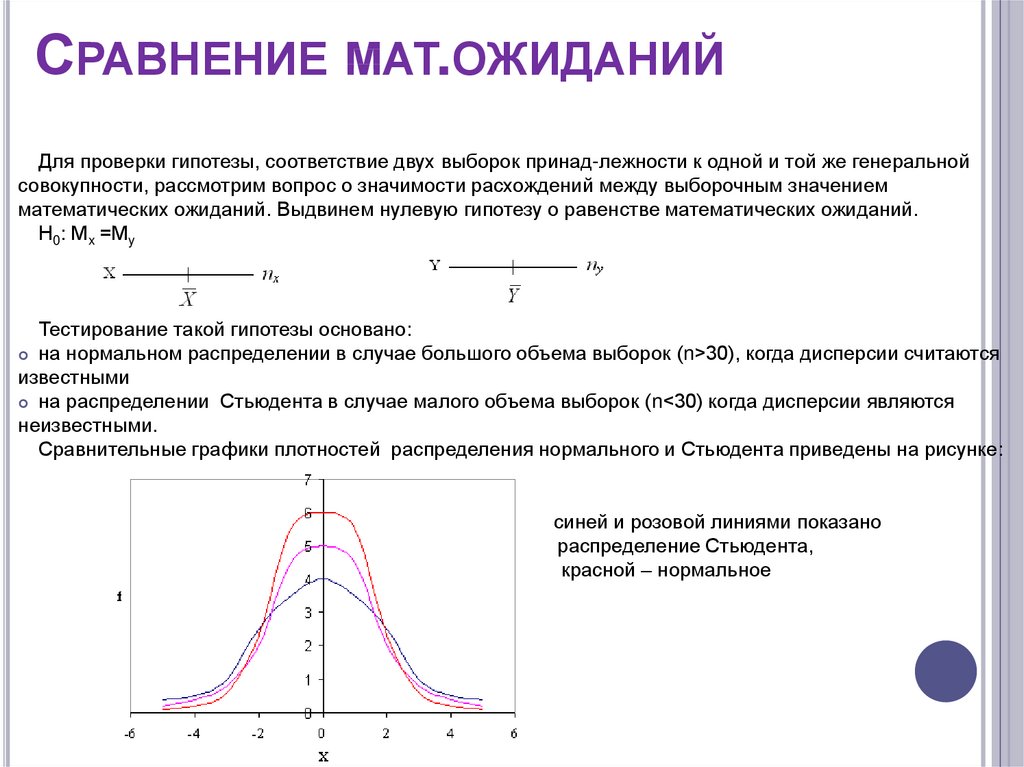
Затем определяют альтернативную гипотезу (), которая принимается, если нулевая гипотеза неверна. Альтернативная гипотеза больше относится к той теории, которую собираются исследовать. Итак, на этом примере альтернативная гипотеза заключается в утверждении, что показатели курения различны у женщин и мужчин в популяции.

Разницу в показателях курения не уточнили, т.е. не установили, имеют ли в популяции мужчины более высокие или более низкие показатели, чем женщины. Такой подход известен как двусторонний критерий, потому что учитывают любую возможность, он рекомендуется постольку, поскольку редко есть уверенность заранее в направлении какого-либо различия, если таковое существует.

В некоторых случаях можно использовать односторонний критерий для гипотезы , в котором направление эффекта задано. Его можно применить, например, если рассматривать заболевание, от которого умерли все пациенты, не получившие лечения; новый препарат не мог бы ухудшить положение дел.

Уровень значимости. Важным этапом проверки статистических гипотез является определение уровня статистической значимости , т.е. максимально допускаемой исследователем вероятности ошибочного отклонения нулевой гипотезы.

Получение статистики критерия, определение критической области

После того как данные будут собраны, значения из выборки подставляют в формулу для вычисления статистики критерия (примеры различных статистик критериев см. ниже). Эта величина количественно отражает аргументы в наборе данных против нулевой гипотезы.

Критическая область. Для принятия решения об отклонении или не отклонении нулевой гипотезы необходимо также определить критическую область проверки гипотезы.

Выделяют 3 вида критических областей:

• двусторонняя:

Рис. 1 Двусторонняя критическая область

• левосторонняя:

Рис. 2 Левосторонняя критическая область



• правосторонняя:

Рис. 3 Правосторонняя критическая область

— заданный исследователем уровень значимости.

Если наблюдаемое значение критерия (K) принадлежит критической области (K_кр, заштрихованная область на рис.1-3), гипотезу отвергают, если не принадлежит — не отвергают.

Для краткости можно записать и так:


| K | > K_кр — отклоняем H₀

| K

| < K_кр — не отклоняем H₀

Получение значения

р (достигнутого уровня значимости)

Все статистики критерия подчиняются известным теоретическим распределениям вероятности. Значение статистики критерия, полученное из выборки, связывают с уже известным распределением, которому она подчиняется, чтобы получить значение р, площадь обоих «хвостов» (или одного «хвоста», в случае односторонней гипотезы) распределения вероятности.


Большинство компьютерных пакетов обеспечивают автоматическое вычисление двустороннего значения р.


Значение р — это вероятность получения нашего вычисленного значения критерия или его еще большего значения, если нулевая гипотеза верна.

Иными словами, p — это вероятность отвергнуть нулевую гипотезу при условии, что она верна.


Нулевая гипотеза всегда относится к популяции, представляющей больший интерес, нежели выборка. В рамках проверки гипотезы мы либо отвергаем нулевую гипотезу и принимаем альтернативу, либо не отвергаем нулевую гипотезу. Подробнее об ошибках при проверке гипотез

Применение значения

р

Следует решить, сколько аргументов позволят отвергнуть нулевую гипотезу в пользу альтернативной. Чем меньше значение р, тем сильнее аргументы против нулевой гипотезы.

• Традиционно полагают, если р < 0,05, (=0,05) то аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс против этого. Тогда можно отвергнуть нулевую гипотезу и сказать, что результаты значимы на 5% уровне.

• Напротив, если р > 0,05, то аргументов недостаточно, чтобы отвергнуть нулевую гипотезу. Не отвергая нулевую гипотезу, можно заявить, что результаты не значимы на 5% уровне. Данное заключение не означает, что нулевая гипотеза истинна, просто недостаточно аргументов (возможно, маленький объем выборки), чтобы ее отвергнуть.

Уровень значимости (т.е. выбранная «граница отсечки») 5% задается произвольно. На уровне 5% можно отвергнуть нулевую гипотезу, когда она верна. Если это может привести к серьезным последствиям, необходимо потребовать более веских аргументов, прежде чем отвергнуть нулевую гипотезу, например, выбрать значение = 0,01 (или 0,001).

Определение результата только как значимого на определенном уровне граничного значения (например 0, 05) может ввести в заблуждение. Например, если р = 0,04, то нулевую гипотезу отвергаем, но если р = 0,06, то ее не отвергли бы. Действительно ли они различны? Мы рекомендуем всегда указывать точное значение р, обычно получаемое путем компьютерного анализа.

Проверка гипотез против доверительных интервалов

Доверительные интервалы и проверка гипотез тесно связаны. Первоначальная цель проверки гипотезы состоит в том, чтобы принять решение и предоставить точное значение р.


Доверительный интервал (ДИ) количественно определяет изучаемый эффект (например, разницу в средних) и дает возможность оценить значение результатов. ДИ предоставляют интервал вероятных значений для истинного эффекта, поэтому его также можно использовать для принятия решения даже без точных значений р.


Например, если бы гипотетическое значение для данного эффекта (например, значение, равное нулю) находилось вне 95% ДИ, можно было бы счесть гипотетическое значение неправдоподобным и отвергнуть . В этом случае станет известно, что р < 0,05, но не станет известно его точное значение

Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии


В начало

Содержание портала

Что это такое, как его рассчитать и почему это важно

Что такое P-значение?

В статистике p-значение – это вероятность получения результатов, по крайней мере столь же экстремальных, как и наблюдаемые результаты проверки статистической гипотезы, при условии, что нулевая гипотеза верна. Значение p служит альтернативой точкам отклонения, чтобы обеспечить наименьший уровень значимости, при котором нулевая гипотеза будет отклонена. Меньшее значение p означает, что есть более сильные доказательства в пользу альтернативной гипотезы.

Р-значение часто используется для повышения доверия к исследованиям или отчетам государственных органов. Например, Бюро переписи США требует, чтобы любой анализ с p-значением, превышающим 0,10, должен сопровождаться заявлением о том, что разница статистически не отличается от нуля. различные публикации.

Ключевые выводы

• Значение p — это статистическое измерение, используемое для проверки гипотезы на основе наблюдаемых данных.
• Значение p измеряет вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна.
• Чем ниже p-значение, тем выше статистическая значимость наблюдаемой разницы.
• Значение p 0,05 или ниже обычно считается статистически значимым.
• P-значение может служить альтернативой или дополнением к предварительно выбранным уровням достоверности для проверки гипотез.

Нажмите «Воспроизвести», чтобы узнать, как рассчитывается P-значение

Как рассчитывается P-значение?

P-значения обычно находятся с помощью таблиц p-значений или электронных таблиц/статистического программного обеспечения. Эти расчеты основаны на предполагаемом или известном распределении вероятностей конкретной тестируемой статистики. P-значения рассчитываются из отклонения между наблюдаемым значением и выбранным эталонным значением с учетом распределения вероятностей статистики, при этом большая разница между двумя значениями соответствует более низкому p-значению.

Математически p-значение рассчитывается с использованием интегрального исчисления на основе площади под кривой распределения вероятностей для всех значений статистики, которые по крайней мере так же далеки от эталонного значения, как и наблюдаемое значение, относительно общей площади под кривой распределения вероятностей. .

Расчет p-значения зависит от типа проведенного теста. Три типа тестов описывают положение на кривой распределения вероятностей: тест с более низким хвостом, тест с верхним хвостом или двусторонний тест.

Короче говоря, чем больше разница между двумя наблюдаемыми значениями, тем меньше вероятность того, что разница вызвана простой случайностью, и это отражается в более низком p-значении.

Подход P-значения к проверке гипотез

Подход p-значения к проверке гипотезы использует рассчитанную вероятность, чтобы определить, есть ли основания отвергать нулевую гипотезу. Нулевая гипотеза, также известная как «гипотеза», представляет собой исходное утверждение о совокупности (или процессе генерации данных). Альтернативная гипотеза утверждает, отличается ли параметр совокупности от значения параметра совокупности, указанного в гипотезе.

На практике уровень значимости указывается заранее, чтобы определить, насколько малым должно быть p-значение, чтобы отвергнуть нулевую гипотезу. Поскольку разные исследователи используют разные уровни значимости при изучении вопроса, у читателя иногда могут возникнуть трудности со сравнением результатов двух разных тестов. P-значения обеспечивают решение этой проблемы.

Например, предположим, что исследование, сравнивающее доходность двух конкретных активов, было проведено разными исследователями, которые использовали одни и те же данные, но с разными уровнями значимости. Исследователи могут прийти к противоположным выводам относительно того, различаются ли активы.

Если бы один исследователь использовал уровень достоверности 90%, а другому требовался уровень достоверности 95%, чтобы отвергнуть нулевую гипотезу, а p-значение наблюдаемой разницы между двумя доходами составляло 0,08 (соответствует уровню достоверности 92%). , то первый исследователь обнаружит, что два актива имеют статистически значимую разницу, в то время как второй не обнаружит статистически значимой разницы между доходностью.

Чтобы избежать этой проблемы, исследователи могли бы сообщить p-значение проверки гипотезы и позволить читателям самим интерпретировать статистическую значимость. Это называется подходом p-значения к проверке гипотез. Независимые наблюдатели могли бы отметить значение p и решить для себя, представляет ли это статистически значимую разницу или нет.

Даже низкое значение p не обязательно является доказательством статистической значимости, так как все еще существует вероятность того, что наблюдаемые данные являются результатом случайности. Только повторные эксперименты или исследования могут подтвердить, является ли связь статистически значимой.

Пример значения P

Инвестор утверждает, что эффективность его инвестиционного портфеля эквивалентна эффективности индекса Standard & Poor’s (S&P) 500. Чтобы определить это, инвестор проводит двусторонний тест.

Нулевая гипотеза утверждает, что доходность портфеля эквивалентна доходности S&P 500 за определенный период, в то время как альтернативная гипотеза утверждает, что доходность портфеля и доходность S&P 500 не эквивалентны — если инвестор провел односторонний тест, альтернативный Гипотеза будет утверждать, что доходность портфеля либо меньше, либо больше, чем доходность S&P 500.

Тест гипотезы p-значения не обязательно использует предварительно выбранный уровень достоверности, при котором инвестор должен сбросить нулевую гипотезу о том, что доходность эквивалентна. Вместо этого он обеспечивает меру того, сколько доказательств есть, чтобы отвергнуть нулевую гипотезу. Чем меньше p-значение, тем больше доказательств против нулевой гипотезы.

Таким образом, если инвестор обнаружит, что p-значение равно 0,001, есть убедительные доказательства против нулевой гипотезы, и инвестор может с уверенностью заключить, что доходность портфеля и доходность S&P 500 не эквивалентны.

Хотя это не дает точного порога того, когда инвестор должен принять или отклонить нулевую гипотезу, у него есть еще одно очень практическое преимущество. Проверка гипотезы P-значения предлагает прямой способ сравнить относительную уверенность, которую может иметь инвестор при выборе между несколькими различными типами инвестиций или портфелей по сравнению с эталоном, таким как S&P 500.

Например, для двух портфелей, A и B, эффективность которых отличается от S&P 500 с p-значениями 0,10 и 0,01 соответственно, инвестор может быть гораздо более уверен, что портфель B с более низким p-значением действительно покажет постоянно разные результаты.

Значимо ли значение Р 0,05?

Значение p менее 0,05 обычно считается статистически значимым, и в этом случае нулевую гипотезу следует отклонить. Значение p больше 0,05 означает, что отклонение от нулевой гипотезы не является статистически значимым, и нулевая гипотеза не отвергается.

Что означает P-значение 0,001?

Значение p, равное 0,001, указывает на то, что если бы проверенная нулевая гипотеза действительно была верной, то был бы один шанс из 1000 увидеть результаты, по крайней мере, столь же экстремальные. Это приводит к тому, что наблюдатель отклоняет нулевую гипотезу, потому что либо наблюдался очень редкий результат данных, либо нулевая гипотеза неверна.

Как можно использовать P-значение для сравнения двух разных результатов проверки гипотез?

Если у вас есть два разных результата, один с p-значением 0,04 и один с p-значением 0,06, результат с p-значением 0,04 будет считаться более статистически значимым, чем p-значение 0,06. Помимо этого упрощенного примера, вы можете сравнить p-значение 0,04 с p-значением 0,001. Оба статистически значимы, но пример 0,001 дает еще более сильный аргумент против нулевой гипотезы, чем пример 0,04.

Итог

Значение p используется для измерения значимости данных наблюдений. Когда исследователи выявляют очевидную взаимосвязь между двумя переменными, всегда существует вероятность того, что эта корреляция может быть совпадением. Расчет p-значения помогает определить, может ли наблюдаемая взаимосвязь возникнуть случайно.

Исправление от 2 апреля 2022 г.: В предыдущей версии p-значение неверно описывалось как вероятность результатов, возникающих в результате случайного совпадения.

S.3.1 Проверка гипотез (подход критического значения)

Подход критического значения включает определение «вероятно» или «маловероятно» путем определения того, является ли наблюдаемая тестовая статистика более экстремальной, чем можно было бы ожидать, если бы нулевая гипотеза была верна. То есть это влечет за собой сравнение наблюдаемой тестовой статистики с некоторым пороговым значением, называемым «критическим значением ». Если тестовая статистика более экстремальна, чем критическое значение, то нулевая гипотеза отклоняется в пользу альтернативной гипотезы. Если тестовая статистика не столь экстремальна, как критическое значение, то нулевая гипотеза не отвергается. 9*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\), которое соответствует t -распределению с n — 1 степенями свободы.

• Определить критическое значение, найдя значение известного распределения тестовой статистики, такое, что вероятность совершения ошибки первого рода — которая обозначается \(\альфа\) (греческая буква «альфа») и называется « уровень значимости теста » — мал (обычно 0,01, 0,05 или 0,10).
• Сравните статистику теста с критическим значением. Если тестовая статистика более экстремальна в направлении альтернативы, чем критическое значение, отклоните нулевую гипотезу в пользу альтернативной гипотезы. Если тестовая статистика менее экстремальна, чем критическое значение, не отвергайте нулевую гипотезу.

Средний средний балл Раздел

 

В нашем примере, касающемся среднего среднего балла, предположим, что мы берем случайную выборку из n = 15 студентов, изучающих математику. Поскольку n = 15, наша тестовая статистика t * имеет n — 1 = 14 степеней свободы. Кроме того, предположим, что мы установили уровень значимости α равным 0,05, так что у нас есть только 5%-й шанс совершить ошибку типа I.

Правохвостый

Критическое значение для проведения Правоюшнего тестирования H ₀ : μ = 3 против H _A : μ > 3 — T 9081 — μ > 3 — T 9081 -VELED T.S. _\(\alpha\) , n — 1, такое, что вероятность справа от равна \(\alpha\). С помощью статистического программного обеспечения или таблицы t можно показать, что критическое значение t _0,05,14 это 1,7613. То есть мы отклоним нулевую гипотезу H ₀ : μ = 3 в пользу альтернативной гипотезы H _A : μ > 3, если критерий статистики t * больше 1,7613. Визуально область отклонения на графике заштрихована красным цветом.

Левосторонний

Критическое значение для проведения левостороннего теста H ₀ : μ = 3 против H _A : μ < 3 есть t -значение, обозначенное -t _{(\(\alpha\), n — 1)} , такое, что вероятность слева из них — это \(\alpha\). С помощью статистического программного обеспечения или таблицы t можно показать, что критическое значение -t _0,05,14 равно -1,7613. То есть мы бы отвергли нулевую гипотезу H ₀ : μ = 3 в пользу альтернативной гипотезы H _A : μ < 3, если тестовая статистика t * меньше -1,7613.

No related posts.