Умножение векторов
Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где .
Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.
Векторным произведением двух векторов и называется вектор , который:
имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;
перпендикулярен к плоскости этого параллелограмма;
направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и называется правой тройкой векторов).

Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: .
Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число.
Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах , и , как на ребрах.
Указанные произведения векторов и их свойства достаточно просто выражаются через их прямоугольные координаты, т.е. координаты векторов в базисе , по сравнению с аналогичными выражениями в произвольном базисе , которых мы не приводим.
Пусть
заданы два вектора и .
Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
.
Угол между векторами вычисляется по формуле
,
или в координатной форме .
Проекция вектора на ось вектора находится из соотношения:
,
или в координатной форме .
Если учесть, что — орт вектора, то .
Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:
.
Векторное произведение ненулевых векторов выражается через координаты данных векторов и следующим образом:
.
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. .
Скаляр , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .
Координаты вектора зависят от выбора базиса. Выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении координат вектора в одном базисе по его координатам в другом базисе. Выясним, как устанавливается связь между координатами одного и того же вектора в различных базисах.
Пусть в пространстве имеются два базиса: старый и новый . Каждый из векторов (i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
.
Матрица (i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы (i =1,2,3) линейно независимы, поэтому матрица неособенная.
Обратный
переход от нового базиса к старому
базису осуществляется с помощью обратной
матрицы .
Найдем зависимость между координатами некоторого вектора в разных базисах. Пусть этот вектор имеет координаты относительно старого базиса и координаты относительно нового базиса, т.е. и
Подставив значения из предыдущей системы в первое равенство
Как нетрудно заметить, матрицей перехода от новых к старым координатам будет транспонированная матрица . В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами:
и .
Пример. В базисе заданы векторы и вектор . Показать, что векторы (i =1,2,3) образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство или
Задача сводится к решению системы:
Определитель
системы не равен нулю. Следовательно, однородная
система имеет только нулевое решение ,
значит векторы
линейно независимы
и образуют базис.
Следовательно, однородная
система имеет только нулевое решение ,
значит векторы
линейно независимы
и образуют базис.
Связь между старым базисом и новым выражается системой уравнений:
Матрица перехода от старого базиса к новому имеет вид
Вычисляем . Она имеет вид
Находим транспонированную матрицу
Координаты в новом базисе находим из равенства
Новые координаты вектора в базисе есть (9/6, 5/6, 1/6) и вектор может быть представлен в виде:
Правда ли что векторное умножение векторов это умножение двух матриц размерностью два и имеет геометрический смысл площади параллелограмма?
Математика и математики
104742 участника сообщества
Правда ли что векторное умножение векторов идентично умножение двух матриц с размерностью два и имеет геометрический смысл площади параллелограмма?
igor simchanko ·
При этом, конечно, для векторного произведения в ортнормированном базисе i, j. k справедлива формула
Более подробно про формулы в других базисах можно почитать в википедии. Так что умножение двумерных матриц (т.е. видимо матриц 2х2) тут ни при чём.
В тоже время, есть и геометрические свойства. Прежде всего модуль векторного произведения |[a,b]| действительно численно равен площади параллелограмма «натянутого» на векторы a,b. Кроме того, векторное произведение ортогонально плоскости векторов a,b. Эти два свойства определяют два противоположных вектора (советую проверить это). По этому для определённости говорят, что векторы a,b, [a,b] образуют «правую тройку», это позволяет выбрать из двух векторов один.
Вообще, векторное произведение очень интересная штука: позволяет не только решать многие стереометрические задачи (например с их помощью очень просто доказывается теорема косинусов для трехранного угла), но они ещё и тесно связаны с кватернионами (см.
А значит трехмерные векторы с операцией векторного произведения образуют алгебру Ли, это очень интересный и важный пример такой алгебраической структуры.
Математика, политика, высшая школа и хейт спич
Перейти на t.me/forodirchNEWS3 оценили·
1,2 K
igor simchanko
24 дек 2022
Почему в двумерном пространстве нельзя произвести векторное умножение двух векторов? Результирующий вектор будет… Читать дальше
Комментировать ответ…Комментировать…
Математика
Бог Царь Отечество · 20 дек 2022
Похоже, автор вопроса слышал что-то о векторной и тензорной алгебре, но особо не вникал.
Речь здесь должна идти об антисимметричных тензорах ранга два. Векторное произведение — это антисимметризация тензорного произведения… Читать далее
Векторное произведение — это антисимметризация тензорного произведения… Читать далее
·
1,1 K
igor simchanko
20 дек 2022
Какой физический смысл имеет векторное произведение векторов . Напишите расчетные примеры примеры.
Комментировать ответ…Комментировать…
Faris Mekhdi-Zadeh
Digital marketer, researcher and data analyst · 20 дек 2022
Векторное умножение векторов, также известное как векторное произведение, это операция, которая применяется к двум векторам и возвращает вектор, который является перпендикуляром к плоскости, в которой расположены исходные… Читать далее
1 оценил·
120
Леонид Коганов
20 дек 2022
Полагаю, что глагол «возвращает» в первой фразе несёт смысл «доставляет в конечном итоге операции (векторного. .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
линейная алгебра — почему мы не определяем векторное умножение по компонентам?
спросил
Изменено 8 лет назад
Просмотрено 17 тысяч раз
$\begingroup$
Мне просто интересно, почему мы никогда не определяем умножение векторов как умножение отдельных компонентов. То есть, почему никто никогда не определяет $\langle a_1,b_1 \rangle \cdot \langle a_2,b_2 \rangle$ как $\langle a_1a_2, b_1b_2 \rangle$? Получающийся вектор просто геометрически не интересен?
- линейная алгебра
$\endgroup$
8
$\begingroup$
В отличие от обычных операций векторного исчисления, произведение $\bullet$, определенное здесь, не является ковариантным для декартовых изменений координат. Это означает, что уравнение, содержащее $\bullet$, не гарантирует, что оно останется верным, если оба члена подвергаются ортогональному изменению координат, например, повороту осей.
Это означает, что уравнение, содержащее $\bullet$, не гарантирует, что оно останется верным, если оба члена подвергаются ортогональному изменению координат, например, повороту осей.
Для двумерного примера рассмотрим следующее уравнение:
\begin{уравнение}
\begin{bmatrix} 1 \\ 0 \end{bmatrix} \bullet \begin{bmatrix} 0 \\ 1\end{bmatrix} = \begin{bmatrix} 0 \\ 0\end{bmatrix}.
\end{уравнение}
Если мы повернем плоскость на 45° против часовой стрелки, то
\начать{выравнивать}
\begin{bmatrix} 1 \\ 0 \end{bmatrix} \to \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{ bmatrix},& & \begin{bmatrix} 0 \\ 1 \end{bmatrix} \to \begin{bmatrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{ 2}} \end{bmatrix},&&\begin{bmatrix} 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} 0 \\ 0 \end{bmatrix},
\end{выравнивание}
но
\begin{уравнение}\тег{!!}
\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \bullet \begin{bmatrix} -\frac{1}{ \sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix} \ne\begin{bmatrix} 0 \\ 0\end{bmatrix}. \end{уравнение}
Таким образом, с точки зрения физика, эта операция некорректна, поскольку она не должна зависеть от конкретной системы координат, выбранной для описания физического пространства. Это не относится к скалярному произведению и перекрестному произведению, которые не зависят от такого выбора.
\end{уравнение}
Таким образом, с точки зрения физика, эта операция некорректна, поскольку она не должна зависеть от конкретной системы координат, выбранной для описания физического пространства. Это не относится к скалярному произведению и перекрестному произведению, которые не зависят от такого выбора.
$\endgroup$
5
$\begingroup$
Это произведение Адамара, которое определено для матриц и, следовательно, для векторных столбцов. См. Страницу Википедии: Продукт Адамара
$\endgroup$
10
$\begingroup$
Еще немного подробнее о том, что уже сказали Джузеппе Негро, Джеймс С. Кук и Майкл Джойс:
Вектор — это , а не набор отдельных компонентов.
Вектор — это элемент некоторого векторного пространства.
Когда вы пишете вектор как такой кортеж, вы имеете в виду только расширение вектора в каком-то конкретном базисе. Но это основание очень часто даже не указывается. Что на самом деле нормально, потому что «обычные» векторные операции на самом деле не зависят от выбора, то есть если вы преобразовали все свои векторы, чтобы они были записаны в каких-то другой базис , у вас будут разные числа, но одни и те же вычисления все равно дадут правильные результаты.
Но это не сработает для покомпонентного умножения, как уже было показано. Эта операция просто , а не работает с векторами, а с их базисным представлением, которое четко определено только для некоторого фиксированного выбора базиса, что на самом деле не интересует вас при изучении векторов.
Конечно, существует множество приложений, в которых вас действительно интересуют кортежи чисел, но тогда это не векторы. В продукте Адамара нет ничего плохого, но он работает не с векторами, а с матрицами 1 . Если вы хотите умножать компоненты, то ваши объекты могут называться кортежами, массивами, списками или чем-то еще, но вряд ли векторами.
В продукте Адамара нет ничего плохого, но он работает не с векторами, а с матрицами 1 . Если вы хотите умножать компоненты, то ваши объекты могут называться кортежами, массивами, списками или чем-то еще, но вряд ли векторами.
К сожалению, многие ошибаются, вот почему, например. Программисты на C++ благословлены классом 2 и std::vector , который на самом деле предназначен для динамических массивов, которые даже менее точно являются векторами, чем статические массивы.
1 Матрицы страдают от аналогичной проблемы: многие люди используют «матрицу» и «линейное отображение» как синонимы, но на самом деле это не одно и то же; матрицы относятся к определенному базису, в то время как линейные отображения не нуждаются в этом. 9n$ как кольцо, вы обычно сосредотачиваетесь на его идентичности в векторном пространстве.
Я думаю, что многие люди, вероятно, когнитивно были обмануты, думая о вашем продукте как о перекрестном продукте или как о внутреннем продукте. Эти два действительно полезны в линейной алгебре, но покоординатное произведение не сравнивается.
Эти два действительно полезны в линейной алгебре, но покоординатное произведение не сравнивается.
$\endgroup$
$\begingroup$
Я часто вижу этот продукт как неправильный ответ на моем курсе механики для первокурсников. Если бы они сказали мне, что, по их мнению, мне нужно прямое произведение $\mathbb{R}$ на саму себя, я бы позволил им вернуть свои баллы. 92y = y+jx $$
Умножение на $j$ отражает строку $y=x$. Это явно отличается от комплексных чисел $\mathbb{R} \oplus i\mathbb{R}$, где умножение на $i$ отображает $(x,y)$ в $(-y,x)$. См. http://en.wikipedia.org/wiki/Split-complex_number для получения информации о геометрии этих гиперболических чисел.
$\endgroup$
2
$\begingroup$
Это действительно просто ответ Джузеппе Негро сказал иначе, но ваше определение ошибочно в том смысле, что оно зависит от выбора основы. Так что на самом деле это не функция двух входных векторов, а скорее функция двух векторов и выбор базиса для векторного пространства.
Так что на самом деле это не функция двух входных векторов, а скорее функция двух векторов и выбор базиса для векторного пространства.
На примере Джузеппе он показывает, что если вы разложите два специально выбранных вектора по двум разным основаниям, вы получите два разных значения для вашего продукта, используя ваше определение.
Сравните это со скалярным произведением. Возьмем любые два вектора $v, w$ в векторном пространстве и вычислим скалярное произведение. Вы открываете свой блокнот и расширяете $v$ и $w$ с точки зрения вашего любимого ортонормированного базиса $e_1, \dots, e_n$, что дает $v = v_1 e_1 + \cdots + v_n e_n$ и $w = w_1 e_1 + \cdots + w_n e_n$, поэтому вы заключаете, что $v \cdot w = v_1 w_1 + \cdots v_n w_n$. Я, с другой стороны, открываю блокнот и раскладываю $v$ и $w$ на мой любимый ортонормированный базис $f_1, \dots, f_n$, дающий $v = v’_1 f_1 + \cdots + v’_n f_n$ и $w = w’_1 f_1 + \cdots + w’_n f_n$, поэтому я заключаю, что $v \cdot w = v’_1 w’_1 + \cdots + v’_n w’_n$. Тот факт, что мы получаем одно и то же число для $v \cdot w$ (даже если мой $v’_i$ не будет таким же, как ваш $v_i$ и аналогично для коэффициентов $w$), говорит нам о том, что что скалярное произведение на самом деле является просто функцией векторов $v$ и $w$, а не функцией их коэффициентов разложения по какому-то конкретному базису.
Тот факт, что мы получаем одно и то же число для $v \cdot w$ (даже если мой $v’_i$ не будет таким же, как ваш $v_i$ и аналогично для коэффициентов $w$), говорит нам о том, что что скалярное произведение на самом деле является просто функцией векторов $v$ и $w$, а не функцией их коэффициентов разложения по какому-то конкретному базису.
$\endgroup$
Замечания по умножению векторов на действительное число
Скалярные и векторные величины — это только два вида величин.
Если мы хотим измерить какую-либо величину, есть два способа измерения: либо только величина, либо и величина, и направление.
Если величина измеряется по ее величине, она называется скалярной величиной.
Если величина измеряется как по величине, так и по направлению, она называется векторной величиной.
В этой статье будет рассмотрено умножение векторов на вещественное число.
Вектор — это величина, которая имеет как величину, так и направление, но не имеет положения.
Скорость и ускорение — два примера таких чисел. Векторный анализ был независимо изобретен Джозайей Уиллардом Гиббсом и Оливером Хевисайдом (соответственно из США и Соединенного Королевства) в конце девятнадцатого века для объяснения новых принципов электромагнитной теории, открытых шотландским ученым Джеймсом Клерком Максвеллом. С тех пор векторы незаменимы в физике, механике, электротехнике и других науках для количественного описания сил.
Можно добавить или удалить два вектора. Например, чтобы добавить или удалить векторы v и w графически, переместите их оба в начало координат и завершите параллелограмм, созданный двумя векторами; v + w — один диагональный вектор параллелограмма.
Умножение двух векторов можно выполнить двумя способами. Скалярное произведение (a・b) и перекрестное произведение (a×b)
Результатом перекрестного произведения является другой вектор. Правило правой руки можно использовать для изображения направления v×w, которое перпендикулярно как v, так и w. Перекрестное произведение обычно используется для получения «нормальи» (линии, перпендикулярной) к поверхности в некоторой точке, а также для расчета крутящего момента и магнитной силы, действующей на движущуюся заряженную частицу.
Перекрестное произведение обычно используется для получения «нормальи» (линии, перпендикулярной) к поверхности в некоторой точке, а также для расчета крутящего момента и магнитной силы, действующей на движущуюся заряженную частицу.
Скалярное произведение — это еще один метод умножения двух векторов. v・w = vw cos θ дает скалярное произведение.
Работа W, выполняемая постоянной силой F, действующей на движущийся объект d, определяется выражением W = Fdcosθ в типичном физическом приложении.
Умножение векторов
Когда мы умножаем вектор A на действительное число k, мы получаем другой вектор A’. Величина A’ в k раз больше величины A. Если она положительна, направление A’ совпадает с направлением A .
Термин «умножение векторов» относится к одному из нескольких способов умножения двух (или более) векторов друг на друга. Это может быть одна из следующих статей:
В результате A・B = |A | |Б | cos θ
В общем случае билинейное произведение в алгебре над полем.
Перекрестное произведение, также называемое «векторным произведением», представляет собой бинарную операцию над двумя векторами, которая дает другой вектор. В трехмерном пространстве вектор, перпендикулярный плоскости, определяемый перекрестным произведением двух векторов, определяется как вектор, величина которого является произведением величин двух векторов плюс синус угла между двумя векторами.
В результате A×B = |A | |Б | sin θ n и где n — единичный вектор, перпендикулярный плоскости, определяемой векторами A и B.
Матрица — это внешнее произведение двух векторов координат. Внешний продукт двух векторов с n и m является матрицей m. В общем, внешнее произведение двух векторов (многомерных массивов чисел) является вектором. Перекрестное произведение, также известное как внешнее произведение векторов.
Произведения с более чем тремя векторами называются множественными перекрестными произведениями.

Существует два типа умножения векторов:
Несколько примеров умножения векторов на скаляр:
Рассмотрим случай, когда вектор, назовем его «а», умножается на скаляр с величиной 0,25. В этой ситуации вектор произведения указывает вектор с тем же направлением, что и вектор a .
Сила является векторной величиной в физическом мире. Величина определяет объем выполненной работы.
И направление силы, приложенной к предмету. Согласно второму закону линейного движения Ньютона эта сила является произведением вектора на скалярное число. F = ma — формула силы. В приведенном выше уравнении «а» означает ускорение объекта, а «м» — массу объекта, скалярную величину. В результате это один из физических примеров умножения векторов на скаляры.
Умножение векторов
Умножение двух векторов сложнее скалярного умножения. Скалярное произведение иногда называют «точечным произведением», а векторное произведение — это способ умножения, использующий два вектора (или «перекрестное произведение»).
Скалярное произведение иногда называют «точечным произведением», а векторное произведение — это способ умножения, использующий два вектора (или «перекрестное произведение»).
Пока мы будем говорить только о скалярном произведении, но у вас должно быть достаточно хороших математических знаний, чтобы понимать и векторное произведение. В двух измерениях определяется скалярное произведение (или скалярное произведение) двух векторов. Это определение, как всегда, можно легко распространить на три измерения, просто следуя шаблону. Чтобы отличить операцию от векторного произведения, в котором используется знак креста (), операция всегда должна обозначаться точкой (•) — отсюда термины скалярное произведение и векторное произведение.
Заключение:
Когда вектор умножается на скаляр, результатом является вектор большей величины с тем же направлением, что и у оригинала.
В физике умножение векторов на скаляры имеет широкий спектр применений. Многие единицы СИ векторных значений представляют собой векторные и скалярные произведения.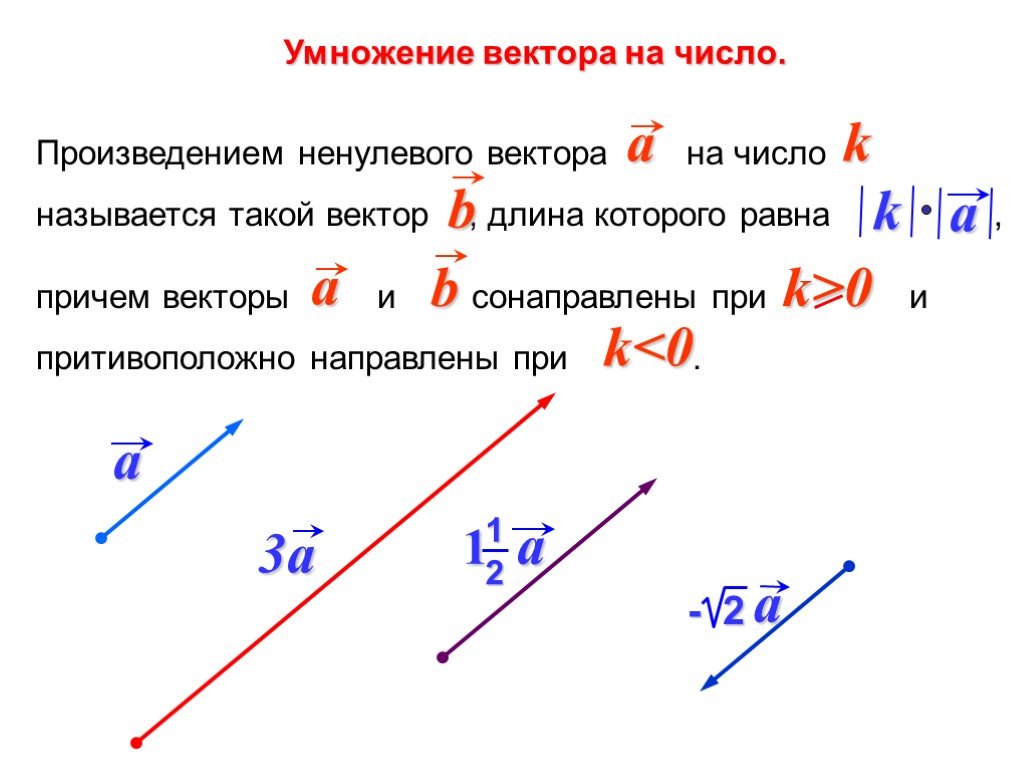


 Вектор — это элемент некоторого векторного пространства.
Вектор — это элемент некоторого векторного пространства.