Какие бывают виды уравнений: Что такое уравнения? и какие виды уравнений есть?

Уравнение плоскости, виды уравнения плоскости, уравнение плоскости в пространстве

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат Oхуz трехмерного пространства.

Определение уравнения плоскости

Определение 1

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х, у и z. Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Теорема 1

Всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида Ax+By+Cz+D=0 , где А,В,С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид Ax+By+Cz+D=0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид Ax+By+Cz+D=0  носит название общего уравнения плоскости. Если не придавать числам А,В,С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение  λ·Ax+λ·By+λ·Cz+λ·D=0, будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства Ax+By+Cz+D=0 и λ·Ax+λ·By+λ·Cz+λ·D=0 равнозначны.

Пример 1

Общим уравнениям плоскости x-2·y+3·z-7=0  и -2·x+4·y-23·z+14=0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению Ax+By+Cz+D=0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида Ax+By+Cz+D=0 .

Уравнение плоскости Ax+By+Cz+D=0 может быть полным и неполным. Все коэффициенты А,B,С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Пример 2

Рассмотрим положение в пространстве плоскости, заданной уравнением 4·y-5·z+1=0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости Oyz. Уравнение z = 0 определяет координатную плоскость Oyz, а общее уравнение плоскости вида 3·x-y+2·z=0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А,В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида Ax+By+Cz+D=0, которое удовлетворяет следующим условиям: длина вектора n→=(A, B, C) равна единице, т.е. n→=A2+B2+C2=1 , а D≤0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α·x+cos β·y+cos γ·z-p=0 , где

p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α, cos β, cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.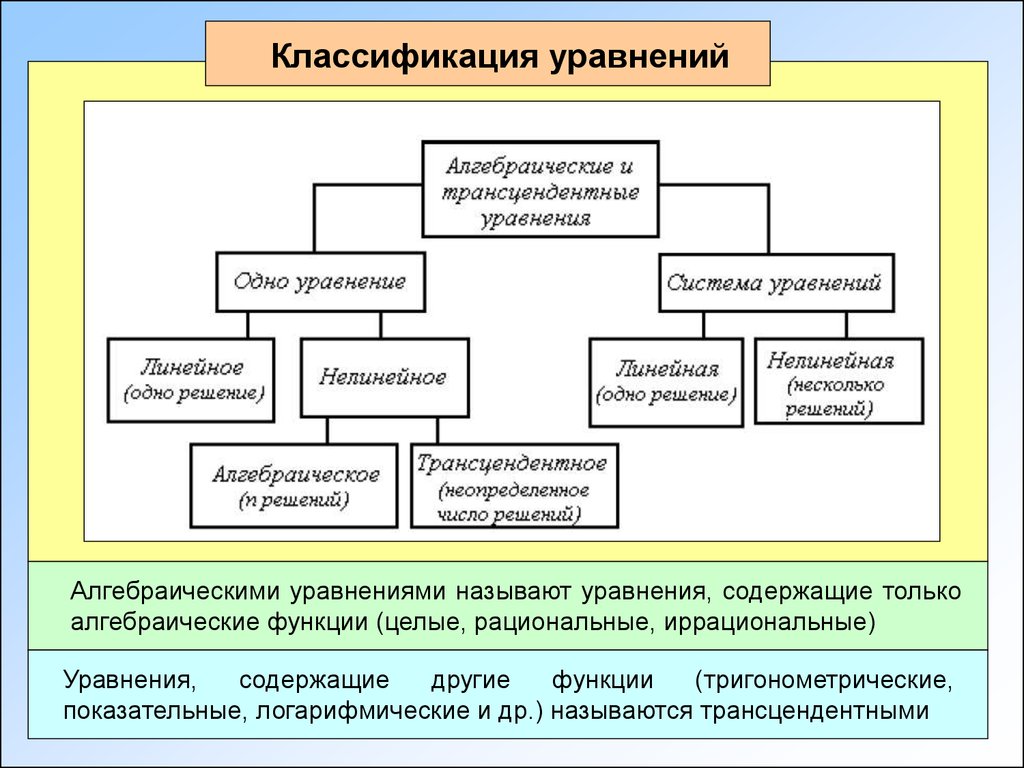

n→=(cos α, cos β, cos γ), n→=cos2α+cos2 β+cos2 γ=1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат Oхуz удалена от начала координат на расстояние pв положительном направлении нормального вектора этой плоскости n→=(cos α, cos β, cos γ) . Если p равно нулю, то плоскость проходит через начало координат.

Пример 3

Плоскость задана общим уравнением плоскости вида -14·x-34·y+64·z-7=0 . D=-7≤0 , нормальный вектор этой плоскости n→=-14, -34, 64 имеет длину, равную единице, так как n→=-142+-342+64=1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях Oх, Oу и Oz отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a, b и с. Уравнение плоскости в отрезках имеет вид xa+yb+zc=1 . Знак чисел а, b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Пример 4

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x-5+y-4+z4=1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x-5+y-4+z4=1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.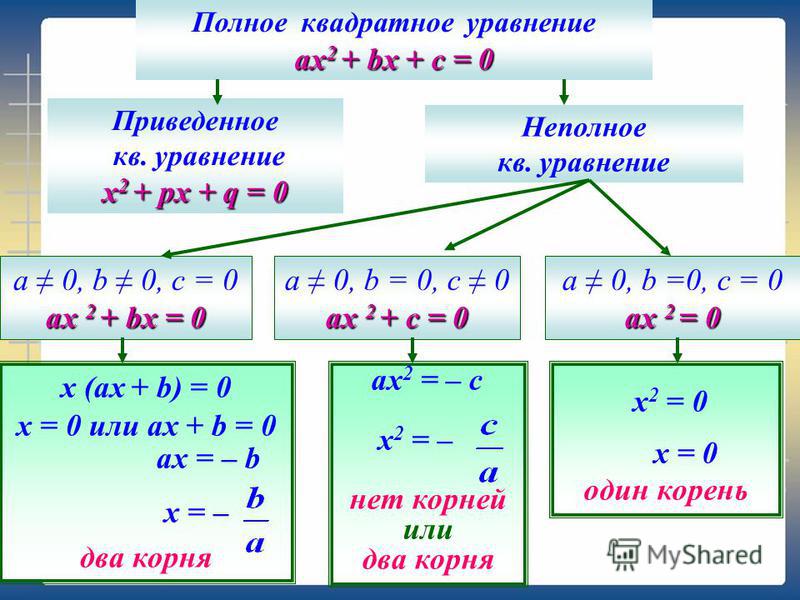

Уравнение прямой, виды уравнения прямой на плоскости, уравнение линии на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы уравнения прямой на плоскости в математике. Теперь же перейдем к изучению определенного уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости. Будем считать, что это большой ликбез для «чайников».

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, котору. можно задавать в прямоугольной декартовой системе координат Oху. Дадим определение прямой.

Определение 1

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой  в декартовой системе Oxy, будет являться общим уравнением прямой на плоскости.

Фактически, уравнением прямой линии на плоскости будем называть уравнение с двумя переменными, которые обозначаются как x и y. Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии (линейной точки).

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости (поверхности). Этому будет посвящен весь следующий раздел нашей статьи. Сколько существует вариантов записи? Отметим, что существует несколько вариантов записи уравнения прямой, которые можно сделать. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Первым делом познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости (пространстве) в декартовой системе координат Oxy и с ее понятием.

Теорема 1

Уравнение вида Ax+By+C=0 , где x и y – переменные, а А, В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат Oxy. В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида Ax+By+C=0 .

Таким образом, общее уравнение прямой на плоскости имеет вид Ax+By+C=0 .

Поясним смысл некоторых важных разных аспектов темы.

Пример 1

Попробуем это нарисовать. Посмотрите на рисунок.

Линию на чертеже стоит определять уравнением вида 2x+3y-2=0, так как координаты любой точки, которые будут составлять эту прямую (составляющие), удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2x+3y-2=0, дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А, В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида Ax+By=0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение Ax+By+C=0 задает прямую, расположенную параллельно оси абсцисс Ox. Если B равно нулю, то можно говорить о параллельности линия оси ординат Oy.

Можно вывести: при некотором наборе значений чисел А, В и C с помощью общего уравнения прямой можно написать любую прямую линию на плоскости в прямоугольной системе координат Oху.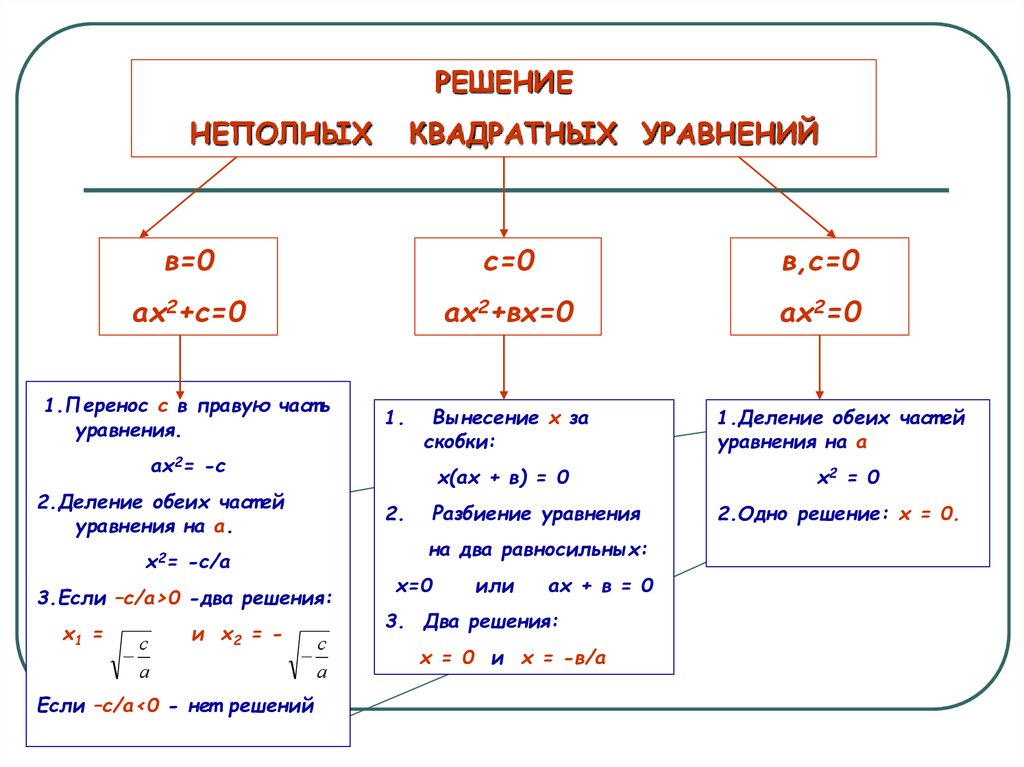

Прямая, заданная уравнением вида Ax+By+C=0 , имеет нормальный вектор прямой с координатами A, B .

Все приведенные уравнения прямых, которые мы по порядку рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале лекции мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид xa+yb=1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению построение прямой линии на чертеже будет простым делом. Для этого необходимо отметить в прямоугольной системе координат точки a, 0  и 0, b , а затем начертить прямую линию, которая будет через них проходить.

Пример 2

Построим прямую, которая задана формулой x3+y-52=1. Отмечаем на графике прямой две точки 3, 0, 0, -52, соединяем их между собой. Как это рисовать.

Что еще можно дополнить? Рекомендуем ознакомиться с аналитическим материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y=k·x+b  должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x.

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси Ox.

Определение 2

Для обозначения угла наклона прямой к положительному направлению оси Ox в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси Ox или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывать это будем следующим образом k=tg α.  Для прямой, которая располагается параллельно оси Oy или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y=k·x+b, проходит через точку 0, b  на оси ординат — это будет означать, что уравнение прямой с угловым коэффициентом y=k·x+b задает на плоскости прямую линию, которая проходит через точку  0, b  и образует угол α с положительным направлением оси Ox, причем k=tg α .

Пример 3

Изобразим прямую линию, которая определяется уравнением вида y=3·x-1.

Записываться это будет так. Эта вертикальная линия должна пройти через точку (0, -1) . Угол наклона α=arctg 3=π3 равен 60 градусов к положительному направлению оси Ox. Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции прямой в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом».  Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x-x1ax=y-y1ay, где x1, y1, ax, ay- это некоторые действительные числа, из которых ax  и ay не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M1(x1, y1) . Числа ax  и ay  в знаменателях дробей представляют собой координаты вектора прямой линии, который будет направлять. Это значит, что каноническое уравнение прямой линии x-x1ax=y-y1ay  в декартовой системе координат Oxy соответствует линии, проходящей через точку M1(x1, y1)  и имеющей направляющий вектор a→=(ax, ay) .

Пример 4

Изобразим в системе координат Oxy прямую линию, которая задается уравнением x-23=y-31. Точка M1(2, 3)  будет иметь принадлежность прямой, вектор a→(3, 1) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x-x1ax=y-y1ay может быть использовано в случаях, когда ax  или ay равно нулю. Наличие ноля в знаменателе делает запись x-x1ax=y-y1ay  условной. Уравнение можно писать следующим образом ay(x-x1)=ax(y-y1).

В том случае, когда ax=0 , каноническое уравнение прямой принимает вид x-x10=y-y1ay  и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что ay=0, принимает вид x-x1ax=y-y10. Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд задач и как их нужно решать, а также многочисленные примеры с решениями, которые позволяют на высоком уровне овладеть темой (и ни в коем случае не путать прямую с кривой).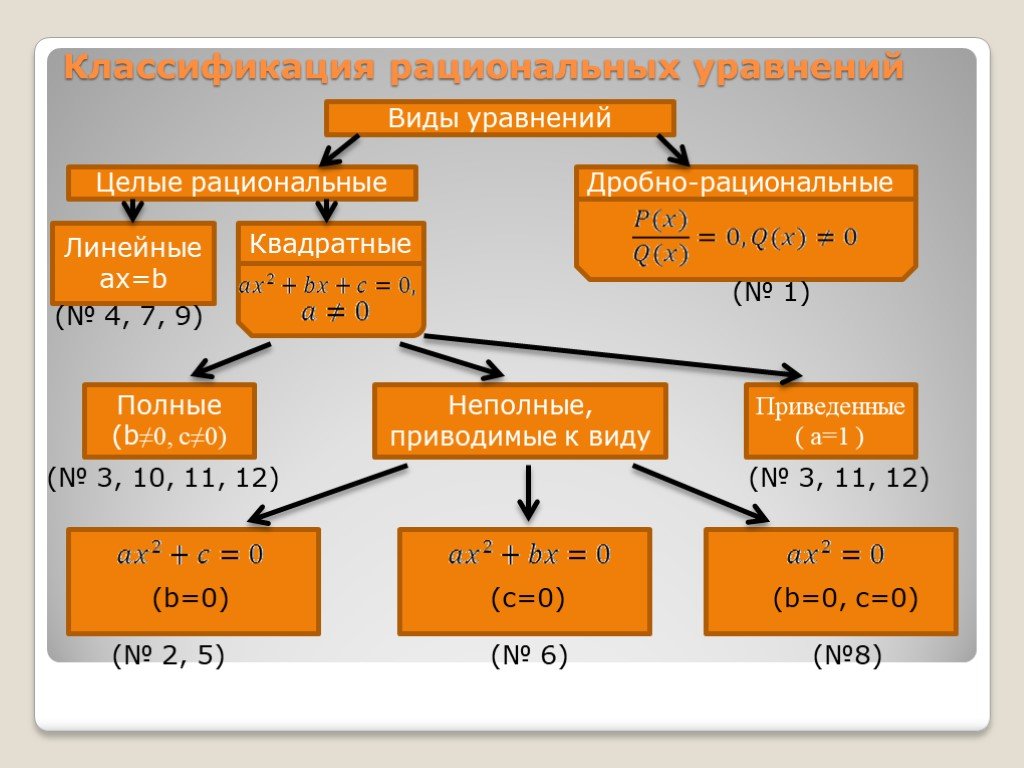

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид  x=x1+ax·λy=y1+ay·λ , где x1, y1, ax, ay — это некоторые действительные числа, из которых ax  и ay  не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы устанавливать неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x, y   представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Пример 5

Предположим, что λ=0 .

Тогда x=x1+ax·0y=y1+ay·0⇔x=x1y=y1 , т. е. точка с координатами (x1, y1)  принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты ax и ay при параметре λ  в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Пример 6

Рассмотрим параметрические уравнения прямой линии вида x=2+3·λy=3+λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку (x1, y1)  и имеет направляющий вектор a→=(3, 1) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид ,Ax+By+C=0, где числа А, В, и C таковы, что длина вектора n→=(A, B) равна единице, а C≤0 .

Нормальным вектором линии, заданной нормальным уравнением прямой  в прямоугольной системе координат Oху, является вектор n→=(A, B) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n→=(A, B) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α·x+cos β·y-p=0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n→=(cos α, cos β) , справедливо равенство n→=cos2 α + cos2 β=1 , величина p≥0  и равна расстоянию от начала координат до прямой.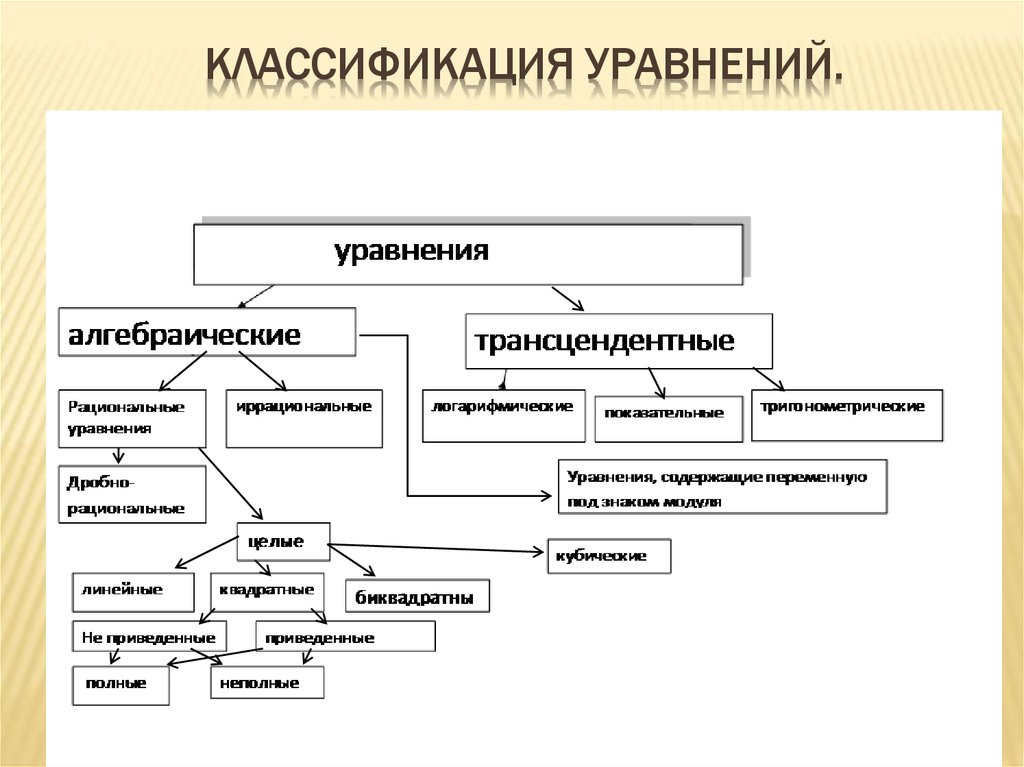

Пример 7

Рассмотрим общее уравнение прямой -12·x+32·y-3=0. Это общее уравнение прямой является нормальным уравнением прямой, так как n→=A2+B2=-122+32=1  и C=-3≤0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты -12, 32 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n→=-12, 32 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой Ax+By+C=0 числа А, В и С таковы, что уравнение Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Уравнение — определение, типы, примеры

Уравнение — это математическое выражение с символом «равно» между двумя выражениями, имеющими одинаковые значения. Например, 3x + 5 = 15. Существуют различные типы уравнений, такие как линейные, квадратные, кубические и т. д. Давайте узнаем больше об уравнениях в математике в этой статье.

1.	Что такое уравнения?
2.	Части уравнения
3.	Как решить уравнение?
4.	Типы уравнений
5.	Уравнение против выражения
6.	Часто задаваемые вопросы по уравнениям

Что такое уравнения?

Уравнения — это математические операторы, содержащие два алгебраических выражения по обе стороны от знака «равно (=)». Он показывает отношение равенства между выражением, записанным в левой части, и выражением, записанным в правой части. В каждом уравнении в математике мы имеем LHS = RHS (левая часть = правая часть). Уравнения могут быть решены, чтобы найти значение неизвестной переменной, представляющей неизвестную величину. Если в выражении нет знака «равно», значит, оно не является уравнением. Это будет считаться выражением. Вы узнаете разницу между уравнением и выражением в следующем разделе этой статьи.

Посмотрите на следующие примеры. Это даст вам представление о значении уравнения в математике.

	Уравнения	Это уравнение?
1.	у = 8х — 9	Да
2.	у + х 2 — 7	Нет, потому что нет символа «равно».
3.	7 + 2 = 10 — 1	Да

Теперь давайте двигаться вперед и узнать о частях уравнения в математике.

Части уравнения

Существуют различные части уравнения, которые включают коэффициенты, переменные, операторы, константы, термины, выражения и знак равенства. Когда мы пишем уравнение, обязательно наличие знака «=» и условий с обеих сторон. Обе стороны должны быть равны друг другу.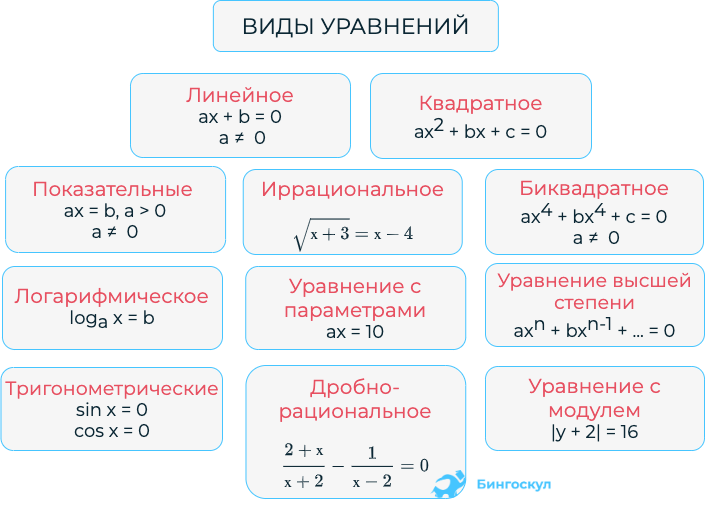 Уравнение не обязательно должно иметь несколько членов с обеих сторон, иметь переменные и операторы. Уравнение можно составить и без них, например, 5 + 10 = 15. Это арифметическое уравнение без переменных. В противоположность этому, уравнение с переменными является алгебраическим уравнением. Посмотрите на изображение ниже, чтобы понять части уравнения.

Как решить уравнение?

Уравнение похоже на весы с одинаковыми весами с обеих сторон. Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется в силе. Точно так же, если мы умножим или разделим одно и то же число на обе части уравнения, оно останется верным. Рассмотрим уравнение прямой, 3x − 2 = 4. Выполним математические операции над левой и правой сторонами так, чтобы равновесие не нарушалось. Давайте добавим 2 с обеих сторон, чтобы уменьшить LHS до 3x. Это не нарушит баланс. Новая левая сторона равна 3x − 2 + 2 = 3x, а новая правая сторона равна 4 + 2 = 6. Таким образом, уравнение принимает вид 3x = 6. Теперь давайте разделим обе части на 3, чтобы уменьшить левую часть до x. Таким образом, решением данного уравнения прямой является x = 2,

Шаги для решения базового уравнения с одной переменной (линейного) приведены ниже:

• Шаг 1: Приведите все члены с переменными с одной стороны и все константы с другой стороны уравнения, применяя арифметические действия. операций с обеих сторон.
• Шаг 2: Объедините все одинаковые термины (термы, содержащие одну и ту же переменную с одинаковым показателем степени), добавляя/вычитая их.
• Шаг 3: Упростите и получите ответ.

Возьмем еще один пример основного уравнения: 3x — 20 = 7. Чтобы вывести все константы на правую сторону, мы должны добавить 20 к обеим частям. Отсюда следует, что 3x — 20 + 20 = 7 + 20, что можно упростить как 3x = 27. Теперь разделите обе части на 3. Это даст вам x = 9, что и является требуемым решением уравнения.

Типы уравнений

В зависимости от степени уравнения можно разделить на три типа.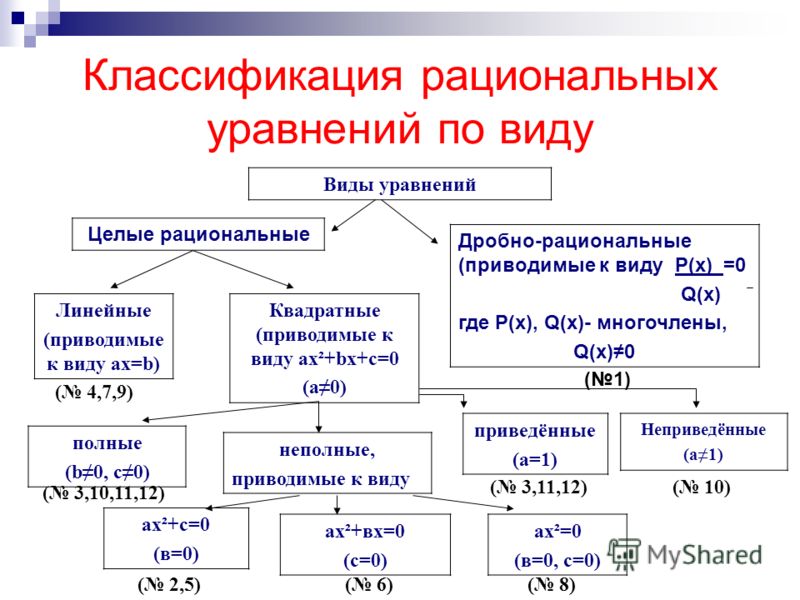 Ниже приведены три типа уравнений в математике:

• Линейные уравнения
• Квадратные уравнения
• Кубические уравнения

Линейное уравнение

Уравнения со степенью 1 в математике называются линейными уравнениями. В таких уравнениях 1 является наивысшим показателем членов. Их можно далее классифицировать на линейные уравнения с одной переменной, линейные уравнения с двумя переменными, с тремя переменными и т. д. Стандартная форма линейного уравнения с переменными X и Y: aX + bY — c = 0, где a и b коэффициенты X и Y соответственно, а c — константа.

Квадратное уравнение

Уравнения второй степени известны как квадратные уравнения. Стандартная форма квадратного уравнения с переменной x: ax ² + bx + c = 0, где a ≠ 0. Эти уравнения можно решить, разделив средний член, дополнив квадрат или дискриминантным методом.

Кубические уравнения

Уравнения степени 3 известны как кубические уравнения. Здесь 3 — это наивысший показатель хотя бы одного из членов. Стандартная форма кубического уравнения с переменной x: ax ³ + bx ² + cx + d = 0, где a ≠ 0.

Уравнение против выражения

Выражения и уравнения в математике используются одновременно в алгебре, но между этими двумя терминами есть большая разница. Когда 2x + 4 является выражением, 2x + 4 = 0 считается уравнением. Давайте поймем основную разницу между уравнением и выражением с помощью приведенной ниже таблицы:

Уравнение	Выражение
Когда два выражения равны по значению и написаны вместе со знаком «равно» между ними, это известно как уравнение в математике.	Это математическое выражение, содержащее хотя бы один термин или несколько терминов, соединенных операторами между ними.
Имеет знак равенства «=».	Выражение не содержит знака равенства «=».
Можно найти значение неизвестной величины.	Можно упростить до самой низкой формы.
Пример: x — 8 = 16, 6y = 33, 3z — 7y = 9 и т. д.	Пример: x — 8, 6y, 3z — 7y — 9 и т. д.

Важные замечания по уравнениям в математике:

• Значения переменной, которая делает уравнение истинным, называются решением или корнем уравнения.
• На решение уравнения не влияет сложение, вычитание, умножение или деление одного и того же числа на обе части уравнения.
• График линейного уравнения с одной или двумя переменными представляет собой прямую линию.
• Кривая квадратного уравнения имеет форму параболы.

☛  Похожие темы:

Ознакомьтесь с интересными статьями, посвященными концепции уравнений в математике.

• Система уравнений
• Простые уравнения и их приложения
• Найдите x

Часто задаваемые вопросы по уравнению

Что такое уравнение в математике?

Уравнение в математике — это отношение равенства между двумя выражениями, написанными по обе стороны от знака равенства. Например, 3y = 16 — это уравнение.

Что такое линейное уравнение?

Линейное уравнение — это уравнение со степенью 1. Это означает, что наивысший показатель степени любого члена может быть равен 1. Примером линейного уравнения в математике является x + y = 24,9.0003

Что такое квадратное уравнение?

Квадратное уравнение — это уравнение со степенью 2. Оно может иметь любое количество переменных, но наивысшая степень членов может быть только 2. Стандартная форма квадратного уравнения с переменной y — это ay ² + by + c = 0, где a ≠ 0.

Как уравнения используются в реальной жизни?

В реальной жизни во многих ситуациях можно использовать уравнения. Всякий раз, когда необходимо найти неизвестную величину, можно составить уравнение и решить его. Например, если стоимость 1 карандаша составляет 1,2 доллара, а общая сумма денег, потраченных вами на карандаши, составляет 9 долларов..6 количество купленных карандашей можно найти, составив уравнение на основе данной информации. Пусть количество купленных карандашей равно х. Тогда уравнение будет 1,2x = 9,6, которое можно решить как x = 8.

Как решать квадратные уравнения?

Квадратные уравнения с одной переменной могут быть решены следующими методами:

• Метод факторизации
• Завершение квадратного метода
• Дискриминантный метод

Какие существуют 3 типа уравнений?

В зависимости от степени уравнения можно разделить на следующие три типа:

• Линейное уравнение
• Квадратное уравнение
• Кубическое уравнение

Какое уравнение не имеет решения?

Уравнения двух параллельных прямых не имеют решений, так как они не пересекаются ни в одной точке. Чтобы идентифицировать уравнения параллельных прямых, мы должны сравнить коэффициенты обеих переменных в данных двух линейных уравнениях с двумя переменными. Если отношение коэффициентов такое же и не равно отношению констант, это означает, что эти уравнения не имеют решений. Для двух уравнений ax + by + c = 0 и px + qy + r = 0 оно не будет иметь решения, когда a/p = b/q ≠ c/r.

Что такое уравнение окружности?

Уравнение окружности с радиусом r и центром (x ₁ , y ₁ ) равно (x − x ₁ ) ² + (y − y ₁ ) 7 0 7 ^{2 90 2} .

10 различных типов математических уравнений – DifferentTypes.net

10 декабря 2020 г. 30 ноября 2019 г. акции

Теперь займемся математикой. Кто бы мог подумать, что алфавиты все еще найдут свое место в математических формулах и функциях?

Уравнение просто определяется как равенство с различными переменными, также известными как неизвестные, которых может быть больше двух. Переменные или неизвестные обычно представляются буквами алфавита.

Наличие уравнения означает, что его нужно решить, что может быть не всегда правильно, но мы решаем уравнения, выясняя идентичность или представления переменных, которые сделают уравнение верным.

Уравнения разделены на две части; первая часть уравнения находится в левой части перед знаком равенства, а другая часть — после знака равенства в правой части.

Уравнение может быть в двух формах, первая форма может содержать то, что мы называем уравнением тождества, в котором переменные истинны для всех значений переменных, тогда как условные уравнения могут быть истинны только для переменных определенного значения.

Без знака равенства выражение перестанет быть уравнением. Вот пример общего уравнения:

X2 + 3b + 234 = 5

См. также:  26 Различные виды математики

Содержание

1. Полиномиальное уравнение

Полиномиальные уравнения будут содержать только положительные целые показатели степени, которые установлены равными нулю. Полиномиальное уравнение — это алгебраическое уравнение, которое записывается в виде: X = y

, где x и y — многочлены с коэффициентами, являющимися действительными числами.

Полиномиальные уравнения могут также содержать более одной переменной, например:

X2 + 3b + 234 = 0

2. Рациональное полиномиальное уравнение

Рациональное полиномиальное уравнение — это просто алгебраическое уравнение, содержащее пропорции.

Примером рационального полиномиального уравнения является:

x/2 = [x + 2] / 4

3. Иррациональное полиномиальное уравнение степени с дробным показателем.

Пример иррационального показателя:

√ [x – 2] = 2x + 1

Такие уравнения решаются путем возведения уравнений в одинаковую степень в обеих частях уравнения или путем введения новой переменной.

Связанные: 7 различных типов дробей

4. Трансцендентное уравнение

Трансцендентное уравнение — это уравнение, содержащее трансцендентные функции, переменные которых должны быть решены.

Пример трансцендентного уравнения:

X = e-x
X = cos x

Трансцендентные уравнения решаются через обратные функции.

5. Линейное уравнение

Это уравнения для прямых линий.

В отношении линейных уравнений следует отметить, что когда они содержат две переменные, их график всегда строится по прямой линии. Каждый член линейного уравнения является константой или произведением константы и переменной.

Существует множество способов записи линейных уравнений, но один фактор заключается в том, что они должны содержать константу c и простые переменные, такие как x и y. Переменные, однако, не имеют показателей степени и не имеют ни квадратов, ни квадратных корней.

Пример линейного уравнения:

Y = mx + c

В этом типичном примере m всегда называется наклоном, тогда как c — это точка на кривой, пересекающая ось y. Линейное уравнение может быть представлено в трех формах:

Одна переменная:
8x – 7 = 0

Две переменные:
45x + 5j = 456

Три переменные:
1 + 16 9017l – 6y

6.

Квадратное уравнение

92 – 4ac))/2a

При этом, применительно к данному примеру, a = 1, b = 3 и c = 234.

Квадратные уравнения могут быть решены с помощью методов факторизации или с помощью метода квадратов или с использованием квадратичной формулы для замены значений, данных в уравнении.

7. Тригонометрическое уравнение

Тригонометрическое уравнение — это любое уравнение, содержащее тригонометрическую функцию. Все тригонометрические уравнения, верные для любых углов, известны как тригонометрические тождества.

Некоторые тригонометрические уравнения могут быть выполнены или решены без использования калькулятора, тогда как остальные могут быть слишком сложными, чтобы не использовать калькулятор.

Пример тригонометрического уравнения:

Tan [x] = 3,2

его показатель степени переменной обычно равен ½ или квадратному корню.

Пример радикального уравнения:

√[x] + 10 = 26

9.