Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
 4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
 The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)Парная регрессия и корреляция, MS Excel
« Назад
Купить работу
- ПРО РОБОТУ
Код роботи: 4353
Вид роботи: Лабораторна робота
Предмет: Економічна кібернетика (Экономическая кибернетика)
Тема: №5, Парная регрессия и корреляция, MS Excel
Кількість сторінок: 9
Дата виконання: 2018
Мова написання: російська
Ціна: безкоштовно
Купить работу
По территориям региона приводятся данные:
Таблица 1
Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, ден. | Среднедневная заработная плата, ден.ед., y |
1 | 85 | 139 |
2 | 86 | 148 |
3 | 87 | 142 |
4 | 79 | 154 |
5 | 106 | 164 |
6 | 113 | 195 |
7 | 67 | 139 |
8 | 98 | 164 |
9 | 79 | 152 |
10 | 87 | 162 |
11 | 86 | 152 |
12 | 117 | 173 |
Требуется:
1. Построить линейное уравнение парной регрессии y по x.
Построить линейное уравнение парной регрессии y по x.
Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.
Таблица 2
№ | x | y | y*x | x2 | y2 | ki | |||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 85 | 139 | 11815 | 7225 | 19321 | 151,80 | -12,80 | 163,93 | 9,21 |
2 | 86 | 148 | 12728 | 7396 | 21904 | 152,69 | -4,69 | 22,04 | 3,17 |
3 | 87 | 142 | 12354 | 7569 | 20164 | 153,59 | -11,59 | 134,21 | 8,16 |
4 | 79 | 154 | 12166 | 6241 | 23716 | 146,46 | 7,54 | 56,88 | 4,90 |
5 | 106 | 164 | 17384 | 11236 | 26896 | 170,51 | -6,51 | 42,40 | 3,97 |
6 | 113 | 195 | 22035 | 12769 | 38025 | 176,75 | 18,25 | 333,16 | 9,36 |
7 | 67 | 139 | 9313 | 4489 | 19321 | 135,77 | 3,23 | 10,45 | 2,33 |
8 | 98 | 164 | 16072 | 9604 | 26896 | 163,38 | 0,62 | 0,38 | 0,38 |
9 | 79 | 152 | 12008 | 6241 | 23104 | 146,46 | 5,54 | 30,71 | 3,65 |
10 | 87 | 162 | 14094 | 7569 | 26244 | 153,59 | 8,41 | 70,81 | 5,19 |
11 | 86 | 152 | 13072 | 7396 | 23104 | 152,69 | -0,69 | 0,48 | 0,46 |
12 | 117 | 173 | 20241 | 13689 | 29929 | 180,31 | -7,31 | 53,45 | 4,23 |
Итого | 1090 | 1884 | 173282 | 101424 | 298624 | 1884 | 0,00 | 918,89 | 54,99 |
Среднее значение | 90,83 | 157 | 14440,17 | 8452 | 24885,33 | 157 | – | 76,57 | 4,58 |
14,19 | 15,37 | – | – | – | – | – |
| – | |
201,31 | 236,33 | – | – | – | – | – |
| – |
По формулам находим параметры регрессии
Получено уравнение регрессии:
.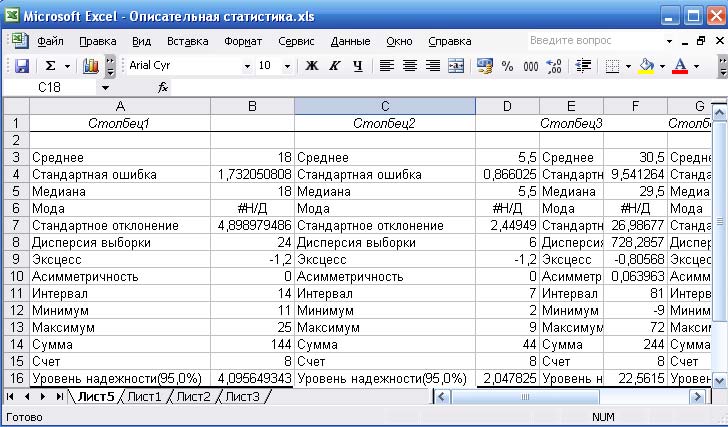
Параметр регрессии позволяет сделать вывод, что с увеличением среднедушевого прожиточного минимума на 1 ден.ед. среднедневная заработная плата возрастает в среднем на 0,89 ден.ед.
После нахождения уравнения регрессии заполняем столбцы 7 – 10 таблицы 2.
2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
Тесноту линейной связи оценит коэффициент корреляции:
Т.к. значение коэффициента корреляции больше 0,7, то это говорит о наличии весьма тесной линейной связи между признаками.
Коэффициент детерминации:
Это означает, что 67,6% вариации заработной платы (y) объясняется вариацией фактора x – среднедушевого прожиточного минимума.
Качество модели определяет средняя ошибка аппроксимации:
Качество построенной модели оценивается как хорошее, так как не превышает 10%.
3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью -критерия Фишера и t-критерия Стьюдента.
Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера. Фактическое значение F-критерия по формуле составит
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k1=1 и k2=12-2=10 составляет Fтабл=4,96. Так как , то уравнение регрессии признается статистически значимым.
Оценку статистической значимости параметров регрессии и корреляции проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.
Табличное значение t-критерия для числа степеней свободы df=n-2=12-2=10 и уровня значимости составит tтабл=2,23.
Определим стандартные ошибки (остаточная дисперсия на одну степень свободы
Тогда
Фактические значения t-статистики превосходят табличное значение:
Поэтому параметры a, b и rxy не случайно отличаются от нуля, а статистически значимы.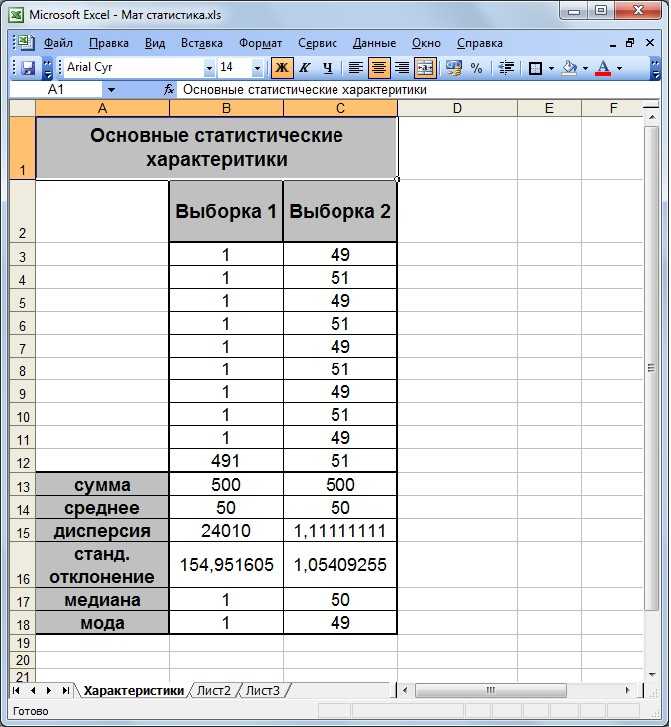
Рассчитаем доверительные интервалы для параметров регрессии a и b. Для этого определим предельную ошибку для каждого показателя:
Доверительные интервалы
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: ден.ед., тогда индивидуальное прогнозное значение заработной платы составит: ден.ед.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Ошибка прогноза составит:
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный интервал прогноза:
Выполненный прогноз среднемесячной заработной платы является надежным () и находится в пределах от 140,16 ден.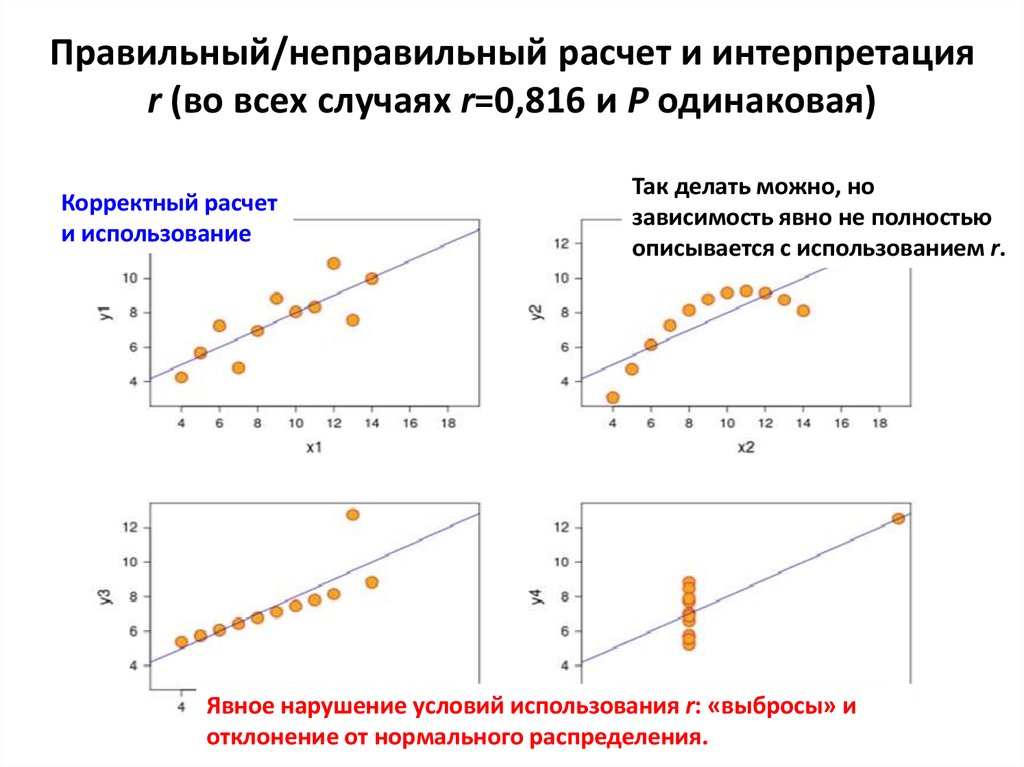 ед. до 185,0 ден.ед.
ед. до 185,0 ден.ед.
6. На одном графике отложить исходные данные и теоретическую прямую.
7. Проверить вычисления в MS Excel.
Выбираем Сервис®Анализ данных®Регрессия. Заполняем диалоговое окно ввода данных и параметров вывода. Получаем следующие результаты:
Откуда выписываем.
Уравнение регрессии:
Коэффициент корреляции:
Коэффициент детерминации:
Фактическое значение F-критерия Фишера:
Остаточная дисперсия на одну степень свободы:
Корень квадратный из остаточной дисперсии (стандартная ошибка):
Стандартные ошибки для параметров регрессии:
Фактические значения t-критерия Стьюдента:
Доверительные интервалы:
Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t-критерия Стьюдента для коэффициента корреляции совпадает с tb). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).
Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).
Множественная корреляция | Реальная статистика с использованием Excel
В основных понятиях корреляции мы определяем коэффициент корреляции , который измеряет размер линейной связи между двумя переменными. Теперь мы расширим это определение на ситуацию, когда имеется более двух переменных. Определение 10012
, где r xz , r yz , r xy определены в определении 2 основных понятий корреляции. Здесь x и y рассматриваются как независимые переменные, а z — как зависимая переменная.
Коэффициент детерминацииМы также определяем множественный коэффициент детерминации как квадрат множественного коэффициента корреляции.
Часто индексы опускаются, а множественный коэффициент корреляции и множественный коэффициент детерминации записываются просто как R и R 2 соответственно. Эти определения также могут быть расширены до более чем двух независимых переменных. Только с одной независимой переменной коэффициент множественной корреляции составляет просто r .
Эти определения также могут быть расширены до более чем двух независимых переменных. Только с одной независимой переменной коэффициент множественной корреляции составляет просто r .
К сожалению, R не является объективной оценкой коэффициента множественной корреляции генеральной совокупности, что очевидно для небольших выборок. Относительно объективная версия R дается скорректированным R .
Определение 2 : Если R равно R z,xy , как определено выше (или аналогично для большего количества переменных), то скорректированный множественный коэффициент детерминации равен
, где k = число k независимые переменные и n = количество элементов данных в выборке для z (которое должно быть таким же, как выборки для x и y).
Средства анализа данных Инструменты анализа данных Excel: В дополнение к различным функциям корреляции, описанным в другом месте, Excel предоставляет инструменты анализа данных Covariance и Correlation . Инструмент Covariance вычисляет попарные ковариации генеральной совокупности для всех переменных в наборе данных. Аналогично инструмент Correlation вычисляет различные коэффициенты корреляции, как описано в следующем примере.
Инструмент Covariance вычисляет попарные ковариации генеральной совокупности для всех переменных в наборе данных. Аналогично инструмент Correlation вычисляет различные коэффициенты корреляции, как описано в следующем примере.
Пример 1 : Мы расширяем данные в примере 2 проверки корреляции с помощью t-теста, чтобы включить ряд других статистических данных. Данные для первых нескольких состояний показаны на рисунке 1.9.Рисунок 1. Данные для примера 1
Рисунок 2 – Коэффициенты корреляции для данных примера 1
Можно также выделить первые три переменные, бедность, младенческую смертность и белые (т. коэффициенты, предполагая, что бедность является зависимой переменной, как определено в определениях 1 и 2. Мы используем данные на рисунке 2 для получения значений , и .
Частичная и полупартийная корреляция Определение 3 : дано x , Y и z Как в определении 1, Частичная корреляция из x и Z Z Z Z Z и Z и Z Z и Z и Z и Z и Z и Z . удерживая константу y, определяется следующим образом:
удерживая константу y, определяется следующим образом:
В получастичной корреляции устраняется корреляция между x и y, но не корреляция между x и z и y и z :
Причинно-следственная связьПредположим, мы смотрим на взаимосвязь между GPA (средним баллом) и зарплатой через 5 лет после выпуска и обнаруживаем, что существует высокая корреляция между этими двумя переменными. Как уже упоминалось в другом месте, это не означает, что хорошая учеба в школе приводит к тому, что человек получает более высокую зарплату. На самом деле вполне возможно, что существует третья переменная, скажем, IQ, которая хорошо коррелирует как со средним баллом, так и с зарплатой (хотя это не обязательно означает, что IQ является причиной более высокого среднего балла и более высокой зарплаты).
В этом случае возможно, что корреляция между средним баллом и зарплатой является следствием корреляции между IQ и средним баллом и между IQ и зарплатой. Чтобы проверить это, нам нужно определить корреляцию между средним баллом и зарплатой, исключив влияние IQ от обеих переменных, то есть частичную корреляцию.
Чтобы проверить это, нам нужно определить корреляцию между средним баллом и зарплатой, исключив влияние IQ от обеих переменных, то есть частичную корреляцию.
Свойство 1 :
Доказательство: Первое утверждение следует из
Второе утверждение следует из:
Пример 2 : Рассчитайте и для данных в Примере 1.
Можно увидеть, что свойство 1 содержит эти данные с
Вариант разделенияС тех пор является мерой доли дисперсии, относящейся к вовлеченным переменным, мы можем посмотреть на значение понятий, определенных выше, используя следующую диаграмму Венна, где прямоугольник представляет общую дисперсию переменной бедности.
Рисунок 3 – Распределение дисперсии по бедности
Используя данные примера 1, мы можем рассчитать разбивку дисперсии по бедности на рисунке 4:
Рисунок 4 – Распределение дисперсии по бедности продолжение
Обратите внимание, что мы можем вычислить B несколькими способами: ( A + B – A , ( B + C ) – C , ( A + B + C ) – ( A + C ) и т. д. и получить в каждом случае один и тот же ответ. Также обратите внимание, что
д. и получить в каждом случае один и тот же ответ. Также обратите внимание, что
где D = 1 – ( A + B + C) .
Рисунок 5 — Распределение дисперсии для бедности Продолжение
Свойство 2 : Из свойства 1 следует, что:
Если независимые переменные не зависят, это уменьшается до
99000.
Функции рабочего листа
Функции реальной статистики : Ресурсный пакет реальной статистики содержит следующие функции, где образцы для z , x, и y содержатся в массивах или диапазонах R, R1 и R2 соответственно.
CORREL_ADJ (R1, R2) = скорректированный коэффициент корреляции для наборов данных, определенных диапазонами R1 и R2 y
PART_CORREL (R, R1, R2) = частная корреляция r zx, y переменных z и x Удерживая константу y
Semipart_correl (R, R1, R2) = полупартийная корреляция R Z ( x , Y)
Несколько корреляций для 5.
Определение 1 определяет множественный коэффициент корреляции R z,x y и соответствующий множественный коэффициент детерминации для трех переменных x, y и z . Мы можем расширить эти определения до более чем трех переменных, как описано в разделе Расширенная множественная корреляция.
Напр. если R1 представляет собой массив m × n , содержащий данные для n переменных, то функция реальной статистики RSquare(R1, k ) вычисляет кратный коэффициент детерминации для k -й переменной по отношению к другие переменные в R1. Множественный коэффициент корреляции для k -й переменной по отношению к другим переменным в R1 может быть затем рассчитан по формуле =SQRT(RSquare(R1, k )).
Таким образом, если R1, R2 и R3 являются тремя столбцами массива данных м × 3 или диапазона R, где R1 и R2 содержат выборки для независимых переменных x , а y и R3 содержат выборки данных для зависимая переменная z , тогда =MCORREL(R3, R1, R2) дает тот же результат, что и =SQRT(RSquare(R, 3)).
Точно так же определение коэффициента частичной корреляции (Определение 3) может быть расширено до более чем трех переменных, как описано в разделе Расширенная множественная корреляция.
Книга примеровНажмите здесь , чтобы загрузить книгу Excel с примерами, описанными на этой веб-странице.
СсылкиHowell, D.C. (2010) Доверительные интервалы по величине эффекта pdf
Schmuller, J. (2009) Статистический анализ с помощью Excel для чайников. Wiley
https://www.wiley.com/en-us/Statistical+Analysis+with+Excel+For+Dummies%2C+3rd+Edition-p-9781118464311
Множественная корреляция, продолжение | Реальная статистика с использованием Excel
В множественной корреляции мы исследуем корреляции с тремя случайными переменными. Теперь мы распространим некоторые из этих результатов на более чем три переменные.
Коэффициент корреляции и коэффициент детерминации Сначала мы суммируем некоторые результаты анализа множественной регрессии, касающиеся коэффициента корреляции и коэффициента детерминации для любого количества переменных. В частности, коэффициент детерминации можно рассчитать по
В частности, коэффициент детерминации можно рассчитать по
Пакет ресурсов Real Statistics предоставляет функцию массива RSquare (R1, R2), которая вычисляет R 2 . Здесь R1 — это массив n × k , содержащий выборочные данные X , а R2 — это массив n × 1, содержащий выборочные данные Y .
Таким образом, мы можем рассчитать коэффициент корреляции по формуле =КОРРЕКЦИЯ(RSквадрат(R1, R2)).
В качестве альтернативы, мы можем рассчитать как коэффициент корреляции, так и коэффициент детерминации, используя Excel 9Инструмент анализа данных 0011 Regression или инструмент анализа данных Real Statistics Linear Regression .
Другое использование RSquare Как описано в разделе «Множественный регрессионный анализ», существует также вторая форма функции RSquare, в которой Данные содержат все столбцы в R1, кроме j -го столбца, а данные Y состоят из j -й столбец R1.
Таким образом, если R1 представляет собой массив n × k , состоящий из всех данных X , за которыми следует столбец данных Y , то R 2 = RSquare(R1, k).
В частности, предположим, что R1, R2 и R3 являются тремя столбцами массива n × 3 R. Далее мы предполагаем, что R1 и R2 содержат выборочные данные для независимых переменных x 1 и х 2 , а R3 содержит выборочные данные для зависимой переменной y. Отсюда следует, что формулы массива =MCORREL(R3, R1, R2) и =SQRT(RSquare(R, 3)) дают одинаковые результаты.
Свойство R 2 Оказывается, что R 2 = RSquare(R1, j ) также можно вычислить для первой корреляции1, найдя корреляцию R1 выделение j -го элемента по диагонали. Если это имеет значение c, тогда желаемое значение R 2 равно 1 – 1/ c .
Таким образом, R 2 также можно рассчитать по формуле:
=1–1/ИНДЕКС(DIAG(MINVERSE(CORR(R1))), j )
4 Частный коэффициент корреляции
Определение 1 : Предположим, что у нас есть случайные величины x 1 , …, x k и для каждого x j у нас есть выборка размером п . Теперь предположим, что Z состоит из всех случайных переменных x 1 ,…, x K , исключая x I и x J , где I c . Затем коэффициент частичной корреляции между переменными x I и x J является коэффициентом корреляции между x I и x J . переменные в константе Z).
Это определение согласуется с определением 3 множественной корреляции, где есть только три переменные (т.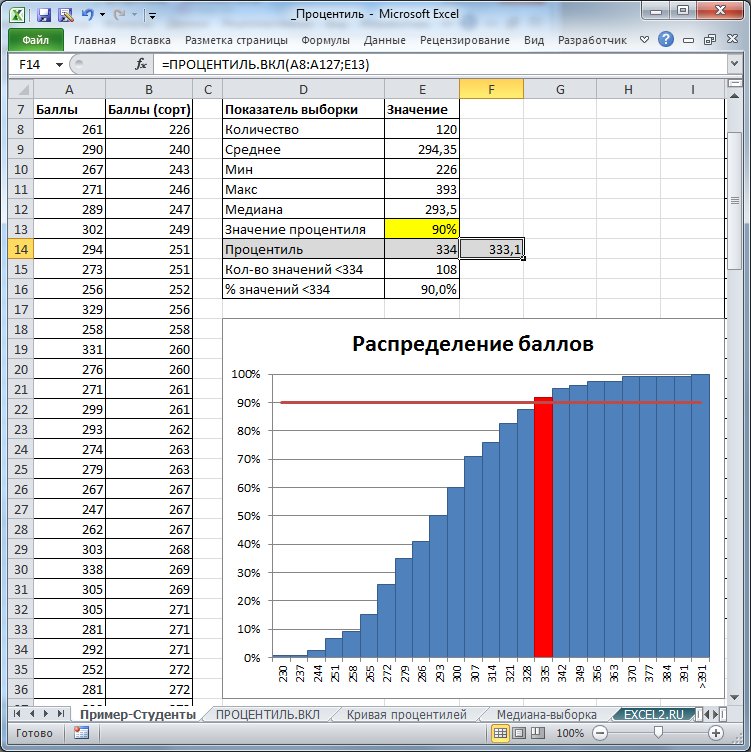 е. k = 3). Оказывается, коэффициент частичной корреляции можно вычислить, как описано в следующем свойстве.
е. k = 3). Оказывается, коэффициент частичной корреляции можно вычислить, как описано в следующем свойстве.
Собственность 1 : Предположим, что x 1 ,…, x K и Z , как в определении 1, и Let x и Z — в определении 1, и Let x и Z — в определении 1, и Let x и Z .0013 n × k матрица X = [ x ij ]. Частный коэффициент корреляции между переменными x i и x j , где i ≠ j с учетом всех остальных переменных, определяется по формуле
, X равно R -1 = [ p ij ]. Пример Пример 1 : Рассчитайте коэффициент частичной корреляции между криминальным и врачебным контролем смертей на дорогах и университетом на основе данных на рисунке 1 (который является подмножеством данных для примера 1 множественной корреляции).
Рисунок 1 – Данные штата США
Сначала мы вычисляем корреляционную матрицу и ее обратную для данных на рисунке 1 (см. рисунок 2).
Рисунок 2 – Обратная корреляционная матрица
Матрицу корреляции в диапазоне h5:K7 можно рассчитать, как описано в методе наименьших квадратов множественной регрессии. Затем мы можем вычислить обратную матрицу корреляции (диапазон h21:K14) с помощью формулы рабочего листа =MINVERSE(CORR(B4:E18)).
Теперь мы можем рассчитать коэффициент частичной корреляции между Преступностью и Врачами с учетом Смертей на дорогах и Университета, используя Свойство 1. В частности, мы используем формулу =–I11/SQRT(h21*I12), что дает значение 0,0919913.
В общем случае коэффициент частичной корреляции между переменными i и j дается формулой i , j )
или, альтернативно, следующая формула, менее ресурсоемкая для расчета:
=ИНДЕКС(-h21:K14/(M11:M14*ТРАНСП(M11:M14)), i , j )
Здесь диапазон M11:M14 представляет собой квадратный корень элементов на диагонали обратной корреляционной матрицы. Это можно рассчитать по формуле массива
Это можно рассчитать по формуле массива
=SQRT(INDEX(h21:K14,G11:G14,G11:G14))
Или формула массива =SQRT(DIAG(h21:K14).
Наблюдение : Как описано выше, мы можем вычислить Для получения значения .103292 используйте любую из следующих формул: =1-1/h21
Матрица частичной корреляцииОпределение 2 : Предположим, что x 1 , …, x k и X соответствуют определению 1 и свойству 1. S = [ S IJ ] где для всех I ♠ J
Пример 2 : Рассчитайте матрицу частичной корреляции для данных на рисунке 1.
Результат показан в результате показан в результате показан в результате показан в результате показан Рис. 3.9Рисунок 3 – Матрица частичной корреляции
Наблюдение : обратите внимание, что определение 2 не определяет значения на диагонали матрицы частичной корреляции (т. е. где i = j ). Приведенная выше формула дает матрицу, главная диагональ которой состоит из минус единиц. Если мы предпочитаем, чтобы главная диагональ состояла из всех единиц, мы можем использовать следующую модифицированную формулу:
Приведенная выше формула дает матрицу, главная диагональ которой состоит из минус единиц. Если мы предпочитаем, чтобы главная диагональ состояла из всех единиц, мы можем использовать следующую модифицированную формулу:
=-h21:K14/(M11:M14*TRANSPOSE(M11:M14))+2*IDENTITY()
Функции рабочего листаФункции реальной статистики : Ресурсный пакет реальной статистики предоставляет следующие функции, где R1 представляет собой матрицу n × k , представляющую выборки размером n для случайных величин x 1 ,…, x k .
PCORREL (R1, i , j ) = коэффициент частной корреляции x i с x j на основе данных в R1
PCORR (R1) — это функция, которая выводит матрицу частичной корреляции для данных in2 50 R1 90 Рисунок 1, PCORREL(B4:E18, 1, 2) = 0,0919913 на рисунке 3.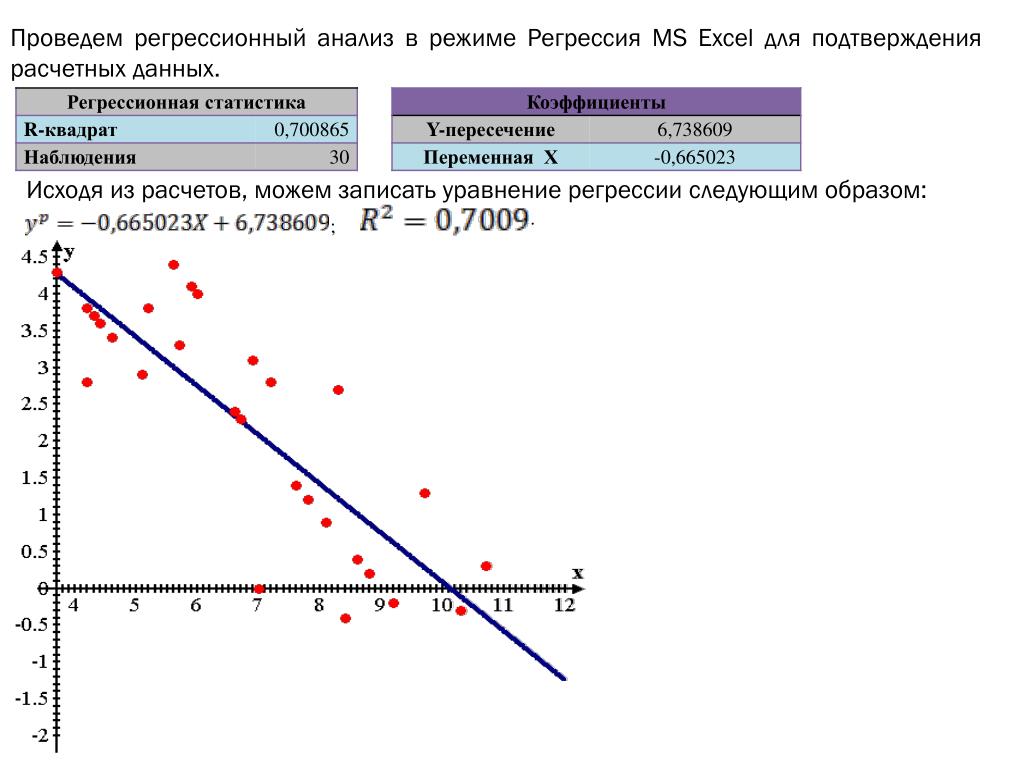

 ед., x
ед., x