Вектора и линейные операции над векторами
Физика — Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс
Вектора и линейные операции над векторами — ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ
Цель: познакомить с векторами и операциями над ними.
Ход урока
I. Повторение. Беседа
1. Что называется перемещением толчки?
2. Каков смысл модуля перемещения?
3. Что называется телом отсчета?
4. Какими способами можно задать положение точки?
5. Что называют радиус-вектором?
II. Изучение нового материала
Известно, что некоторые физические величины полностью характеризуются числом, которое выражает отношение этой величины к единице измерения. Такие величины называют скалярными.
— Приведите пример таких величин. (Примерами могут служить масса, температура, плотность, энергия.)
Для характеристики других физических величин, например скорости, силы, недостаточно знать число, измеряющее их величину, необходимо знать и их направление. Такие величины называют векторными. В физике они играют большую роль. Вектор — направленный отрезок прямой.
У вектора есть начало и конец. Начало вектора называют так же точкой его приложения.
Если точка А является началом вектора а, то мы будем говорить, что вектор а приложен к точке А (рис. 4).
Число, выражающее длину направленного отрезка, называют модулем вектора, и обозначают той же буквой, что и сам вектор, но без стрелки сверху.
Если начало вектора совпадает с его концом, такой вектор называют нулевым.
Вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 5).
5).
Два вектора называют равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление.
Из определения равенства векторов вытекает утверждение: каковы бы ни были вектор а и т. Р, существует единственный вектор с началом в т. Р, равный вектору а.
В физике принципиальное значение имеют линия, вдоль которой направлен вектор, и точка приложения вектора.
1. Сумма векторов.
Пусть даны два вектора а и b. Для нахождения их суммы нужно вектор в перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора а. Тогда вектор, проведенный из начала вектора а в конец перенесенного вектора b, и будет являться суммой а и b. с = а + b = b + а — правило треугольника.
Если два вектора коллинеарны и сонаправлены, то их сумма представляет собой вектор, направленный в ту же сторону и равный по модулю сумме модулей векторов слагаемых.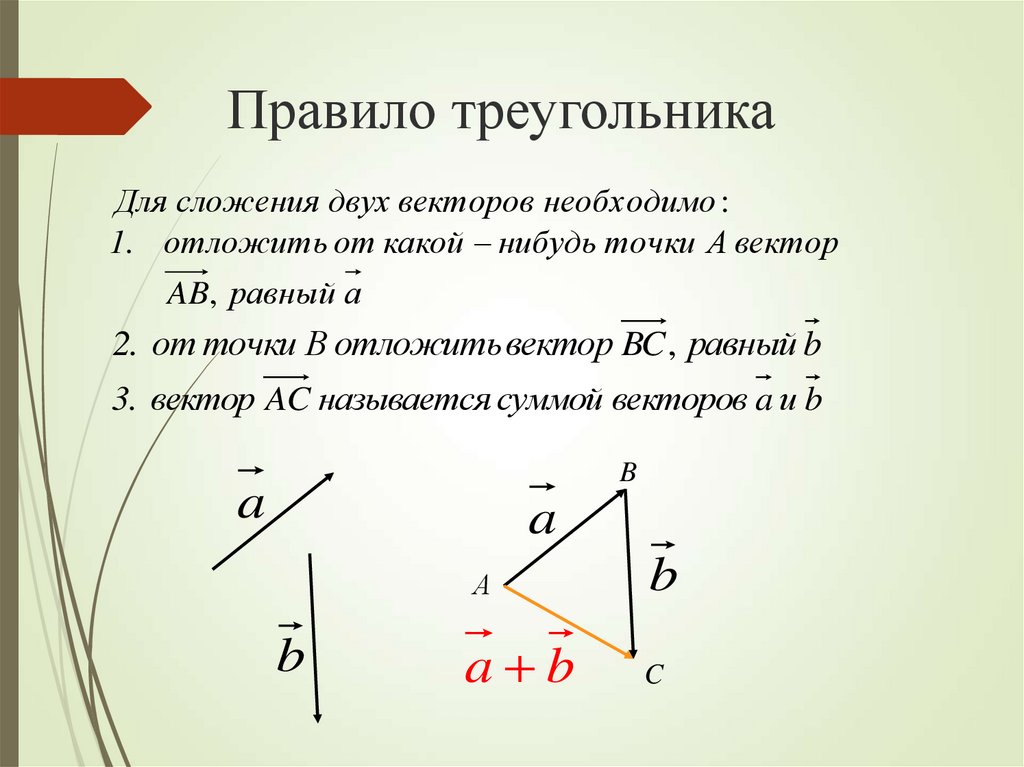
Если два вектора коллинеарны и направлены в противоположные стороны, то их сумма будет представлять собой вектор, модуль которого равен разности модулей векторов слагаемых, направленный в сторону того вектора-слагаемого, модуль которого больше.
Сумма векторов может быть найдена и по правилу параллелограмма (рис. 6).
В этом случае параллельным переносом нужно совместить начала векторов а ив и построить на них параллелограмм. Тогда сумма а и b будет представлять собой диагональ этого параллелограмма.
2. Умножение вектора на скаляр.
Произведением вектора а на число k называют вектор b, коллинеарный вектору а, направленный в сторону, что и вектор а, если k 0 и в направлен в противоположную сторону, если k
Если два вектора коллинеарны, то они отличаются только скалярным множителем.
Если k = -1, то b = -а. Вектор -а имеет модуль равный модулю вектора а, но направлен в противоположную сторону.
Два вектора, противоположно направленные и имеющие равные длины, называются противоположными. А и -а представляют собой противоположные векторы.
3. Разность векторов.
Вычитание векторов есть действие, обратное сложению.
Пусть необходимо из вектора b вычесть вектор а и тем самым найти их разность, т. е. h = b — a. Чтобы найти вектор разности, нужно по правилу параллелограмма (или треугольника) сложить вектор b с вектором, противоположным вектору а, т. е. с вектором -а (рис. 7).
Разностью векторов b и а называют такой вектор h, который в сумме с вектором а дает вектор b. h = b — a и h + a = b по определению одно и то же.
III. Закрепление изученного
1. Какие величины называют скалярными, а какие — векторными?
2. Чем отличается векторная величина от скалярной?
3. Какие правила сложения векторов вы знаете?
Какие правила сложения векторов вы знаете?
4. Как производится сложение нескольких векторов?
5. Как определить разность двух векторов?
6. Какие вектора называются коллинеарными?
7. Как производится сложение и вычитание коллинеарных векторов?
IV. Решение задач
1. Начало вектора а задано координатами точки А (2;2), конец В (6;5). Построить вектор.
2. Эквивалентно замените силу F = 0,6 Н, приложенную в т. А, двумя силами, действующими на ту же точку вдоль той же прямой, но противоположные стороны. Меньшая из этих сил равна 1,1 Н. Каким должен быть модуль второй силы? (Ответ: 1,7 Н)
3. В одной точке приложены силы F1 = 15 Н, F2 = 24 Н, F3 = 19 Н, F4 = 20 Н. Определите их равнодействующую для случаев, когда
а) все данные силы действуют вдоль одной прямой в одну сторону.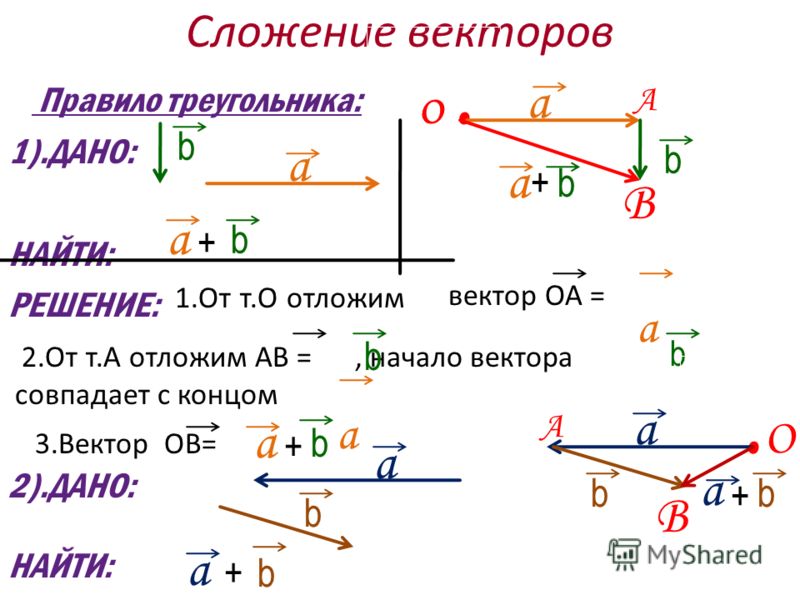
б) все данные силы действуют вдоль одной прямой, первые две в одну сторону, а вторые две — в сторону, противоположную первым.
Домашнее задание
П. 5.
Сложение векторов. Сложение сил. Геометрия. 8 класс. | Методическая разработка по геометрии (8, 9 класс) на тему:
Слайд 1
Басня «Лебедь, Щука и Рак» И.А. Крылов
Слайд 2
1 . Бывает … тяжести, … упругости 2. 2 вектора, которые лежат на параллельных прямых или на одной прямой называются… 4. Арифметическое действие. 5. Направленный отрезок. 7. F – так обозначают физическую величину… 8. Направленный отрезок прямой, который соединяет начало движения и конец движения. 9. Вектор — это … отрезок. 10. Ускорение, скорость — это величины… 12. Длина вектора — это … величина. 13. Величина, характеризующая быстроту изменения 14. t, m, t 0 — величины… 15. Каждый вектор имеет… 6. 16. 11.
Слайд 4
Сложение векторов. Сложение сил 21.04.16
Сложение сил 21.04.16
Слайд 5
Защита проектов Скорость. Ускорение. Импульс тела.
Слайд 6
Вспомним! Тело из точки 1 переместилось вправо на расстояние 3 м в точку 2, а затем переместилось перпендикулярно предыдущему направлению в точку 3 на расстояние 4 м. Найти путь и перемещение. s = √ s 1 2 + s 2 2 = √9 м 2 +16м 2 = 5 м. Путь L = s 1 + s 2 = 7 м. 1 2 3 s s 1 s 2
Слайд 7
Разминка для глаз
Слайд 8
Две силы направлены вдоль одной прямой в одну сторону: R F 2 F 1 R = F 1 + F 2 R = F 1 + F 2 Равнодействующая двух сил, направленных вдоль одной прямой в одну сторону, направлена в ту же сторону , а её модуль равен сумме модулей этих сил. Например: F 1 = 7 Н, F 2 = 4 Н, Тогда R = 7 Н + 4 Н = 11 Н, направлена вправо.
Слайд 9
Две силы направлены вдоль одной прямой в противоположные стороны: R F 2 F 1 R = F 1 + F 2 R = F 2 — F 1 Равнодействующая двух сил, направленных вдоль одной прямой в противоположные стороны, направлена в сторону силы с большим модулем, а её модуль равен разности модулей этих сил.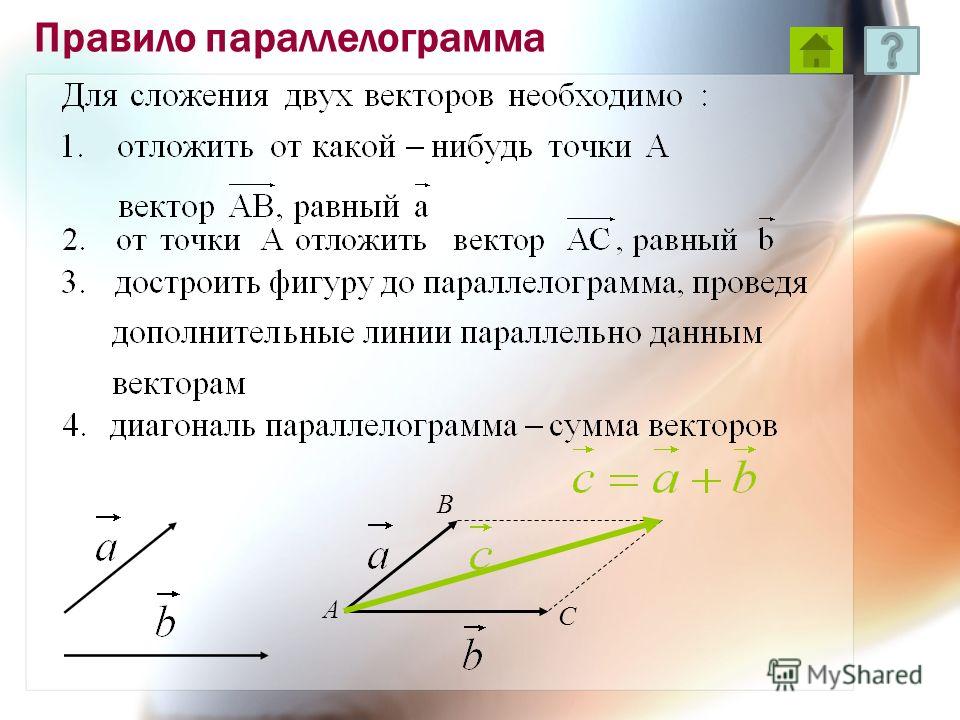 Например: F 1 = 7 Н, F 2 = 4 Н, Тогда R = 7 Н — 4 Н = 3 Н, направлена влево.
Например: F 1 = 7 Н, F 2 = 4 Н, Тогда R = 7 Н — 4 Н = 3 Н, направлена влево.
Слайд 10
Если на тело действуют две силы, направленные вдоль одной прямой в противоположные стороны: F 1 F 2 R = F 1 + F 2 R = F 1 – F 2 = 0, при этом F 1 = F 2 , то: при этом тело может либо находиться в покое, либо двигаться равномерно и прямолинейно.
Слайд 11
Нахождение равнодействующей силы в случае, когда силы направлены под прямым углом друг к другу: R = F 1 + F 2 В данном случае её можно найти по теореме Пифагора: F 1 F 2 R
Слайд 12
Работа с текстом Прочитайте внимательно текст и ответьте на вопросы после текста.
Слайд 13
Ответы: Правило треугольника, правило параллелограмма и правило многоугольника. По правилу параллелограмма. Правило многоугольника. Нулевому вектору. в) начало первого и конец второго.
Слайд 14
6.
Слайд 15
7. 3 м/с 4 м/с Скорость приземления равна 5 м/с.
Слайд 16
Лебедь, щука и рак
Слайд 17
Лебедь, щука и рак l r s Р m
Слайд 18
Домашнее задание «3» П. 94, 95, № 9(1,3) с. 149 «4» П.94, 95, № 9(1,3), № 16 с. 149 «5» П.94, 95, № 9(1-4), № 16 с. 149 Творческая задача . Подобрать задачи из учебника физики, по теме «Сложение векторов». Дополнительно. Творческое задание . Придумать кроссворд (или тест) на тему: «Векторы».
94, 95, № 9(1,3) с. 149 «4» П.94, 95, № 9(1,3), № 16 с. 149 «5» П.94, 95, № 9(1-4), № 16 с. 149 Творческая задача . Подобрать задачи из учебника физики, по теме «Сложение векторов». Дополнительно. Творческое задание . Придумать кроссворд (или тест) на тему: «Векторы».
Слайд 19
Закончи предложения: Я знаю умею могу
Слайд 20
Ниже приведены семь вопросов, на каждый из которых можно дать только один из ответов: БОЛЬШИНСТВО, НЕКОТОРЫЕ, ВСЕ, НИКТО. Дайте ответ на каждый из вопросов, предварительно обсудив его с соседом по парте: 1. Принимали участие в совместной работе — 2. Помогали в выборе правильных решений — 3. Предлагали новые идеи и направления — 4. Ждали помощи от класса — 5. Находили и исправляли ошибки — 6. Оказывали помощь другим — 7. Понимали, что делаем общее дело —
Слайд 21
Спасибо за урок!
Что такое результат?
Результирующее число представляет собой векторную сумму двух или более векторов. Это результат сложения двух или более векторов вместе. Если сложить векторы смещения A, B и C, результатом будет вектор R. Как показано на диаграмме, вектор R можно определить с помощью точно нарисованной масштабированной диаграммы сложения векторов.
Если сложить векторы смещения A, B и C, результатом будет вектор R. Как показано на диаграмме, вектор R можно определить с помощью точно нарисованной масштабированной диаграммы сложения векторов.
Сказать, что вектор R есть результирующее перемещение векторов смещения A, B и C означает, что человек, который шел со смещением A, затем B, а затем C, сместится на ту же величину, что и человек, который шел со смещением R. Вектор смещения R дает то же самое результат в виде векторов смещения A + B + C. Поэтому можно сказать, что
Вышеприведенное обсуждение относится к результату сложения векторов смещения. При добавлении векторов смещения результатом будет результирующее смещение . Но любые два вектора могут быть добавлены, если они являются одной и той же векторной величиной. Если добавить два или более векторов скорости, результатом будет результирующая скорость .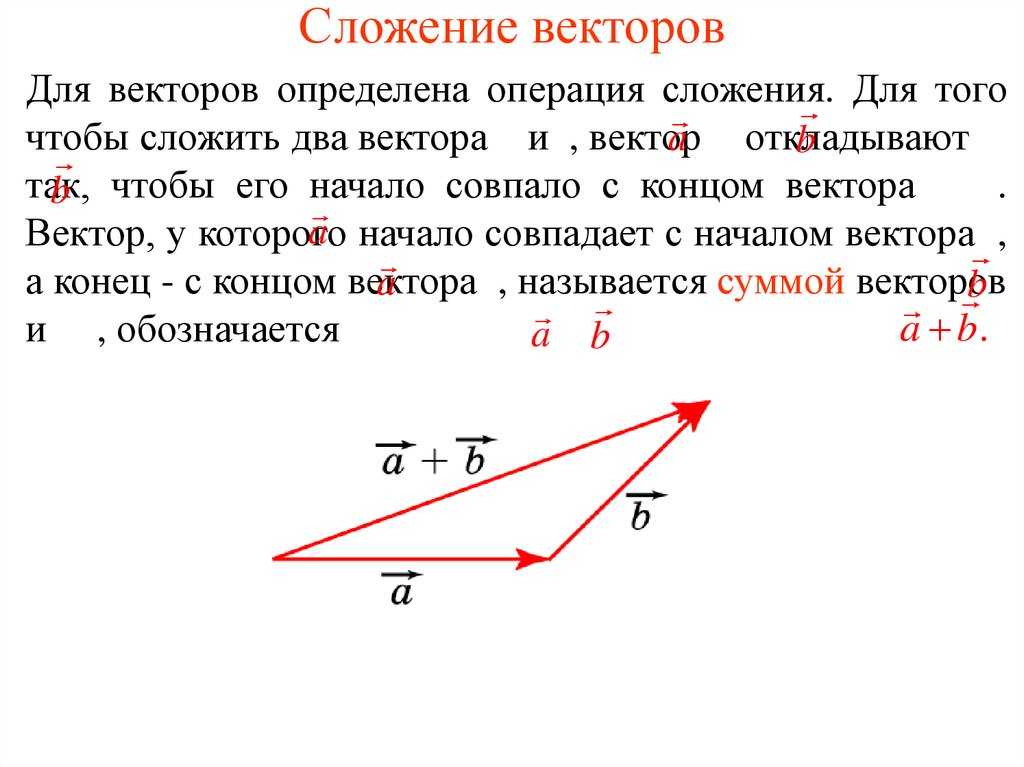 Если добавить два или более векторов силы, то результатом будет равнодействующая сила . Если сложить два или более векторов импульса, то результатом будет …
Если добавить два или более векторов силы, то результатом будет равнодействующая сила . Если сложить два или более векторов импульса, то результатом будет …
Во всех таких случаях результирующий вектор (будь то вектор смещения, вектор силы, вектор скорости и т. д.) является результатом сложения отдельных векторов. Это то же самое, что добавить А + В + С + … . «Делать A + B + C — это то же самое, что делать R». В качестве примера рассмотрим футболиста, которого одновременно бьют три игрока противоположной команды (игроки A, B и C). Футболист испытывает на себе воздействие трех различных сил. Каждая приложенная сила вносит свой вклад в общую или результирующую силу. Если сложить три силы вместе с помощью методов сложения векторов (обсуждавшихся ранее), то можно определить результирующий вектор R. В этом случае испытать три силы A, B и C — это то же самое, что испытать силу R. Если вас ударят игроки A, B и C, это приведет к той же силе, что и удар, нанесенный одним игроком, применяющим силу R». Сделать A + B + C — это то же самое, что сделать R». Вектор R — это тот же результат, что и векторы A + B + C!!
Сделать A + B + C — это то же самое, что сделать R». Вектор R — это тот же результат, что и векторы A + B + C!!
Таким образом, результат представляет собой векторную сумму всех отдельных векторов. Результат является результатом объединения отдельных векторов вместе. Результирующую можно определить путем сложения отдельных сил с использованием методов сложения векторов.
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей интерактивной игры Name That Vector, нашей интерактивной игры с добавлением вектора или нашей интерактивной игры с угадыванием вектора. Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Посетите: Назовите этот вектор | Добавление вектора | Игра «Угадай вектор»
Следующий раздел:
Перейти к следующему уроку:
3.3 Сложение и вычитание векторов: аналитические методы
Сложение векторов с использованием аналитических методов
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рис. 3.30, на котором векторы размера AA 12{A} {} и размера BB 12{B} {} складываются для получения результирующего размера RR 12{R} {} .
Рис. 3.30 Векторы размера AA 12{A} {} и размера BB 12{B} {} представляют собой два участка пути, а размер RR 12{R} {} представляет собой результирующее или полное перемещение. Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.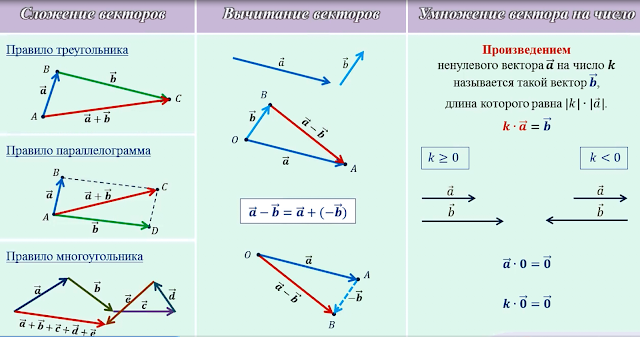
Если AA и BB представляют два этапа ходьбы (два перемещения), то RR представляет собой общее перемещение. Человек, совершающий прогулку, оказывается на вершине RR. Есть много способов попасть в одну и ту же точку. В частности, человек мог ходить первым в x -направление, а затем в y -направление. Эти пути являются x — и y -компонентами результирующего, RxRx и RyRy size 12{R rSub { size 8{y} } } {}. Если мы знаем RxRx и RyRy size 12{R rSub { size 8{y} } } {} мы можем найти РР и θθ с помощью уравнений A=Ax2+Ay2A=Ax2+Ay2 и θ=tan–1(Ay/Ax)θ=tan–1(Ay/Ax) размер 12{θ=»tan» rSup { размер 8{–1}} \( A rSub { размер 8{y}} /A rSub { размер 8 {x} } \) } {}. Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого вектора, которые должны быть добавлены вдоль выбранных перпендикулярных осей . Используйте уравнения
Ax=AcosθAx=Acosθ размер 12{A rSub {размер 8{x}} =A»cos»θ} {} и
Ay=AsinθAy=Asinθ size 12{A rSub { size 8{y} } =A»sin»θ} {}, чтобы найти компоненты. На рис. 3.31 эти компоненты
Размер AxAx 12 {A rSub { размер 8 {x} } } {},
AyAy размер 12 {A rSub { размер 8 {y} } } {},
BxBx размер 12{B rSub { размер 8{x} } } {}, и
ByBy size 12{B rSub { size 8{y} } } {}. Углы, которые составляют векторы размера AA 12{A} {} и размера BB 12{B} {} с x -ось θAθA размера 12{θ rSub {размер 8{A} } } {} и θBθB размера 12{θ rSub {размер 8{B} } } {} соответственно.
Затем найдите компоненты каждого вектора, которые должны быть добавлены вдоль выбранных перпендикулярных осей . Используйте уравнения
Ax=AcosθAx=Acosθ размер 12{A rSub {размер 8{x}} =A»cos»θ} {} и
Ay=AsinθAy=Asinθ size 12{A rSub { size 8{y} } =A»sin»θ} {}, чтобы найти компоненты. На рис. 3.31 эти компоненты
Размер AxAx 12 {A rSub { размер 8 {x} } } {},
AyAy размер 12 {A rSub { размер 8 {y} } } {},
BxBx размер 12{B rSub { размер 8{x} } } {}, и
ByBy size 12{B rSub { size 8{y} } } {}. Углы, которые составляют векторы размера AA 12{A} {} и размера BB 12{B} {} с x -ось θAθA размера 12{θ rSub {размер 8{A} } } {} и θBθB размера 12{θ rSub {размер 8{B} } } {} соответственно.
Рисунок 3.31. Чтобы добавить векторы размера AA 12{A} {} и размера BB 12{B} {}, сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы AxAx size 12{A rSub { size 8{x} } } {}, AyAy size 12{A rSub { size 8{y} } } {}, BxBx size 12{B rSub { size 8{x } } } {} и ByBy size 12{B rSub { size 8{y} } } {} показаны на изображении.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано на рисунке 3.32,
3.12 Rx=Ax+BxRx=Ax+Bx размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8 {x} } } {}
и
3.13 Ry=Ay+By.Ry=Ay+By. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}
Рисунок 3.32. Величина векторов AxAx размера 12{A rSub { size 8{x} } } {} и BxBx размера 12{B rSub { size 8{x} } } {} складывается для получения величины RxRx размера 12{ R rSub { size 8{x} } } {} результирующего вектора в горизонтальном направлении. Аналогично, величины векторов AyAy size 12{A rSub { size 8{y} } } {} и ByBy size 12{B rSub { size 8{y} } } {} в сумме дают величину RyRy size 12{R rSub { size 8{y} } } {} результирующего вектора в вертикальном направлении.
Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси y . Например, пройти 9 кварталов на восток можно двумя этапами: первые три квартала на восток и вторые шесть кварталов на восток, всего девять, потому что они идут в одном направлении. Таким образом, разложение векторов на компоненты вдоль общих осей облегчает их добавление. Теперь, когда компоненты размера RR 12{R} {} известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину RR size 12{R } {} результанта, используйте теорему Пифагора.
3.14 R=Rx2+Ry2.R=Rx2+Ry2. размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup { размер 8{2} } } «.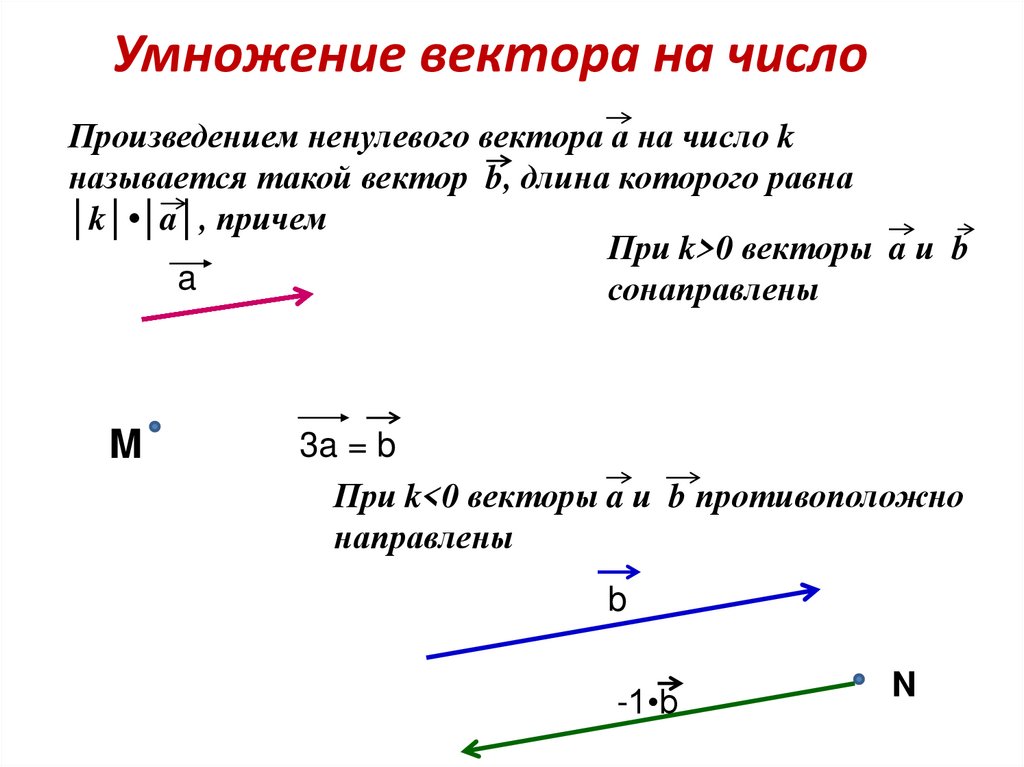
Шаг 4. Чтобы получить направление равнодействующей
3,15 θ=tan-1(Ry/Rx).θ=tan-1(Ry/Rx). size 12{θ=»tan» rSup { size 8{- 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «.»} {}
В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.
Пример 3.3 Добавление векторов с использованием аналитических методов
Добавьте вектор размера AA 12{A} {} к вектору размера BB 12{B} {}, показанному на рисунке 3.33, используя перпендикулярные компоненты вдоль x — и и -оси. Оси x — и y — направлены соответственно с востока на запад и с севера на юг.
Рис. 3.33 Вектор AA размера 12{A} {} имеет величину 53,0 м53,0 м размера 12{«53» «.» «0 м»} {} и направление 20,0º20,0º размер 12{«20» «.» 0 { size 12{ circ } } } {} к северу от оси x . Вектор BB размера 12{B} {} имеет звездную величину 34,0 м34,0 м размера 12{«34» «.» «0 м»} {} и направление 63,0º63,0º размер 12{«63» «.» 0° } {} к северу от оси x . Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.
Стратегия
Компоненты размера AA 12{A} {} и BB размера 12{B} {} вдоль x — и y -осей представляют собой ходьбу строго на восток и строго на север, чтобы добраться до одного и того же конечная точка. После обнаружения они объединяются для получения результирующего.
После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты Размер AA 12{A} {} и BB размер 12{B} {} вдоль x — и y -оси. Обратите внимание, что A=53,0 мА=53,0 м размер 12{«A» «=» «53,0 м»} {}, θA=20,0ºθA=20,0º размер 12{«θ» «subA» «=» «20,0°» } {}, B=34,0 mB=34,0 м размер 12{«B» «=» «34,0» «м»} {} и θB=63,0ºθB=63,0º размер 12{θ rSub {размер 8{B} } } {}. Мы находим x -компоненты, используя Ax=AcosθAx=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}, что дает
3,16 Ax=AcosθA=(53,0 m)(cos 20,0º)=(53,0 м)(0,940)=49,8 мAx=AcosθA=(53,0 м)(cos 20,0º)=(53,0 м)(0,940)=49,8 malignl { stack {
size 12{A rSub { size 8{x} } =A»cos»θ rSub {size 8{A}} = \(«53» «. 0″ m» \) \( «cos»»20″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «53» «.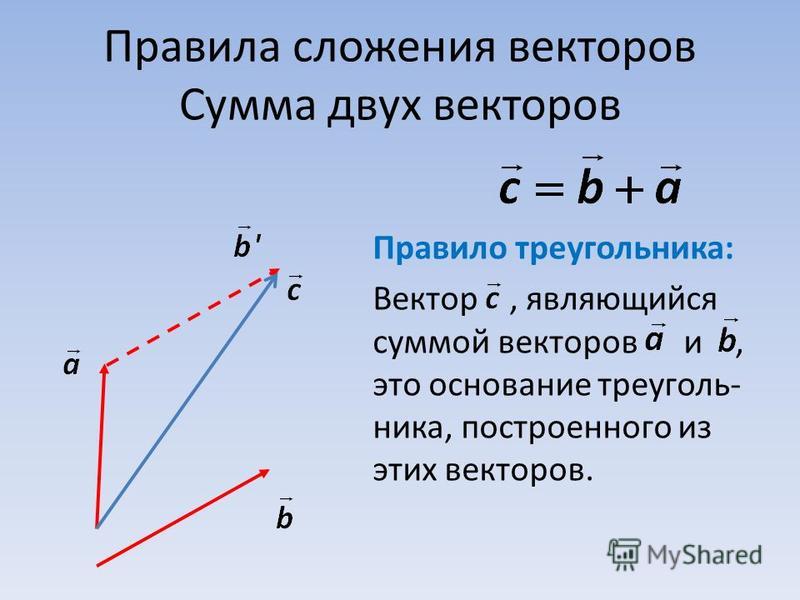 » 0″ м» \) \( 0 «.» «940» \) = «49» «.» 8″ м» {}
} } {}
» 0″ м» \) \( 0 «.» «940» \) = «49» «.» 8″ м» {}
} } {}
и
3,17 Bx=BcosθB=(34,0 м)(cos 63,0°)=(34,0 м)(0,454)=15,4 м.Bx=BcosθB=(34,0 м)(cos 63,0°)=( 34,0 м)(0,454)=15,4 м.alignl { stack { размер 12{B rSub { размер 8{x} } =B»cos»θ rSub { размер 8{B}} = \(«34» «. 0″ m» \) \( «cos»»63″ » .» 0 { размер 12 { круг } } \) } {} # » «= \( «34» «. 0″ м» \) \( 0 «.» «454» \) =»15″ «.» 4 «м» {} } } {}
Аналогично, y -компоненты находятся с помощью Ay=AsinθAAy=AsinθA size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A} } } { }.
3,18 Ay=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 мAy=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 malignl { куча { size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A}} = \(«53» «.» 0″ m» \) \( «sin»»20″ » .» 0 { размер 12 { круг } } \) } {} # » «= \(«53» «. 0″ м» \) \( 0 «.» «342» \) =»18″ «.» 1 «м» {} } } {}
и
3,19 By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891)=30,3 м.By=BsinθB=(34,0 м)(sin 63,0º)=( 34,0 м)(0,891)=30,3 м.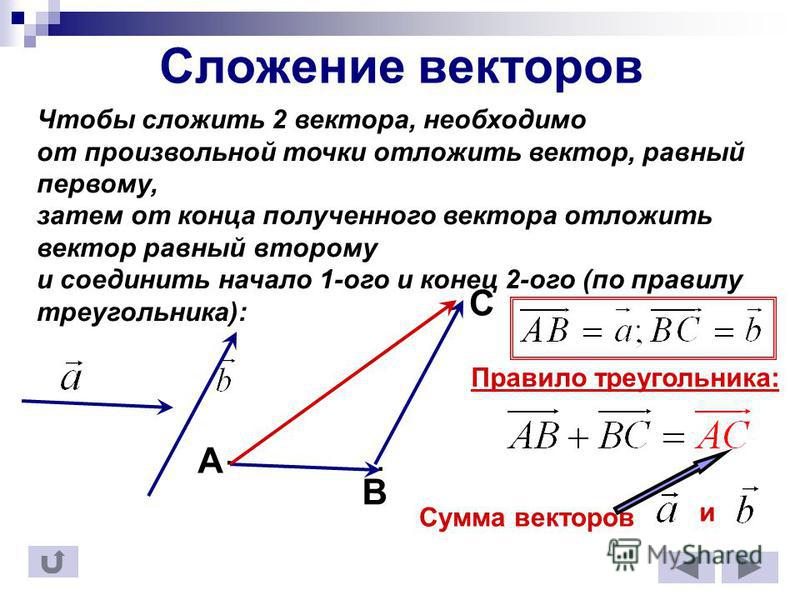 alignl {стек {
size 12{B rSub { size 8{y} } =B»sin»θ rSub { size 8{B}} = \(«34» «. 0″ m» \) \( «sin»»63″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «34» «.» 0″ м» \) \( 0 «.» «891» \)=»30″ «.» 3″ м» «.» {}
} } {}
alignl {стек {
size 12{B rSub { size 8{y} } =B»sin»θ rSub { size 8{B}} = \(«34» «. 0″ m» \) \( «sin»»63″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «34» «.» 0″ м» \) \( 0 «.» «891» \)=»30″ «.» 3″ м» «.» {}
} } {}
Таким образом, x — и y -компоненты равнодействующей равны
3,20 Rx=Ax+Bx=49,8 m+15,4 m=Ax=65,2 mRx= +15,4 м=65,2 м размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8{x} } =»49″ «.» 8″ м»+»15″ «.» 4″ м»=»65″ «.» 2″ м»} {}
и
3,21 Ry=Ay+By=18,1 м+30,3 м=48,4 м. Ry=Ay+By=18,1 м+30,3 м=48,4 м. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y}} =»18″ «.» 1″ м»+»30″ «.» 3″ м»=»48″ «.» 4″ м.»} {}
Теперь мы можем найти величину равнодействующей по теореме Пифагора
3,22 R=Rx2+Ry2=(65,2)2+(48,4)2 mR=Rx2+Ry2=(65,2)2+(48,4)2 m размер 12 {R = sqrt {R rSub { размер 8 {x} } rSup { размер 8 {2} } +R rSub { размер 8 {y} } rSup { размер 8 {2} } } = sqrt { \ («65 » «. » 2 \) rSup { size 8{2} } + \( «48» «.» 4 \) rSup { size 8{2} } } » m»} {}
» 2 \) rSup { size 8{2} } + \( «48» «.» 4 \) rSup { size 8{2} } } » m»} {}
так что
3.23 R =81,2 м.R=81,2 м. size 12{R =»81.2″ «m.»} {}
Наконец, мы находим направление равнодействующей
3,24 θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2).θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2). size 12{θ=»tan» rSup { size 8{ — 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «=+»»tan» rSup { size 8{ — 1} } \(«48» «.» 4/»65″ «.» 2 \) «.»} {}
Таким образом,
3,25 θ=tan−1(0,742)=36,6º. θ=тангенс-1(0,742)=36,6º. size 12{θ=»tan» rSup { size 8{ — 1} } \( 0 «.» «742» \) =»36″ «.» 6 {размер 12{круг}} «.»} {}
Рисунок 3.34 Используя аналитические методы, мы видим, что величина RR размера 12{R} {} составляет 81,2 м81,2 м размера 12{«81» «.» «2 м»} {} и его направление 36,6º36,6º размер 12{«36» «.» 6°} {} к северу от востока.
Обсуждение
В этом примере показано сложение векторов с использованием перпендикулярных компонентов.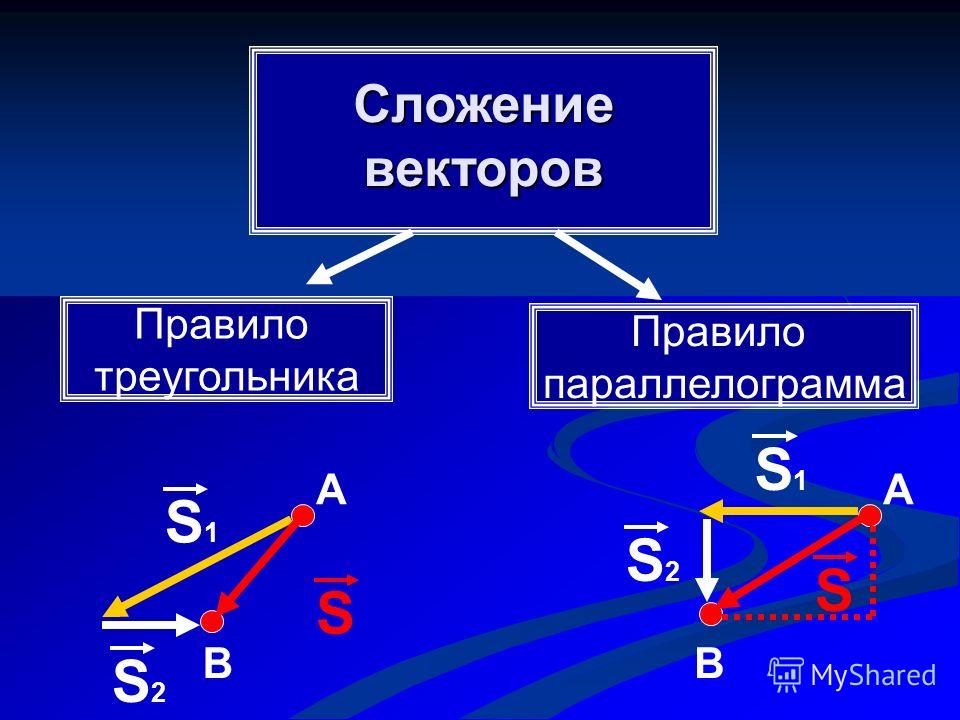 Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A−B≡A+(–B)A−B≡A+(–B) размер 12{A – B эквивалент A+ \(- B \)} {}. Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты –B–B – минусы компонентов Размер каретки 12{B} {}. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R size 12{A- полужирный «B = R»} {} равны
3,26 Rx=Ax+(–Bx )Rx=Ax+(–Bx) размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +-B rSub { размер 8{x} } } {}
и
3,27 Ry=Ay+(–By)Ry=Ay+(–By) размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +-B rSub { размер 8{y} } } {}
, а в остальном описанный выше метод идентичен методу сложения (см.
