Метод интерполяции онлайн расчет: Линейная интерполяция. Онлайн калькулятор

Интерполяционный многочлен Ньютона (полином Ньютона)

УчебаМатематика

Этот онлайн калькулятор строит интерполяционный многочлен Ньютона для заданного набора точек. Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график.

Калькулятор ниже строит интерполяционный многочлен Ньютона (полином Ньютона) в общем виде (то есть ему не требуется, чтобы точки из набора значений находились друг от друга на равном расстоянии), после чего упрощает его, раскрывая скобки, и получает результат, пригодный для расчетов. Помимо этого калькулятор интерполирует значения неизвестной функции в указанных точках и строит график полинома, отмечая точки интерполяции и точки из заданного набора данных.

Как пользоваться

Сначала вводите набор точек — одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек, в которых надо найти значения интерполяционного многочлена в следующее поле в виде значений x, разделенных пробелом.

Теория и формулы, как обычно, описаны под калькулятором.

Интерполяционный многочлен Ньютона (полином Ньютона)

0 -1 1 1 4 1

Набор точек, одна точка на строку, значения разделяются пробелом

Точки для интерполяции

Точность вычисления

Округленно

Полином Ньютона

 

Полином Ньютона после упрощений

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Полином Ньютона

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Интерполяционный многочлен Ньютона (полином Ньютона)

В общем виде интерполяционный многочлен Ньютона записывается в следующем виде:

,

где n — степень полинома,
— разделенная разность k-го порядка, вычисляемая как
.

Разделенную разность k-го порядка также можно выразить через значения функции в точках с помощью такой формулы:
.
Последняя формула и используется в калькуляторе.

Полином Ньютона — это форма записи полинома n-ной степени, который проходит через все заданные точки из набора значений. Такая форма является более удобной формой представления интерполяционного полинома для ручных расчетов, так как при добавлении дополнительного узла все вычисленные ранее слагаемые остаются без изменения, а к выражению добавляется только одно новое слагаемое.

При этом сам интерполяционный полином для заданного набора данных является единственным, и по сути, полином Ньютона только по форме отличается от полинома Лагранжа, после упрощения превращаясь в один и тот же полином.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Интерполяционный многочлен Лагранжа (полином Лагранжа)
• • Метод Ньютона
• • Умножение многочленов
• • Расширенный НОД полиномов в конечном поле
• • Метод выделения полного квадрата
• • Раздел: Математика ( 265 калькуляторов )

 #интерполяция #полином интерполяционный многочлен Ньютона интерполяция Математика математический анализ Многочлены полином полином Ньютона

 PLANETCALC, Интерполяционный многочлен Ньютона (полином Ньютона)

Timur2020-11-29 11:12:36

Метод Пауэлла онлайн

Примеры решенийМетод Зейделя Метод Ньютона Метод хорд Решение уравненийМетод LU-разложения Метод Гаусса Матрица Гессе Градиент функции Экстремум функции

Этот метод основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации.

Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом Пауэлла (см. также калькулятор для двух переменных). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

f(x) =

Начиная из точки x₀ = . Точность ξ =
Шаг приращения h = .
Множитель приращения a = .

Правила ввода функций:

пусть x₁ — начальная точка; Δx- выбранная величина шага по оси х.
Шаг 1: Вычислить x₂=x₁+Δx.
Шаг 2: Вычислить f(x₁) и f(x₂).
Шаг 3: Если f(x

1)>f(x₂), положить x₃=x₁+2Δx, если f(x₁)≤f(x₂), то x₃=x₁-Δx.
Шаг 4: Вычислить f(x₃) и найти F_min = min{f₁, f₂, f₃}
X_min равно точке x_i, которая соответствует F_min.
Шаг 5: По трем точкам x₁, x₂, x₃ вычислить x, используя квадратичную аппроксимацию.



Шаг 6: Проверка на окончание поиска:
а) является ли разность |F_min-f(z)|≤ε;
б) является ли разность |X_min-x|≤δ,
где ε>0 и δ>0 — заданные точности.
Если условия а) и б) выполняются одновременно, то закончить поиск. Иначе переход на Шаг 7.
Шаг 7: Выбрать «наилучшую» точку (X _min или x) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти на Шаг 4.
Замечание: после пятого шага необходимо провести дополнительную проверку, т.к. точка x может находиться за точкой x₃. В этом случае точка x заменяется точкой, координата которой вычисляется c учетом заранее установленной длины шага.
Пусть полученная точка x лежит вне отрезка интерполяции. Смысл здесь заключается в следующем. О характере функции, в общем случае, ничего неизвестно, но при помощи аппроксимации происходит замена ее по трем точкам параболой (на рисунке обозначена пунктиром). Вид параболы полностью определяется выбранными точками. Если точки выбраны неудачно, то минимум параболы может оказаться весьма далеко от минимума функции. Причем, если у функции имеются несколько локальных минимумов, в итоге можно найти не тот минимум, что является ближайшим к начальной точке. Применение же вышеописанного правила предотвращает подобную ситуацию.

Пример. Найти .
Пусть начальная точка x₁=1 и длина шага Δx=1.
Критерии останова:

Замечание. Оба критерия должны выполняться одновременно.
Итерация 1:
Шаг 1: x₂=x₁+ Δx =2
Шаг 2: f(x₁)=18; f(x₂)=16
Шаг 3: f(x₁)>f(x₂), следовательно x₃=1+2 = 3;
Шаг 4: f(x₃)=23. 33;F_min=16; X_min=x₂.
Шаг 5: Вычислим x: Шаг 6: Проверка на окончание поиска:
а) . Критерий останова не выполняется, следовательно поиск продолжается. Переход на Шаг 7.
Шаг 7: Выбираем x как «наилучшую» точку, а x ₁=1, x₂=2 – как точки, которые ее окружают. Обозначим эти точки в естественном порядке и переходим к Шагу 4.
Итерация 2:
Шаг 4: x₁=1; f₁=18; x₂=1.714, f₂=15.21 = F_min;
X_min = x₂ = 1.714, x₃= 2; f₃ = 16
Шаг 5: Шаг 6: Проверка на окончание поиска: а) .
Первый критерий останова не выполняется. Переход на Шаг 7.
Шаг 7: Выбираем x как «наилучшую» точку, а x₁ = 1, x₂ = 1,714 – как точки, которые ее окружают. Обозначим эти точки в естественном порядке и переходим к Шагу 4.
Итерация 3:
Шаг 4:
x₁ = 1, f₁ = 18; x₂ = 1. 65; f₂ = 15.142; = F_min; X_min= x₂ = 1.65
x₃ = 1.174; f₃ = 15.21
Шаг 5: Шаг 6: Проверка на окончание поиска:
а) б)
Оба критерия останова выполняются, следовательно, поиск закончен.
Ответ: x=1,6124 (точное решение x=1.5874).

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Онлайн-калькулятор: интерполяция многочленов Ньютона

  Исследование  Математика  Алгебра  Полиномы

Полиномы

Этот онлайн-калькулятор интерполяции точек строит полиномы Ньютона. Калькулятор также показывает общую форму и упрощенную форму, интерполирует дополнительные точки, если они введены, и строит график

Этот онлайн-калькулятор строит интерполяционный полином Ньютона для заданного набора точек данных.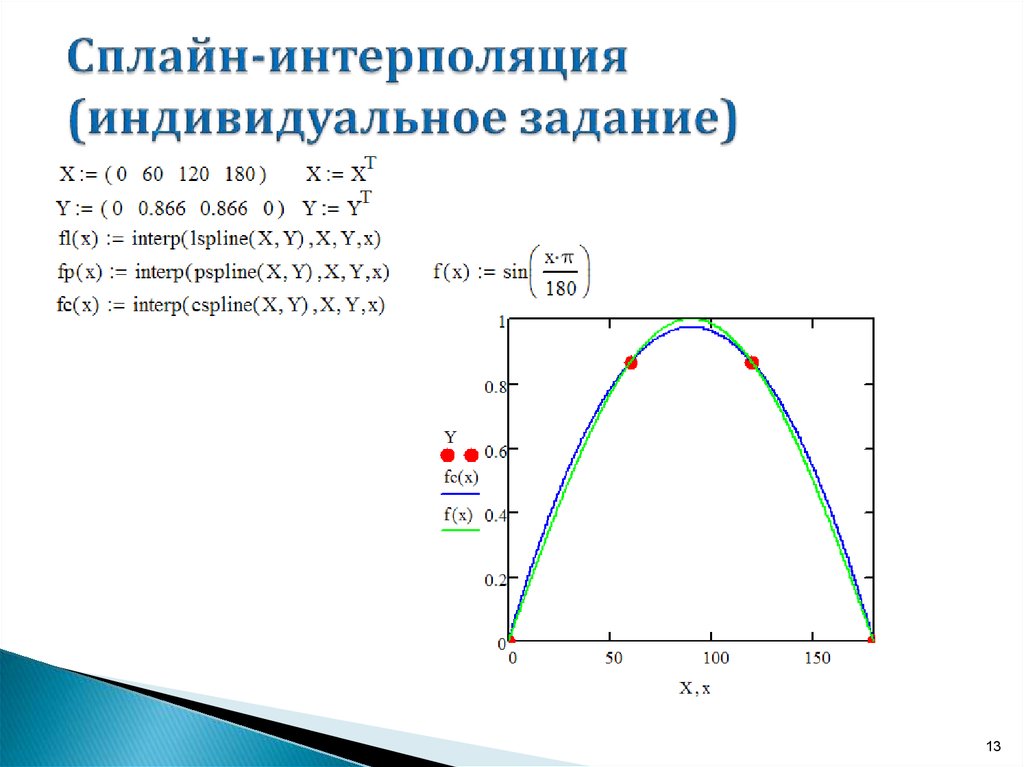 Он также вычисляет интерполированное значение для введенных точек и строит график.

Использование

Сначала введите точки данных, по одной точке в строке, в формате x f(x) , разделенные пробелами. Если вы хотите интерполировать функцию, используя интерполирующий полином, введите точки интерполяции в следующее поле в виде значений x , разделенных пробелами.

Вы также можете найти теорию об интерполяционном многочлене Ньютона под калькулятором.

Полиномиальная интерполяция Ньютона

0 -1 1 1 4 1

Точки данных, одна точка на строку, разделенная по пространству

Точки интерполяции

Расчет Точность

Окружные

Полином Ньютона

NEWTON POLYNOMIAL После упрощения

. Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Многочлен Ньютона

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Полиномиальная интерполяция Ньютона

Общая форма интерполяционного многочлена Ньютона:

,

где n — степень полинома,
— _k_th деленная разность, определяемая как
.

k разделенная разница также может быть выражена как:
.
Последняя форма используется в калькуляторе.

При интерполяции Ньютона дополнительные базисные полиномы и соответствующие коэффициенты могут быть рассчитаны, когда необходимо использовать больше точек данных, а все существующие базисные полиномы и их коэффициенты остаются неизменными. Это больше подходит для ручных вычислений, поскольку, например, дополнительные точки в интерполяции Лагранжа требуют пересчета всех базисных полиномов.

Обратите внимание, что из-за уникальности полиномиальной интерполяции интерполяция Ньютона аналогична интерполяции Лагранжа. Это один и тот же полином n-й степени, выраженный через разные базисные полиномы, взвешенные с разными коэффициентами.

URL скопирован в буфер обмена

Похожие калькуляторы

• • Калькулятор полиномов Лагранжа
• • Метод Ньютона
• • Численное интегрирование
• • Простая математика в любой системе счисления
• • Greatest common divisor of several polynomials
• • Polynomials section ( 19 calculators )

  #interpolation #Newton interpolation Math newton numerical analysis Polynomials

  PLANETCALC, The Newton Polynomial Interpolation

 Тимур  2022-09-26 16:45:11

Калькулятор линейной интерполяции

Создано Bogna Szyk

Отзыв Стивена Вудинга и Джека Боуотера

Последнее обновление: 7 октября 2022 г.

Содержание:

• Что такое линейная интерполяция?
• Формула линейной интерполяции
• Как использовать этот калькулятор для решения y

Этот калькулятор линейной интерполяции является удобным инструментом для поиска точек на определенной линии, определяемой либо двумя координатами, либо непосредственно формой наклона-отрезка. Эта статья предоставит вам уравнение линейной интерполяции и подробно объяснит, как его использовать. Благодаря этому калькулятору вы сможете найти линейную интерполяцию (или экстраполяцию) в кратчайшие сроки!

Что такое линейная интерполяция?

Представьте, что вы пытаетесь измерить зависимость между количеством муки, которое вы используете для выпечки печенья, и количеством печенья, которое вы получаете. В первый раз израсходовали 200 г муки и получили 15 печений , а во второй раз при использовании 300 г — 20 печений. Вы хотите узнать, сколько печенья получится, если использовать 250 г муки. Если вы предполагаете, что зависимость является линейной, вам нужна линейная интерполяция . Если бы вы искали значение, выходящее за пределы тестируемого диапазона (например, 500 г муки), оно называлось бы экстраполяцией .

Формула линейной интерполяции

Если вы хотите найти y, уравнение линейной интерполяции выглядит следующим образом:

y = (x — x₁) × (y₂ — y₁) / (x₂ — x₁) + y₁

где:

• (x₁, y₁) — Координаты первой известной точки данных;
• (x₂, y₂) — Координаты первой известной точки данных; и
• (x, y) — Координаты искомой точки.

Формула экстраполяции идентична. Однако следует помнить, что экстраполяция часто дает результаты, которые не подтверждаются экспериментальными данными , поэтому, если вы не уверены, что зависимость является линейной, всегда лучше использовать вместо нее интерполяцию.

💡 Вас также может заинтересовать наш калькулятор формы пересечения уклонов.

Как использовать этот калькулятор для решения y

Давайте вместе решим проблему с куки. Сколько печенья можно испечь из 250 г муки ?

1. Определите координаты первой точки данных. В нашем случае х₁ = 200 и у₁ = 15 .

2. Определите координаты второй точки данных. В нашем случае х₁ = 300 и у₁ = 20 .

3. Выберите значение x для точки, которую вы анализируете . В этом случае х = 250 .

4. Введите все эти значения в формулу линейной интерполяции:

   у = (х — х₁) × (у₂ — у₁) / (х₂ — х₁) + у₁

   г = (250 — 200) × (20 — 15) / (300 — 200) + 15

   у = 17,5

5. Калькулятор линейной интерполяции предоставит вам наклон и точку пересечения линейного уравнения, определяемые двумя точками.

   No related posts.