Каким знаком обозначается подобие фигур как записывается подобие фигур: Каким знаком обозначается подобие фигур? Как записывается подобие треугольников?

Подобие фигур в математике: определение и примеры

Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.

Содержание:

1. Понятие подобия фигур
2. Подобие треугольников
3. Подобие многоугольников

Понятие подобия фигур

В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.

Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.

Для обозначения подобия фигур употребляется знак . На рисунке 2.434 изображены подобные фигуры . Запись читается: фигура подобна фигуре 

Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.

Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.

Определение. Масштаб — это коэффициент подобия соответствующих фигур.

Подобие треугольников

На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза:  У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны:  Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.

Подобие треугольников записывается так:  Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников  будет число 2. Если же взять отношения , коэффициент подобия будет равен .

Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.

Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.

Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.

Для выявления подобия треугольников существуют признаки подобия треугольников.

Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Следствия из этой теоремы.

1.    Равносторонние треугольники подобны.

2.    Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3.    Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

4.    Равнобедренные прямоугольные треугольники подобны.

Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 4. (Третий признак — по пропорциональности трех сторон.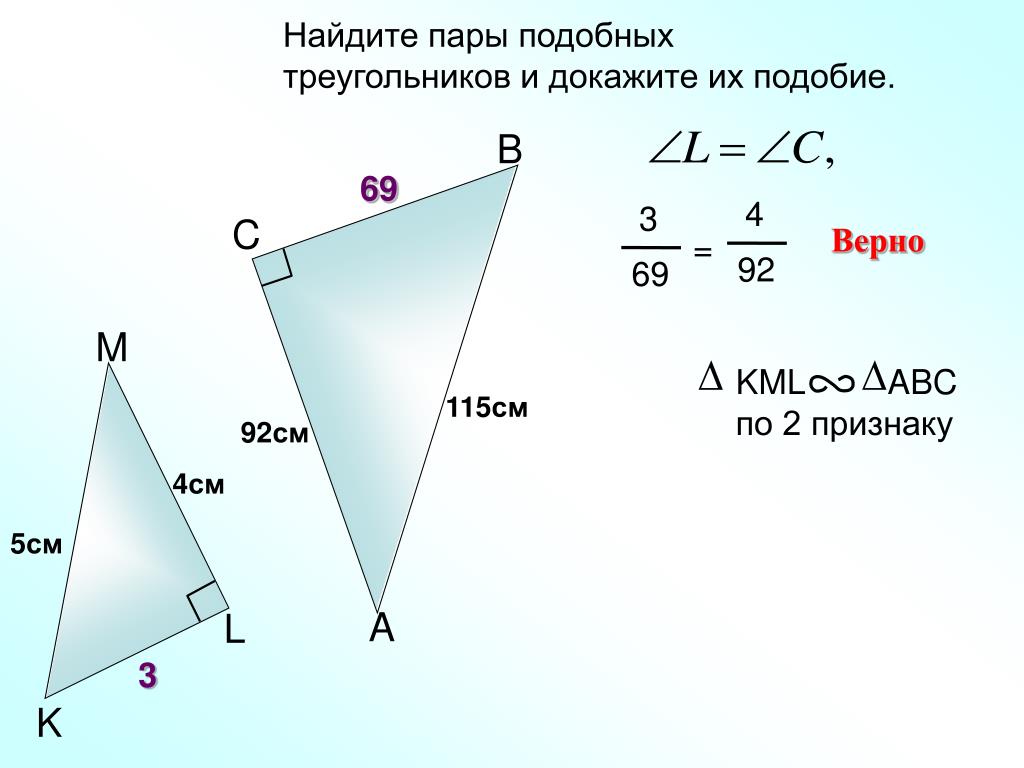 ) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.

Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Подобие многоугольников

Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.

На рисунке 2.436 изображены два подобных пятиугольника , у них  а также  k — коэффициент подобия.

Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).

Теорема 6.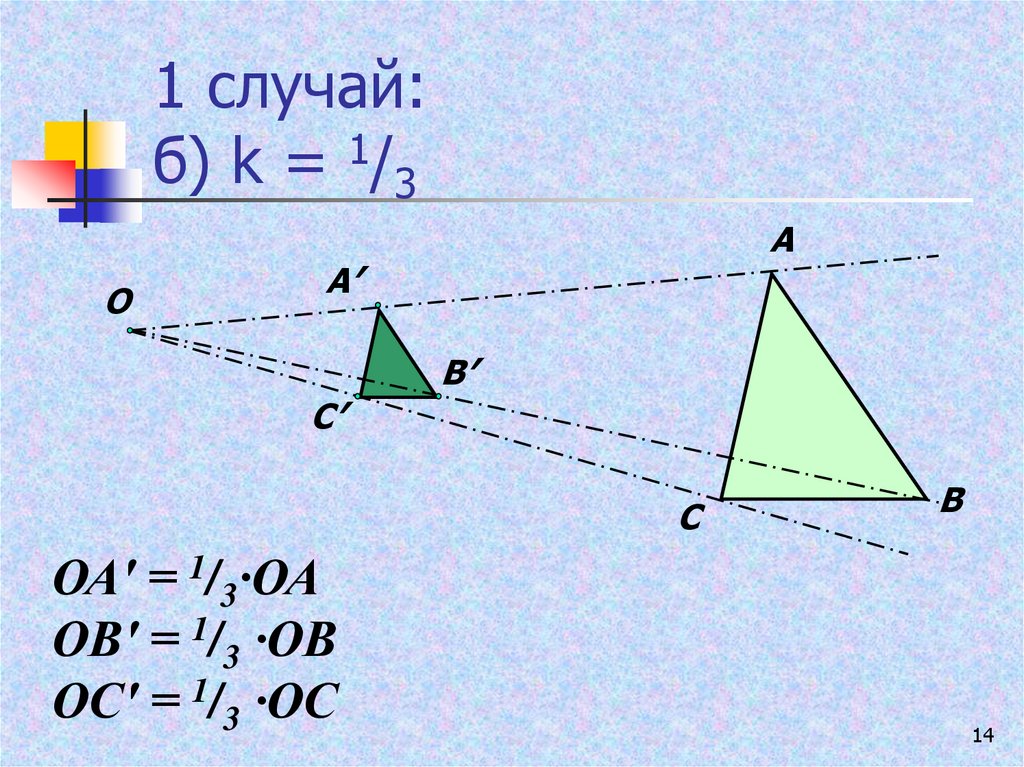 Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).

Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.

 

 

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету «Математика»:

А.В. Погорелов. Геометрия. 9 класс. §11. Контрольные вопросы, ответы — Решебник

Страница 1 из 2

Вопрос 1. Что такое преобразование подобия?
Ответ. Преобразование фигуры \(F\) в фигуру \(F’\) называется преобразованием подобия, если при этом проеобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки \(X\), \(Y\) фигуры \(F\) при преобразовании подобия переходят в точки \(X’\), \(Y’\) фигуры \(F’\), то \(X’Y’ = k\cdot XY\), причем число \(k\) — одно и то же для всех точек \(X\), \(Y\).

Число \(k\) называется коэффициентом подобия. При \(k = 1\) преобразование подобия, очевидно, является движением.

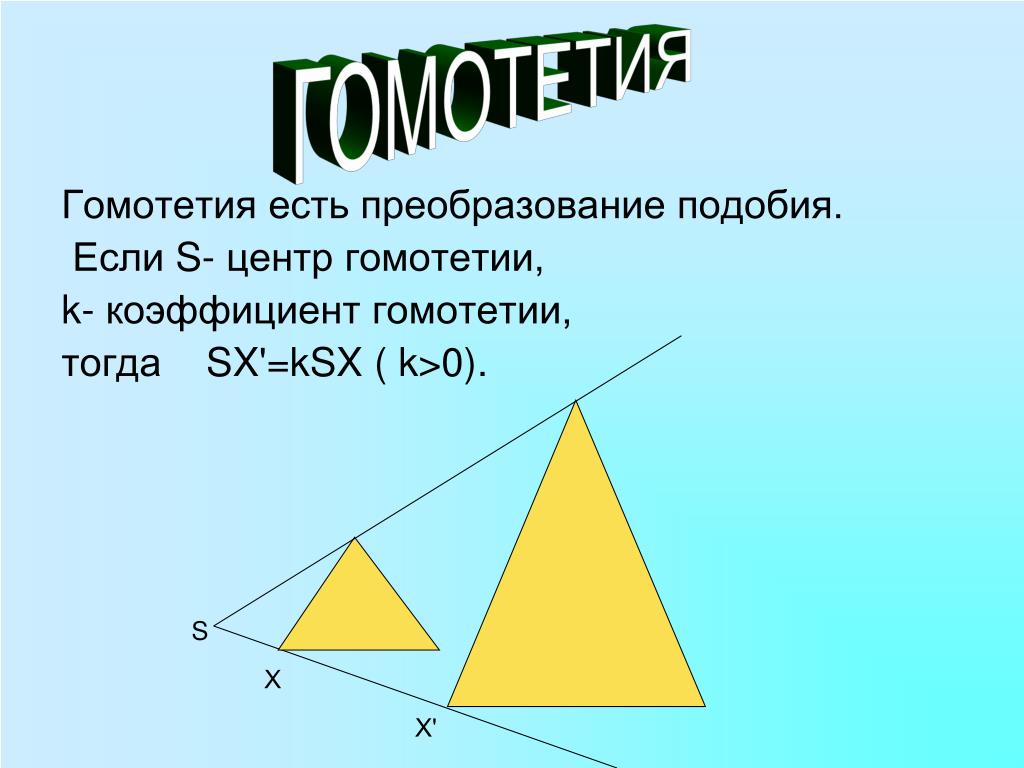
Вопрос 2. Что такое гомотетия (центр гомотетии, коэффициент гомотетии)?
Ответ. Пусть \(F\) — данная фигура и \(O\) — фиксированная точка (рис. 234). Проведем через произвольную точку \(X\) фигуры \(F\) луч \(OX\) и отложим на нем отрезок \(OX’\), равный \(k\cdot OX\), где \(k\) — положительное число. Преобразование фигуры \(F\), при котором каждая ее точка \(X\) переходит в точку \(X’\), построенную указанным способом, называется гомотетией относительно центра \(O\)

. Число \(k\) называется коэффициентом гомотетии, фигуры \(F\) и \(F’\) называется гомотетичными.

Вопрос 3. Докажите, что гомотетия есть преобразование подобия.

Ответ. Теорема 11.1. Гомотетия есть преобразование подобия.

Доказательство. Пусть \(O\) — центр гомотетии, \(k\) — коэффициент гомотетии, \(X\) и \(Y\) — две произвольные точки фигуры (рис.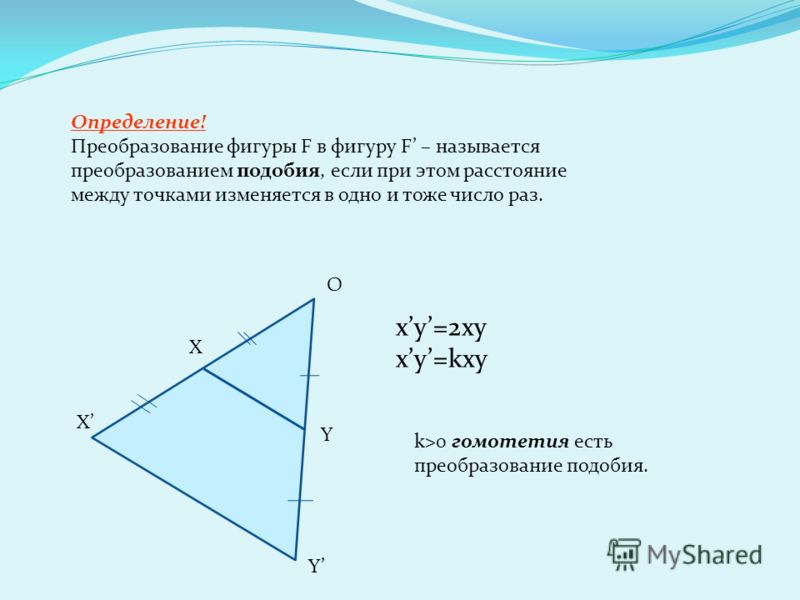 235).

При гомотетии точки \(X\) и \(Y\) переходят в точки \(X’\) и \(Y’\) на лучах \(OX\) и \(OY\) соответственно, причем \(OX’ = k\cdot OX\), \(OY’ = k\cdot OY\). Отсюда следуют векторные равенства

\(\overline{OX’} = k\overline{OX},\, \overline{OY’} = k\overline{OY}\).

Вычитая эти равенства почленно, получим:

\(\overline{OY’} — \overline{OX’} = k(\overline{OY} — \overline{OX})\).

Так как \(\overline{OY’} — \overline{OX’} = \overline{X’Y’}\), \(\overline{OY} — \overline{OX} = \overline{XY}\), то \(\overline{X’Y’} = k\overline{XY}\). Значит, \(|\overline{X’Y’}| = k|\overline{XY}|\), т.е. \(X’Y’ = kXY\). Следовательно, гомотетия есть преобразование подобия. Теорема доказана.

Вопрос 4. Какие свойства преобразования подобия вы знаете? Докажите, что преобразование подобия сохраняет углы между полупрямыми.

Ответ. Так же как и для движения, доказывается, что при преобразовании подобия три точки \(A, B, C\), лежащие на одной прямой, переходят в три точки \(A_1, B_1, C_1\), также лежащие на одной прямой. Причем если точка \(B\) лежит между точками \(A\) и \(C\), то точка \(B_1\) лежит между точками \(A_1\) и \(C_1\). Отсюда следует, что преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки.

Докажем, что

преобразование подобия сохраняет углы между полупрямыми.

Действительно, пусть угол \(ABC\) преобразованием подобия с коэффициентом \(k\) переводится в угол \(A_1B_1C_1\) (рис. 237). Подвергнем угол \(ABC\) преобразованию гомотетии относительно его вершины \(B\) с коэффициентом гомотетии \(k\). При этом точки \(A\) и \(C\) перейдут в точки \(A_2\) и \(C_2\). Треугольники \(A_2BC_2\) и \(A_1B_1C_1\) равны по третьему признаку. Из равенства треугольников следует равенство углов \(A_2BC_2\) и \(A_1B_1C_1\). Значит, углы \(ABC\) и \(A_1B_1C_1\) равны, что и требовалось доказать.

Вопрос 5. Какие фигуры называются подобными?

Ответ. Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия.

Вопрос 6. Каким знаком обозначается подобие фигур? Как записывается подобие треугольников?

Ответ. Для обозначения подобия фигур используется специальный значок: \(\sim\).

Запись \(F\sim F’\) читается так: «Фигура \(F\) подобна фигуре \(F’\)».

Запись подобия треугольников \(ABC\) и \(A_1B_1C_1\): \(\triangle ABC \sim \triangle A_1B_1C_1\).

Вопрос 7. Сформулируйте и докажите признак подобия треугольников по двум углам.

Ответ. Теорема 11.2. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(\angle A = \angle A_1\), \(\angle B = \angle B_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).

Пусть \(k = \frac{AB}{A_1B_1}\). Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 238).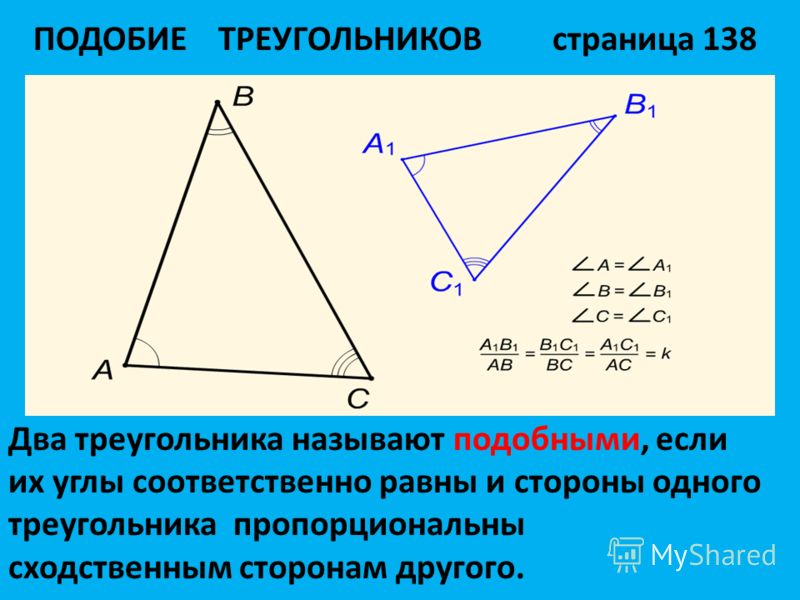 При этом получим некоторый треугольник \(A_2B_2C_2\), равный треугольнику \(ABC\). Действительно, так как преобразование подобия сохраняет углы, то \(\angle A_2 = \angle A_1\), \(\angle B_2 = \angle B_1\). А значит, у треугольников \(ABC\) и \(A_2B_2C_2\) \(\angle A = \angle A_2\), \(\angle B = \angle B_2\). Далее, \(A_2B_2 = kA_1B_1 = AB\). Следовательно, треугольники \(ABC\) и \(A_2B_2C_2\) равны по второму признаку (по стороне и прилежищим к ней углам).

Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.

Теорема доказана.

Вопрос 8. Сформулируйте и докажите признак подобия треугольников по двум сторонам и углу между ними.

Ответ. Теорема 11.3. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.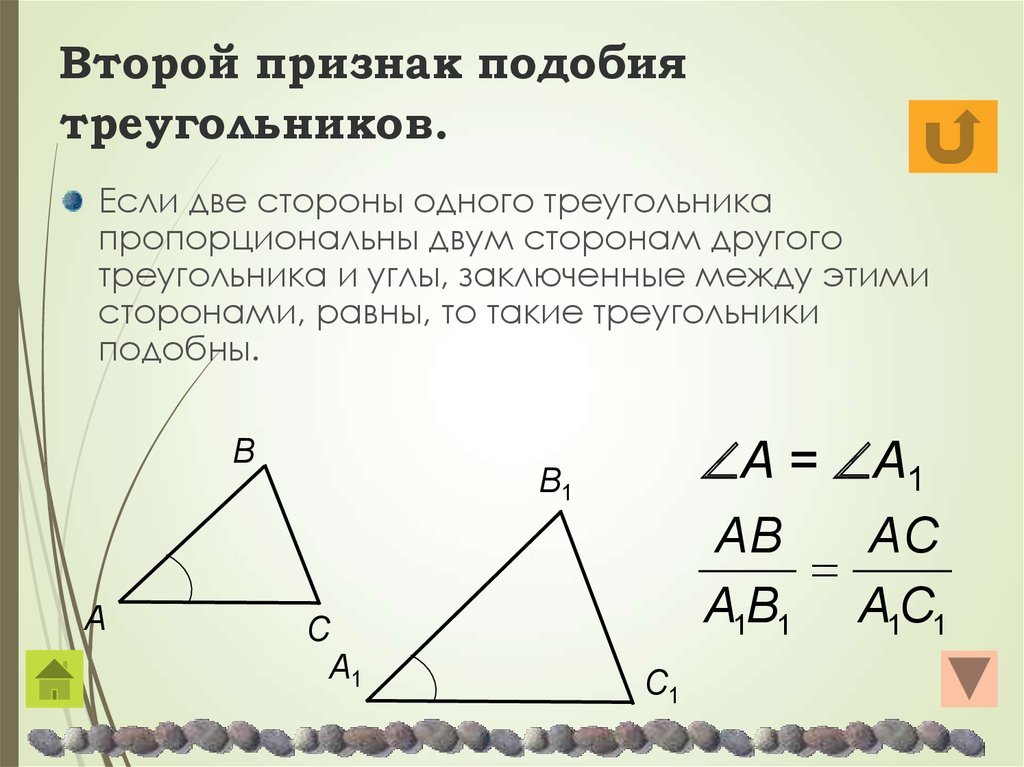

Доказательство (аналогично доказательству теоремы 11.2). Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(\angle C = \angle C_1\) и \(AC = kA_1C_1\), \(BC = kB_1C_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).

Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 240). При этом получим некоторый треугольник \(A_2B_2C_2\), равный треугольнику \(ABC\). Действительно, так как преобразование подобия сохраняет углы, то \(\angle C_2 = \angle C_1\). А значит, у треугольников \(ABC\) и \(A_2B_2C_2\) \(\angle C = \angle C_2\). Далее, \(A_2C_2 = kA_1C_1 = AC\), \(B_2C_2 = kB_1C_1 = BC\). Следовательно, треугольники \(ABC\) и \(A_2B_2C_2\) равны по первому признаку (по двум сторонам и углу между ними).

Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.

Теорема доказана.

Вопрос 9. Сформулируйте и докажите признак подобия треугольников по трем сторонам.

Ответ. Теорема 11.4. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Доказательство (аналогично доказательству теоремы 11.2). Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(AB = kA_1B_1\), \(AC = kA_1C_1\), \(BC = kB_1C_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).

Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 242). При этом получим некоторый треугольник \(A_2B_2C_2\), равный треугольнику \(ABC\). Действительно, у треугольников соответствующие стороны равны:

\(A_2B_2 = kA_1B_1 = AB\),

\(A_2C_2 = kA_1C_1 = AC\),

\(B_2C_2 = kB_1C_1 = BC\).

Следовательно, треугольники \(ABC\) и \(A_2B_2C_2\) равны по третьему признаку (по трем сторонам).

Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.

Теорема доказана.

Вопрос 10. Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Ответ. У прямоугольного треугольника один угол прямой. Поэтому по теореме 11.2 для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.

Пусть \(ABC\) — прямоугольный треугольник с прямым углом \(C\). Проведем высоту \(CD\) из вершины прямого угла (рис. 243).

Треугольники \(ABC\) и \(CBD\) имеют общий угол при вершине \(B\). Следовательно, они подобны: \(\triangle ABC \sim \triangle CBD\). Из подобия треугольников следует пропорциональность соответствующих сторон:

\[\frac{AB}{BC} = \frac{BC}{BD},\, или\, BC = \sqrt{AB\cdot BD}.\]

Это соотношение обычно формулируют так: катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

• Вперед

Подобие общих фигур 8 класс онлайн-подготовка на Ростелеком Лицей

Равенство геометрических фигур

 

Как мы уже знаем, фигурой в геометрии называется множество точек на плоскости.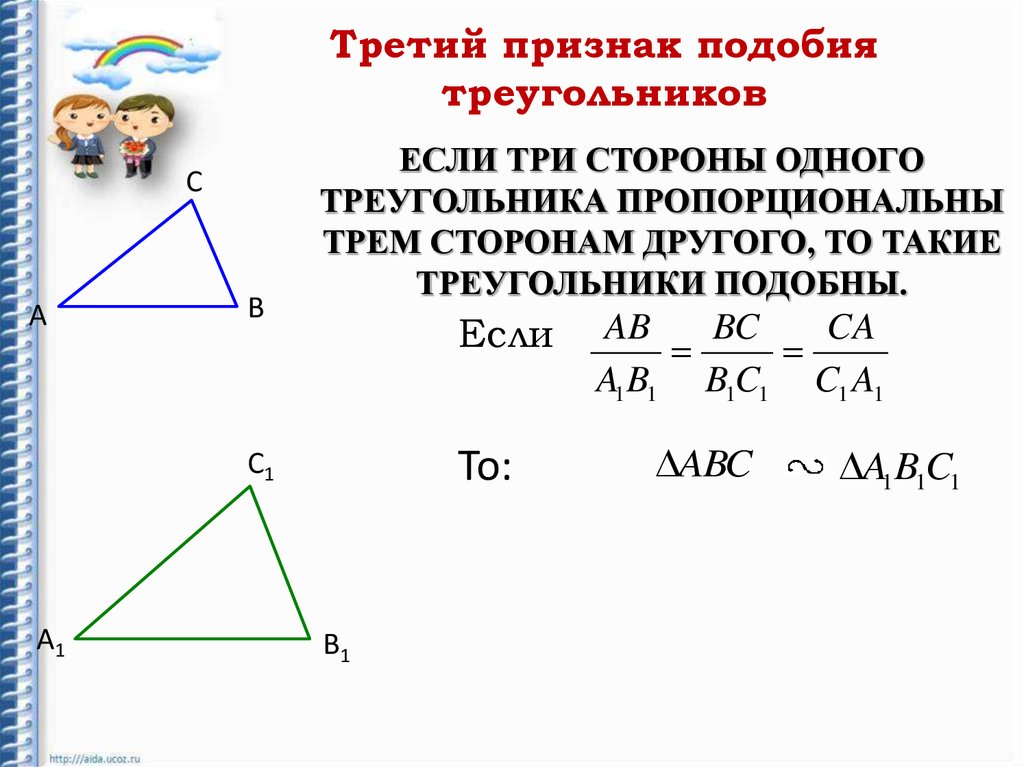 Прямая, отрезок, луч, треугольник, окружность, квадрат и так далее – всё это примеры геометрических фигур.

 

В повседневной жизни нас с вами окружают множество различных предметов. Часть из них имеют одинаковые размеры и одинаковую форму. Например, две одинаковые ручки или две одинаковых монеты и т.д. В геометрии фигуры, имеющие одинаковые размеры и форму, называются равными фигурами.

Из этого определения следует, например, что если прямоугольник и квадрат имеют равные площади, то это не значит, что они являются равными фигурами, так как это разные по форме фигуры. Другой пример: любые две окружности имеют одну и ту же форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами.

Следует отметить, что не все фигуры можно сравнивать. Нельзя определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.

Если же мы имеем дело с произвольными фигурами, то иногда даже сложно определить, имеют ли они одинаковую форму. Таким образом, нужно иметь надежный метод сравнения фигур. Он заключается в следующем: две геометрические фигуры называются равными, если их можно совместить наложением.

Но как быть в том случае, когда, скажем, длина стороны треугольника равна  км? В данном случае можно воспользоваться признаками равенства треугольников, которые мы рассматривали на предыдущих уроках. Смысл этих признаков в следующем: равенство трех элементов треугольников гарантирует равенство самих треугольников, а значит, и равенство остальных элементов, которые совместятся при наложении (биссектрис, высот, медиан).

 

Примеры подобия фигур

 

 

А что если форму оставить без изменений, а все размеры пропорционально изменить (увеличить или уменьшить в одинаковое количество раз)?

 

Рассмотрим данную ситуацию на примере треугольника.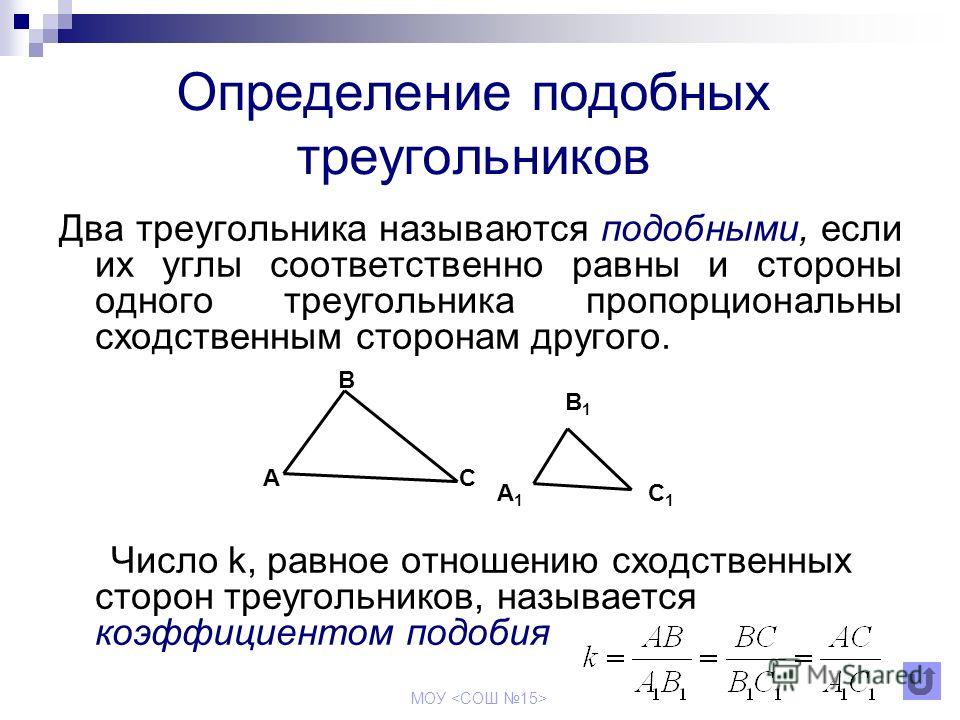

Пример 1

Пусть дан правильный треугольник  со стороной  (см. рис. 1).

Рис. 1. Правильный треугольник

Уменьшив стороны треугольника  в  раза, получим правильный треугольник  со стороной  (см. рис. 2). То есть форма треугольника осталась прежней, а все размеры изменились (уменьшились) в  раза. Докажем это.

Рис. 2. Правильный треугольник  с уменьшенными сторонами

Доказательство:

Такой треугольник мы уже встречали на предыдущих уроках. Это треугольник, вершины которого лежат на серединах сторон исходного треугольника (см. рис. 3).

Рис. 3. Иллюстрация к доказательству

То есть из исходного правильного треугольника мы получили другой правильный треугольник, длина стороны которого уменьшилась в  раза.

Такие треугольники в геометрии называются подобными.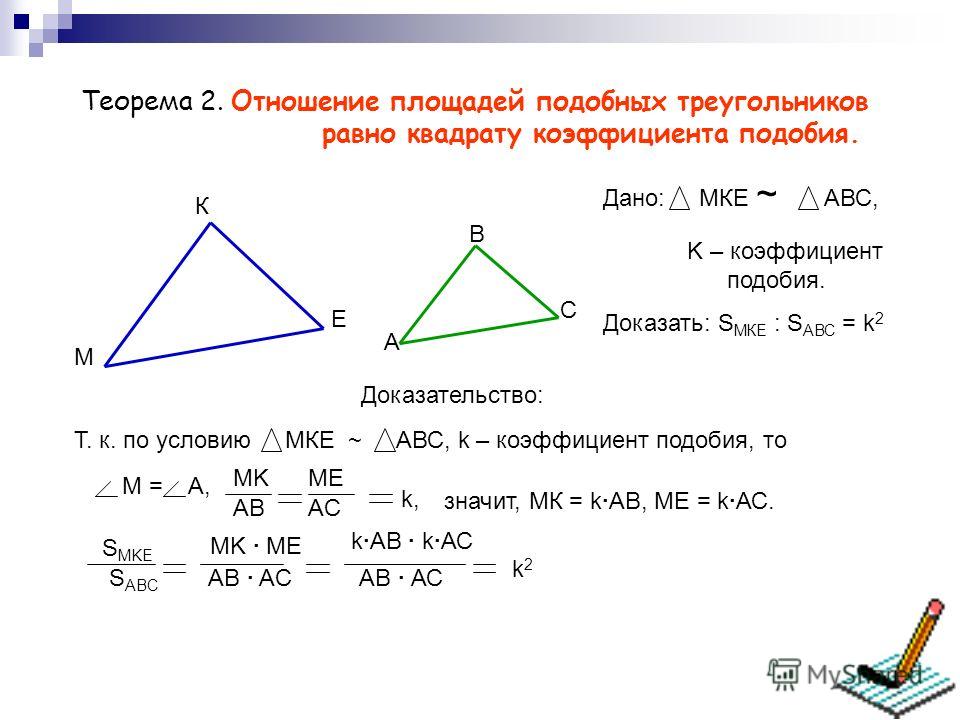

Обозначение:.

Коэффициент подобия – это число, равное отношению сходственных сторон в подобных фигурах. В нашем случае коэффициент подобия равен .

Обозначение:.

Пример 2

Дом на большом расстоянии имеет форму прямоугольника. Если постепенно приближаться к нему можно заметить, что его форма не меняется, но его размеры увеличиваются. Из этого можно сделать вывод, что его размеры изменяются в одинаковое число раз. Это ещё один пример подобных фигур.

Пример 3

Подобие фигур также используется при нанесении местности на карту. Возьмем, например, Крым и его изображение на карте с масштабом . Понятно, что форма Крыма на карте аналогична реальной форме, но размеры изменены в  раз.

Таковы при­ме­ры подобных фигур – фигур, ко­то­рые имеют оди­на­ко­вую форму, но раз­ные раз­ме­ры. При­чем раз­ме­ры из­ме­ня­ют­ся в одно и то же число раз.

 

Примеры применения подобия фигур

 

 

Можно сформулировать признаки подобия треугольников. Эти признаки позволяют по некоторой информации об исходных треугольниках получить более подробную (дополнительную) информацию о них.

 

Пример 4

Пусть есть  подобных треугольника  с коэффициентом подобия . Тогда можно утверждать, что соотношение длин соответствующих сторон треугольников пропорционально . То есть: . Как и в случае признаков равенства, гарантируется пропорциональность соответствующих элементов треугольников (медиан, биссектрис, высот и т.д.).

Рассмотрим еще один подобный пример.

Пример 5

Предположим, что коэффициент подобия треугольников  и  равен . Тогда для них можно записать следующее соотношение: . Из этого следует, что . Как мы уже знаем, по третьему признаку эти треугольники будут равными (Второй и третий признаки равенства треугольников). Отсюда можно сделать вывод, что равенство фигур является частным случаем подобия фигур с коэффициентом .

Признаки подобия фигур, в частности признаки подобия треугольников, являются полезными приемами в математике, они применяются для упрощения и решения множества задач. Однако для изучения этих признаков необходимо перевести некоторые понятия на строгий математический язык. 

---

 

Пропорциональные отрезки

Понятия «отношение» и «пропорциональность» играют важную роль в изучении признаков подобия фигур.

Для начала рассмотрим понятие отношения отрезков на примере отрезков  и  (см. рис. 4).

Рис. 4. Отрезки  и

Определение

Отношение длин отрезков  и  называется отношением отрезков  и .

Рассмотрим задачу на данное определение.

Задача 1

Дано

Два отрезка  и

Найти

Отношение отрезков  и

Решение

Поскольку отношение отрезков – это отношение длин соответствующих отрезков, то имеем:

Ответ:.

Отметим, что отношение отрезков – это безразмерная величина.

Теперь предположим, что отношение пары отрезков   и   равно отношению пары других отрезков  и . Это записывается следующим образом:

В таком случае говорят о пропорциональности отрезков. А именно: отрезки  и   пропорциональны отрезкам  и  соответственно.

По свойству пропорции  и  можно поменять местами: . От этого смысл выражения не поменяется.

Пропорциональные отрезки встречаются в формулировке обобщенной теоремы Фалеса (Задачи на параллелограмм).

Теорема Фалеса

Стороны угла рассекаются параллельными прямыми на пропорциональные части (см. рис.5). То есть:

Аналогичное соотношение можно записать и для суммы длин отрезков:

Рис. 5. Иллюстрация к теореме Фалеса

---

 

 

Подобие треугольников

 

 

Рассмотрим два треугольника  и , у которых соответствующие углы равны (см.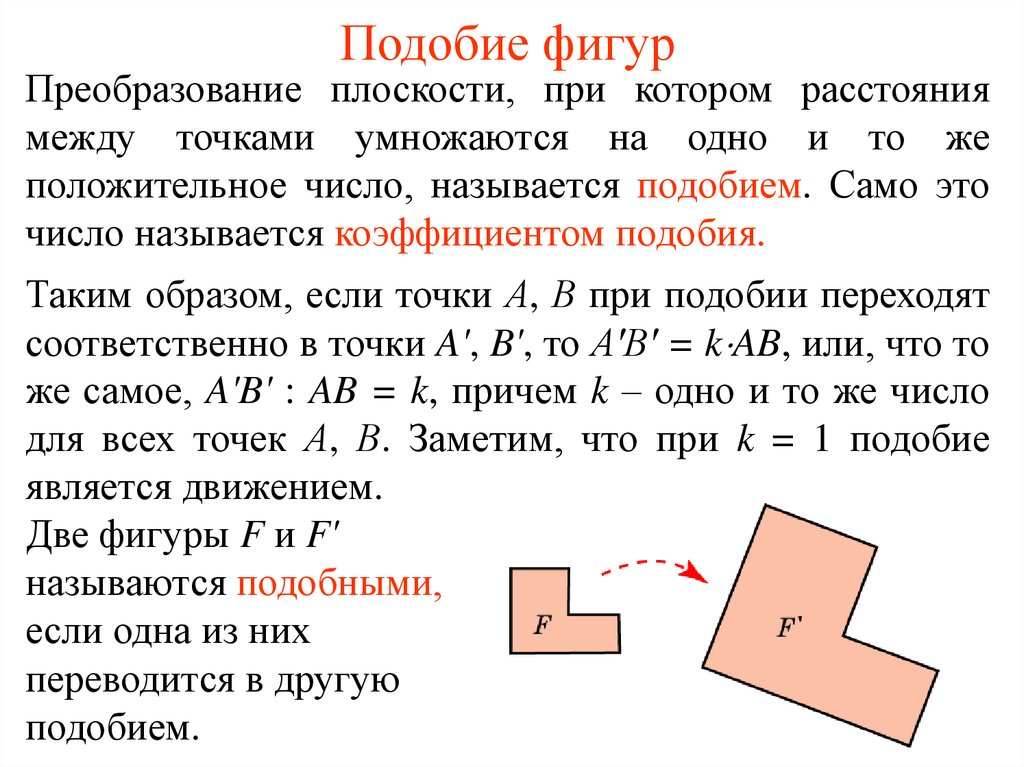 рис. 6):

 

Рис. 6. Треугольники с равными углами

Стороны, которые лежат против равных углов треугольников, называются сходственными.

Перечислим сходственные стороны:  и  (лежат против равных углов  ),  и  (лежат против равных углов  ),  и  (лежат против равных углов  ).

Определение

Два треугольника  и  называются подобными, если соответствующие углы равны, а сходственные стороны – пропорциональны:

Причем  , где  – это коэффициент подобия треугольников.

Оказывается, можно ограничиться лишь некоторыми из этих равенств чтобы гарантировать факт подобия. В этом заключается суть признаков подобия треугольников, которые подробно будут рассмотрены на следующих уроках.

Можно заметить, что пропорциональные отрезки играют важную роль в определении подобных треугольников. Рассмотрим задачу на пропорциональность отрезков.

---

 

Задача на пропорциональность отрезков

Теорема

Биссектриса угла треугольника рассекает противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Докажем эту теорему.

Дано

Произвольный треугольник ,  – биссектриса угла .

Доказать

Доказательство

Запишем выражения для площадей образовавшихся треугольников   и . Для этого опустим высоту из вершины .Выполним рисунок к задаче (см. рис. 1).

Рис. Иллюстрация к доказательству теоремы

Поскольку площадь треугольника равна половине произведения основания на высоту получаем: , . Теперь найдем отношение этих площадей:

С другой стороны, биссектриса – это геометрическое место точек, равноудаленных от сторон угла. Этим свойством обладают все точки, принадлежащие биссектрисе, в том числе точка . Поэтому расстояние от точки  до сторон одинаковое, обозначим его . Тогда высоты треугольников   и , опущенные к соответствующим основаниям  и , равны . Можно переписать отношение площадей этих треугольников:

Левые части этих двух равенств равна, значит и правые часть также равны:

Теорема доказана.

 

---

 

На данном уроке мы рас­смот­ре­ли по­до­бие фигур, вспомнили признаки равенства треугольников, дали опре­де­ле­ние по­доб­ным тре­уголь­ни­кам. Вспом­ни­ли о про­пор­ци­о­наль­но­сти от­рез­ков, тео­ре­му Фа­ле­са и их роль в ре­ше­нии дан­ных задач.

 

Спи­сок ре­ко­мен­до­ван­ной ли­те­ра­ту­ры

1. Алек­сан­дров А.Д. и др. Гео­мет­рия, 8 класс. – М.: Про­све­ще­ние, 2006.
2. Бу­ту­зов В. Ф., Ка­дом­цев С.Б., Пра­со­лов В.В. Гео­мет­рия, 8 класс. – М.: Про­све­ще­ние, 2011.
3. Мерз­ляк А.Г., По­лон­ский В.Б., Якир С.М. Гео­мет­рия, 8 класс. – М.: ВЕН­ТА­НА-ГРАФ, 2009.

 

Ре­ко­мен­до­ван­ные ссыл­ки на ре­сур­сы сети Ин­тер­нет:

1. Интернет-портал «egemaximum.ru» (Источник)
2. Интернет-портал «ru.solverbook.com» (Источник)
3. Интернет-портал «math20.com» (Источник)

 

До­маш­нее за­да­ние

1. Могут ли быть по­доб­ны­ми: а) пря­мо­уголь­ный и рав­но­сто­рон­ний тре­уголь­ни­ки; б) рав­но­бед­рен­ный и рав­но­сто­рон­ний тре­уголь­ни­ки; в) тре­уголь­ник с углом  и тре­уголь­ник с углом ?
2. Из от­рез­ков дли­ной , , , ,  и  см со­ста­ви­ли два по­доб­ных между собой тре­уголь­ни­ка. Най­ди­те ко­эф­фи­ци­ент по­до­бия этих тре­уголь­ни­ков.

 

Похожие фигурки

Горячая математика

Говорят, что две фигуры похожий если они одинаковой формы. Говоря более математическим языком, две фигуры подобны, если их соответствующие углы равны конгруэнтный , а отношения длин их соответствующих сторон равны.

Это обычное отношение называется масштаб .

Символ ∼ используется для обозначения сходства.

Пример 1:

На рисунке ниже пятиугольник А Б С Д Е ∼ пятиугольник В Вт Икс Д Z .

(Обратите внимание, что порядок, в котором вы пишете вершины, имеет значение; например, пятиугольник А Б С Д Е является нет похоже на пятиугольник В Z Д Икс Вт .)

Пример 2:

Два цилиндра похожи. Найдите масштабный коэффициент и радиус второго цилиндра.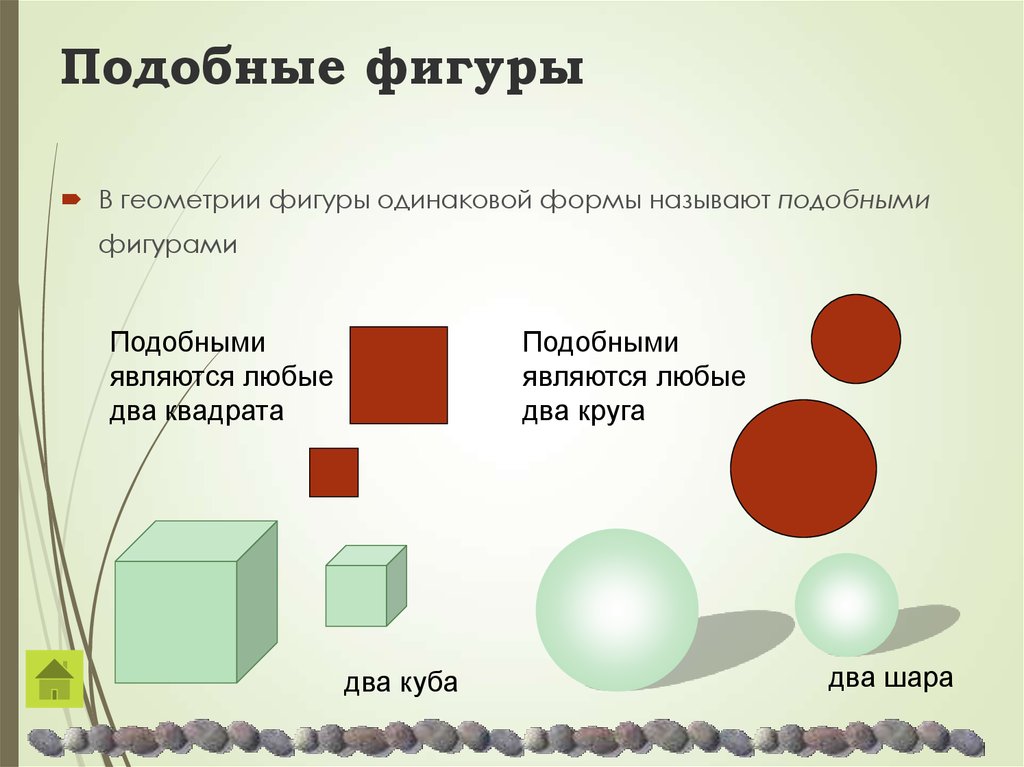

Высота цилиндра справа 1 3 высота цилиндра слева. Итак, масштабный коэффициент 1 3 .

Чтобы получить радиус меньшего цилиндра, разделите 1,8 по 3 .

1,8 ÷ 3 знак равно 0,6

Значит, радиус меньшего цилиндра 0,6 см.

Заметим, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью вращения , размышления , переводы , а также расширения .

Пример 3:

На рисунке выше шестиугольник А 1 Б 1 С 1 Д 1 Е 1 Ф 1 переворачивается горизонтально, чтобы получить А 2 Б 2 С 2 Д 2 Е 2 Ф 2 .

Затем шестиугольник А 2 Б 2 С 2 Д 2 Е 2 Ф 2 переводится как получить А 3 Б 3 С 3 Д 3 Е 3 Ф 3 .

Шестиугольник А 3 Б 3 С 3 Д 3 Е 3 Ф 3 расширяется на масштабный коэффициент 1 2 получить А 4 Б 4 С 4 Д 4 Е 4 Ф .

Обратите внимание, что

А 1 Б 1 С 1 Д 1 Е 1 Ф 1 ∼ А 2 Б 2 С 2 Д 2 Е 2 Ф 2 ∼ А 3 Б 3 С 3 Д 3 Е 3 Ф 3 ∼ А 4 Б 4 С 4 Д 4 Е 4 Ф 4 .

То есть все четыре шестиугольника подобны. (На самом деле, первые три конгруэнтны.)

Пример 4:

Рассмотрим пятиугольник п Вопрос р С Т на координатной плоскости.

Ротация на 180 ° о происхождении отводит пятиугольник к п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ .

Теперь расширение относительно начала координат с помощью масштабного коэффициента 2 берет пятиугольник п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ к п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ .

Обратите внимание, что п Вопрос р С Т ∼ п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ ∼ п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ . То есть все три пятиугольника подобны. (И первые два совпадают.)

Обобщение пропорций из подобных фигур

ВведениеСоздание подобных фигур с помощью расширенийЗапись пропорций из расширенийКраткий обзор

Подобные фигуры — это многоугольники или другие фигуры, пропорциональные по форме.

Если у вас одинаковые цифры, вы узнали в предыдущих классах, что верны две вещи.

На этом уроке вы распространите свои знания о подобных фигурах на расширения. Расширение — это увеличение или уменьшение фигуры на заданный масштабный коэффициент.

В этом разделе вы будете использовать расширения для создания похожих фигур.

Используйте интерактивное создание подобных фигур с помощью расширения, чтобы расширить Δ ABC . Нажмите и перетащите ползунок, чтобы расширить Δ ABC , чтобы создать Δ DEF . Число на ползунке указывает коэффициент масштабирования, используемый для создания расширения. Используйте интерактив, чтобы заполнить следующую таблицу. Используйте таблицу, чтобы ответить на вопросы после таблицы.

Скопируйте и вставьте приведенную ниже таблицу в свои заметки или текстовый документ, чтобы ввести свои данные.

Масштабный коэффициент ( f )	DEAB\frac{DE}{AB}	EFBC\frac{EF}{BC}	DFAC\frac{DF}{AC}
0,25
0,75
2
2,5

Проверьте свой ответ

1. Как соотносится отношение длин каждой пары соответствующих сторон для расширения, созданного с использованием заданного коэффициента масштабирования?
2. Если два или более отношения равны, что это говорит вам о длинах соответствующих сторон?
3. Как расширение соотносится с парой подобных фигур?

Пауза и размышление

В интерактивном режиме вы использовали расширение для создания пары подобных треугольников. Считаете ли вы, что те же самые отношения сохранятся, если вы расширите четырехугольник? Почему или почему нет?

 

В последнем разделе вы исследовали, как расширение используется для создания новой фигуры (изображения) из исходной фигуры (прообраза). Вы также видели, что отношения любых пар соответствующих сторон дилатации равны. Это означает, что длины соответствующих сторон пропорциональны, что является одним из признаков подобных фигур.

Теперь, когда вы увидели, как можно использовать расширения для создания похожих фигур, вы можете использовать расширения для настройки и решения пропорций.

Рассмотрим расширение, показанное ниже. Трапеция JKLM получается путем расширения трапеции ABCD .

1. Как определить пару соответствующих сторон?
2. После того, как вы определили две пары соответствующих сторон, как вы можете использовать эту информацию, чтобы составить пропорцию?

Используйте ссылку для завершения интерактивного задания.

Пример 1: Решите пропорцию для x .

38=12x\frac{3}{8} = \frac{12}{x}

• Найдите масштабный коэффициент. В этом примере коэффициент масштабирования равен 4 (3 × 4 = 12).
• Умножить на коэффициент масштабирования.

3(4)8(4)=12x\frac{3(4)}{8(4)} = \frac{12}{x}

• ​Поскольку x стоит в знаменателе, найдите знаменатель. x = 8(4) = 32
  0090 = 32

Пример 2: Решите пропорцию для x.

27=x21\frac{2}{7} = \frac{x}{21}

• Найдите масштабный коэффициент. В этом примере коэффициент масштабирования равен 3 (7 × 3 = 21).
• Умножить на коэффициент масштабирования.

​2(3)7(3)=x21\frac{2(3)}{7(3)} = \frac{x}{21}

• Поскольку x находится в числителе, найдите числитель. x = 2(3) = 6
  0090 = 6

Пауза и размышление

После того, как вы написали пропорцию, как вы можете решить ее?

На этом уроке вы применили то, что узнали ранее о подобных фигурах, к расширениям. Расширение — это когда вы создаете вторую фигуру из исходной фигуры с определенным коэффициентом масштабирования. Поскольку соответствующие стороны как увеличенной фигуры, так и исходной фигуры пропорциональны, эти две фигуры подобны.

На приведенном ниже рисунке Δ FGH получается путем расширения Δ ABC с масштабным коэффициентом, равным 2.

Выполните следующую пропорцию:

ADMP=?OP\frac{AD}{MP} = \frac{ ?}{OP}

Используйте приведенную выше информацию и конгруэнтность углов, чтобы составить пропорцию.

• Сторона OP соответствует ∠O и ∠P.
• ∠C и ∠D конгруэнтны ∠O и ∠P.
• Сторона, отсутствующая в пропорции, это CD.

• Печать
• Поделиться

пропорций и подобных фигур — объяснение!

СоотношенияПропорцииПропорциональностьРешение словесных задачСолнечные лучи / Части

Purplemath

Уравнения пропорциональности можно использовать для «решения» «подобных фигур».

Что такое «похожие фигуры»?

«Подобный» — это геометрический термин, относящийся к геометрическим фигурам (квадратам, треугольникам и т. д.), которые имеют одинаковую форму, но одна из пар фигур больше другой.

Содержание продолжается ниже

MathHelp.com

Решение пропорций

Чтобы мысленно представить похожие фигуры, подумайте о том, что происходит, когда вы используете настройку «увеличить» или «уменьшить» на копировальном аппарате или когда вы получаете восьмерку. увеличение изображения размером три на пять раз, которое вам действительно нравится, или, если вы использовали графическую программу, подумайте о сохранении «соотношения сторон» изображения, размер которого вы изменяете. Результатом каждого из этих примеров является пара похожих фигур (или, во всяком случае, похожих картинок).

Как вы «решаете» подобные фигуры?

В контексте соотношений и пропорций точка подобия заключается в том, что соответствующие стороны подобных фигур пропорциональны; то есть длины совпадающих сторон пропорциональны.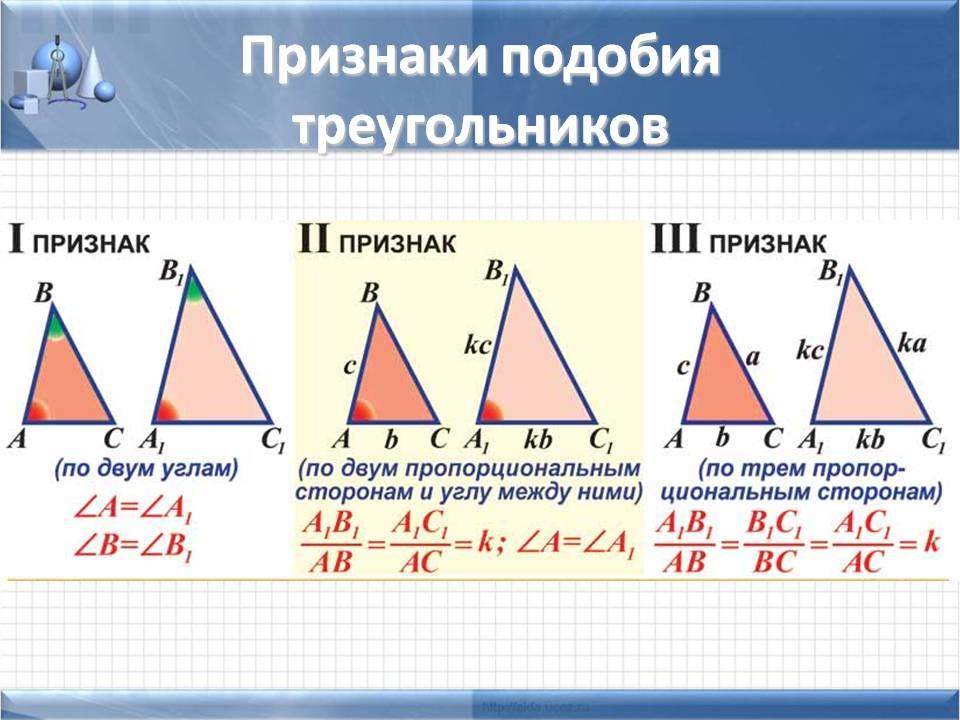 Таким образом, имея две похожие фигуры, не все стороны которых отмечены их длинами, вы можете создать уравнение пропорциональности, смешивая известную и неизвестную информацию, и найти неизвестное значение.

Примечание. Чтобы этот процесс работал, у подобных фигур должна быть хотя бы одна пара соответствующих сторон, обе длины которых известны. Эта пара будет вашей эталонной парой, формируя одну сторону вашего уравнения пропорциональности.

Например, посмотрите на подобные треугольники ABC и abc ниже:

«Соответствующие стороны» — это пары сторон, которые «совпадают», за исключением аспекта увеличения или уменьшения их относительных размеров. Таким образом, А соответствует а, В соответствует b, а С соответствует с.

Так как эти треугольники подобны, то пары соответствующих сторон пропорциональны. То есть A : a = B : b = C : c. Другими словами, это уравнение, состоящее из трех частей, гласит: «Большой-А относится к маленькому-А, как большой-В к маленькому-В и как большой-С к маленькому-С».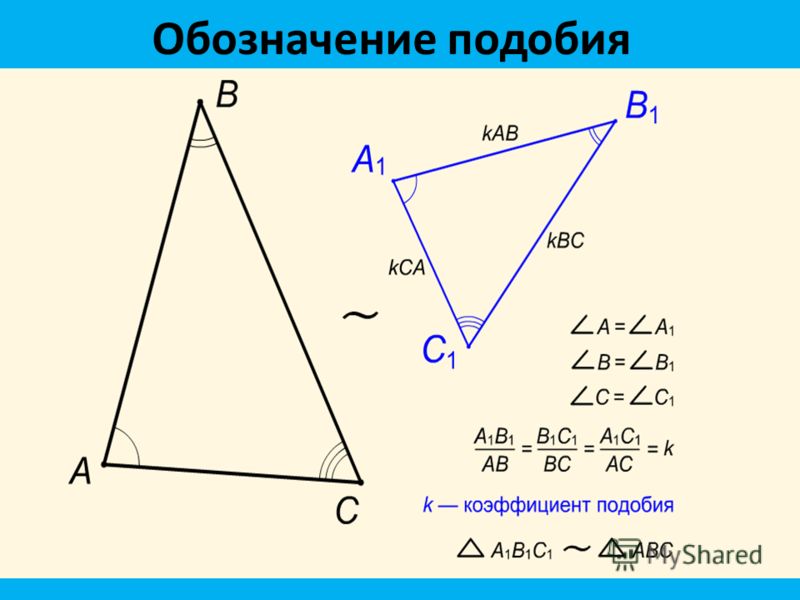 Эта пропорциональность соответствующих сторон может быть использована для нахождения длины стороны фигуры, учитывая аналогичную фигуру, для которой известны достаточные измерения.

• В показанных треугольниках длины сторон даны как A = 48 мм, B = 81 мм, C = 68 мм и a = 21 мм. Найдите длины сторон b и c, округлив до ближайшего целого числа.

Я составлю свои пропорции, используя отношения в форме (длина большого треугольника) ÷ (длина маленького треугольника), а затем решу пропорции. (Кстати, вы можете установить свои пропорции по своему усмотрению; нет правила, которое гласит, что «чем больше, тем выше».)

Так как они дали мне только длину стороны a для маленького треугольника, мое эталонное соотношение будет A : a.

Сначала я найду длину b. Вот моя установка:

(Нет необходимости, чтобы вы маркировали вещи, как я сделал выше с начальной дробью, содержащей слова «большой» и «маленький», но это может быть очень полезно, чтобы напомнить себе, как вы Я хочу все уладить. Это быстрый способ уберечь себя от неприятностей.)

Заполнив мои известные значения, я получаю:

б = [21 × 81]/48

б = 1701/48

b = 35,4375

(мне нужно будет не забыть дать округленное до целого значение длины этой стороны (другими словами, мне нужно будет не забыть округлить до «35») в моей руке -в ответ.)

Теперь, когда я нашел одну длину, я тем же методом найду длину оставшейся стороны, c.

с × 48 = 21 × 68

с = 1428/48

c = 29,75

В качестве ответа я мог бы просто записать два числа, которые я нашел, но эти числа не будут иметь большого смысла без их единиц измерения. Кроме того, при повторной проверке исходного упражнения мне напомнили, что я должен округлить свои значения до ближайшего целого числа, поэтому «29,75» с единицами измерения или без них будет неправильным.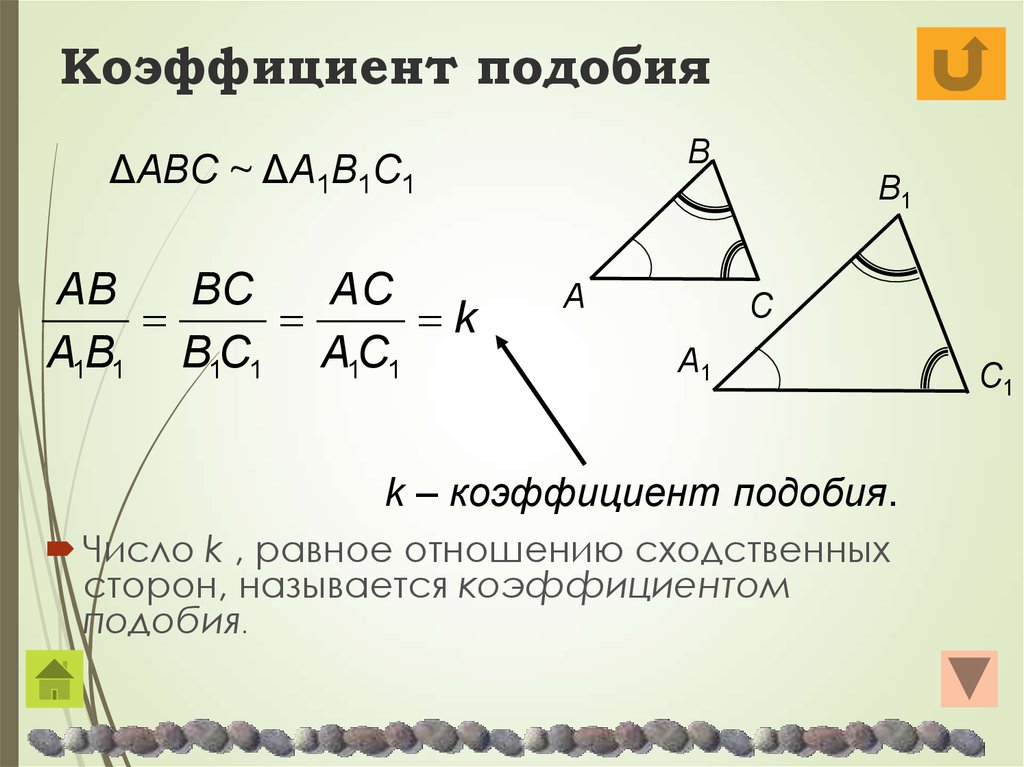 Правильный ответ:

b = 35 мм, c = 30 мм

---

Хотя я мог бы использовать длину, найденную для b, для нахождения длины c в приведенном выше упражнении, вместо этого я вернулся к значению а. Почему? Потому что это было заведомо хорошее «точное» значение.

Хотя десятичное значение в этом случае было точным значением (то есть значение b не округлялось), обычно лучше иметь привычку возвращаться к заведомо правильным значениям, когда это возможно. Таким образом, когда десятичное значение округлено до , вы игнорируете округленное производное значение и возвращаетесь к точному исходному значению.

Эта практика поможет вам избежать потенциальных ошибок округления.

---

• Изображение размером 3,5″ (то есть 3,5 дюйма) в высоту и 5″ в ширину необходимо увеличить так, чтобы ширина была 9″. Какой высоты будет картина?

Фотолаборатория при увеличении исходного изображения будет сохранять пропорции оригинала; то есть прямоугольники, представляющие внешние края исходного и увеличенного изображения, будут похожими фигурами.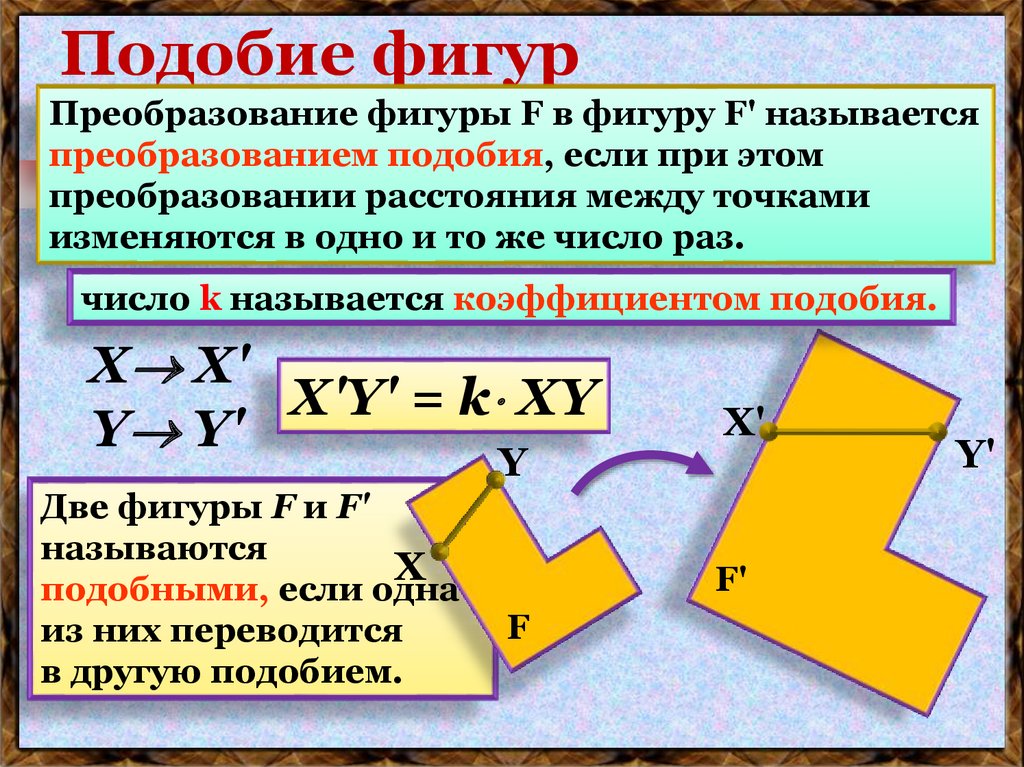 Используя этот факт, я могу установить пропорцию и решить, используя « h » для обозначения значения высоты, которое я ищу:

h = [(9)(3,5)]/5

31,5 = 5 ч = 31,5/5

h = 6,3

Высота изображения будет:

6,3 дюйма

---

В первом упражнении выше отношения были между соответствующими сторонами, и пропорциональность была сформирована из этих пар сторон. Соотношения в пропорциях содержали дроби, образованные от деления первоначального большого значения на новое малое значение. Во втором упражнении выше отношения были между двумя разными измерениями, а пропорциональность была сформирована из наборов измерений. Соотношения в пропорции содержат дроби, образованные от старой высоты и старой ширины, и от новой высоты и новой ширины.

Во многих упражнениях вы сможете устанавливать соотношения и пропорции несколькими способами.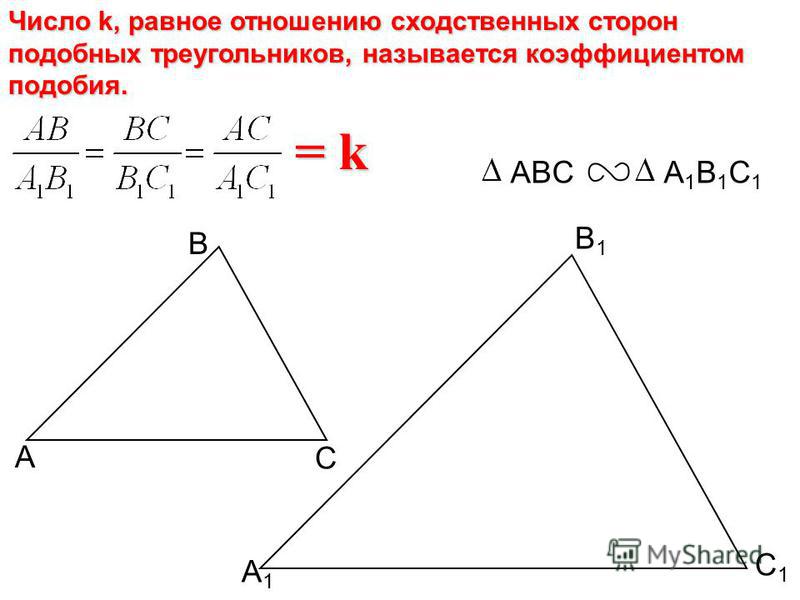 Это совершенно нормально. Просто убедитесь, что вы хорошо маркируете вещи, четко определяете свои переменные и настраиваете их разумным и последовательным образом. Это должно помочь вам найти правильные решения. Если вы когда-либо сомневались в своем решении, не забудьте снова подключить его к исходному упражнению и убедиться, что оно работает.

---

Есть еще одна тема, своего рода ответвление подобных вопросов, с которыми вы можете столкнуться. Он основан на том факте, что если две фигуры (или трехмерные фигуры) подобны, то пропорциональны не только их длины, но и их квадраты (будучи их площадями) и их кубы (будучи их объемами).

• Две прямоугольные призмы подобны, одна пара соответствующих длин составляет 15 см и 27 см соответственно. (а) Если объем меньшей призмы равен 2000 см ³ , каков объем большей призмы? (b) Если площадь одной грани большей призмы составляет 243 см ² , какова площадь соответствующей стороны меньшей призмы?

«Прямоугольная призма» — это просто причудливая геометрическая фраза для «кирпича», поэтому я знаю, что работаю с трехмерными фигурами. Мне известно, что формы похожи, и мне предоставлены две сравнительные длины. Это дает мне мое основное соотношение:

(маленький)/(большой): 15/27 = 5/9

Это

5/9 представляет собой упрощенное (т. буду использовать для нахождения моих ответов для объема и площади поверхности.

(a) Чтобы найти объем большей призмы, мне нужно возвести в куб линейное отношение, которое они мне дали (то есть мне нужно возвести в куб уменьшенную дробь, которую я получил, когда поместил две длины в отношение выше). Помещая значения для меньшей призмы в верхнюю часть коэффициентов, я получаю:

(5/9) ³ = 125/729

Это соотношение, которое я буду использовать для настройки пропорции объема:

В 909090 = [(200090] /125

В = 11664

Проверив свои единицы измерения, я получил ответ:

(а) 11 664 см ³

(б) Чтобы найти площадь одной стороны меньшей призмы, мне нужно чтобы возвести в квадрат линейное отношение, которое они мне дали (то есть мне нужно возвести в квадрат уменьшенную дробь, полученную путем помещения двух длин в отношение).