Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Тема урока: Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Цель урока: изучить понятия множество, подмножество, элементы множества, пустое множество и операций над множествами: пересечение, объединение; проводить несложные систематизации; приводить примеры различных множеств и подмножеств, правильно проводить логические рассуждения.Воспитание аккуратности при работе в тетради, самостоятельности, грамотной математической речи. Развитие мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего урока). внимания учащихся (выполнение заданий на нахождение соответствия). Развитие памяти учащихся
СТРУКТУРА УРОКА
1.Организационный момент
2.Устный счет
3. Изучение нового материала
4.Закрепление
5.Подведение итогов
6.Рефлексия
7.Домашнее задание
Ход урока
1.Организационный момент
Вступительное слово учителя
2. Устный счет
1) 52 + 32 2)67 – 25 3) 51:10 4) 47 -3 : 2
3. Изучение нового материала
Часть 1
Эпиграф:
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Ф. Хаусдорф
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.Обозначают А,В,Р,…
Например:
множество зверей,
множество учеников;
множество столов;
множество стульев;
Предметы, составляющие данное множество, называются его элементами.
Обозначают .
Если множество А состоит из элементов a , c , k , то записывают это так: А = { a , c , k }.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел.
Виды множеств
Подмножество
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
Пустое множество, по определению, считают подмножеством всякого множества.Обозначают Ø
Если два множества состоят из одних и тех же элементов, то они называются равными.
Например, А = { a , c , k , m , n } и В = { m , n , a , c , k }, А = В.
Множество является заданным, т.е. известным, если ясно, какие у него элементы. Поэтому, чтобы задать множество, можно просто перечислить все его элементы.
Круги́ Э́йлера[— геометрическая схема, с помощью которой можно изобразить отношения междуподмножествами, для наглядного представления. Изобретены Леонардом Эйлером.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Практическая работа
Задание1
Перечислите множество фруктов
Перечислите множество овощей
Перечислите множество школьных предметов учеников 6 класса
Задание 2
Начертите три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
1.Дано множество {11; 34; 60; 16; 90}. Принадлежит ли этому множеству число, которое получится при сложении 60 и 30, при вычитании 9 из 17, при делении 72 на 8, при вычитании И из 48, при умножении 20 на 3? [да; нет; нет; да; да].
2.По какому признаку составлено множество {зима, весна, лето, осень}, {11. 13, 15, 17, 19}? [времена года, [нечетные числа большие 10 и меньшие 20].
3.По какому признаку составлено множество {6,3,5,2,4}? [Множество чисел, больших 1 и меньших 7. Является ли это мно жество подмножеством натуральных чисел? [Да].
4.Назовите множество дней одной недели; множество месяцев одного года. Является ли множество дней одной недели подмно жеством множества дней одного месяца? [Да].
5.Даны следующие множества:
А — множество учеников данной школы;
В — множество учеников пятых классов данной школы;
С — множество учащихся всех школ данного города;
Д — множество учащихся пятых классов, посещающих кружковые занятия по математике;
Е — множество всех учащихся школ России.
[ Д ВАСЕ].
Перечислить буквы, обозначающие множества, так, чтобы каждая буква (кроме последней) обозначала подмножество следующего множества.
6.Даны множества:
А — множество натуральных чисел;
В — множество четных чисел;
С — множество нечетных чисел;
Д — множество чисел, делящихся на 5;
Е — множество чисел, делящихся на 10.
[ВА, СА, ДА, ЕА, ДС, ЕВ, ДЕ].
Указать, какие из данных множеств являются подмножествами других данных множеств.
7.Назовите множество натуральных чисел, расположенных между числами 21 и 22.
[Ø]
(Объяснение учителя).
Часть 2.Решим ЗАДАЧУ № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
Введем обозначения:
В — множество всех учащихся;
М — множество учащихся (кружковцев), увлекающихся мате матикой;
JI — множество учащихся (кружковцев), увлекающихся лите ратурой;
И — множество учащихся (кружковцев), увлекающихся историей.
Из условия задачи следует, что все условия пересекаются.
Для составления схемы воспользуемся «кругами Эйлера».
Пересечение множеств М, JI и Д содержит 6 элементов (МЛИ|=6 это следует из условия задачи).
Пересечение множеств М и Л содержит 32 элемента (|MЛ|=32), но 6 элементов принадлежат множеству И (смотри рисунок).
Можно определить, сколько человек записать в кружки по мате матике и литературе (32-6=26 человек).
Пересечение множеств М и И содержит 11 элемента (|МИ|=11), но 6 элементов принадлежат множеству JI; следовательно в кружки по математике и истории записалось 11-6=5 человек.
ЛИ содержит 8 человек (|ЛИ|=8), но 6 элементов принадлежат множеству М, значит в кружки по литературе и истории записалось 8-6=2 человека.
Теперь легко определить сколько учащихся посещают только один кружок:
по математике — 51-(6+26+5)= 14 человек;
по литературе — 40-(6+26+2)=6 человек;
по истории — 22-(6+5+2)=9 человек;
всего записалось — 14+6+9+26+5+6+2=68 человек;
не записалось — 70-68=2 человека.
Решим ЗАДАЧУ № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Введем обозначения:
Л — множество лыжников;
Б — множество баскетболистов;
П — множество пловцов.
По условию задачи все три множества пересекаются. Число эле ментов пересечения трёх множеств обозначим через X.
Пересечение множеств Б и П (БП) содержит 15 человек (|БП| = 15), но X человек принадлежат множеству Л. Можно определить, сколько человек занимаются баскетболом и плава нием: 15-Х (чел.).
Пересечение множеств JI и П (ЛП) содержит 18 человек (|ЛП|=18), но X человек принадлежат множеству Б. Можно определить, сколько человек занимаются лыжами и плаванием: 18-Х (чел.).
Пересечение множеств Б и JI (БЛ) содержит 16 человек (|БЛ|= 16), но X человек принадлежат множеству П. Можно определить, сколько человек занимаются баскетболом и лыжами: 16-Х (чел.).
Теперь легко определить, сколько учащихся занимаются только баскетболом:
26-(16-Х+Х+15-Х)=26-(31 -X).
Сколько учащихся занимаются только плаванием:
25-(18-Х+Х+15-Х)=25-(33-Х).
Сколько учащихся занимаются только лыжами:
27-(16-Х+Х+18-Х)=27-(34-Х).
По условию задачи известно, что в классе 40 человек и один чело век освобожден от занятий по физкультуре. Следовательно, можно составить уравнение:
25-(33-Х)+27-(34-Х)+26-(31 -Х)+15-X+l 8-Х+16-Х+Х+1 =40.
Отсюда, Х= 10, т. е. 10 человек одновременно занимаются баскет болом, плаванием и лыжами.
3 (чел.) занимаются только лыжами.
25-(33-10)=2 (чел.) занимаются только плаванием.
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
32-15=17 (чел.) — выписывают только газету.
21-15=6 (чел.) — выписывают только журнал.
40—(15+17+6)=2 (чел.).
Ответ: 2 человека не выписывают ни газеты, ни журнала.
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
35-10=25 (чел.) — посещают кружки.
Пусть X чел. посещают и биологический, и математический кружки, тогда 20-Х (чел.) — посещают математический кружок, а 11 -X (чел.) — посещают биологический кружок.
Известно, что всего в кружках занимаются 25 человек. Следо вательно, можно составить уравнение:
20-Х+11-Х+Х=25
Х=6
Ответ: 6 биологов увлекаются математикой.
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Пусть X чел. владеют тремя языками, тогда (85-Х) чел. Владе ют только английским языком,(80-Х) чел. — только испанским, (75-Х) чел. — только немецким. По условию задачи известно, что среди 100 человек нет таких, которые знают только два иностранных языка, но все владеют по крайней мере одним иностранным языком. Следовательно, можно составить уравнение:
85-Х+Х+80-Х+75-Х=100
Х=70.
Ответ: 70 человек знают три иностранных языка.
Часть 3. Отношения между множествами. Операции над множествами. Разбиение множества на классы.
Между двумя множествами существует несколько видов отношений. Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В =∅ . Например, А = { a , c , k }, В = { d , e , m , n }, общих элементов у этих множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅ . Например, множества А = { a , c , k } и В = { c , k , m , n } пересекаются, т. к. у них есть общие элементы c , k .
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.
а) б) в) г) д)
Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∩ В = { a , c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2) Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х∈В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∪ В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?
Р е ш е н и е. Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников, изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму. Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А \ В = { k , m , n }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В’А. Дополнение можно изобразить как показано на рис. 5. Если В – подмножество универсального множества U, то дополнение подмножества В до U обозначают В’.
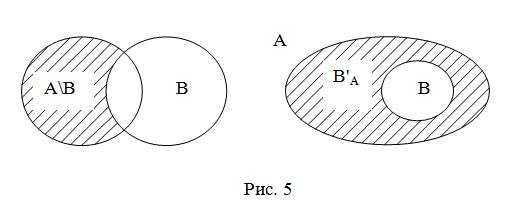
Например, если В – множество однозначных натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С’ – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По определению разность данных множеств состоит из натуральных чисел, кратных 3 и не кратных 5. Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
Задания для самостоятельной работы по теме :
Приведите примеры множеств А, В, С, если отношения между ними таковы:
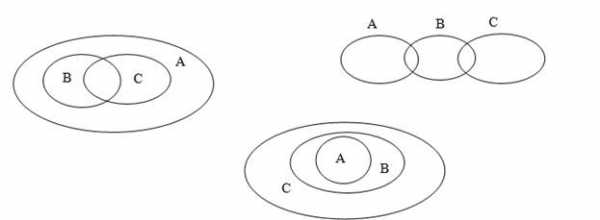
2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a , b , c , d , e , f , k } и В = { a , c , e , k , m , p }. Найдите А ∪ В , А ∩ В , А \ В , В \ А .
4. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x N/ 1 x 15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
6. Рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Раздаточный материал
ЗАДАЧа № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
ЗАДАЧа № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
infourok.ru
Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Тема урока: Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Цель урока: изучить понятия множество, подмножество, элементы множества, пустое множество и операций над множествами: пересечение, объединение; проводить несложные систематизации; приводить примеры различных множеств и подмножеств, правильно проводить логические рассуждения.Воспитание аккуратности при работе в тетради, самостоятельности, грамотной математической речи. Развитие мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего урока). внимания учащихся (выполнение заданий на нахождение соответствия). Развитие памяти учащихся
СТРУКТУРА УРОКА
1.Организационный момент
2.Устный счет
3. Изучение нового материала
4.Закрепление
5.Подведение итогов
6.Рефлексия
7.Домашнее задание
Ход урока
1.Организационный момент
Вступительное слово учителя
2. Устный счет
1) 52 + 32 2)67 – 25 3) 51:10 4) 47 -3 : 2
3. Изучение нового материала
Часть 1
Эпиграф:
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Ф. Хаусдорф
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.Обозначают А,В,Р,…
Например:
множество зверей,
множество учеников;
множество столов;
множество стульев;
Предметы, составляющие данное множество, называются его элементами.
Обозначают .
Если множество А состоит из элементов a , c , k , то записывают это так: А = { a , c , k }.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел.
Виды множеств
Подмножество
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
Пустое множество, по определению, считают подмножеством всякого множества.Обозначают Ø
Если два множества состоят из одних и тех же элементов, то они называются равными.
Например, А = { a , c , k , m , n } и В = { m , n , a , c , k }, А = В.
Множество является заданным, т.е. известным, если ясно, какие у него элементы. Поэтому, чтобы задать множество, можно просто перечислить все его элементы.
Круги́ Э́йлера[— геометрическая схема, с помощью которой можно изобразить отношения междуподмножествами, для наглядного представления. Изобретены Леонардом Эйлером.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Практическая работа
Задание1
Перечислите множество фруктов
Перечислите множество овощей
Перечислите множество школьных предметов учеников 6 класса
Задание 2
Начертите три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
1.Дано множество {11; 34; 60; 16; 90}. Принадлежит ли этому множеству число, которое получится при сложении 60 и 30, при вычитании 9 из 17, при делении 72 на 8, при вычитании И из 48, при умножении 20 на 3? [да; нет; нет; да; да].
2.По какому признаку составлено множество {зима, весна, лето, осень}, {11. 13, 15, 17, 19}? [времена года, [нечетные числа большие 10 и меньшие 20].
3.По какому признаку составлено множество {6,3,5,2,4}? [Множество чисел, больших 1 и меньших 7. Является ли это мно жество подмножеством натуральных чисел? [Да].
4.Назовите множество дней одной недели; множество месяцев одного года. Является ли множество дней одной недели подмно жеством множества дней одного месяца? [Да].
5.Даны следующие множества:
А — множество учеников данной школы;
В — множество учеников пятых классов данной школы;
С — множество учащихся всех школ данного города;
Д — множество учащихся пятых классов, посещающих кружковые занятия по математике;
Е — множество всех учащихся школ России.
[ Д ВАСЕ].
Перечислить буквы, обозначающие множества, так, чтобы каждая буква (кроме последней) обозначала подмножество следующего множества.
6.Даны множества:
А — множество натуральных чисел;
В — множество четных чисел;
С — множество нечетных чисел;
Д — множество чисел, делящихся на 5;
Е — множество чисел, делящихся на 10.
[ВА, СА, ДА, ЕА, ДС, ЕВ, ДЕ].
Указать, какие из данных множеств являются подмножествами других данных множеств.
7.Назовите множество натуральных чисел, расположенных между числами 21 и 22.
[Ø]
(Объяснение учителя).
Часть 2.Решим ЗАДАЧУ № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
Введем обозначения:
В — множество всех учащихся;
М — множество учащихся (кружковцев), увлекающихся мате матикой;
JI — множество учащихся (кружковцев), увлекающихся лите ратурой;
И — множество учащихся (кружковцев), увлекающихся историей.
Из условия задачи следует, что все условия пересекаются.
Для составления схемы воспользуемся «кругами Эйлера».
Пересечение множеств М, JI и Д содержит 6 элементов (МЛИ|=6 это следует из условия задачи).
Пересечение множеств М и Л содержит 32 элемента (|MЛ|=32), но 6 элементов принадлежат множеству И (смотри рисунок).
Можно определить, сколько человек записать в кружки по мате матике и литературе (32-6=26 человек).
Пересечение множеств М и И содержит 11 элемента (|МИ|=11), но 6 элементов принадлежат множеству JI; следовательно в кружки по математике и истории записалось 11-6=5 человек.
ЛИ содержит 8 человек (|ЛИ|=8), но 6 элементов принадлежат множеству М, значит в кружки по литературе и истории записалось 8-6=2 человека.
Теперь легко определить сколько учащихся посещают только один кружок:
по математике — 51-(6+26+5)= 14 человек;
по литературе — 40-(6+26+2)=6 человек;
по истории — 22-(6+5+2)=9 человек;
всего записалось — 14+6+9+26+5+6+2=68 человек;
не записалось — 70-68=2 человека.
Решим ЗАДАЧУ № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Введем обозначения:
Л — множество лыжников;
Б — множество баскетболистов;
П — множество пловцов.
По условию задачи все три множества пересекаются. Число эле ментов пересечения трёх множеств обозначим через X.
Пересечение множеств Б и П (БП) содержит 15 человек (|БП| = 15), но X человек принадлежат множеству Л. Можно определить, сколько человек занимаются баскетболом и плава нием: 15-Х (чел.).
Пересечение множеств JI и П (ЛП) содержит 18 человек (|ЛП|=18), но X человек принадлежат множеству Б. Можно определить, сколько человек занимаются лыжами и плаванием: 18-Х (чел.).
Пересечение множеств Б и JI (БЛ) содержит 16 человек (|БЛ|= 16), но X человек принадлежат множеству П. Можно определить, сколько человек занимаются баскетболом и лыжами: 16-Х (чел.).
Теперь легко определить, сколько учащихся занимаются только баскетболом:
26-(16-Х+Х+15-Х)=26-(31 -X).
Сколько учащихся занимаются только плаванием:
25-(18-Х+Х+15-Х)=25-(33-Х).
Сколько учащихся занимаются только лыжами:
27-(16-Х+Х+18-Х)=27-(34-Х).
По условию задачи известно, что в классе 40 человек и один чело век освобожден от занятий по физкультуре. Следовательно, можно составить уравнение:
25-(33-Х)+27-(34-Х)+26-(31 -Х)+15-X+l 8-Х+16-Х+Х+1 =40.
Отсюда, Х= 10, т. е. 10 человек одновременно занимаются баскет болом, плаванием и лыжами.
26-(31-10)=5 (чел.) занимаются только баскетболом.
3 (чел.) занимаются только лыжами.
25-(33-10)=2 (чел.) занимаются только плаванием.
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
32-15=17 (чел.) — выписывают только газету.
21-15=6 (чел.) — выписывают только журнал.
40—(15+17+6)=2 (чел.).
Ответ: 2 человека не выписывают ни газеты, ни журнала.
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
35-10=25 (чел.) — посещают кружки.
Пусть X чел. посещают и биологический, и математический кружки, тогда 20-Х (чел.) — посещают математический кружок, а 11 -X (чел.) — посещают биологический кружок.
Известно, что всего в кружках занимаются 25 человек. Следо вательно, можно составить уравнение:
20-Х+11-Х+Х=25
Х=6
Ответ: 6 биологов увлекаются математикой.
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Пусть X чел. владеют тремя языками, тогда (85-Х) чел. Владе ют только английским языком,(80-Х) чел. — только испанским, (75-Х) чел. — только немецким. По условию задачи известно, что среди 100 человек нет таких, которые знают только два иностранных языка, но все владеют по крайней мере одним иностранным языком. Следовательно, можно составить уравнение:
85-Х+Х+80-Х+75-Х=100
Х=70.
Ответ: 70 человек знают три иностранных языка.
Часть 3. Отношения между множествами. Операции над множествами. Разбиение множества на классы.
Между двумя множествами существует несколько видов отношений. Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В =∅ . Например, А = { a , c , k }, В = { d , e , m , n }, общих элементов у этих множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅ . Например, множества А = { a , c , k } и В = { c , k , m , n } пересекаются, т. к. у них есть общие элементы c , k .
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.
а) б) в) г) д)
Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∩ В = { a , c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2) Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х∈В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∪ В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?
Р е ш е н и е. Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников, изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму. Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А \ В = { k , m , n }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В’А. Дополнение можно изобразить как показано на рис. 5. Если В – подмножество универсального множества U, то дополнение подмножества В до U обозначают В’.
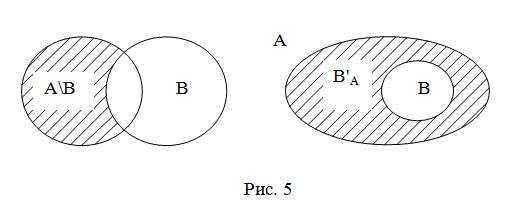
Например, если В – множество однозначных натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С’ – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По определению разность данных множеств состоит из натуральных чисел, кратных 3 и не кратных 5. Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
Задания для самостоятельной работы по теме :
Приведите примеры множеств А, В, С, если отношения между ними таковы:
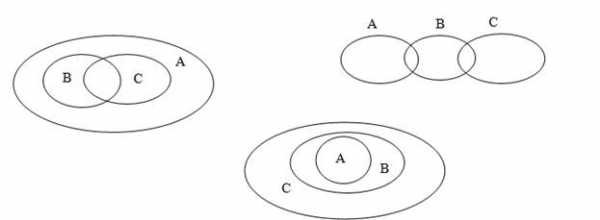
2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a , b , c , d , e , f , k } и В = { a , c , e , k , m , p }. Найдите А ∪ В , А ∩ В , А \ В , В \ А .
4. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x N/ 1 x 15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
6. Рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Раздаточный материал
ЗАДАЧа № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
ЗАДАЧа № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
infourok.ru
I.3. Способы задания множеств
Множество считается заданным, если о каждом элементе можно однозначно сказать, принадлежит он этому множеству или нет.
А) Простейший способ задания множества состоит просто в перечислении всех элементов данного множества.
Если множество A конечное, состоящее из элементов A1, A2, …, AN, то пишут A = {A1, A2, …, AN} . В частности, {A} — множество, состоящее из одного элемента A.
Но такой способ задания применим, разумеется, лишь к конечным множествам.
Б) Другой, универсальный способ: задание множества A С помощью характеристического свойства элементов данного множества, то есть такого свойства, которым обладают все элементы множества A и не обладают другие элементы, не принадлежащие A.
Если P(X) — такое свойство, то пишут: .
Например, для конечного множества A = {A1, A2,…, AN} можно записать: A = {X | x = A1, или X = a2, или …, или X = AN}. Множество всех депутатов парламента можно задать так: D = {X | X — депутат}. Множество всех студентов S = { x | X — студент}.
В) Еще один способ — это задание множества с помощью порождающей процедуры, или алгоритмический способ.
Например, пусть M = {1, 2, 4, 8, 16,…} — множество степеней числа 2. Тогда его можно задать так:
1) ; 2) если , то .
Другой пример: множество МP = {314, 159, 256, 358, …} задается как последовательность троек подряд идущих цифр десятилетней записи числа p = 3,141592653589793238462… . (В действительности, учитывая трансцендентность числа p, множество МP содержит все целые числа от 0 до 999.)
Г) Четвертый способ — задание множеств с помощью операций над уже известными множествами.
К описанию свойств, задающих множество, естественно предъявить требования точности и недвусмысленности. Например, множество хороших фильмов 1999г. разные люди зададут разными списками. Даже сами критерии отбора фильмов могут оказаться различными.
Надежный способ точного описания множества — распознающая (разрешающая) процедура. Например, для множества степеней двойки М2N разрешающей процедурой может служить разложение числа на простые множители.
Задание множества М4 нельзя отнести ни к одному из перечисленных способов; оно по сути совсем не задано, а только названо. Задать его можно списком футболистов, или описанием: М4 есть множество лиц, имеющих удостоверение футболиста клуба «Динамо-Минск». В этом случае разрешающая процедура — это проверка документов.
I.4. Пустое и универсальное множества
В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом Æ. Если A есть пустое множество, то пишут: A = Æ. Зачем же его вообще вводят? Стоит отметить, что когда множество задано своим характеристическим свойством, то не всегда заранее известно, существует ли хоть один элемент с таким свойством. Например, пусть множество А состоит из всех четырехугольников таких, что) все их углы прямые,)диагонали имеют различную длину.
Для человека, не знающего геометрии, ничего противоречивого в этих требованиях нет. Однако из теоремы о равенстве диагоналей прямоугольника следует, что множество таких четырехугольников пусто. Пустыми являются также множества треугольников, сумма углов которых отлична от 180, множество квадратных трехчленов, имеющих больше двух корней и т.д.
В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным. Оно обычно обозначается U (от англ. Свойства универсального множества:
-Любой объект, какова бы ни была его природа, является элементом универсального множества
-В частности, само универсальное множество содержит себя в качестве одного из многих элементов
-Любое множество является подмножеством
-В частности, само универсальное множество является своим подмножеством
-Объединение
-В частности, объединение универсального множества с самим собой равно универсальному множеству
-Пересечение
-В частности, пересечение универсального множества с самим собой равно универсальному множеству
-Исключение
-В частности, исключение универсального множества из себя равно пустому множеству
-Исключение любого множества из универсального множества равно дополнению
-Дополнение универсального множества есть пустое множество.
studfiles.net
| |||||||||||||||
| |||||||||||||||
dl.nure.ua
Глава I. Элементы логики
§ 1. Множества и операции над ними
Изучая математику, необходимо усвоить определенную систему понятий, предложений и доказательств.
Изучение этого материала связано с овладением теоретико-множественным языком.
В конце XIXвека возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор. Знания в этой области нужны учителю начальных классов для понимания содержания начального курса математики и для освоения таких важных понятий, как взаимно однозначное соответствие, отношение, число, геометрическая фигура.
Лекция 1. Понятие множества
План:
1. Понятие множества. Элемент множества. Пустое множество. Примеры конечных и бесконечных множеств.
2. Способы задания множеств. Равные множества.
3. Отношения между множествами. Подмножество. Универсальное множество. Круги Эйлера.Числовые множества.
1. Понятие множества и элемента множества
В математике часто рассматриваются те или иные группы объектов как единое целое: натуральные числа, треугольники, квадраты и др. Все эти различные совокупности называют множествами.
Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах: множество гласных букв русского языка, множество натуральных чисел, множество треугольников.
Математический смысл слова «множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим числом предметов. В математике этого не требуется. Здесь можно рассматривать множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
Множества принято обозначать прописными буквами латинского алфавита: A,B,C,D, …,Z. Множество, не содержащее ни одного объекта, называетсяпустым и обозначается символом∅.
Объекты, из которых образовано множество, называются элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: а, b,c,…,z.
Предложение «Объект а принадлежит множеству А» можно записать, используя символы:а ∈ А». Предложение«Объект а не принадлежит множеству А»можно записать так:а ∉ А.
Например, если А – множество однозначных чисел, то утверждение «Число 3 – однозначное» можно записать в таком виде: 3 ∈ А. Запись 12∉ А означает, что «Число 12 не является однозначным», или «Число 12 не принадлежит множеству А», или «Множество А не содержит числа 12».
В геометрии точки обозначают заглавными буквами. «Точка Р лежит на отрезке АВ» можно записать: Р ∉ АВ или Р∉ Х.
Множества бывают конечные и бесконечные. Конечные: множество дней недели, множество месяцев в году. Бесконечные: множество точек на прямой, множество натуральных чисел.
Для ряда числовых множеств в математике приняты стандартные обозначения:
N– множество натуральных чисел;
Z– множество целых чисел;
Q– множество рациональных чисел;
R– множество действительных чисел.
2. Способы задания множеств
Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?
Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
1. Множество можно задать, перечисливвсе его элементы. Запись: А = {3, 4, 5, 6.
2. Если множество бесконечно, то его элементы перечислить нельзя. В таких случаях указывают характеристическое свойство его элементов.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Например: А = {х׀ х – двузначные числа}
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными соседними сторонами и как множество ромбов с прямыми углами.
Очень важно умение переходить от одного способа задания множества к другому.
studfiles.net
Способы задания множеств
Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?
Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5 и 6, то мы зададим это множество, поскольку все его элементы окажутся перечисленными. При этом возможна запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {3,4, 5,6}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества: указывают характеристическое свойство его элементов.
Характеристическое свойство- это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Рассмотрим, например, множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, — «быть двузначным числом». Это характеристическое свойство дает возможность решать вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так, число 45 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит, так как оно не является двузначным.
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными смежными сторонами и как множество ромбов с прямым углом.
В тех случаях, когда характеристическое свойство элементов множества можно представить в символической форме, возможна соответствующая запись множества. Например, множество А натуральных чисел, меньших 7, можно задать так: А = {х | х N и х<7}.
При такой записи буквой х обозначается элемент множества А. Для этих целей можно использовать и другие буквы латинского алфавита.
Итак, для того чтобы задать некоторое множество, достаточно либо перечислить все его элементы, либо указать их характеристическое свойство. Второй способ более общий: он позволяет задавать и конечные, и бесконечные множества.
Очень важно умение переходить от одного способа задания множества к другому. Этому обучаются уже младшие школьники, выполняя упражнения такого характера.
З а д а ч а 1. Запишите числа, которые больше, чем 65 и меньше, чем 75.
Р е ш е н и е. Множество чисел задано при помощи характеристического свойства «быть больше 65 и меньше 75». Требу-
ется перечислить элементы этого множества: 66, 67, 68,69, 70, 71,72,73,74.
З а д а ч а 2. Укажите характеристическое свойство элементов множества А = {12, 22, 32, 42, 52, 62, 72, 82,92}.
Р е ш е н и е. Перечислены все элементы множества А. Их характеристическое свойство: «быть двузначным и оканчиваться цифрой 2».
Похожие статьи:
poznayka.org
Множества,их элементы,поджмножества
Определение 1
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Предметы или объекты, образующие данное множество, называются его элементами. Например, число $6$ будет являться элементом множества натуральных чисел, а число $0,9$ не будет являться элементом множества натуральных чисел.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Определение 2
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Определение 3
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
В математике часть множества называют — подмножество. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества.
Обозначение множеств, подмножеств и их элементов
Чаще всего множества обозначаются латинскими буквами- $A, B, C , D, X, Y, Z, W$ и Т.Д.
Элементы множеств обозначаются строчными буквами $a,b,c,d,x,y,z$ и Т.Д.
Записать принадлежность некоторого элемента к некоторому множеству, например то, что некоторой элемент $a$ будет входить в множество $A$ математически можно так: $a\in A$.Прочитать данную запись можно так: a принадлежит множеству $A$.
Если же некоторый элемент, например, $b$ не принадлежит множеству $B$, то это записывается так: $b\notin B$.Читают эту запись так: $b$ не принадлежит множеству $B$
Например, если обозначить множество целых чисел за $A$, что тогда можно записать: $3\in A$, $7,5\notin B$
Пустое множество в математике обозначают так: $ᴓ$
Для обозначения того, что множество $B$ является подмножеством множества $A$, используют обозначение: Знак $\subset $ обозначает включение одного множества в другое множество.
Пример 1
Определить какие элементы из перечисленных $12,38,54,79,934$ будут входить в множество $A$- чисел кратных $3$.
Решение: По условию множество $A$ содержит в себе элементы, каждый из которых должен быть кратным, т.е. делится без остатка на $3.$ Значит для того чтобы определить будут ли заданные числа являться элементами множества $A$ нам надо проверить какие из них будут делится на $3$ без остатка, какие нет.
Вспомним признак делимости на $3$: Если сумма цифр, входящих в состав числа делится на $3$, то число делится на $3$ без остатка.
$12$ делится на $3$, т.к. сумма цифр числа $12$ равна $3$
число $38$ на $3$ без остатка делится не будет, т.к. сумма цифр $3+8=11$ не делится на $3$ без остатка
аналогично т.к. суммы цифр числа $54$ равна $9$ доказываем, что на $3$ оно делится, в число $74$ на $3$ делится не будет, т.к. сумма цифр равна $11.$
Найдем сумму цифр числа $934: 9+3+4=16$, число $16$ не кратно $3$ ,значит и число $934$ на $3$ без остатка делится не будет
Теперь сделаем вывод, какие числа будут являться элементами множества $A$:
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ {\rm :\ }54\in A.\]Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
Конечные множества с небольшим количеством элементов обычно записывают в фигурных скобках $\left\{a,b,c\right\}$
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Второй способ задания множеств применим как для конечных. так и для бесконечных множеств. Он заключается в том, что указывается свойство, которым обладает каждый элемент данного множества — множество задают описанием, т.е. указав его характеристическое свойство, т. е свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.
Пример 2
Например, с помощью описания можно задать такие множество натуральных чисел от $1$ до $9$ включительно. Характеристическим свойством, т. е. свойством, которым обладают все элементы этого множества для данных элементов будет являться то, что все они являются натуральными числами и каждое из них не меньше $1$ и не больше $9$. Перечислением указанное множество можно задать следующим образом:
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Пример 3
Например, рассмотрим множества
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
$B=\left\{9,8,7,6,5,4,3,2,1\right\}$
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Пример 4
Например, рассмотрим два множества:
$A=\left\{1\ ,2,3,4,5\right\}$
$B=\left\{9,7,5,3,\right\}$
Общей частью этих множеств будет множество $C=\left\{3,5,\right\}$
Математически это можно обозначить так: $А\cap B=\left\{3,5\right\}$
Пересечением множеств $A$ и $B$ называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество $A$ и в множество $B$.
Объединение множеств
Из двух множеств $A$ и $B$ можно образовать новое множество, объединяя все элементы множества $A$ и все элементы множества $B$
Математически это можно обозначить так:$\ А\ \cup B$
Объединением множеств $A$ и $B$ называется новое множество$\ А\ \cup B$, состоящее из тех и только из тех элементов, которые входят хотя бы в одно из множеств $A$ или $B$.
Разность множеств
Разностью двух множеств $A$ и $B$ называют такое множество, в которое входят все элементы из множества $A$, не принадлежащие множеству $B$.
spravochnick.ru
