Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..Клеммы wago -клемма wago 243-808 Украина ecshop ООО Электроконтроль
Мало кто знает о том, где именно, чаще всего появляются проблемы и неисправности, когда речь идет об электросетях, но если подумать, то можно прийти к правильному выводу, ведь редко, когда в ровном проводе появится неисправность при отсутствии внешней деформации. Это значит, что проблемы возникают в соединениях смежду проводами или с розетками, выключателем и тому подобное. Обрыв в проводе случается редко, а вот в местах, где соединяют провода, вызванные сопротивлением, обрыв образуется именно в сайках. Можно легко прийти к выводу, что надежные спайки — хороший контакт, не столь большое сопротивление, а значит проводимость выше и безопасней цепью.
Строительно-монтажная клемма должна отвечать нескольким параметрам, среди которых: строк эксплуатации, устойчивость, напряжение, сила тока и так далее.
Клеммники ваго очень удобные и в принципе просты в использовании. Они обладают неоспоримыми преимуществами, которых здесь достаточно:
- монтаж.нет нужды в спайке, что значит отсутствие необходимости наличия дополнительных материалов, достаточно зачистить проводник и провести коммуникацию.
- при зажиме по винтовому типу есть возможность испортить, деформировать провод, недожимая или пережимая его, что в принципе, чревато последствиями. Пружинные клеммы wago адаптируются непосредственно под сечение.
- клеммная колодка не требует дополнительного обеспечения изоляции.
- надежный контакт
Используя клеммы Вы можете быть уверенны в том, что проводимость не утратит своей силы во все время использования.
Клеммы wago 222 предназначены для распределительных коробок.
- номинальное напряжение 400 В / 4 кВ
- соединение CAGE CLAMP
- номинальный ток: 32 А для 4 мм2; 24 А для 2,5 мм2
- подключение без инструмента
Wago 222 подходит для использования и подсоединения всех типов проводников.
Клеммы wago 2273 для распределительных коробок предоставляются заполненные пастой и без пасты вовсе.
- сечение провода: 0,5 — 2,5 мм2
- номинальный ток 24 А
Wago 773 соединяет проводники в распределительных коробках. 773 серия отличается прозрачностью и предназначена для подключения только медных проводников. Поставляется без пасты.
Ваго клеммы лучший выбор, если Вы заботитесь о безопасности электросетей, но все равно, необходимо быть внимательным. Стоит помнить о том, что превышение тока, заставит клемму начать плавиться, поэтому следует предусмотреть дополнительный запас.
Покупая клеммы для проводов wago цена не столь велика, в среднем от 5 до 50 гривен, что, в принципе является приятным диапазоном ценовой политики, особенно на столь качественный продукт.
Купить клеммы для проводов в Одессе, да и по всей территории Украины, не так уж и сложно. Стоит просто обратится в наше представительство, и заказать интересующий Вас товар, на себе прочувствовав все позитивные стороны, столь качественной продукции.
Движущая сила WAGO, позволяющая компании разрабатывать и продвигать на рынок новейшие продукты, заключается в комплексном подходе к проектам по автоматизации. WAGO специализируется на электрических и электронных компонентах с техникой пружинных зажимов. WAGO, будучи изобретателем техники пружинных зажимов, продолжает разработку электронных подсистем и продуктов подсоединительной электротехники на основе этой успешной технологии.
В отделе ЭЛЕКТРОТЕХНИКИ разрабатываются компоненты электрической соединительной техники. В отделе ЭЛЕКТРОНИКИ — электронные компоненты для распределительных систем управления технологическими процессами.
Идея соединять электрические проводники не винтом, а силой пружины была впервые осуществлена в компании WAGO еще в 1951 году.
Таким образом мы — пионеры в области пружинных соединительных систем для электроники и электротехники. В основе всех наших продуктов лежит дна и та же философия: Не требующие ухода виброустойчивые клеммные соединения, независимые от силы приложения монтировщика.
Сертификация DIN ISO (Немецкий промышленный стандарт/Международной организации стандартизации ИСО) 14001 WAGO придает большое значение высокой степени безопасности работ и бережному отношению к природным ресурсам и энергии. Сертификационная комиссия TÜV Mangagement Service GmbH засвидетельствовала, что в Германии и Швейцарии соблюдены все требования ИСО 14001: 2004. Это еще раз доказывает, что мы заботимся не только о качестве нашей продукции, но и о состоянии экологии и окружающих людуй.
Сертификация DIN ISO (Немецкого промышленного стандарта/Международной организации стандартизации ИСО) 9001: 2000 На сегодняшний день в условиях жесткой конкуренции необходимо не только гарантировать качествот самой продукции, но и быть представителем системы гарантии качества.
Требования к такой системе изложены в ИСО 9001: 2000. Чтобы подтвердить соответствие наших стандартов качества международным требованиям, мы прошли сертификационные испытания в независимой инстанции и получили для заводов.
Q2 Найдите наименьшее число, на которое нужно умножить каждое из следующих чисел, чтобы получить.
..Перейти к
- Упражнение 7.1
- Упражнение 7.2
- Рациональное число
- Линейные уравнения с одной переменной
- Понимание четырехугольников
- Практическая геометрия
- Обработка данных
- Квадраты и квадратные корни
- Кубы и кубические корни
- Сравнение количеств
- Алгебраические выражения и тождества
- Визуализация твердых фигур
- Измерение
- Показатели и силы
- Прямые и обратные пропорции
- Факторизация
- Введение в графики
- Игра с числами
Главная >
Решения НЦЭРТ
Класс 8
Математика
>
Глава 7.
Кубы и кубические корни
>
Упражнение 7.1
>
Вопрос 3
Вопрос 3 Упражнение 7.1
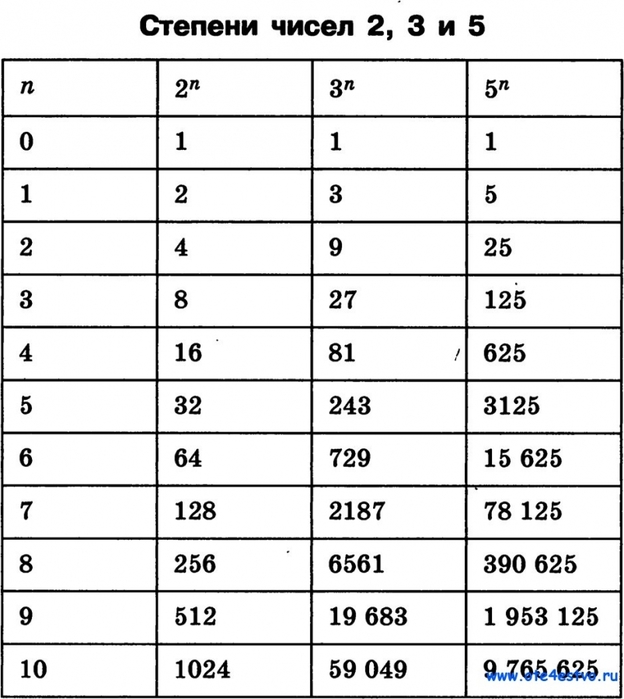
В2) Найдите наименьшее число, на которое нужно умножить каждое из следующих чисел, чтобы получить полный куб:
(i)243
(ii)256
(iii)72
(iv)675
(v)100
Ответ:
Решение:
(i) 243
Простые множители числа 243 =
Здесь 3 не входят в группу троек.
Следовательно, 243 нужно умножить на 3, чтобы получить идеальный куб.
(ii) 256
Простые множители числа 256 = 2\times2\times2\times2\times2\times2\times2\times2
Здесь требуется один множитель 2, чтобы получить тройку.
Следовательно, 256 нужно умножить на 2, чтобы получить идеальный куб.
(iii) 72
Простые множители 72 = 2\times2\times2\times3\times3
Здесь 3 не появляется в группе 3.
Следовательно, 72 нужно умножить на 3, чтобы получить идеальный куб.
(iv) 675
Простые множители числа 675 = 3\times3\times3\times5\times5
Здесь множитель 5 не появляется в группе 3.
Следовательно, 675 нужно умножить на 3, чтобы получить идеальный куб.
(в) 100
Простые множители 100 = 2\x2\times5\times5
Здесь множитель 2 и 5 не появляются в группе 3.
Следовательно, 100 нужно умножить на 2\times5= 10, чтобы получить идеальный куб.
Связанные вопросы
Какие из следующих чисел не являются совершенными кубами? (i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
Q1) Какие из следующих чисел не являются совершенными кубами: (i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
Найдите наименьшее число, на которое нужно умножить каждое из следующих чисел, чтобы получить…
Найдите наименьшее число, на которое нужно разделить каждое из следующих чисел, чтобы получить совершенное.