Значения синуса косинуса: Нахождение значений синуса и косинуса, тангенса и котангенса — методическая рекомендация. Алгебра, 10 класс.

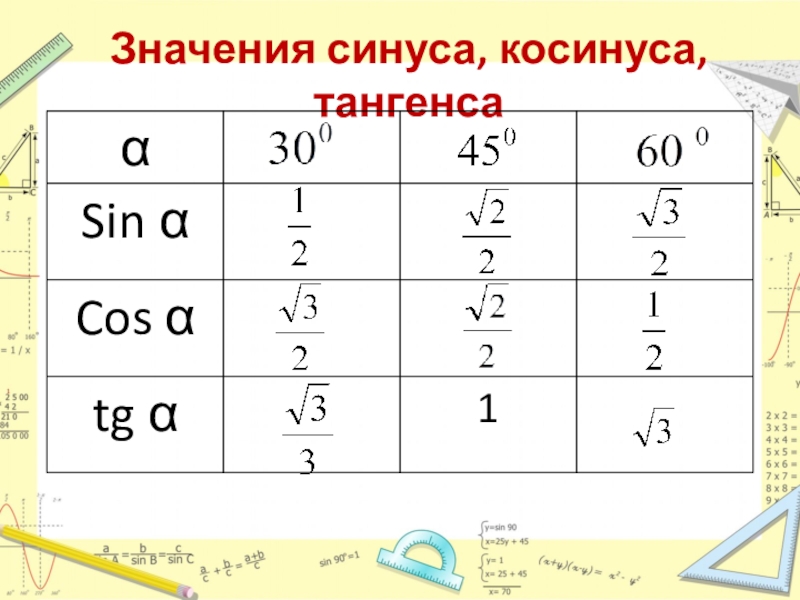
Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№32 – Рамблер/класс

Найдите значения синуса и косинуса а, если а равно: Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№32 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Всем приветик, плиз помогайте с этой занудной алгеброй, нике не решу(((  Найдите значения синуса и косинуса а, если а равно: 

ответы

Сейчас все сделаем, лови ответик))

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309

Привет! Поможете с решением?)
Скорость изменяется по закону 
(скорость измеряется в метрах в секунду). В какой момент времени (Подробнее…)

ГДЗ11 классКолмогоров А.Н.10 классАлгебра

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Это правда, что будут сокращать иностранные языки в школах?

 Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее…)

ШколаНовостиИностранные языки

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых). ..

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Как найти значение синуса, косинуса и тангенса углов от 0 до 180 градусов. ТФ Часть 16

12+

6 месяцев назад

Математика от Баканчиковой311 подписчиков

Геометрия 8-9 класс. Как найти значение синуса, косинуса и тангенса углов от 0° до 180°? Сегодня мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в геометрии», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. На примере трех задач мы покажем Вам: как найти значения тригонометрических функций для тупых углов; как найти значение одной тригонометрической функции, зная значение другой тригонометрической функции и величину угла; как вычислить выражение, состоящее из тригонометрических функций с заданными углами.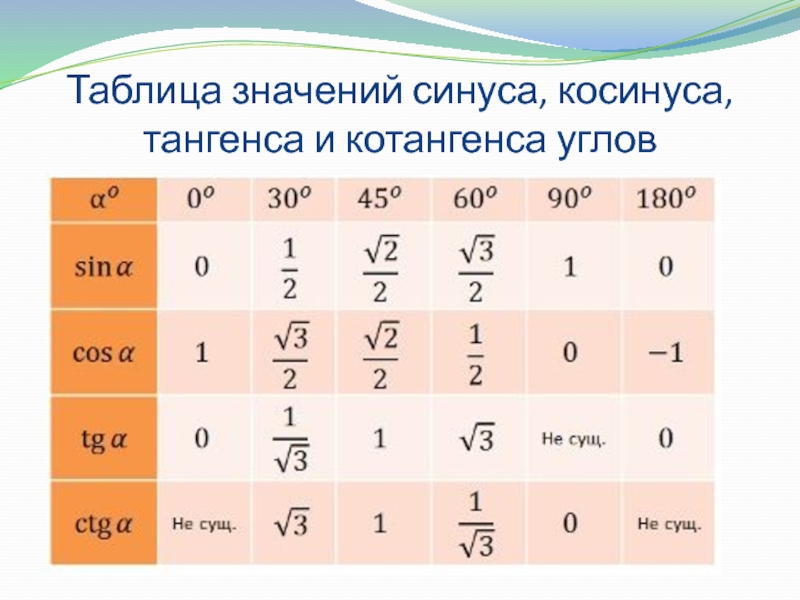 Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео. 00:00 Начало видео. 00:17 Задача 1. Найти sin 120°, cos 135°, tg 150°, sin 160°. 05:27 Задача 2. Найти cos α, если а). sin α = 0,6; угол α – острый. 07:10 Задача 2. Найти cos α, если б). sin α = 0,6; угол α – тупой. 08:34 Как найти tg α, зная sin α или cos α? 09:06 Задача 3. Вычислить… Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео: Определение синуса, косинуса и тангенса для любых углов от 0° до 180°. Тригонометрические функции в геометрии. Часть 15. https://rutube.ru/video/f7bb29d13b83a98c2fdbde34d8d7a5dd/ Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.ru/video/b99256c0e2a5f1411c87731142e2a822/ Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии.

Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/ Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/ Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/ Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°. Тригонометрические функции в геометрии. Часть 5. Геометрия 9 класс. https://rutube.ru/video/9393cb6043b9878b49883195db02d251/ Функция в математике. Определение. Пример, на котором функцию понимают ВСЕ. https://rutube.ru/video/e39b203540be6b34b1c6728b8a73a8c4/ Компоненты функции: аргумент, значение функции, область определения функции, область значений функции https://rutube.ru/video/b244f058080abfb736bb53076b8ad8cc/ Способы задания функции. 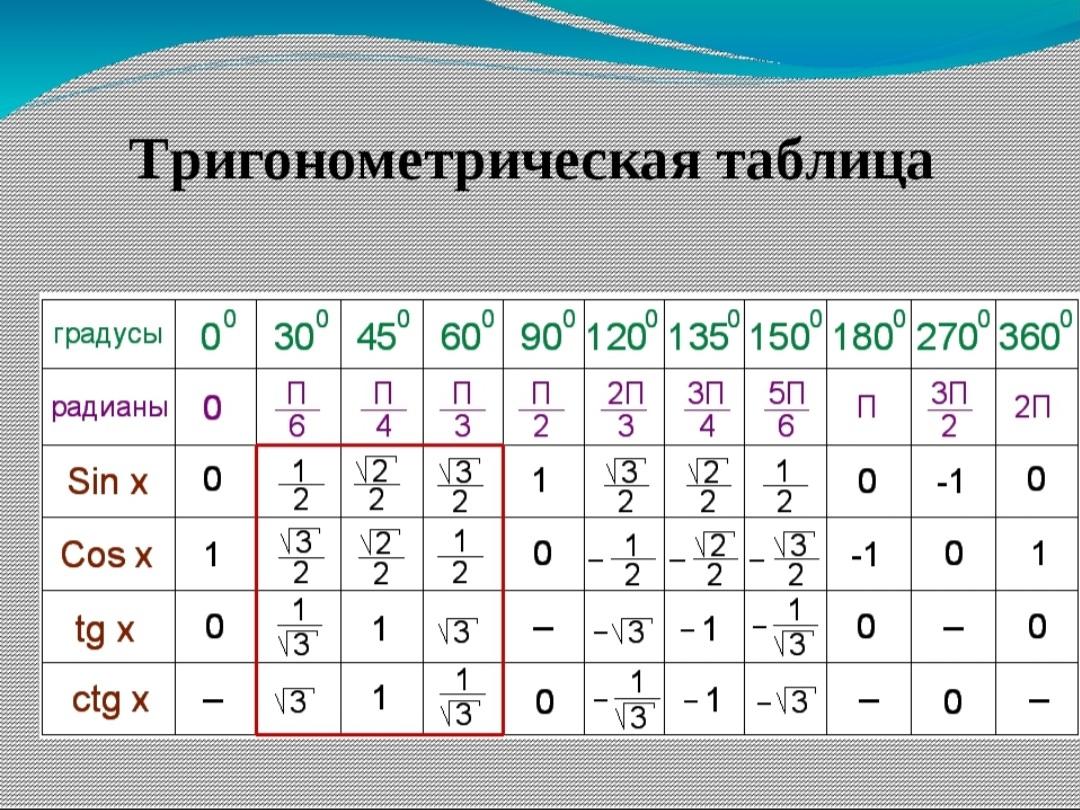Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/ #ТригонометрическиеФункцииВГеометрии #значениетригонометрическихфункцийот0до180 #найдитезначениетригонометрическихфункций #значениетригонометрическихфункцийлюбогоугла #найтикосинусеслисинусравен #найтисинусесликосинусравен #найтитангенсеслисинусравен #найтитангенсесликосинусравен #вычислитесуммусинусовикосинусов # вычислитесуммусинусовкосинусовтангенсов #вычислитьтригонометрическоевыражение #МатематикаОтБаканчиковой геометрия 8-9 класс, значение тригонометрических функций от 0 до 180, найдите значение тригонометрических функций, значение тригонометрических функций любого угла, найти косинус если синус равен, найти синус если косинус равен, найти тангенс если синус равен, найти тангенс если косинус равен, вычислите сумму синусов и косинусов, вычислите сумму синусов косинусов тангенсов, вычислить тригонометрическое выражение

Калькулятор синуса, косинуса, тангенса

С помощью нашего калькулятора синуса, косинуса, тангенса вы узнаете все, что вам нужно о наиболее важных тригонометрических функциях: узнаете, как их идентифицировать, как они связаны с прямоугольными треугольниками и как вычислить их в мгновение ока. !

Тригонометрические функции: вычисление синуса, косинуса и тангенса

Тригонометрические функции — это математические функции, которые связывают числовых значений с углами в соответствии с определенными правилами. Существует много тригонометрических функций, но наиболее важными являются синус, косинус и тангенс. Поскольку в качестве аргумента они принимают угол, естественно идентифицировать их на окружности.

На изображении ниже вы можете увидеть тригонометрический круг , круг с радиусом 111, где для определенного угла α\alphaα мы выделили сегменты, соответствующие синусу и косинусу.

Обратите внимание, что касательная лежит вне круга, касаясь его, как следует из названия. Хотя синус и косинус легко идентифицировать как проекций радиуса на вертикальную и горизонтальную оси , нам нужно увидеть определение тангенса, чтобы понять, как его найти и визуализировать:

tan⁡(α)=sin⁡(α)cos⁡(α)\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}tan(α)=cos( α)sin(α)​

На рисунке ниже мы представили три тригонометрические функции: мы вычислили значения синуса, косинуса и тангенса для углов между 0°0\градус0° и 360°360\градус360°.

Даже из этого беглого взгляда на тригонометрию можно определить многие свойства этих функций:

• Значения, рассчитанные для синуса, косинуса и тангенса, являются периодическими . В частности:
  • Синус и косинус имеют периодичность, равную 360°360\градус360°; и
  • Тангет имеет периодичность 180°180\градус180°.
• Синус и косинус имеют значения от -1-1-1 до 111. Тангенс принимает значения от -∞-\infty-∞ до ∞\infty∞.
• Значения синуса и косинуса периодически переключаются в четырех квадрантах круга;
• Синус и косинус «сдвинуты по фазе» на 90°90\градус90° друг к другу.

Продолжайте изучать эти функции, чтобы открыть множество других почти бесконечных свойств!

После этого введения в тригонометрические функции пришло время научиться вычислять синус, косинус и тангенс в треугольнике. Перейти к следующему разделу!

Как вычислить синус, косинус и тангенс треугольника?

Прямоугольные треугольники и тригонометрические функции имеют глубокую связь: вы можете быстро вычислить значения последних и геометрическую характеристику первых, не запоминая никаких формул: благодаря аккуратному графическому представлению функций вы всегда можете нарисовать то, что вам нужно на листе бумаги, и вы быстро вспомните математику!

Чтобы понять связь между прямоугольными треугольниками и тригонометрическими функциями, посмотрите на детали предыдущего изображения.

2(\alpha) = 1 ,sin2(α)+cos2(α)=1,

которые мы получаем из теоремы Пифагора . Но одно это не подскажет нам, как вычислять синус, косинус и тангенс в треугольнике. Если вы рассматриваете угол α\alphaα, вы можете найти значения функций благодаря набору соотношений между длинами сторон треугольника :

α) = противоположный смежный \ начало {разделение} \ sin (\ alpha) & = \ frac {\ mathrm {напротив}} {\ mathrm {гипотенуза}} \\ [1em] \cos(\alpha) & = \frac{\mathrm{смежный}}{\mathrm{гипотенуза}}\\[1em] \ tan (\ alpha) & = \ frac {\ mathrm {напротив}} {\ mathrm {смежно}} \end{split}sin(α)cos(α)tan(α)​=hypotenuseopposite​=hypotenuseadjacent​=adjacentopposite​​

Повернув треугольник и поместив нужный острый угол в центр тригонометрической окружности, вы можете вычислить синус, косинус и тангенс второго угла.

Другие инструменты Omni

Наш калькулятор синуса, косинуса и тангенса позволяет вам видеть значения тригонометрических функций непосредственно для определенного угла.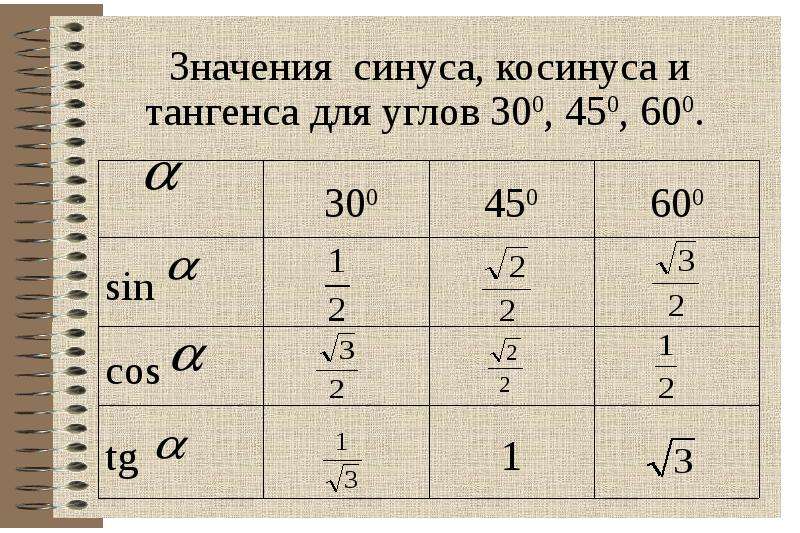 Вы также можете вставить известную информацию о прямоугольном треугольнике и посмотреть, достаточно ли их для расчета остальных. Если вы нашли этот инструмент полезным, ознакомьтесь с другими нашими калькуляторами:

• Тригонометрический калькулятор;
• Калькулятор косинуса треугольника;
• Калькулятор синусоидального треугольника;
• Калькулятор триггерного треугольника;
• Калькулятор тригонометрии прямоугольного треугольника;
• Калькулятор триггеров;
• Калькулятор отношения тангенса; и
• Калькулятор угла касательной.

Часто задаваемые вопросы

Почему я могу вычислять синус, косинус и тангенс в треугольнике?

Прямоугольные треугольники и тригонометрические функции тесно связаны. Если вы посмотрите на синус и косинус на тригонометрическом круге, вы увидите, что они образуют прямой угол, что позволяет вам определяют прямоугольный треугольник с катетами, соответствующими синусу и косинусу.

Вычисляя отношения между гипотенузой и катетисом, вы можете найти меру «наклона» отрезка в анализе, который есть не что иное, как результат тригонометрической функции.

Как вычислить синус, косинус и тангенс в треугольнике 3-4-5?

Чтобы вычислить синус, косинус и тангенс в треугольнике 3-4-5, выполните следующие простые шаги:

1. Поместите треугольник в тригонометрический круг с острым углом в центре.

2. Определите катеты , расположенные рядом с катетами и напротив , к углу.

3. Вычислите результаты тригонометрических функций для этого угла, используя следующие формулы:

   • sin(α) = противоположность / гипотенуза ;

   • cos(α) = смежная / гипотенуза ; и

   • tan(α) = напротив / рядом .

4. Поверните и переверните треугольник , чтобы найти значения синуса, косинуса и тангенса для другого острого угла, выполнив те же действия.

Как вычислить синус прямоугольного треугольника?

Чтобы вычислить синус прямоугольного треугольника, выполните следующие действия:

1. Определите угол α в анализе.

2. Присвоить метку напротив катета , не касаясь угла .

3. Назначьте метку рядом с катету , касающемуся угла .

4. Вычислите синус с отношением противолежащего катета к гипотенузе:
   sin(α) = противоположный/гипотенуза .

5. Чтобы вычислить синус другого острого угла ß , повторите шаги 2-4 или обратите внимание, что в этом случае sin(ß) = cos(α) благодаря свойству sin(90° - α) = cos(α) .

Как вычислить тангенс, зная синус и косинус?

Чтобы вычислить тангенс, если вы знаете синус и косинус, просто вычислите отношение между этими двумя величинами :

tan(α) = sin(α)/cos(α) к нулю в некоторых случаях (но никогда одновременно), функция имеет особенностей, где она не определена: мы находим их при каждом аргументе вида 90° + k × π , где k — целое число.

Видео-вопрос: Использование единичного круга для выражения значений синуса, косинуса и тангенса для 2𝜋 − 𝑥 через их значения для 𝑥, где 𝑥 — любое действительное число

На рисунке точки 𝑀(cos 𝜃, sin 𝜃) и 𝑁 лежат на единичной окружности, и ∠𝐴𝑂𝑁 = 2𝜋 − 𝜃. Выразите значения синуса, косинуса и тангенса 2𝜋 − 𝜃 через их значения для 𝜃. Проверьте, верно ли это для всех значений 𝜃.

Стенограмма видео

На рисунке точки 𝑀 cos 𝜃, sin 𝜃 и 𝑁 лежат на единичной окружности, а угол 𝐴𝑂𝑁 равен двум 𝜋 минус 𝜃. Выразите значения sin, cos и тангенс двух 𝜋 минус 𝜃 с точки зрения их значений для 𝜃. Проверьте, верно ли это для всех значения 𝜃.

В вопросе нам говорят, что точка 𝑀 имеет координаты cos 𝜃, sin 𝜃. И из схемы мы видим, что угол 𝐴𝑂𝑀 равен 𝜃. Мы знаем, что это справедливо для любого точка, лежащая на единичной окружности, где 𝜃 измеряется против часовой стрелки направление от положительной оси 𝑥. Так как угол рефлекса 𝐴𝑂𝑁 равен равно двум 𝜋 минус 𝜃, точка 𝑁 имеет координаты cos два 𝜋 минус 𝜃, sin два 𝜋 минус 𝜃. Используя тот факт, что существует два 𝜋 радианы в полном круге и мы измеряем отрицательные углы по часовой стрелке от положительной оси 𝑥, то координаты точки 𝑁 также можно записать в виде cos отрицательный 𝜃, отрицательный sin 𝜃.

От симметрии агрегата круг, точки 𝑀 и 𝑁 будут иметь одну и ту же 𝑥-координату. Это означает, что cos отрицательного 𝜃 равно cos 𝜃. Это на самом деле стандартный результат что мы можем процитировать продвижение вперед. Поскольку функция косинуса четная, cos отрицательного 𝜃 равен cos 𝜃. А так как кос два 𝜋 минус 𝜃 равно cos отрицательного 𝜃, оно также должно быть равно cos 𝜃.

𝑥-координата точки 𝑁 на единичный круг также можно записать как cos 𝜃. При работе с 𝑦-координаты точек 𝑀 и 𝑁, мы видим, что 𝑀 находится на одинаковом расстоянии над 𝑥-ось, так как точка 𝑁 находится ниже 𝑥-оси.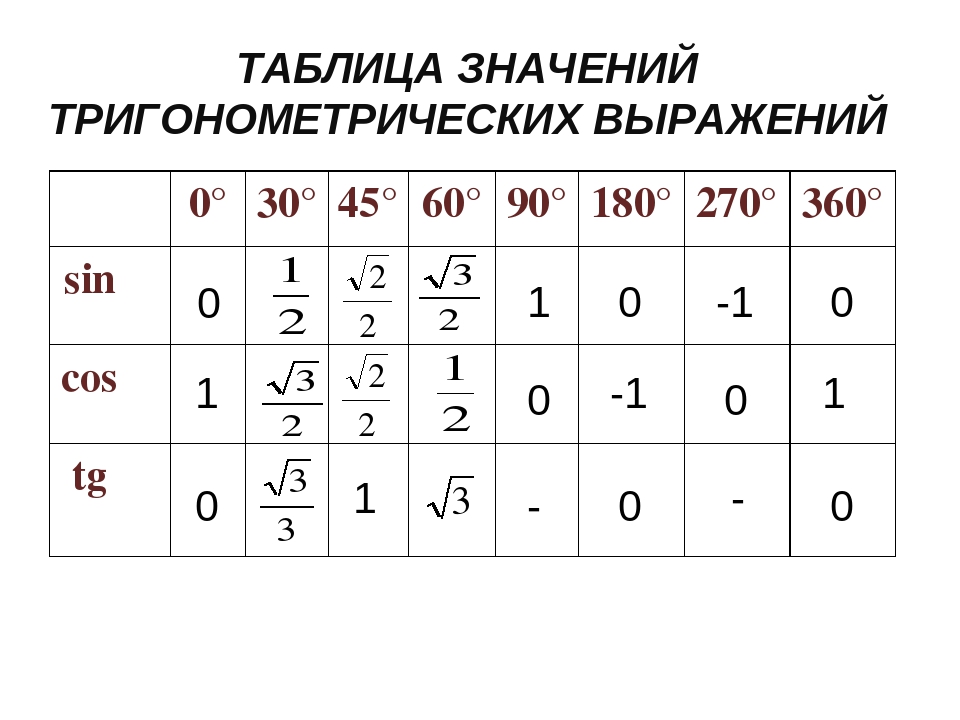 Это означает, что грех отрицательного 𝜃 равно отрицательному греху 𝜃. Так же, как результат для потому что отрицательный 𝜃, этот результат верен для всех значений 𝜃, так как синус является нечетным функция. Грех отрицательного 𝜃 всегда равно отрицательному греху 𝜃. Это означает, что поскольку грех двух 𝜋 минус 𝜃 равен греху отрицательного 𝜃, он также равен отрицательному греху 𝜃. 𝑦-координата точки 𝑁 может быть записано как отрицательный грех 𝜃.

Теперь мы выразили значения sin и cos двух 𝜋 минус 𝜃 с точки зрения их значений для 𝜃. грех двух 𝜋 минус 𝜃 равно отрицательный грех 𝜃 и потому что два 𝜋 минус 𝜃 равно cos 𝜃. Теперь мы можем найти выражение для тангенс двух 𝜋 минус 𝜃, используя одно из наших тригонометрических тождеств. Мы знаем, что загар под любым углом 𝛼 равно sin 𝛼, деленному на cos 𝛼. Если разделить первое уравнение на во-вторых, у нас есть грех двух 𝜋 минус 𝜃 над потому что два 𝜋 минус 𝜃 равен к отрицательному греху 𝜃 над потому что 𝜃. Используя приведенное ниже тождество, левая часть упрощается до тангенса двух 𝜋 минус 𝜃, а правая — до негативный загар 𝜃.

Теперь у нас есть три выражения требуется, значения sin, cos и тангенса двух 𝜋 минус 𝜃 с точки зрения их значения для 𝜃. Нас также просят проверить, это справедливо для всех значений 𝜃. Если мы позволим точке 𝑃 лежать в первом квадрант, как показано на схеме, где угол 𝐴𝑂𝑃 равен некоторому другому значение 𝜃, то точка 𝑄, где угол против часовой стрелки 𝐴𝑂𝑄 равен два 𝜋 минус 𝜃, будут лежать в четвертом квадранте, как показано.

И снова эти точки будут одна и та же 𝑥-координата, тогда как 𝑦-координаты будут аддитивными, обратными друг друга. Если точка 𝑃 имеет координаты 𝑥, 𝑦, то точка 𝑄 будет иметь координаты 𝑥, минус 𝑦. И поэтому мы можем сделать вывод, что выражения для sin, cos и tan двух 𝜋 минус 𝜃 с точки зрения их значения 𝜃 верны для всех значений 𝜃 в единичном круге.