Трапеция, Средняя линия трапеции, треугольник
Четырёхугольник, у которого только две стороны параллельны называются трапецией.
Параллельные стороны трапеции называются её основаниями, а те стороны, которые не параллельны, называются боковыми сторонами. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC =>
MN || AB
MN = AB/2
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA1 = A1A2 = A 2A3 = A3A4 = A4A5
Мы соединяем A5 с B и проводим такие прямые через A4, A3, A2 и A1, которые параллельны A5B. Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB3A3A5 мы видим, что BB4 = B4B3. Таким же образом, из трапеции B4B2A2A4 получаем B4B3 = B3B2
Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB3A3A5 мы видим, что BB4 = B4B3. Таким же образом, из трапеции B4B2A2A4 получаем B4B3 = B3B2
В то время как из трапеции B3B1A1A3, B3B2 = B2B1.
Тогда из B2AA2 следует, что B2B1 = B1A. В заключении получаем :
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
Средняя линия трапеции ABCD: определение, свойства, признак, длина
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое средняя линия трапеции
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
- Определение средней линии трапеции
- Свойства средней линии трапеции
- Свойство 1
- Свойство 2
- Свойство 3
- Признак средней линии трапеции
- Вторая средняя линия
- Пример задачи
Определение средней линии трапеции
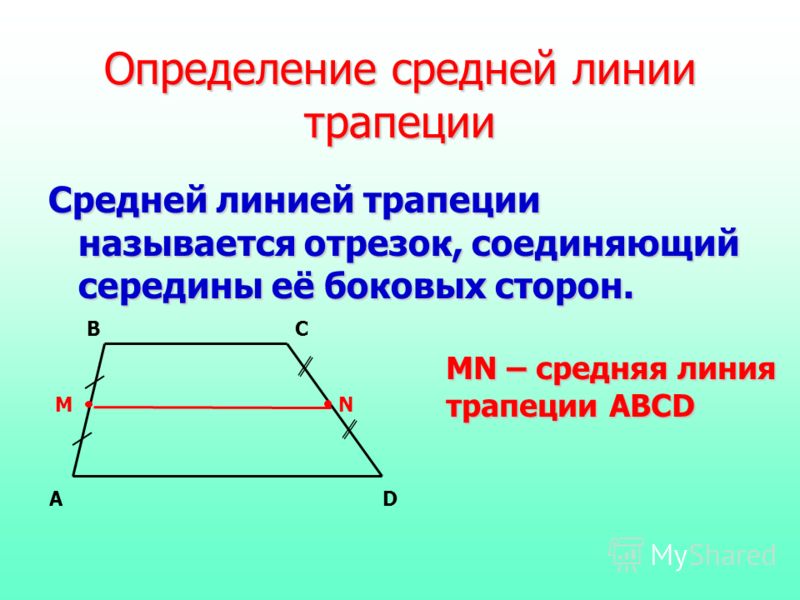
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.
- LM – средняя линия трапеции ABCD
- L – середина стороны AB, т.е. AL = LB
- M – середина стороны CD, т.
 е. CM = MD
е. CM = MD
Свойства средней линии трапеции
Свойство 1
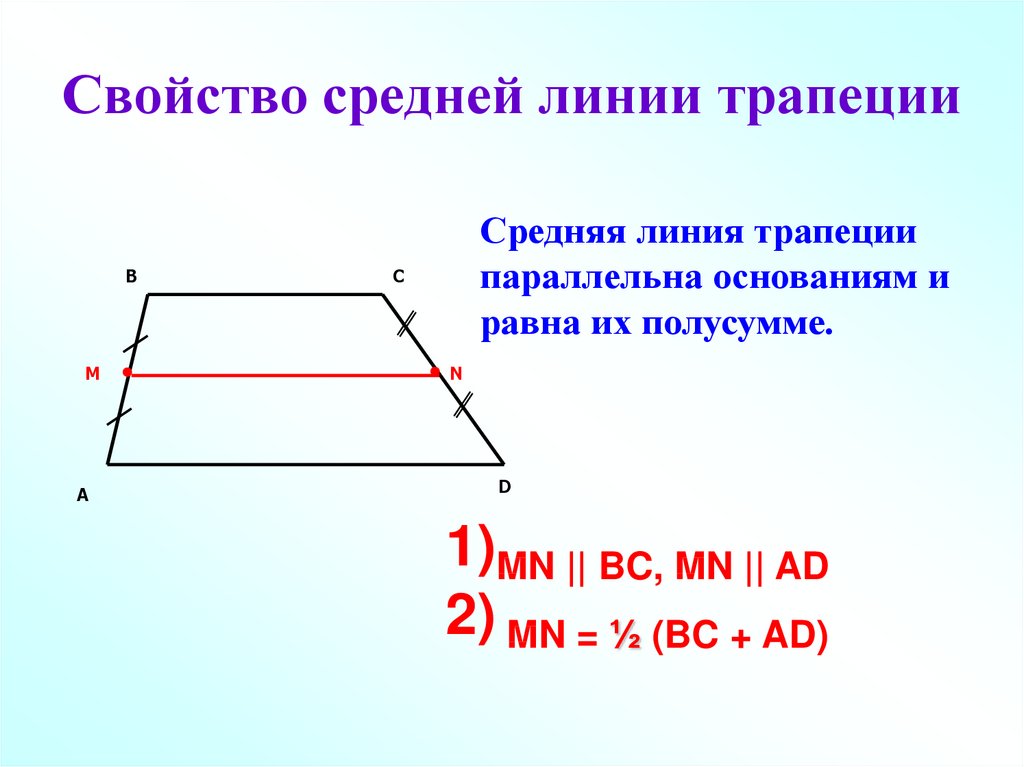
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Для рисунка выше:
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.
Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.
Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Решение
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b)/2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b)/2.
Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Трапеция, средняя линия и средний сегмент трапеции и треугольника
Четырехугольник с двумя противоположными параллельными сторонами называется трапецией (трапецией) .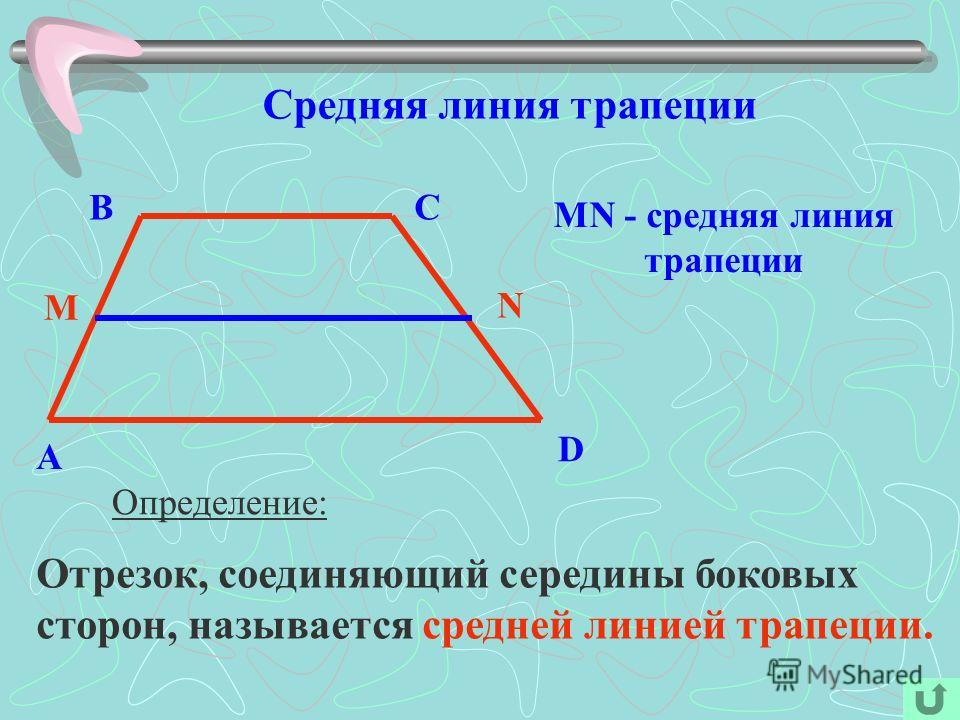
Параллельные стороны трапеции называются основаниями (AB и CD), а те, которые не параллельны, называются катетами (AD и BC).
Если катеты равны по длине, трапеция называется равнобедренной .
DE и CF — это высоты .
Средняя линия трапеции
Линия, соединяющая середины непараллельных сторон, называется средней линией (или средней линией) трапеции.
Линия MN является средней линией ABCD. А отрезок MN является средним отрезком ABCD.
AM = MD
BN = НЗ
Средняя линия трапеции параллельна ее сторонам.
В нашем случае — MN || АБ || ОКРУГ КОЛУМБИЯ.
Теорема 1:
Если прямая, проходящая через середину катета трапеции, параллельна ее основаниям, затем линия проходит через середину другой ноги.
Теорема 2:
Средний сегмент трапеции равен половине длин двух параллельных сторон.
Другими словами:
$\overline{MN} = \frac{\overline{AB} + \overline{DC}}{2}$
Середина треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется серединой треугольника.
Он параллелен третьей стороне и его длина вдвое меньше третьей стороны.
Теорема : Если отрезок пересекает середину одной стороны треугольника и параллелен другой стороне того же треугольника, то этот отрезок делит третью сторону пополам.
$\overline{AM} = \overline{MC}$ и $\overline{BN} = \overline{NC}$ =>
$ млн || AB$
$\overline{MN} = \frac{\overline{AB}}{2}$
Применение свойств средних сегментов
Разделите отрезок на равные отрезки, не измеряя.
Задание: Разделить заданный отрезок $\overline{AB}$ на 5 равных отрезков без измерения.
Решение:
Пусть p — произвольный луч с началом A, не лежащий на AB.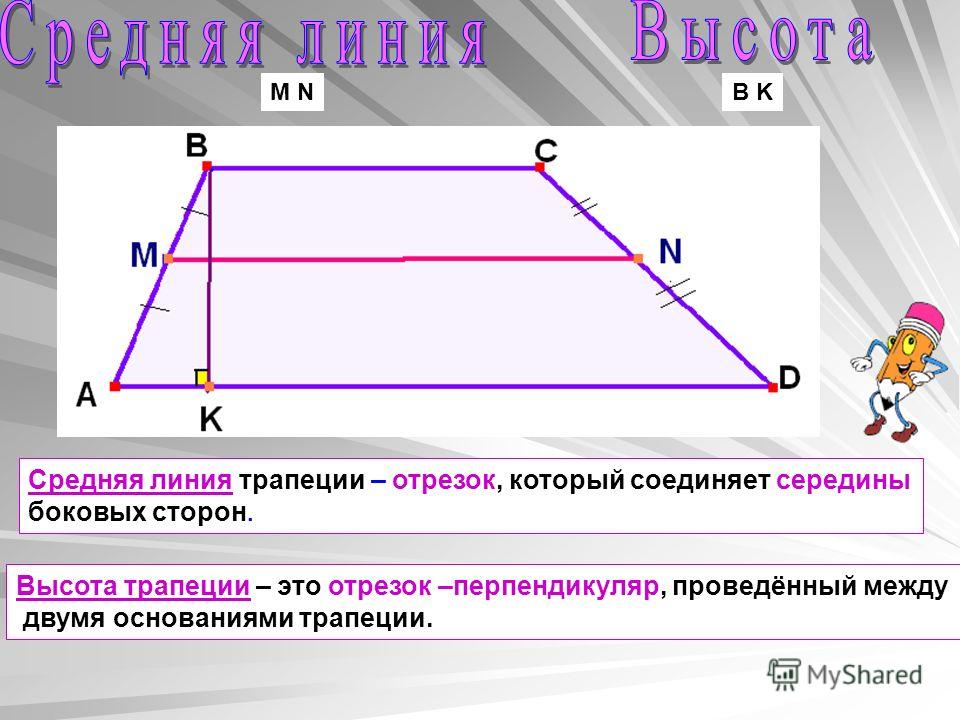 Проводим последовательно пять равных отрезков на с.
Проводим последовательно пять равных отрезков на с.
$\overline{AA_1} = \overline{A_1A_2} = \overline{A_2A_3} = \overline{A_3A_4} = \overline{A_4A_5}$
Соединяем A 5 с B и проводим линии через A 4
Они пересекают АВ в точках B 4 , B 3 , B 2 и B 1 соответственно. Эти точки делят отрезок $\overline{AB}$ на пять равных отрезков.
Действительно, из трапеции BB 3 A 3 A 5 мы видим, что $\overline{BB_4} = \overline{B_4B_3}$. Таким же образом из трапеции В 4 В 2 А 2 А 4 , получаем $\overline{B_4B_3} = \overline{B_3B_2}$
А из трапеции B 3 B 1 A 1 A 3 ,
$\overline{B_3B_2} = \overline{B_2B_1}$.
Тогда из B 2 AA 2 следует, что $\overline{B_2B_1} = \overline{B_1A}$.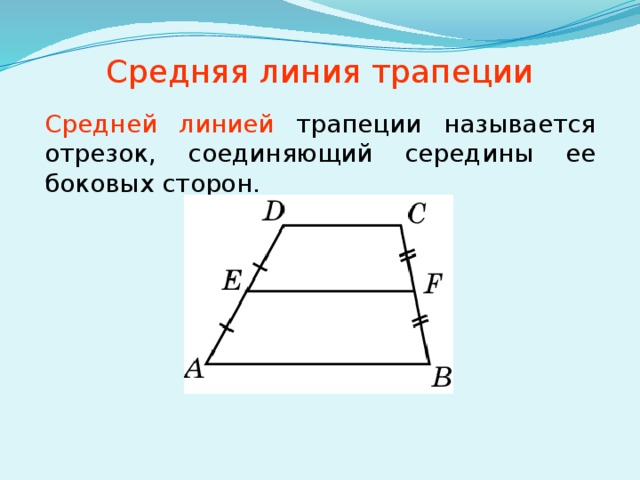 В итоге получаем:
В итоге получаем:
$\overline{AB_1} = \overline{B_1B_2} = \overline{B_2B_3} = \overline{B_3B_4} = \overline{B_4B}$
Ясно, что если AB нужно разделить на другое количество равных отрезков, мы должны спроецировать такое же количество равных отрезков на p. Дальше поступаем так же.
Определение медианы трапеции (средняя линия, средний сегмент)
Определение медианы трапеции (средняя линия, средний сегмент) — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Отрезок между серединами катетов трапеции
Также известен как средняя линия или средний сегмент
Попробуйте это Перетащите оранжевые точки на каждой вершине изменить форму трапеции. Обратите внимание на поведение красной срединной линии.
Недвижимость
Срединная линия всегда параллельна основаниям. Отрегулируйте трапецию выше, перетащив любую вершину, и убедитесь, что это так.
Длина медианы равна средней длине оснований, или по формуле:
Если одно из оснований имеет нулевую длину, результатом будет треугольник.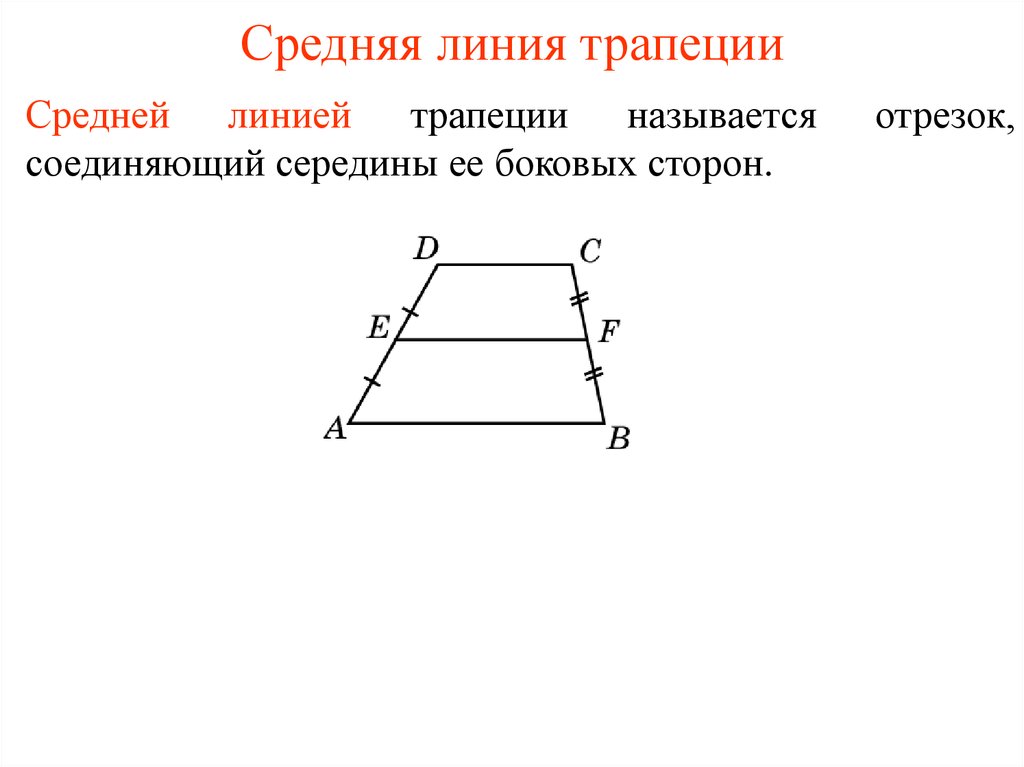

 е. CM = MD
е. CM = MD