Коэффициент корреляции рассчитать онлайн: Онлайн калькулятор: Коэффициент корреляции Пирсона

Онлайн калькулятор: Коэффициент корреляции Пирсона

РаботаСтатистика

Расчет коэффициента корреляции двух случайных величин.

Приведем парочку определений, если кто вдруг подзабыл.

Практически все определения можно найти в википедии.

Корреляция в математической статистике — это вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия.

Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.

Если значение по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 — связь слабая или вообще отсутствует. При коэффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть, изменения двух величин можно описать математической функцией.

Наиболее широко известен коэффициент корреляции Пирсона (Карл Пирсон (Pearson), английский математик, 1857-1936), характеризующий степень линейной зависимости между переменными. Он определяется, как

где буква M обозначает математическое ожидание.

Собственно, тут больше и говорить нечего — вводим случайные величины в таблицу (значения по умолчанию можно удалить), калькулятор рассчитывает коэффициент корреляции по формуле Пирсона

Коэффициент корреляции Пирсона

Изменения случайных величин

	X	Y

Записей:

51020501001000

Изменения случайных величин

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;-50.5

Загрузить данные из csv файла

Точность вычисления

Знаков после запятой: 4

Коэффициент корреляции Пирсона

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Коэффициент корреляции Спирмена
• • Коэффициент Танимото
• • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
• • Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли.
• • Таблица независимых испытаний по формуле Бернулли
• • Раздел: Статистика ( 31 калькуляторов )

 корреляция коэффициент корреляции Пирсона Статистика теория вероятности

 PLANETCALC, Коэффициент корреляции Пирсона

Timur2020-11-03 14:19:27

‘; return ret; } }

Функция КОРРЕЛ

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

Функция КОРРЕЛ возвращает коэффициент корреляции двух диапазонов ячеев. Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера.

Синтаксис

КОРРЕЛ(массив1;массив2)

Аргументы функции КОРРЕЛ описаны ниже.

Замечания

• Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако ячейки с нулевыми значениями включаются.

• Если массив1 и массив2 имеют различное количество точек данных, то correl возвращает #N/A.

• org/ListItem»>

  Если массив1 или массив2 пуст или если

  s (стандартное отклонение) их значений равно нулю, то corREL возвращает значение #DIV/0! ошибку «#ВЫЧИС!».

• Так как коэффициент корреляции ближе к +1 или -1, он указывает на положительную (+1) или отрицательную (-1) корреляцию между массивами. Положительная корреляция означает, что при увеличении значений в одном массиве значения в другом массиве также увеличиваются. Коэффициент корреляции, который ближе к 0, указывает на отсутствие или неабную корреляцию.

• Уравнение для коэффициента корреляции имеет следующий вид:

  где 

  являются средними значениями выборок СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Пример

В следующем примере возвращается коэффициент корреляции двух наборов данных в столбцах A и B.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Калькулятор коэффициента корреляции — MathCracker.com

Решатели Статистика

---

Инструкции: Вы можете использовать этот пошаговый калькулятор коэффициента корреляции для двух переменных X и Y. Все, что вам нужно сделать, это ввести данные X и Y в формате, разделенном запятыми или пробелами (например: «2, 3, 4, 5″, или «3 4 5 6 7»).

X данные (через запятую)

Данные Y (через запятую)

Имя переменной X (необязательно)

Имя переменной Y (необязательно)

---

Вычисленный выше коэффициент корреляции соответствует коэффициенту корреляции Пирсона. Требования для его вычисления заключаются в том, что две переменные X и Y измеряются по крайней мере на уровне интервала (что означает, что он не работает с номинальными или порядковыми переменными). 92}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]

Если у вас есть две или более переменных, вы можете использовать наш калькулятор корреляционной матрицы . Кроме того, если данные для переменных \(X\) и \(Y\) не соответствуют параметрическим предположениям для корреляции Пирсона, вам следует использовать это Калькулятор корреляции Спирмена вместо.

Могу ли я использовать z-показатели для вычисления коэффициента корреляции

Безусловно! Вы видели z-показатели повсюду в статистике и, естественно, задаетесь вопросом, можете ли вы вычислить корреляцию с z-значениями . Вы определенно можете это сделать, и на самом деле это обычный способ сделать это в статистике социальных наук.

Другие калькуляторы, похожие на этот калькулятор корреляции

Кроме того, существует понятие множественный коэффициент корреляции , когда у вас есть более одного предиктора, который получается путем вычисления корреляции между наблюдаемыми значениями \(Y\) и прогнозируемыми значениями \(\hat Y\) с помощью регрессии.

---

Базовый пакет статистики Калькулятор коэффициента корреляции Коэффициент корреляции Коэффициент корреляции Пирсона Решатель статистики

Коэффициент корреляции (ρ) Калькулятор

GENERATE WORK

сообщите об этом объявлении

GENERATE WORK

Коэффициент корреляции (ρ) — работа со ступенями случайные выборки $X$ и $Y$ или два набора популяционных данных.

Для этого онлайн-инструмента статистики и вероятности требуются две случайные выборки $X$ и $Y$ или два набора данных о населении. Другими словами, он измеряет, насколько сильно и в каком направлении линейная связь между двумя наборами данных.
Необходимо выполнить следующие шаги:

1. Ввести в поле две выборки $X$ и $Y$ (наблюдаемые значения). Эти значения должны быть действительными числами или переменными и могут быть разделены запятыми. Значения можно скопировать из текстового документа или электронной таблицы.
2. Нажмите кнопку «СОЗДАТЬ РАБОТУ» , чтобы выполнить расчет.
3. Калькулятор коэффициента корреляции даст линейную корреляцию между наборами данных.

Ввод: Два списка действительных чисел, разделенных запятой
Результат: Действительное число

Калькулятор коэффициента корреляции дает нам пошаговую процедуру и понимание каждого шага расчета. Прежде чем будет получен окончательный результат коэффициента корреляции, он вычисляет выборочное среднее и стандартное отклонение двух наборов данных. Эти значения выборочного среднего и стандартных отклонений могут быть полезны для дальнейшего решения задач и приложений.

Формула коэффициента корреляции:
9N\frac{(x_i-\mu_X)(y_i-\mu_Y)}{\sigma_X\sigma_Y}\end{align}$$

, где $\sigma_x$ и $\sigma_y$ – стандартные отклонения генеральной совокупности, а $\ mu_x$ и $\mu_y$ — средние значения населения.

Что такое коэффициент корреляции?

Рассмотрим две переменные,

$$X=(x_1,\ldots,x_n)\quad \mbox{and}\quad Y=(y_1,\ldots, y_n)$$

Если большие значения $ X$ связаны с высокими значениями $Y$, то существует положительная корреляция. Если высокие значения $X$ связаны с низкими значениями $Y$, то существует отрицательная корреляция. Об этих корреляциях можно судить по графикам рассеяния. Точечная диаграмма — это график, который использует декартовы координаты для отображения значений двух переменных набора данных.

Коэффициент корреляции

, обычно обозначаемый $r_{XY}$, измеряет, насколько набор точек данных близок к линейности. Другими словами, он измеряет степень зависимости или линейной корреляции (статистической связи) между двумя случайными выборками или двумя наборами данных о населении. Коэффициент корреляции использует значения от $-1$ до $1$.
Например, на первом рисунке $r_{XY}=1$, а точки данных находятся на линии с положительным наклоном. На втором рисунке $r_{XY}=-1,$ и точки данных находятся на линии с отрицательным наклоном.

Есть некоторая корреляция:

• Если $|r_{XY}|=1$, то существует совершенная корреляция между $X$ и $Y$;
• Если $r_{XY}=0$, корреляции между $X$ и $Y$ нет.

Корреляция с большим абсолютным значением имеет более сильную линейную корреляцию между наборами данных $X$ и $Y$.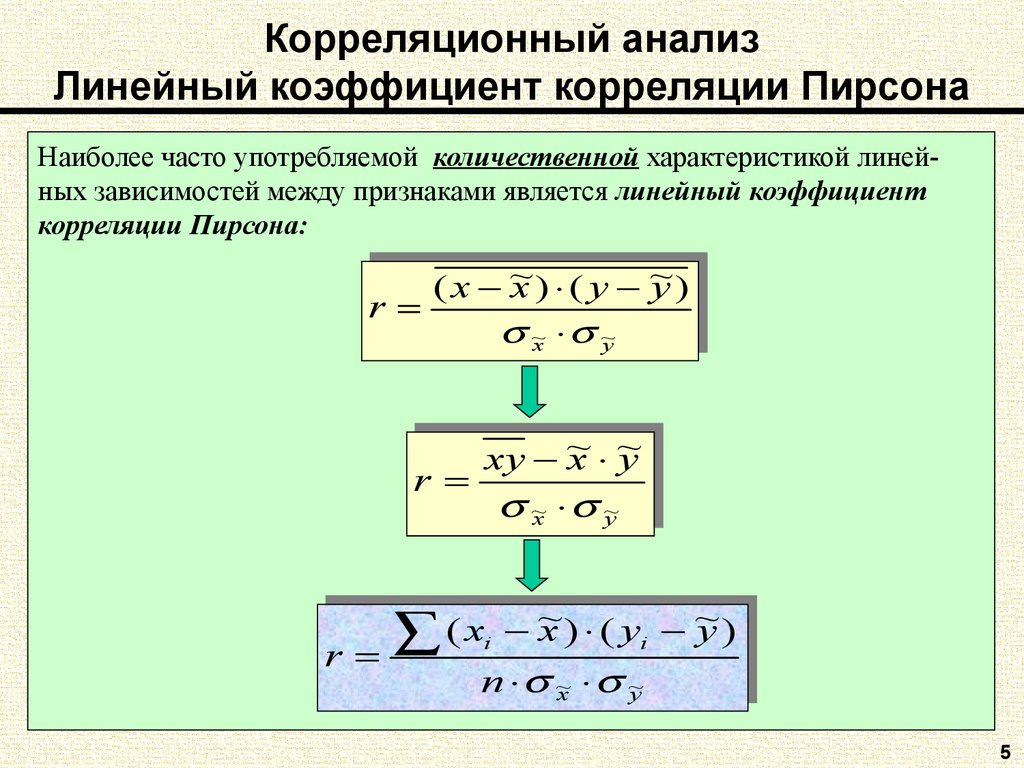 Корреляция с меньшим абсолютным значением имеет более слабую линейную корреляцию между наборами данных $X$ и $Y$. Если значения корреляций равны, то они имеют одинаковую силу. 9N\frac{(x_i-\mu_X)(y_i-\mu_Y)}{\sigma_X\sigma_Y}\end{align}$$

, где $\sigma_x$ и $\sigma_y$ – стандартные отклонения генеральной совокупности, а $\ mu_x$ и $\mu_y$ — средние значения населения.
Чтобы найти выборочный коэффициент корреляции, необходимо выполнить следующие шаги:

1. Найти выборочное среднее $\bar{X}$ для набора данных $X$;
2. Найти выборочное среднее $\bar{Y}$ для набора данных $Y$;
3. Найти стандартное отклонение выборки $s_X$ для набора выборочных данных $X$;
4. Найдите стандартное отклонение выборки $s_Y$ для набора данных $Y$;
5. Подставьте значения в формулу для коэффициента корреляции, чтобы получить результат.

Во многих случаях мы можем рассчитать коэффициент корреляции вручную, особенно для небольших вычислений. Но, если у нас большой набор данных для расчета или мы хотим получить точный результат, то стоит воспользоваться калькулятором коэффициента корреляции.
В работе с шагами показан полный пошаговый расчет того, как найти коэффициент корреляции двух выборок $X: 1,2,4,5,8$ и $Y: 5,20,40,80,100$ с помощью табличного метода. Для любых других образцов просто укажите два списка чисел и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор для создания работы, проверки результатов, полученных вручную, или эффективного решения домашних заданий.

Практические задачи для коэффициента корреляции

Коэффициент корреляции полезен в финансах. Например, при определении того, насколько хорошо взаимный фонд работает по сравнению с его эталонным индексом или другим фондом. Практические задачи коэффициента корреляции предоставляются с использованием данных статистического моделирования, а также реальных данных.

Практическая задача 1: Найдите коэффициент корреляции данных в таблице, которая показывает связь между температурой и слабостью, ощущаемой в различных конечностях. 9o$ $5$

Практическая задача 2 : Найдите коэффициент корреляции между количеством взятых напрокат книг по геометрии и статистике на пятой неделе с понедельника по пятницу.

	Number of extremities	Statistics
Monday	134	231
Tuesday	156	127
Wednesday	234	276
Thursday	214	265
Friday	301	124

The correlation coefficient calculator, formula, work with steps (tabular method) and practice problems would be очень полезно для учащихся начальных классов образования K-12, чтобы узнать, что такое коэффициент корреляции набора данных в статистике и вероятности, как его найти.