Угол. Прямой и развернутый угол. Чертежный треугольник 5 класс онлайн-подготовка на Ростелеком Лицей
Введение
Данная тема рассматривалась ранее.
Повторить эту тему можно, перейдя по ссылке
Полный, развернутый, прямой угол
1. Полный угол (см. Рис. 1)
Рис. 1. Полный угол
Стороны угла совпадают.
Меньший угол не виден. Он называется нулевым углом.
Зато второй угол, больший, захватил плоскость полностью. Такой угол называется полным. Вот он имеет для нас важное значение. Поделив его пополам, а потом еще раз пополам, мы получим еще два типа важных углов.
2. Развернутый угол (см. Рис. 2.)
Рис. 2. Развернутый угол
Если стороны угла будут смотреть в разные стороны, составляя прямую, то два полученных угла будут равны друг другу. При этом вместе они составляют полный угол.
То есть угол, образованный такими лучами, является половиной полного угла.
Сам угол похож на то, как если бы ножки циркуля развернули в разные стороны. Угол так и назвали – развернутым.
Угол так и назвали – развернутым.
3. Прямой угол
Поделим уже развернутый угол пополам. Получим два равных угла (см. Рис. 3).
Рис. 3. Прямой угол
Если столб стоит на земле прямо, то мы видим, что углы с двух сторон равны друг другу. Угол так и называется – прямой. Для него вместо дуги договорились использовать специальную отметку, маленький уголок.
Способы черчения углов
1. Чтобы начертить полный угол, нужно из точки провести луч, подразумевая, что это два совпадающих луча.
2. Чтобы начертить развернутый угол, нужно провести прямую и поставить на ней точку. Получим два луча, идущих в разные стороны, то есть развернутый угол.
3. Чтобы начертить прямой угол, легче всего воспользоваться готовым деревянным или металлическим прямым углом, который называется чертежным треугольником, или угольником (см. Рис. 4).
Рис. 4. Чертежный треугольник
Перпендикулярные прямые
Часто уже есть прямая и точка на ней и нужно провести через эту точку вторую прямую под прямым углом к первой.
Совместим угольник одной стороной с имеющейся прямой так, чтобы его вершина совместилась с точкой на прямой. Теперь проведем вторую прямую. Она расположена под прямым углом к первой прямой. Такие прямые называют перпендикулярными (см. Рис. 5).
Рис. 5. Перпендикулярные прямые и угольник
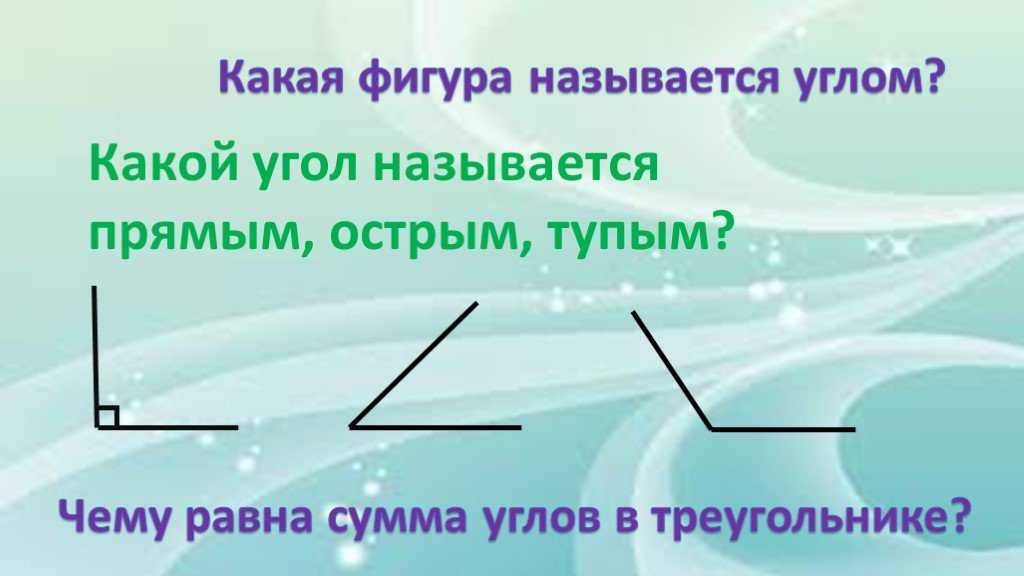
Прямой, острый, тупой угол
Дан развернутый угол (см. Рис. 6).
Рис. 6. Развернутый угол AOB
Поделим его пополам.
Угол – прямой (см. Рис. 7).
Рис. 7. Прямой угол
Угол меньше прямого угла. Такие углы называются острыми (см. Рис. 8).
Рис. 8. Острый угол ЕОВ
Угол больше прямого угла. Такие углы называются тупыми (см. Рис. 9).
Рис. 9. Тупой угол
Итак, все это можно сформулировать короткими определениями:
1. Прямой угол – это половина развернутого угла.
2. Острый угол – это угол меньше прямого.
3. Тупой угол – это угол больше прямого и меньше развернутого.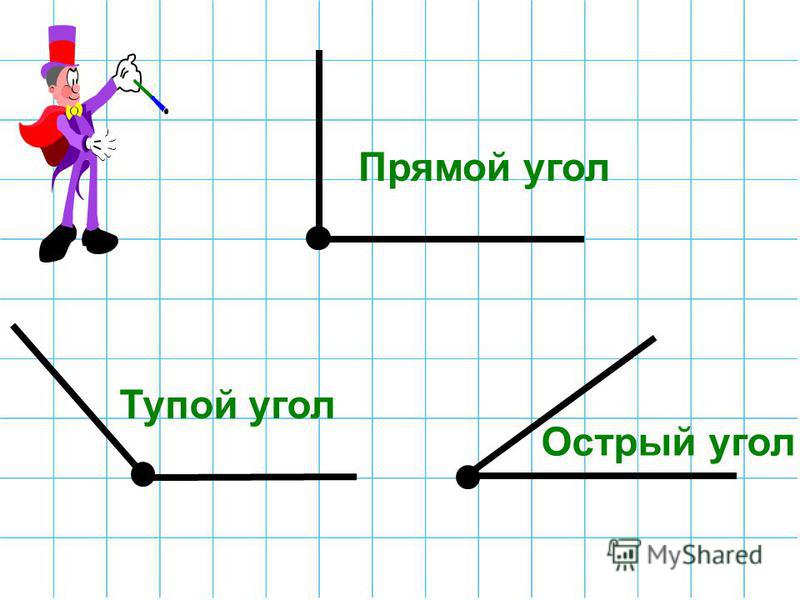
Различные способы построения прямого угла
Построение прямого угла с помощью циркуля
На листе бумаги можно построить прямой угол, даже если у вас нет угольника.
Помните, что прямой угол – это половина развернутого.
Сначала изобразим развернутый угол (см. Рис. 10).
Рис. 10. Построение прямого угла
Теперь поделим его пополам. Для этого возьмем циркуль и от вершины угла отложим в обе стороны одинаковое расстояние (см. Рис. 11).
Рис. 11. Построение прямого угла (продолжение)
Увеличим чуть-чуть расстояние между ножками циркуля и отложим две дуги с центрами в полученных точках, чтобы они пересеклись над вершиной угла (см. Рис. 12).
Рис. 12. Построение прямого угла (продолжение)
Мы получим новую точку прямо над вершиной . Соединим точки (см. Рис. 13).
Рис. 13. Построение прямого угла (продолжение)
Мы все делили симметрично, углы получились равными, а значит, прямыми.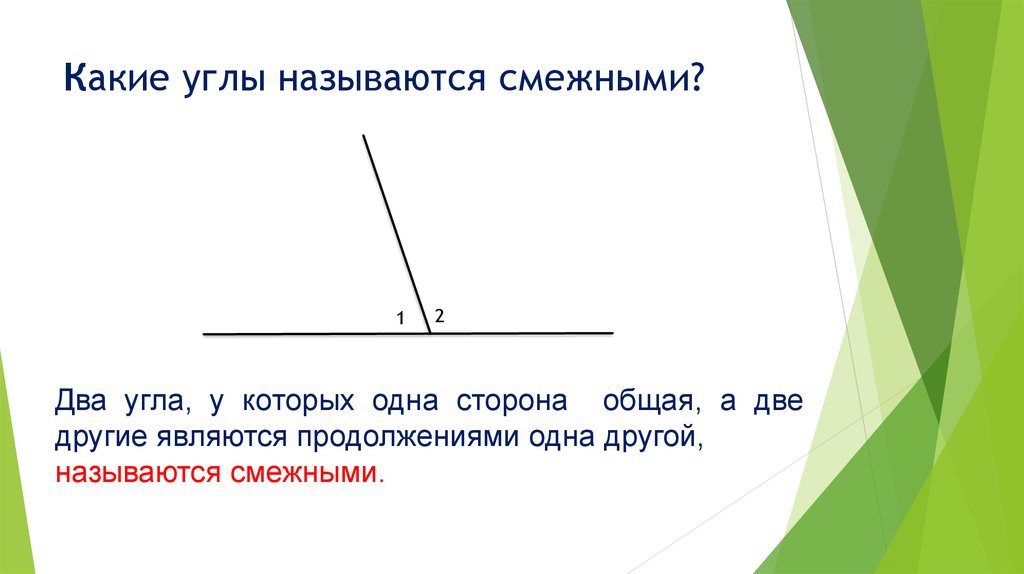
«Египетский треугольник»
Представьте теперь себе землемера в Древнем Египте. Ему нужно разделить поле на прямоугольники, а для этого нужно уметь делать прямые углы. У него нет огромного деревянного угольника. А даже если бы и был, его же тоже нужно уметь сделать.
Египтяне использовали треугольник со сторонами в соотношении 3:4:5. Один угол этого треугольника прямой. Его потом так и назвали – «египетский треугольник».
Чтобы на земле начертить такой треугольник, можно взять веревку 12 метров, отметить на ней три части – 3, 4 и 5 метров. Концы веревки соединить. В отметках привязать колышки. Натянуть за колышки все части веревки и вбить колышки в землю. Получится египетский треугольник, а значит, один прямой угол (см. Рис. 14).
Рис. 14. «Египетский треугольник»
Отвес
Если у нас ровный пол, то веревка с грузом на конце будет составлять с линией пола прямой угол. Такой инструмент используют строители. Он называется отвес (см. Рис. 15).
Он называется отвес (см. Рис. 15).
Рис. 15. Отвес
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
- Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
- Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Shkolo.ru (Источник).
- Cleverstudents.ru (Источник).
- Festival.1september.ru (Источник).
Домашнее задание
- Постройте полный, прямой и развернутый углы.
- Назовите все углы на рисунке, а также укажите их вид:
Внеклассный урок — Углы
Углы
Основные понятия.
Угол – это фигура, образованная двумя лучами, выходящими из одной точки.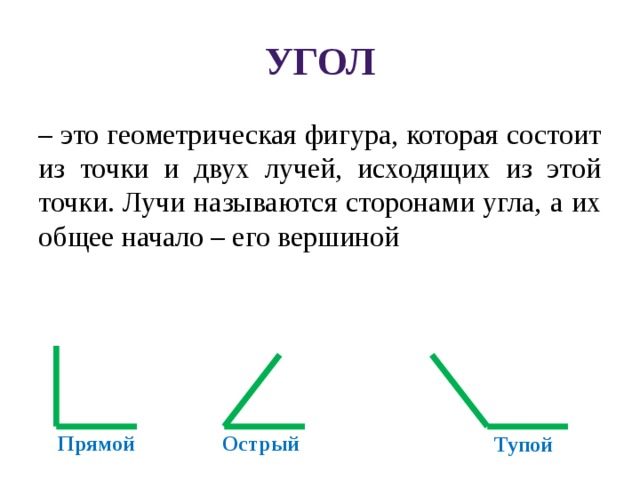
Вершина угла – это точка, из которой выходят два луча, образующих этот угол.
Биссектриса – это луч, который выходит из вершины угла и делит угол пополам.
Развернутый угол – это угол, стороны которого лежат на одной плоскости; равен 180˚ и является прямой.
Прямой угол – это угол, равный половине развернутого угла; равен 90˚.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого, но меньше развернутого.
Угол разбивает плоскость на две части. Каждая из частей называется плоским углом.
Плоские углы с общими сторонами называются дополнительными.
Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.
Если плоский угол содержит полуплоскость, то его градусная мера равна 360º – α, где α – градусная мера дополнительного плоского угла.
Равные углы.
Это углы, которые совпадают при наложении.
Смежные углы.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке углы (ad) и (cd) смежные. У них сторона d общая, а стороны a и c – дополнительные полупрямые.
Теорема:
Сумма смежных углов равна 180º.
Из теоремы следует:
— если два угла равны, то смежные с ними углы равны.
— если угол не развернутый, то его градусная мера меньше 180º.
— угол, смежный с прямым углом, есть прямой угол.
Вертикальные углы.
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Они созданы пересечением двух прямых и не являются прилегающими, имеют общую вершину и одинаковую градусную меру.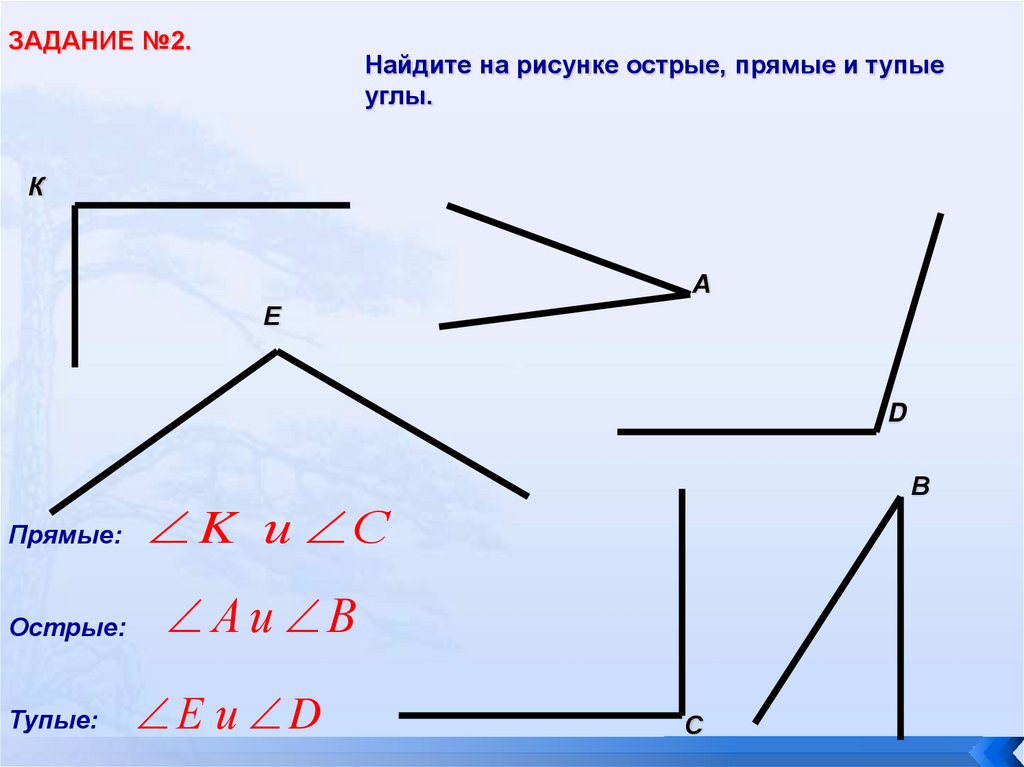
На рисунке углы (A1 B1) и (A2 B2) вертикальные. Стороны A2 и B2 второго угла являются дополнительными полупрямыми сторон A1 и B1 первого угла.
Центральный угол.
Центральным углом в окружности называется плоский угол с вершиной в ее центре (рис.1).
Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (на рис.1 дуга AB является дугой окружности).
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, вписанный в окружность.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис.2).
Свойства:
1) Вписанный угол равен половине соответствующего центрального угла (на рис. 2) Вписанный угол, опирающийся на диаметр, равен 90° (рис.4). 3) Вписанный угол, опирающийся на хорду, равную радиусу окружности, равен 30°. |
Углы при пересечении двух прямых третьей.
При пересечении прямых a и b секущей c образуется восемь углов, которые на рисунке обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Q2 Классифицируйте каждый из следующих углов как прямой прямой острый тупой или рефлекторный 1 2 3 4 5 6 …
Перейти к
- Упражнение 5.1
- Упражнение 5.
 2
2 - Упражнение 5.3
- Упражнение 5.4
- Упражнение 5.5
- Упражнение 5.6
- Упражнение 5.7
- Упражнение 5.8
- Упражнение 5.
 9
9
- Зная наши цифры
- Целые числа
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная > Решения НЦЭРТ Класс 6 Математика >
 Понимание элементарных форм
>
Упражнение 5.3
>
Вопрос 2
Понимание элементарных форм
>
Упражнение 5.3
>
Вопрос 2Вопрос 2 Упражнение 5.3
Q2) Классифицируйте каждый из следующих углов как прямой, прямой, острый, тупой или загнутый:
Ответ:
РЕШЕНИЕ:
Острый угол
тупой угол
прямой угол
угол рефлекса
прямой угол
острый угол
Связанные вопросы
Q1) 1. Сопоставьте следующее: (i) Прямой угол (a) Меньше одной четверти оборота (ii) Ri…
(i) Прямой угол ——- (a) Менее одной четверти оборота (ii) Прямой угол ——— (b) Больше…
Классифицируйте каждый из следующих углов как прямой, прямой, острый, тупой или рефлекторный:
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 5.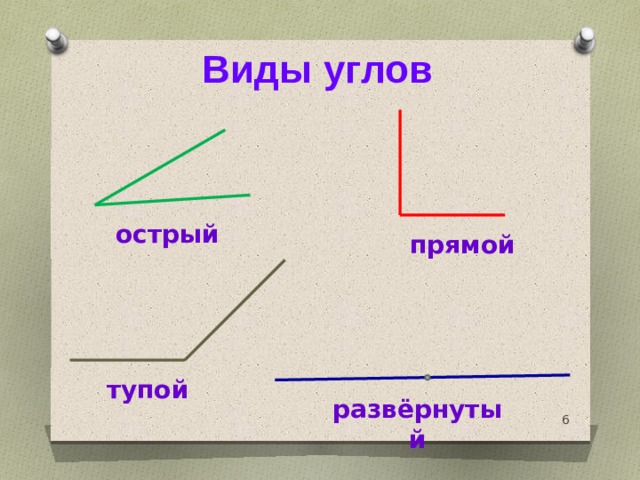 1
1
Упражнение 5.2
Упражнение 5.3
Упражнение 5.4
Упражнение 5.5
Упражнение 5.6
Упражнение 5.7
Упражнение 5.8
ГЛАВА
НАЙДЕНИ Цифры
Игра с цифрами
Основные геометрические идеи
Понимание элементарных форм
Целые числа
Фракции
Десятиц
Обработка данных
MENSURATION
Алгебра
Соотношение и доля
Симметрия
Практика
.
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
видов углов | Свойства острых, прямых, прямых, тупых и рефлекторных углов
Все типы углов, свойства острых, прямых, прямых, тупых и рефлекторных углов, различные типы углов, типы угловой диаграммы привязки и типы углов Видео.
РЕЗЮМЕ
Угол
Угол образуется при пересечении двух прямых или отрезков прямых. В нашей повседневной жизни мы видим различные типы Углов, образованных между краями плоских поверхностей. Мы видим разные Типы углов , такие как острый угол, прямой угол, тупой угол, прямой угол, угол отражения и угол полного вращения.
В нашей повседневной жизни мы видим различные типы Углов, образованных между краями плоских поверхностей. Мы видим разные Типы углов , такие как острый угол, прямой угол, тупой угол, прямой угол, угол отражения и угол полного вращения.
Типы угловых привязок Диаграмма
Типы углов | Острые, прямые, прямые, тупые и рефлекторные углыТакже проверьте: — 1–30 Cube Value [PDF Download]
Типы углов Диаграмма PDF
Типы углов
- Острый угол 0 Прямой угол 6 09056
- Прямоугольный
- Тупоугольный
- Угол отражения
- Угол полного вращения
Различные типы углов
Мы обсудим типы углов и их свойства: —
Острый угол
Угол, который больше 0° и меньше 90° называется острым Угол. Примеры острых углов: 10°, 60°, 70° и 55°. Вы можете наблюдать следующий острый угол ∠ABC.
Прямой угол
Угол, равный ровно 180°, называется прямым углом.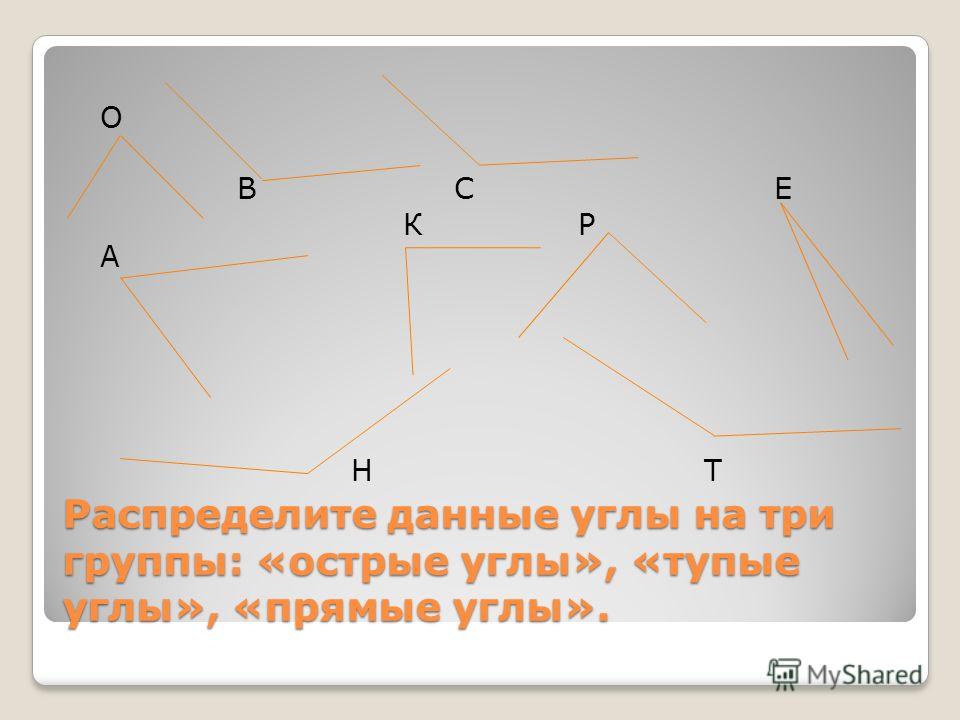 Обратите внимание на следующий рисунок, который представляет собой прямой угол.
Обратите внимание на следующий рисунок, который представляет собой прямой угол.
Прямой угол
Угол, равный ровно 90°, называется прямым углом.
Тупой угол
Угол, который больше 90° и меньше 180°, называется тупым углом. Примеры тупых углов: 95°, 100°, 120° и 140°. Вы можете наблюдать следующее изображение.
Угол рефлекса
Угол больше 180° и меньше 360° называется углом рефлекса. Примеры углов рефлекса: 190°, 220°, 240° и 250°. Вы можете наблюдать следующее изображение.
Полный угол поворота
Угол, равный точно 360°, называется полным углом поворота.
SUMMARY
| Types of Angles | Measurement of Angle |
|---|---|
| Acute Angle | More than 0°, Less than 90° |
| Straight Angle | 180° |
| Right Угол | 90° |
| Тупой угол | Более 90°, Меньше 180° |
| Рефлекторный угол | Более 180 °, меньше 360 ° |
| Угол вращения | 360 ° |

 3 вписанный угол ABC равен половине соответствующего ему центрального угла AOC).
3 вписанный угол ABC равен половине соответствующего ему центрального угла AOC).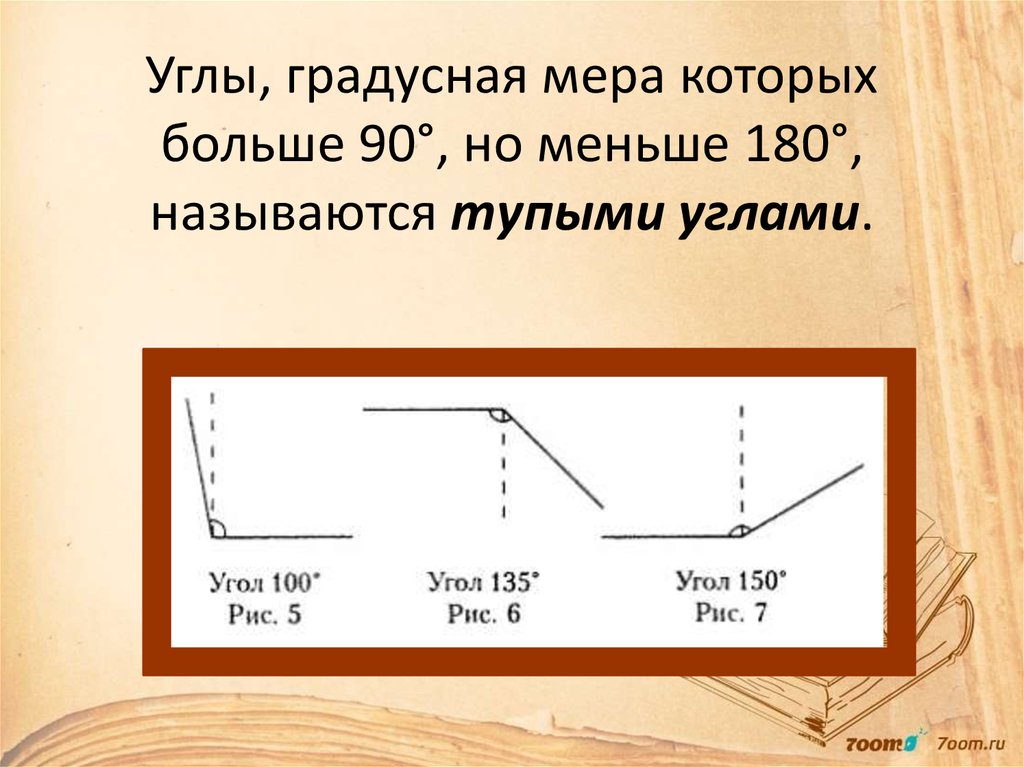 2
2 9
9