Калькулятор арифметической прогрессии: Онлайн калькулятор: Арифметическая прогрессия

Содержание

Арифметическая прогрессия калькулятор

Вычислить:

Член арифметической прогрессии с номером nСумма членов арифметической прогрессии (если известные только два любых члена прогрессии)Сумма первых n членов арифметической прогрессииСумма членов арифметической прогрессии от n-ого до m-огоШаг (разность) арифметической прогрессииПостроить арифметическую прогрессию

Известный член арифметической прогрессии

a_m =

Номер m известного члена прогрессии

m =

Номер n члена арифметической прогрессии (который необходимо найти)

n =

Шаг (разность) арифметической прогрессии

d =

Отобразить члены арифметической прогрессии без нумерациис нумерациейв строкув столбик

с по

Идет расчет …

Арифметическая прогрессия

Арифметическая прогрессия – это числовая последовательность, каждый член в которой начиная со второго равен сумме предыдущего члена и числа d.

Число d – называется шагом или разностью прогрессии.

Приведем примеры, построим арифметическую прогрессию с шагом d = 2, первый член которой a₁ будет равен 3, тогда прогрессия будет построена следующим образом:
3, 3+2, (3+2)+2, (3+2+2)+2, (3+2+2+2)+2… либо
3, 3+2, 5+2, 7+2, 9+2… либо
3, 3+2, 3+(2·2), 3+(2·3), 3+(2·4)… и так далее, прогрессия имеет вид:
3, 5, 7, 9, 11…

Приведем еще один пример, построим арифметическую прогрессию с шагом d = −2, первый член которой a₁ равен 5, тогда прогрессия будет построена следующим образом:
5, 5−2, (5−2)−2, (5−2−2)−2, (5−2−2−2)−2… либо
5, 5−2, 3−2, 1−2, −1−2… либо
5, 5−2, 5+(2·(−2)), 5+(3·(−2)), 5+(4·(−2))… и так далее, прогрессия имеет вид:

5, 3, 1, −1, −3…

Любой член a_n арифметической прогрессии может быть вычислен по формуле:

a_n − член арифметической прогрессии, который необходимо найти
n − номер n члена арифметической прогрессии (который необходимо найти)
a_m − известный член арифметической прогрессии
m − номер m известного члена прогрессии
d − шаг (разность) арифметической прогрессии

Если известен первый член прогрессии, то формула примет вид:

a_n − член арифметической прогрессии, который необходимо найти
a₁ − первый член арифметической прогрессии
d − шаг (разность) арифметической прогрессии

Возьмём для примера, заданную выше прогрессию 5, 3, 1, -1, -3… и найдем ее 4-й член.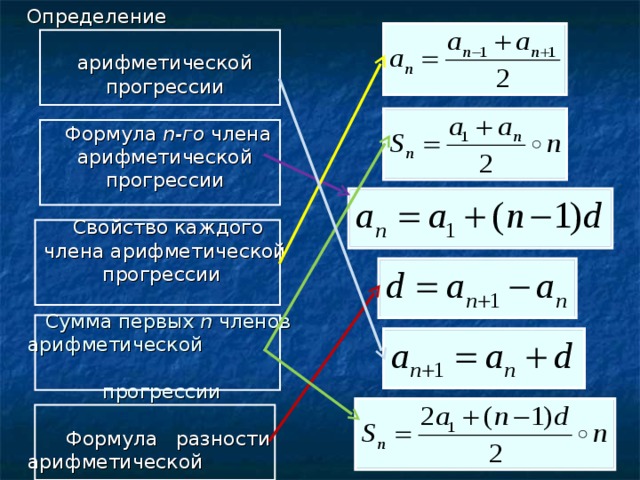

В данной прогрессии d = -2. В качестве a_m − мы можем использовать любой известный член прогрессии, возьмем a₂ = 3, тогда
a₄ = a_n = a_m − (m − n) · d = 3 − (2 − 4) · (−2) = −1

Решим еще один пример. Дана арифметическая прогрессия

(a_n):

…

Разность прогрессии d = ½. Найти a₁₀. В данном случае можно воспользоваться второй формулой, так как известен первый член прогрессии:

a₁₀ =

a ₁ + (n − 1) · d =

0 + (10 − 1) · 1/2 =

= 4.5

Шаг (разность) арифметической прогрессии

a_n − известный член арифметической прогрессии член с номером n
a_m − следующий известный член арифметической прогрессии член с номером m
n − номер n члена арифметической прогрессии
m − номер m члена арифметической прогрессии

Приведем пример.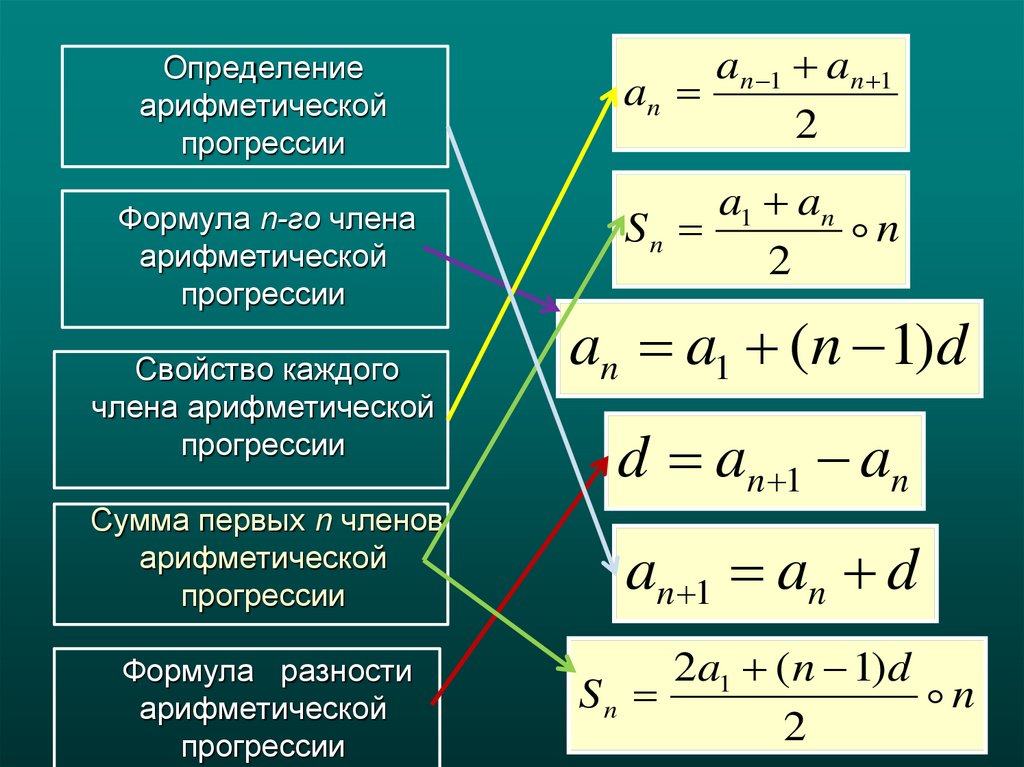 Дана прогрессия (a_n): −3, −1, 1, 3… найти ее разность. Членами a_n и a_m могут быть любые известные члены прогрессии, тогда в качестве a_n, возьмём 1-й член в качестве a_m второй.
a_n = -3
a_m = -1 тогда:

d =

a_m − a_n

m − n

−1 − (−3)

2 − 1

Сумма членов арифметической прогрессии

Сумма первых n членов арифметической прогрессииa₁ − первый член арифметической прогрессии
a_n − член арифметической прогрессии
n − номер n члена арифметической прогрессии (количество суммируемых членов)

Приведем пример. Дана прогрессия (a_n): −3, −1, 1, 3… Найти сумму первых десяти членов. Чтобы воспользоваться формулой, приведенной выше, необходимо сначала вычислить значение разности прогрессии, затем значение 10-го члена прогрессии, и затем уже находить сумму.

Значение разности d уже было найдено в примере выше, продублируем его:

d =

a_m − a_n

m − n

-1 − (-3)

2 − 1

Теперь найдем значение 10-го члена прогрессии:
a₁₀ = a₁ + (n − 1) · d = −3 + (10 − 1) · 2 = 15
a₁₀ = 15

Найдем сумму первых 10-ти членов:

S₁₀ =

-3 + 15

· 10 =

Сумма членов арифметической прогрессии от n-ого до m-огоa_n − член арифметической прогрессии член с номером n
a_m − член арифметической прогрессии член с номером m
n − номер n члена арифметической прогрессии
m − номер m члена арифметической прогрессии

Решим пример на нахождение суммы арифметической прогрессии, когда известно только два ее члена. Даны члены прогрессии a₃ = 4 и a₁₆ = -7. Найти сумму первых 20-ти членов прогрессии.

Вычислим шаг (разность) арифметической прогрессии:

d =

a_m − a_n

m − n

-7 − 4

16 − 4

= −0.916666666666667

Найдем значение 1 члена арифметической прогрессии (первого члена суммы):

a_n – член арифметической прогрессии с номером n, который необходимо найти.
a_m – известный член прогрессии с номером m.
n = 1
a_m = -7, m = 16

a₁ =

a _m − (m − n) · d =

−7 − (16 − 1) · (-11/12) =

= 6.75

Найдем значение 20 члена арифметической прогрессии (последнего члена суммы):
a_n – член арифметической прогрессии с номером n, который необходимо найти.
a_m – известный член прогрессии с номером m.
n = 20
a_m = -7, m = 16

a₂₀ =

a _m − (m − n) · d =

−7 − (16 − 20) · (-11/12) =

= −10. 6666666666667

Найдем сумму членов арифметической прогрессии с 1 по 20:
a_n = a

1 = 27/4
a_m = a₂₀ = -32/3

S_1,20 =

a_n + a_m

· (m − n + 1) =

27/4 + (-32/3)

· (20 − 1 + 1) =

= −39.1666666666667

Общая разница арифметической прогрессии Калькулятор

✖N-й член AP — это член, соответствующий индексу или позиции числа n от начала в данной арифметической прогрессии.ⓘ N-й срок AP [T_n]

+10%

-10%

✖Первый член AP — это значение, соответствующее первому члену арифметической прогрессии.ⓘ Первый срок АП [a]

+10%

-10%

✖Номер индекса n-го члена AP — это значение n для n-го члена или положение n-го члена в арифметической прогрессии.ⓘ Номер индекса n-го срока действия ПД [n]

+10%

-10%

✖Общая разность АР — это разница произвольного члена с предшествующим ему членом арифметической прогрессии.

ⓘ Общая разница арифметической прогрессии [d]

⎘ копия

👎

Формула

сбросить

👍

Общая разница арифметической прогрессии Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

N-й срок AP: 20 —> Конверсия не требуется
Первый срок АП: 3 —> Конверсия не требуется
Номер индекса n-го срока действия ПД: 9 —> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

2. 125 —> Конверсия не требуется

< 3 Общая разница арифметической прогрессии Калькуляторы

Общая разница арифметической прогрессии формула

Общая разница AP = (N-й срок AP-Первый срок АП)/(Номер индекса n-го срока действия ПД-1)
d = (T_n-a)/(n-1)

Что такое арифметическая прогрессия?

Арифметическая прогрессия или просто AP — это последовательность чисел, в которой последующие члены получаются путем добавления постоянного числа к первому члену. Это фиксированное число называется общей разностью арифметической прогрессии. Например, последовательность 2, 5, 8, 11, 14,… является арифметической прогрессией с первым членом, равным 2, и общей разностью, равной 3. AP является сходящейся последовательностью тогда и только тогда, когда общая разность равна 0, иначе AP всегда расходится.

Copied!

Калькулятор арифметической последовательности | Формула

Авторы: Богна Шик и Анна Щепанек, доктор философии

Рецензию сделали Стивен Вудинг и Джек Боуотер

Последнее обновление: 29 декабря 2022 г.

Содержание:

Что такое арифметическая последовательность?
Определение и наименование арифметической последовательности
Примеры арифметической последовательности
Формула арифметической последовательности
Различие между последовательностью и рядом
Арифметический ряд до бесконечности
Арифметические и геометрические последовательности
Арифметико-геометрическая последовательность
Калькулятор арифметической последовательности: пример использования 0031 анализ последовательности числа, которые создаются путем добавления постоянного значения каждый раз . Вы можете использовать его, чтобы найти любое свойство последовательности — первое слагаемое, общую разность, nᵗʰ слагаемое или сумму первых n слагаемых. Вы можете сразу приступить к его использованию или прочитать дальше, чтобы узнать, как он работает.
В этой статье мы объясняем определение арифметической последовательности, поясняем уравнение последовательности, которое использует калькулятор, и даем вам формулу для нахождения арифметического ряда (сумма арифметической прогрессии). Мы также предоставляем обзор различий между арифметическими и геометрическими последовательностями и простой для понимания пример применения нашего инструмента.
Что такое арифметическая прогрессия?
Чтобы ответить на этот вопрос, сначала нужно узнать, что такое термин последовательность означает. По определению, последовательность в математике — это набор объектов, таких как числа или буквы, которые идут в определенном порядке. Эти объекты называются элементами или элементами последовательности. Довольно часто один и тот же объект появляется несколько раз в одной последовательности.
Арифметическая последовательность также является набором объектов, точнее, чисел. Каждое последовательное число создается путем добавления постоянного числа (называемого общей разностью 9).0032 ) к предыдущему. Такая последовательность может быть конечной, когда в ней есть определенное количество членов (например, 20), или бесконечной, если мы не указываем количество членов.
Каждая арифметическая последовательность однозначно определяется двумя коэффициентами: общей разностью и первым членом . Если вы знаете эти два значения, вы можете записать всю последовательность.
Определение арифметической последовательности и наименование
Как только вы начнете углубляться в тему что такое арифметическая последовательность , вполне вероятно, что вы столкнетесь с некоторой путаницей. Это происходит из-за различных соглашений об именах, которые используются.
Два наиболее распространенных термина, с которыми вы можете столкнуться, это арифметическая последовательность и ряд . Первую также часто называют арифметической прогрессией , а вторую также называют частичной суммой .
Основное различие между последовательностью и последовательностью состоит в том, что по определению арифметическая последовательность — это просто набор чисел, каждый раз складывающий общую разность. Арифметический ряд, с другой стороны, представляет собой сумму n членов последовательности. Например, вы можете обозначить сумму первых 12 членов как S ₁₂ = a ₁ + a ₂ + … + a ₁₂ .
Примеры арифметической последовательности
Некоторые примеры арифметической последовательности включают:
- 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, …
- 6, 3, 0, -3, -6, -9, -12, -15, …
- 50, 50.1, 50.2, 50.3, 50.4, 50.5, …
Сможете ли вы найти общее отличие каждой из этих последовательностей? Подсказка: попробуйте вычесть термин из следующего термина.

Основываясь на этих примерах арифметических последовательностей, вы можете заметить, что общая разность не обязательно должна быть натуральным числом — это может быть дробь. На самом деле, это даже не должно быть положительным!
Если общая разность арифметической последовательности положительна, мы называем ее возрастающей последовательностью . Естественно, если разность отрицательна, последовательность будет уменьшающейся на . Что происходит в случае нулевой разницы? Ну, вы получите монотонная последовательность , где каждый член равен предыдущему.
Теперь давайте внимательно посмотрим на эту последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Можете ли вы определить, в чем состоит общее различие в этом случае? ?
На самом деле, у вас не должно быть возможности. Это не пример арифметической последовательности, а частный случай, называемый последовательностью Фибоначчи. Каждый термин находится путем сложения двух предшествующих ему терминов. Интересно, не так ли? Так что, если вы хотите узнать больше, воспользуйтесь калькулятором Фибоначчи. Это стоит вашего времени.
Отличным применением последовательности Фибоначчи является построение спирали. Если вы нарисуете квадраты со сторонами, длина которых равна последовательным членам этой последовательности, вы получите идеальную спираль.
Идеальная спираль — прямо как эта! (Источник: Викимедиа.)
Математикам всегда нравилась последовательность Фибоначчи! Если вы хотите обнаружить последовательность, которая пугала их почти столетие, воспользуйтесь нашим калькулятором гипотез Коллатца.
Формула арифметической последовательности
Предположим, вы хотите найти 30ᵗʰ член любой из последовательностей, упомянутых выше (кроме последовательности Фибоначчи, конечно). Записывать первые 30 терминов было бы утомительно и отнимало много времени. Однако вы, наверное, заметили, что вам не нужно записывать их все! Достаточно, если вы добавите 29 общих отличий к первому члену.
Обобщим это утверждение, чтобы сформулировать уравнение арифметической последовательности. Это формула для любого nᵗʰ члена последовательности.
a = a₁ + (n-1)d
где:
a — nᵗʰ член последовательности;
d — Отличие общее; и
a₁ — Первый член последовательности.
Эта формула арифметической последовательности применяется в случае всех общих разностей, положительных, отрицательных или равных нулю. Естественно, что в случае нулевой разности все слагаемые равны друг другу, что делает ненужными какие-либо вычисления.
Разница между последовательностью и последовательностью
Наш калькулятор арифметической последовательности также может найти сумму последовательности (называемой арифметической последовательностью ) для вас. Поверьте, вы можете сделать это сами — это не так сложно!
Посмотрите на первый пример арифметической последовательности: 3, 5, 7, 9, 11, 13, 15, 17, 19, 21. Мы могли бы просуммировать все члены вручную, но это не обязательно. Попробуем суммировать термины более организованным образом. Мы сложим первое и последнее слагаемые вместе, затем второе и предпоследнее, третье и третье с последним и т. д. Вы быстро заметите, что:
3 + 21 = 24
5 + 19 = 24
7 + 17 = 24
Сумма каждой пары постоянна и равна 24 . Это означает, что нам не нужно складывать все числа. Все, что вам нужно сделать, это сложить первый и последний член последовательности и умножить эту сумму на количество пар (т. е. на n/2).
Математически это записывается как:
S = n/2 × (a₁ + a)
Подставляя уравнение арифметической последовательности вместо члена nᵗʰ:
S = n/2 × [a₁ + a₁ + (n-1)d]
После упрощения:
S = n/2 × [2a₁ + (n-1)d]
9000 2 Это формула позволит вам найти сумму арифметической прогрессии.
Арифметический ряд до бесконечности
При поиске суммы арифметической последовательности вы, вероятно, заметили, что вам нужно выбрать значение n , чтобы вычислить частичную сумму. Что, если вы хотите просуммировать всех членов последовательности?
Интуитивно понятно, что сумма бесконечного числа слагаемых будет равна бесконечности независимо от того, является ли общая разность положительной, отрицательной или даже равной нулю. Однако это относится не ко всем типам последовательностей. Если вы выберете другую, например геометрическую последовательность, сумма до бесконечности может оказаться конечным членом .
Арифметические и геометрические последовательности
Очевидно, что наш калькулятор арифметических последовательностей не может анализировать никакие другие типы последовательностей. Например, последовательность 2, 4, 8, 16, 32, … не имеет общего различия. Это потому, что это другой вид последовательности — геометрическая прогрессия.
В чем основное отличие арифметической последовательности от геометрической? В то время как арифметическая последовательность использует общую разность для построения каждого последующего члена, геометрическая последовательность использует обыкновенное отношение . Это означает, что мы умножаем каждый термин на определенное число каждый раз, когда хотим создать новый термин.
Одним из интересных примеров геометрической последовательности является так называемая цифровая вселенная . Вы, наверное, слышали, что объем цифровой информации удваивается каждые два года. Это означает, что вы можете записать числа, представляющие количество данных в геометрической последовательности, с общим отношением, равным двум.
Арифметико-геометрическая последовательность
Вы также можете анализировать специальный тип последовательности, называемый арифметико-геометрической последовательностью . Он создается путем умножения членов двух прогрессий — арифметической и геометрической.
Например, рассмотрим следующие две прогрессии:
Арифметическая последовательность: 1, 2, 3, 4, 5, …
Геометрическая последовательность: 1, 2, 4, 8, 16, …
Чтобы получить n-й член арифметико-геометрического ряда, нужно умножить n-й член арифметической прогрессии на n-й член геометрической прогрессии. В этом случае результат будет выглядеть так:
Первый член: 1 × 1 = 1
Второй член: 2 × 2 = 4
Третий член: 3 × 4 = 12
Четвертый член: 4 × 8 = 32
Пятый член: 5 × 16 = 80
Такая последовательность определяется четырьмя параметрами : начальным значением арифметической прогрессии a , общей разностью d , начальным значением геометрической прогрессии b , а обыкновенное отношение r .
Калькулятор арифметической прогрессии: пример использования
Разберем простой пример, который можно решить с помощью формулы арифметической прогрессии . Мы внимательно рассмотрим пример свободного падения.
Камень свободно падает в глубокую шахту. За первую секунду он опускается на четыре метра. Каждую следующую секунду расстояние, на которое он падает, увеличивается на 9,8 метра. Какое расстояние прошел камень между пятой и девятой секундами?
Пройденное расстояние следует арифметической прогрессии с начальным значением a = 4 м и общей разностью d = 9,8 м .
Сначала мы найдем общее расстояние, пройденное за первые девять секунд свободного падения, вычислив частичную сумму S₉ ( n = 9 ):
S₉ = n/2 × [2a₁ + ( n-1)d] = 9/2 × [2 × 4 + (9–1) × 9,8] = 388,8 м
За первые девять секунд камень проходит в общей сложности 388,8 м. Однако нас интересует только расстояние, пройденное с пятой по девятую секунду. Как рассчитать это значение? Это легко — все, что нам нужно сделать, это вычесть расстояние, пройденное за первые четыре секунды, S₄, из частичной суммы S₉.
S₄ = n/2 × [2a₁ + (n-1)d] = 4/2 × [2 × 4 + (4-1) × 9,8] = 74,8 м
S₄ равно 74,8 м. Теперь мы можем найти результат простым вычитанием:
расстояние = S₉ — S₄ = 388,8 — 74,8 = 314 м
Существует альтернативный метод решения этого примера. Вы можете использовать формулу арифметической последовательности , чтобы вычислить расстояние, пройденное за пятую, шестую, седьмую, восьмую и девятую секунды, и сложить эти значения вместе. Попробуйте сделать это сами — скоро вы поймете, что результат точно такой же!
Часто задаваемые вопросы
Как найти n-й член арифметической прогрессии?
Чтобы найти nᵗʰ член арифметической прогрессии, aₙ :
Умножьте на обыкновенную разность d на (n-1) .
Добавить этого продукта к первому члену a₁ .
Результатом является термин nᵗʰ. Хорошая работа!
В качестве альтернативы можно использовать формулу: aₙ = a₁ + (n-1) × d .
Как найти общую разность в арифметической прогрессии?
Вычтите любые два соседних члена , чтобы получить общую разность последовательности. Можно взять любые последующие, например, a₂-a₁ , a₇-a₆ или a₁₀₀-a₉₉ . Если вы не получили одинаковый результат для всех различий, ваша последовательность не является арифметической.
Какая общая разница в следующей арифметической последовательности: -12, -1, 10, 21?
Общая разница 11 . Вы можете оценить его, вычитая любую последовательную пару членов, например, a₂ — a₁ = -1 — (-12) = 11 или a₄ — a₃ = 21 — 10 = 11
В чем разница между арифметикой и геометрическая последовательность?
разность между любыми соседними элементами постоянна для любой арифметической последовательности , в то время как отношение любой последовательной пары термов одинаково для любой геометрической последовательности .
Чтобы получить следующий член арифметической прогрессии, нужно добавить общее отличие к предыдущему .
Чтобы получить следующий член геометрической последовательности, нужно умножить предыдущий член на знаменатель .
Как определить, является ли последовательность арифметической?
Разница между любой последовательной парой чисел должна быть одинаковой. Чтобы проверить, является ли последовательность арифметической, найдите различия между каждой соседней парой терминов. Если какое-либо из значений отличается, ваша последовательность не является арифметической.
Богна Шик и Анна Щепанек, доктор философии
Этот калькулятор использует следующую формулу для нахождения n-го члена последовательности:
Введите любые два значения:
Общая разность, d
Как ввести больше членов?
Выберите расширенный режим ниже, если вам даны термины с индексами больше 5 и вы хотите, чтобы мы определили по ним последовательность.
Как найти больше терминов?
Здесь можно распечатать любую часть последовательности (или найти отдельные термины)
Хотите записать?
Сумма любого количества начальных членов
Найдите сумму a₁ + . .. + aₚ для p =
Для произвольного первого индекса выберите расширенный режим ниже.
Ознакомьтесь с 7 калькуляторами похожих последовательностей 🔗
Гипотеза КоллатцаФибоначчиГеометрическая последовательность… Еще 4
Калькулятор арифметической последовательности — Калькулятор N-го члена
Введите значения в поля ввода ниже, чтобы вычислить n-й член и сумму арифметического прогресса ион с помощью арифметической последовательности /серийный калькулятор.
Формула
а _n = а ₁ + (n — 1)d
Тип метода:
Базовый калькулятор
Решение для a ₁ и d
Решение для n
Введите общее количество терминов (n ^th термин):
Введите первый член (a ₁ ):
Введите общую разность (d):
Я хочу вычислить:
N-й член Сумма последовательности
РЕКЛАМА
РЕКЛАМА
Вычислить геометрическую последовательность
Содержание:
Калькулятор N-го члена
Что такое арифметическая прогрессия?
Формула арифметической прогрессии
Нахождение n-го члена арифметической прогрессии и ее суммы
Дайте нам отзыв
✎
✉
Nth Term Calculator
Калькулятор арифметической последовательности — это онлайн-инструмент, который вычисляет:
Арифметическую последовательность
Значение N-го члена
Сумма арифметической прогрессии
Что такое арифметическая прогрессия?
Арифметическая последовательность может быть определена как
» Арифметическая последовательность – это последовательность, в которой каждый член увеличивается путем прибавления или вычитания некоторого постоянного значения, известного как общая разность (d) . »
Арифметическая последовательность широко известна как арифметический ряд и арифметическая прогрессия.
Формула арифметической последовательности
Формула для нахождения n-го члена:
n ^th член = a + (n — 1)d найдите сумму арифметической прогрессии:
S = n/2 × [2a ₁ + (n — 1)d]
Где:
a относится к nᵗʰ члену последовательности,
d относится к общей разнице, а
a₁ относится к первому члену последовательности.
Специальной формулы для нахождения арифметической прогрессии не существует. В следующем разделе мы объясним метод вычисления арифметической последовательности с использованием общей разности и первого члена.
Нахождение n-го члена, арифметической последовательности и ее суммы
Для вычисления n-го члена, арифметической последовательности и ее суммы вы можете просто использовать калькулятор арифметических рядов выше.
Пример:
Найдите n-й член и сумму арифметической последовательности для 15 количество членов, если первый член равен 5 900 76 а разница 4.
Решение:
Шаг 1: Определите значения.
n = 15
a = 5
d = 4
Шаг 2: Используйте формулу арифметической последовательности и поместите значения.
Для нахождения n-го члена
n ^й член = a + (n — 1)d
= 5 + (15 — 1) × 4
= 61
n ^th срок = 61
Для нахождения суммы арифметической прогрессии
S = n/2 × [2a₁ + (n — 1)d]
S = 15/2 × [2(5) + ( 15 — 1) × 4]
S = 495
Для нахождения арифметической последовательности
Добавьте общую разность в первый член, чтобы получить арифметическую последовательность.
No related posts.