Калькулятор дробей — множитель дробей, сложение
Калькулятор дробей
Что такое дробь? Части и значение
Дробь в самом простом значении этого слова относится к количеству, которое не является целым, таким образом выражая отношение часть-целое. С точки зрения математики дробь представляет собой количество частей целого. Итак, если мы представим 7 частей целого, состоящего из 10 частей, то дробь будет представлена как 7 ÷ 10.
Дробь представлена в терминах части и целого, разделенных линией деления. Математическая дробь также имеет 2 части:
- Числитель: появляется в верхней части линии деления и представляет часть.
- Знаменатель: появляется под чертой деления и представляет собой целое, частью которого является числитель.
Например, в дроби 2 ÷ 7 2 — числитель, а 7 — знаменатель.
Типы дробей
В математике дроби могут быть 6 основных типов, в которых категории не являются исключительными (т.
е. конкретная дробь может попадать более чем в одну категорию).
- Правильная дробь
Правильная дробь – это дробь, у которой числитель меньше знаменателя. Так, 8 ÷ 17, 2 ÷ 5, 1 ÷ 5 и т. д. — все это примеры правильных дробей в качестве их числителей, т. е. числа над чертой деления (8, 2, 1) меньше знаменателей, т. е. числа, выраженные ниже линия разделения (17, 5, 5).
- Неправильная дробь
Неправильной дробью называется дробь, в которой знаменатель меньше числителя (и наоборот, числитель больше знаменателя). Так, например, примеры неправильных дробей включают 8 ÷ 5, 4 ÷ 3, 3 ÷ 2.
- Одинаковые дроби
Одинаковые дроби состоят из пары дробей с одинаковым знаменателем. Такие операции, как сложение и вычитание, можно выполнять непосредственно над одинаковыми дробями. Так, например, 49 и 79 похожи на дроби. Точно так же 3 ÷ 5 и 2 ÷ 5 также похожи на дроби
- В отличие от дробей
В отличие от дробей относятся к паре дробей, в которых знаменатели различны.
Чтобы выполнять такие действия, как сложение и вычитание над неправильными дробями, их нужно сначала преобразовать в одинаковые дроби. Например, 4 ÷ 9и 5 ÷ 8 являются парой непохожих дробей, так как их знаменатели (9 и 8) различны и не равны.Во многих математических операциях вам может понадобиться преобразовать неправильную дробь в правильную дробь. Вот как это сделать:
Чтобы выполнять такие действия, как сложение и вычитание над неправильными дробями, их нужно сначала преобразовать в одинаковые дроби. Например, 4 ÷ 9и 5 ÷ 8 являются парой непохожих дробей, так как их знаменатели (9 и 8) различны и не равны.Во-первых, найдите наименьшее общее кратное (НОК) дробей. Например, для 4 ÷ 6 и 5 ÷ 8 знаменатели равны 6 и 8, а НОК 6 и 8 равен 24.
вам придется умножить знаменатели, чтобы получить LCM. (Легкий трюк — разделить НОК на знаменатель). Например, в случае числа 8 его нужно умножить на 3, чтобы получить 24, а в случае 6 его нужно умножить на 4, чтобы получить 24 9.0007
Узнав коэффициент, на который нужно умножить знаменатель, умножьте и числитель, и знаменатель на одно и то же число, т.е. 4 x 4 ÷ 6 x 4 = 16 ÷ 24 и 5 x 3 ÷ 8 x 3 = 15 ÷ 24
Теперь у вас есть похожие дроби, то есть 16 ÷ 24 и 15 ÷ 24
Смешанная дробь, как следует из названия, состоит из целого, части и его объединенное целое.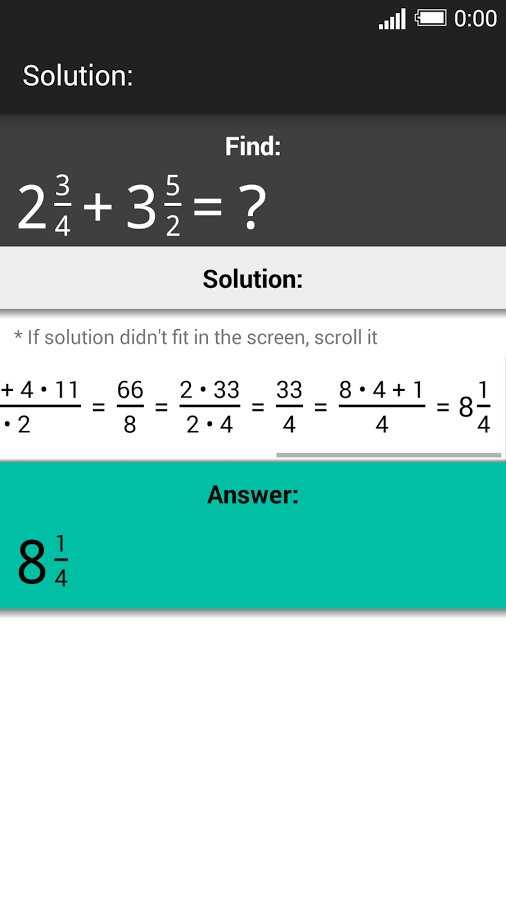
Он состоит из двух частей: целого числа и дроби. Смешанная дробь получается из неправильной дроби при ее делении. Частное, полученное после деления, образует целое число, остаток образует числитель оставшейся дроби, а делитель образует знаменатель.
Вот пример:
Если мы рассмотрим неправильную дробь 85 и разделим числитель на знаменатель путем деления в большую сторону, мы получим:Делитель = 5
Частное = 1
Остаток = 3
Чтобы преобразовать это в смешанной дроби частное становится целым, остаток становится числителем, а делитель становится знаменателем, то есть 1 x 3 ÷ 5 .
Эквивалентные дроби – это те дроби, которые имеют одинаковую приведенную форму, т.е. при приведении к простейшим формам эти дроби эквивалентны. Например, при приведении двух дробей 3 ÷ 6 и 2 ÷ 4 к их простейшему виду они будут равны 1 ÷ 2 и, следовательно, образуют пару эквивалентных дробей.
Аналогично пара дробей 9 ÷ 9 и 4 ÷ 4 будет равна 1 ÷ 1 при приведении к простейшему виду, т.
е. образует пару равнозначных дробей.
Как выполнять операции с дробями
Выполнение математических операций с дробями может показаться запутанным или сложным, но если вы помните определенные эмпирические правила приближения к операциям с дробями, вы можете легко их выполнять. Здесь мы разбили для вас процесс решения математических операций с дробями на простые шаги.
- Сложение и вычитание
Самый первый и главный фактор, о котором следует помнить, это то, что всякий раз, когда вы выполняете сложение или вычитание пары дробей, они должны быть подобны дробям. Следовательно, если пара дробей, которые вы добавляете/вычитаете, представляет собой пару одинаковых дробей, вы можете напрямую добавлять или вычитать их. Но в случае, если они не похожи на дроби, вы должны сначала преобразовать их в подобные дроби, как указано выше.
- Умножение и деление
Для таких операций, как умножение и деление, вы можете напрямую выполнять вычисления с непохожей парой дробей.
Умножение дробей очень просто: сначала нужно перемножить числовые значения числителей и знаменателей. Потом просто полученный ответ в сокращенной форме.
Преобразование обычных инженерных дробей в десятичные числа
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже. (Необходимо изменить описание)
| 64th | 32th | 16th | 8th | 4th | 2nd | Decimal | Decimal (inch to mm) | |
| 1/64 | 0.015625 | 0.396875 | ||||||
| 2/64 | 1/32 | 1/16 | 0.03125 | 0.79375 | ||||
| 3/64 | 0. 046875 | 1.1 | ||||||
| 4/64 | 2/32 | 0.0625 | 1.5875 | |||||
| 5/64 | 0.078125 | 1.984375 | ||||||
| 6/64 | 3/32 | 0.09375 | 2.38125 | |||||
| 7/64 | 0.109375 | 2.778125 | ||||||
| 8/64 | 4/32 | 2/16 | 1/8 | 0.125 | 3.175 | |||
| 9/64 | 0.140625 | 3.571875 | ||||||
| 10/64 | 5/32 | 0.15625 | 3.96875 | |||||
| 11/64 | 0.171875 | 4.365625 | ||||||
| 12/64 | 6/32x | 3/16 | 0. 1875 | 4.7625 | ||||
| 13/64 | 0.203125 | 5.159375 | ||||||
| 14/64 | 7/32 | 0.21875 | 5.55625 | |||||
| 15/64 | 0.234375 | 5.953125 | ||||||
| 16/64 | 8/32 | 4/16 | 2/8 | 1/4 | 1/4 | 0.25 | 6.35 | |
| 17/64 | 0.265625 | 6.746875 | ||||||
| 18/64 | 9/32 | 0.28125 | 7.14375 | |||||
| 19/64 | 0.296875 | 7.540625 | ||||||
| 20/64 | 10/32 | 5/16 | 0.3125 | 7.9375 | ||||
| 21/64 | 0. 328125 | 8.334375 | ||||||
| 22/64 | 11/32 | 0.34375 | 8.73125 | |||||
| 23/64 | 0.359375 | 9.128125 | ||||||
| 24/64 | 12/32 | 6/16 | 3/8 | 0.325 | 9.525 | |||
| 25/64 | 0.3 | 9.921875 | ||||||
| 26/64 | 13/32 | 0.40625 | 10.31875 | |||||
| 27/64 | 0.421875 | 10.715625 | ||||||
| 28/64 | 14/32 | 7/16 | 0.4375 | 11.1125 | ||||
| 29/64 | 0.453125 | 11.509375 | ||||||
| 30/64 | 15/32 | 0. 46875 | 11. | |||||
| 31/64 | 0.484375 | 12.303125 | ||||||
| 32/64 | 16/32 | 8/16 | 4/8 | 2/4 | 2/4 | 0.5 | 12.7 | |
| 33/64 | 0.515625 | 13.096875 | ||||||
| 34/64 | 17/32 | 0.53125 | 13.49375 | |||||
| 35/64 | 0.546875 | 13.8 | ||||||
| 36/64 | 18/32 | 9/16 | 0.5625 | 14.2875 | ||||
| 37/64 | 0.578125 | 14.684375 | ||||||
| 38/ 64 | 9/32 | 0.59375 | 15.08125 | |||||
| 39/64 | 0. 609375 | 15.478125 | ||||||
| 40/64 | 20/32 | 10/16 | 5/8 | 0.625 | 15.875 | |||
| 41/64 | 0.640625 | 16.271875 | ||||||
| 42 /64 | 21/32 | 0.65625 | 16.66875 | |||||
| 43/64 | 0.671875 | 17.065625 | ||||||
| 44/64 | 22/32 | 11/16 | 0.6875 | 17.4625 | ||||
| 45/64 | 0.703125 | 17.859375 | ||||||
| 46/64 | 23/32 | 0.71875 | 18.25625 | |||||
| 47/64 | 0.734375 | 18.653125 | ||||||
| 48/64 | 24/32 | 12/16 | 6/8 | 3/6 | 3/6 | 0. 75 | 19.05 | |
| 49/64 | 0.765625 | 19.446875 | ||||||
| 50/ 64 | 25/32 | 0.78125 | 19.84375 | |||||
| 51/64 | 0.796875 | 20.240625 | ||||||
| 52/64 | 26/32 | 13/16 | 0.8125 | 20.6375 | ||||
| 53/64 | 0.828125 | 21.034375 | ||||||
| 54/64 | 27/32 | 0.84375 | 21.43125 | |||||
| 55/64 | 0.859375 | 21.828125 | ||||||
| 56/64 | 28/32 | 14/16 | 7/8 | 0.875 | 22.225 | |||
| 57/64 | 0. 8 | 22.621875 | ||||||
| 58/64 | 29/32 | 0. | 23.01875 | |||||
| 59/64 | 0.921875 | 23.415625 | ||||||
| 60/64 | 30/32 | 15/16 | 0.9375 | 23.8125 | ||||
| 61/64 | 0.953125 | 24.209375 | ||||||
| 62/64 | 31/32 | 0.96875 | 24.60625 | |||||
| 63/64 | 0,984375 | 25,003125 | ||||||
| 64/64 | 32/329 | 933/64/6432/32 | ||||||
| 64/64 | 32/32 | |||||||
| 64/64 | 32/32 | |||||||
| .0133 | 2/2 | 1 | 25.4 |
Часто задаваемые вопросы о Калькуляторе дробей
Вычислять дроби очень просто: для сложения и вычитания преобразуйте дроби в одну и ту же пару, а затем выполняйте их.
Для умножения или деления вы можете напрямую выполнять вычисления с дробями.
3/4 разделить на 2 будет равно 3/8.
½ от ¾ равно ⅜.
¼ x ¼, так как дробь будет ⅛
Вы можете разделить дроби, сначала инвертировав дробь делителя и умножив на нее дробь делимого. Ответ следует привести к простейшей форме. Например:
Чтобы сравнить дроби, сначала преобразуйте их в подобные дроби. После этого сравните числители одинаковых дробей и больше та, у которой числитель больше. В отличие от дробей нельзя сравнивать напрямую.
Чтобы сложить дроби с разными знаменателями, сначала преобразуйте дроби в подобные дроби, чтобы получить одинаковый знаменатель (который будет НОК двух знаменателей). После этого сложите числители и приведите полученный ответ к простейшему виду.
Смешанная дробь — это дробная фигура, состоящая из двух частей: целого числа и дроби.
Нет, смешанные дроби можно получить только из неправильных дробей, так как их знаменатели меньше числителей, а значит, при длинном делении получится положительный остаток.