28 разделить на 7 умножить на 5
Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см.
Этот онлайн калькулятор поможет вам понять как умножить целые числа и десятичные дроби столбиком. Калькулятор умножения столбиком очень просто и быстро вычислит произведение и выдаст подробное решение задачи.
Содержание
- Калькулятор умножение столбиком
- Ввод данных в калькулятор умножение столбиком
- Дополнительные возможности калькулятора умножения столбиком
- Инструкция использования калькулятора для умножения столбиком
- Как работать с математическим калькулятором
- Алгоритм работы онлайн-калькулятора на примерах
- Сложение.
- Вычитание.
- Умножение.
- Деление.
Калькулятор умножение столбиком
Ввод данных в калькулятор умножение столбиком
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора умножения столбиком
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Инструкция использования калькулятора для умножения столбиком
Для вычисления достаточно ввести числа (целые иди десятичные дроби) и нажать кнопку «=».
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
. | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 /x | дробь | Вывод в десятичные дроби.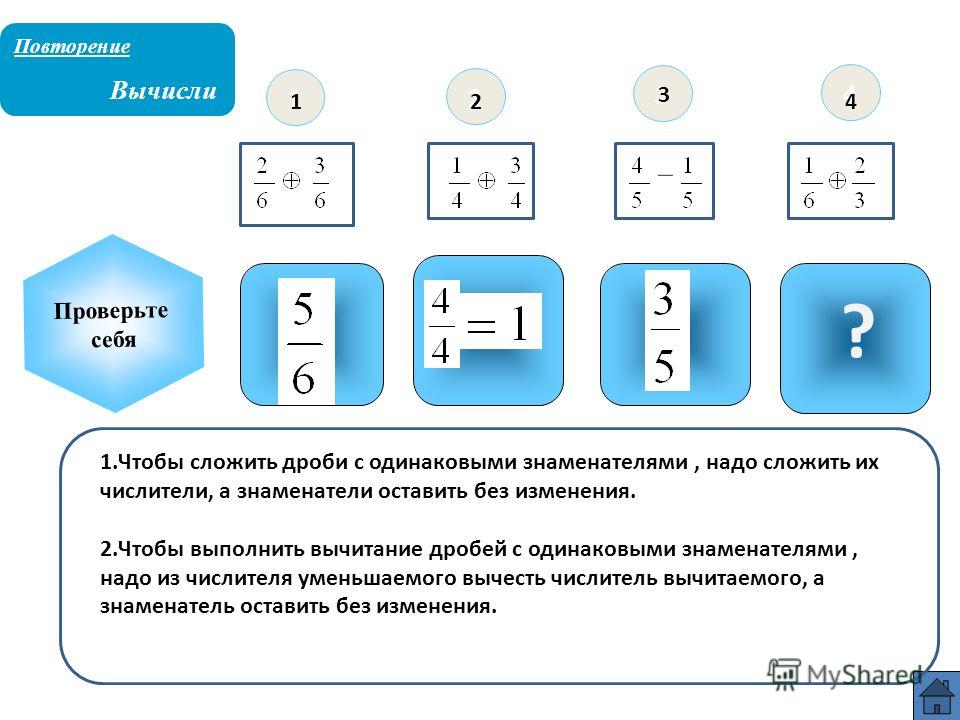 В числителе 1, в знаменателе вводимое число В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.

Сложение целых натуральных чисел
Сложение целых натуральных и отрицательных чисел
Сложение десятичных дробных чисел
Вычитание.
Вычитание целых натуральных чисел
Вычитание целых натуральных и отрицательных чисел
Вычитание десятичных дробных чисел
Умножение.
Произведение целых натуральных чисел
Произведение целых натуральных и отрицательных чисел
Произведение десятичных дробных чисел
Деление.
Деление целых натуральных чисел
Деление целых натуральных и отрицательных чисел
Деление десятичных дробных чисел
РусскийКалькулятор дроби в десятичную — MathCracker.com
Инструкции:
Используйте этот калькулятор, чтобы преобразовать заданную вами дробь в десятичную дробь, показав все шаги. Пожалуйста, введите одно десятичное число в форму ниже:
Пожалуйста, введите одно десятичное число в форму ниже:
Подробнее об этом Калькулятор дроби в десятичную дробь
Все мы знаем, что такое дробь, но иногда забываем, что существует тесная связь между дробью и десятичным числом. Действительно, дробь \(\displaystyle \frac{a}{b}\) — это буквально число \(a\), деленное на \(b\), поэтому в результате можно ожидать десятичную дробь.
Например, если вы вычисляете дробь \(\displaystyle \frac{6}{5}\) и интерпретируете ее как «6, деленное на 5», то, когда вы фактически выполняете расчет, вы получаете, что 6, деленное на 5, равно 1,2, что является десятичным числом с целая часть.
Однако есть одно предостережение: при вычислении десятичной дроби путем деления числителя на знаменатель мы не всегда получим такое простое десятичное число, как «1,2», как в предыдущем примере. Например, если я вычисляю 1/3 как 1, деленное на 3, я получаю 0,33333…. с бесконечной последовательностью троек.
Например, если я вычисляю 1/3 как 1, деленное на 3, я получаю 0,33333…. с бесконечной последовательностью троек.
Как перевести дробь в десятичную?
Процедура проста: для дроби \(\displaystyle \frac{a}{b}\) нужно разделить \(a\) на \(b\). Это кажется простым, но на самом деле мы обычно используем для этого калькулятор.
Если бы мы должны были сделать расчет вручную, как преобразовать дробь в десятичную без калькулятора? Существует изящная теорема Евклида об остатках, которая показывает, что для двух чисел \(a\) и \(b\) у вас есть число \(q\) (частное) и \(r\) (остаток), поэтому что \(a = b q + r\) с \(r
Например, если у нас есть \(a = 34\) и \(b = 12\), мы получаем \(34 = 2 \cdot 12 + 10\), поэтому частное равно 2, а остаток равен 10.
Дроби и повторяющиеся десятичные дроби
Описанный выше процесс не обязательно заканчивается с нулевым остатком в какой-то момент, потому что мы можем найти рекуррентный десятичный , как, например, в случае \(\displaystyle \frac{1}{3}\)
Как мы узнаем, когда мы закончим с повторяющимся десятичным числом?
. Ну и что интересно, это зависит от знаменателя: если простые множители разложения знаменателя всего 2 или 5, или если единственное простое число равно 2, или если единственное простое число равно 5, то десятичная дробь, найденная из дроби, будет иметь и конечную цифру (будет неповторяющейся).
Например, в случае \(\displaystyle \frac{1}{3}\) знаменатель равен 3, а 3 — простое число, поэтому знаменатель имеет простое число, которое не равно 2 и не 5 в его разложении, поэтому тогда мы получим повторяющееся (повторяющееся ) десятичный
Конвертер этой дроби в десятичную
Этот калькулятор предоставит соответствующее десятичное число, связанное с предоставленной дробью, и оценит, повторяется ли десятичное число или нет, путем анализа простого разложения знаменателя.
Преимущества и недостатки использования дроби по сравнению с десятичной дробью
- Использование десятичной дроби может быть более конкретным, потому что это число
-
Однако проблема десятичных дробей заключается в том, что может быть громоздко выражать повторяющиеся десятичные дроби.

- В самом деле, для повторяющегося десятичного числа 0,3333… с бесконечными тройками нам, возможно, придется придумать способ сделать действительно ясным, что последовательность троек не заканчивается.
- С другой стороны, с дробями тривиально выразить повторяющиеся десятичные дроби, такие как «1/3» для 0,33333……
Подробнее о дробях и процентах
Обычно нам приходится работать и преобразовывать обратно и вперед между десятичными числами и процентами, а также дробями. Переход от дроби к десятичному является обычным явлением, но иногда вам будет интересно перейти от дроби к процентам, а, как мы знаем, между процентами и десятичными дробями существует прямая эквивалентность.
Также с этим Калькулятор десятичной дроби вы можете провести обратный процесс, начав с десятичной дроби и придя к дроби.
Кроме того, очень распространен процесс преобразования десятичных чисел в проценты и процентов в десятичные. Например, когда мы имеем дело со ставками и видим, что ставка равна \(r = 0.04\), мы сразу же видим ее как \(r = 4\%\), которая просто получается путем умножения десятичной дроби на 100.
В зависимости от того, как вы его используете, вы можете использовать это
калькулятор доли в проценты
, так как иногда вы предпочитаете видеть связь дроби непосредственно с процентом.
Пример: Преобразование дроби в десятичную
Вопрос : вычислить дробь \(\displaystyle\frac{33}{75}\) как десятичную.
Доля до десятичной вопрос 2
Вопрос Выразите 3/81 в виде десятичной дроби. Является ли он рецидивирующим?
Доля до десятичной вопрос 3
Вопрос
Преобразование \(\displaystyle\frac{4597784}{2323453498}\) в десятичное число. Является ли он рецидивирующим?
Является ли он рецидивирующим?
Как решать десятичные дроби. Деление на десятичную дробь Деление десятичных дробей онлайн
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Выполнить сложение дробей путем сложения их числителей.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.

- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.

- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Онлайн калькуляторы и конвертеры:
Деление на десятичную дробь сводится к делению на натуральное число.
Правило деления числа на десятичную дробь
Чтобы разделить число на десятичную дробь, надо и в делимом, и в делителе запятую перенести на столько цифр вправо, сколько их в делителе после запятой. После этого выполнить деление на натуральное число.
Примеры.
Выполнить деление на десятичную дробь:
Чтобы разделить на десятичную дробь, нужно и в делимом, и в делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, то есть, на один знак. Получаем: 35,1: 1,8 =351: 18. Теперь выполняем деление уголком. В итоге получаем: 35,1: 1,8 = 19,5.
В итоге получаем: 35,1: 1,8 = 19,5.
2) 14,76: 3,6
Чтобы выполнить деление десятичных дробей, и в делимом, и в делителе переносим запятую вправо на один знак: 14,76: 3,6 = 147,6: 36. Теперь выполняемна натуральное число. Результат: 14,76: 3,6 = 4,1.
Чтобы выполнить деление на десятичную дробь натурального числа, надо и в делимом, и в делителе перенести на столько знаков вправо, сколько их в делителе после запятой. Поскольку в делителе в этом случае запятая не пишется, недостающее количество знаков заполняем нулями: 70: 1,75 = 7000: 175. Делим уголком полученные натуральные числа: 70: 1,75 = 7000: 175 =40.
4) 0,1218: 0,058
Чтобы разделить одну десятичную дробь на другую, переносим запятую вправо и в делимом, и в делителе на столько знаков, сколько их в делителе после запятой, то есть на три знака. Таким образом, 0,1218: 0,058 = 121,8: 58. Деление на десятичную дробь заменили делением на натуральное число. Делим уголком. Имеем: 0,1218: 0,058 = 121,8: 58 = 2,1.
5) 0,0456: 3,8
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей.
Допустим, дано уравнение следующего вида:
Данное уравнение можно решить двумя разными способами.
Способ № 1:
Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит число, то умножаем это число на каждый член в скобках:
Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону, целый числе в другую:
\[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\]
Делим 2 части на число перед \
\[ — 2x = — 17\]
Ответ: \
Способ № 2:
В этом способе умножим левую и правую части на 10:
Это линейное уравнение, которое решается по аналогии с 1 способом:
\[ — 72x + 52x = 17 — 144 — 43\]
\[ — 20x = — 170\]
Ответ: \
Где можно решить десятичные уравнения онлайн?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Простые арифметические действия — это основа дальнейшего обучения детей точным наукам. Математика сопровождает людей повсюду на протяжении всей жизни, а потому важно понимать её с самых азов. Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.
Как вычитать десятичные дроби в столбик
При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными
Действия с десятичными дробями производятся так же, как и с натуральными. Основные правила, которые важно знать при решении примеров на вычитание в столбик:
Основные правила, которые важно знать при решении примеров на вычитание в столбик:
- Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
- Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего.
 Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними. - Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
- Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.
Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее
Вычитание всегда можно проверить сложением.
Карточки для уроков
Чтобы было проще изучить алгоритм действий, можно распечатать для детей специальные карточки-памятки, которые помогут быстрее освоить новый материал.
Фотогалерея: варианты карточек для занятий
Видео: как вычитать десятичные дроби столбиком
Освоив это простое действие, дети смогут в дальнейшем лучше учиться, ведь примеры с десятичными дробями решают не только на математике, но и на физике, химии, астрономии. Главное — понять алгоритм.
Главное — понять алгоритм.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Калькулятор десятичных дробей
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Этот калькулятор может преобразовать дробь в десятичную, сделать знаменатель таким, как 10, 100, 1000 и т. д., определить, является ли дробь продолжением, и дает подробное решение.

Как преобразовать дробь в десятичную
Десятичные числа стали использоваться для более удобного написания дробей. Чтобы записать десятичное число, нужно разделить целую часть числа и дробную часть запятой. Если дробь не содержит целой части, перед запятой необходимо поставить ноль. Если дробь имеет знаменатель типа 10, 100, 1000 и т. д. и количество цифр в числителе меньше, чем в знаменателе, то для преобразования такого числа в дробь необходимо подсчитать количество цифр в знаменателе. числитель и количество нулей в знаменателе. Например, дробь
| 12 | ||
| 1000 |
(ноль целых 12 тысячных) 2 цифры в числителе и 3 нуля в знаменателе. 3 — 2 = 1, следовательно, после запятой необходимо написать один ноль:
| 12 | = 0,012 | |
| 1000 |
Приведем другой пример, дробь
| 3 | ||
| 1000 |
В этой дроби 1 цифра в числителе, 3 нуля в знаменателе. 3 — 1 = 2, следовательно, после запятой необходимо написать два нуля:
3 — 1 = 2, следовательно, после запятой необходимо написать два нуля:
| 3 | = 0,003 | |
| 1000 |
И последний пример, дробь
| 12 | ||
| 100 |
Эта дробь имеет 2 цифры в числителе и 2 нуля в знаменателе. 2 — 2 = 0, поэтому не нужно добавлять ноль после запятой:
| 12 | = 0,12 | |
| 100 |
Если знаменатель дроби является числом, отличным от таких чисел, как 10, 100, 1000 и т. д., то необходимо сделать знаменатель такой дроби равным 10, 100, 1000 и т. д. Первый шаг — упростить дробная часть. Затем разложите знаменатель дроби на простые множители. Если разложение содержит хотя бы один множитель, отличный от 2 или 5, то такая дробь может быть представлена только как бесконечное десятичное число. Если в разложении дроби все множители числа 2 или 5, то необходимо следить за тем, чтобы количество двоек и пятерок было одинаковым. Для этого нужно умножить числитель и знаменатель дроби на недостающее количество двоек или пятерок.
Например,
д., то необходимо сделать знаменатель такой дроби равным 10, 100, 1000 и т. д. Первый шаг — упростить дробная часть. Затем разложите знаменатель дроби на простые множители. Если разложение содержит хотя бы один множитель, отличный от 2 или 5, то такая дробь может быть представлена только как бесконечное десятичное число. Если в разложении дроби все множители числа 2 или 5, то необходимо следить за тем, чтобы количество двоек и пятерок было одинаковым. Для этого нужно умножить числитель и знаменатель дроби на недостающее количество двоек или пятерок.
Например,
| 1 | = | |
| 40 |
| 1 | = | |
| 2∙2∙2∙5 |
| 1∙5∙5 | = | |
| 2∙2∙2∙5∙5∙5 |
| 25 | = | |
| 1000 |
Приведем другой пример
| 5 | 301 | = |
| 200 |
| 6 | 101 | = |
| 200 |
| 6 | 101 | = |
| 2∙2∙2∙5∙5 |
| 6 | 101∙5 | = |
| 2∙2∙2∙5∙5∙5 |
| 6 | 505 | = |
| 1000 |
Приведем пример бесконечной десятичной дроби.
| 0,3333333333333333… | ||
При преобразовании этой дроби в десятичное число получается бесконечное десятичное число.
| You may also find the following calculators helpful | |
| Fraction Calculators | |
| Simplifying Fractions Calculator | |
| Improper to Mixed Fraction Calculator | |
| Mixed Fraction to Improper Calculator | |
| Fractions Calculator С пошаговым решением | |
| Возведение дроби в степень. Онлайн калькулятор. | |
| Калькулятор десятичной дроби | |
| Fraction to Decimal Calculator | |
| Compare Fractions Calculator | |
| Common Denominator Calculator | |
| Trigonometers Calculators | |
| Sine Calculator | |
| Cosine Calculator | |
| Tangent Calculator | |
| Вычислитель котангенса | |
| Вычислитель секанса | |
| Cosecant Calculator | |
| Arcsine Calculator | |
| Arccosine Calculator | |
| Arctangent Calculator | |
| Arccotangent Calculator | |
| Arcsecant Calculator | |
| Arccosecant Calculator | |
| Numeral Systems Calculators | |
| Калькулятор римских цифр | |
| Римские цифры От 1 до 3999 | |
| Калькулятор систем счисления | |
Двоичный калькулятор. Сложение, вычитание, умножение и деление двоичных чисел. Сложение, вычитание, умножение и деление двоичных чисел. | |
| Calculators (Number theory) | |
| Mathematical Expressions Calculator | |
| Calculator Parentheses | |
| Prime Factorization Calculator | |
| Gcd and Lcm Calculator With Steps | |
| Gcd and Lcm calculator using Euclidean алгоритм | |
| Калькулятор Gcd и Lcm для любого количества чисел | |
| Разбить число на его значение | |
| Разделить число на отношение. Онлайн -калькулятор с шагами | |
| Процентный калькулятор с этапами | |
| Научная нотация в калькулятор с десятичным преобразованием | |
| Научные нотации | |
| Факторский калькулятор с шагами | |
| . Факторский калькулятор со ступенями | |
| . Факторский калькулятор с шагами | |
. 1098 1098 | Logarithm Calculator |
| Quadratic Equations Calculator With Steps | |
| Remainder Calculator | |
| Root Calculator | |
| Decimal Period Calculator | |
| Big Number Calculator | |
| Rounding Numbers Calculator | |
| Калькулятор свойств корней и показателей | |
| Калькулятор комплексных чисел | |
| Area Calculators | |
| Area of a Square Calculator | |
| Area of a Rectangle Calculator | |
| Combinatorics Calculators | |
| Permutations of N Elements Calculator | |
| Combinations of N Elements by M Calculator | |
| Перестановки N элементов с помощью М-калькулятора | |
| Математические тренажеры | |
| Дополнительный математический тренажер | |
| Тренер по математике вычитания | |
| Умножение математического тренера | |
| Дивизион | |
| Математический тренажер | 11111111111110 | 111111111111111111111111111111111110 гг. Тренажер по математике отдела умножения вычитания. Найдите правильный ответ. Тренажер по математике отдела умножения вычитания. Найдите правильный ответ. |
| Онлайн-тренажер числовых выражений | |
| Linear Algebra and Analytical Geometers Calculators | |
| Matrix Addition and Subtraction Calculator | |
| Matrix Multiplication Calculator | |
| Matrix Transpose Calculator | |
| Matrix Determinant Calculator | |
| Inverse Matrix Calculator | |
| Длина сегмента линии. Онлайн-калькулятор расстояния между точками. | |
| Калькулятор векторных координат по двум точкам | |
| Калькулятор векторного модуля (длины) | |
| Калькулятор сложения и вычитания векторов | |
| Калькулятор векторного скалярного произведения. Используя длину векторов и косинус угла между векторами. | |
Калькулятор векторного скалярного произведения. Используя векторные координаты. | |
| Калькулятор векторного произведения. Используя векторные координаты. | |
| Векторный калькулятор тройного произведения | |
| Vector Multiplication by Number Calculator | |
| Angle Between Vectors Calculator | |
| Vector Collinearity Check Calculator | |
| Vector Coplanarity Calculator | |
| Converters | |
| Length Converter | |
| Speed Converter | |
| Преобразователь ускорения | |
| Калькуляторы физики | |
Механика | |
| Speed Time Distance Calculator | |
| Acceleration Speed Distance Calculator | |
| Displacement Time Calculator | |
| Time Calculator | |
| Newton’s Second Law Calculator | |
| Gravitational Force Calculator | |
| Momentum Калькулятор | |
| Калькулятор импульсов | |
| Калькулятор веса объекта | |
ОПТИКА | |
Калькулятор отражения и преломлений. Калькулятор электрического заряда Q Калькулятор электрического заряда Q | |
| Калькулятор силы, действующей на заряд | |
| Distance From Charge Calculator | |
| Potential Charge Energy Calculator | |
| Electric Field Potential Calculator | |
| Conductor and Sphere Capacitance Calculator | |
Capacitors | |
| Калькулятор емкости параллельных пластинчатых, цилиндрических и сферических конденсаторов | |
| Калькулятор напряженности электрического поля в пластинчато-параллельных, цилиндрических и сферических конденсаторах | |
| Напряжение (потенциальная разность) параллельной пластины, цилиндрического и сферического конденсатора калькулятор | |
| Расстояние между пластинками в калькуляторе плиты параллельной пластины | |
| Площадь пластин в параллельной пластинке калькулятор | |
| Площадь пластин в параллельной пластинке калькулятор | |
| Площадь пластин в параллельной пластинке калькулятор | |
| Площадь пластины в параллельной пластинке калькулятор | |
Площадь пластин. Калькулятор Калькулятор | |
| Калькулятор энергии, запасенной в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах | |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов | |
| Астрономические калькуляторы | |
| Вес объекта на других планетах | |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках | |
| Генераторы | |
| Генератор случайных чисел | |
| Генератор паролей |
Рабочие листы с десятичными дробями
Благодарим вас за посещение страницы рабочих листов с десятичными дробями и процентами в американском формате на сайте Math-Drills.Com, где мы ОБЯЗАТЕЛЬНО помогаем учащимся учиться. На этой странице вы найдете рабочие листы Decimals по различным темам, включая сравнение и сортировку десятичных дробей, сложение, вычитание, умножение и деление десятичных дробей, а также преобразование десятичных дробей в другие числовые форматы. Для начала вы обнаружите, что печатные формы общего назначения могут быть полезны при обучении понятиям десятичных дробей и разрядного значения. Более подробная информация о них содержится сразу под подзаголовком. Если вы предпочитаете десятичные дроби неанглоязычного формата (т. е. запятые, используемые в качестве десятичных дробей), посетите страницу десятичных дробей европейского формата.
Для начала вы обнаружите, что печатные формы общего назначения могут быть полезны при обучении понятиям десятичных дробей и разрядного значения. Более подробная информация о них содержится сразу под подзаголовком. Если вы предпочитаете десятичные дроби неанглоязычного формата (т. е. запятые, используемые в качестве десятичных дробей), посетите страницу десятичных дробей европейского формата.
Ниже на странице рабочие листы по округлению, сравнению и упорядочению десятичных дробей позволяют учащимся более комфортно работать с десятичными дробями, прежде чем они перейдут к выполнению операций с десятичными дробями. На странице есть много операций с десятичными знаками. Было бы неплохо, если бы учащиеся хорошо знали сложение, вычитание, умножение и деление, прежде чем пытаться ответить на эти вопросы. В конце страницы вы найдете десятичные числа, используемые в порядке выполнения вопросов.
Самые популярные рабочие листы с десятичными знаками на этой неделе
Умножение трехзначных чисел на двузначные числа с различными десятичными знаками ( 2048 просмотров на этой неделе )Сложение и вычитание десятичных знаков с тремя разрядами до и после запятой ( 1572 просмотров на этой неделе )Умножение 2-значных чисел на 2-значные числа с различными десятичными знаками ( 1366 просмотров на этой неделе )Деление десятичных знаков на различные десятичные числа с различными размерами частных ( 1151 просмотров на этой неделе )Округление различных десятичных знаков до различных десятичных знаков ( 1080 просмотров на этой неделе )Универсальные печатные формы
Универсальные десятичные печатные формы используются в различных контекстах и помогают учащимся решать математические вопросы, связанные с десятичными дробями.
Сетка тысячных является полезным инструментом для представления десятичных дробей. Каждый маленький прямоугольник представляет собой тысячную. Каждый квадрат представляет сотую часть. Каждая строка или столбец представляет десятую часть. Вся сетка представляет собой одно целое. Сетка сотых может использоваться для моделирования процентов или десятичных дробей. Таблица десятичных разрядов — это инструмент, используемый учащимися, которые впервые изучают разрядные значения, связанные с десятичными знаками, или для тех учащихся, у которых возникают трудности с разрядными значениями при работе с десятичными знаками.
Тысячные Сетка Сотые Сетки ( 4 на странице) Сотые Сетки ( 9 на странице) Сотки Сетки ( 20 на странице) Таблица десятичных разрядов (от до сотых долей ) Таблица десятичных разрядов (от единиц до тысячных ) Таблица десятичных разрядов ( от сотен до сотых ) Таблица десятичных разрядов ( тысячных до тысячных ) Таблица десятичных разрядов ( от сотен тысяч до тысячных ) Таблица десятичных разрядов ( от сотен миллионов до миллионных долей )
Расширенная форма с десятичными знаками
Расширенная форма с десятичными знаками Рабочие листы, включая преобразование из стандартной в расширенную форму и из расширенной формы в стандартную форму.
Учащимся, у которых есть трудности с развернутой формой, попробуйте ознакомить их с таблицей значений десятичных разрядов и разрешить им использовать ее при преобразовании чисел стандартной формы в расширенную форму. На самом деле существует пять способов (на два больше, чем с целыми числами) для записи расширенной формы для десятичных дробей, и какой из них вы используете, зависит от вашего приложения или предпочтений. Вот краткий обзор различных способов использования десятичного числа 1,23.
1. Расширенная форма с использованием десятичных знаков: 1 + 0,2 + 0,03
2. Расширенная форма с использованием дробей: 1 + 2 ⁄ 10 + 3 ⁄ 100
)
4. Расширенная форма коэффициентов с использованием дробей: (1 × 1) + (2 × 1 ⁄ 10 ) + (3 × 1 ⁄ 100 )
5. Расширенная экспоненциальная форма: (1 × 10 0 ) + (2 × 10 -1 ) + (3 × 10 9 )2023 -2 )
Расширенная экспоненциальная форма: (1 × 10 0 ) + (2 × 10 -1 ) + (3 × 10 9 )2023 -2 )
Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 3 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 4 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 5 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 6 десятичных разрядов) Преобразование десятичных знаков из стандартных в Расширенная форма с использованием десятичных знаков ( 7 десятичных знаков) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 8 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием десятичных знаков ( 9 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием дробей ( 3 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в расширенную форму с использованием дробей ( 4 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием дробей ( 5 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием дробей ( 6 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием дробей ( 7 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в расширенную форму с использованием дробей ( 8 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму с использованием дробей ( 9 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием десятичных знаков ( 3 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием десятичных знаков ( 4 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в расширенную форму коэффициентов с использованием десятичных дробей ( 5 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием десятичных знаков ( 6 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием десятичных знаков ( 7 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием десятичных знаков ( 8 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в форму расширенных коэффициентов с использованием десятичных дробей ( 9 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 3 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 4 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 5 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в расширенную форму множителей с использованием дробей ( 6 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 7 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 8 десятичных разрядов) Преобразование десятичных знаков из стандартной формы в расширенную форму коэффициентов с использованием дробей ( 9 десятичных разрядов) Преобразование десятичных дробей из стандартной формы в расширенную экспоненциальную форму ( 3 десятичных знаков) Преобразование десятичных знаков из стандартных в расширенную экспоненциальную форму ( 4 десятичных разрядов) Преобразование десятичных знаков из стандартных в расширенную экспоненциальную форму ( 5 десятичных разрядов) Преобразование десятичных знаков из стандартных в расширенную экспоненциальную форму ( 6 десятичных разрядов) Преобразование десятичных знаков из стандартных в расширенную экспоненциальную форму ( 7 десятичных разрядов) Преобразование десятичных знаков из стандартных в Расширенная экспоненциальная форма ( 8 десятичных разрядов) Преобразование десятичных знаков из стандартных в расширенную экспоненциальную форму ( 9 десятичных разрядов) СТАРЫЙ стандарт в расширенную форму (3 цифры до десятичной точки; 2 после) СТАРЫЙ стандарт в расширенную форму (4 цифры до десятичной точки; 3 после) СТАРЫЙ стандарт в расширенную форму (6 цифр до десятичной точки; 4 после) СТАРЫЙ стандарт в расширенную форму (12 цифр до десятичной точки; 3 после)
Запись расширенной формы десятичных чисел в стандартной форме Конечно, возможность конвертировать числа уже в расширенном виде в стандартный вид также важна. В эти рабочие листы включены все пять версий десятичной развернутой формы.
В эти рабочие листы включены все пять версий десятичной развернутой формы.
Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 3 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 4 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 5 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 6 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 7 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 8 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием десятичных знаков в стандартную форму ( 9 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием дробей в стандартную форму ( 3 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием дробей в стандартную форму ( 4 десятичных разрядов) Преобразование десятичных дробей из расширенной формы с использованием дробей в стандартную форму ( 5 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием дробей в стандартную форму ( 6 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием дробей в стандартную форму ( 7 десятичных разрядов) Преобразование десятичных знаков из расширенной формы с использованием дробей в стандартную форму ( 8 десятичных разрядов) Преобразование десятичных дробей из расширенной формы с использованием дробей в стандартную форму ( 9 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 3 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 4 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 5 десятичных разрядов) Преобразование десятичных дробей из расширенной формы коэффициентов с использованием десятичных дробей в стандартную форму ( 6 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 7 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 8 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием десятичных знаков в стандартную форму ( 9 десятичных разрядов) Преобразование десятичных дробей из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 3 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 4 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 5 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 6 десятичных разрядов) Преобразование десятичных дробей из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 7 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 8 десятичных разрядов) Преобразование десятичных знаков из расширенной формы коэффициентов с использованием дробей в стандартную форму ( 9 десятичных разрядов) Преобразование десятичных знаков из расширенной экспоненциальной формы в стандартную форму ( 3 десятичных разрядов) Преобразование десятичных дробей из расширенной экспоненциальной формы в стандартную форму ( 4 десятичных разрядов) Преобразование десятичных знаков из расширенной экспоненциальной формы в стандартную форму ( 5 десятичных разрядов) Преобразование десятичных знаков из расширенной экспоненциальной формы в стандартную форму ( 6 десятичных разрядов) Преобразование десятичных знаков из расширенной экспоненциальной формы в стандартную форму ( 7 десятичных разрядов) Преобразование десятичных дробей из расширенной экспоненциальной формы в стандартную форму ( 8 десятичных разрядов) Преобразование десятичных знаков из расширенной экспоненциальной формы в стандартную форму ( 9 десятичных разрядов) СТАРЫЙ Расширенный до стандартной формы (3 цифры перед запятой; 2 после) СТАРЫЙ Расширенный до стандартной формы (4 цифры перед запятой; 3 после) СТАРЫЙ Расширенный до стандартной формы (6 цифр до десятичной точки; 4 после) СТАРЫЙ Расширенный до стандартной формы (12 цифр перед запятой; 3 после)
Рабочие листы для округления десятичных чисел
Рабочие листы для округления десятичных знаков с опциями для округления различных десятичных чисел до различных разрядов.
Округление десятичных дробей аналогично округлению целых чисел; Вы должны знать свою стоимость места! Изучая округление, также полезно узнать об усечении, поскольку это может помочь учащимся правильно округлить. Простая стратегия округления включает в себя усечение, использование цифр после усечения, чтобы определить, остается ли новая конечная цифра той же самой или увеличивается, затем предпринимаются действия, увеличивая, если необходимо, и отбрасывая остальные. Вот простой пример. Округлите 4,567 до десятых. Во-первых, усекаем число после десятых долей 4,5|67. Далее посмотрите на усеченную часть (67). Это больше половины пути к 9?9 (т.е. 50 или больше)? Это так, поэтому решение будет заключаться в увеличении. Наконец, увеличьте значение десятых долей на 1, чтобы получить 4,6. Конечно, ситуация немного усложняется, если завершающая цифра — 9. В этом случае может потребоваться некоторая перегруппировка. Например: округлить 6,959 до ближайшей десятой. Обрезать: 6,9 | 59. Решаем увеличить, поскольку 59 — это больше половины пути к 99. Увеличение приводит к необходимости перегруппировать десятые доли в дополнительное целое, поэтому результат равен 7,0. Следите за тем, чтобы ученики не писали 6.10. В этом случае вы захотите исправить их сразу. Последнее замечание: если есть три усеченные цифры, то возникает вопрос, является ли число более чем на полпути к 999. Аналогично для одной цифры; это число более чем на полпути к 9. И так далее…
Обрезать: 6,9 | 59. Решаем увеличить, поскольку 59 — это больше половины пути к 99. Увеличение приводит к необходимости перегруппировать десятые доли в дополнительное целое, поэтому результат равен 7,0. Следите за тем, чтобы ученики не писали 6.10. В этом случае вы захотите исправить их сразу. Последнее замечание: если есть три усеченные цифры, то возникает вопрос, является ли число более чем на полпути к 999. Аналогично для одной цифры; это число более чем на полпути к 9. И так далее…
Следует также отметить, что в некоторых научных и математических «кружках» округление немного отличается «на 5». Например, большинство людей будут округлять до 5, например: 6,5 —> 7; 3,555 —> 3,56; 0,60500 —> 0,61; и т. д. Однако другой способ округления числа 5 — это округление до ближайшего четного числа, поэтому 5,5 будет округлено до 6, а 8,5 — в меньшую сторону до 8. Основная причина этого — не исказить результаты большого количества событий округления. Если вы всегда округляете до 5, в среднем вы получите немного более высокие результаты, чем должны. Поскольку большинство студентов предуниверситетского образования округляют число до 5, именно это мы и сделали в следующих рабочих листах.
Поскольку большинство студентов предуниверситетского образования округляют число до 5, именно это мы и сделали в следующих рабочих листах.
Округлить десятых долей до целого числа Округлить сотых до целого числа Округлить тысячных до целого числа Округлите десятитысячных до целого числа Округлить различных десятичных дробей до целого числа Округлить Сотые до Десятые Округлить Тысячные до Десятые Раунд Десятитысячные от до Десятые доли Округлить Разные Десятичные до Десятичные Округлить Тысячные до Сотые Раунд Десятитысячные до Сотые Округлить Разные Десятичные до Сотые Раунд Десятитысячные до Тысячные Округлить Сотые от до Различные Десятичные разряды Раунд Тысячных 9От 1959 до Различные десятичных разрядов Раунд Десятитысячные до Различные Десятичные разряды Округлить различных десятичных разрядов до различных десятичных разрядов
Рабочие листы для сравнения и упорядочивания десятичных чисел
Рабочие листы для сравнения и упорядочивания десятичных знаков, чтобы помочь учащимся распознавать порядковый номер в десятичных числах.
В таблицах сравнения десятичных дробей учащиеся сравнивают пары чисел, а в таблицах упорядочения десятичных дробей учащиеся сравнивают список чисел, сортируя их.
Сравнение листов с десятичными дробями. Учащиеся, которые научились сравнивать целые числа, обнаружат, что сравнивать десятичные дроби довольно легко. Самая простая стратегия состоит в том, чтобы сначала сравнить числа до десятичной (целая часть числа) и сравнить только десятичные части, если целые части числа равны. Такого рода вопросы позволяют учителям/родителям получить хорошее представление о том, усвоили ли учащиеся концепцию десятичных дробей или нет. Например, если студент считает, что 4,93 больше, чем 8,7, то им может понадобиться немного больше инструкций по разрядности. Близкие числа означают, что были предприняты некоторые меры, чтобы числа выглядели одинаково. Например, они могут быть близки по стоимости, т.е. 3.3. и 3.4, или одна из цифр может быть изменена, как в 5. 86 и 6.86.
86 и 6.86.
Сравнение десятичных дробей до Десятых долей ( Оба числа случайные ) Сравнение десятичных дробей до десятых ( отличается одной цифрой от ) Сравнение десятичных дробей до Десятые ( Оба числа близки по значению ) Сравнение десятичных дробей до десятых ( различных трюков ) Сравнение десятичных дробей до сотых ( оба числа случайные ) Сравнение десятичных дробей до сотых ( одна цифра отличается от ) Сравнение десятичных знаков до сотых ( две цифры заменены местами ) Сравнение десятичных долей до сотых ( Оба числа близки по значению ) Сравнение десятичных знаков до сотых ( Одно число имеет лишнюю цифру ) Сравнение десятичных дробей до сотых ( Различные приемы ) Сравнение десятичных долей до тысячных Сравнение десятичных дробей до тысячных ( одна цифра отличается от ) Сравнение десятичных знаков до тысячных ( две цифры заменены местами ) Сравнение десятичных долей до тысячных ( Оба числа близки по значению ) Сравнение десятичных дробей до тысячных ( Одно число имеет лишнюю цифру ) Сравнение десятичных дробей до тысячных ( различных трюков ) Сравнение десятичных долей до десятитысячных Сравнение десятичных дробей до десятитысячных ( отличается одной цифрой от ) Сравнение десятичных знаков до десятитысячных ( две цифры заменены местами ) Сравнение десятичных дробей до Десять тысячных ( Оба числа близки по значению ) Сравнение десятичных дробей до десятитысячных ( Одно число имеет лишнюю цифру ) Сравнение десятичных дробей до Десятитысячных ( Различные приемы ) Сравнение десятичных долей до сотен тысячных Сравнение десятичных дробей до стотысячных ( отличается одной цифрой от ) Сравнение десятичных долей до сотен тысячных ( две цифры заменены местами ) Сравнение десятичных дробей до стотысячных ( оба числа близки по значению ) Сравнение десятичных дробей до стотысячных ( Одно число имеет лишнюю цифру ) Сравнение десятичных дробей до стотысячных ( различные приемы )
Заказ или сортировка десятичных чисел Упорядочивание десятичных дробей очень похоже на сравнение десятичных дробей, за исключением того, что числовых значений больше двух. Как правило, учащиеся определяют наименьшее (или наибольшее) десятичное число для начала, вычеркивают его из списка, затем повторяют процесс, чтобы найти следующее наименьшее/наибольшее число, пока не доберутся до последнего числа. Всегда полезно проверить список в конце.
Как правило, учащиеся определяют наименьшее (или наибольшее) десятичное число для начала, вычеркивают его из списка, затем повторяют процесс, чтобы найти следующее наименьшее/наибольшее число, пока не доберутся до последнего числа. Всегда полезно проверить список в конце.
Порядок десятичных сотых Порядок десятичных тысячных
Преобразование десятичных дробей в дроби и другие числовые форматы
Преобразование рабочих листов десятичных дробей в основном для преобразования десятичных дробей и дробей, а также в проценты и отношения.
Преобразование десятичных чисел в дроби и другие числовые форматы Есть много веских причин для преобразования десятичных дробей в другие числовые форматы. Работать с дробью в операциях часто проще, чем с эквивалентным десятичным числом. Рассмотрим 0,333… что эквивалентно 1/3. Умножить 300 на 0,333… сложно, но умножить 300 на 1/3 очень просто! Учащиеся должны быть знакомы с некоторыми наиболее распространенными преобразованиями дробей в десятичные числа, чтобы они могли переключаться между ними по мере необходимости.
Преобразование дробей в конечные десятичные дроби Преобразование дробей в завершающие и повторяющиеся десятичные дроби Преобразование конечных десятичных дробей в дроби Преобразование завершающих и повторяющихся десятичных дробей в дроби Преобразование дробей в сотые Преобразование дробей в десятичные дроби, проценты и отношения части к части Преобразование дробей в десятичные дроби, проценты и отношения части к целому Преобразование десятичных знаков г. в дроби, проценты и отношения частей к частям Преобразование десятичных чисел в дроби, проценты и отношения части к целому Преобразование процентов в дроби, десятичные дроби и отношения части к части Преобразование процентов в дроби, десятичные дроби и отношения части к целому Преобразование соотношений частей в дроби, десятичные дроби и проценты Преобразование отношений части к целому в дроби, десятичные дроби и проценты Преобразование различных дробей , десятичных знаков, процентов и отношений частей к частям Преобразование различных дробей , десятичных знаков, процентов и отношений части к целому Преобразование различных дробей , десятичных знаков, процентов и отношений частей к частям с помощью 7-х и 11-х Преобразование различных дробей, десятичных знаков, процентов и отношений части к целому с помощью 7-х и 11-х
Листы сложения и вычитания десятичных дробей
Листы сложения и вычитания десятичных дробей с различными трудностями, включая сложение и вычитание сами по себе, а также смешанные на странице.
Попробуйте следующую стратегию мысленного сложения десятичных дробей. Начните с игнорирования десятичных знаков в вопросе о сложении. Сложите числа, как если бы они были целыми числами. Например, 3,25 + 4,98 можно рассматривать как 325 + 498 = 823. Используйте оценку, чтобы решить, где разместить десятичную дробь. В примере 3,25 + 4,98 приблизительно равно 3 + 5 = 8, поэтому десятичный знак в сумме должен стоять между 8 и 2 (т.е. 8,23)
Добавление десятичной дроби Десятые доли с 0 перед запятой (диапазон от 0,1 до 0,9) Добавление десятичной дроби Десятичных долей с 1 цифрой перед десятичной дробью (диапазон от 1,1 до 9,9) Добавление десятичного числа Десятичных долей с двумя цифрами перед десятичным числом (диапазон от 10,1 до 99,9) Добавление десятичного числа сотых долей с 0 перед десятичным числом (диапазон от 0,01 до 0,99) Сложение десятичного числа с сотыми долями с 1 цифрой перед десятичным числом (диапазон от 1,01 до 9). .99) Добавление десятичного числа Сотые доли с двумя цифрами перед десятичным числом (диапазон от 10,01 до 99,99) Добавление десятичного числа тысячных с 0 перед десятичным числом (диапазон от 0,001 до 0,999) Сложение десятичного числа с тысячными долями с 1 цифрой перед десятичным числом (диапазон от 1,001 до 9,999) Сложение десятичного числа с тысячными долями с двумя цифрами перед десятичным числом (диапазон от 10,001 до 99,999) Добавление десятичной дроби Десятитысячные с 0 перед запятой (диапазон от 0,0001 до 0,9999) Добавление десятичной дроби Десятитысячных с 1 цифрой перед десятичной дробью (диапазон от 1,0001 до 9,9999) Добавление десятичной дроби Десятитысячных с двумя цифрами перед десятичной дробью (диапазон от 10,0001 до 99,9999) Добавление различных десятичных знаков с 0 перед запятой
Добавление различных десятичных знаков с 1 цифрой перед запятой
Добавление Различные десятичных знаков с 2 цифрами перед запятой
Добавление различных десятичных знаков с различным количеством цифр перед запятой
.99) Добавление десятичного числа Сотые доли с двумя цифрами перед десятичным числом (диапазон от 10,01 до 99,99) Добавление десятичного числа тысячных с 0 перед десятичным числом (диапазон от 0,001 до 0,999) Сложение десятичного числа с тысячными долями с 1 цифрой перед десятичным числом (диапазон от 1,001 до 9,999) Сложение десятичного числа с тысячными долями с двумя цифрами перед десятичным числом (диапазон от 10,001 до 99,999) Добавление десятичной дроби Десятитысячные с 0 перед запятой (диапазон от 0,0001 до 0,9999) Добавление десятичной дроби Десятитысячных с 1 цифрой перед десятичной дробью (диапазон от 1,0001 до 9,9999) Добавление десятичной дроби Десятитысячных с двумя цифрами перед десятичной дробью (диапазон от 10,0001 до 99,9999) Добавление различных десятичных знаков с 0 перед запятой
Добавление различных десятичных знаков с 1 цифрой перед запятой
Добавление Различные десятичных знаков с 2 цифрами перед запятой
Добавление различных десятичных знаков с различным количеством цифр перед запятой
Блоки с основанием десять можно использовать для десятичного вычитания. Просто переопределите блоки так, чтобы большой блок был единицей, плоскость — десятой, стержень — сотой, а маленький куб — тысячной. Смоделируйте и вычтите десятичные дроби, используя блоки с основанием десять, чтобы учащиеся могли «увидеть», как на самом деле работают десятичные дроби.
Просто переопределите блоки так, чтобы большой блок был единицей, плоскость — десятой, стержень — сотой, а маленький куб — тысячной. Смоделируйте и вычтите десятичные дроби, используя блоки с основанием десять, чтобы учащиеся могли «увидеть», как на самом деле работают десятичные дроби.
Вычитание десятичной дроби Десятых долей с Без целочисленной части Вычитание десятичной дроби Десятых долей с целой частью в уменьшаемом Вычитание десятичных долей Десятых долей с целой частью в уменьшаемом и вычитаемом Вычитание десятичной дроби Сотые доли с Без целочисленной части Вычитание десятичной дроби сотых с целой частью в уменьшаемом и вычитаемом г.
Вычитание десятичной сотых с большей целой частью в уменьшаемом Вычитание десятичной дроби Тысячных с Без целочисленной части Вычитание десятичной дроби тысячных с целой частью в уменьшаемом и вычитаемом Вычитание десятичной дроби Десятитысячных с Без целочисленной части Вычитание десятичной дроби десятитысячных с целой частью в уменьшаемом и вычитаемом г. Вычитание различных десятичных долей до сотых Вычитание различных десятичных долей до тысячных Вычитание различных десятичных долей до десятитысячных
Вычитание различных десятичных долей до сотых Вычитание различных десятичных долей до тысячных Вычитание различных десятичных долей до десятитысячных
Складывать и вычитать десятичные дроби довольно просто, когда все десятичные дроби выстроены в ряд. С вопросами, расположенными горизонтально, учащимся предлагается понять разрядное значение, связанное с десятичными знаками. Прекрасная стратегия для размещения десятичной дроби — использовать оценку. Например, если вопрос 490,2 + 20,1, ответ без десятичной дроби — 693. Оцените, округлив 49,2 до 50 и 20,1 до 20. 50 + 20 = 70. Десятичная запятая в 693 должна быть помещена между 9 и 3, как в 69,3, чтобы получить число близко к оценке 70.
Вышеупомянутая стратегия поможет учащимся понять операции с десятичными дробями, но также важно, чтобы у них была прочная основа для численного значения и мастерства в эффективных стратегиях, чтобы полностью преуспеть в этих операциях. вопросы. Как и в случае любого математического навыка, неразумно демонстрировать его учащимся, пока они не приобретут необходимые предварительные навыки и знания.
вопросы. Как и в случае любого математического навыка, неразумно демонстрировать его учащимся, пока они не приобретут необходимые предварительные навыки и знания.
Сложение десятичных знаков с десятыми по горизонтали Добавление десятичных знаков к сотым по горизонтали Добавление десятичных знаков к тысячным по горизонтали Добавление десятичных знаков к десятитысячным по горизонтали Добавление десятичных знаков по горизонтали до двух разрядов До и после десятичной дроби Добавление десятичных знаков по горизонтали до Три знака До и после десятичной дроби Добавление десятичных знаков по горизонтали до четырех разрядов До и после десятичной дроби Вычитание десятичных знаков до десятых По горизонтали Вычитание десятичных долей до сотых По горизонтали Вычитание десятичных долей до тысячных По горизонтали Вычитание Десятичных долей до Десятитысячных По горизонтали Вычитание десятичных знаков по горизонтали до двух знаков до и после десятичной дроби Вычитание десятичных знаков по горизонтали до трех разрядов До и после десятичной дроби Вычитание десятичных знаков по горизонтали до четырех разрядов До и после десятичной дроби Сложение и вычитание десятичных знаков до десятых По горизонтали Сложение и вычитание десятичных знаков до Сотые По горизонтали Сложение и вычитание Десятичных долей до тысячных По горизонтали Сложение и вычитание десятичных дробей до десятитысячных по горизонтали Сложение и вычитание десятичных знаков по горизонтали до двух разрядов До и после десятичной дроби Сложение и вычитание десятичных знаков по горизонтали до трех разрядов До и после десятичной дроби Сложение и вычитание десятичных знаков по горизонтали до четырех знаков до и после десятичной дроби
Рабочие листы по умножению и делению десятичных дробей
Рабочие листы по умножению и делению десятичных дробей различных уровней сложности.
Умножение десятичных дробей на целые числа очень похоже на умножение целых чисел, за исключением того, что нужно иметь дело с десятичной дробью. Хотя поначалу у учащихся могут возникнуть проблемы с этим, из-за возможности округления и оценки они обычно могут понять это довольно быстро. Многие учителя советуют ученикам игнорировать десятичные дроби и умножать числа так же, как и целые числа. Это хорошая стратегия для использования. Выяснить, где десятичная дробь идет в конце, можно, подсчитав, сколько знаков после запятой было в исходном вопросе, и дав ответ, сколько знаков после запятой. Чтобы лучше понять этот метод, учащиеся могут округлить два коэффициента и умножить их в уме, чтобы получить оценку, а затем поставить десятичную дробь на основе своей оценки. Например, умножение 90,84 × 91, студенты могут сначала округлить числа до 10 и 91 (оставить 91, так как умножить на 10 легко), а затем получить оценку 910. На самом деле умножение (игнорируя десятичную дробь) дает вам 89544. Чтобы получить это число близко к 910 , десятичная дробь должна находиться между 5 и 4, то есть 895,44. Обратите внимание, что в факторах есть два десятичных знака, а в ответе два десятичных знака, но оценка сделала его более понятным, а не просто методом.
На самом деле умножение (игнорируя десятичную дробь) дает вам 89544. Чтобы получить это число близко к 910 , десятичная дробь должна находиться между 5 и 4, то есть 895,44. Обратите внимание, что в факторах есть два десятичных знака, а в ответе два десятичных знака, но оценка сделала его более понятным, а не просто методом.
Умножить Двузначные десятые по 1-значное целых чисел Умножьте двузначных сотых на однозначных целых чисел. Умножьте двузначных тысячных на однозначных целых чисел. Умножьте 3-значных десятых на 1-значных целых чисел Умножьте трехзначных сотых на однозначных целых чисел. Умножьте трехзначных тысячных на однозначных целых чисел. Умножить различных десятичных дробей на 1 цифра целых чисел Умножение двузначных десятых на двузначных целых чисел Умножение двузначных сотых на двузначных целых чисел Умножение 3-значных десятых на 2-значных целых чисел Умножение трехзначных сотых на двузначных целых чисел Умножение трехзначных тысячных на двузначных целых чисел Умножение различных десятичных дробей на двузначных целых чисел
Умножение
на десятичные числа Умножение двузначных целых на двузначные десятых Умножение двузначных десятых на двузначное десятых Умножение двузначных сотых на двузначное десятых Умножение 3-значных целых на 2-значные десятых Умножение 3-значные десятые на 2-значные десятых Умножение 3-значных сотых на 2-значное десятых Умножение 3-значных тысячных на 2-значное десятых Умножение различных десятичных дробей на двузначные десятых Умножение двузначного целого числа на двузначное число сотых Умножение двузначных десятых на двузначное сотых Умножение двузначных сотых г. двузначным числом сотых Умножение трехзначного целого числа на двузначное число сотых Умножение 3-значных десятых на 2-значное сотых Умножение трехзначных сотых на двузначное сотых Умножение 3-значных тысячных на 2-значное сотых Умножение различных десятичных дробей на двузначные сотых Умножение двузначных чисел на двузначные с различных знаков после запятой
Умножение трехзначных чисел на двузначные с различными десятичными знаками
двузначным числом сотых Умножение трехзначного целого числа на двузначное число сотых Умножение 3-значных десятых на 2-значное сотых Умножение трехзначных сотых на двузначное сотых Умножение 3-значных тысячных на 2-значное сотых Умножение различных десятичных дробей на двузначные сотых Умножение двузначных чисел на двузначные с различных знаков после запятой
Умножение трехзначных чисел на двузначные с различными десятичными знаками
Десятичное умножение (диапазон от 0,1 до 0,9) Десятичное умножение (диапазон от 1,1 до 9,9) Десятичное умножение (диапазон от 10,1 до 99,9) Десятичное умножение (от 0,01 до 0,99) Десятичное умножение (диапазон от 1,01 до 9,99) Десятичное умножение (диапазон от 10,01 до 99,99) Случайное количество цифр Случайное количество мест
Деление десятичных дробей на целые числаРазделить десятые доли на целое число Разделить сотые доли на целое число Разделить тысячные на целое число Разделить десять тысячных на целое число Разделить различные десятичные дроби на целое число
Деление на частных, что дает хороший результат Если вы не знакомы с делением с помощью десятичного делителя, то общий метод заполнения вопросов — избавиться от десятичной дроби в делителе. Это делается путем умножения делителя и делимого на одну и ту же величину, обычно на степень десяти, такую как 10, 100 или 1000. Например, если вопрос о делении 5,32/5,6, вы должны умножить делитель и делимое на 10, чтобы получить получить эквивалентную задачу деления, 53,2/56. Завершение этого деления даст точно такое же частное, что и исходное (попробуйте на своем калькуляторе, если не верите нам). Основная причина завершения десятичного деления таким образом состоит в том, чтобы получить десятичную дробь в правильном месте при использовании алгоритма длинного деления США.
Это делается путем умножения делителя и делимого на одну и ту же величину, обычно на степень десяти, такую как 10, 100 или 1000. Например, если вопрос о делении 5,32/5,6, вы должны умножить делитель и делимое на 10, чтобы получить получить эквивалентную задачу деления, 53,2/56. Завершение этого деления даст точно такое же частное, что и исходное (попробуйте на своем калькуляторе, если не верите нам). Основная причина завершения десятичного деления таким образом состоит в том, чтобы получить десятичную дробь в правильном месте при использовании алгоритма длинного деления США.
Гораздо более простая стратегия, на наш взгляд, состоит в том, чтобы сначала полностью игнорировать десятичные дроби и использовать оценку, чтобы поместить десятичную дробь в частное. В том же примере, что и выше, вы получите 532/56 = 95. Если вы «гибко» округлите оригинал, вы получите около 5/5, что примерно равно 1, поэтому десятичная запятая в 95 должна быть помещена так, чтобы 95 было близко к 1. В этом случае вы должны поместить его непосредственно перед 9, чтобы получить 0,95. Сочетание этой стратегии с описанной выше также может очень помочь с более сложными вопросами. Например, 4,584184 ÷ 0,461 можно сначала преобразовать в эквивалент: 4584,184 ÷ 461 (вы можете оценить частное примерно как 10). Заполните вопрос о делении без десятичных знаков: 4584184 ÷ 461 = 9944, затем поместите десятичную дробь так, чтобы 9944 было примерно 10. В результате получится 9,944.
Сочетание этой стратегии с описанной выше также может очень помочь с более сложными вопросами. Например, 4,584184 ÷ 0,461 можно сначала преобразовать в эквивалент: 4584,184 ÷ 461 (вы можете оценить частное примерно как 10). Заполните вопрос о делении без десятичных знаков: 4584184 ÷ 461 = 9944, затем поместите десятичную дробь так, чтобы 9944 было примерно 10. В результате получится 9,944.
Деление десятичных чисел не должно быть слишком сложным, особенно с рабочими листами ниже, где десятичные числа работают хорошо. Чтобы сделать эти рабочие листы, мы сначала случайным образом сгенерировали делитель и частное, а затем перемножили их вместе, чтобы получить делимое. Конечно, вы увидите частное только на странице ответов, но генерация вопросов таким образом позволяет хорошо решить любую задачу на десятичное деление.
Деление десятичных дробей на различные десятичные дроби с различными размерами частных
Деление десятичных дробей на однозначные десятые (например, 0,72 ÷ 0,8 = 0,9)
Деление десятичных дробей на однозначные десятые с большими частными (например, 3,2 ÷ 0,5 = 6,4)
Деление десятичных дробей на двузначные десятые (например, 10,75 ÷ 2,5 = 4,3)
Деление десятичных дробей на двузначные десятые с большими частными (например, 387,75 ÷ 4,7 = 82,5)
Деление десятичных дробей на трехзначные десятые (например, 1349,46 ÷ 23,8 = 56,7)
Деление десятичных дробей на двузначные сотые (например, 0,4368 ÷ 0,56 = 0,78)
Деление десятичных дробей на двузначные сотые доли с большими коэффициентами (например, 1,7277 ÷ 0,39). = 4,43)
Деление десятичных дробей на трехзначные сотые (например, 31,4863 ÷ 4,61 = 6,83)
Деление десятичных дробей на 4-значные сотые (например, 7628,1285 ÷ 99,91 = 76,35)
Деление десятичных дробей на трехзначные тысячные (например, 0,076504 ÷ 0,292 = 0,262)
Деление десятичных дробей на трехзначные тысячные с большими частными (например, 2,875669 ÷ 0,551 = 5,219)
= 4,43)
Деление десятичных дробей на трехзначные сотые (например, 31,4863 ÷ 4,61 = 6,83)
Деление десятичных дробей на 4-значные сотые (например, 7628,1285 ÷ 99,91 = 76,35)
Деление десятичных дробей на трехзначные тысячные (например, 0,076504 ÷ 0,292 = 0,262)
Деление десятичных дробей на трехзначные тысячные с большими частными (например, 2,875669 ÷ 0,551 = 5,219)
Эти рабочие листы, вероятно, будут использоваться для оценки и вычислений.
Случайное количество цифр Случайное количество мест
Порядок действий с десятичными знаками. Рабочие листы
Порядок операций с
десятичными знакамиРабочие листы с порядком операций в этом разделе фактически находятся на странице «Порядок операций», но они включены сюда для вашего удобства.
2-шаговый Порядок операций с положительными десятичными знаками 3 шага Порядок операций с положительными десятичными знаками 4-шаговый Порядок операций с положительными десятичными знаками 5-шаговый Порядок операций с положительными десятичными знаками 6-шаговый Порядок операций с положительными десятичными знаками 2-шаговый Порядок операций с положительными и отрицательными десятичными знаками 3 шага Порядок операций с положительными и отрицательными десятичными знаками 4 шага Порядок операций с положительными и отрицательными десятичными знаками 5-шаговый Порядок операций с положительными и отрицательными десятичными знаками 6-шаговый Порядок операций с положительными и отрицательными десятичными знаками
Порядок операций с десятичными запятыми Рабочие листы с порядком операций в этом разделе фактически находятся на странице «Порядок операций», но они включены сюда для вашего удобства.

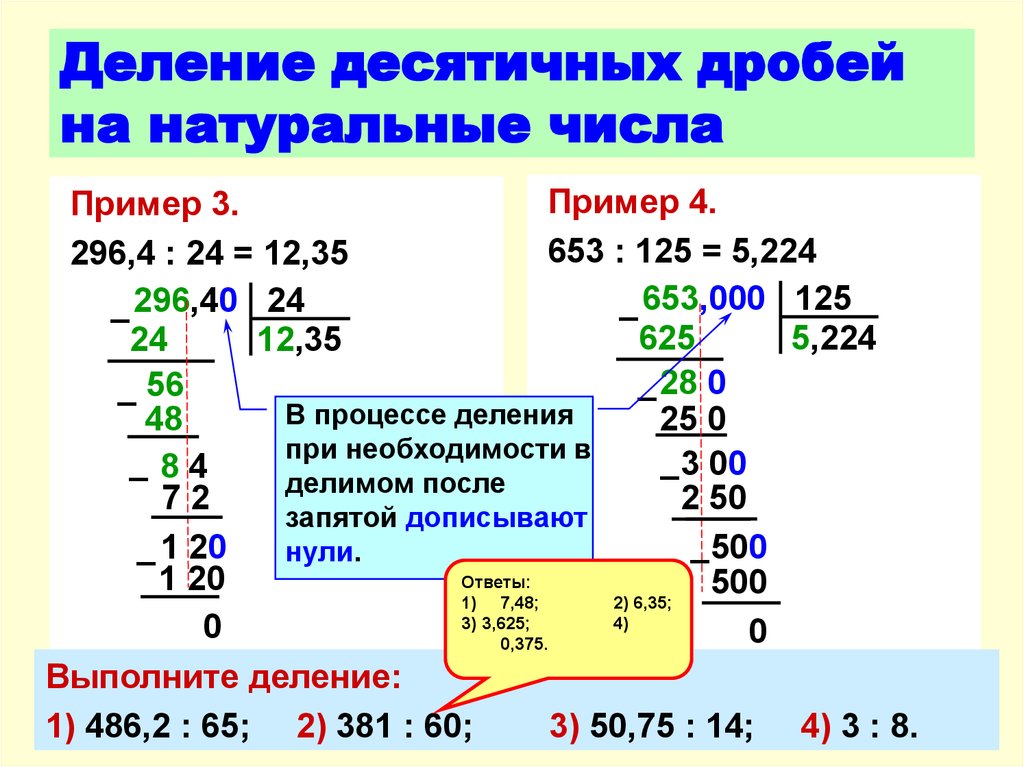

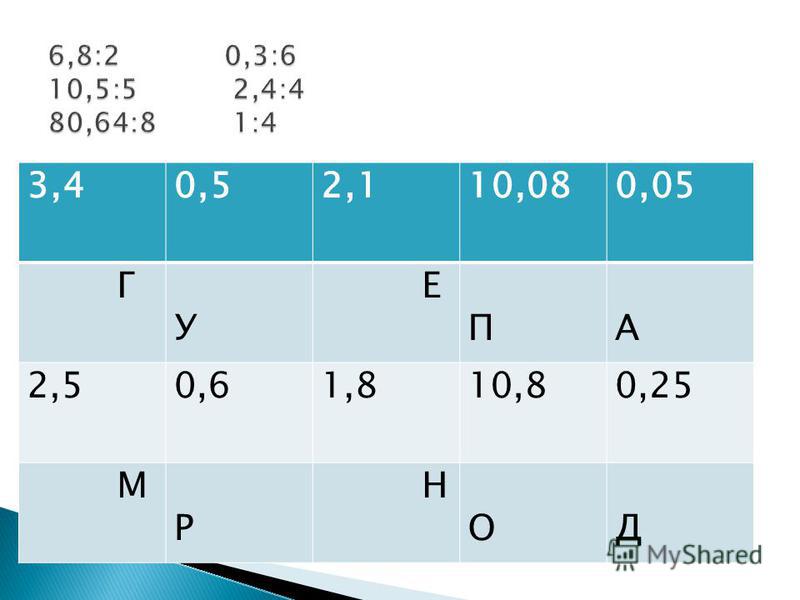
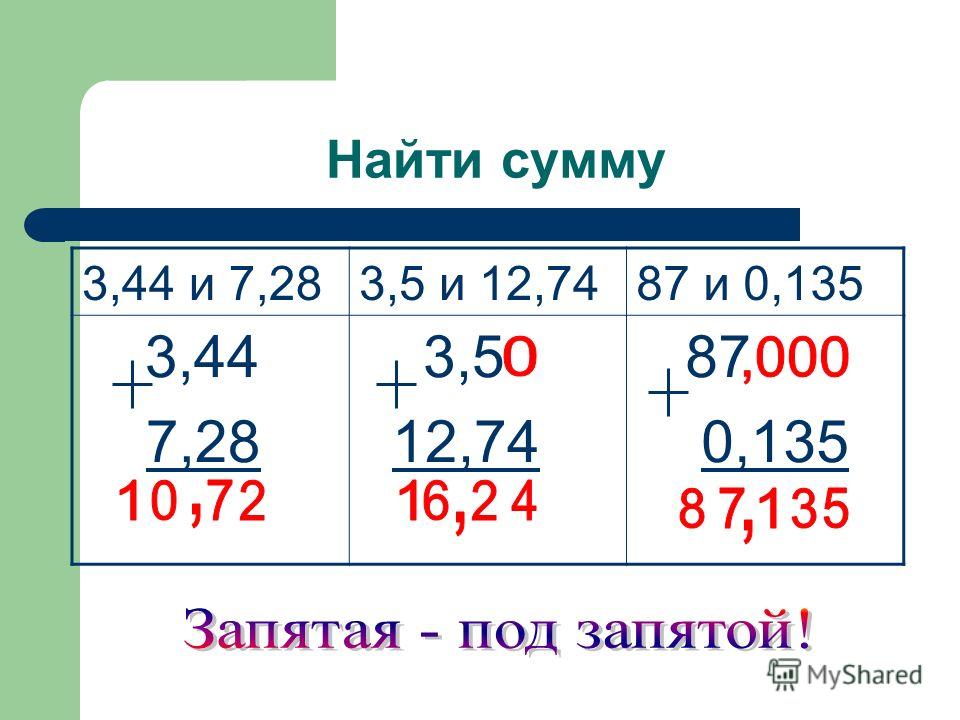
 Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.