Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Содержание
- Понятие степени
- Правило возведения дроби
- Нулевая и отрицательная степень
- Рациональный показатель
- Примеры решения
- Расчёт на онлайн-калькуляторе
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
- квадраты, образующиеся при произведении чисел или цифр самих на себя;
- кубы, получающиеся при умножении квадрата на сторону;
- биквадраты, произведение квадрата на квадрат;
- квадрато-кубы, возникающие при умножении квадратов на кубы;
- бикубы, произведение кубов на самих себя.
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Но при этом существует нюанс возведения в нулевую степень. Любое число, вне зависимости от вида, в нулевой степени даст единицу. Например, (2/32)0 = 1, -1420 = 1. Выражение же ноль в нулевой степени не имеет смысла, поэтому ответ считается неопределённым.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,52 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Утверждение справедливо для любого вида дроби с произвольной степенной функцией. Например, (11 / 14)3. Используя закон, можно записать следующее: (11 / 14)3 = 113 / 143 = (11 * 11 * 11) / (14 * 14 * 14) = 1331 / 2744. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14)3 = (0,78)3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:

Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32)3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Так, согласно алгебраическим правилам, для простых чисел a и b, при условии, что a < b, справедливо выражение: ca / cb = ca — b. Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Для нулевой степени такой подход использовать будет некорректно. При основании, которое равно нулю, применяя предыдущее равенство, можно записать, что ноль в степени a умноженный на ноль в степени ноль, равняется нулю с показателем a. То есть выражение может быт переписано как 0 = 0. Оно будет правильным при любом натуральном показателе, при этом не будет зависеть от того, чему равно выражение 00.
Ответ на 00 может быть любым. Поэтому для избежания путаницы считают, что решение записи 00 не имеет смысла, так же как и деление на ноль. Например, (12 / 34)0 = 120 / 340 = 1 / 1 = 1 или (-3 / 4)0 = 1, а вот для (0 / 23)0 ответ будет не определён.
Чтобы знать, как возвести дробь в отрицательную степень, нужно вспомнить свойство произведения с равными основаниями: ca * cb = ca+ b. Предположив, a = -b, при условии, что основание не равняется нулю, можно записать: c−a * ca = c-a+a = a0 = 1. Несложно сделать вывод о том, что положительный и отрицательный показатель взаимно обратный. Отсюда выходит, что если число нужно возвести в отрицательную степень, то его можно представить в виде дроби: c—a = 1 / ca.
Получается, что для минусового показателя ответ определяется дробью, при условии, что основание отлично от нуля и показатель — натуральное число. Фактически необходимо перевернуть дробь и возвести её по правилу, при этом знак показателя изменить на положительный. Например, (23 / 37)-2 = 1 / (11 / 37)2 = (37 / 22)2 или (1 / 5)-2 = (5 / 1)2 = 52 = 25.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Пусть имеется число n, которое необходимо возвести в степень a / b. Необходимо будет извлечь корень из n. Чтобы выражение соответствовало таблицам степени, должна выполняться формула: n(a / b) * b = na * b / b = na.
Используя полученное выражение, логично предположить, что ca / b = a√cb, но это лишь справедливо, когда показатель степени целый. Можно сделать вывод о том, что если выражение a√cb справедливо, что степенью числа c дробным показателем b / a является корень из c в степени b.
Если принять, что основание больше либо равно нулю, когда b является положительным числом, то буде справедливым равенство: сa / b = a√cb. При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0a / b = a√0b = 0.
Тут нужно оговориться, что для некоторых одночленов приведённое правило не работает. Например, для 3√ (-12 /3)2 или 4√ -122 оно верное, а для (-1 / 3)-2 / 3 или (-3 / 2)2 / 5 не имеет смысла, так как основание не может быть отрицательным. Поэтому вводится условие, по которому выражение a√ cb имеет смысл, при любых значениях неотрицательного основания.
Что же касается минусовой величины в показателе корней, оно в основании должно отличаться от нуля. Иными словами, если в любом уравнении или равенстве выражение a / b нельзя упростить (сократить), то a * i / b * I = ca — i / b —, причём степень можно заменить на ca / b.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
 Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35.
Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35. Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049
Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049Таким образом, чтобы возвести в степень дробь необходимо знать: правило, свойства степеней, порядок выполнения арифметических операций. А также учитывать знак показателя и вид основания.
Расчёт на онлайн-калькуляторе
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.
Предыдущая
АлгебраФункция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач
Следующая
АлгебраОдночлен 7 класс объяснение понятия, что называют коэффициентом и степенью одночлена стандартного вида, действия над выражением, принцип преобразования, примеры записи и решение типовых задач
Чтобы возвести рациональную дробь в степень нужно – dj-sensor.
 ru
ruСодержание
- Как возвести в степень смешанное число
- Правило возведения алгебраической дроби в степень, его доказательство
- Примеры, решения
Возведение дроби в степень. Наш онлайн-калькулятор позволяет возводить в степень любую дробь. Чтобы задать смешанную дробь заполните поля, соответствующие целой части, числителю и знаменателю. Если дробь не имеет целой части, то тогда оставьте соответствующее поле незаполненным. Если необходимо задать отрицательную дробь – для этого нажмите кнопку [+/-].После нажатия на кнопку «Вычислить» калькулятор выдаст ответ. Ниже под калькулятором будет приведено подробное решение с последовательностью действий, которые необходимо совершить.
При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.
Данное свойство соответствует другой записи свойства № 5 «Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
- (
3 · b 5c ) 2 =
3 2 · b 2 5 2 · c 2 =
9 · b 2 25 · c 2 =
9b 2 25c 2
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь. После этого возводим в степень и числитель, и знаменатель.
Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления и возвести число в степень онлайн.
Тема сводится к тому, что нам необходимо производить умножение одинаковых дробей. Данная статья расскажет, какое необходимо использовать правило, чтобы верно возводить алгебраические дроби в натуральную степень.
Правило возведения алгебраической дроби в степень, его доказательство
Перед тем, как начать возводить в степень, необходимо углубить знания при помощи статьи про степень с натуральным показателем, где имеется произведение одинаковых множителей, которые находятся в основании степени, причем их количество определено показателем. К примеру, число 2 3 = 2 · 2 · 2 = 8 .
Читайте также: Составить уравнение касательной к гиперболе перпендикулярной прямой
При возведении в степень чаще всего используем правило. Для этого в отдельности возводят в степень числитель и отдельно знаменатель. Рассмотрим на примере 2 3 2 = 2 2 3 2 = 4 9 . Правило применимо для возведения дроби в натуральную степень.
При возведении алгебраической дроби в натуральную степень получаем новую, где числитель имеет степень исходной дроби, а знаменатель – степень знаменателя. Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Доказательство данного правила записывается в виде дроби, которую необходимо возвести в степень, основываясь на самом определении с натуральным показателем. Тогда получаем умножение дробей вида a b n = a b · a b · . . . · a b = a · a · . . . · a b · b · . . . · b = a n b n
Примеры, решения
Правило возведения алгебраической дроби в степень производится последовательно: сначала числитель , потом знаменатель. Когда в числителе и знаменателе имеется многочлен, тогда само задание сведется к возведению заданного многочлена в степень. После чего будет указана новая дробь, которая равна исходной.
Произвести возведение дроби x 2 3 · y · z 3 в квадрат.
Необходимо зафиксировать степень x 2 3 · y · z 3 2 . По правилу возведения алгебраической дроби в степень получаем равенство вида x 2 3 · y · z 3 2 = x 2 2 3 · y · z 3 2 . Теперь необходимо произвести преобразование полученной дроби к виду алгебраической, выполняя возведение в степень. Тогда получим выражение вида
Тогда получим выражение вида
x 2 2 3 · y · z 3 2 = x 2 · 2 3 2 · y 2 · z 3 2 = x 4 9 · y 2 · z 6
Все случаи возведения в степень не предполагают подробного разъяснения, поэтому сам решение имеет краткую запись. То есть, получаем, что
x 2 3 · y · z 3 2 = x 2 2 3 · y · z 3 2 = x 4 9 · y 2 · z 6
Ответ: x 2 3 · y · z 3 2 = x 4 9 · y 2 · z 6 .
Если числитель и знаменатель имеют многочлены, тогда необходимо возводить всю дробь в степень, после чего применять формулы сокращенного умножения для его упрощения.
Возвести дробь 2 · x – 1 x 2 + 3 · x · y – y в квадрат.
Из правила имеем, что
Читайте также: Телевизор lg сбрасывает каналы после выключения
2 · x – 1 x 2 + 3 · x · y – y 2 = 2 · x – 1 2 x 2 + 3 · x · y – y 2
Чтобы преобразовать выражение, необходимо воспользоваться формулой квадрата суммы трех слагаемых в знаменателе, а в числителе – квадратом разности, что позволит упростить выражение. Получим:
2 · x – 1 2 x 2 + 3 · x · y – y 2 = = 2 · x 2 – 2 · 2 · x · 1 + 1 2 x 2 2 + 3 · x · y 2 + – y 2 + 2 · x 2 · 3 · x · y + 2 · x 2 · ( – y ) + 2 · 3 · x · y · – y = = 4 · x 2 – 4 · x + 1 x 4 + 9 · x 2 · y 2 + y 2 + 6 · x 3 · y – 2 · x 2 · y – 6 · x · y 2
Ответ: 2 · x – 1 2 x 2 + 3 · x · y – y 2 = 4 · x 2 – 4 · x + 1 x 4 + 9 · x 2 · y 2 + y 2 + 6 · x 3 · y – 2 · x 2 · y – 6 · x · y 2
Заметим, что при возведении в натуральную степень дробь, которую не можем сократить, получаем также несократимую дробь. Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Калькулятор десятичной дроби — MathCracker.com
Инструкции: Используйте этот калькулятор, чтобы преобразовать заданное десятичное число, которое вы предоставляете, в дробь, показывая все шаги. Введите одно десятичное число (например, число типа «3,4673» или число типа «.345279») в форму ниже:
Об этом калькуляторе десятичной дроби
Что такое десятичная дробь?
Десятичная дробь относится к способу выражения чисел с использованием числа десять в качестве основания, а также степеней десяти и десятых долей.
Проще говоря, десятичные дроби — это числа, какими вы их знаете, это последовательность цифр (числа от 0 до 9), за которой, возможно, следуют десятые части, представленные точкой «.» и последовательность цифр
Пример цифры: Например, 45,34556 и 0,5678 — это цифры. Цифры, которые имеют только «0» слева от «.» обычно пишут как .4534, для краткости.
Как преобразовать десятичную дробь в дробь?
Стратегия проста: нам нужно попытаться «исключить» десятичные дроби (цифры справа от «.»), умножив число на степень 10.
Как только вы это сделаете, вы обратите внимание на степень 10, которую вы использовали для достижения этого, потому что затем вы будете использовать ее для преобразования данного числа в десятичное число. k}\]
k}\]
и, возможно, вы захотите уменьшить дробь справа от наименьшего выражения.
Таблица десятичных дробей
Преимущества и недостатки использования диаграммы по сравнению с формулой преобразования десятичных знаков в дробь
-
Использование диаграммы прямое: вы просто смотрите на диаграмму и сразу получаете преобразование десятичной дроби в дробь.

- Проблема с диаграммой заключается в том, что там нет точного десятичного числа или дроби, которую вы ищете.
- Используя формулу преобразования, вы уверены, что можете преобразовать ЛЮБОЕ число, но вам действительно нужно поработать над расчетом.
Калькуляторы о дробях и процентах
Естественно, как вы, вероятно, уже поняли, дроби, десятичные числа и проценты тесно связаны между собой. И часто это просто разные форматы для представления одной и той же информации более удобным способом для данного контекста.
Например, использование калькулятора процентов в дроби выполняет ту же работу, что и этот калькулятор десятичных дробей, с той разницей, что сначала вам нужно будет преобразовать десятичную дробь в проценты.
Естественно, вы можете столкнуться с обратной ситуацией. Может быть, вы хотите преобразовать дробь до десятичной , который является просто общим алгоритмом арифметики деления. Обратите внимание, что преобразование дроби в десятичную может привести к конечному десятичному числу или потенциально к повторяющемуся десятичному числу.
Например, дробь \(\displaystyle \frac{3}{5}\) соответствует простому числу 0,6 (простому конечному десятичному числу), а дробь \(\displaystyle \frac{1}{3}\) соответствует повторяющемуся десятичному числу 0,33333.
Пример: Преобразование десятичной дроби в дробь
Вопрос : Вычислите число 3,4563 как дробь.
Решение:
Вы ввели следующее десятичное число \(D = \displaystyle 3.4563\), и цель состоит в том, чтобы преобразовать его в дробь.
Шаг 1:
Нам нужно умножить \(D = 3. {4} \]
\[ = 3.4563 \times 10000= 34563 \]
{4} \]
\[ = 3.4563 \times 10000= 34563 \]
Итак, разделив обе части на \(10000\), мы получим
\[ 3.4563 = \displaystyle \frac{34563}{10000} \]
а поскольку найденная дробь уже упрощена, делается вывод, что простейшая дробь, эквивалентная \(3.4563\), равна \(3.4563\).
Следовательно, выражение десятичной дроби в простейшем виде — \(\displaystyle 3.4563 = \frac{ 34563}{ 10000}\), что завершает вычисление.
Пример 2
Вопрос
Выразите 0,625 в виде дроби.
Решение:
Алгебра
|
|
|
|||||||||||||||||||||
Eˣ Калькулятор | Возведен В Степень X
Математические Калькуляторы
Этот удивительный инструмент позволит вам вычислить e в степени любого числа, которое вы выберете. X)
X)
Оглавление
| ◦Каково значение e на дисплее калькулятора калькулятора? — е к числу х |
| ◦Как ввести e в калькулятор? — Рассчитать e до числа x |
| ◦Что это означает на практике? Как вы вычисляете от е до х? |
| ◦Что означает эксп? |
| ◦Как перевести е в степень х без калькулятора? |
| ◦Что эквивалентно e отрицательной бесконечности? |
| ◦Чему равна производная от е до х? |
Каково значение e на дисплее калькулятора калькулятора? — е к числу х
e — две самые фундаментальные константы в математике. е нельзя записать в виде дроби. Оно также имеет бесконечное количество десятичных разрядов, как и его двоюродный брат пи ( ).
e можно назвать много вещей в математике. Оно может быть известно как число Эйлера или натуральные числа. Его значение равно 2,7182818284590452353602… и продолжает считать!
Теперь мы знаем, что это такое и сколько это стоит. x.
x.
Автор статьи
Parmis Kazemi
Пармис — создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Eˣ Калькулятор русский
Опубликовано: Mon May 16 2022
В категории Математические калькуляторы
Добавьте Eˣ Калькулятор на свой сайт
Eˣ Калькулятор на других языках
هˣ آلة حاسبةCalculatrice EˣEˣ RechnerEˣ計算機ईˣ कैलकुलेटरEˣ Hesap MakinesiEˣ KalkulatorEˣ CalculatorEˣ КалькулятарEˣ Kalkulačka
Как добавить Eˣ Калькулятор на мой сайт?
Вы можете легко добавить Eˣ Калькулятор на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!
Как добавить виджет Eˣ Калькулятор на сайт WordPress?
Добавить Eˣ Калькулятор на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.
Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кода
Другие математические калькуляторы
Калькулятор Векторного Произведения
Калькулятор Треугольников 30 60 90
Калькулятор Ожидаемой Стоимости
Математический Онлайн Калькулятор
Калькулятор Стандартного Отклонения
Калькулятор Процентов
Калькулятор Дробей
Конвертер Фунтов В Чашки: Мука, Сахар, Молоко..
Калькулятор Окружности
Калькулятор Формулы Двойного Угла
Вычисление Корня
Калькулятор Площади Треугольника
Калькулятор Котерминального Угла
Калькулятор Скалярного Произведения
Калькулятор Средней Точки
Конвертер Значащих Цифр (калькулятор Sig Figs)
Калькулятор Длины Дуги Для Круга
Калькулятор Балльной Оценки
Калькулятор Процентного Увеличения
Калькулятор Процентной Разницы
Калькулятор Линейной Интерполяции
Калькулятор QR-разложения
Калькулятор Транспонирования Матрицы
Калькулятор Гипотенузы Треугольника
Калькулятор Тригонометрии
Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника)
45 45 90 Калькулятор Треугольника (калькулятор Прямоугольного Треугольника)
Калькулятор Умножения Матриц
Калькулятор Среднего
Генератор Случайных Чисел
Калькулятор Погрешности
Калькулятор Угла Между Двумя Векторами
LCM Calculator — Калькулятор Наименьшего Общего Кратного
Калькулятор Площади В Квадратных Футах
Калькулятор Экспоненты (калькулятор Мощности)
Калькулятор Математического Остатка
Правило Трех Калькуляторов — Прямая Пропорция
Калькулятор Квадратичных Формул
Калькулятор Суммы
Калькулятор Периметра
Калькулятор Z-счета (значение Z)
Калькулятор Фибоначчи
Калькулятор Объема Капсулы
Калькулятор Объема Пирамиды
Калькулятор Объема Треугольной Призмы
Калькулятор Объема Прямоугольника
Калькулятор Объема Конуса
Калькулятор Объема Куба
Калькулятор Объема Цилиндра
Калькулятор Масштабного Коэффициента Расширения
Калькулятор Индекса Разнообразия Шеннона
Калькулятор Теоремы Байеса
Калькулятор Антилогарифмов
Калькулятор Простых Чисел
Калькулятор Экспоненциального Роста
Калькулятор Размера Выборки
Калькулятор Обратного Логарифма (логарифма)
Калькулятор Распределения Пуассона
Мультипликативный Обратный Калькулятор
Калькулятор Процента Оценок
Калькулятор Отношения
Калькулятор Эмпирических Правил
Калькулятор P-значения
Калькулятор Объема Шара
Калькулятор Чистой Приведенной Стоимости
1 целая минус 1 2 в кубе
Автор Сфера закона На чтение 5 мин Просмотров 4 Опубликовано
Содержание
- Калькулятор дробей
- Онлайн калькулятор дробей с решением со степенями со скобками с буквами
- Таблица кубов
- Таблица кубов
- Теория
- Скачать таблицу кубов
- Калькулятор степеней — возвести в степень онлайн
- Что такое натуральная степень числа?
- Как возвести число в натуральную степень?
- Что такое отрицательная степень числа?
- Как возвести число в целую отрицательную степень?
Калькулятор дробей
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».
Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».
Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Источник
Онлайн калькулятор дробей с решением со степенями со скобками с буквами
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
- Сложение, вычитание, деление и умножение дробей.
- Расчет дробей с подробнейшим решением.
- Расчет дробей со степенями, скобками и буквами.
- Сокращение дробей.
- Поддержка до трех дробей онлайн.
Постоянная ссылка на результат этого расчета
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей. (-2) +1.
(-2) +1.
Источник
Таблица кубов
Таблица кубов или таблица возведения чисел в третью степень. Интерактивная таблица кубов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175616 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Таблица кубов
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Скачать таблицу кубов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
Источник
Калькулятор степеней — возвести в степень онлайн
Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.
Что такое натуральная степень числа?
Число p называют n -ой степенью числа a , если p равно числу a , умноженному само на себя n раз: p = a n = a·. ·a
·a
n — называется показателем степени, а число a — основанием степени.
Как возвести число в натуральную степень?
Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:
Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 3 4
Решение: как было сказано выше, 3 4 = 3·3·3·3 = 81 .
Ответ: 3 4 = 81 .
Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 5 5
Решение: аналогично, 5 5 = 5·5·5·5·5 = 3125 .
Ответ: 5 5 = 3125 .
Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.
Что такое отрицательная степень числа?
При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.
Как возвести число в целую отрицательную степень?
Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.
Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2 -4
Решение: как было сказано выше, 2 -4 =
Источник
Сложение, вычитание, деление и умножение дробей
Инструкции по использованию
- Введите дроби в приведенный выше калькулятор.
- Выберите математическую операцию, которую вы хотите выполнить (сложение, вычитание, умножение, деление), используя серый раскрывающийся список между двумя дробями.
- Результаты будут обновляться автоматически при каждом изменении любого значения в калькуляторе.
- Флажок под калькулятором позволяет выбрать между сокращением дроби до эквивалента наименьшего общего знаменателя (если флажок установлен) или не уменьшением (если флажок не установлен).
Как вручную считать дроби
Как складывать дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.

- Сложите числители.
- Уменьшить результат до максимально упрощенного числа.
Как вычитать дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Добавьте второй числитель к первому.
- Уменьшить результат до максимально упрощенного числа.
Как умножать дроби
- Перемножьте числа в верхней части вместе.
- Перемножьте числа внизу вместе.
- Уменьшить результат до максимально упрощенного числа.
Как делить дроби
- Переверните вторую дробь вверх ногами, чтобы получить обратное число.
- Умножьте дроби вместе (точно так же, как в разделе умножения выше).
- Уменьшить результат до максимально упрощенного числа.
Дроби: история, актуальность и популярное использование
— Руководство Автор Corin B. Arenas , опубликовано 22 октября 2019 г.
Arenas , опубликовано 22 октября 2019 г.
Практически каждый день мы имеем дело с дробями. Подумай об этом. Получаете ли вы монеты за размен, покупаете одежду со скидкой 75 % или готовите на полстакана масла, вы используете дроби.
В этом разделе мы поговорим о происхождении дробей, их значении для передачи информации и золотом сечении.
Что такое дроби?
Дроби представляют собой части целого числа или любого количества равных частей. Он функционирует чтобы описать, как части соотносятся с целым числом.
Для иллюстрации представьте целое число как торт. Если вы разрежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 часть всего торта.
- 1 представляет одну часть или часть целого числа, которое называется числителем .
- 4 представляет собой общее количество частей в целом числе, которое называется знаменателем .
Краткая история дробей
Происхождение слова: Термин дробь происходит от латинского
слово дробь что означает «сломать». В раннем английском языке это означает «отломанный кусок или
фрагмент». Английское слово «перелом» также
имеет такое же происхождение слова.
В раннем английском языке это означает «отломанный кусок или
фрагмент». Английское слово «перелом» также
имеет такое же происхождение слова.
Концепция дробей существует уже более 4000 лет. Но разные цивилизации по-своему стандартизируют дроби для универсального использования.
Египтяне
Согласно Математика сквозь века : Нежная история для учителей и других, египтяне были одними из первых, кто изобрел форму дроби еще в 1800 г. до н.э. Их концепция в основном ограничивалась частями, иначе известными как единичные дроби. Единичные дроби используют 1 в качестве числителя.
Египетские математики создали систему с основанием 10 идея, которая похожа на системы счисления, которые мы используем сегодня. Цифра иероглифы представляли их числа, а значит, символы соответствовали определенное значение.
Так как числитель всегда равен 1, нужно было указать только знаменатель. Египтяне отмечали знаменатель овалом или точкой над значением. Вот несколько примеров из Math Through the Ages :
Вот несколько примеров из Math Through the Ages :
Части были выражены в виде суммы единичных дробей. Однако система не позволяла повторять дробные единицы в этой последовательности, что затрудняло расчеты. Чтобы решить эту проблему, египтяне создали обширные списки таблиц, в которых были указаны двойные значения различных частей.
Вавилоняне
Еще одна цивилизация, создавшая сложную систему для Фракции были вавилонянами, по словам преподавателя математики и автора Лиз Памфри.
Вавилоняне организовали фракции в группы по 60 человек (базовое 60). Сегодня мы обычно объединяем числа в группы по 10. Но для вычислений, таких как углы и минуты для времени, мы также используем основание 60. Система группировала дроби по 10 и использовала два символа, один для единицы, а другой для 10.
Ниже приведены символы, представляющие вавилонскую систему счисления от 1 до 20:
Однако у них не было символа для нуля (который они позже добавили около 311 г. до н.э.) или знака, функционирующего как десятичная точка для указать доли целого числа. Это затрудняло интерпретацию чисел.
до н.э.) или знака, функционирующего как десятичная точка для указать доли целого числа. Это затрудняло интерпретацию чисел.
Например, приведенные ниже числа читаются как 12 и 15.
Согласно Памфри, символы также могут значения:
- 12 и 15 отдельными номерами
- 15/12
- 12 15/60
- 720 + 15
Как видите, отсутствие индикатора дроби делает его трудно отделить целые числа от дробей. Вероятно, они полагались на контекст, чтобы разобраться в числовых значениях.
И египетская, и вавилонская системы позже были переданы людям в Греции, а затем и средиземноморской цивилизации.
Греки
В Греции практика использования дробных значений в качестве сумм
долей единицы была довольно распространена до средневековья. Например, Либер
Abbaci итальянского математика Фибоначчи
известный текст 13 века. Он широко использовал дроби, описывая
различные способы преобразования других дробей в суммы единичных дробей.
Чтобы лучше понять, ниже приведена таблица греческих цифровые символы. Обратите внимание, что они такие же, как буквы в греческом языке. алфавит:
греческий запись дробей требует от читателей понимания контекста для правильного интерпретация. Чтобы выделить дробь, они ставят диакритический знак (‘) после знаменателя дроби.
Например, число β (2) становится ½ при записи через диакритический знак, β’ .
Аналогично, µβ (42) становится 1/42 при записи в виде µβ’ .
Однако здесь возникает путаница: µβ’ также может означать 40 ½. Вот почему понимание контекста имеет решающее значение при интерпретации греческих дробей.
Римлянам
Для римлян дроби выражались только словами, которые затрудняло какие-либо расчеты.
Их система была основана на единице веса, называемой «ас».
При таком подходе 1 «ас» равнялся 12 унциям (римская
основная единица измерения, положенная в основу современной унции). Таким образом, дроби
имеют знаменатели со значениями, делящимися на 12.
Таким образом, дроби
имеют знаменатели со значениями, делящимися на 12.
В таблице ниже показаны римские дроби с соответствующими терминами:
Китайцы
Китайцы написали Девять Главы по математическому искусству , датируемому примерно 100 г. до н.э. Он включает в себя текст о дробях, похожих на те, которые мы используем сегодня.
В соответствии с Math Through the Ages , он содержал большинство обычных правил вычисления с дробями, например, как складывать, делить и умножать дроби, а также приводить дробь к наименьшему значению.
Однако их система избегала использования неправильных дробей. Например, вместо неправильной дроби 9/4 они использовали эквивалентную ей смешанную дробь 2 1/4.
В отличие от западной математики, китайцы сосредоточились на практических приложениях, а не на теоретических рассуждениях и геометрии.
Индийцы
Индийцы разработали способ записи дробей,
ближе к тому, что мы используем сегодня.
Согласно ресурсному сайту The Story of Mathematics, до 1000 г. до н.э. индуистские мантры в ранний ведический период вызывали силы от десяти до сотен и даже до триллиона. Это свидетельствует о том, что ранняя индийская цивилизация использовала сложные математические операции, включая дроби, квадраты, кубы и корни.
Около 500 г. до н.э. они придумали систему письма под названием брахми, которая состояла из 9числовые символы и ноль. Учитель математики и писатель Лиз Памфри отмечает, что эти числа во многом повлияли на современные числа, которыми мы пользуемся сегодня. См. изображение ниже.
Индийская система записывала дроби, помещая одно значение поверх другого, точно так же, как сегодня числитель пишется над знаменателем. Тем не менее, они не провели черту между ними. Например, дробь 4/5 будет выглядеть так:
Позднее эту систему использовали арабы при торговле с индийцами. Именно арабы провели черту, чтобы отличить верхнее число от младшего в дроби. Это в конечном итоге привело к тому, как мы пишем дроби в современную эпоху.
Это в конечном итоге привело к тому, как мы пишем дроби в современную эпоху.
Как дроби улучшают способ передачи информации
По словам доктора Петерсона из MathForum.org: «Дроби были изобретены, чтобы обеспечить способ работы с величинами меньше единицы».
Если бы люди использовали только целые числа, единственный способ обратиться к меньшее количество заключается в использовании меньших единиц. Так поступали римляне — они использовали целые числа для измерения футов и использовали дюймы, когда им нужно было учитывать более мелкие единицы.
Например, вместо 1/12 фута длина будет равна 1 дюйму, а 1/4 фута будет равна 3 дюймам. Но что, если вы имеете в виду 2 с половиной фута? Как насчет 1 и 3/4 футов?
Если вы основываете стандартную длину на футах, это
сбивает с толку постоянное обращение к футам и дюймам одновременно. В принципе,
дроби позволяют проводить измерения, не обязательно создавая
новые юниты. Было бы лучше учитывать измерения в
последовательная мода.
В США чаще используют дроби (английское измерение), поскольку они используют чашки, а не весы для измерения при приготовлении пищи и выпечке.
Американцам еще предстоит перейти на метрическую систему, которая десятичная система, в которой используются единицы, связанные с коэффициентами 10. метрическая система обычно использует граммы и литры вместо американской системы измерения для унций, чашек, пинт и так далее.
В таблице ниже показано преобразование объема из английского измерения в его метрический эквивалент:
Преобразование объема в США в метрическую единицу
Кроме того, сохранение измерений в одной единице позволяет нам легко складывать, вычитать, умножать и делить дроби. Это устраняет проблему преобразования, которая невозможна, если измерение производится между двумя разными единицами измерения.
Для более простого расчета дробей используйте калькулятор в верхней части этой страницы.
Хотя десятичные дроби обеспечивают альтернативный способ указания
дроби (и более простой способ расчета дробей с помощью калькулятора), это
необходимо понимать традиционные дроби и то, как их значения влияют на
целое число.
По данным Thoughtco.com, учащиеся, не усвоившие дроби в первые годы жизни, склонны запутаться и испытать математическую тревогу. Они также упомянули половину американской восьмерки оценщики не могут расположить дроби в порядке их значения.
Интуитивное изучение дробей помогает детям лучше понять теоретические математические концепции, позволяя им использовать их в реальной жизни. Это намного лучше, чем запоминать таблицы с единицами измерения или символами.
Золотое сечение и последовательность Фибоначчи
В математике отношение — это сравнение двух числа, которые зависят от вида сравниваемых чисел.
Вы можете встретить пример, написанный так: 1:3 или 1 из 3. Например, бутылка концентрата апельсинового сока состоит из 1 части апельсинового сока и 3 части воды. Это также может быть записано в виде дроби, 1/3.
Соотношения связаны с дробями, потому что они сравнивают разные
значения, которые могут представлять собой целое. В этом примере вся часть — это бутылка. апельсинового сока.
апельсинового сока.
Золотое сечение это специальное число, представленное греческим символом фи ( φ ) с приблизительным значением 1,618.
Получается путем деления линии на 2 части так, чтобы длинная часть (а) деленная на короткий участок (б) равна всей длине, деленной на длинный раздел.
Чтобы дать вам лучшее представление, вот иллюстрация со стандартным уравнением: сооружения, такие как Парфенон и пирамиды Египта. В Великой пирамиде Гизы, отношение основания к высоте составляет примерно 1,5717, что составляет близко к золотому сечению. Он также встречается в повторяющихся закономерностях в природе, таких как как лепестки цветов, ракушки, ветки деревьев и спиральные галактики.
С другой стороны, Фибоначчи
последовательность — еще одна известная формула в математике. Последовательность получена из
сумма двух предшествующих ему чисел. Многие источники говорят, что Леонардо Фибоначчи
(Леонардо Пизанский) популяризировал его в своей книге Либер Абакчи .
Но согласно Live Science, математик Кит Девлин, автор книги « В поисках Фибоначчи: поиски Откройте для себя заново забытого математического гения, изменившего мир 90 100 что Леонардо Фибоначчи на самом деле не «открыл» эту последовательность.
Древние санскритские писания, в которых использовалось индийско-арабское числительное системы были первыми, кто обсудил ее за столетия до Леонардо Фибоначчи.
Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 и так далее…
Когда математики строят квадраты на основе этой последовательности, они могут нарисовать спираль.
Как золотое сечение связано с последовательностью Фибоначчи?
Исследователи заметили, что когда вы берете любые два последовательных числа Фибоначчи, их соотношение очень близко к золотому сечению. Таким образом, φ примерно равно 1,618. Чтобы дать вам представление, посмотрите таблицу ниже.
Чтобы дать вам представление, посмотрите таблицу ниже.
Итог
Концепция дробей была разработана различными древними цивилизациями. Одними из первых, кто разработал дробную систему с обширными таблицами, были египтяне. Другие древние общества, такие как вавилоняне, греки, римляне и китайцы, также внесли свой вклад в его улучшение. Но на современные цифры и то, как мы пишем дроби, больше всего повлияли индийцы, которые ввели индийско-арабскую систему счисления.
Использование дробей помогает нам легко передавать информацию об измерениях. Это удерживает людей от использования разных единиц измерения, облегчая их вычисление.
Наконец, дроби связаны со знаменитой золотой пропорцией и последовательностью Фибоначчи, которые в значительной степени повлияли на то, как мы проектируем всевозможные структуры.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Забавные математические мультфильмы
efunda: Калькулятор дробей
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор дробей
Этот калькулятор дробей можно использовать для сложения, вычитания, умножения и деления дробей и смешанных чисел. Чтобы вычислить смешанные числа, установите флажок «Рассчитать смешанные числа». Входные данные числителя и знаменателя принимают только целые числа. При вычислении смешанных чисел можно использовать десятичные дроби, если числитель и знаменатель пусты. После вычисления десятичные дроби будут преобразованы в дроби.
Чтобы вычислить смешанные числа, установите флажок «Рассчитать смешанные числа». Входные данные числителя и знаменателя принимают только целые числа. При вычислении смешанных чисел можно использовать десятичные дроби, если числитель и знаменатель пусты. После вычисления десятичные дроби будут преобразованы в дроби.
Ответы представляют собой дроби в низших единицах или смешанные числа в сокращенной форме. Процесс, используемый для поиска ответа, также предоставляется.
Что такое дробь?
Дробь представляет собой количество равных частей целого и состоит из числителя и знаменателя:
Числитель — это верхнее число (1) дроби, а знаменатель — нижнее число (8 ). Линия, разделяющая числитель и знаменатель дроби, называется чертой дроби и указывает на деление. Вышеупомянутая дробь читается как «одна восьмая», что означает, что она представляет собой 1 равную часть от восьми полных частей, например, 1 кусок пиццы для пиццы, нарезанной на 8 кусочков. Если вы съели 3 куска пиццы, значит, вы съели 3 части всей пиццы или, используя дроби, пиццы. Дроби — это эффективный способ представления частей целого с помощью чисел, вместо того чтобы описывать понятие словами.
Если вы съели 3 куска пиццы, значит, вы съели 3 части всей пиццы или, используя дроби, пиццы. Дроби — это эффективный способ представления частей целого с помощью чисел, вместо того чтобы описывать понятие словами.
Дроби можно разделить на несколько категорий. Например, это и простая дробь, и правильная дробь. Это правильная дробь, потому что числитель меньше знаменателя, и простая дробь, потому что и числитель, и знаменатель — целые числа.
Что такое правильные дроби, неправильные дроби и смешанные числа?
Правильные дроби
Дроби представляют собой часть целого, поэтому имеет смысл считать «правильными» дробями дроби, у которых числитель меньше знаменателя. Числитель представляет количество равных частей целого, а знаменатель представляет собой целое. Таким образом, правильная дробь всегда имеет значение меньше 1. Используя пример пиццы, разрезанной на 8 ломтиков, ломтики считаются правильной дробью, но (или 1) не является правильной дробью, поскольку значение равно 1, и 8 частей из 8 представляют всю пиццу, а не часть целого.
Неправильные дроби
Неправильная дробь — это дробь, у которой числитель больше или равен знаменателю. Для неправильной дроби дробь представляет больше, чем целое. Используя пример пиццы, разрезанной на 8 кусков, мы можем думать о неправильной дроби как о наличии более 1 целой пиццы; если у нас есть кусочки пиццы, то у нас есть 1 целая пицца, но если у нас есть кусочки пиццы, у нас есть 1 целая пицца и 1 часть из 8 пиццы 2 и . Неправильные дроби — это эффективный способ выражения частей целого таким образом, который сообщает нам размер целого, а также позволяет нам представлять значения, превышающие 1.
Смешанные числа
Смешанные числа (или смешанные дроби) — еще один способ представления неправильных дробей. Вместо неправильной дроби, где числитель больше знаменателя, смешанные числа записываются как комбинация целого числа и правильной дроби. Например, 1 целая пицца и 1 дополнительный кусок пиццы представлены как неправильная дробь; чтобы записать это как смешанное число, посчитайте количество целых и количество частей целого.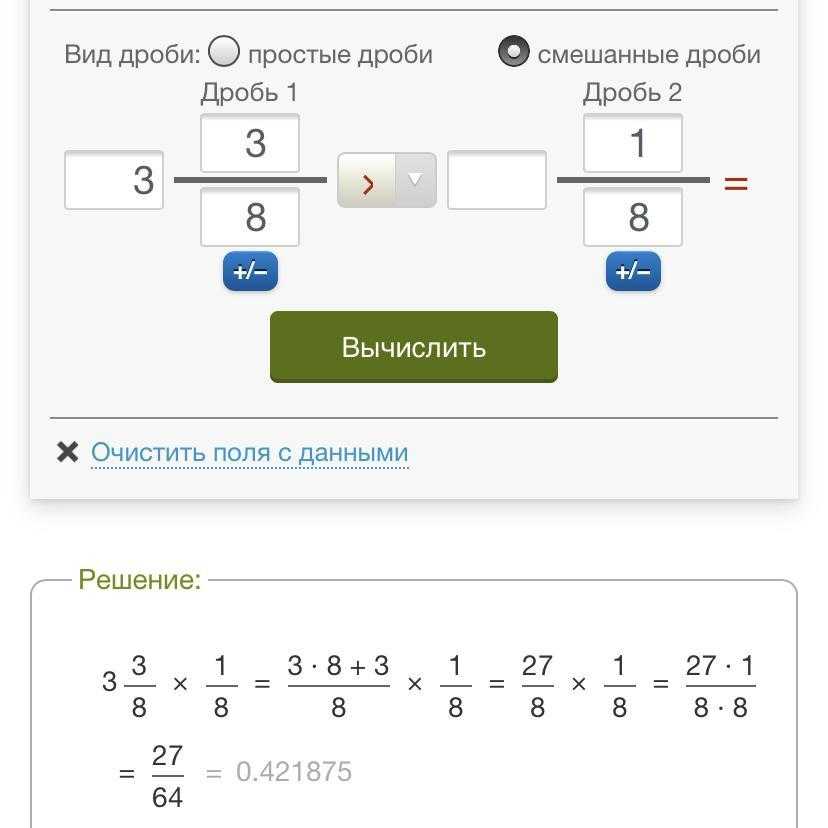 В этом случае имеется 1 целое, или , и 1 часть целого, или . Объединив их, неправильная дробь записывается как смешанное число.
В этом случае имеется 1 целое, или , и 1 часть целого, или . Объединив их, неправильная дробь записывается как смешанное число.
Преобразование смешанных чисел в неправильные дроби
Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число, затем добавьте числитель. Например:
Преобразование неправильных дробей в смешанные числа
Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель и запишите целое число, а затем остаток над знаменателем. Например:
Сложение дроби
Чтобы складывать дроби, знаменатели дробей должны совпадать. Это связано с тем, что дроби используются для представления частей целого, где знаменатель говорит нам, сколько частей составляет целое, а числитель говорит нам, сколько частей целого у нас есть. Тогда имеет смысл, что дроби нельзя складывать, если знаменатели дробей различны, поскольку 1 часть целого, состоящая из 8 частей, отличается от 1 части целого, состоящего из 4 частей.
Когда знаменатели совпадают
Если знаменатели складываемых дробей одинаковы, сложите числители и запишите результат над общим знаменателем. Например:
Это верно независимо от того, является дробь правильной или неправильной. Например:
В этом случае одна из складываемых дробей является неправильной дробью, поэтому в результате получается также неправильная дробь. Однако обратите внимание, что дроби добавляются таким же образом. Пока знаменатели одинаковы, сложение дробей относительно простое.
Когда знаменатели не совпадают
Когда знаменатели не совпадают, преобразуйте дроби так, чтобы все дроби имели одинаковый знаменатель, затем сложите числители и запишите результат над общим знаменателем.
Процесс преобразования набора дробей в дроби с общим знаменателем называется нахождением общего знаменателя. Существует бесконечное количество способов представить одно и то же значение в виде дроби. Например:
Все приведенные выше дроби представляют одно и то же значение (половину целого), но имеют разные числитель и знаменатель. является наиболее упрощенной формой дроби, представляющей половину целого. Каждая последующая дробь, указанная выше, представляет собой просто первую дробь , умноженную на дробное представление числа 1. Напомним, что любое значение, умноженное на 1, равно тому же самому значению, и что любая дробь, в которой числитель и знаменатель имеют одинаковое значение равно 1. Эти факты позволяют преобразовать любую дробь в дробь, имеющую одно и то же значение, представленное разными числителями и знаменателями; эти дроби называются эквивалентными дробями. Например, отметив, что умножение дробей включает умножение числителя на числитель и знаменателя на знаменатель,
является наиболее упрощенной формой дроби, представляющей половину целого. Каждая последующая дробь, указанная выше, представляет собой просто первую дробь , умноженную на дробное представление числа 1. Напомним, что любое значение, умноженное на 1, равно тому же самому значению, и что любая дробь, в которой числитель и знаменатель имеют одинаковое значение равно 1. Эти факты позволяют преобразовать любую дробь в дробь, имеющую одно и то же значение, представленное разными числителями и знаменателями; эти дроби называются эквивалентными дробями. Например, отметив, что умножение дробей включает умножение числителя на числитель и знаменателя на знаменатель,
и так далее. Таким образом, один из способов найти общий знаменатель между двумя дробями — просто умножить их знаменатели, не забывая также умножать числители на соответствующий знаменатель, чтобы значения дробей не менялись. Например:
В этом случае 32 является общим знаменателем. Мы всегда можем найти общий знаменатель, просто перемножая каждый другой знаменатель, но, как мы видим из приведенного выше примера, это не всегда приводит к дроби в простейшей форме.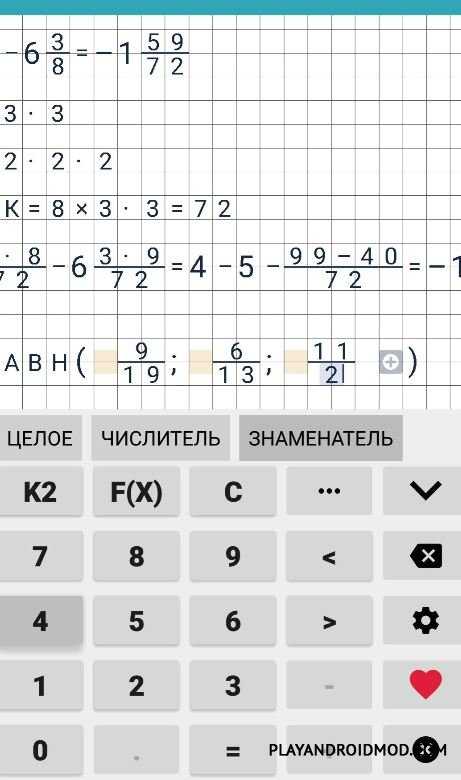 Для этого примера мы могли бы оставить в покое, если бы знали, что 8 является общим знаменателем для двух дробей:
Для этого примера мы могли бы оставить в покое, если бы знали, что 8 является общим знаменателем для двух дробей:
8 в этом примере обозначается как наименьший общий знаменатель. Если мы найдем наименьший общий знаменатель двух или более дробей, возможно, нам не придется упрощать результат.
Вычитание дробей
Подобно сложению дробей, вычитание дробей требует, чтобы знаменатели дробей были одинаковыми. Обратитесь к разделу сложения фракций для более подробной информации.
Когда знаменатели одинаковы
Когда знаменатели дробей одинаковы, вычтите числители дробей, затем запишите результат над общим знаменателем и упростите:
Когда знаменатели не совпадают
Когда знаменатели дробей не совпадают, преобразуйте дроби в эквивалентные дроби с общим знаменателем, затем вычтите их числители и запишите результат над общим знаменателем. Есть несколько способов найти общий знаменатель. Самый простой способ найти общий знаменатель — это умножить знаменатели участвующих дробей, но этот метод часто приводит к дроби не самой простой формы. Например, предположим, что мы хотим вычесть следующее:
Например, предположим, что мы хотим вычесть следующее:
Числители пока нельзя вычитать, так как знаменатели дробей не совпадают. Умножение 4×8=32 дает нам общий знаменатель дробей. Чтобы преобразовать дроби в эквивалентные дроби с этим общим знаменателем, умножьте числитель и знаменатель каждой дроби на знаменатель другой дроби:
Теперь, когда дроби имеют одинаковый знаменатель, числители можно вычесть, и дроби упрощены следующим образом:
Также можно найти наименьший общий знаменатель, но методы для этого здесь не обсуждаются. В этом случае мы могли бы заметить, что 8 является наименьшим общим знаменателем между двумя дробями, и могли бы вместо этого вычесть дроби, преобразовав их в эквивалентную дробь со знаменателем 8:
Умножение дроби
Умножение дроби почти так же, как обычное умножение; просто найдите произведение числителей перемножаемых дробей и запишите результат над произведением знаменателей. Количество перемножаемых дробей не меняет процесс. Например:
Количество перемножаемых дробей не меняет процесс. Например:
Чтобы умножить смешанные числа, сначала преобразуйте их в неправильные дроби, а затем умножьте:
При умножении двух смешанных чисел следите за тем, чтобы не умножать целые и дробные части по отдельности. Сначала нужно преобразовать смешанные числа в неправильные дроби.
Деление дробей
Деление дробей аналогично умножению дробей, за исключением того, что мы умножаем дробь, которую делим, на то, что называется обратной величиной другой дроби. Обратная дробь — это та дробь, в которой местами числитель и знаменатель поменялись местами. Например, обратная величина . Таким образом, чтобы разделить две дроби, просто найдите обратную величину делителя, затем умножьте числитель на числитель и знаменатель на знаменатель. Например:
Упрощение дробей
Упрощение дробей включает в себя нахождение формы дроби, в которой все общие делители числителя и знаменателя вынесены на множители так, что единственный общий делитель между числителем и знаменателем равен 1; эта окончательная форма дроби называется ее простейшей формой. Этот процесс также иногда называют уменьшением фракции.
Этот процесс также иногда называют уменьшением фракции.
Одним из способов упрощения дробей является деление числителя и знаменателя на общие простые множители (или их кратные), начиная с первого простого числа 2 через каждое последующее простое число до тех пор, пока дробь уже нельзя будет сократить. Это может быть утомительно в зависимости от дроби, но это надежный и простой способ уменьшить дробь. Например, учитывая, что мы хотим упростить , мы знаем, что 78 и 156 имеют общий делитель 2, потому что они оба четные, поэтому мы можем начать с деления обоих на 2:
Следующее простое число равно 3, и в этом случае 39 и 78 делят этот множитель, поэтому разделите оба на 3: разделите их оба на 13:
Поскольку единственный общий множитель в этой точке равен 1, дробь не может быть уменьшена дальше, и поэтому она имеет простейшую форму. Несмотря на то, что числитель и знаменатель в этом примере относительно малы, мы видим, что сокращение дробей с помощью этого процесса может быстро стать утомительным.
Еще один более эффективный способ упрощения дробей заключается в нахождении наибольшего общего делителя (НОД), хотя процесс нахождения НОД здесь подробно обсуждаться не будет. Короче говоря, мы, возможно, поняли, что 78 — это GCF 78 и 156, и мы могли бы немедленно разделить оба числа на 78, чтобы получить простейшую форму. Таким образом, если мы можем определить НОД числителя и знаменателя, упрощение дробей просто включает деление и числителя, и знаменателя на их НОД.
Преобразование дробей в десятичные числа
Дроби и десятичные дроби — это два разных способа выражения одного и того же значения. В зависимости от ситуации мы можем предпочесть выражать значение в дробной или десятичной форме, поэтому полезно иметь возможность конвертировать между ними.
Преобразование десятичных дробей в дроби
Преобразование десятичных дробей в дроби относительно просто, если мы понимаем, что такое десятичные дроби и разрядные значения. Вкратце, каждая позиция в десятичной дроби соответствует степени 10. Например, 0,5 читается как «пять десятых», потому что 5 стоит на 10-й позиции, что соответствует 10 -1 . 0,05 читается как «пять сотых» и соответствует 10 -2 . 0,005 читается как «пятитысячные» и соответствует 10 -3 и так далее.
Например, 0,5 читается как «пять десятых», потому что 5 стоит на 10-й позиции, что соответствует 10 -1 . 0,05 читается как «пять сотых» и соответствует 10 -2 . 0,005 читается как «пятитысячные» и соответствует 10 -3 и так далее.
Чтобы преобразовать десятичную дробь в дробную, сдвиньте десятичную точку вправо, отслеживая, сколько раз она смещается, пока она не окажется после последнего ненулевого значения (крайнего справа). Тогда число должно быть целым числом, и это число является числителем дроби. Знаменатель дроби равен 10, возведенному в степень, сколько раз мы сдвигали запятую. Для 0,5 нам пришлось бы один раз сдвинуть запятую, чтобы получить целое число 5. Таким образом, числитель равен 5, а знаменатель равен 10 1 , так как мы один раз передвинули десятичную точку. Таким образом, 0,5 в форме дроби:
Если десятичная дробь также имеет целую часть, например 1,5, процесс такой же, за исключением того, что значение до десятичной точки будет целой частью смешанного числа. Таким образом, 1,5 в форме смешанного числа:
Таким образом, 1,5 в форме смешанного числа:
Преобразование дробей в десятичные
Преобразование дробей в десятичные обычно сложнее, чем преобразование десятичных дробей в дроби. В тех случаях, когда мы можем преобразовать дробь в эквивалентную дробь со знаменателем, равным степени 10, мы можем использовать обратную логику, используемую для преобразования десятичных дробей в дроби (см. выше). Например:
Однако во многих случаях это невозможно, а преобразование дробей в десятичные представляет собой утомительный процесс, требующий длительного деления. Даже в этом случае многие дроби могут не иметь конечного десятичного знака. Например, в десятичной форме это 0,3333…, где «…» означает, что 3 повторяется бесконечно. Другие значения, такие как π, просто никогда не заканчиваются и не имеют повторяющихся значений. Таким образом, если нам придется прибегнуть к делению в большую сторону, десятичная форма дроби часто будет оценочной.
Чтобы преобразовать дробь с помощью деления в большую сторону, разделите числитель на знаменатель, оставив десятичную точку в частном на том же месте, что и в числителе. Вот и все, но в идеале это нужно делать с помощью компьютера или калькулятора, так как преобразование дробей таким способом очень утомительно.
Вот и все, но в идеале это нужно делать с помощью компьютера или калькулятора, так как преобразование дробей таким способом очень утомительно.
Калькулятор неполных дробей + онлайн-решатель с бесплатными шагами
Калькулятор неполных дробей используется для решения задач на неполные дроби. Этот калькулятор приводит к двум составляющим дробям, которые составляют исходную дробь в наших задачах, и используется процесс 9.0067 Расширение неполной дроби .
Что такое калькулятор неполных дробей?
Калькулятор частичных дробей — это онлайн-калькулятор, предназначенный для разложения полиномиальной дроби на составляющие ее части.
Этот калькулятор работает по методу Расширение частичной дроби .
Мы рассмотрим это подробнее по мере продвижения вперед.
Как пользоваться калькулятором неполных дробей?
Для использования калькулятора частичных дробей , вы должны ввести числитель и знаменатель в поля ввода и нажать кнопку «Отправить». Теперь пошаговое руководство по использованию этого калькулятора можно увидеть здесь:
Теперь пошаговое руководство по использованию этого калькулятора можно увидеть здесь:
Шаг 1
Введите числитель и знаменатель в соответствующие поля ввода.
Шаг 2
Нажмите кнопку «Отправить», и будет создано решение вашей проблемы.
Шаг 3
Если вы хотите продолжать пользоваться калькулятором, введите новые данные и получите новые результаты. Количество раз, когда вы можете использовать этот калькулятор, не ограничено.
Как работает калькулятор неполных дробей?
Калькулятор неполных дробей работает, разлагая предоставленную ему многочленную дробь на составляющие дроби, используя метод неполных дробей. Он также упоминается как частичное расширение дроби , и мы углубимся в этот метод далее в этой статье.
Теперь давайте посмотрим на многочлены, из которых состоят дроби.
Многочлены
Многочлены представляют класс математических функций , которые выражаются в определенном формате, это может включать алгебраические, экспоненциальные, основные математические операции и т. д. . И этот процесс называется LCM или также известен как наименьшее общее кратное . А теперь мы рассмотрим этот метод ниже.
д. . И этот процесс называется LCM или также известен как наименьшее общее кратное . А теперь мы рассмотрим этот метод ниже.
Наименьшее общее кратное
Итак, Наименьшее общее кратное — очень распространенный метод сложения дробей. Он всемирно известен как LCM , и его работу можно увидеть следующим образом.
Здесь мы примем пару полиномиальных дробей:
\[ \frac {p} {q} + \frac {r} {s} \]
Чтобы решить эту задачу, мы должны умножить Знаменатель на каждой дроби на числитель другой, а также умножить их друг на друга, чтобы создать новый знаменатель .
Это можно увидеть в действии следующим образом:
\[ \frac{ p x s } { q x s } + \ frac { r x q } { s x q } = \ frac { ( p x s ) + ( r x q ) } { q x s } \]
Можно удивиться, что этот метод не используется в Ultimate Solution , но действительно важно знать, как работает этот метод. Учитывая, что метод, который мы рассматриваем, а именно метод разложения на частичные дроби , является противоположностью этому математическому процессу .
Учитывая, что метод, который мы рассматриваем, а именно метод разложения на частичные дроби , является противоположностью этому математическому процессу .
Неполные дроби
Частичная дробь — это метод преобразования дроби в составные полиномы, которые можно сложить вместе, чтобы получить эту дробь, используя метод НОК . Теперь мы можем углубиться в то, как работает этот метод, и разделить дробь на две дроби.
Пусть есть полиномиальная дробь, и она выражается следующим образом:
\[ f (x) = \frac {p(x)} {q_1(x) q_2(x)} \]
Здесь мы возьмем числители для двух дробей, составляющих эту дробь, и назовем их А и В. Это делается здесь:
\[ f (x) = \frac {p(x)} { q_1(x) q_2(x)} = \frac {A} {q_1(x)} + \frac {B} {q_2(x) } \]
Теперь возьмем знаменатель исходной дроби, умножим и разделим его на обе части уравнения. Это можно увидеть здесь:
\[ p(x) = \frac {A} {q_1(x)} \times ( q_1(x) q_2(x)) + \frac {B} {q_2(x)} \times ( q_1(x) q_2(x)) \]
p(x) = A . q2(x) + B . q1(x)
q2(x) + B . q1(x)
На этом этапе мы берем выражения q1(x) и q2(x) и решаем их по отдельности, противопоставляя их нулю. Это дает два результата, в одном из которых член, содержащий q1(x), обращается в нуль, а в другом q2(x) обращается в нуль. Таким образом, мы получаем наши значения A и B.
Где q1(x) = 0, p(x) = A x q2(x), $\frac { p(x) }{ q_2(x) }$ = A
Аналогично,
Где q2(x) = 0, p(x) = B x q1(x), $\frac { p(x)}{q_1(x)}$ = B
Здесь мы в основном сравниваем переменных чтобы получить наши результаты. Таким образом, мы получаем решение нашей задачи о дробях.
Решенные примеры
Теперь давайте рассмотрим несколько примеров, чтобы лучше понять концепции.
Пример 1
Рассмотрим полиномиальную дробь: 92 – x – 2 } = \frac { 5x – 4 } { ( x – 2 ) ( x + 1 ) } \]
Теперь давайте разделим числитель на A и B. И это делается здесь:
\[ \frac { 5x – 4 } { ( x – 2 ) ( x + 1 ) } = \ frac { A } { ( x – 2 ) } + \ frac { B } { ( x + 1 ) } \]
Здесь мы умножим и разделим знаменатель на обе части.


 Первые полторы тысяч разложений.
Первые полторы тысяч разложений. Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн