Калькулятор перевода из радиан в градусы. Радианы в градусы, градусы в радианы
С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки» . Углы бывают разные: тупые, острые, прямые , развёрнутые, центральные, смежные . Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
Что означают градус и радиан
Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние . Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления. Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.
Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.
Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир .
Кроме градусной меры для измерения углов применяют меру радианную . Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l.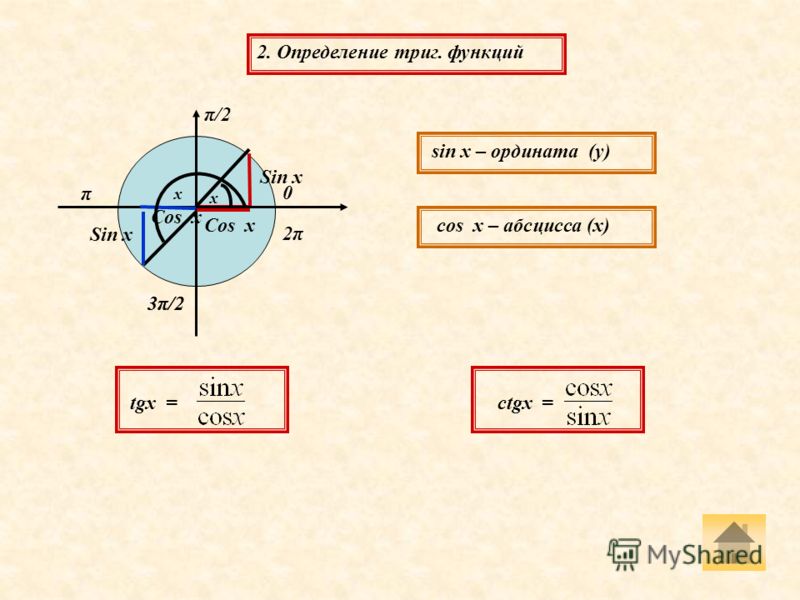
Как перевести градусы в радианы и обратно
Мы знаем, что центральному углу в 360° соответствует вся окружность, длина которой вычисляется по известной формуле l=2 π R. Разделим это выражение на R и получим: α= 2 π R/R=2 π рад≈6,28 рад. Если взять какое-то угловое расстояние в A град., то его радианная мера α получится из пропорции: А/360°=α/(2 π). Решив это уравнение, получим формулу перевода градусов в радианы — α=(π/180°) А, или формулу перевода радиан в градусы — А=(180°/π) α. Из этих формул мы придём к следующим соотношениям:
- 1 рад=180°/π≈57,2958°;
- 1°=π/180 рад≈0,01745 рад.
Сколько составит 180 градусов в радианах и 90 градусов в радианах? Воспользовавшись полученными выше формулами, придём к таким соотношениям:
- 90°=π/2 рад≈1,571 рад;
- 180°=π рад≈3,142 рад.

Итак, как правильно переводить градусную меру в радианную и обратно? В этом вам поможет следующее правило:
Чтобы найти число радиан, нужно градусную меру умножить на число π и поделить на 180. Чтобы найти число градусов, нужно радианную меру умножить на 180 и поделить на число π .
Примеры решения задач
Задача 1. Чему равна длина дуги окружности, если R=1 см, α=1 рад?
Решение. По формуле длины дуги найдём: l=R α=1 1=1 см.
Задача 2. Сколько рад в 45°?
Решение. Используя правило, получим: α=45 π/180=π/4 рад.
Задача 3. Сколько град. в π² рад?
Решение. Используя правило, найдём: А=π² 180/π=180π град.≈565,5°.
Задача 4. Чему равен средний угловой размер лунного диска, если среднее расстояние до Луны равно R=384399 км, а диаметр самой Луны D=3476 км?
Решение. Если мысленно на Луну с Земли провести два луча, которые пройдут через крайние точки диаметра её диска, мы получим центральный угол, исходящий из глаз наблюдателя.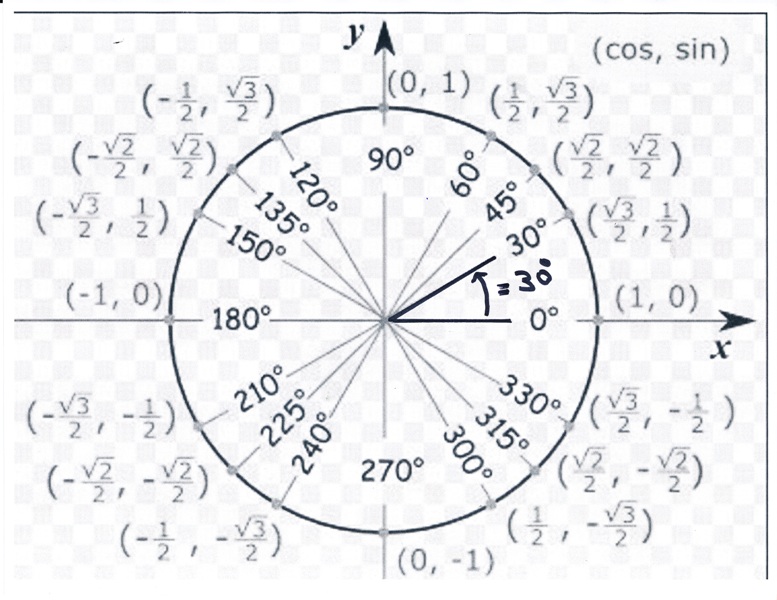 Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05”≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.
Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05”≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.
Минуты и секунды
Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления . В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «»”, а секунды — значком «””. Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения:
- 1°=60’=3600”;
- 1’=(1/60)°=60”;
- 1”=(1/3600)°=(1/60)’;
- 1 рад≈3438′.
Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.
Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.
Что такое градусы?
Градус — общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления. Градус тоже делится на 60 минут, а минуты — на 60 секунд. Общепринятыми обозначениями являются:
° — угловые градусы
’ — минуты,
’’ — секунды.
За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники — от картографии до расчета орбит искусственных спутников Земли.
Что такое радианы?
Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра.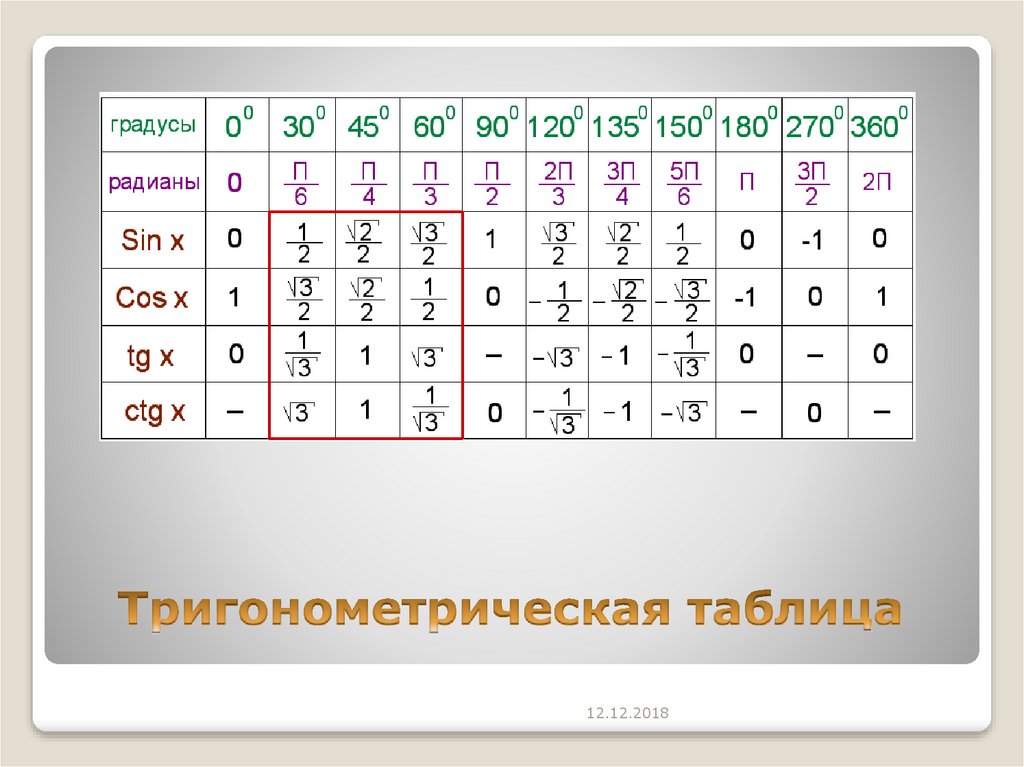 Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.
Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.
Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.
По определению, радиан — угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности. Международное обозначение радиана — rad, отечественное — рад. Размерности он не имеет.
Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.
Зачем понадобилось вводить новую единицу измерения угла?
Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Как переводить градусы в радианы
Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.
И простая формула перевода из радианов в градусы: 1 рад = 180/π.
Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.
Остались вопросы?
Ответы на них можно найти , где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.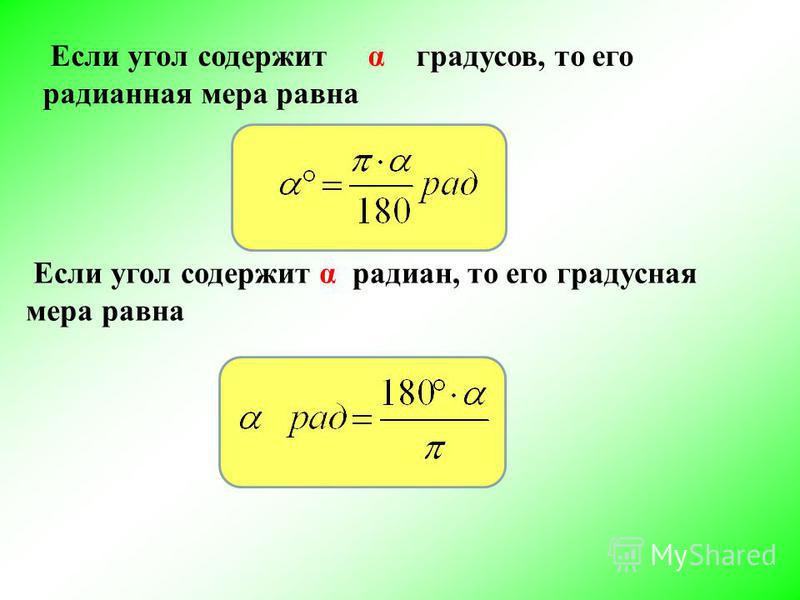
Калькулятор онлайн выполняет перевод градусов в радианы , перевевод радиан в градусы , перевод дробных градусов (градусы представленные десятичной дробью) в вид градусов, минут и секунд и выводит формулы с подробным решением.
Перевести градусы в радианы : градусы необходимо умножить на π/180. Если градусы заданы в виде «градусов, минут и секунд», то вначале их необходимо перевести в десятичную форму по формуле: градусы + минуты/60 + секунды/3600;
Формула перевода радиан в градусы : если угол равен α rad радиан, то он равен формула перевода радиан в градусы градусов, где π ≈ 3,1415.
Перевести радианы в градусы : радианы необходимо умножить на 180/π. Целая часть полученного произведения — это количество градусов. Чтобы перевести дробную часть в минуты, необходимо ее умножить на 60. Целая часть полученного произведения — количество минут. Для вычисления секунд необходимо снова умножить дробную часть от предыдущей операции на 60, округлить полученное произведение до ближайшего целого — это количество секунд.
Формула перевода градусов в радианы : если угол равен α deg радиан, то он равен формула перевода градусы в радианы радиан, где π ≈ 3,1415.
| Дано: | Решение: | |
Перевод градусов, минут и секунд в радианы | ||
| α° deg = градусов | перевод градусов в радианы | |
| α» deg = минут | ||
| α» deg = секунд | ||
Перевод радиан в градусы, минуты и секунды | ||
| α rad = радиан | перевод радиан в градусы, минуты и секунды | |
Перевод десятичных градусов в вид градусов, минут и секунд | ||
| α deg = градусов | выделение из десятичных градусов градусов, минут и секунд перевод десятичных градусов в вид градусов, минут и секунд | |
| округление до 1 2 3 4 5 знаков после запятой | ||
Помощь на развитие проекта сайт
Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до десятитысячных).
II. Для справки:
- Градусна мера угла — угловая мера, в которой за единицу принимается угол в 1 градус и показывающая сколько раз градус и его части (минута и секунда) укладывается в данном угле.
- Радианная мера угла — угловая мера, в которой за единицу принимается угол в 1 радиан и показывающая сколько раз радиан укладывается в данном угле.

- Градусы и радианы — единицы измерения плоских углов в геометрии.
- Один градус равен 1/180 части развернутого угла.
- Радиан — угол, соответствующий дуге, длина которой равна ее радиусу.
Номограмма для перевода радиан в градусы и градусов в радианы.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.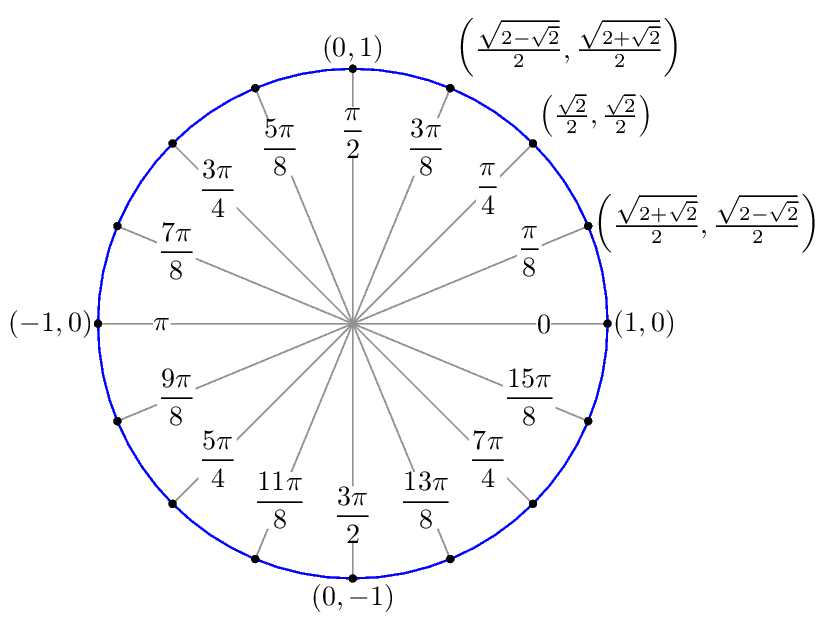 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.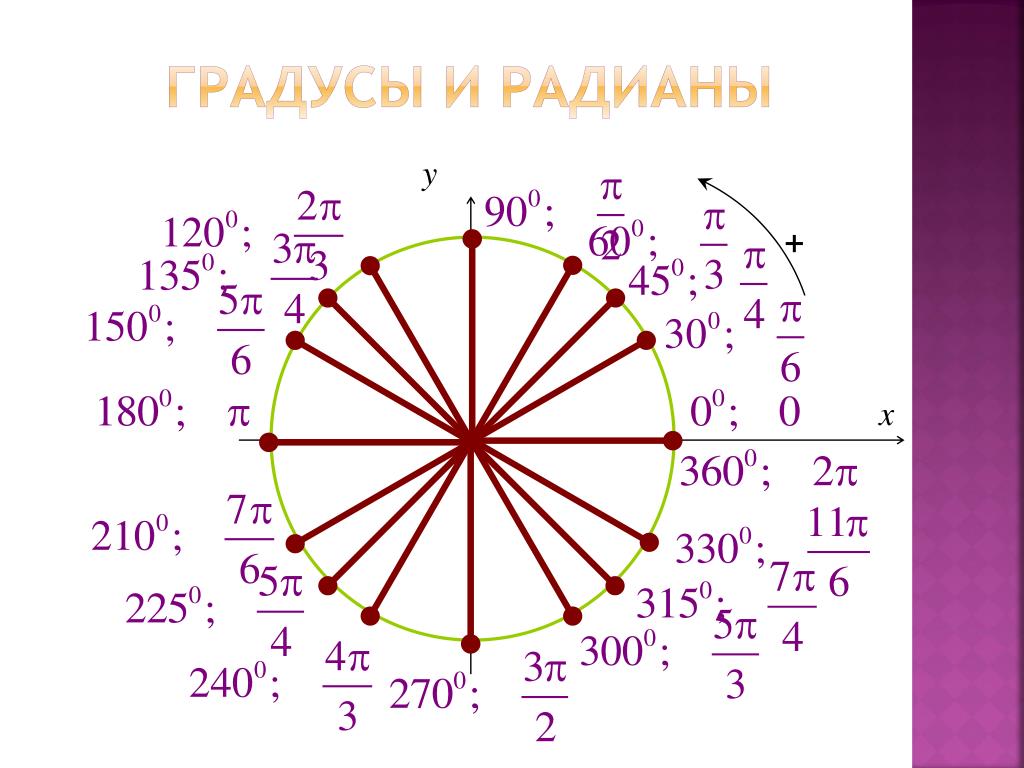 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.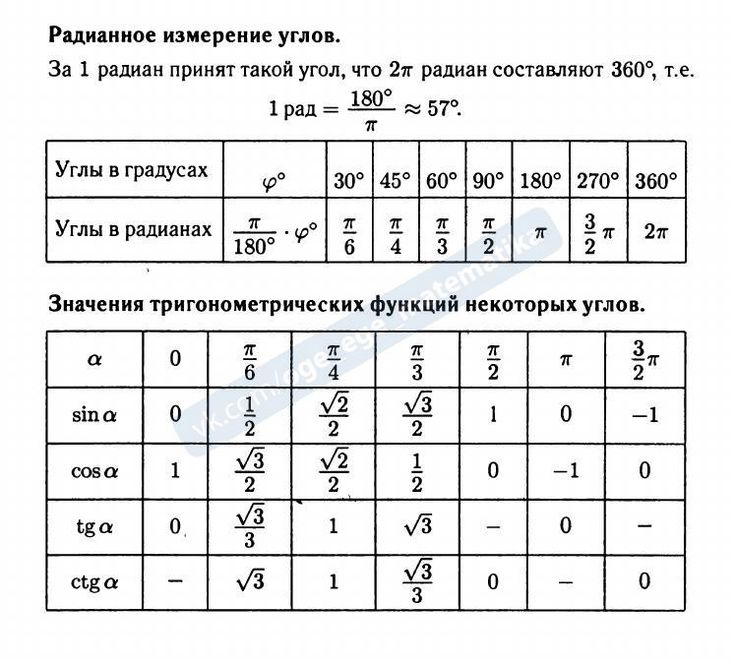 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
градусов в радианы | Преобразователь Кайла
- Преобразователь Кайла > org/ListItem»> Угол >
- градусов >
- Градусов в Радиан
| Градусы (°) | Радиан (рад) |
| Точность: 0123456789121518 |
Обратное преобразование?
Радиан в Градусы (или просто введите значение в поле «до»)
Пожалуйста, поделитесь, если вы нашли этот инструмент полезным:
| Описание устройства | |
|---|---|
|
|
| Conversions Table | |||||||
|---|---|---|---|---|---|---|---|
| 1 Degrees to Radians = 0.0175 | 70 Degrees to Radians = 1.2217 | ||||||
| 2 Degrees to Radians = 0.0349 | 80 Degrees to Radians = 1.3963 | ||||||
| 3 градуса до радиан = 0,0524 | 90 градусов до радиан = 1,5708 | ||||||
| 4 градуса с радианами = 0,0698 | 100 градусов до радиан = 1,7453 | ||||||
| 5 градусов = 1,7453 | |||||||
| 5 градусов.0019 | 200 градусов до радиан = 3,4907 | ||||||
| 6 градусов с радианами = 0,1047 | 300 градусов с радианами = 5,236 | ||||||
| 7 градусов с радианами = 0,1222 | 77 | 7 градусов с радианами = 0,1222 | 7777777 40077 7 градусов с радианами = 0,1222 | 777777777 40077 7. | 7 градусов. Радианы = 0,1396 | 500 градусов до радиан = 8,7266 | |
| 9 градусов с радианами = 0,1571 | 600 градусов с радианами = 10,472 | ||||||
| 10 градусов до Радиана = 0.1745 | |||||||
| 10 градусов до радио = 0.1745 | |||||||
| 10 градусов.0019 | 800 градусов до радиан = 13,9626 | ||||||
| 20 градусов с радианами = 0,3491 | 900 градусов до радиан = 15,708 | ||||||
| 30 градусов к радианам = 0,5236 | |||||||
| 30 градусов к радианам = 0,5236 | |||||||
| 30 градусов с радианами = 0,5236 | |||||||
| 30 градусов. to Radians = 0.6981 | 10,000 Degrees to Radians = 174.5329 | ||||||
| 50 Degrees to Radians = 0.8727 | 100,000 Degrees to Radians = 1745.3293 | ||||||
| 60 Degrees to Radians = 1.0472 | 1,000,000 Degrees to Radians = 17453.2925 | ||||||
Similar Angle Units
- Degrees to Diameter Parts
- Degrees to Gradians
- Degrees to Binary Degrees
Common Units
- Degrees to Radians
- Degrees to Minutes of time
- Градусов в Угловые секунды
Градусов в Радианы Генератор таблиц
Онлайн калькулятор градусов(°) в радианы(рад), таблица, формулы.
Градусы
Радианы
Точность
No DecimalsRounded to 1 DecimalRounded to 2 DecimalsRounded to 3 DecimalsRounded to 4 DecimalsRounded to 5 DecimalsRounded to 6 DecimalsRounded to 7 DecimalsRounded to 8 DecimalsRounded to 9 DecimalsRounded to 10 DecimalsRounded to 11 DecimalsRounded to 12 Decimals
Radians to Degrees converter ►
| Градусы | Радианы | |
|---|---|---|
| 1° | 0.017453293 rad | |
| 2° | 0.034 | 5 rad|
| 3° | 0.052359878 rad | |
| 4° | 0.06981317 rad | |
| 5° | 0.087266463 rad | |
| 6° | 0.104719755 rad | |
| 7° | 0.122173048 rad | |
| 8° | 0. 13962634 rad 13962634 rad | |
| 9° | 0.157079633 rad | |
| 10° | 0.174532925 rad | |
| 11° | 0.191986218 rad | |
| 12° | 0.20943951 rad | |
| 13° | 0.226892803 rad | |
| 14° | 0.244346095 rad | |
| 15° | 0.261799388 rad | |
| 16° | 0.27925268 rad | |
| 17° | 0.296705973 rad | |
| 18° | 0.314159265 rad | |
| 19° | 0.331612558 rad | |
| 20° | 0.34 | 5 rad|
| 21° | 0.366519143 rad | |
| 22° | 0.383972435 rad | |
| 23° | 0.401425728 rad | |
| 24° | 0.41887902 rad | |
| 25° | 0.436332313 rad | |
| 26° | 0. 453785606 rad 453785606 rad | |
| 27° | 0.471238898 rad | |
| 28° | 0.488692191 rad | |
| 29° | 0.506145483 rad | |
| 30° | 0.523598776 rad | |
| 31° | 0.541052068 rad | |
| 32° | 0.558505361 rad | |
| 33° | 0.575958653 rad | |
| 34° | 0.593411946 rad | |
| 35° | 0.610865238 rad | |
| 36° | 0.628318531 rad | |
| 37° | 0.645771823 rad | |
| 38° | 0.663225116 rad | |
| 39° | 0.680678408 rad | |
| 40° | 0.698131701 rad | |
| 41° | 0.715584993 rad | |
| 42° | 0.733038286 rad | |
| 43° | 0.750491578 rad | |
| 44° | 0. 767944871 rad 767944871 rad | |
| 45° | 0.785398163 rad | |
| 46° | 0.802851456 rad | |
| 47° | 0.820304748 rad | |
| 48° | 0.837758041 rad | |
| 49° | 0.855211333 rad | |
| 50° | 0.872664626 rad | |
| 51° | 0.8 | |
| 52° | 0. | 1211 rad |
| 53° | 0.925024504 rad | |
| 54° | 0.942477796 rad | |
| 55° | 0.959931089 rad | |
| 56° | 0.977384381 rad | |
| 57° | 0.994837674 rad | |
| 58° | 1.012290966 rad | |
| 59° | 1.029744259 rad | |
| 60° | 1.047197551 rad | |
| 61° | 1.064650844 rad | |
| 62° | 1. 082104136 rad 082104136 rad | |
| 63° | 1.099557429 rad | |
| 64° | 1.117010721 rad | |
| 65° | 1.134464014 rad | |
| 66° | 1.151917306 rad | |
| 67° | 1.169370599 rad | |
| 68° | 1.186823891 rad | |
| 69° | 1.204277184 rad | |
| 70° | 1.221730476 rad | |
| 71° | 1.239183769 rad | |
| 72° | 1.256637061 rad | |
| 73° | 1.2740 | |
| 74° | 1.291543646 rad | |
| 75° | 1.308996939 rad | |
| 76° | 1.326450232 rad | |
| 77° | 1.343 | 4 rad|
| 78° | 1.361356817 rad | |
| 79° | 1.378810109 rad | |
| 80° | 1. 396263402 rad 396263402 rad | |
| 81° | 1.413716694 rad | |
| 82° | 1.431169987 rad | |
| 83° | 1.448623279 rad | |
| 84° | 1.466076572 rad | |
| 85° | 1.483529864 rad | |
| 86° | 1.500983157 rad | |
| 87° | 1.518436449 rad | |
| 88° | 1.535889742 rad | |
| 89° | 1.553343034 rad | |
| 90° | 1.570796327 rad | |
| 91° | 1.588249619 rad | |
| 92° | 1.605702912 rad | |
| 93° | 1.623156204 rad | |
| 94° | 1.640609497 rad | |
| 95° | 1.658062789 rad | |
| 96° | 1.675516082 rad | |
| 97° | 1.692969374 rad | |
| 98° | 1. |


